Evaluating the Influence of Rain Event Characteristics on Rainfall Interception by Urban Trees Using Multiple Correspondence Analysis
Abstract
1. Introduction
2. Materials and Methods
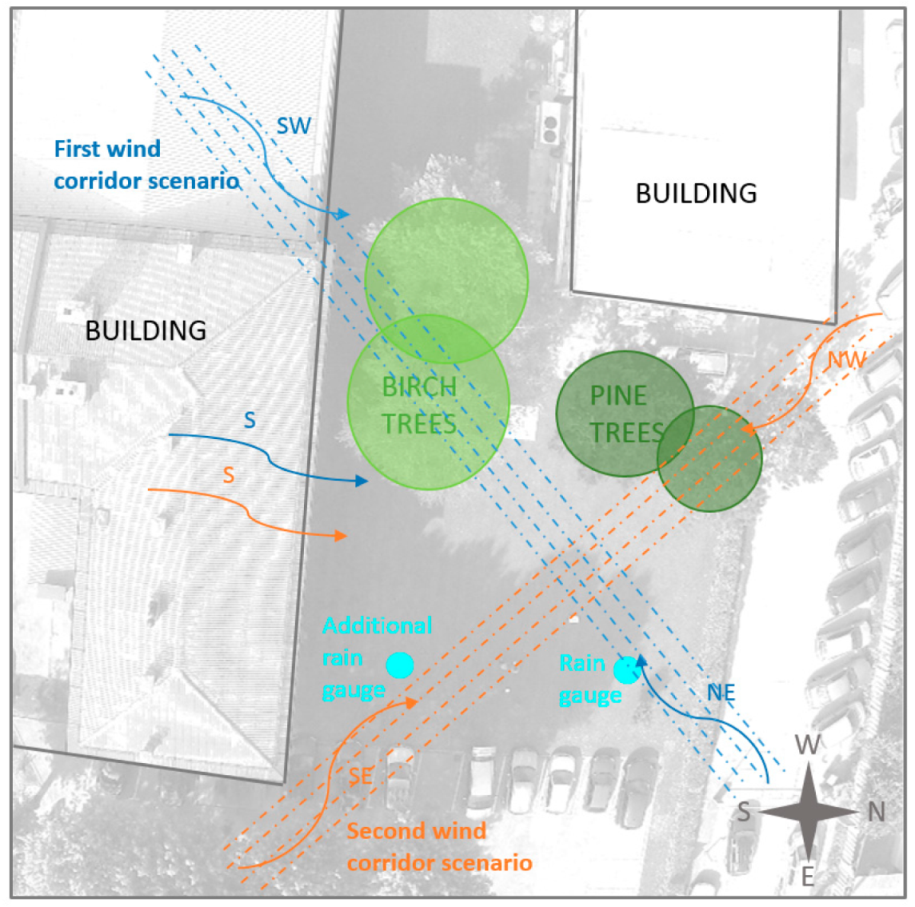
2.1. Study Site
2.2. Measurements
2.3. Data Analysis Methods
3. Results and Discussion
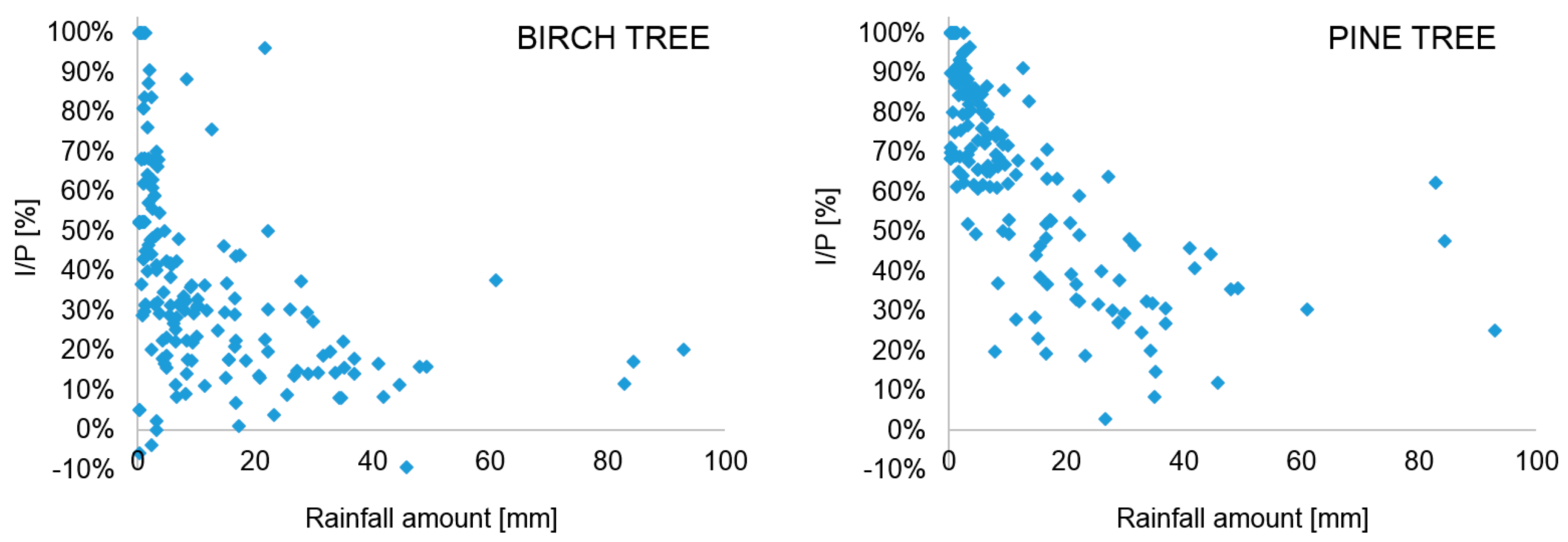
3.1. Rainfall Event Characteristics, Rainfall Interception, Throughfall, and Stemflow
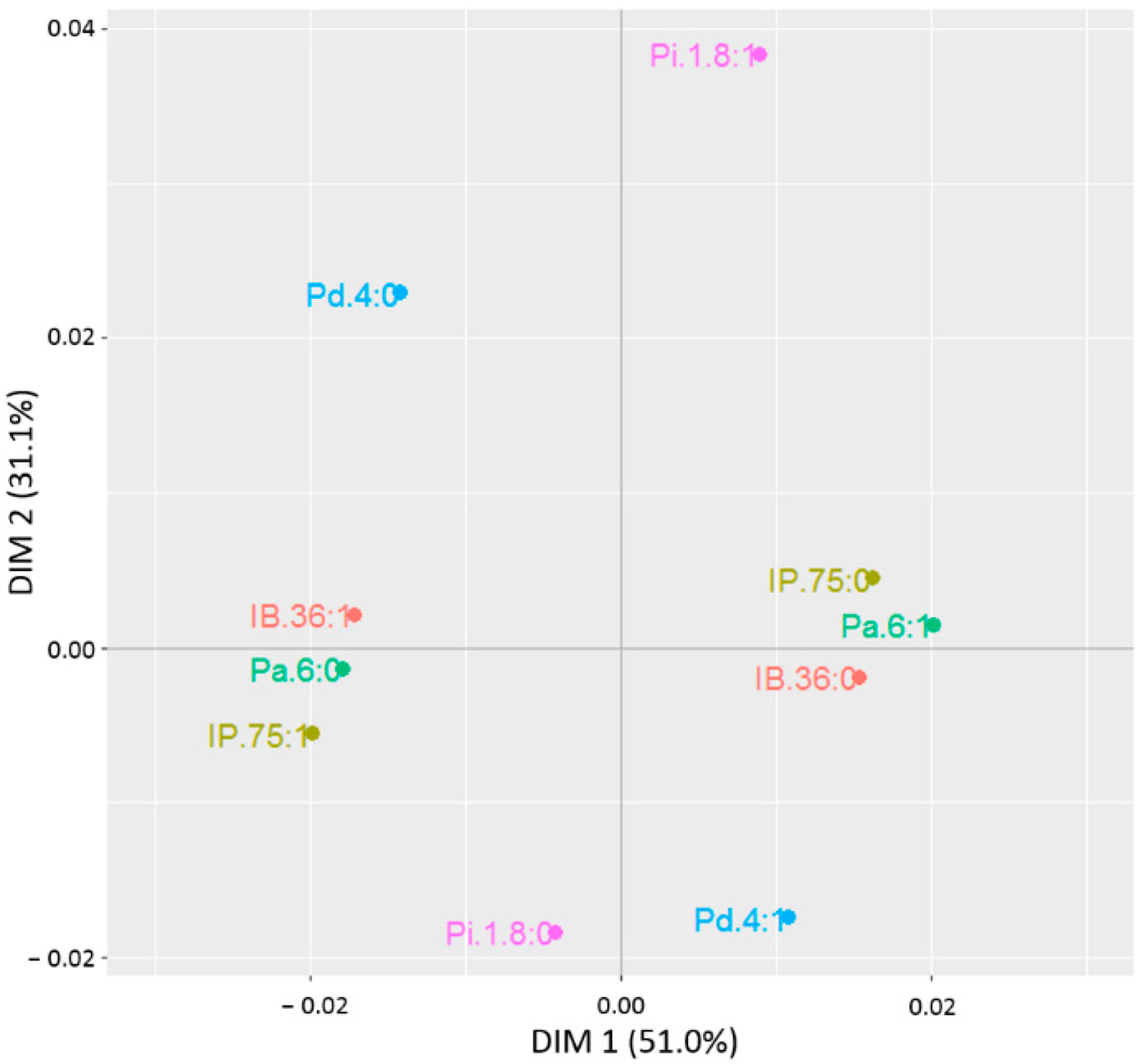
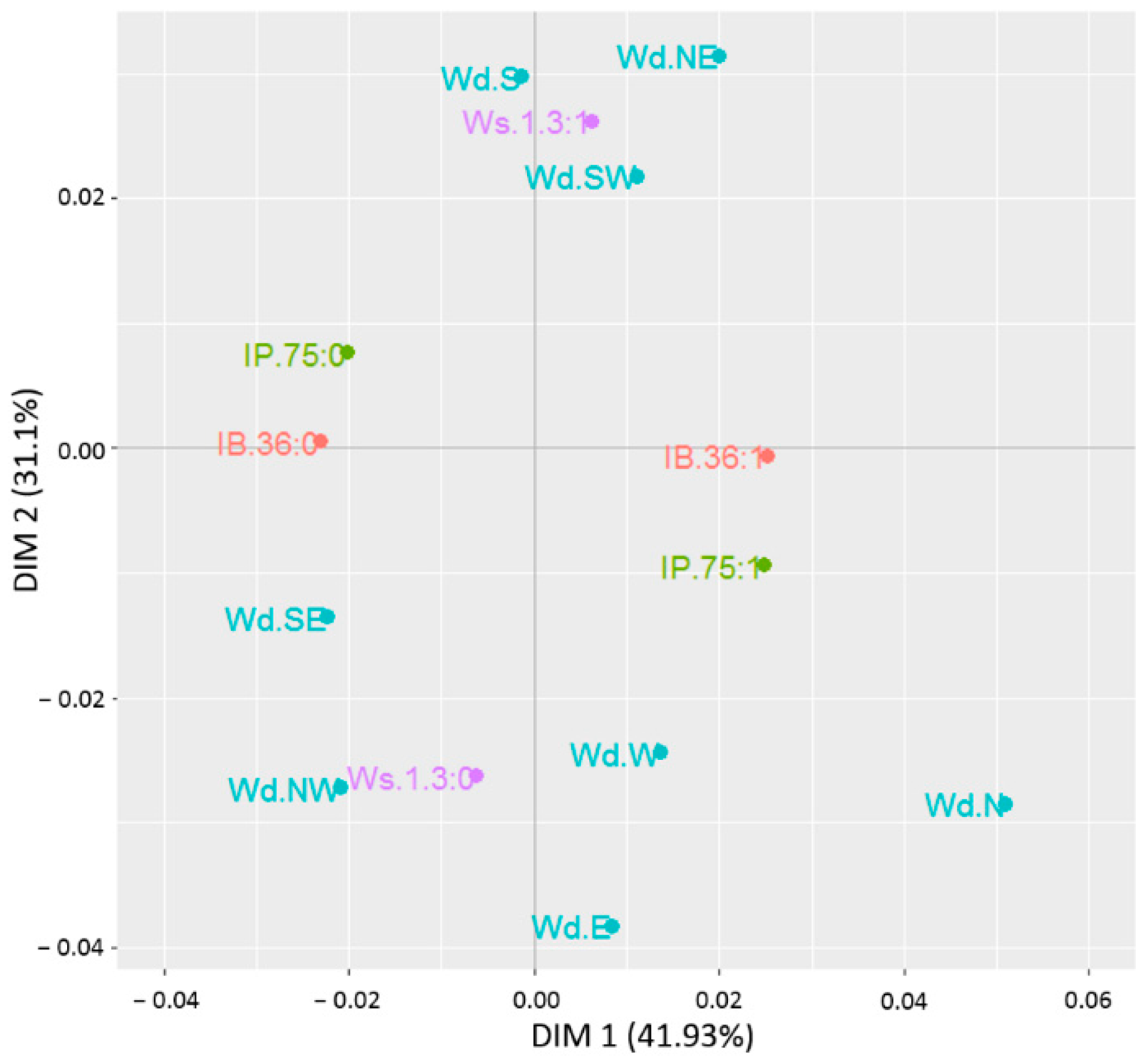
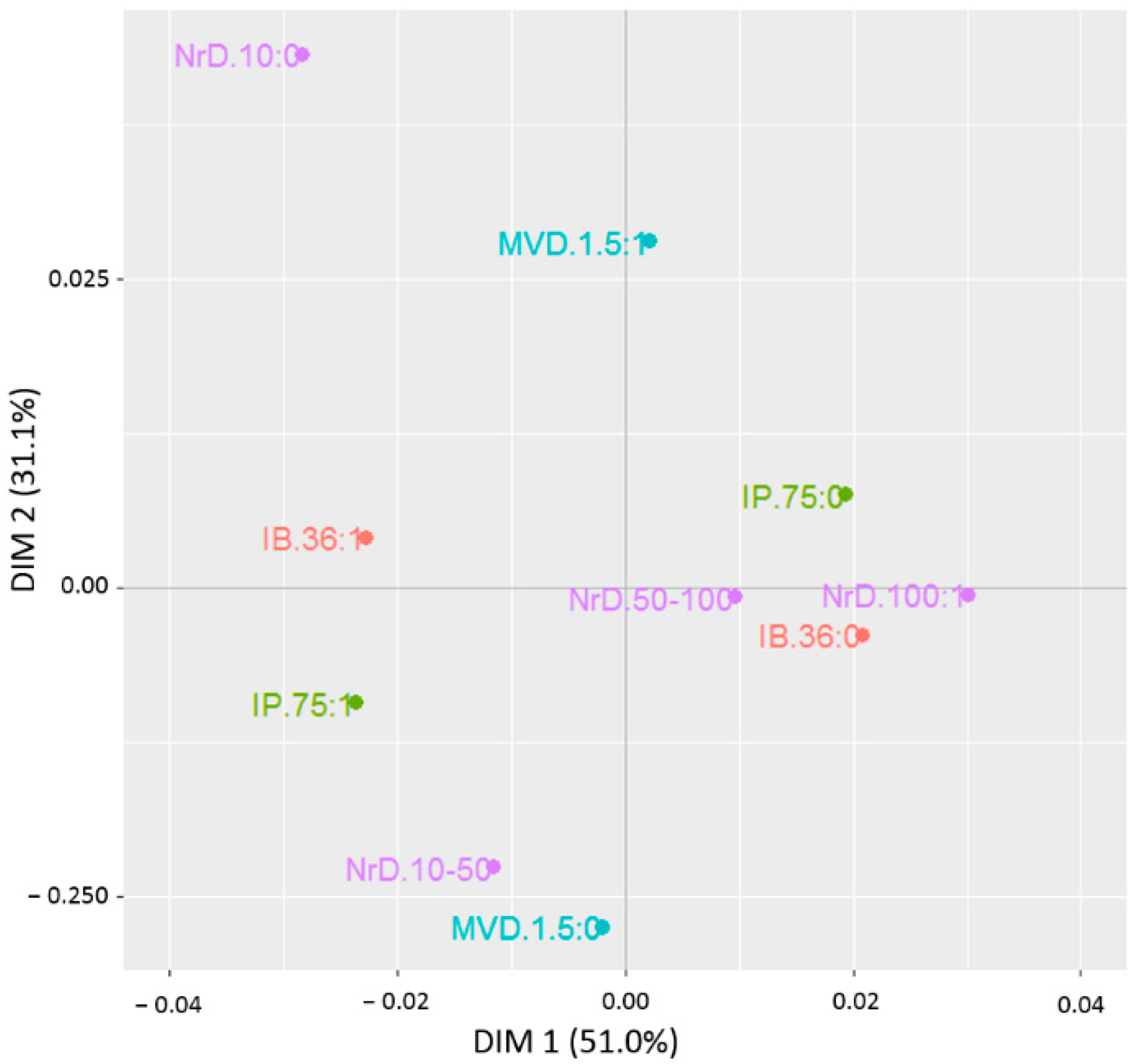
3.2. Multiple Correspondence Analysis (MCA)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chang, S.C.; Matzner, E. The effect of beech stemflow on spatial pattern of soil solution chemistry and seepage fluxes in a mixed beech/oak stand. Hydrol. Process. 2000, 14, 135–144. [Google Scholar] [CrossRef]
- Friesen, J.; Van Stan, J.T. Early European Observations of Precipitation Partitioning by Vegetation: A Synthesis and Evaluation of 19th Century Findings. Geosciences 2019, 9, 423. [Google Scholar] [CrossRef]
- Zabret, K.; Rakovec, J.; Mikoš, M.; Šraj, M. Influence of raindrop size distribution on throughfall dynamics under pine and birch trees at the rainfall event level. Atmosphere 2017, 8, 240. [Google Scholar] [CrossRef]
- Levia, D.F.; Nanko, K.; Amasaki, H.; Giambelluca, T.W.; Hotta, N.; Iida, S.; Mudd, R.G.; Nullet, M.A.; Sakai, N.; Shinohara, Y.; et al. Throughfall partitioning by trees. Hydrol. Process. 2019, 33, 1698–1708. [Google Scholar] [CrossRef]
- Levia, D.F.; Frost, E.E. A review and evaluation of stemflow literature in the hydrologic and biogeochemical cycles of forested and agricultural ecosystems. J. Hydrol. 2003, 274, 1–29. [Google Scholar] [CrossRef]
- Guevara-Escobar, A.; Gonzalez-Sosa, E.; Veliz-Chavez, C.; Ventura-Ramos, E.; Ramos-Salinas, M. Rainfall interception and distribution patterns of gross precipitation around an isolated Ficus benjamina tree in an urban area. J. Hydrol. 2007, 333, 532–541. [Google Scholar] [CrossRef]
- Livesley, S.J.; Baudinette, B.; Glover, D. Rainfall interception and stemflow by eucalypt street trees—The impacts of canopy density and bark type. Urban For. Urban Green. 2014, 13, 192–197. [Google Scholar] [CrossRef]
- Yang, B.; Lee, D.K.; Heo, H.K.; Biging, G. The effects of tree characteristics on rainfall interception in urban areas. Landsc. Ecol. Eng. 2019, 15, 289–296. [Google Scholar] [CrossRef]
- Zabret, K.; Šraj, M. Rainfall Interception by Urban Trees and Their Impact on Potential Surface Runoff. Clean Soil Air Water 2019, 47, 1800327. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, D.Q.; Su, J.; Trzcinski, A.P.; Dong, J.W.; Tan, S.K. Future Scenarios Modeling of Urban Stormwater Management Response to Impacts of Climate Change and Urbanization. Clean Soil Air Water 2017, 45, 1700111. [Google Scholar] [CrossRef]
- Rahman, M.A.; Moser, A.; Anderson, M.; Zhang, C.; Rötzer, T.; Pauleit, S. Comparing the infiltration potentials of soils beneath the canopies of two contrasting urban tree species. Urban For. Urban Green. 2019, 38, 22–32. [Google Scholar] [CrossRef]
- Xiao, Q.; McPherson, E.G.; Ustin, S.L.; Grismer, M.E.; Simpson, J.R. Winter rainfall interception by two mature open-grown trees in Davis, California. Hydrol. Process. 2000, 14, 763–784. [Google Scholar] [CrossRef]
- Asadian, Y.; Weiler, M. A New Approach in Measuring Rainfall Interception by Urban Trees in Coastal British Columbia. Water Qual. Res. J. Can. 2009, 44, 16–25. [Google Scholar] [CrossRef]
- Zabret, K.; Rakovec, J.; Šraj, M. Influence of meteorological variables on rainfall partitioning for deciduous and coniferous tree species in urban area. J. Hydrol. 2018, 558, 29–41. [Google Scholar] [CrossRef]
- Armson, D.; Stringer, P.; Ennos, A.R. The effect of street trees and amenity grass on urban surface water runoff in Manchester, UK. Urban For. Urban Green. 2013, 12, 282–286. [Google Scholar] [CrossRef]
- Wang, J.; Endreny, T.A.; Nowak, D.J. Mechanistic Simulation of Tree Effects in an Urban Water Balance Model. JAWRA 2008, 44, 75–85. [Google Scholar] [CrossRef]
- Sjöman, J.D.; Gill, S.E. Residential runoff—The role of spatial density and surface cover, with a case study in the Höjeå river catchment, southern Sweden. Urban For. Urban Green. 2014, 13, 304–314. [Google Scholar] [CrossRef]
- Huang, J.Y.; Black, T.A.; Jassal, R.S.; Les Lavkulich, L.M. Modelling rainfall interception by urban trees. Water Qual. Res. J. Can. 2017, 42. [Google Scholar] [CrossRef]
- Smets, V.; Wirion, C.; Bauwens, W.; Hermy, M.; Somers, B.; Verbeiren, B. The importance of city trees for reducing net rainfall: Comparing measurements and simulations. Hydrol. Earth Syst. Sci. 2019, 23, 3865–3884. [Google Scholar] [CrossRef]
- Crockford, R.H.; Richardson, D.P. Partitioning of rainfall into throughfall, stemflow and interception: Effect of forest type, ground cover and climate. Hydrol. Process. 2000, 14, 2903–2920. [Google Scholar] [CrossRef]
- Staelens, J.; De Schrijver, A.; Verheyen, K.; Verhoest, N.E.C. Rainfall partitioning into throughfall, stemflow, and interception within a single beech (Fagus sylvatica L.) canopy: Influence of foliation, rain event characteristics, and meteorology. Hydrol. Process. 2008, 22, 33–45. [Google Scholar] [CrossRef]
- Zabret, K.; Šraj, M. Spatial variability of throughfall under single birch and pine tree canopies. Acta Hydrotech. 2018, 31, 1–20. [Google Scholar] [CrossRef]
- Magliano, P.N.; Whitworth-Hulse, J.I.; Florio, E.L.; Aguirre, E.C.; Blanco, J.L. Interception loss, throughfall and stemflow by Larrea divaricata: The role of rainfall characteristics and plant morphological attributes. Ecol. Res. 2019, 34, 753–764. [Google Scholar] [CrossRef]
- Šraj, M.; Brilly, M.; Mikoš, M. Rainfall interception by two deciduous Mediterranean forests of contrasting stature in Slovenia. Agric. For. Meteorol. 2008, 148, 121–134. [Google Scholar] [CrossRef]
- Van Stan, J.T.; Van Stan, J.H.; Levia, D.F. Meteorological influences on stemflow generation across diameter size classes of two morphologically distinct deciduous species. Int. J. Biometeorol. 2014, 58, 2059–2069. [Google Scholar] [CrossRef]
- Bezak, N.; Zabret, K.; Šraj, M. Application of Copula Functions for Rainfall Interception Modelling. Water 2018, 10, 995. [Google Scholar] [CrossRef]
- Nanko, K.; Hotta, N.; Suzuki, M. Evaluating the influence of canopy species and meteorological factors on throughfall drop size distribution. J. Hydrol. 2006, 329, 422–431. [Google Scholar] [CrossRef]
- Barbier, S.; Balandier, P.; Gosselin, F. Influence of several tree traits on rainfall partitioning in temperate and boreal forests: A review. Ann. For. Sci. 2009, 66, 602. [Google Scholar] [CrossRef]
- Zabret, K. The influence of tree characteristics on rainfall interception. Acta Hydrotech. 2013, 26, 99–116. (In Slovenian) [Google Scholar]
- Siegert, C.M.; Levia, D.F. Seasonal and meteorological effects on differential stemflow funneling ratios for two deciduous tree species. J. Hydrol. 2014, 519, 446–454. [Google Scholar] [CrossRef]
- Holder, C.D.; Gibbes, C. Influence of leaf and canopy characteristics on rainfall interception and urban hydrology. Hydrol. Sci. J. 2016, 26, 182–190. [Google Scholar] [CrossRef]
- Fleischbein, K.; Wilcke, W.; Goller, R.; Boy, J.; Valarezo, C.; Zech, W.; Knoblich, K. Rainfall interception in a lower montane forest in Ecuador: Effects of canopy properties. Hydrol. Process. 2005, 19, 1355–1371. [Google Scholar] [CrossRef]
- Dohnal, M.; Černy, T.; Votrubova, J.; Tesar, M. Rainfall interception and spatial variability of throughfall in spruce stand. J. Hydrol. Hydromech. 2014, 62, 277–284. [Google Scholar] [CrossRef]
- Schooling, J.T.; Carlyle-Moses, D.E. The influence of rainfall depth class and deciduous tree traits on stemflow production in an urban park. Urban Ecosyst. 2015, 18, 1261–1284. [Google Scholar] [CrossRef]
- Honda, E.A.; Mendonça, A.H.; Durigan, G. Factors affecting the stemflow of trees in the Brazilian Cerrado. Ecohydrology 2014, 8, 1351–1362. [Google Scholar] [CrossRef]
- Nytch, C.J.; Meléndez-Ackerman, E.J.; Pérez, M.E.; Ortiz-Zayas, J.R. Rainfall interception by six urban trees in San Juan, Puerto Rico. Urban Ecosyst. 2019, 22, 103. [Google Scholar] [CrossRef]
- Nanko, K.; Hudson, S.A.; Levia, D.F. Differences in throughfall drop size distributions in the presence and absence of foliage. Hydrol. Sci. J. 2016, 61, 620–627. [Google Scholar] [CrossRef]
- Tanaka, N.; Levia, D.; Igarashi, Y.; Yoshifuji, N.; Tanaka, K.; Tantasirin, C.; Nanko, K.; Suzuki, M.; Kumagai, T. What factors are most influential in governing stemflow production from plantation-grown teak trees? J. Hydrol. 2017, 544, 10–20. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Wang, X.P.; Pan, Y.X.; Hu, R. Relative contribution of biotic and abiotic factors to stemflow production and funneling efficiency: A long-term field study on a xerophytic shrub species in Tengger Desert of northern China. Agric. For. Meteorol. 2020, 280, 107781. [Google Scholar] [CrossRef]
- Van Stan, J.T.; Gay, T.E.; Lewis, E.S. Use of multiple correspondence analysis (MCA) to identify interactive meteorological conditions affecting relative throughfall. J. Hydrol. 2016, 533, 452–460. [Google Scholar] [CrossRef]
- Richards, G.; van der Ark, L.A. Dimensions of cultural consumption among tourists: Multiple correspondence analysis. Tour. Manag. 2013, 37, 71–76. [Google Scholar] [CrossRef]
- Husson, F.; Josse, J. Multiple Correspondence Analysis. In The Visualization and Verbalization of Data; Greenacre et Blasius; CRC/PRESSE: Boca Raton, FL, USA, 2014. [Google Scholar]
- Ali, F.; Dissanayake, D.; Bell, M.; Darrow, M. Investigating car users’ attitudes to climate change using multiple correspondence analysis. J. Transp. Geogr. 2018, 72, 237–247. [Google Scholar] [CrossRef]
- Dussault, M.C.; Smith, M.; Hanson, I. Evaluation of trauma patterns in blast injuries using multiple correspondence analysis. Forensic Sci. Int. 2016, 267, 66–72. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Benseler, S.M.; Tyrrell, P.N. Cluster and Multiple Correspondence Analyses in Rheumatology: Paths to Uncovering Relationships in a Sea of Data. Rheum. Dis. Clin. N. Am. 2018, 44, 349–360. [Google Scholar] [CrossRef] [PubMed]
- Mancini, R.; Pattaro, G.; Diodoro, M.G.; Sperduti, I.; Garufi, C.; Stigliano, V.; Perri, P.; Grazi, G.L.; Cosimelli, M. Tumor Regression Grade after Neoadjuvant Chemoradiation and Surgery for Low Rectal Cancer Evaluated by Multiple Correspondence Analysis: Ten Years as Minimum Follow-up. Clin. Colorectal Cancer 2018, 17, e13–e19. [Google Scholar] [CrossRef]
- ARSO. Available online: http://www.meteo.si/met/sl/archive/ (accessed on 11 November 2019).
- Pérez-Harguindeguy, N.; Díaz, S.; Garnier, E.; Lavorel, S.; Poorter, H.; Jaureguiberry, P.; Bret-Harte, M.S.; Cornwell, W.K.; Craine, J.M.; Gurvich, D.E.; et al. New handbook for standardized measurement of plant functional traits worldwide. Aust. J. Bot. 2013, 61, 167–234. [Google Scholar] [CrossRef]
- IGI Global. Available online: https://www.igi-global.com/dictionary/fundamentals-of-electrostatic-spraying/49548 (accessed on 20 November 2019).
- Van Stan, J.T.; Siegert, C.M.; Levia, D.F.; Scheick, C.E. Effects of wind-driven rainfall on interception and stemflow generation between two codominant tree species with differing crown characteristics. Agric. For. Meteorol. 2016, 151, 1277–1286. [Google Scholar] [CrossRef]
- Ripley, B.; Venables, B.; Bates, D.M.; Hornik, K.; Gebhardt, A.; Firth, D. Package “Mass”. Available online: https://cran.r-project.org/web/packages/MASS/MASS.pdf (accessed on 7 November 2019).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: http://www.R-project.org/ (accessed on 7 November 2018).
- Murakami, S. A proposal for a new forest canopy interception mechanism: Splash droplet evaporation. J. Hydrol. 2006, 319, 72–82. [Google Scholar] [CrossRef]
- Dunkerley, D.L. Evaporation of impact water droplets in interception processes: Historical precedence of the hypothesis and a brief literature overview. J. Hydrol. 2009, 376, 599–604. [Google Scholar] [CrossRef]
- Saito, T.; Matsuda, H.; Komatsu, M.; Xiang, Y.; Takahashi, A.; Shinohara, Y.; Otsuki, K. Forest canopy interception loss exceeds wet canopy evaporation in Japanese cypress (Hinoki) and Japanese cedar (Sugi) plantations. J. Hydrol. 2013, 507, 287–299. [Google Scholar] [CrossRef]
- Iida, S.; Levia, D.F.; Shimizu, A.; Shimizu, T.; Tamai, K.; Nobuhiro, T.; Kabeya, N.; Noguchi, S.; Sawano, S.; Araki, M. Intrastorm scale rainfall interception dynamics in a mature coniferous forest stand. J. Hydrol. 2017, 548, 770–783. [Google Scholar] [CrossRef]
- Lüpke, M.; Leuchner, M.; Levia, D.; Nanko, K.; Iida, S.; Menzel, A. Characterization of differential throughfall drop size distributions beneath European beech and Norway spruce. Hydrol. Process. 2019, 33, 3391–3406. [Google Scholar] [CrossRef]
- Calder, I.R. Dependence of rainfall interception on drop size: 1. Development of the two-layer stochastic model. J. Hydrol. 1996, 185, 363–378. [Google Scholar] [CrossRef]
- Hall, R.L. Interception loss as a function of rainfall and forest types: Stochastic modelling for tropical canopies revisited. J. Hydrol. 2003, 280, 1–12. [Google Scholar] [CrossRef]

| Variable’s Acronym | Threshold Value | Less than Threshold | More than Threshold |
|---|---|---|---|
| Rainfall amount–Pa | 6 mm | Pa6:0 | Pa6:1 |
| Rainfall duration–Pd | 4 h | Pd4:0 | Pd4:1 |
| Rainfall intensity–Pi | 1.8 mm/h | Pi1.8:0 | Pi1.8:1 |
| Wind speed–Ws | 1.3 m/s | Ws1.3:0 | Ws1.3:1 |
| Wind direction–Wd | S, N, E, W, SE, NE, SW, NW | WdS/WdN/WdE/WdW/WdSE/WdNE/WdSW/WdNW | |
| Median volume diameter–MVD | 1.5 mm | MVD1.5:0 | MVD1.5:1 |
| Number of raindrops-NrD | 10,000/50,000/100,000 | NrD10:0/NrD10-50/NrD50-100/NrD100:1 | |
| Pa (mm) | Pd (h) | Pi (mm/h) | Ws (m/s) | MVD (mm) | NrD |
|---|---|---|---|---|---|
| 6 | 1.5 | 0.8 | 0.5 | 1 | 10,000 |
| 8 | 3 | 1.2 | 1 | 1.3 | 30,000 |
| 10 | 4 | 1.4 | 1.3 | 1.5 | 50,000 |
| 12 | 5.5 | 1.8 | 1.8 | 1.8 | 10,000, 100,000 |
| 14 | 8 | 2.2 | 2 | 2 | 10,000, 50,000, 100,000 |
| Acronym | NrD10:0 | NrD10–50 | NrD50–100 | NrD100:1 |
|---|---|---|---|---|
| Number of Raindrops Per Class | <10,000 | 10,000–50,000 | 50,001–100,000 | >100,000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zabret, K.; Šraj, M. Evaluating the Influence of Rain Event Characteristics on Rainfall Interception by Urban Trees Using Multiple Correspondence Analysis. Water 2019, 11, 2659. https://doi.org/10.3390/w11122659
Zabret K, Šraj M. Evaluating the Influence of Rain Event Characteristics on Rainfall Interception by Urban Trees Using Multiple Correspondence Analysis. Water. 2019; 11(12):2659. https://doi.org/10.3390/w11122659
Chicago/Turabian StyleZabret, Katarina, and Mojca Šraj. 2019. "Evaluating the Influence of Rain Event Characteristics on Rainfall Interception by Urban Trees Using Multiple Correspondence Analysis" Water 11, no. 12: 2659. https://doi.org/10.3390/w11122659
APA StyleZabret, K., & Šraj, M. (2019). Evaluating the Influence of Rain Event Characteristics on Rainfall Interception by Urban Trees Using Multiple Correspondence Analysis. Water, 11(12), 2659. https://doi.org/10.3390/w11122659






