Optimization of Spring Wheat Irrigation Schedule in Shallow Groundwater Area of Jiefangzha Region in Hetao Irrigation District
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Design of the Experiment
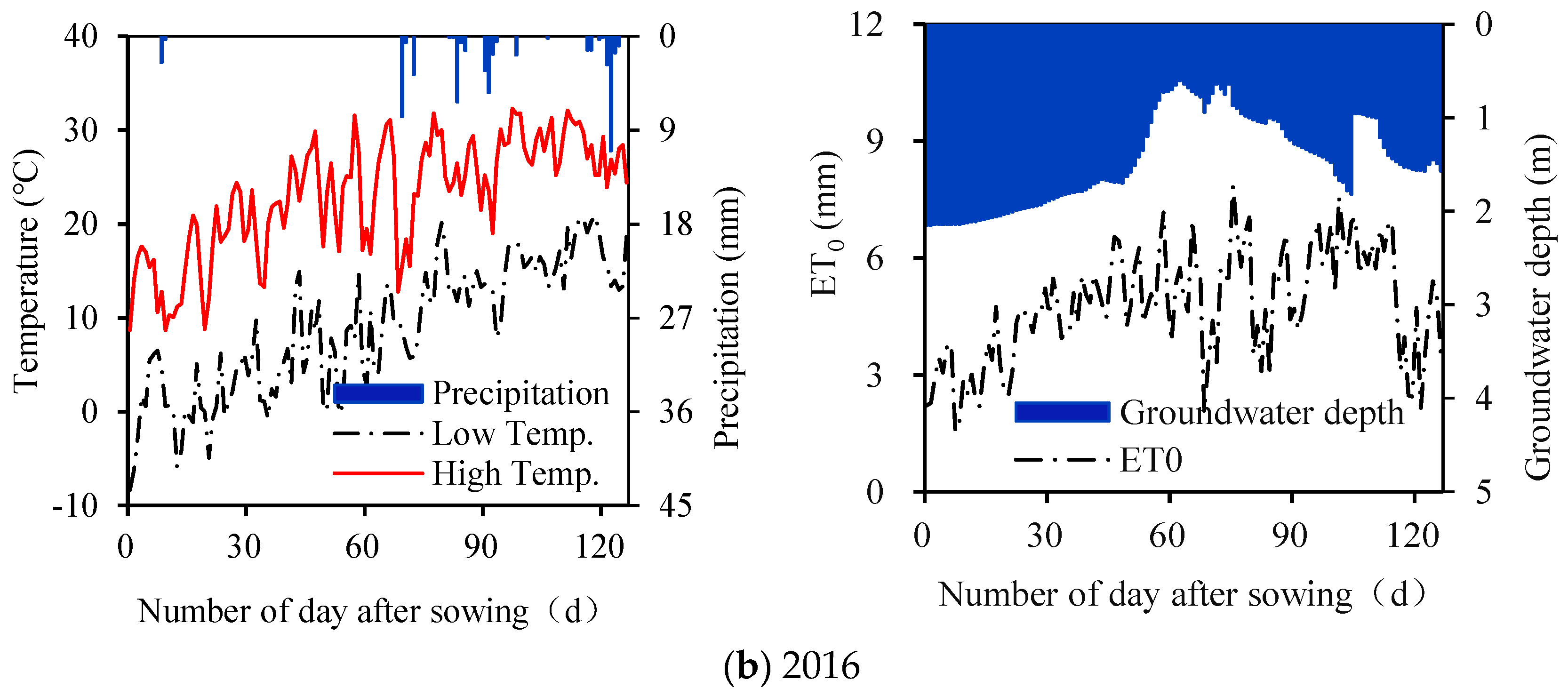
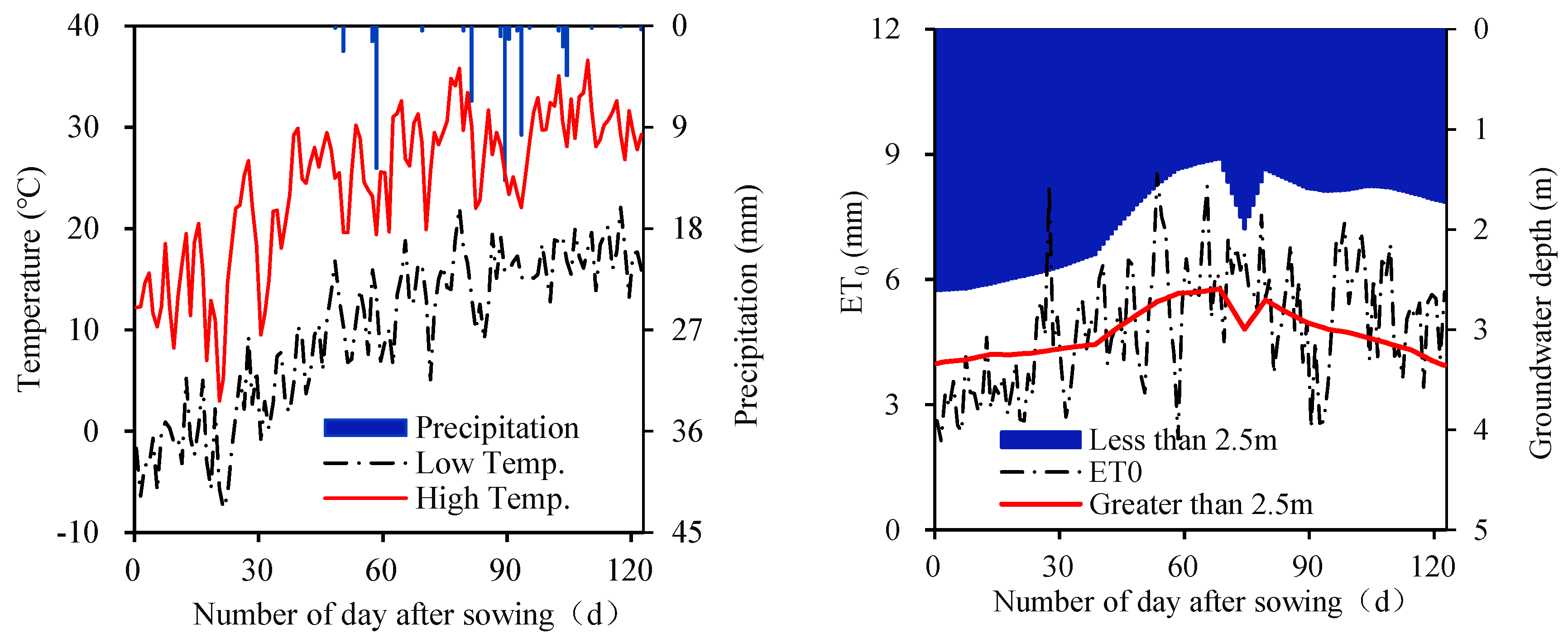
2.3. Data Observation
2.4. The Aquacrop Model
2.5. Model Verification
2.6. Scenarios
2.6.1. Determination of the Typical Year
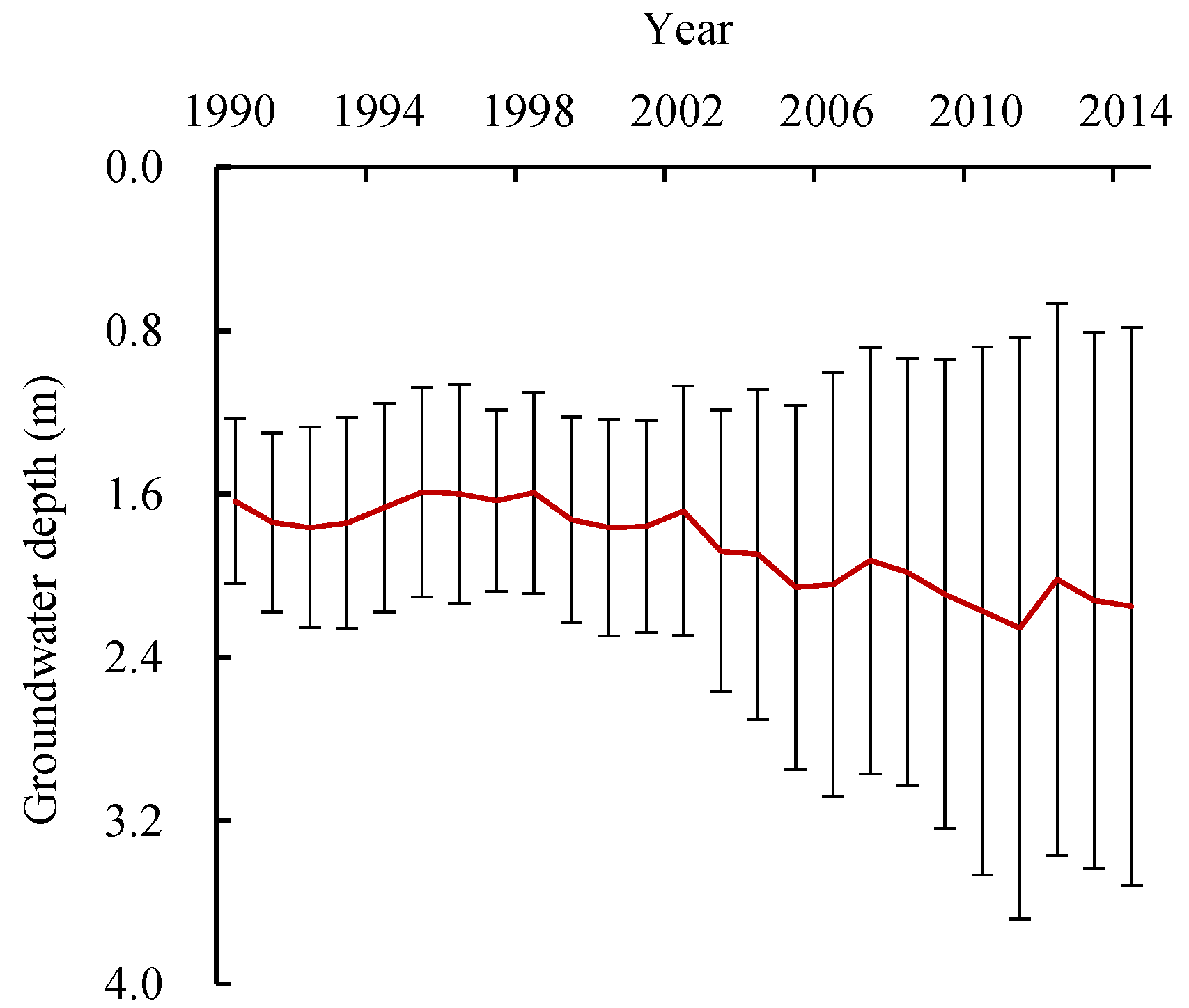
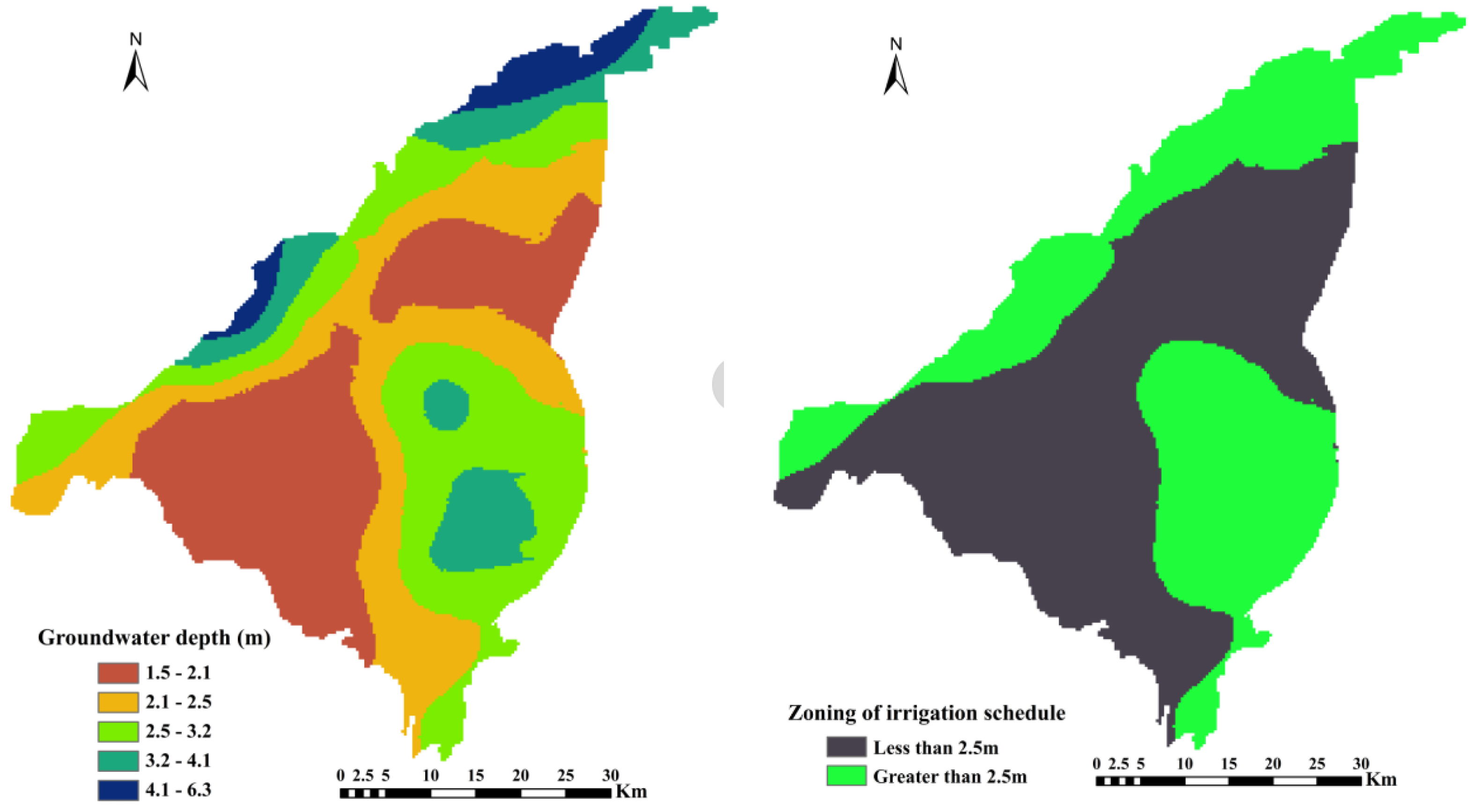
2.6.2. Determination of Groundwater Depth
2.6.3. Irrigation Schedule Scenarios
3. Results
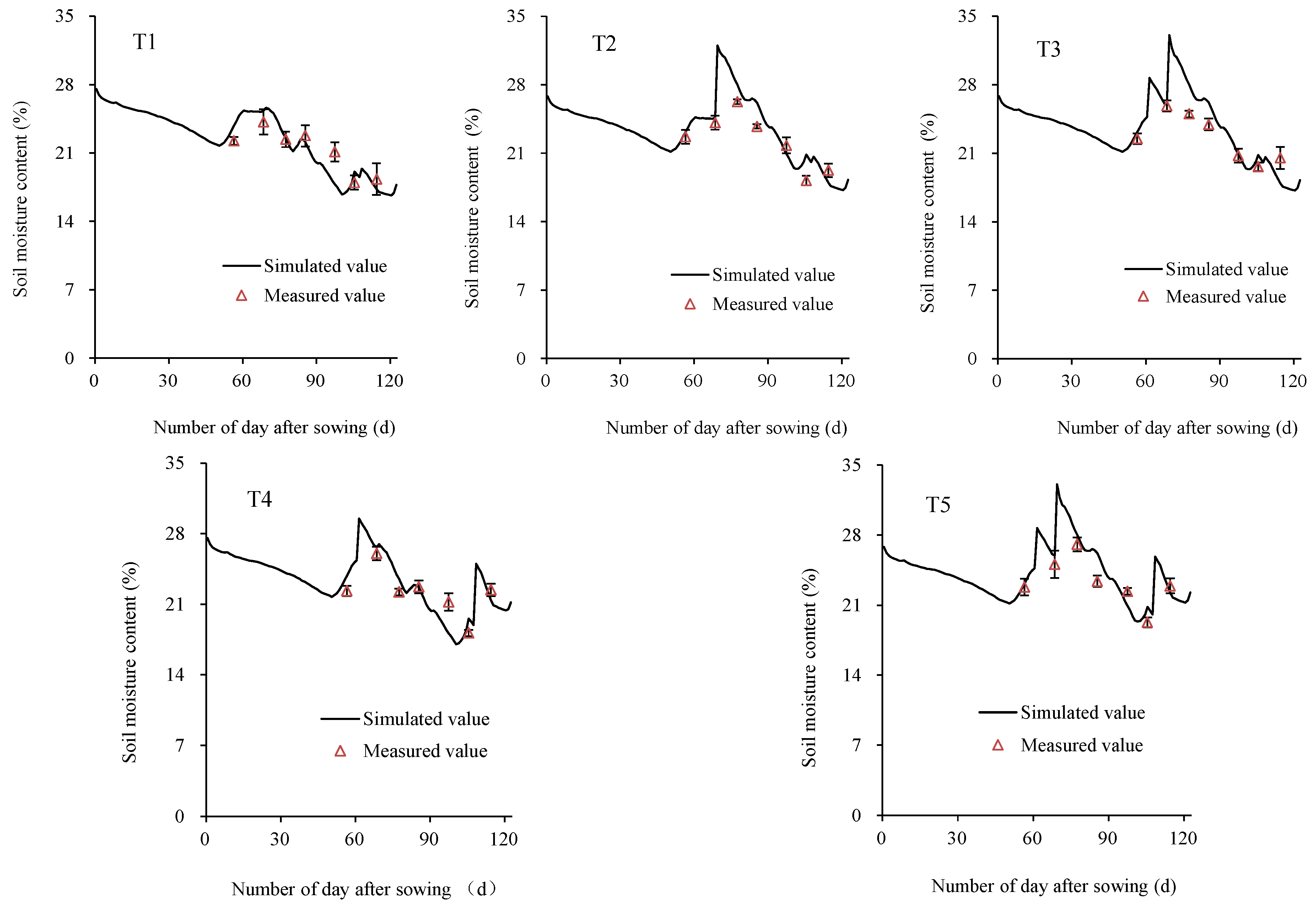
3.1. Model Verification
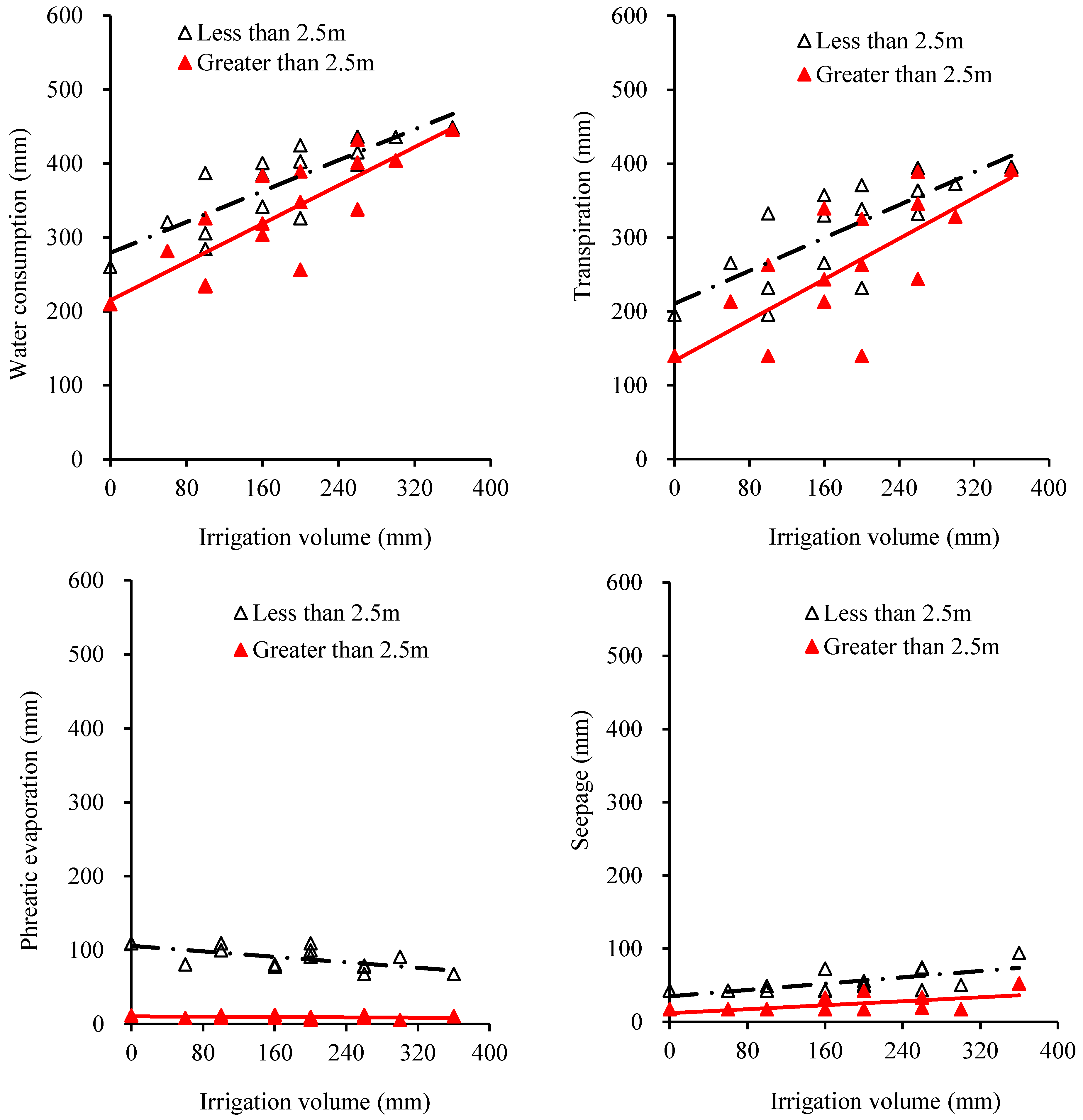
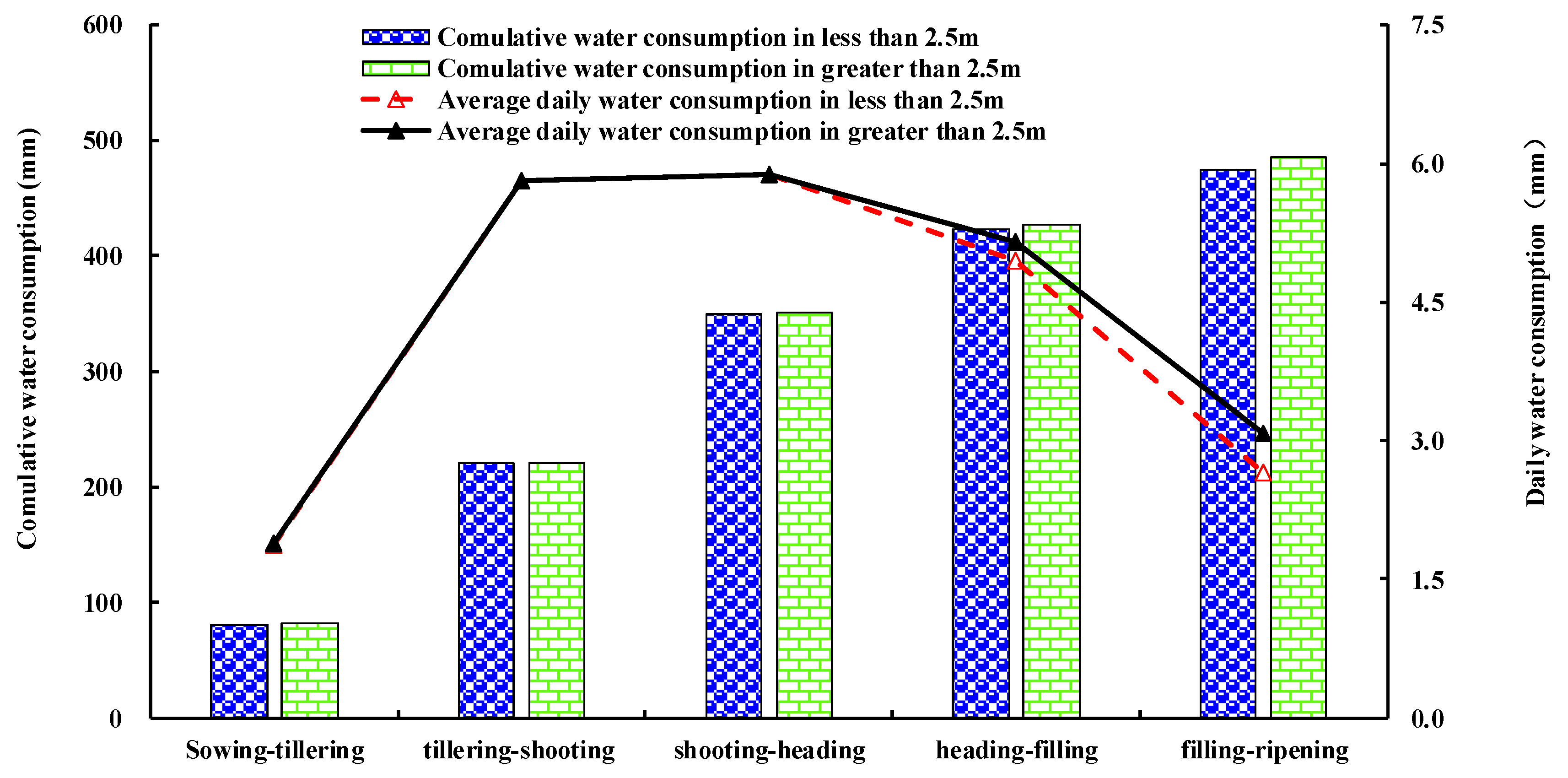
3.2. Water Consumption by Spring Wheat in Different Zones under Different Irrigation Schedules
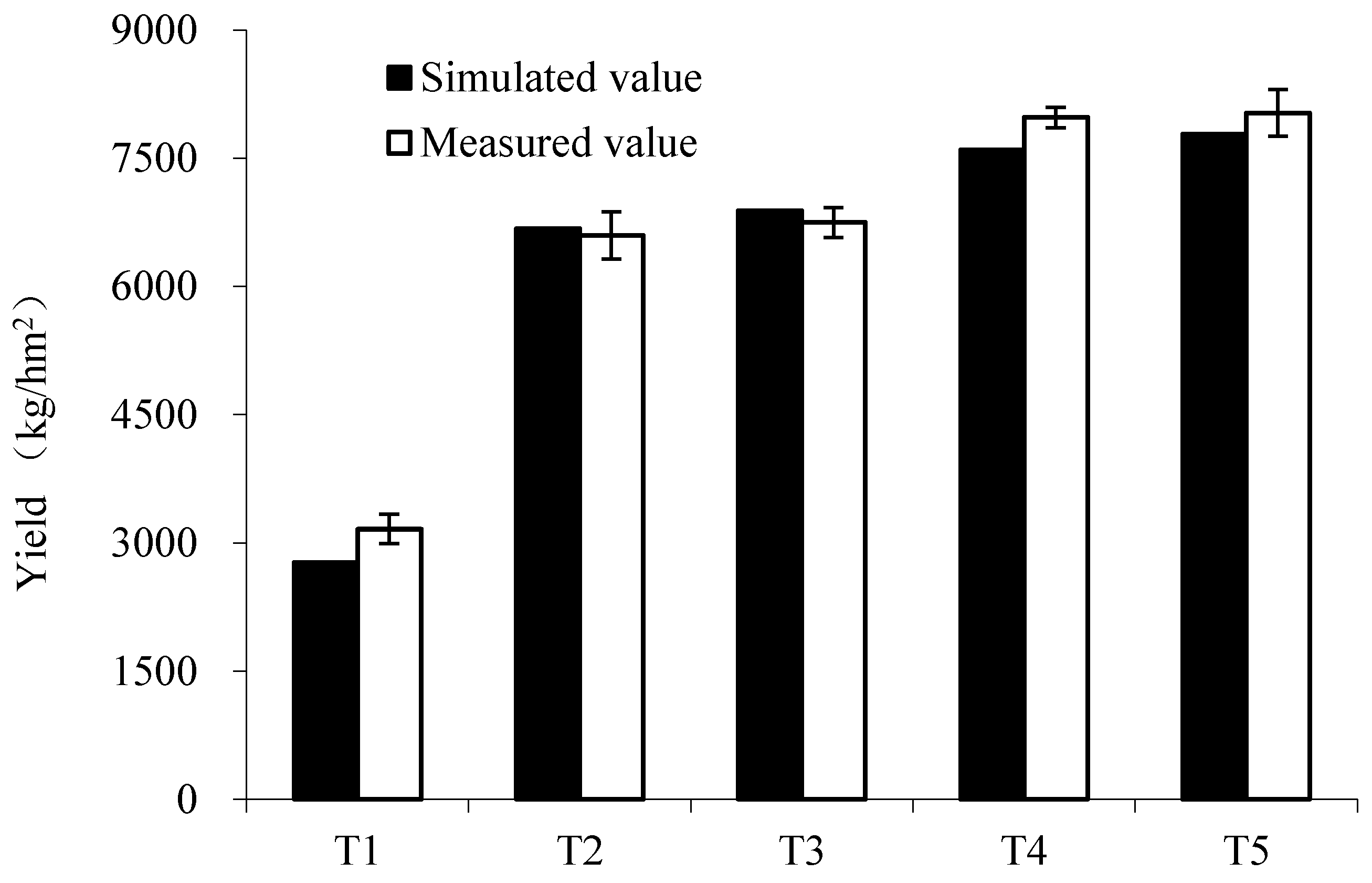
3.3. Yield of Spring Wheat in Different Zones under Different Irrigation Schedules
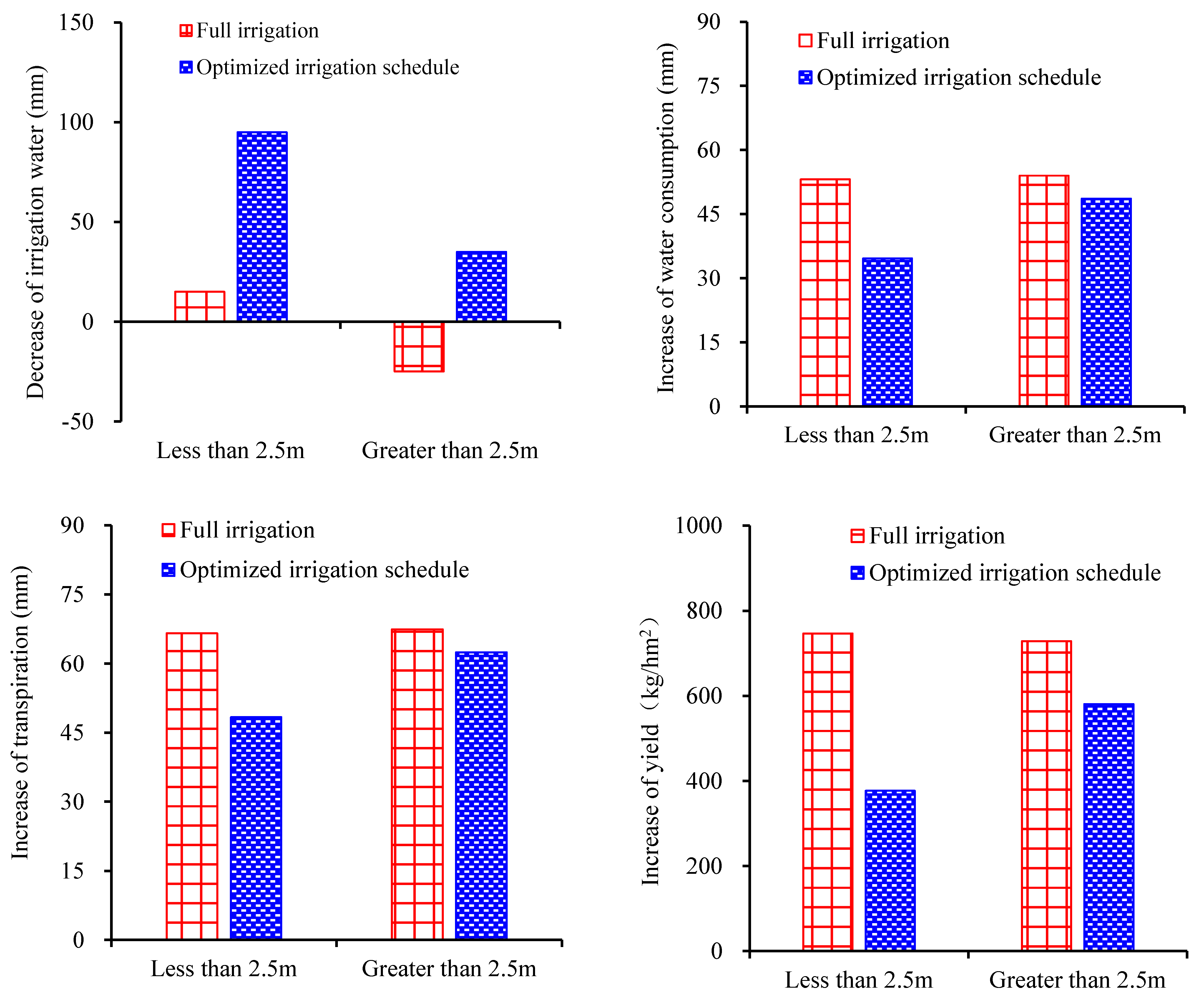
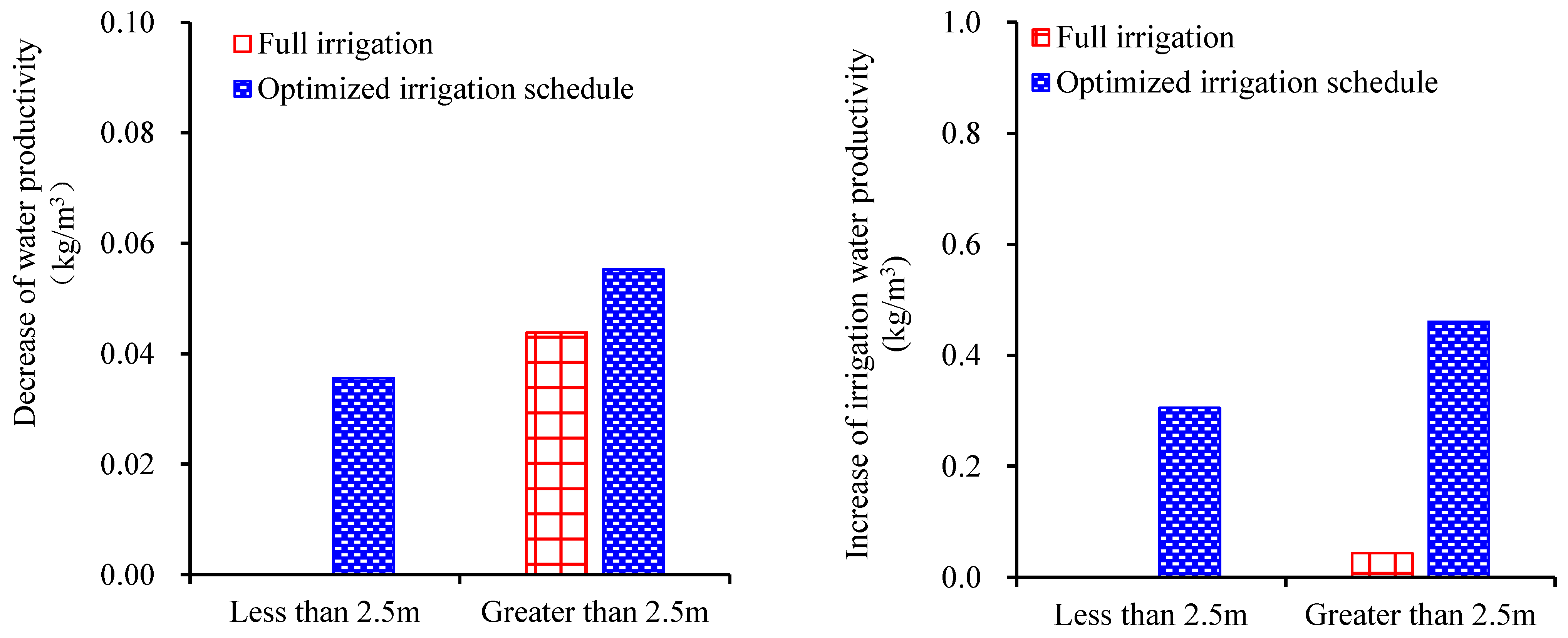
3.4. Optimization of Spring Wheat Irrigation Schedule Considering Groundwater Spatial Variability
4. Discussion
4.1. Water Saving Performance Analysis
4.2. Water Consumption Characteristics
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, P.; Yu, J.J.; Pozdniakov, S.P.; Grinevsky, S.O. Shallow groundwater dynamics and its driving forces in extremely arid areas: A case study of the lower Heihe River in northwestern China. Hydrol. Process. 2014, 28, 1539–1553. [Google Scholar] [CrossRef]
- Satchithanantham, S.; Krahn, V.; Ranjan, R.S.; Sager, S. Shallow groundwater uptake and irrigation water redistribution within the potato root zone. Agric. Water Manag. 2014, 132, 101–110. [Google Scholar] [CrossRef]
- Ghamarnia, H.; Golamian, M.; Sepehri, S.; Arji, I. Shallow groundwater use by Safflower (Carthamus tinctorius L.) in a semi-arid region. Irrig. Sci. 2011, 29, 147–156. [Google Scholar] [CrossRef]
- Gao, X.Y.; Huo, Z.L.; Qu, Z.Y. Modeling contribution of shallow groundwater to evapotranspiration and yield of maize in an arid area. Sci. Rep. 2017, 7, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Kong, F.R.; Qu, Z.Y.; Liu, Y.J.; Ma, Y.X. Experimental research on the effect of different kinds of groundwater buried depth on soil water, salinity and crop growth. China Rural Water Hydropower 2009, 5, 44–48. (In Chinese) [Google Scholar]
- Kruse, E.G.; Champion, D.F.; Cuevas, D.L.; Yoder, R.E.; Young, D. Crop water use from shallow, saline water tables. Trans. Asae 1993, 36, 697–707. [Google Scholar] [CrossRef]
- Wang, X.H.; Hou, H.B. The influence of shallow groundwater on crops growth laws. J. Irrig. Drain. 2006, 25, 13–16. (In Chinese) [Google Scholar]
- Zhang, C.X. Study on groundwater utilization by dry crops. J. Irrig. Drain. 1989, 8, 20–24. (In Chinese) [Google Scholar]
- Yang, P.Y.; Wu, B.; Wang, S.X.; Dong, X.G.; Liu, L. Research on irrigation schedule of cotton drip irrigation under plastic film based on the different ground water table in arid areas. Agric. Res. Arid Areas 2014, 32, 76–82. (In Chinese) [Google Scholar]
- Zhuang, Y.; Lu, J.; Jiao, X. Effect of groundwater table on cotton irrigation regulation. Water Sav. Irrig. 2015, 3, 15–17. (In Chinese) [Google Scholar]
- Wang, B.L. Experimental study on the utilization of shallow groundwater for spring wheat. Agric. Sci. Technol. 2011, 12, 108–132. [Google Scholar]
- Liu, Z.D.; Liu, Z.G.; Yu, J.H.; Nan, J.Q.; Qin, A.Z.; Xiao, J.F. Effects of groundwater depth on maize growth and water use efficiency. J. Drain. Irrig. Mach. Eng. 2014, 32, 617–624. (In Chinese) [Google Scholar]
- Xue, J.Y.; Guan, H.; Huo, Z.L.; Wang, F.X.; Huang, G.H.; Boll, J. Water saving practices enhance regional efficiency of water consumption and water productivity in an arid agricultural area with shallow groundwater. Agric. Water Manag. 2017, 194, 78–89. [Google Scholar] [CrossRef]
- Ghamarnia, H.; Farmanifard, M. Yield production and water-use efficiency of wheat (Triticum aestivum L.) cultivars under shallow groundwater use in semi-arid region. Arch. Agron. Soil Sci. 2014, 60, 1677–1700. [Google Scholar] [CrossRef]
- Ren, D.Y.; Xu, X.; Huang, Q.Z.; Huo, Z.L. Analyzing the Role of Shallow Groundwater Systems in the Water Use of Different Land-Use Types in Arid Irrigated Regions. Water 2018, 10, 634. [Google Scholar] [CrossRef]
- Wang, X.W.; Huo, Z.L.; Guan, H.; Guo, P. Drip irrigation enhances shallow groundwater contribution to crop water consumption in an arid area. Hydrol. Process. 2018, 32, 747–758. [Google Scholar] [CrossRef]
- Chen, H.; Liu, Z.Y.; Huo, Z.L.; Qu, Z.Y.; Xia, Y.H.; Fernald, A. Impacts of agricultural water saving practice on regional groundwater and water consumption in an arid region with shallow groundwater. Environ. Earth Sci. 2016, 75, 1204. [Google Scholar] [CrossRef]
- Ebrahimi, H.; Ghazavi, R.; Karimi, H. Estimation of Groundwater Recharge from the Rainfall and Irrigation in an Arid Environment Using Inverse Modeling Approach and RS. Water Resour. Manag. 2016, 30, 1939–1951. [Google Scholar] [CrossRef]
- Gao, X.Y.; Bai, Y.N.; Huo, Z.L.; Xu, X.; Huang, G.H.; Xia, Y.H.; Steenhuisc, T.S. Deficit irrigation enhances contribution of shallow groundwater to crop water consumption in arid area. Agric. Water Manag. 2017, 185, 116–125. [Google Scholar] [CrossRef]
- Xue, J.Y.; Huo, Z.L.; Wang, F.X.; Kang, S.Z.; Huang, G.H. Untangling the effects of shallow groundwater and deficit irrigation on irrigation water productivity in arid region: New conceptual model. Sci. Total Environ. 2018, 619, 1170–1182. [Google Scholar] [CrossRef]
- Gao, X.Y.; Huo, Z.L.; Xu, X.; Qu, Z.Y. Shallow groundwater plays an important role in enhancing irrigation water productivity in an arid area: The perspective from a regional agricultural hydrology simulation. Agric. Water Manag. 2018, 208, 43–58. [Google Scholar] [CrossRef]
- Karimov, A.K.; Šimůnek, J.; Hanjra, M.A.; Avliyakulov, M.; Forkutsa, I. Effects of the shallow water table on water use of winter wheat and ecosystem health: Implications for unlocking the potential of groundwater in the Fergana Valley (Central Asia). Agric. Water Manag. 2014, 131, 57–69. [Google Scholar] [CrossRef]
- Liu, J.; Sun, S.K.; Wang, Y.B.; Zhao, X.N. Evaluation of crop production, trade, and consumption from the perspective of water resources: A case study of the Hetao irrigation district, China, for 1960–2010. Sci. Total Environ. 2015, 505, 1174–1181. [Google Scholar] [CrossRef] [PubMed]
- Bai, L.L.; Cai, J.B.; Liu, Y.; Chen, H.; Zhang, B.Z.; Huang, L.X. Responses of field evapotranspiration to the changes of cropping pattern and groundwater depth in large irrigation district of Yellow River basin. Agric. Water Manag. 2017, 166, 17–32. [Google Scholar] [CrossRef]
- Du, J.; Yang, P.L.; Ren, S.M.; Li, Y.K.; Wang, Y.Z.; Yuan, X.Q.; Li, X.Y.; Du, J. The canal-lining project on groundwater and ecological environment in Hetao irrigation District of Inner Mongolia. Chin. J. Appl. Ecol. 2011, 22, 144–150. (In Chinese) [Google Scholar]
- Li, Z.Z.; Fu, X.J.; Tian, Y.; Zhen, Q. Study on the Change of Soil Moisture and Groundwater by Jiefangzha Region in Hetao Irrigation District. Inn. Mong. Water Resour. 2018, 5, 16–17. (In Chinese) [Google Scholar]
- Allen, R.; Periera, L.; Raes, D.; Smith, M. Crop Evapotranspriation: Guidelines for Computing Crop Water Requirement; FAO Irrigation and Drainage Paper No.56; FAO: Rome, Italy, 1998. [Google Scholar]
- Hsiao, T.; Heng, L.; Steduto, P.; Rojas-Lara, B.; Raes, D.; Fereres, E. AquaCrop—The FAO Crop Model to Simulate Yield Response to Water: III. Parameterization and Testing for Maize. Agron. J. 2009, 101, 448–459. [Google Scholar] [CrossRef]
- Raes, D.; Steduto, P.; Hsiao, T.; Fereres, E. AquaCropThe FAO Crop Model to Simulate Yield Response to Water: II. Main Algorithms and Software Description. Agron. J. 2009, 101, 438–447. [Google Scholar] [CrossRef]
- Steduto, P.; Hsiao, T.; Raes, D.; Fereres, E. AquaCrop—The FAO Crop Model to Simulate Yield Response to Water: I. Concepts and Underlying Principles. Agron. J. 2009, 101, 426–437. [Google Scholar] [CrossRef]
- Andarzian, B.; Bannayan, M.; Steduto, P.; Mazraeh, H.; Barati, M.E.; Barati, M.A.; Rahnama, A. validation and testing of the Aquacrop model under full and deficit irrigated wheat production in Iran. Agric. Water Manag. 2011, 100, 1–8. [Google Scholar] [CrossRef]
- Kahimba, F.C.; Bullock, P.R.; Sri-Ranjan, R.; Cutforth, H.W. Evaluation of the SolarCalc model for simulating hourly and daily incoming solar radiation in the Northern Great Plains of Canada. Can. Biosyst. Eng. 2009, 51, 1–11. [Google Scholar]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Willmott, C.J.; Maasuura, K. Advantages of the meanabsolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Zhao, S.Z.; Kong, F.J.; Wang, X.K.; Li, S.B.; Meng, K.W. Confirming of critical depth of groundwater level and discussion on it’s significance-take Hetao Irrigation Area for example. J. Inn. Mong. Agric. Univ. 2008, 29, 164–167. (In Chinese) [Google Scholar]
- Ruan, B.Q.; Han, Y.P.; Jiang, R.F.; Xu, F.R. Appropriate water saving extent for ecological vulnerable area. J. Hydraul. Eng. 2008, 39, 809–814. (In Chinese) [Google Scholar]




| Depth (cm) | Dry Bulk Density (g/cm3) | Saturated Moisture Content (m3/m3) | Field Capacity (m3/m3) | Wilting Point (m3/m3) |
|---|---|---|---|---|
| 0–10 | 1.45 | 0.46 | 0.36 | 0.09 |
| 10–20 | 1.40 | 0.47 | 0.38 | 0.09 |
| 20–40 | 1.34 | 0.49 | 0.41 | 0.09 |
| 40–60 | 1.38 | 0.48 | 0.41 | 0.08 |
| 60–100 | 1.34 | 0.50 | 0.42 | 0.09 |
| Treatment | Tillering–Shooting | Shooting–Heading | Heading–Filling | Irrigation Quota (mm) | |
|---|---|---|---|---|---|
| 2015 | 2016 | ||||
| T1 | - | - | |||
| T2 | √ | 100 | 100 | ||
| T3 | √ | √ | 160 | 160 | |
| T4 | √ | √ | 160 | 135 | |
| T5 | √ | √ | √ | 260 | 235 |
| Parameter | Default | Calibrated |
|---|---|---|
| Cutoff temperature (°C) | 26 | 26 |
| Crop coefficient | 1.10 | 1.05 |
| Upper and lower thresholds of soil water depletion coefficient | 0.20~0.65 | 0.15~0.35 |
| Shape factor for water stress coefficient for canopy expansion | 5.0 | 5.0 |
| Upper stomatal control limit coefficient of soil stress | 0.65 | 0.35 |
| Soil water depletion fraction for stomatal control-upper threshold | 2.5 | 2.5 |
| Canopy growth coefficient | 0.04901 | 0.07600 |
| Canopy decline coefficient | 0.07179 | 0.18506 |
| Maximum canopy cover in fraction soil cover | 0.96 | 0.98 |
| Minimum effective rooting depth (m) | 0.30 | 0.30 |
| Maximum effective rooting depth (m) | 1.50 | 0.90 |
| Normalized water productivity (g/m2) | 15.0 | 19.7 |
| Harvest index (%) | 48 | 48 |
| Number of plants per hectare | 4,500,000 | 6,500,000 |
| Treatment | Tillering–Shooting | Shooting–Heading | Heading–Filling | Filling–Ripening | Irrigation Quota (mm) |
|---|---|---|---|---|---|
| T00 | - | ||||
| T11 | √ | 60 | |||
| T12 | √ | 100 | |||
| T13 | √ | 100 | |||
| T14 | √ | 100 | |||
| T21 | √ | √ | 160 | ||
| T22 | √ | √ | 160 | ||
| T23 | √ | √ | 160 | ||
| T24 | √ | √ | 200 | ||
| T25 | √ | √ | 200 | ||
| T26 | √ | √ | 200 | ||
| T31 | √ | √ | √ | 260 | |
| T32 | √ | √ | √ | 260 | |
| T33 | √ | √ | √ | 260 | |
| T34 | √ | √ | √ | 300 | |
| T44 | √ | √ | √ | √ | 360 |
| R2 | RMSE (%) | MAE (%) | MBE (%) | EF | ||
|---|---|---|---|---|---|---|
| Model calibration | T1 | 0.927 | 1.481 | 1.290 | −1.045 | 0.747 |
| T2 | 0.887 | 1.417 | 1.083 | 0.495 | 0.869 | |
| T3 | 0.887 | 1.740 | 1.526 | 0.735 | 0.862 | |
| T4 | 0.825 | 1.522 | 1.343 | 0.473 | 0.784 | |
| T5 | 0.764 | 1.635 | 1.383 | 0.066 | 0.722 | |
| All treatments | 0.860 | 1.203 | 0.780 | 0.037 | 0.849 | |
| Model verification | T1 | 0.710 | 1.578 | 1.278 | −0.136 | 0.464 |
| T2 | 0.810 | 1.647 | 1.431 | 0.825 | 0.601 | |
| T3 | 0.805 | 1.802 | 1.429 | 0.691 | 0.349 | |
| T4 | 0.651 | 1.564 | 1.288 | 0.090 | 0.472 | |
| T5 | 0.755 | 1.445 | 1.241 | 0.633 | 0.581 | |
| All treatments | 0.761 | 1.612 | 1.333 | 0.421 | 0.538 | |
| R2 | RMSE (kg/hm2) | MAE (kg/hm2) | MBE (kg/hm2) | EF | |
|---|---|---|---|---|---|
| Model calibration | 0.985 | 275.883 | 246.190 | −159.370 | 0.976 |
| Model verification | 0.970 | 357.097 | 242.402 | 145.004 | 0.618 |
| Groundwater Depth | Model | Tillering–Shooting | Shooting–Heading | Heading–Filling | Filling–Ripening | R2 | RMSE (kg/hm2) | MAE (kg/hm2) | MBE (kg/hm2) |
|---|---|---|---|---|---|---|---|---|---|
| Greater than 2.5 m | Jensen | −2.4901 | 4.3914 | −0.4899 | 0.0252 | 0.77 | 1565.50 | 1059.55 | 128.87 |
| Minhas | 38.0809 | 4.9308 | 0.3486 | 0.0112 | 0.94 | 692.37 | 441.15 | 141.82 | |
| Blank | −0.3555 | 0.8647 | 0.4171 | 0.0344 | 0.97 | 458.34 | 327.79 | −4.24 | |
| Stewart | 0.7614 | 0.6691 | 0.506 | −0.0109 | 0.98 | 410.58 | 306.51 | 22.58 | |
| Singh | −0.6875 | 0.8138 | 0.6344 | 0.0714 | 0.96 | 530.17 | 459.80 | 0.11 | |
| Less than 2.5 m | Jensen | 0.9930 | 0.3591 | 0.6202 | −0.0280 | 0.99 | 165.32 | 136.03 | 30.87 |
| Minhas | 37.7041 | −0.0287 | 0.8584 | 0.0743 | 0.95 | 487.17 | 319.54 | −265.34 | |
| Blank | −0.0437 | 0.4508 | 0.5864 | −0.0434 | 0.98 | 198.21 | 166.18 | −2.04 | |
| Stewart | 1.0475 | 0.3265 | 0.5562 | −0.0134 | 0.99 | 145.73 | 125.48 | −2.28 | |
| Singh | −0.7359 | 0.9530 | 0.5868 | 0.0490 | 0.98 | 231.57 | 169.90 | −0.54 |
| Groundwater Depth | Irrigation Schedule | Input (mm) | Output (mm) | Soil Water Use (mm) | |||
|---|---|---|---|---|---|---|---|
| Precipitation | Irrigation Quota | Phreatic Evaporation | Seepage | Water Consumption | |||
| Greater than 2.5 m | Current irrigation schedule | 57 | 335 | 8 | 87 | 438 | 102 |
| Full irrigation | 57 | 360 | 7 | 84 | 492 | 129 | |
| Optimized irrigation schedule | 57 | 300 | 7 | 47 | 486 | 147 | |
| Less than 2.5 m | Current irrigation schedule | 57 | 335 | 65 | 127 | 440 | 65 |
| Full irrigation | 57 | 320 | 55 | 70 | 493 | 85 | |
| Optimized irrigation schedule | 57 | 240 | 62 | 68 | 474 | 139 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Z.; Zhang, B.; Cai, J.; Wei, Z.; Chen, H.; Liu, Y. Optimization of Spring Wheat Irrigation Schedule in Shallow Groundwater Area of Jiefangzha Region in Hetao Irrigation District. Water 2019, 11, 2627. https://doi.org/10.3390/w11122627
Peng Z, Zhang B, Cai J, Wei Z, Chen H, Liu Y. Optimization of Spring Wheat Irrigation Schedule in Shallow Groundwater Area of Jiefangzha Region in Hetao Irrigation District. Water. 2019; 11(12):2627. https://doi.org/10.3390/w11122627
Chicago/Turabian StylePeng, Zhigong, Baozhong Zhang, Jiabing Cai, Zheng Wei, He Chen, and Yu Liu. 2019. "Optimization of Spring Wheat Irrigation Schedule in Shallow Groundwater Area of Jiefangzha Region in Hetao Irrigation District" Water 11, no. 12: 2627. https://doi.org/10.3390/w11122627
APA StylePeng, Z., Zhang, B., Cai, J., Wei, Z., Chen, H., & Liu, Y. (2019). Optimization of Spring Wheat Irrigation Schedule in Shallow Groundwater Area of Jiefangzha Region in Hetao Irrigation District. Water, 11(12), 2627. https://doi.org/10.3390/w11122627






