Numerical Analysis of Woltman Meter Accuracy under Flow Perturbations
Abstract
1. Introduction
2. Materials and Methods
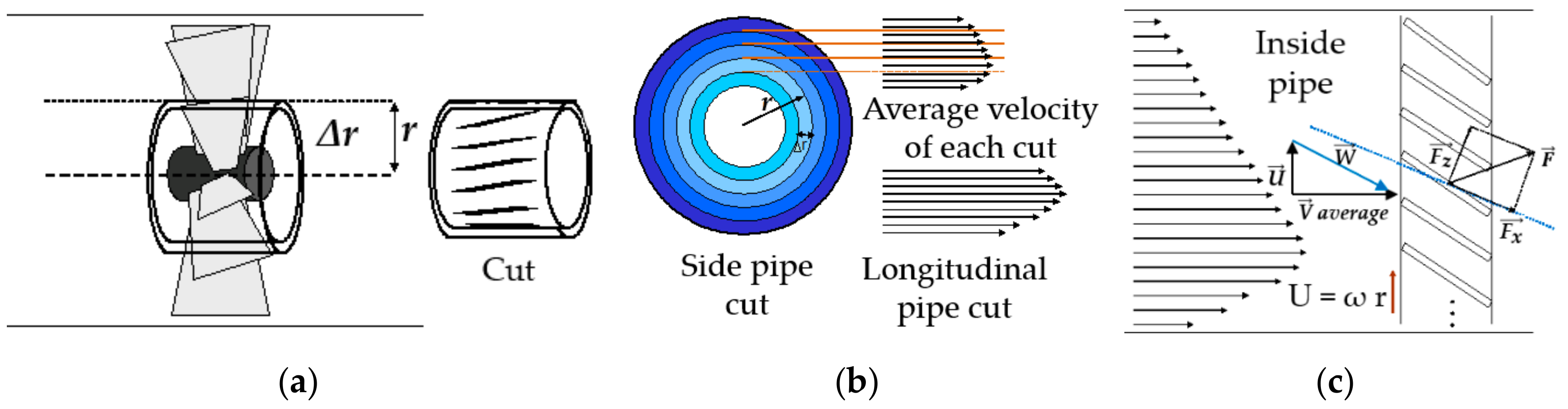
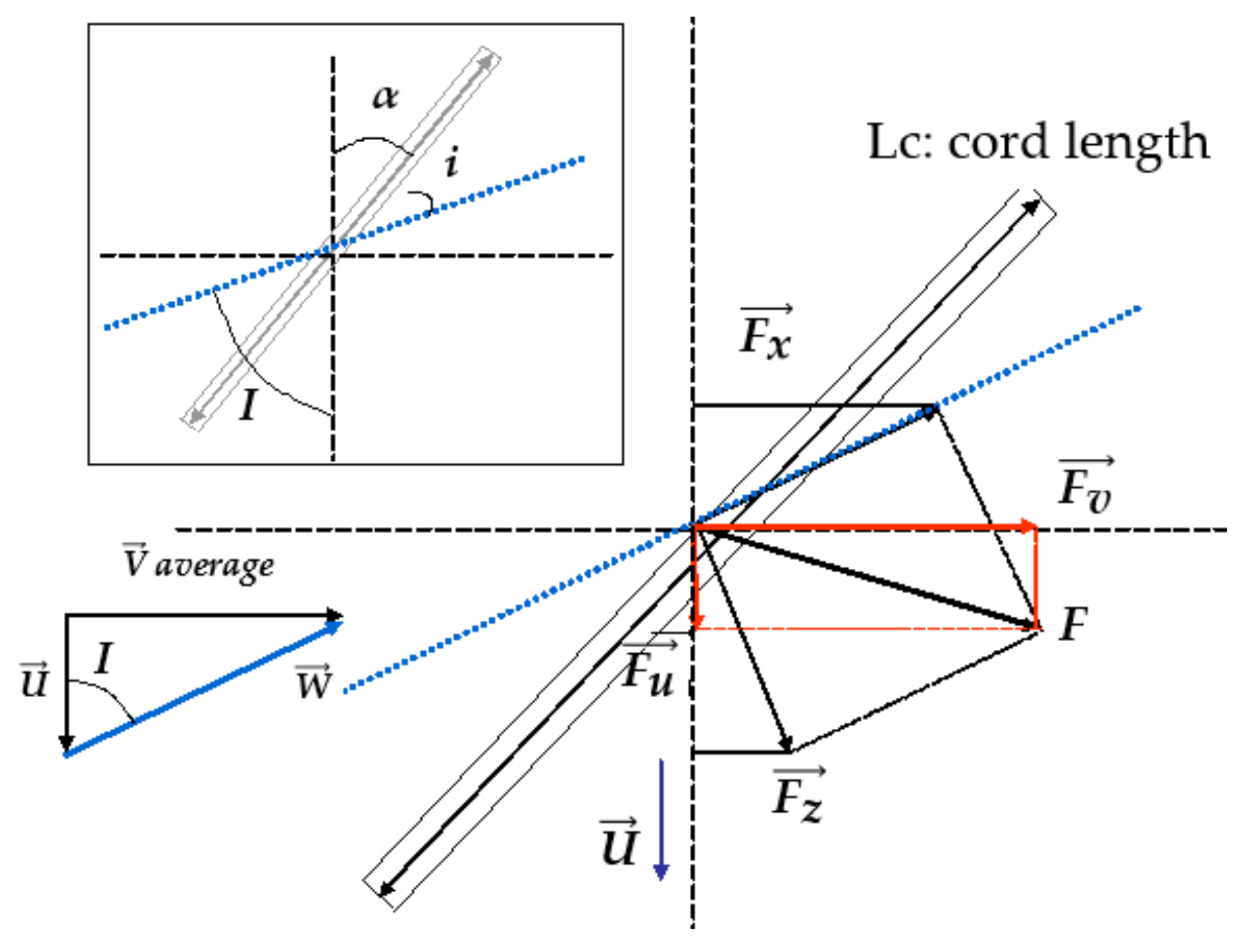
2.1. Theoretical Analysis
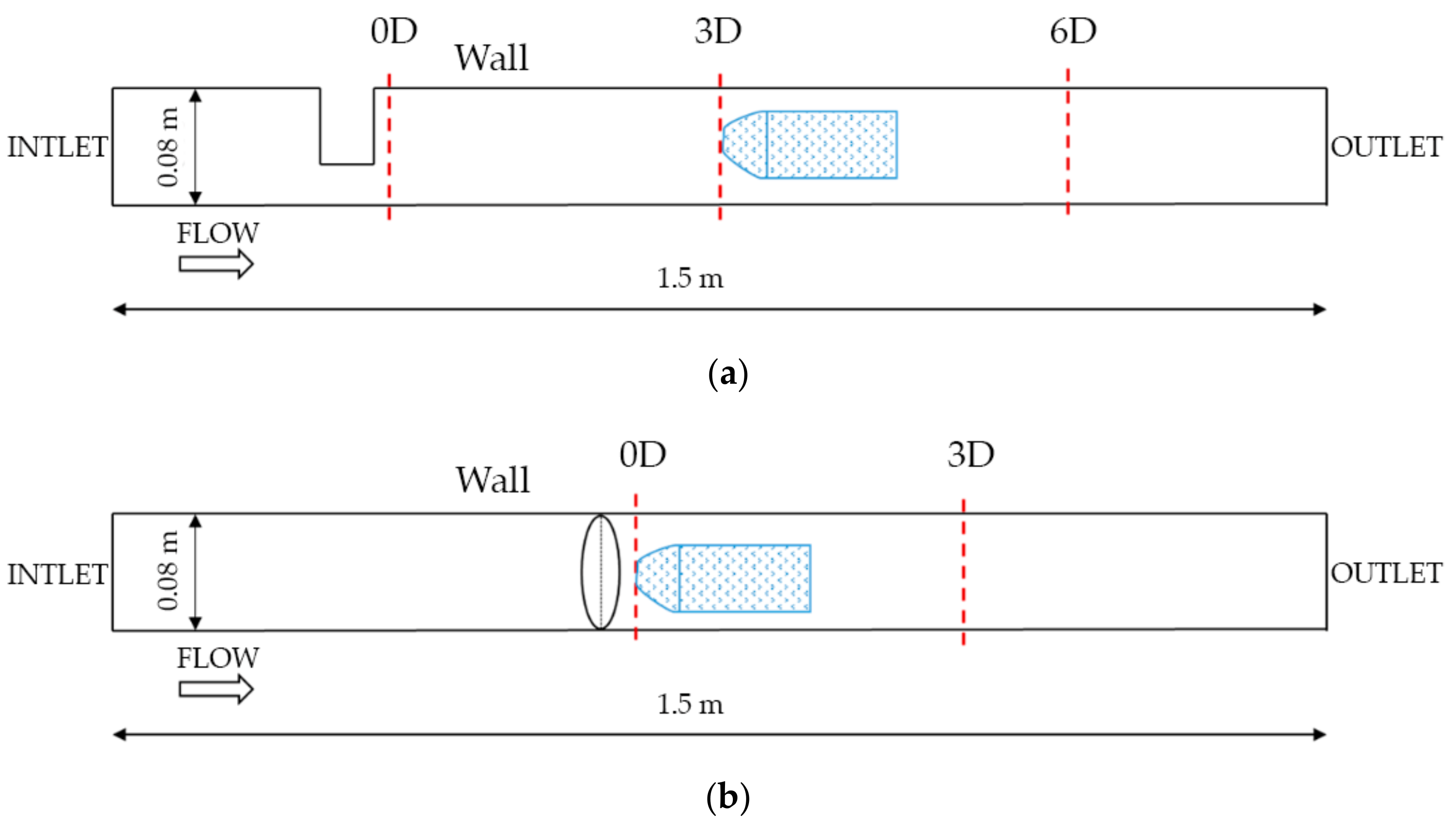
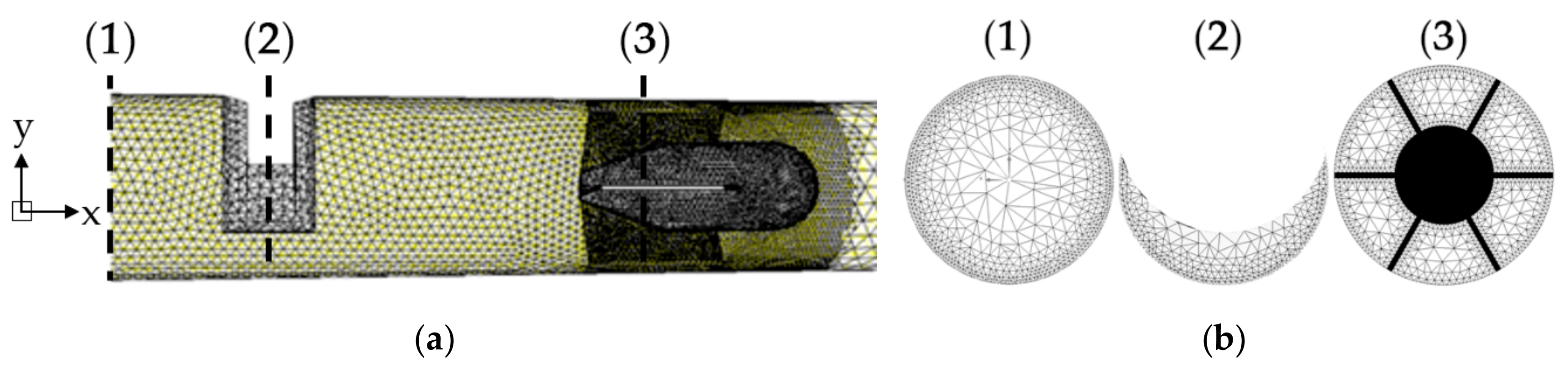
2.2. Computational Simulation
2.3. Numerical Analysis
2.4. Experimental Validation
3. Results and Discussion
3.1. Theoretical Analysis
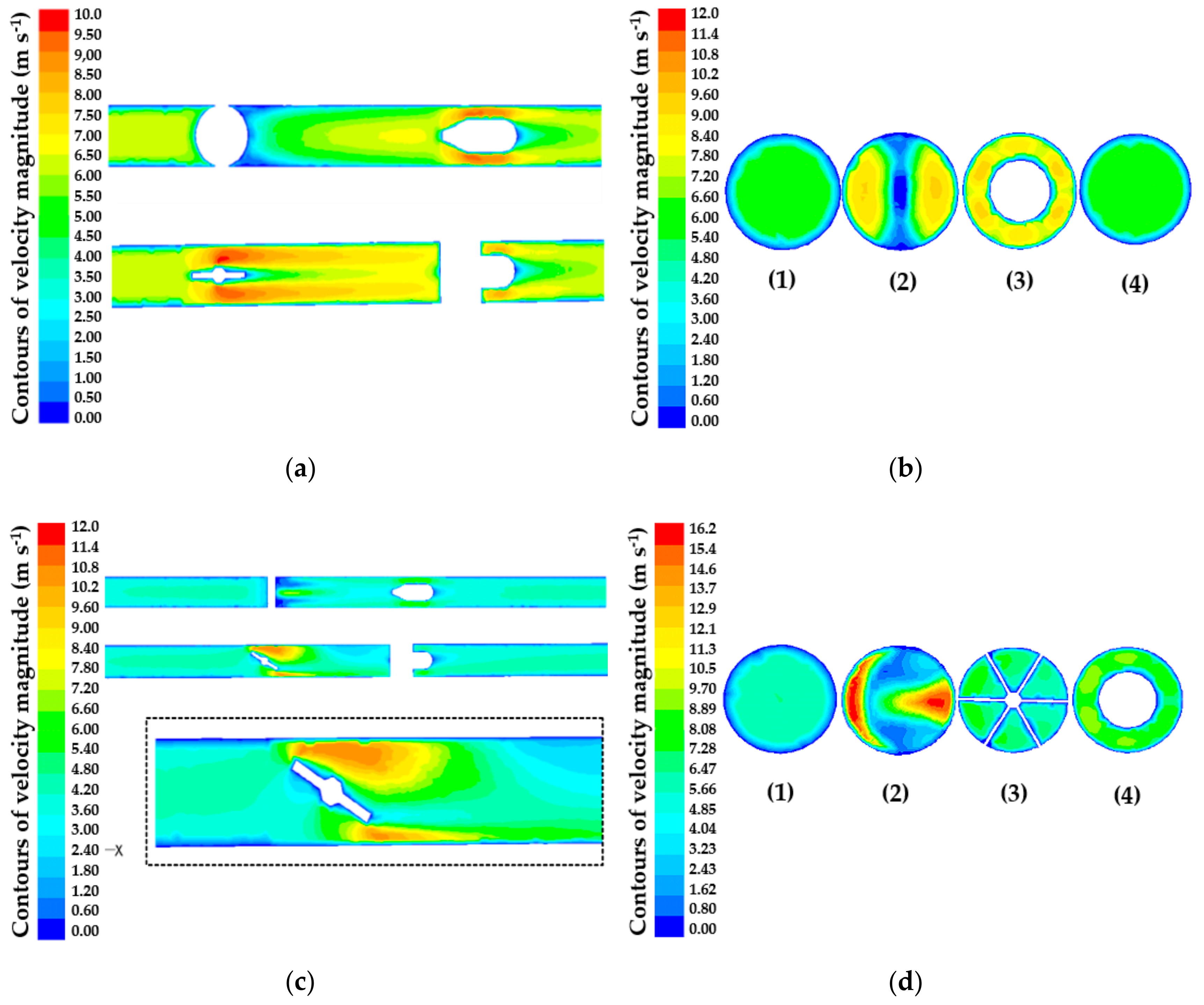
3.2. Computational Fluid Simulation
3.3. Numerical Analysis
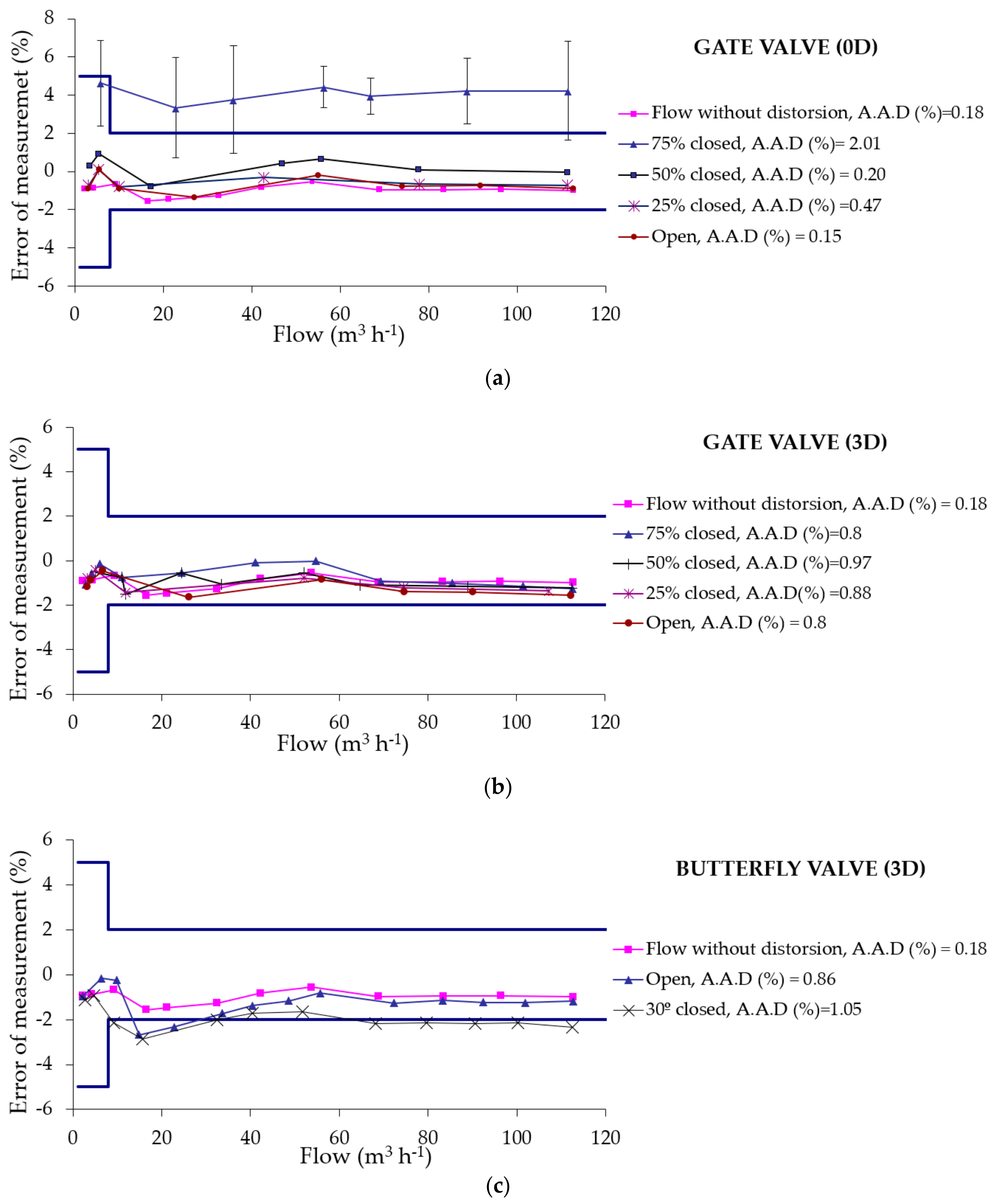
3.4. Experimental Validation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pardo, M.A.; Manzano, J.; Cabrera, E.; García-Serra, J. Energy audit of irrigation networks. Biosyst. Eng. 2013, 115, 89–101. [Google Scholar] [CrossRef]
- Zapata, N.; Salvador, R.; Cavero, J.; Lecina, S.; López, C.; Mantero, N.; Anadón, R.; Playán, E. Field test of an automatic controller for solid-set sprinkler irrigation. Irrig. Sci. 2013, 31, 1237–1249. [Google Scholar] [CrossRef]
- Arregui, F.; Cabrera, E., Jr.; Cobacho, R. Integrated Water Meter Management, 1st ed.; International Water Association: London, UK, 2007; ISBN 978-1-84339-034-3. [Google Scholar]
- Sapra, M.K.; Bajaj, M.; Kundu, S.N.; Sharma, B.S.V.G. Experimental and CFD investigation of 100 mm size cone flow elements. Flow Meas. Instrum. 2011, 22, 469–474. [Google Scholar] [CrossRef]
- Baker, R.C. Turbine and related flowmeters. In Flow Measurement Handbook: Industrial Designs, Operating Principles, Performance, and Applications; Cambridge University Press: Cambridge, UK, 2016; pp. 279–326. ISBN 978-1-107-05414-1. [Google Scholar]
- Lysak, P.D.; Jenkins, D.M.; Capone, D.E.; Brown, W.L. Analytical model of an ultrasonic cross-correlation flow meter, part 1: Stochastic modeling of turbulence. Flow Meas. Instrum. 2008, 19, 1–7. [Google Scholar] [CrossRef]
- Venugopal, A.; Agrawal, A.; Prabhu, S.V. Influence of blockage and upstream disturbances on the performance of a vortex flowmeter with a trapezoidal bluff body. Measurement 2010, 43, 603–616. [Google Scholar] [CrossRef]
- Singh, R.K.; Singh, S.N.; Seshadri, V. CFD prediction of the effects of the upstream elbow fittings on the performance of cone flowmeters. Flow Meas. Instrum. 2010, 21, 88–97. [Google Scholar] [CrossRef]
- Piechota, P.; Synowiec, P.; Andruszkiewicz, A.; Wędrychowicz, W. Selection of the relevant turbulence model in a CFD simulation of a flow disturbed by hydraulic elbow — comparative analysis of the simulation with measurements results obtained by the ultrasonic flowmeter. J. Therm. Sci. 2018, 27, 413–420. [Google Scholar] [CrossRef]
- Zhuang, Y.; Zhang, N.; Ma, L.; Huang, Y. Numerical investigation of liquid flowmeter calibration device based on CFD. J. Phys. Conf. Ser. 2018, 1074, 1–7. [Google Scholar] [CrossRef]
- Liu, W.; Xu, Y.; Zhang, T.; Qi, F. Experimental optimization for dual support structures cone flow meters based on cone wake flow field characteristics. Sens. Actuator A Phys. 2015, 232, 115–131. [Google Scholar] [CrossRef]
- Blocken, B.; Gualtieri, C. Ten iterative steps for model development and evaluation applied to Computational Fluid Dynamics for environmental fluid mechanics. Environ. Model. Softw. 2012, 33, 1–22. [Google Scholar] [CrossRef]
- Bonakdari, H.; Zinatizadeh, A.A. Influence of position and type of Doppler flow meters on flow-rate measurement in sewers using computational fluid dynamic. Flow Meas. Instrum. 2011, 22, 225–234. [Google Scholar] [CrossRef]
- Singh, R.K.; Singh, S.N.; Seshadri, V. Study on the effect of vertex angle and upstream swirl on the performance characteristics of cone flowmeter using CFD. Flow Meas. Instrum. 2009, 20, 69–74. [Google Scholar] [CrossRef]
- Tang, P.; Juárez, J.M.; Li, H. Investigation on the effect of structural parameters on cavitation characteristics for the Venturi tube using the CFD method. Water 2019, 11, 2194. [Google Scholar] [CrossRef]
- Zheng, D.; Zhang, P.; Xu, T. Study of acoustic transducer protrusion and recess effects on ultrasonic flowmeter measurement by numerical simulation. Flow Meas. Instrum. 2011, 22, 488–493. [Google Scholar] [CrossRef]
- Qin, L.; Hu, L.; Mao, K.; Chen, W.; Fu, X. Flow profile identification with multipath transducers. Flow Meas. Instrum. 2016, 52, 148–156. [Google Scholar] [CrossRef]
- Palau, C.V.; do Bomfim, G.V.; de Azevedo, B.M.; Peralta, I.B. Numerical study of upstream disturbances on the performance of electromagnetic and ultrasonic flowmeters. Sci. Agric. (Piracicaba, Braz.) 2019, 77, 1–8. [Google Scholar] [CrossRef]
- Ribeiro, A.S.; Loureiro, D.; Martins, L.; Sousa, J.A.; Batista, E.; Dias, L.; Soares, A.C. Measurement uncertainty of turbine flow meter calibration used in conformity assessment for water management. J. Phys. Conf. Ser. 2018, 1065, 092006. [Google Scholar] [CrossRef]
- Simão, M.; Besharat, M.; Carravetta, A.; Ramos, H.M. Flow velocity distribution towards flowmeter accuracy: CFD, UDV, and field tests. Water 2018, 10, 1807. [Google Scholar] [CrossRef]
- Moosa, M.; Hekmat, M.H. Numerical investigation of turbulence characteristics and upstream disturbance of flow through standard and multi-hole orifice flowmeters. Flow Meas. Instrum. 2019, 65, 203–218. [Google Scholar] [CrossRef]
- Borkar, K.; Venugopal, A.; Prabhu, S.V. Pressure measurement technique and installation effects on the performance of wafer cone design. Flow Meas. Instrum. 2013, 30, 52–59. [Google Scholar] [CrossRef]
- Weissenbrunner, A.; Fiebach, A.; Schmelter, S.; Bär, M.; Thamsen, P.U.; Lederer, T. Simulation-based determination of systematic errors of flow meters due to uncertain inflow conditions. Flow Meas. Instrum. 2016, 52, 25–39. [Google Scholar] [CrossRef]
- Liu, Q.; Ye, J.; Zhang, G.; Lin, Z.; Xu, H.; Jin, H.; Zhu, Z. Study on the metrological performance of a swirlmeter affected by flow regulation with a sleeve valve. Flow Meas. Instrum. 2019, 67, 83–94. [Google Scholar] [CrossRef]
- Zhen, W.; Tao, Z. Computational study of the tangential type turbine flowmeter. Flow Meas. Instrum. 2008, 19, 233–239. [Google Scholar] [CrossRef]
- Mu, Y.; Liu, M.; Ma, Z. Research on the measuring characteristics of a new design butterfly valve flowmeter. Flow Meas. Instrum. 2019, 70, 101651. [Google Scholar] [CrossRef]
- Mignot, E.; Bonakdari, H.; Knothe, P.; Lipeme Kouyi, G.; Bessette, A.; Rivière, N.; Bertrand-Krajewski, J.-L. Experiments and 3D simulations of flow structures in junctions and their influence on location of flowmeters. Water Sci. Technol. 2012, 66, 1325–1332. [Google Scholar] [CrossRef]
- Saboohi, Z.; Sorkhkhah, S.; Shakeri, H. Developing a model for prediction of helical turbine flowmeter performance using CFD. Flow Meas. Instrum. 2015, 42, 47–57. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Education Ltd: Harlow, UK, 2007; ISBN 978-0-13-127498-3. [Google Scholar]
- ISO 4064-2. Water Meters for Cold Potable Water and Hot Water—Part 2: Test Methods; ISO: Geneva, Switzerland, 2014. [Google Scholar]
- Tsukamoto, H.; Hutton, S.P. Theoretical prediction of meter factor for a helical turbine flowmeter. In Proceedings of the Conference on Fluid Control and Measurement, Tokyo, Japan, 2–5 September 1985. [Google Scholar]
- Wallis, R.A. Axial Flow Fans; Academic Press: New York, NY, USA, 1961; ISBN 978-1-4832-2784-9. [Google Scholar]
- Augusto, P.E.D.; Cristianini, M. Using Computational Fluid Dynamics (CFD) for evaluation of fluid flow through a gate valve. Int. J. Food Eng. 2012, 8, 1–11. [Google Scholar] [CrossRef]
- Corbera, S.; Olazagoitia, J.L.; Lozano, J.A. Multi-objective global optimization of a butterfly valve using genetic algorithms. ISA Trans. 2016, 63, 401–412. [Google Scholar] [CrossRef]
- Azad, A.; Baranwal, D.; Arya, R.; Diwakar, N. Flow analysis of butterfly valve using CFD. Int. J. Mod. Eng. Res. Technol. 2014, 4, 50–56. [Google Scholar]
- Dawy, A.; Sharara, A.; Hassan, A. A numerical investigation of the incompressible flow through a butterfly valve using CFD. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 1–7. [Google Scholar]
- Toro, A.D.; Johnson, M.C.; Spall, R.E. Computational fluid dynamics investigation of butterfly valve performance factors. J. Am. Water Works Assoc. 2015, 107, E243–E254. [Google Scholar] [CrossRef]
- Li, S.; Zhu, L.; Wang, W.; Xiao, K.; Xu, X.; Zhang, B. Analysis of Thermal-Fluid-Structure Coupling and Resonance Forecast for Link Butterfly Valve Under Small Opening. J. Shanghai Jiaotong Univ. (Sci.) 2019, 24, 341–350. [Google Scholar] [CrossRef]
- Lin, Z.; Ma, G.; Cui, B.; Li, Y.; Zhu, Z.; Tong, N. Influence of flashboard location on flow resistance properties and internal features of gate valve under the variable condition. J. Nat. Gas Sci. Eng. 2016, 33, 108–117. [Google Scholar] [CrossRef]




| Cases Studied | ||||||
|---|---|---|---|---|---|---|
| Configuration | Reference | Gate Valve | Butterfly Valve | |||
| Opening degree | - | 75% closed | 50% closed | 25% closed | open | 30° closed |
| Distance | - | 0D, 3D | 0D, 3D | 0D, 3D | 3D | 3D |
| Boundary conditions | ||||||
| Input velocity (m s−1) | 1, 2, 3, 4, 6 | 1, 2, 3, 4, 6 | 1, 2, 3, 4, 6 | 1, 2, 3, 4, 6 | 1, 2, 3, 4, 6 | 1, 2, 3, 4, 6 |
| Outlet pressure (bar) | 3 | 3 | 3 | 3 | 3 | 3 |
| Wall condition k (mm) | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Symmetry wall | yes | yes | yes | yes | no | no |
| Degree Closure | Variable | Distance to Woltman Meter (0D) | Distance to Woltman Meter (3D) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 75% | Flow (m3 h−1) | 17.35 | 34.70 | 52.10 | 69.40 | 104.10 | 17.5 | 35.1 | 52.67 | 70.21 | 105.3 |
| ωdeveloped (rad s−1) | 24.27 | 48.57 | 72.85 | 97.13 | 145.69 | 24.6 | 49.1 | 73.69 | 98.24 | 147.4 | |
| ωdistorted (rad s−1) | 34.55 | 69.86 | 105.45 | 141.01 | 212.20 | 25.1 | 50.4 | 75.03 | 100.6 | 149.9 | |
| Error (%) | 42.36 | 43.83 | 44.75 | 45.18 | 45.65 | 1.66 | 2.56 | 1.82 | 2.4 | 1.72 | |
| 50% | Flow (m3 h−1) | 17.27 | 34.55 | 51.83 | 69.11 | 103.66 | - | - | - | - | - |
| ωdeveloped (rad s−1) | 24.17 | 48.34 | 72.52 | 96.69 | 145.04 | - | - | - | - | - | |
| ωdistorted (rad s−1) | 24.56 | 49.26 | 73.88 | 98.54 | 147.83 | - | - | - | - | - | |
| Error (%) | 1.63 | 1.90 | 1.87 | 1.91 | 1.92 | - | - | - | - | - | |
| 25% | Flow (m3 h−1) | 17.33 | 34.68 | 52.02 | 69.36 | 104.04 | - | - | - | - | - |
| ωdeveloped (rad s−1) | 24.25 | 48.53 | 72.79 | 97.05 | 145.58 | - | - | - | - | - | |
| ωdistorted (rad s−1) | 24.05 | 48.15 | 72.21 | 96.25 | 144.40 | - | - | - | - | - | |
| Error (%) | −0.82 | −0.78 | −0.80 | −0.83 | −0.81 | - | - | - | - | - | |
| Variable | Open | Closed 30° | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Flow (m3 h−1) | 17.51 | 35.30 | 52.70 | 70.45 | 105.33 | 17.50 | 35.15 | 52.00 | 70.32 | 104.85 |
| ωdeveloped (rad s−1) | 24.60 | 49.08 | 73.50 | 98.10 | 147.38 | 24.55 | 49.30 | 73.80 | 98.45 | 147.80 |
| ωdistorted (rad s−1) | 24.40 | 48.90 | 73.05 | 97.70 | 146.85 | 24.30 | 49.10 | 73.50 | 98.20 | 147.15 |
| Error (%) | −0.81 | −0.37 | −0.61 | −0.41 | −0.36 | −1.02 | −0.41 | −0.41 | −0.25 | −0.44 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palau, C.V.; Balbastre, I.; Manzano, J.; Azevedo, B.M.; Bomfim, G.V. Numerical Analysis of Woltman Meter Accuracy under Flow Perturbations. Water 2019, 11, 2622. https://doi.org/10.3390/w11122622
Palau CV, Balbastre I, Manzano J, Azevedo BM, Bomfim GV. Numerical Analysis of Woltman Meter Accuracy under Flow Perturbations. Water. 2019; 11(12):2622. https://doi.org/10.3390/w11122622
Chicago/Turabian StylePalau, Carmen V., Iban Balbastre, Juan Manzano, Benito M. Azevedo, and Guilherme V. Bomfim. 2019. "Numerical Analysis of Woltman Meter Accuracy under Flow Perturbations" Water 11, no. 12: 2622. https://doi.org/10.3390/w11122622
APA StylePalau, C. V., Balbastre, I., Manzano, J., Azevedo, B. M., & Bomfim, G. V. (2019). Numerical Analysis of Woltman Meter Accuracy under Flow Perturbations. Water, 11(12), 2622. https://doi.org/10.3390/w11122622





