Likely and High-End Impacts of Regional Sea-Level Rise on the Shoreline Change of European Sandy Coasts Under a High Greenhouse Gas Emissions Scenario
Abstract
1. Introduction
2. Materials and Methods
2.1. Regional Sea-Level Rise
2.1.1. Sterodynamic Sea-Level Change ()
2.1.2. Barystatic-GRD Induced Sea-Level Change ()
2.1.3. GIA-Induced Relative Sea-Level Change ()
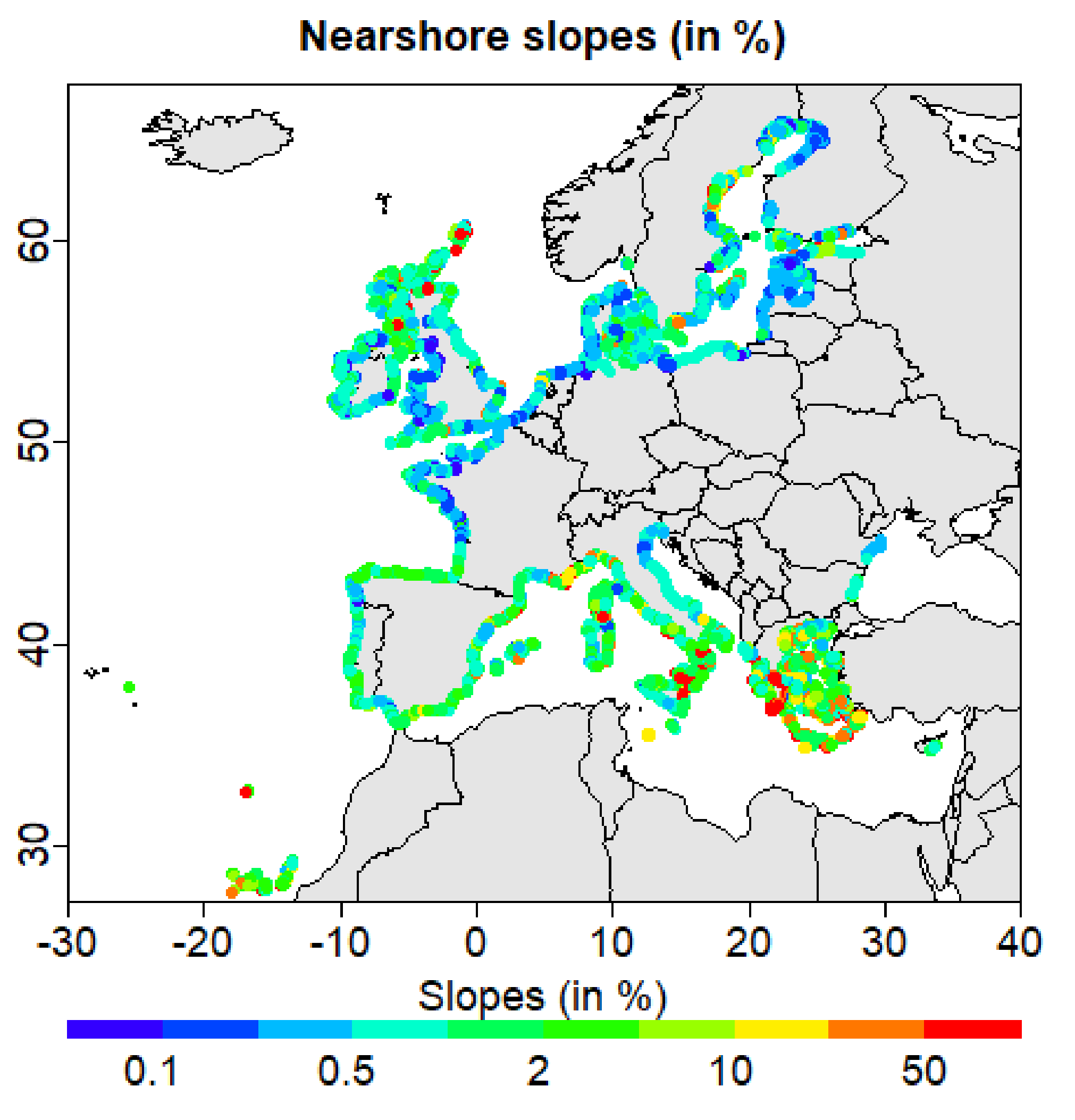
2.2. Shoreline Changes
2.2.1. The EUROSION Database
2.2.2. Shoreline Changes Induced by Sea-Level Rise
3. Approach for the Assessment of High-End Coastal Impacts
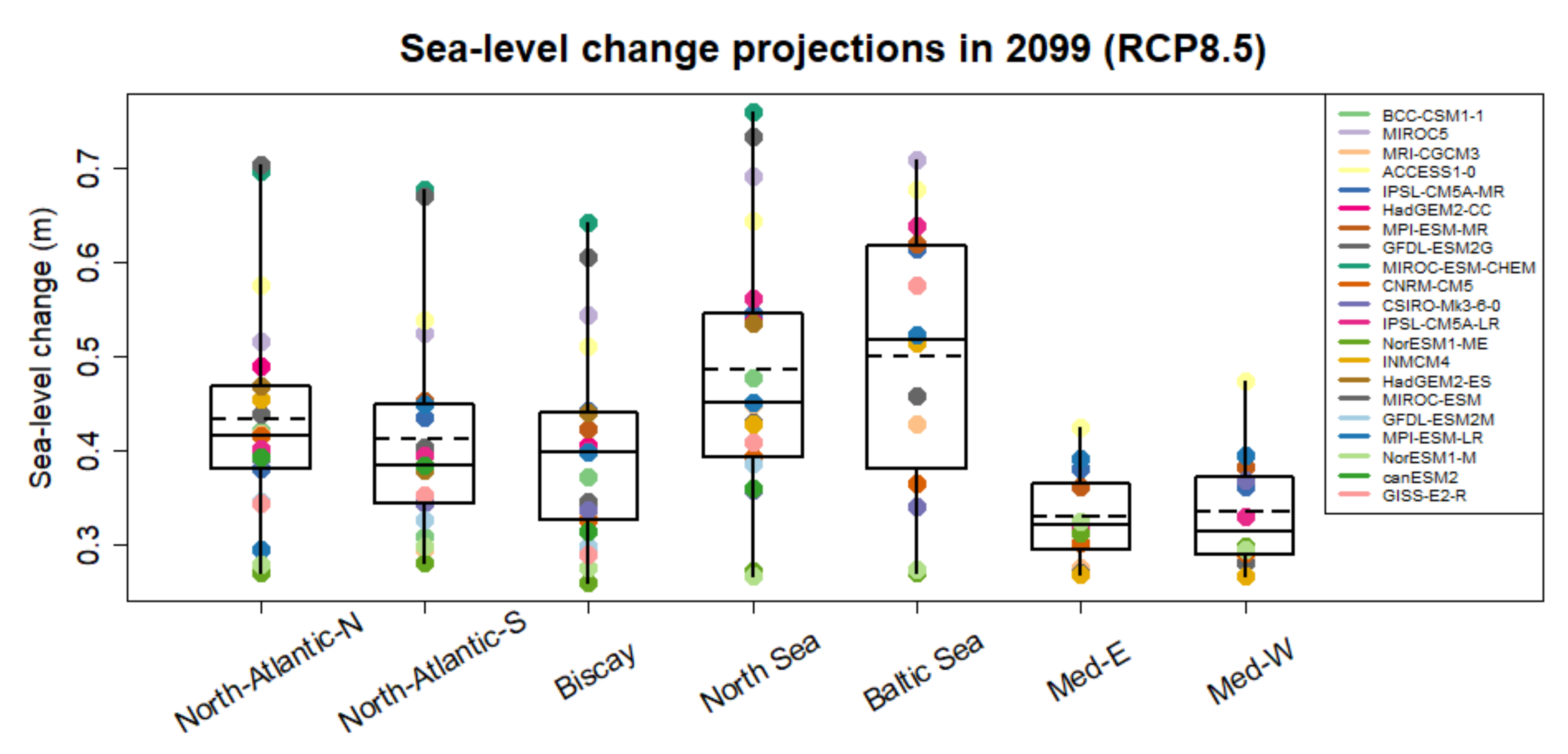
3.1. Sterodynamic Component: CMIP5 Model Selection and High-End Definition
3.2. Barystatic-GRD Components
4. Results
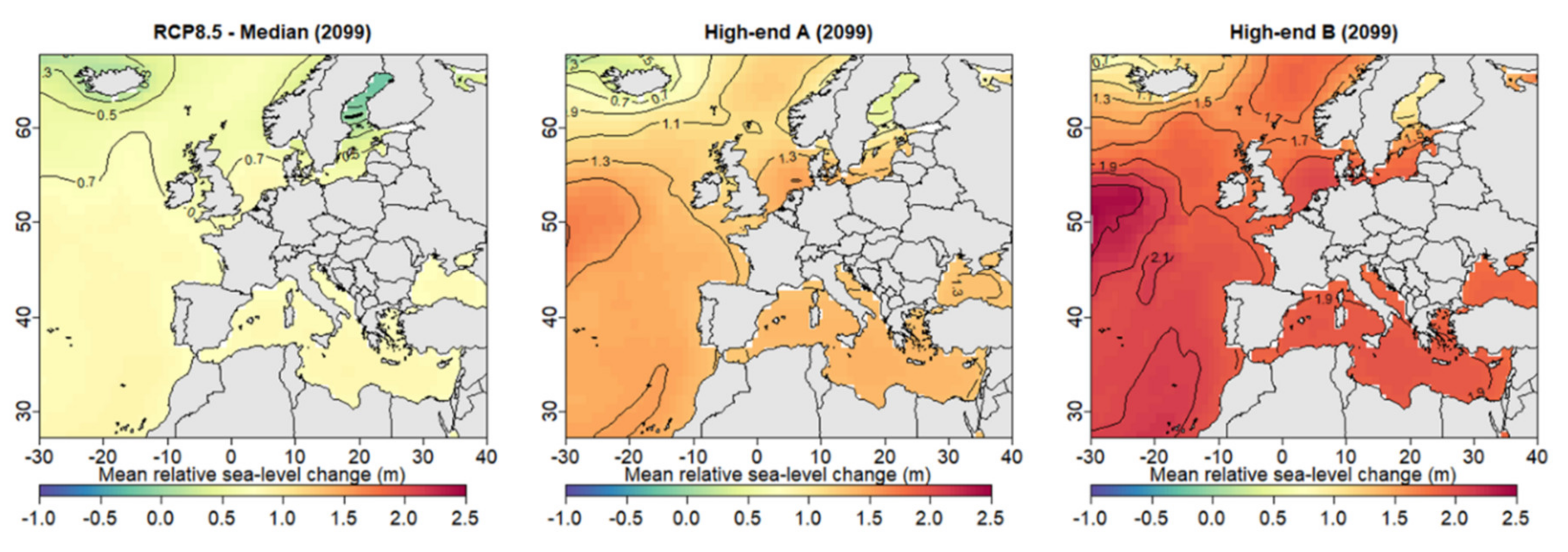
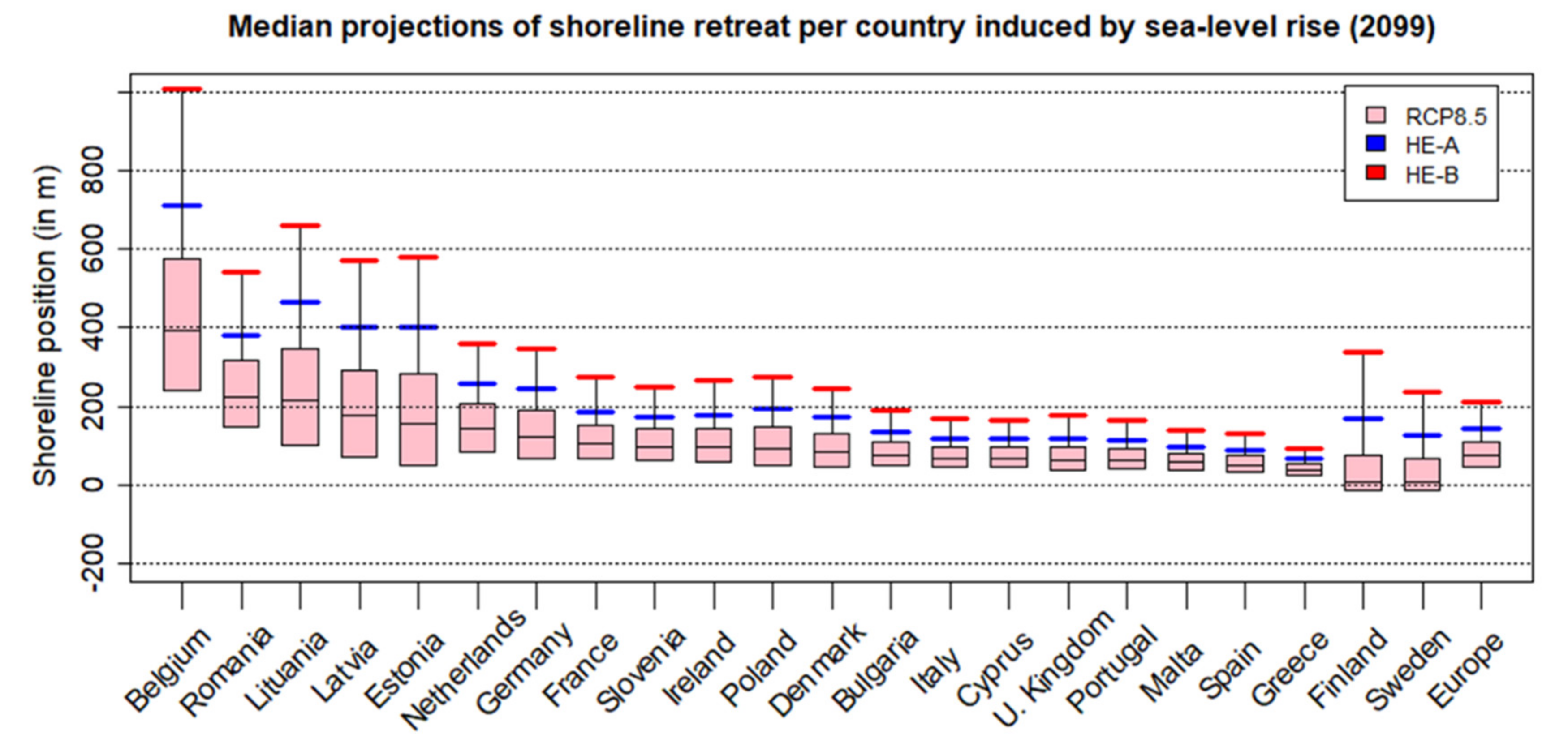
4.1. Shoreline Changes at the European Scale
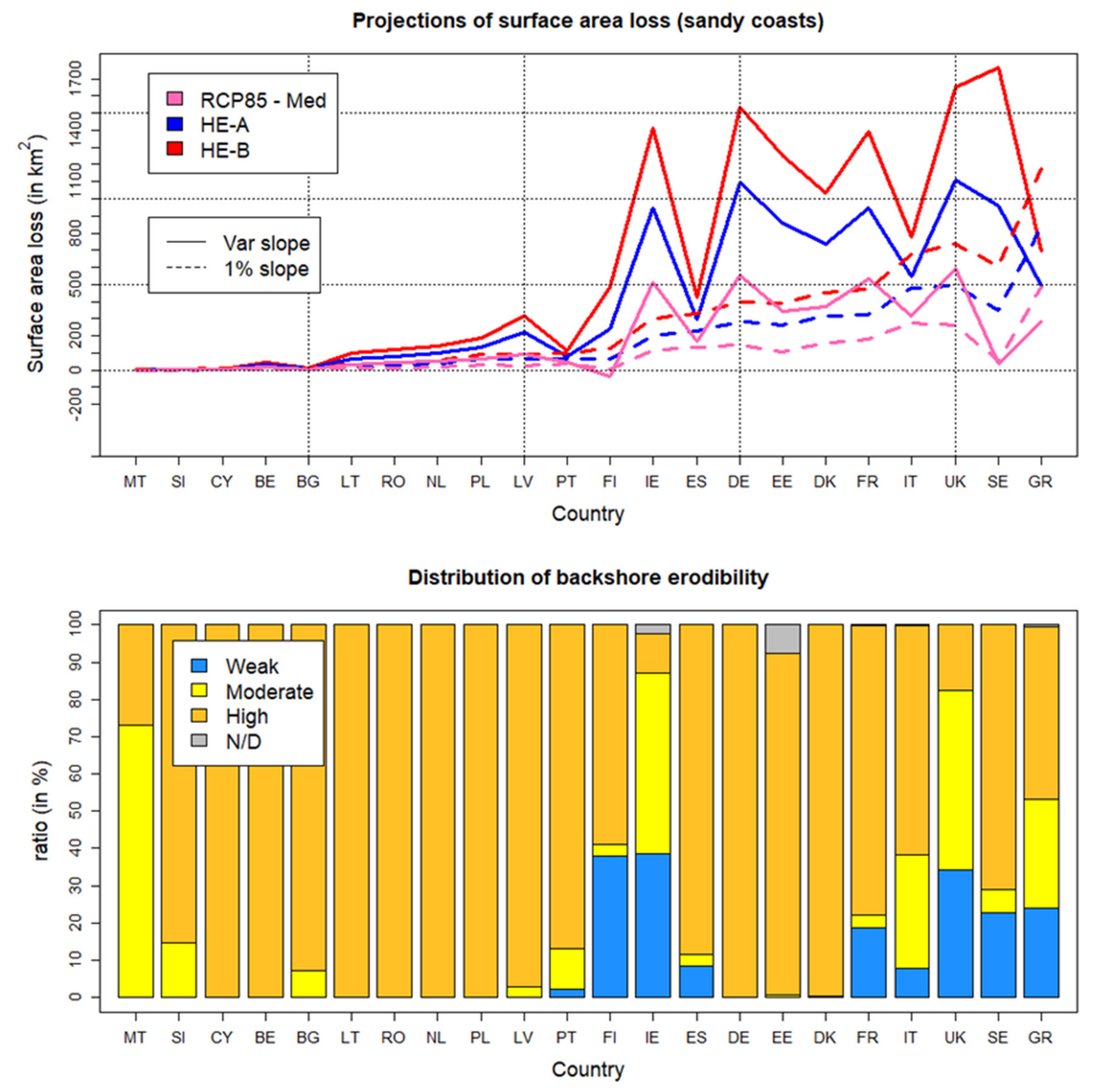
4.2. Shoreline Changes at Country Scale
5. Discussion and Conclusions
- The magnitude and regional distribution of SLR-induced shoreline change projections by 2100 utterly depend on the nearshore slope, the regional distribution of sea-level changes (i.e., hence the various regional contributions) and the trajectory of the future scenario.
- Ignoring the variability of nearshore slopes and assuming a 1% constant uniform nearshore slope instead may lead to a substantial underestimation of SLR-induced shoreline retreat and beach area removal (reduction by 50%) in Europe. In the absence of any coastal adaptation measure, and assuming an infinite erosion potential of each EUROSION segment, we found that Europe is projected to accumulate a land loss area of 4040 km2, 8950 km2, and 13,470 km2 for the RCP8.5 median, High-end A and High-end B scenarios, respectively.
- The sequencing of countries with respect to their exposure to future shoreline retreat varies very importantly with scenarios. In particular, in Northern Europe, the impacts of high-end sea-level scenarios are disproportionately high compared to those of likely scenarios and to those of the Mediterranean area. This is because the softer the nearshore slope, the more sensitive to sea-level changes in the shoreline. Subsequently, large uncertainties in future regional sea-level changes affect primarily coastal regions with gentle nearshore slopes. This results in substantial changes in the ranking of coastal impacts and adaptation needs in Europe, which may be relevant to consider in adaptation finance mechanisms.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Definition of European Main Basins

References
- Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.M.; Jevrejeva, S.; Levermann, A.; Merrifield, M.A.; Milne, G.A.; Nerem, R.S.; Nunn, P.D.; et al. Sea Level Change. In Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- IPCC. IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; Pörtner, H.-O., Roberts, D.C., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Nicolai, M., Okem, A., Petzold, J., et al., Eds.; IPCC: Geneva, Switzerland, 2019. [Google Scholar]
- Nicholls, R.J.; Cazenave, A. Sea-Level Rise and Its Impact on Coastal Zones. Science 2010, 328, 1517–1520. [Google Scholar] [CrossRef]
- Slangen, A.B.A.; Church, J.A.; Agosta, C.; Fettweis, X.; Marzeion, B.; Richter, K. Anthropogenic forcing dominates global mean sea-level rise since 1970. Nat. Clim. Change 2016, 6, 701. [Google Scholar] [CrossRef]
- Cazenave, A.; Meyssignac, B.; Ablain, M.; Balmaseda, M.; Bamber, J.; Barletta, V.; Beckley, B.; Benveniste, J.; Berthier, E.; Blazquez, A.; et al. Global sea-level budget 1993-present. Earth Syst. Sci. Data 2018, 10, 1551–1590. [Google Scholar] [CrossRef]
- Chen, X.Y.; Zhang, X.B.; Church, J.A.; Watson, C.S.; King, M.A.; Monselesan, D.; Legresy, B.; Harig, C. The increasing rate of global mean sea-level rise during 1993–2014. Nat. Clim. Change 2017, 7, 492. [Google Scholar] [CrossRef]
- Dieng, H.B.; Cazenave, A.; Meyssignac, B.; Ablain, M. New estimate of the current rate of sea level rise from a sea level budget approach. Geophys. Res. Lett. 2017, 44, 3744–3751. [Google Scholar] [CrossRef]
- DeConto, R.M.; Pollard, D. Contribution of Antarctica to past and future sea-level rise. Nature 2016, 531, 591–597. [Google Scholar] [CrossRef]
- Edwards, T.L.; Brandon, M.A.; Durand, G.; Edwards, N.R.; Golledge, N.R.; Holden, P.B.; Nias, I.J.; Payne, A.J.; Ritz, C.; Wernecke, A. Revisiting Antarctic ice loss due to marine ice-cliff instability. Nature 2019, 566, 58. [Google Scholar] [CrossRef]
- Golledge, N.R.; Kowalewski, D.E.; Naish, T.R.; Levy, R.H.; Fogwill, C.J.; Gasson, E.G.W. The multi-millennial Antarctic commitment to future sea-level rise. Nature 2015, 526, 421. [Google Scholar] [CrossRef]
- Ritz, C.; Edwards, T.L.; Durand, G.; Payne, A.J.; Peyaud, V.; Hindmarsh, R.C.A. Potential sea-level rise from Antarctic ice-sheet instability constrained by observations. Nature 2015, 528, 115. [Google Scholar] [CrossRef]
- Meyssignac, B.; Cazenave, A. Sea level: A review of present-day and recent-past changes and variability. J. Geodyn. 2012, 58, 96–109. [Google Scholar] [CrossRef]
- Little, C.M.; Horton, R.M.; Kopp, R.E.; Oppenheimer, M.; Yip, S. Uncertainty in Twenty-First-Century CMIP5 Sea Level Projections. J. Clim. 2015, 28, 838–852. [Google Scholar] [CrossRef]
- Mitrovica, J.X.; Tamisiea, M.E.; Davis, J.L.; Milne, G.A. Recent mass balance of polar ice sheets inferred from patterns of global sea-level change. Nature 2001, 409, 1026–1029. [Google Scholar] [CrossRef]
- Peltier, W.R.; Tushingham, A.M. Influence of glacial isostatic adjustment on tide gauge measurements of secular sea level change. J. Geophys. Res. Solid Earth 1991, 96, 6779–6796. [Google Scholar] [CrossRef]
- Zhang, X.B.; Church, J.A.; Monselesan, D.; McInnes, K.L. Sea level projections for the Australian region in the 21st century. Geophys. Res. Lett. 2017, 44, 8481–8491. [Google Scholar] [CrossRef]
- Poitevin, C.; Woppelmann, G.; Raucoules, D.; Le Cozannet, G.; Marcos, M.; Testut, L. Vertical land motion and relative sea level changes along the coastline of Brest (France) from combined space-borne geodetic methods. Remote Sens. Environ. 2019, 222, 275–285. [Google Scholar] [CrossRef]
- Woppelmann, G.; Marcos, M. Coastal sea level rise in southern Europe and the nonclimate contribution of vertical land motion. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.M.; Jevrejeva, S.; Levermann, A.; Merrifield, M.A.; Milne, G.A.; Nerem, R.S.; Nunn, P.D.; et al. Sea-Level Rise by 2100. Science 2013, 342, 1445. [Google Scholar] [CrossRef]
- Stephens, A.S.; Bell, G.R.; Lawrence, J. Applying Principles of Uncertainty within Coastal Hazard Assessments to Better Support Coastal Adaptation. J. Mar. Sci. Eng. 2017, 5, 40. [Google Scholar] [CrossRef]
- Bakker, A.M.R.; Louchard, D.; Keller, K. Sources and implications of deep uncertainties surrounding sea-level projections. Clim. Change 2017, 140, 339–347. [Google Scholar] [CrossRef]
- Kopp, R.E.; DeConto, R.M.; Bader, D.A.; Hay, C.C.; Horton, R.M.; Kulp, S.; Oppenheimer, M.; Pollard, D.; Strauss, B.H. Evolving Understanding of Antarctic Ice-Sheet Physics and Ambiguity in Probabilistic Sea-Level Projections. Earths Future 2017, 5, 1217–1233. [Google Scholar] [CrossRef]
- Le Cozannet, G.; Manceau, J.C.; Rohmer, J. Bounding probabilistic sea-level projections within the framework of the possibility theory. Environ. Res. Lett. 2017, 12, 014012. [Google Scholar] [CrossRef]
- Le Cozannet, G.; Nicholls, R.J.; Hinkel, J.; Sweet, W.V.; McInnes, K.L.; Van de Wal, R.S.W.; Slangen, A.B.A.; Lowe, J.A.; White, K.D. Sea Level Change and Coastal Climate Services: The Way Forward. J. Mar. Sci. Eng. 2017, 5, 49. [Google Scholar] [CrossRef]
- Brasseur, G.P.; Gallardo, L. Climate services: Lessons learned and future prospects. Earths Future 2016, 4, 79–89. [Google Scholar] [CrossRef]
- Hinkel, J.; Church, J.A.; Gregory, J.M.; Lambert, E.; Le Cozannet, G.; Lowe, J.; McInnes, K.L.; Nicholls, R.J.; van der Pol, T.D.; van de Wal, R. Meeting User Needs for Sea Level Rise Information: A Decision Analysis Perspective. Earths Future 2019, 7, 320–337. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Hanson, S.E.; Lowe, J.A.; Warrick, R.A.; Lu, X.F.; Long, A.J. Sea-level scenarios for evaluating coastal impacts. Wiley Interdiscip. Rev. Clim. Change 2014, 5, 129–150. [Google Scholar] [CrossRef]
- Stammer, D.; van de Wal, R.S.W.; Nicholls, R.J.; Church, J.A.; Le Cozannet, G.; Lowe, J.A.; Horton, B.P.; White, K.; Behar, D.; Hinkel, J. Framework for high-end estimates of sea-level rise for stakeholder applications. Earths Future 2019, 7. [Google Scholar] [CrossRef]
- Le Bars, D. Uncertainty in Sea Level Rise Projections Due to the Dependence Between Contributors. Earths Future 2018, 6, 1275–1291. [Google Scholar] [CrossRef]
- Hinkel, J.; Jaeger, C.; Nicholls, R.J.; Lowe, J.; Renn, O.; Shi, P.J. Sea-level rise scenarios and coastal risk management. Nat. Clim. Change 2015, 5, 188–190. [Google Scholar] [CrossRef]
- Rohmer, J.; Le Cozannet, G.; Manceau, J.-C. Addressing ambiguity in probabilistic assessments of future coastal flooding using possibility distributions. Clim. Change 2019, 155, 95–109. [Google Scholar] [CrossRef]
- Hinkel, J.; Lincke, D.; Vafeidis, A.T.; Perrette, M.; Nicholls, R.J.; Tol, R.S.J.; Marzeion, B.; Fettweis, X.; Ionescu, C.; Levermann, A. Coastal flood damage and adaptation costs under 21st century sea-level rise. Proc. Natl. Acad. Sci. USA 2014, 111, 3292–3297. [Google Scholar] [CrossRef]
- Hinkel, J.; van Vuuren, D.P.; Nicholls, R.J.; Klein, R.J.T. The effects of adaptation and mitigation on coastal flood impacts during the 21st century. An application of the DIVA and IMAGE models. Clim. Change 2013, 117, 783–794. [Google Scholar] [CrossRef]
- Grinsted, A.; Jevrejeva, S.; Riva, R.E.M.; Dahl-Jensen, D. Sea level rise projections for northern Europe under RCP8.5. Clim. Res. 2015, 64, 15–23. [Google Scholar] [CrossRef]
- Howard, T.; Pardaens, A.K.; Bamber, J.L.; Ridley, J.; Spada, G.; Hurkmans, R.T.W.L.; Lowe, J.A.; Vaughan, D. Sources of 21st century regional sea-level rise along the coast of northwest Europe. Ocean Sci. 2014, 10, 473–483. [Google Scholar] [CrossRef]
- Katsman, C.A.; Sterl, A.; Beersma, J.J.; van den Brink, H.W.; Church, J.A.; Hazeleger, W.; Kopp, R.E.; Kroon, D.; Kwadijk, J.; Lammersen, R.; et al. Exploring high-end scenarios for local sea level rise to develop flood protection strategies for a low-lying delta—The Netherlands as an example. Clim. Change 2011, 109, 617–645. [Google Scholar] [CrossRef]
- Jiménez, J.A.; Valdemoro, H.I.; Bosom, E.; Sánchez-Arcilla, A.; Nicholls, R.J. Impacts of sea-level rise-induced erosion on the Catalan coast. Reg. Environ. Change 2017, 17, 593–603. [Google Scholar] [CrossRef]
- Toimil, A.; Losada, I.J.; Camus, P.; Díaz-Simal, P. Managing coastal erosion under climate change at the regional scale. Coast. Eng. 2017, 128, 106–122. [Google Scholar] [CrossRef]
- Enríquez, A.R.; Marcos, M.; Álvarez-Ellacuría, A.; Orfila, A.; Gomis, D. Changes in beach shoreline due to sea level rise and waves under climate change scenarios: Application to the Balearic Islands (western Mediterranean). Nat. Hazards Earth Syst. Sci. 2017, 17, 1075–1089. [Google Scholar] [CrossRef]
- Allenbach, K.; Garonna, I.; Herold, C.; Monioudi, I.; Giuliani, G.; Lehmann, A.; Velegrakis, A.F. Black Sea beaches vulnerability to sea level rise. Environ. Sci. Policy 2015, 46, 95–109. [Google Scholar] [CrossRef]
- Stive, M.J.F. How Important is Global Warming for Coastal Erosion? Clim. Change 2004, 64, 27–39. [Google Scholar] [CrossRef]
- Le Cozannet, G.; Garcin, M.; Yates, M.; Idier, D.; Meyssignac, B. Approaches to evaluate the recent impacts of sea-level rise on shoreline changes. Earth Sci. Rev. 2014, 138, 47–60. [Google Scholar] [CrossRef]
- Luijendijk, A.; Hagenaars, G.; Ranasinghe, R.; Baart, F.; Donchyts, G.; Aarninkhof, S. The State of the World’s Beaches. Sci. Rep. 2018, 8, 6641. [Google Scholar] [CrossRef]
- Mentaschi, L.; Vousdoukas, M.I.; Pekel, J.-F.; Voukouvalas, E.; Feyen, L. Global long-term observations of coastal erosion and accretion. Sci. Rep. 2018, 8, 12876. [Google Scholar] [CrossRef]
- Yates, M.L.; Guza, R.T.; O’Reilly, W.C. Equilibrium shoreline response: Observations and modeling. J. Geophys. Res. Ocean. 2009, 114. [Google Scholar] [CrossRef]
- Robinet, A.; Idier, D.; Castelle, B.; Marieu, V. A reduced-complexity shoreline change model combining longshore and cross-shore processes: The LX-Shore model. Environ. Model. Softw. 2018, 109, 1–16. [Google Scholar] [CrossRef]
- Splinter, K.D.; Turner, I.L.; Davidson, M.A.; Barnard, P.; Castelle, B.; Oltman-Shay, J. A generalized equilibrium model for predicting daily to interannual shoreline response. J. Geophys. Res. Earth Surf. 2014, 119, 1936–1958. [Google Scholar] [CrossRef]
- Ranasinghe, R. Assessing climate change impacts on open sandy coasts: A review. Earth Sci. Rev. 2016, 160, 320–332. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Mentaschi, L.; Voukouvalas, E.; Verlaan, M.; Feyen, L. Extreme sea levels on the rise along Europe’s coasts. Earths Future 2017, 5, 304–323. [Google Scholar] [CrossRef]
- Ranger, N.; Reeder, T.; Lowe, J. Addressing ‘deep’ uncertainty over long-term climate in major infrastructure projects: Four innovations of the Thames Estuary 2100 Project. EURO J. Decis. Process. 2013, 1, 233–262. [Google Scholar] [CrossRef]
- Haasnoot, M.; Kwakkel, J.H.; Walker, W.E.; ter Maat, J. Dynamic adaptive policy pathways: A method for crafting robust decisions for a deeply uncertain world. Glob. Environ. Change 2013, 23, 485–498. [Google Scholar] [CrossRef]
- Athanasiou, P.; van Dongeren, A.; Giardino, A.; Vousdoukas, M.; Gaytan-Aguilar, S.; Ranasinghe, R. Global distribution of nearshore slopes with implications for coastal retreat. Earth Syst. Sci. Data 2019, 11, 1515–1529. [Google Scholar] [CrossRef]
- Gregory, J.M.; Griffies, S.M.; Hughes, C.W.; Lowe, J.A.; Church, J.A.; Fukimori, I.; Gomez, N.; Kopp, R.E.; Landerer, F.; Le Cozannet, G.; et al. Concepts and Terminology for Sea Level: Mean, Variability and Change, Both Local and Global. Surv. Geophys. 2019, 1–39. [Google Scholar] [CrossRef]
- Carson, M.; Kohl, A.; Stammer, D.; Slangen, A.B.A.; Katsman, C.A.; van de Wal, R.S.W.; Church, J.; White, N. Coastal sea level changes, observed and projected during the 20th and 21st century. Clim. Change 2016, 134, 269–281. [Google Scholar] [CrossRef]
- Meyssignac, B.; Slangen, A.B.A.; Melet, A.; Church, J.A.; Fettweis, X.; Marzeion, B.; Agosta, C.; Ligtenberg, S.R.M.; Spada, G.; Richter, K.; et al. Evaluating Model Simulations of Twentieth-Century Sea-Level Rise. Part II: Regional Sea-Level Changes. J. Clim. 2017, 30, 8565–8593. [Google Scholar] [CrossRef]
- Mitrovica, J.X.; Gomez, N.; Clark, P.U. The sea-level fingerprint of West Antarctic collapse. Science 2009, 323, 753. [Google Scholar] [CrossRef]
- Slangen, A.B.A.; Carson, M.; Katsman, C.A.; van de Wal, R.S.W.; Kohl, A.; Vermeersen, L.L.A.; Stammer, D. Projecting twenty-first century regional sea-level changes. Clim. Change 2014, 124, 317–332. [Google Scholar] [CrossRef]
- Peltier, W.R. Global glacial isostasy and the surface of the ice-age earth: The ice-5G (VM2) model and grace. Annu. Rev. Earth Planet. Sci. 2004, 32, 111–149. [Google Scholar] [CrossRef]
- Lambeck, K.; Johnston, P. The Viscosity of the Mantle: Evidence from Analyses of Glacial-Rebound Phenomena. In The Earth’s Mantle: Composition, Structure, and Evolution; Jackson, I., Ed.; Cambridge University Press: Cambridge, UK, 1998; pp. 461–502. [Google Scholar]
- Vafeidis, A.T.; Nicholls, R.J.; McFadden, L.; Tol, R.S.J.; Hinkel, J.; Spencer, T.; Grashoff, P.S.; Boot, G.; Klein, R.J.T. A New Global Coastal Database for Impact and Vulnerability Analysis to Sea-Level Rise. J. Coast. Res. 2008, 917–924. [Google Scholar] [CrossRef]
- Hinkel, J.; Nicholls, R.; Tol, R.; Wang, Z.; Hamilton, J.; Boot, G.; Vafeidis, A.; McFadden, L.; Ganopolski, A.; Klein, R. A global analysis of erosion of sandy beaches and sea-level rise: An application of DIVA. Glob. Planet. Change 2013, 111, 150–158. [Google Scholar] [CrossRef]
- Hinkel, J.; Klein, R.J.T. Integrating knowledge to assess coastal vulnerability to sea-level rise: The development of the DIVA tool. Glob. Environ. Change 2009, 19, 384–395. [Google Scholar] [CrossRef]
- Yates, M.L.; Le Cozannet, G. Brief communication Evaluating European Coastal Evolution using Bayesian Networks. Nat. Hazards Earth Syst. Sci. 2012, 12, 1173–1177. [Google Scholar] [CrossRef]
- Le Cozannet, G.; Bulteau, T.; Garcin, M.; Garnier, C.; Muller, H.; Hoareau, A.; Mallet, C. Detecting errors in coastal databases using Bayesian Networks. J. Coast. Res. 2016, 75, 1162–1166. [Google Scholar] [CrossRef]
- Bruun, P. Sea-Level Rise as a Cause of Shore Erosion. J. Waterw. Harb. Div. 1962, 88, 117–132. [Google Scholar]
- Cooper, J.A.G.; Pilkey, O.H. Sea-level rise and shoreline retreat: Time to abandon the Bruun Rule. Glob. Planet. Change 2004, 43, 157–171. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Stive, M.J.F. Rising seas and retreating coastlines. Clim. Change 2009, 97, 465. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Callaghan, D.; Stive, M.J.F. Estimating coastal recession due to sea level rise: Beyond the Bruun rule. Clim. Change 2012, 110, 561–574. [Google Scholar] [CrossRef]
- Zhang, K.; Douglas, B.C.; Leatherman, S.P. Global Warming and Coastal Erosion. Clim. Change 2004, 64, 41. [Google Scholar] [CrossRef]
- Nicholls, R.J. Assessing erosion of sandy beaches due to sea-level rise. Geol. Soc. Lond. Eng. Geol. Spec. Publ. 1998, 15, 71. [Google Scholar] [CrossRef]
- Hinkel, J.; Nicholls, R.J.; Vafeidis, A.T.; Tol, R.S.J.; Avagianou, T. Assessing risk of and adaptation to sea-level rise in the European Union: An application of DIVA. Mitig. Adapt. Strateg. Glob. Change 2010, 15, 703–719. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Grinsted, A.; Moore, J.C. Upper limit for sea level projections by 2100. Environ. Res. Lett. 2014, 7, 104008. [Google Scholar] [CrossRef]
- Bamber, J.L.; Oppenheimer, M.; Kopp, R.E.; Aspinall, W.P.; Cooke, R.M. Ice sheet contributions to future sea-level rise from structured expert judgment. Proc. Natl. Acad. Sci. USA 2019, 116, 11195. [Google Scholar] [CrossRef]
- Horton, B.P.; Rahmstorf, S.; Engelhart, S.E.; Kemp, A.C. Expert assessment of sea-level rise by AD 2100 and AD 2300. Quat. Sci. Rev. 2014, 84, 1–6. [Google Scholar] [CrossRef]
- Jackson, L.P.; Jevrejeva, S. A probabilistic approach to 21st century regional sea-level projections using RCP and High-end scenarios. Glob. Planet. Change 2016, 146, 179–189. [Google Scholar] [CrossRef]
- Le Cozannet, G.; Thiéblemont, R.; Rohmer, J.; Idier, D.; Manceau, J.-C.; Quique, R. Low-End Probabilistic Sea-Level Projections. Water 2019, 11, 1507. [Google Scholar] [CrossRef]
- Landerer, F.W.; Gleckler, P.J.; Lee, T. Evaluation of CMIP5 dynamic sea surface height multi-model simulations against satellite observations. Clim. Dyn. 2014, 43, 1271–1283. [Google Scholar] [CrossRef]
- Marcos, M.; Tsimplis, M.N. Coastal sea level trends in Southern Europe. Geophys. J. Int. 2008, 175, 70–82. [Google Scholar] [CrossRef]
- Slangen, A.B.A.; Adloff, F.; Jevrejeva, S.; Leclercq, P.W.; Marzeion, B.; Wada, Y.; Winkelmann, R. A Review of Recent Updates of Sea-Level Projections at Global and Regional Scales. Surv. Geophys. 2017, 38, 385–406. [Google Scholar] [CrossRef]
- Kopp, R.E.; Horton, R.M.; Little, C.M.; Mitrovica, J.X.; Oppenheimer, M.; Rasmussen, D.J.; Strauss, B.H.; Tebaldi, C. Probabilistic 21st and 22nd century sea-level projections at a global network of tide-gauge sites. Earths Future 2014, 2, 383–406. [Google Scholar] [CrossRef]
- Calafat, F.M.; Chambers, D.P.; Tsimplis, M.N. Mechanisms of decadal sea level variability in the eastern North Atlantic and the Mediterranean Sea. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Gräwe, U.; Klingbeil, K.; Kelln, J.; Dangendorf, S. Decomposing Mean Sea Level Rise in a Semi-Enclosed Basin, the Baltic Sea. J. Clim. 2019, 32, 3089–3108. [Google Scholar] [CrossRef]
- Weisse, R.; Hünicke, B. Baltic Sea Level: Past, Present, and Future. In Oxford Research Encyclopedia of Climate Science; Oxford University Press: New York, NY, USA, 2019. [Google Scholar]
- Slangen, A.B.A.; Katsman, C.A.; van de Wal, R.S.W.; Vermeersen, L.L.A.; Riva, R.E.M. Towards regional projections of twenty-first century sea-level change based on IPCC SRES scenarios. Clim. Dyn. 2012, 38, 1191–1209. [Google Scholar] [CrossRef]
- Slangen, A.B.A.; van de Wal, R.S.W. An assessment of uncertainties in using volume-area modelling for computing the twenty-first century glacier contribution to sea-level change. Cryosphere 2011, 5, 673–686. [Google Scholar] [CrossRef]
- Marzeion, B.; Jarosch, A.H.; Hofer, M. Past and future sea-level change from the surface mass balance of glaciers. Cryosphere 2012, 6, 1295–1322. [Google Scholar] [CrossRef]
- Radic, V.; Bliss, A.; Beedlow, A.C.; Hock, R.; Miles, E.; Cogley, J.G. Regional and global projections of twenty-first century glacier mass changes in response to climate scenarios from global climate models. Clim. Dyn. 2014, 42, 37–58. [Google Scholar] [CrossRef]
- Huss, M.; Hock, R. A new model for global glacier change and sea-level rise. Front. Earth Sci. 2015, 3, 54. [Google Scholar] [CrossRef]
- Wada, Y.; van Beek, L.P.H.; Weiland, F.C.S.; Chao, B.F.; Wu, Y.H.; Bierkens, M.F.P. Past and future contribution of global groundwater depletion to sea-level rise. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Lemperiere, F.; Lafitte, R. The role of dams in the XXI Century to achieve a sustainable development target. In Proceedings of the International Symposium on Dams in the Societies of the 21st Century, Barcelona, Spain, 18–23 June 2006; p. 1065. [Google Scholar]
- Wada, Y.; Lo, M.-H.; Yeh, P.J.F.; Reager, J.T.; Famiglietti, J.S.; Wu, R.-J.; Tseng, Y.-H. Fate of water pumped from underground and contributions to sea-level rise. Nat. Clim. Change 2016, 6, 777. [Google Scholar] [CrossRef]
- Furst, J.J.; Goelzer, H.; Huybrechts, P. Ice-dynamic projections of the Greenland ice sheet in response to atmospheric and oceanic warming. Cryosphere 2015, 9, 1039–1062. [Google Scholar] [CrossRef]
- Delhasse, A.; Fettweis, X.; Kittel, C.; Amory, C.; Agosta, C. Brief communication: Impact of the recent atmospheric circulation change in summer on the future surface mass balance of the Greenland Ice Sheet. Cryosphere 2018, 12, 3409–3418. [Google Scholar] [CrossRef]
- Joughin, I.; Smith, B.E.; Medley, B. Marine Ice Sheet Collapse Potentially Under Way for the Thwaites Glacier Basin, West Antarctica. Science 2014, 344, 735. [Google Scholar] [CrossRef]
- Rignot, E.; Mouginot, J.; Morlighem, M.; Seroussi, H.; Scheuchl, B. Widespread, rapid grounding line retreat of Pine Island, Thwaites, Smith, and Kohler glaciers, West Antarctica, from 1992 to 2011. Geophys. Res. Lett. 2014, 41, 3502–3509. [Google Scholar] [CrossRef]
- Frieler, K.; Clark, P.U.; He, F.; Buizert, C.; Reese, R.; Ligtenberg, S.R.M.; van den Broeke, M.R.; Winkelmann, R.; Levermann, A. Consistent evidence of increasing Antarctic accumulation with warming. Nat. Clim. Change 2015, 5, 348. [Google Scholar] [CrossRef]
- Yin, J.J.; Schlesinger, M.E.; Stouffer, R.J. Model projections of rapid sea-level rise on the northeast coast of the United States. Nat. Geosci. 2009, 2, 262–266. [Google Scholar] [CrossRef]
- Yin, J.; Goddard, P.B. Oceanic control of sea level rise patterns along the East Coast of the United States. Geophys. Res. Lett. 2013, 40, 5514–5520. [Google Scholar] [CrossRef]
- Li, F.; van Gelder, P.H.A.J.M.; Ranasinghe, R.; Callaghan, D.P.; Jongejan, R.B. Probabilistic modelling of extreme storms along the Dutch coast. Coast. Eng. 2014, 86, 1–13. [Google Scholar] [CrossRef]
- Wainwright, D.J.; Ranasinghe, R.; Callaghan, D.P.; Woodroffe, C.D.; Jongejan, R.; Dougherty, A.J.; Rogers, K.; Cowell, P.J. Moving from deterministic towards probabilistic coastal hazard and risk assessment: Development of a modelling framework and application to Narrabeen Beach, New South Wales, Australia. Coast. Eng. 2015, 96, 92–99. [Google Scholar] [CrossRef]
- Dastgheib, A.; Jongejan, R.; Wickramanayake, M.; Ranasinghe, R. Regional Scale Risk-Informed Land-Use Planning Using Probabilistic Coastline Recession Modelling and Economical Optimisation: East Coast of Sri Lanka. J. Mar. Sci. Eng. 2018, 6, 120. [Google Scholar] [CrossRef]
- Le Cozannet, G.; Bulteau, T.; Castelle, B.; Ranasinghe, R.; Woppelmann, G.; Rohmer, J.; Bernon, N.; Idier, D.; Louisor, J.; Salas-y-Melia, D. Quantifying uncertainties of sandy shoreline change projections as sea level rises. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef]
- Sunamura, T. Quantitative predictions of beach-face slopes. GSA Bull. 1984, 95, 242–245. [Google Scholar] [CrossRef]
- Bricheno, L.M.; Wolf, J. Future Wave Conditions of Europe, in Response to High-End Climate Change Scenarios. J. Geophys. Res. Ocean. 2018, 123, 8762–8791. [Google Scholar] [CrossRef]
| Geomorphology | Coastline Length (in km) | Coastline Ratio (in %) |
|---|---|---|
| Sandy shore | 34,661 | 26.6 |
| Hard-rock | 35,720 | 27.4 |
| Soft-rock | 11,832 | 9.0 |
| Muddy | 11,436 | 8.8 |
| Artificial | 7252 | 5.6 |
| N-D | 29,405 | 22.6 |
| Total | 130,031 | 100 |
| Component | RCP8.5 IPCC AR5/SROCC | High-End A Moderate | High-End B Worst Model |
|---|---|---|---|
| Glaciers | 0.18 [0.10 to 0.26] m | 0.26 m | 0.29 m 2 |
| Greenland 1 | 0.15 [0.09 to 0.28] m | 0.28 m | 0.34 m 3 |
| Antarctic SMB | −0.05 [−0.09 to −0.02] m | −0.02 m | 0 m 4 |
| Antarctic DYN | 0.16 [0.02 to 0.37] m | 0.37 m | 0.8 m |
| Groundwater | 0.05 [−0.01 to 0.11] m | 0.11 m | 0.11 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thiéblemont, R.; Le Cozannet, G.; Toimil, A.; Meyssignac, B.; Losada, I.J. Likely and High-End Impacts of Regional Sea-Level Rise on the Shoreline Change of European Sandy Coasts Under a High Greenhouse Gas Emissions Scenario. Water 2019, 11, 2607. https://doi.org/10.3390/w11122607
Thiéblemont R, Le Cozannet G, Toimil A, Meyssignac B, Losada IJ. Likely and High-End Impacts of Regional Sea-Level Rise on the Shoreline Change of European Sandy Coasts Under a High Greenhouse Gas Emissions Scenario. Water. 2019; 11(12):2607. https://doi.org/10.3390/w11122607
Chicago/Turabian StyleThiéblemont, Rémi, Gonéri Le Cozannet, Alexandra Toimil, Benoit Meyssignac, and Iñigo J. Losada. 2019. "Likely and High-End Impacts of Regional Sea-Level Rise on the Shoreline Change of European Sandy Coasts Under a High Greenhouse Gas Emissions Scenario" Water 11, no. 12: 2607. https://doi.org/10.3390/w11122607
APA StyleThiéblemont, R., Le Cozannet, G., Toimil, A., Meyssignac, B., & Losada, I. J. (2019). Likely and High-End Impacts of Regional Sea-Level Rise on the Shoreline Change of European Sandy Coasts Under a High Greenhouse Gas Emissions Scenario. Water, 11(12), 2607. https://doi.org/10.3390/w11122607






