Next Article in Journal
Effects of a Large Irrigation Reservoir on Aquatic and Riparian Plants: A History of Survival and Loss
Previous Article in Journal
Climate Change Impact Assessment on Freshwater Inflow into the Small Aral Sea
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 11
Issue 11
10.3390/w11112378
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Model Performance Indicator of Aging Pipes in a Domestic Water Supply Distribution Network

by
Norzaura Abd Rahman
1,2,
Nur Shazwani Muhammad
1,*,
Jazuri Abdullah
3 and
Wan Hanna Melini Wan Mohtar
1
1
Smart and Sustainable Township Research Center (SUTRA), Faculty of Engineering & Built Environment, Universiti Kebangsaan Malaysia, 43600 Bangi, Selangor, Malaysia
2
Department of Mathematics, Centre for Defence Foundation Studies, Universiti Pertahanan Nasional Malaysia, 57000 Kuala Lumpur, Malaysia
3
Faculty of Civil Engineering, Universiti Teknologi MARA, 40450 Shah Alam, Selangor, Malaysia
*
Author to whom correspondence should be addressed.
Water 2019, 11(11), 2378; https://doi.org/10.3390/w11112378
Submission received: 19 September 2019 / Revised: 16 October 2019 / Accepted: 4 November 2019 / Published: 14 November 2019
(This article belongs to the Section Hydraulics and Hydrodynamics)
Browse Figures
Versions Notes

Abstract

:
Aging pipes in the domestic water distribution network have the potential to decrease the quality and quantity of the treated water supplied to the consumers. Therefore, a calibrated water distribution model is helpful to monitor and understand the behaviour of a real water distribution network. However, a comprehensive performance indicator and an integrated method to assess the efficiency of model performance have not been well established in the literature. This study developed a methodology for a model calibration exercise, with consideration of two uncertainty parameters, i.e., Hazen–Williams roughness coefficient of the pipes and Non-Revenue Water (NRW) in each nodal demand. Following this, a statistical color-coded performance indicator was established, based on the Nash–Sutcliffe Efficiency Coefficient (NSEC), the coefficient of determination (R2), the correlation coefficient (r), and the Mean Absolute Error (MAE). The accuracy of the calibrated model was measured by Discrepancy Ratio (DR) analysis. This study concluded that the model performed well when NRW was added to the nodal demand in zone(s) with suspected water loss activities. The suggested Hazen–Williams roughness coefficient for PVC pipes was between 130 and 140 for pipes aged more than 20 years. The threshold error value to determine the accuracy of the simulated model was proposed to be between –0.05 and 0.05.

1. Introduction

Malaysia gained its independence from the British on 31st August, 1957, more than 60 years ago. Since then, the country has rapidly developed with modern infrastructures. As a result, the current water supply coverage is more than 95% of the total population, as compared to 80% in 1990 [1]. Although treated water is easily accessible, a low percentage of national Non-Revenue Water (NRW) remains elusive, due to the aging pipe networks [2]. NRW refers to the unaccountable water in the distribution networks that cause losses to the water service provider. High NRW has also been reported in several developed countries, such as Italy [3] and USA [4], where the value exceeds the acceptable level of 25%, as suggested by the International Water Association (IWA). The unaccountable water can be divided into two components; 1) unbilled authorised consumption that might be due to water theft and metering faults and 2) water losses from leakage or bursts at pipelines [5]. Over time, the pipelines deteriorate, due to internal and external factors such as pipe age, pipe material, pipe size, soil type, pipe location, and water quality [6,7]. Aging pipelines have caused frequent pipe leakage and burst events [8], and consequently affect the quality and the quantity of water received by the consumers. The leakage also leads to financial loss to the water service provider due to unaccounted treated water, thus resulting in high operational costs.
A few successful strategies are available in minimising the leakage, such as pressure management, active leakage control activities, pipe rehabilitation, asset management and implementation of District Metered Area (DMA) [9]. However, before any appropriate countermeasures can be taken, a preliminary analysis through water network modelling is needed to provide a basal scenario on finding the best water leakage reduction strategies. A calibrated water distribution model is an important tool to help researchers, engineers and water operators to evaluate and analyse the impacts of any plan or improvisation in the water distribution network. This calibrated model must consider the known and unknown parameters related to the water distribution networks, so that the model is able to represent the behaviour and operation of the real systems with acceptable estimation and accuracy. Some parameter adjustments have been proposed to obtain a good calibration model. One of the approaches is adjusting the pipe roughness coefficient with sufficiently accurate nodal demand data [10,11,12]. There have also been a few methods suggested to consider adjustment of both the pipe roughness coefficient and the nodal demand [13] in model calibration of water distribution networks. Therefore, a model calibration exercise is important to represent the real water distribution network. The main challenge in calibrating a water distribution model is the availability and consistency of reliable data [14,15], such as detailed information on the pipe distribution network and consumers’ behaviour. Data requirements include water consumption of each connection, pipe size, pressure, material and elevation of each nodal point. Most water companies consider the data acquisition exercise as challenging, due to the high cost of specialised equipment, difficult installation and the need of continuous monitoring. These constraints also deter researchers in the evolution of research related to aging pipes in the water distribution network. Nevertheless, with a good or poor dataset, calibration model can still be developed with suitable model performance indicators and acceptable error. Ref. [12] presented the whole process of calibration of the water network where an iterative trial and error method is used to determine the unknown parameter of the pipe roughness coefficient. Good performance of their model suggests that the proposed setup may serve as a good guidance for other calibration networks. Complete data availability, namely nodal demands, pipe profiles (length, diameter, type of pipe and year of installation) and valve status (locations, size, operational status) is the most important factor in obtaining good agreement between simulated and observed data. However, most of the aging water distribution networks, especially those in developing countries, have a limited data availability. Therefore, the calibration network process could be a challenging task with some uncertainty on parameter values. This paper provides a better insight on the performance evaluation of the calibration process for a water distribution network with limited data, for example in this case, no data on status of valves.
In evaluating the performance of a calibrated water distribution network model, most researchers commonly used mean absolute error or relative error (e.g., refs. [16,17]) and correlation coefficient (e.g., ref. [18]) to compare the simulated results and observed data. However, further analysis on the efficiency and accuracy of the calibrated model has been less covered and discussed, especially for water distribution network modelling. The Nash–Sutcliffe efficiency coefficient (NSEC) is found to be the best statistical approach for model performance evaluation especially in hydrological modelling [19,20,21,22]. Refs. [22] and [23] proposed a threshold value to represent an acceptable simulated model, i.e., 0.5 < NSEC < 0.65. NSEC is an example of a dimensionless statistical indicator and needs to be further supported by an absolute error in terms of the units of the variable to provide an extensive quantitative relative assessment of model performance.
Average error approach, such as mean absolute error (MAE) is more suitable to represent model performance as compared to those approaches based on squared differences like RMSE [24,25]. The formula of MAE considers absolute differences between simulated and observed values avoiding error concentration in outliers, an attribute which is deemed more appropriate in water distribution modelling instead of RMSE. The combination of MAE and NSEC analyses were also used by ref. [26] in predicting model analysis of flow discharge hydrographs using a genetic algorithm.
Discrepancy Ratio (DR) analysis is useful to evaluate the accuracy of the models. DR is used to evaluate the percentage distribution of the difference between simulated values and observed data. Additionally, DR determines whether the model is over-predicted or under-predicted, based on the direction of skewness of the distribution. The symmetrical/normal distribution (when high concentration at DR is equal to zero), shows that the model performs well. Refs. [27] and [28] suggested a threshold value to indicate the accuracy of predicted model for dispersion coefficient studies in natural streams, based on the proportion numbers of DR between −0.3 and 0.3 for the total number of data.
Utilising simplicity and objectivity, this method offers a new perspective in the classification of performance indicators for water distribution network modelling. Furthermore, the novelty of this study is scarce review of aging pipe networks which simultaneously correlates with high NRW. Additionally, establishing a methodology to calibrate simulated models of aging pipes in a domestic water supply distribution network would be useful and practical to assess the current condition of the waning pipes. This study also evaluates the suitability of statistical indicators in the efficiency or performance of the simulated model, through quantification based on Mean Absolute Error (MAE), Nash–Sutcliffe Efficiency Coefficient (NSEC) and correlation coefficient, r. The accuracy of the model is evaluated using DR analysis. Following this, the most suitable model performance indicator for an aging domestic water supply distribution network is proposed.

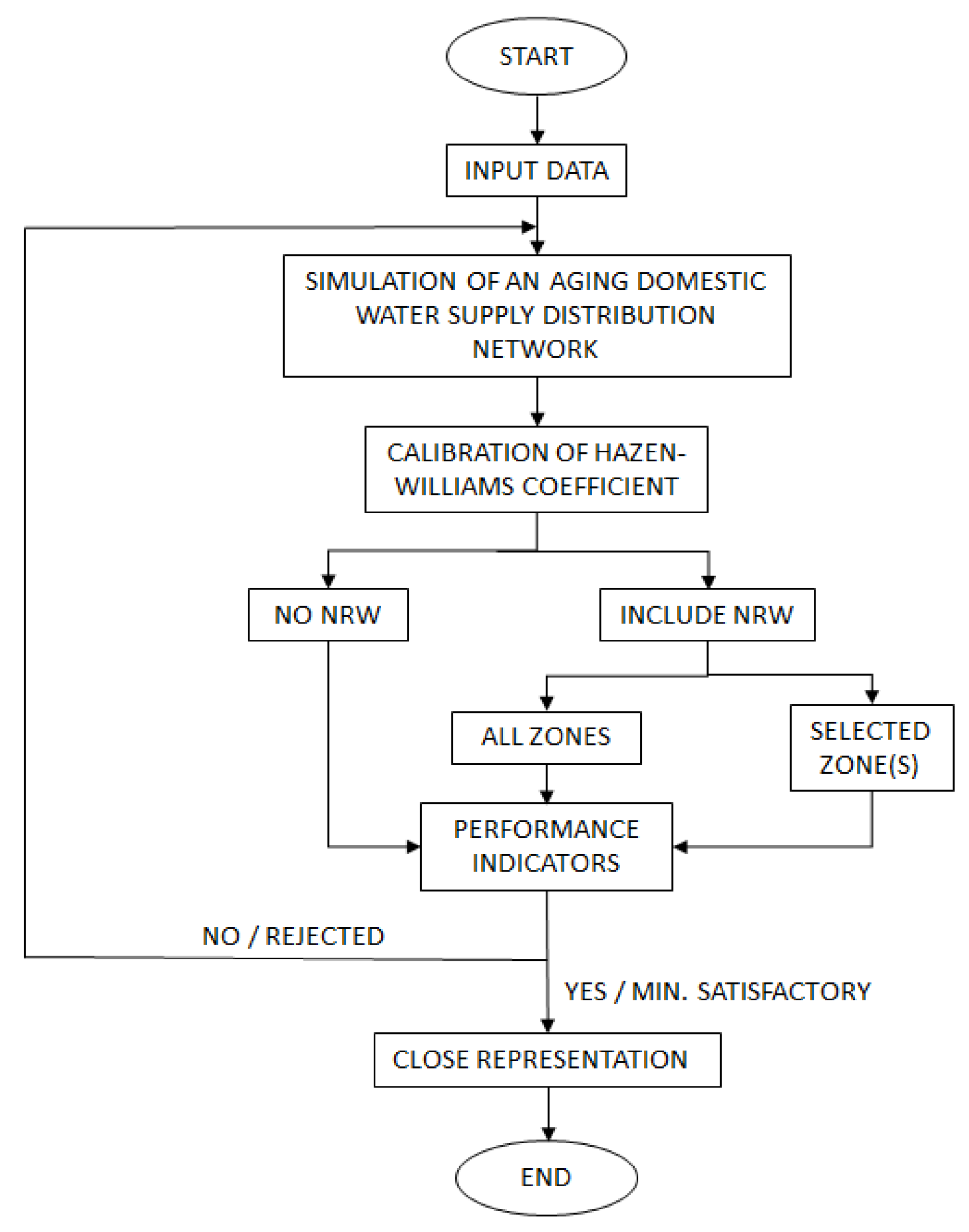
2. Materials and Methods

An open source water distribution network software, EPANET (version 2.0), developed by the United States Environmental Protection Agency was used in this study (Westlake, OH, USA). EPANET has been widely used in previous studies to model the hydraulic characteristics of a water distribution system, including demand-pressure [29], water age [30,31], water quality, such as chlorine content [18,32] and contaminants [33]. EPANET is also helpful in a new water network design in obtaining the preliminary analysis and information about the hydraulics operation of the proposed area, e.g., the cost-effectiveness analysis of the background leakage control strategy [34]. An overview of the proposed methodology is shown in Figure 1. It starts with the simulation of the distribution network in EPANET. In this study, the detailed characteristics of the water supply system at the study area, i.e., the schematic pipe distribution network, nodal demands, pipe characteristics (material, length and diameter) and demand pattern were obtained. The details of these input data are given in the following sections.
The model is assessed varying the Hazen–Williams coefficient, inclusion of the NRW value and zones using the proposed performance indicators of NSEC, R2, MAE and r. To determine the accuracy of the model, the performance indicator of DR was used. If the performance analysis for the calibration model is satisfied, a conclusion will be made. Otherwise, the simulation and performance analysis process will be repeated until a satisfactory calibration result is obtained.

2.1. Study Area

A water distribution network of a semi urban area in Peninsular Malaysia was chosen as the case study. This area was first occupied in 1997 and fully developed in 2012. The network receives its water supply from a reservoir, with an elevation of 44 m higher than the supply area. The water distribution network consists of 1784 domestic connections, with a total pipe length of 11.54 km. This is a mixed development area, where there are active connections consisting of 52 single storey shops, 93 double storey shops, 14 bungalows, 121 semi-detached houses, 28 double storey houses and 1267 single storey terrace houses. Based on the schematic pipe plan provided by the respective water operator, the network distribution system is drawn in the EPANET software. A flow meter and a Pressure Reducing Valve (PRV) were installed at the inlet of the main pipe. The PRV was installed by the water operator in 2015 to reduce the high pressure and water leakage, especially at night when the demand is low. The PRV was set to automatically switch on at 12 AM and shut at 5 AM.

2.2. Pipe Distribution Network

The water distribution network is divided into four sub-zones, i.e., Z1, Z2, Z3 and Z4 (Figure 2a) according to the single-entry water inlet points. Detailed information for each subzone is also given in Figure 2a. Z3 has the longest pipeline which is 3500 m with 606 active connections. The total demand for this sub-zone is 533,800 L/day. This is followed by the second largest area, Z1 with 3050 m pipe length, 606 active connections which consume 381,667 L/day. Sub-zone Z2 comprises of 181 active connections along 2805 m pipeline, with total usage of 146,300 L/day. The shortest pipeline is in sub-zone Z4 with 2180 m length and 273 active connections, where the total daily demand in this area is 239,830 L/day. Most of the pipes are polyvinyl chloride (PVC) and the diameter is 150 mm, except for subzone Z2 which are mostly Anti Bacteria High Impact 3 Layer (AB3P) pipes with 150 mm diameter. The source of water from the reservoir terminal is supplied to the network area through a 2000 m long Asbestos Cement (AC) pipe with a diameter of 450 mm. The main pipes located at the entrance of the water network area (where the flow meter and PRV are installed) are mild steel (MS) pipes with 300 mm diameter.
For the calibration purposes, six pressure loggers were installed, i.e., P1 (before PRV), P2 (after PRV), P3, P4, P5 and P6 (see Figure 2a). Pressure data were collected continuously for three days (from 29–31 March 2018), to obtain the flow and pressure patterns during a weekday (Thursday), weekend eve (Friday) and holiday/weekend (Saturday).
As mentioned in the introduction, the status of valves in this pipe distribution network is unknown. This includes the data on the location and settings of the valves. Due to the data limitation from the water company, the valves are assumed to be fully opened and receive continuous water supply during the simulation period.

2.3. Nodal Base Demand and Demand Pattern

Two input parameters are required in the EPANET software, i.e., base demand and demand pattern at every node. The flow pattern, based on the data collected at the main inlet is analysed to develop a representative demand pattern for all nodes, as shown in Figure 2b. Two distinctive peaks of daily demand pattern were observed from the 3-day data. In general, the demand pattern for the first two days (Thursday and Friday), look relatively similar even though there is a noticeably high peak at hour 37 (that is at 1 PM), due to the long lunch break and Muslim canonical Friday prayer. Other than in the afternoon, the highest peak for both days was found in the morning at 7 AM. (7- and 31-hours, respectively), when the residents are up and getting ready for their daily routines of work and school. The water consumption activities start to slow down after 12 AM each day. During the weekend (Saturday), it can be seen that the highest water consumption starts from hour 57 to 59, i.e., 9–11 AM, slightly later than during the weekday. This is somewhat expected as routine in the weekend changes due to off days for both working and school.
For nodal base demands, the values were estimated based on the actual usage by each active connection, obtained from the monthly billing data provided by the water operator. The monthly usage was divided by 30 days giving an approximation of the average daily demand. This value was then multiplied by three (3), to represent the three-day base demand at every connection.

2.4. Estimation of NRW

The NRW percentage is estimated based on the difference between the volume of water supplied to the network area and the volume that was billed to the consumers. This assumption is valid, since there is no elevated tank after the inlet and the majority of the connecting pipes has the same diameter of 150 mm. The treated water volume supplied by the water company for that three-day period was 5296.86 m3. The average volume of water that was billed to the consumers for the same study period was 3778.94 m3. Therefore, the difference of 1517.92 m3 of water that was unbilled was considered as the NRW. A sample of the NRW rate calculation is given below:
NRW = 5296.86   m 3 - 3778.94   m 3 5296.86   m 3 = 1517.92   m 3 5296.86   m 3 = 0.286 ≈ 29 %
Following this, the value of NRW for the simulated network is rounded up to 30% and used in the simulation cases. Note that this value is much lower than the national averaged NRW at 35% [35] and slightly higher than the suggested NRW value of 25%.

2.5. Uncertainty Parameter

Two uncertainty parameters of the Hazen–Williams roughness coefficient of the pipes and NRW in each nodal demand, as previously discussed, were given focus for the calibration process. The age of pipes influences the roughness coefficient of the pipes [18]. The performance of pipes reduces with age, and this condition is reflected in the value of the roughness coefficient. The age of the pipes in this study area is more than 20 years, except at subzone Z2, which was built in 2012. Recall that most of the pipes in the network area are PVC pipes, whereas a small portion of the pipe network is composed of AC, MS and AB3P pipes. The suggested Hazen–Williams roughness coefficient values for AC and MS, AB3P, and PVC pipes are 130, 150, and 140–150, respectively [36]. However, after 20 years, these values may decrease.
The EPANET software is based on the demand-driven assumption to determine the nodal pressure, thus, the amount of water losses in the network area should be considered in the nodal demand estimations for the water distribution network simulation analysis [37]. Based on the previously calculated NRW, the estimated water loss for the study area is about 30%.
The uncertainty analysis was done using the combination of these two uncertainty parameters in all zones or selected nodal demands, which are discussed for nine different cases. Three Hazen–Williams roughness coefficient values for all PVC pipes are considered, specifically 130, 140 and 150. CASE 1 to CASE 3 considering a Hazen–Williams roughness coefficient of 130. CASE 1 does not include NRW in every nodal demand, CASE 2 includes NRW at all nodal demands, whereas for CASE 3, NRW was added at nodal demand at certain zone(s) with suspected water leakage. CASES 4 to 9 present similar considerations as CASES 1 to 3, however, the Hazen–Williams roughness coefficients used in these simulations were 140 or 150. The details of each case are given in Table 1.

2.6. Performance Indicators

In hydraulic modelling, it is important to evaluate the efficiency and accuracy of the calibrated models to see how well the simulated model imitates the trend or behaviour of an actual water distribution system [38]. The details of efficiency and accuracy of the calibrated models are given in the following sections.

2.6.1. Efficiency of the Simulated Models

1. Mean Absolute Error (MAE)

MAE and correlation coefficient are used in this study as one of the performance indicators. The MAE is commonly used to measure error in model testing [39]. The MAE is much related to the correlation coefficient, r. The lower the value of MAE, the higher the value of correlation coefficient. The correlation coefficient, r value ranging from 0 to 1; approaching to 1 indicates that the simulated and observed data are strongly correlated to each other. The formula for MAE is given as:
MAE = 1 n ∑ i = 1 n | O b s i − S i m i |
where i is the ith number of the sample and n is the total number of samples; O b s i and S i m i represent the observed and simulated values, respectively.
Ref. [40] recommended that a model with a good dataset should be able to achieve an average difference between the simulated and observed pressure of 1.5 m, with a maximum difference of 5.0 m. For a model with a poor dataset, the achievable average difference between simulated and observed pressure is 3.1 m, with a maximum difference of 10.0 m. These propositions led to the development of the performance indicator given in Table 2, where an MAE of less than 1.5 m is considered as Very Good, an MAE value ranging between 1.5 m to 3.1 m is Good and an MAE between 3.1 m and 5.0 m is categorised as Acceptable. Additionally, an MAE of 5.0 to 10.0 m is considered as Satisfied, whereas if the MAE is more than 10.0 m, the model is rejected.

2. Nash–Sutcliffe Efficiency Coefficient (NSEC)

The NSEC is commonly used in hydrological modelling, e.g., runoff simulation and floods [19,20,41]. This performance indicator was developed by ref. [42] and the equation is given below:
NSEC = 1 − ∑ i = 0 n ( O b s i − S i m i ) 2 ∑ i = 0 n ( O b s i − O b s ¯ ) 2
where O b s i and S i m i represent the observed and simulated values, respectively and O b s   ¯ represents the average of observed values.
The NSEC value ranging between 1 to –∞. The value of 1 represents a perfect fit model, whereas an efficiency value less than zero indicates that the observed mean is a better predictor compared to the simulated model. In other words, NSEC < 0 shows that the model is no better than the actual mean.
The threshold value for NSEC that represents sufficient model quality was proposed by refs. [22,23] and these studies were used as a reference for the model performance indicator shown in Table 2, where 0.5 < NSEC < 0.65 is considered as Acceptable. An NSEC value between 0.66 and 0.79 is categorised as Good, whereas an NSEC value in the range of 0.80 to 1.00 is nominated as Very Good and therefore considered as the best fitted model. An NSEC value from 0.35 to 0.49 is classified as Satisfactory, whilst an NSEC value of less than 0.34 indicates that the model should be Rejected.

3. Coefficient of Determination, R2

The coefficient of determination, R2 was found to be nearly identical and highly associated with NSEC, where high R2 corresponds to the high value of NSEC [43]. Unlike NSEC, the R2 value ranges from 0 to 1; the higher the R2, the better the model fits the data. The R2 measures how closely the data is to the fitted regression. For this study, NSEC is used to evaluate the performance of calibrated points (P1–P6), whereas R2 is used to evaluate the performance of the whole calibration model. The value of R2 for each model case in this study is obtained from the EPANET calibration data analysis. The classification of the performance indicator for R2 is the same as NSEC, since the characteristics of these two indicators are similar.

2.6.2. Accuracy of the Simulated Models

The accuracy analysis is conducted with the purpose to evaluate the residual difference of the simulated data to the observed or actual data. The relative difference between the simulated and actual data represents the amount of error that the simulated model possesses, which can be measured by the Discrepancy Ratio (DR) [44]. A DR value equal to zero means an exact prediction, while DR > 0 is over prediction and DR < 0 is under prediction. Therefore, to get a higher accuracy, the value of the error must be as close to zero as possible. The formula for DR is given as:
DR = log ( S i m i O b s i )   ,   i = 1 , 2 , … , n
DR was widely used in measuring errors in predicting the dispersion coefficient for natural channel studies (e.g., refs. [44,45] where the threshold value for the model accuracy was proposed to be a DR value between −0.3 and 0.3 [27,28].

3. Results

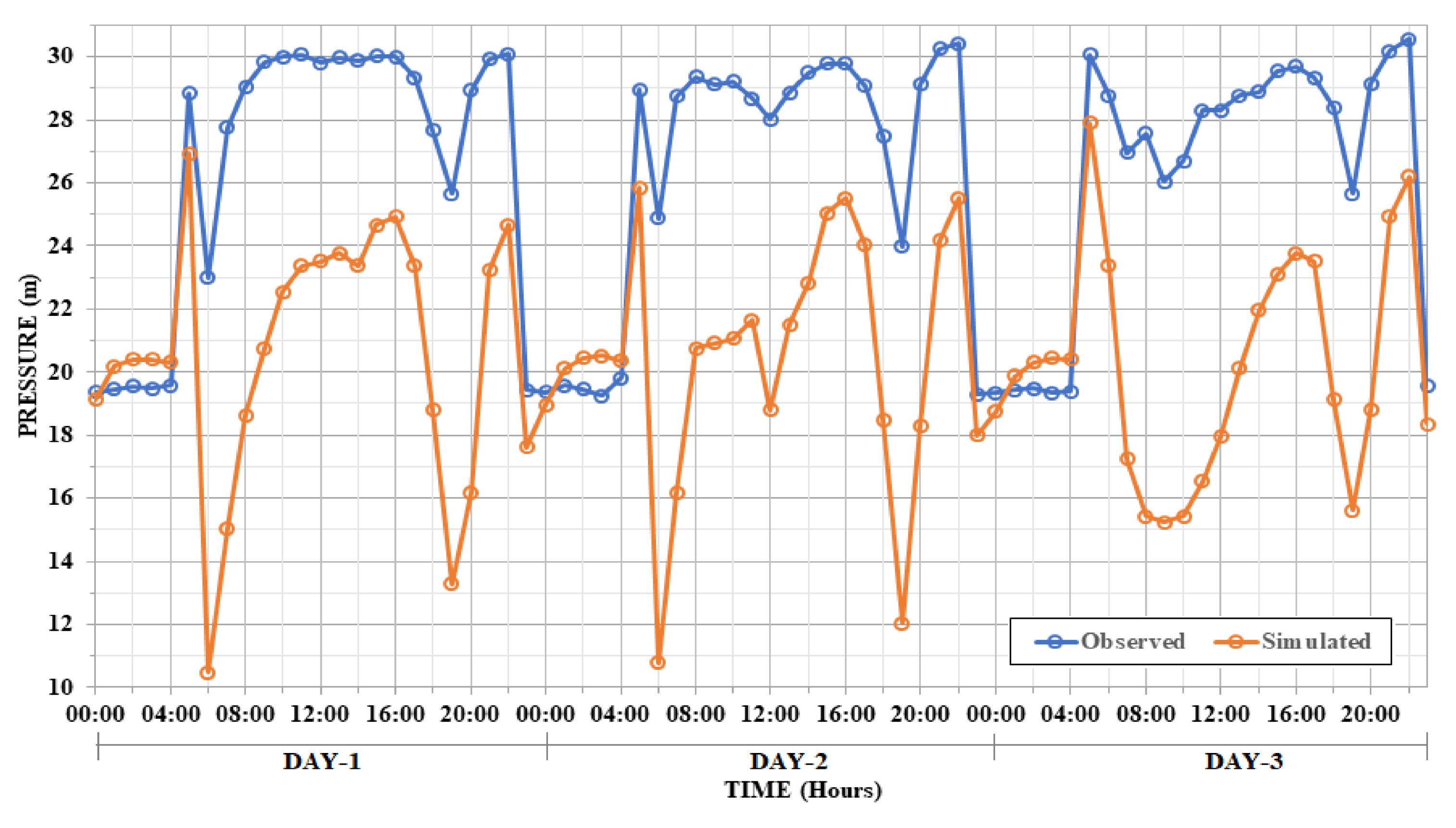
3.1. Performance Analysis o fthe Calibration Model

The simulated pressure estimated from the EPANET software is calibrated with the observed data obtained from the site at these respective pressure points, i.e., P1, P2, P3, P4, P5 and P6. The results are color-coded based on the model performance of each observed pressure points, as shown in Table 2. Model performance is evaluated based on NSEC, R2 and MAE and the accuracy of each model case.
For CASE 1 (Hazen–Williams coefficient of 130 and no NRW in the demand), the NSEC values for P4 and P5 (located in subzone Z4) are negative, −0.11 and −0.15, respectively. The simulated and observed pressures at P4 and P5 are shown in Figure 3a,b, respectively. These figures show an acceptable difference between the observed and simulated values. The MAE of 1.97 m for CASE 1 is considered under the Good category. It can also be observed that the simulated pressures are over- estimated. This led to an early assumption that there is a higher demand in subzone Z4, believed to be caused by NRW. Following this, we decided to simulate CASE 2, which includes 30% of NRW in the water demand for all connections, to examine the model performance and efficiency. This approach was suggested by refs. [12,37] in the nodal demand estimations for the water distribution network simulation analysis.
In CASE 2, (see Table 2), by adding 30% of NRW in the nodal demand, the NSEC value for P4 and P5 significantly improved to 0.66 and 0.72, respectively, which is classified as Good model performance. Therefore, a preliminary conclusion was made for CASE 2, i.e., possibility of NRW occurrence in the subzone Z4 is likely due to the improved pressure resulting from the addition of 30% of NRW at the nodal demands. However, the NSEC value at P6 (located at Z3) is −2.04, which indicates that this value should be rejected. It can be seen that Z3 has the highest total demand compared to Z1, Z2 and Z4 (refer Figure 2a). The overestimated demand (after adding 30% of NRW) caused the under estimation of the simulated pressures at P6, as shown in Figure 4. This explains the negative NSEC value for P6 in CASE 2. Take note that the R2 and MAE of CASE 2 is still under the Good category, 0.73 and 2.08 m respectively, despite the negative value of NSEC at P6.
A similar approach was also conducted for CASE 3, where 30% NRW was included in the nodal demands in subzone Z4 only. Model performance results for CASE 3 showed some improvement, i.e., positive NSEC values at all points. However, the model is still considered as not acceptable due to poor performances at P5 and P6. The average error for CASE 3 shows the lowest value (comparing to all CASES), i.e., MAE of 1.74 m.
The simulations of different Hazen–Williams coefficient values of 140 and 150 were conducted in the next six cases, to observe the uncertainty of this coefficient to the model performance, forming CASES 4 to 9. In general, the results show a similar pattern with CASES 1 to 3. Without the inclusion of NRW in the nodal demand, i.e., CASES 4 and 7, measuring points of P4 and P5 which are located in subzone Z4 showed negative NSEC values. By adding 30% of NRW in the nodal demand in CASE 5 and CASE 8, the NSEC at all points changed to positive values, except for P6, which is located in subzone Z3. The similar justification for poor performance of P6 was discussed earlier as in CASE 2, where an addition of 30% NRW to the nodal demand caused the simulated pressure to further decrease as compared to the observed pressure (see Figure 4). Interestingly for P6, although there is a significant difference of pressures during the higher demand (from 6 AM. to 10 PM.), believed to be the overestimation of demand due to the inclusion of the 30% NRW model, the simulated pressure at low demand (i.e., at night from 11 PM. to 5 AM.) showed a very close match to the observed data as in Figure 4. Essentially, with reference to CASES 2 and 5, by adding 30% NRW in the simulations, the model performance becomes good in estimating the pressure, provided the Hazen–Williams coefficients of 130 and 140, respectively, are used.
The coefficients of determination, R2 for all cases are more than 0.70, which indicates good-fitted models. The MAE values for all cases are also considered small, ranging from 1.74 to 2.03 m. Therefore, the EPANET model performance for the study area is classified as good, following the classification established by ref. [40]. The correlation coefficients for all cases are more than 0.88, indicating that the model parameters are strongly correlated.
From the results, there is a systematic error between observed and simulated values, especially in P4 and P5 (refer to Figure 3), and P6 (refer to Figure 4), although the simulated pressure is able to follow the pattern of the observed pressure. These systematic errors occurred due to the unknown status of valves that were installed in the pipe network. Missing or incomplete data on valves is one of the main challenges in the model calibration process. The water operator acknowledged that there are old valves that were buried underground, thus the location and status of the valves are unknown. There are also some valves that were suspected to be partially opened after a water system test that was carried out a long time ago. These factors caused lower water flow and pressure, especially at P4 and P5 which are located at Z4. Therefore, we assumed that all valves are fully opened and receive continuous water supply. Additionally, the water demand pattern for this particular water network is solely obtained from a flow meter located at the main pipe entrance to the network (refer to Figure 2). The demand pattern at all nodal demands was assumed to be the same, which mainly represents houses and shop lots. However, each subzone has a different total water demand, as shown in Figure 2a. Thus, it can be seen that the simulated pressure can follow the trends of the actual pressure, but there is a noticeable difference between both pressures. If there are flow meters installed at each subzones Z1, Z2, Z3 and Z4, the respective demand pattern can be determined and assigned according to their respective nodal demands, with which more accurate and closely simulated values to the actual values can be obtained.

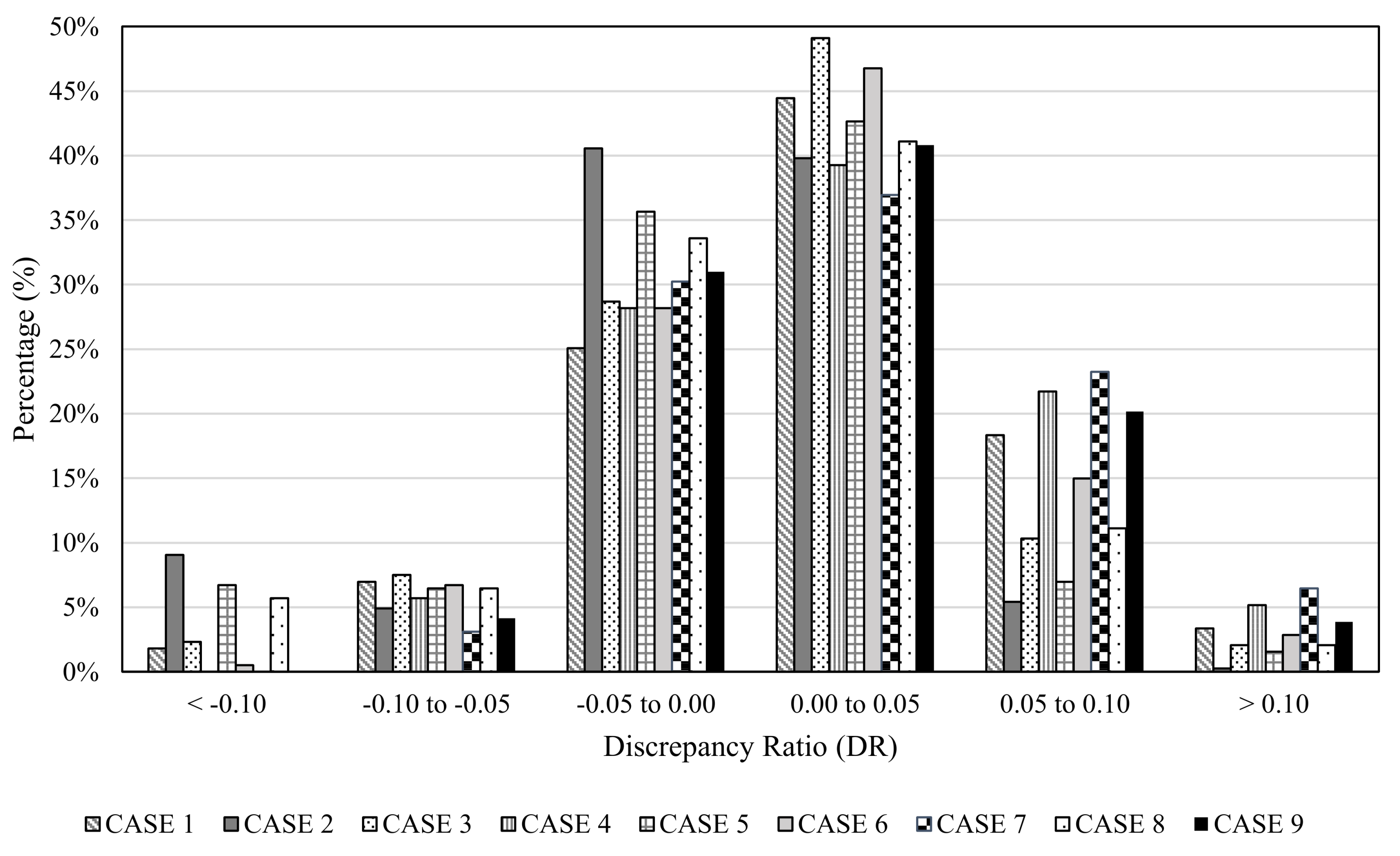
3.2. Accuracy Analysis of the Calibration Model

The DR values are divided into six categories based on the range of values, where the percentage for each case accordingly categorised, is given in Figure 5.
Overall, the distribution of DR is symmetric, although there is a slight positive skewness for CASES 3, 6 and 9 which implies that the simulated pressure values are slightly overestimated as compared to the observed data. Recall that a DR value equal to zero means an exact prediction, while DR > 0 is over prediction and DR < 0 is under prediction. The value of the error must be as close to zero as possible to get a higher accuracy. With reference to Figure 5, the DR values are concentrated between –0.05 to 0.05. This indicates that the error for all models is mostly ±5%. Therefore, the threshold error value for the simulated model in this study is taken as between –0.05 to 0.05. From the proposed threshold error value, the accuracy of each model is compared in Table 2. The highest accuracy is shown in CASE 2 with 81%, followed by CASE 5 and CASE 3, with accuracies of 79% and 78%, respectively. Note that, although CASE 2 has shown the highest accuracy, it has the worst performance for P6. In general, CASE 5 shows a much more balanced behaviour. While CASE 3 also has a high accuracy, both performance indicators at P5 and P6 showed unsatisfactory values. These accuracy values support the performance model evaluation using NSEC, especially for CASES 2 and 5 which showed the highest accuracies. All nodes (except P6) have NSEC values of more than 0.5, which indicate that the simulated results from the EPANET model can be used for further analysis and the NRW value must be included in the nodal demand, with a Hazen–Williams coefficient range of 130 to 140 for 20-year pipes.

4. Conclusions

This study proposed a comprehensive methodology to simulate and calibrate a model for an aging domestic water distribution network of more than 20 years old. The model performance, in terms of efficiency and accuracy, was also presented. The major conclusions from this study are as follows:
a)
A colour-coded performance indicator for model calibration of water distribution systems was established based on statistical values of NSEC, R2 and MAE. The model performance efficiency evaluation was proposed, supported with the accuracy analysis using the Discrepancy Ratio.
b)
There appears to be a systematic error between observed and simulated values in the model calibration process, especially for an aging network with limitation of data. However, with a certain range of average error, i.e.,MAE, the calibrated model can be acceptable with some missing data, in this case, valves’ status and respective demand pattern for each subzone.
c)
This study proposed an extended period of simulation based on observed data of three days, instead of a common, single period simulation. The calibrated model was proven to represent the behaviour of an aging domestic water distribution network in terms of the demand and pressure during weekdays, weekend eve and also weekends.
d)
Identifying the sole demand pattern of the study area is sufficient to perform a simulation, without knowing the actual demand pattern at each node.
e)
For pipes aged 20 years or more, the Hazen–Williams coefficient for PVC pipes was estimated between 130 and 140.
f)
The estimated NRW value should be included, particularly for an aging domestic water distribution network.
g)
The threshold error value for calibrated water distribution network models is proposed as ±5%.

Author Contributions

N.A.R. designed the overall concept of the methodology, carried out the analysis, data collection and curation and wrote the article; N.S.M. worked on the overall concept of the research, designed the methodology, carried out the formal analysis, funding acquisition, supervision, project administration and wrote the article; J.A. actively involved in the methodology, model calibration and validation, carried out the formal analysis, and wrote the article; W.H.M.W.M. contributed in the overall concept of the research, validation and wrote the article. All of the authors contributed substantially to the work reported.

Funding

This research was funded by the MINISTRY OF EDUCATION, MALAYSIA, under Fundamental Research Grant (Grant No. FRGS/1/2015/TK01/UKM/02/3). The authors appreciate the data provided by the water company.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ahmed, F.; Siwar, C.; Begum, R.A. Water resources in Malaysia: Issues and challenges. J. Food Agric. Environ. 2014, 12, 1100–1104. [Google Scholar]
  2. New Straits Times. Aged Pipes, Some Since 1960s, to Finally be Replaced in Five States. Available online: https://www.nst.com.my/news/nation/2018/01/326479/aged-pipes-some-1960s-finally-be-replaced-five-states (accessed on 14 May 2019).
  3. ISTAT. Press Release: WORLD WATER DAY 2019: ISTAT WATER STATISTICS. Available online: https://www.istat.it/en/archivio/228780 (accessed on 14 May 2019).
  4. Folkman, S. Water Main Break Rates in the USA and Canada: A Comprehensive Study. Available online: https://digitalcommons.usu.edu/cgi/viewcontent.cgi?article=1173&context=mae_facpub (accessed on 8 May 2019).
  5. Lambert, A.; Hirner, W. Losses from Water Supply Systems: Standard Terminology and Recommended Performance Measures. In IWA The Blue Pages; IWA Publishing: London, UK, 2000. [Google Scholar]
  6. Marzouk, M.; Hamid, S.A.; El-Said, M. A methodology for prioritizing water mains rehabilitation in Egypt. HBRC J. 2015, 11, 114–128. [Google Scholar] [CrossRef]
  7. Yoo, D.; Kang, D.; Jun, H.; Kim, J. Rehabilitation priority determination of water pipes based on hydraulic importance. Water 2014, 6, 3864–3887. [Google Scholar] [CrossRef]
  8. Punurai, W.; Davis, P. Prediction of asbestos cement water pipe aging and pipe prioritization using Monte Carlo simulation. Eng. J. 2017, 21, 1–13. [Google Scholar] [CrossRef]
  9. Abd Rahman, N.; Muhammad, N.S.; Wan Mohtar, W.H.M. Evolution of research on water leakage control strategies: Where are we now? Urban Water J. 2018, 15, 812–826. [Google Scholar] [CrossRef]
  10. Koppel, T.; Vassiljev, A. Calibration of a model of an operational water distribution system containing pipes of different age. Adv. Eng. Softw. 2009, 40, 659–664. [Google Scholar] [CrossRef]
  11. Alvisi, S.; Franchini, M. Pipe roughness calibration in water distribution systems using grey numbers. J. Hydroinformatics 2010, 12, 424–445. [Google Scholar] [CrossRef]
  12. Jadhao, R.D.; Gupta, R. Calibration of water distribution network of the Ramnagar zone in Nagpur City using online pressure and flow data. Appl. Water Sci. 2018, 8, 1–10. [Google Scholar] [CrossRef]
  13. Bhave, P.R.; Gupta, R. Analysis of Water Distribution Network; Narosa Publication House Pvt. Ltd.: New Delhi, India, 2006. [Google Scholar]
  14. Pernot, P.; Cailliez, F. A critical review of statistical calibration/prediction models handling data inconsistency and model inadequacy. AIChE J. 2017, 63, 4642–4665. [Google Scholar] [CrossRef]
  15. Savic, D.A.; Kapelan, Z.S.; Jonkergouw, P.M. Quo vadis water distribution model calibration? Urban Water J. 2009, 6, 3–22. [Google Scholar] [CrossRef]
  16. Dini, M.; Tabesh, M. A new method for simultaneous calibration of demand pattern and Hazen–Williams coefficients in water distribution systems. Water Resour. Manag. 2014, 28, 2021–2034. [Google Scholar] [CrossRef]
  17. Takahashi, S.; Saldarriaga, J.G.; Vega, M.C.; Hernández, F. Water distribution system model calibration under uncertainty environments. Water Sci. Technol. Water Supply 2010, 10, 31–38. [Google Scholar] [CrossRef]
  18. Mohapatra, S.; Sargaonkar, A.; Labhasetwar, P.K. Distribution network assessment using EPANET for intermittent and continuous water supply. Water Resour. Manag. 2014, 28, 3745–3759. [Google Scholar] [CrossRef]
  19. Abdullah, J.; Muhammad, N.S.; Julien, P.Y.; Ariffin, J.; Shafie, A. Flood flow simulations and return period calculation for the Kota Tinggi watershed, Malaysia. Flood Risk Manag. 2018, 11, S766–S782. [Google Scholar] [CrossRef]
  20. Abdullah, J.; Muhammad, N.S.; Muhammad, S.A.; Julien, P.Y. Envelope curves for the specific discharge of extreme floods in Malaysia. J. Hydro-Environ. Res. 2019, 25, 1–11. [Google Scholar] [CrossRef]
  21. Rosli, M.H.; Sulaiman, W.N.A.; Jamil, N.; Toriman, M.E.; Kamarudin, M.K.A. Integration of spatially hydrological modelling on bentong catchment, pahang, peninsular Malaysia using distributed GIS-based rainfall runoff model. Environ. Asia 2017, 10, 65–79. [Google Scholar] [CrossRef]
  22. Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
  23. Ritter, A.; Muñoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
  24. Willmott, C.J.; Robeson, S.M.; Matsuura, K. A refined index of model performance. Int. J. Climatol. 2012, 32, 2088–2094. [Google Scholar] [CrossRef]
  25. Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
  26. Tayfur, G.; Moramarco, T. Predicting hourly-based flow discharge hydrographs from level data using genetic algorithms. J. Hydrol. 2008, 352, 77–93. [Google Scholar] [CrossRef]
  27. Seo, I.W.; Cheong, T.S. Predicting longitudinal dispersion coefficient in natural streams. J. Hydraul. Eng. 1998, 124, 25–32. [Google Scholar] [CrossRef]
  28. Kashefipour, S.M.; Falconer, R.A. Longitudinal dispersion coefficients in natural channels. Water Res. 2002, 36, 1596–1608. [Google Scholar] [CrossRef]
  29. Sivakumar, P.; Prasad, R.K. Extended period simulation of pressure-deficient networks using pressure reducing valves. Water Resour. Manag. 2015, 29, 1713–1730. [Google Scholar] [CrossRef]
  30. Chen, J.; Zeidan, M.; Ostfeld, A. Analysis of Relations between Pressure and Water Age in Water Distribution Systems. In Proceedings of the 1st International WDSA/CCWI Joint Conference, Kingston, ON, Canada, 23–25 July 2018. [Google Scholar]
  31. Cheng, W.P.; Liu, E.H.; Liu, J.Q. A novel statistical model for water age estimation in water distribution networks. Math. Probl. Eng. 2015, 2015, 1–9. [Google Scholar] [CrossRef]
  32. Akdeniz, T.; Muhammetoğlu, H. Chlorine residual management for water utilities using GIS, SCADA and modeling tools. Desalin. Water Treat. 2017, 59, 135–143. [Google Scholar] [CrossRef]
  33. Adedoja, O.; Hamam, Y.; Khalaf, B.; Sadiku, R. Towards development of an optimization model to identify contamination source in a water distribution network. Water 2018, 10, 579. [Google Scholar] [CrossRef]
  34. Giustolisi, O.; Berardi, L.; Laucelli, D.; Savic, D.; Walski, T.; Brunone, B. Battle of background leakage assessment for water networks (BBLAWN) at WDSA conference 2014. Proced. Eng. 2014, 89, 4–12. [Google Scholar] [CrossRef]
  35. National Water Service Commission. Non-Revenue Water Year 2016–2017. Available online: https://www.span.gov.my/article/view/non-revenue-water-nrw-2015-2016 (accessed on 4 June 2019).
  36. Malaysian Water Association. MWA Design Guidelines for Water Supply Systems; MWA: Kuala Lumpur, Malaysia, 1994. [Google Scholar]
  37. Adeniran, A.E.; Oyelowo, M.A. An EPANET analysis of water distribution network of the University of Lagos, Nigeria. J. Eng. Res. 2013, 18, 69–83. [Google Scholar]
  38. Walski, T.M. Procedure for hydraulic model calibration. J.-Am. Water Work. Assoc. 2017, 109, 55–61. [Google Scholar] [CrossRef]
  39. Tayfur, G. Artificial neural networks, fuzzy logic and genetic algorithms. In Soft Computing in Water Resources Engineering; WIT Press: Southampton, UK, 2014; pp. 55–59. [Google Scholar]
  40. Walski, T.M. Technique for calibrating network models. J. Water Resour. Plan. Manag. 1983, 109, 360–372. [Google Scholar] [CrossRef]
  41. Abdullah, J.; Julien, P.Y. Distributed flood simulations on a small topical watershed with the TREX model. J. Flood Eng. 2014, 5, 17–37. [Google Scholar]
  42. Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models, Part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
  43. Hwang, S.H.; Ham, D.H.; Kim, J.H. A new measure for assessing the efficiency of hydrological data-driven forecasting models. Hydrol. Sci. J. 2012, 57, 1257–1274. [Google Scholar] [CrossRef] [Green Version]
  44. Tayfur, G.; Singh, V.P. Predicting longitudinal dispersion coefficient in natural streams by artificial neural network. J. Hydraul. Eng. 2005, 131, 991–1000. [Google Scholar] [CrossRef] [Green Version]
  45. Ibrahim, S.L.; Abdullah, J.; Hashim, K.; Ariffin, J. Establishment of Jet index for soil erodibility coefficient using jet erosion device (JEd). GEOMATE 2017, 12, 152–157. [Google Scholar] [CrossRef]
Water 11 02378 g001 550
Figure 1. Flowchart of the proposed methodology.
Figure 1. Flowchart of the proposed methodology.
Water 11 02378 g001
Water 11 02378 g002 550
Figure 2. Water distribution network of the study area (a) schematic diagram and input parameters (b) demand pattern.
Figure 2. Water distribution network of the study area (a) schematic diagram and input parameters (b) demand pattern.
Water 11 02378 g002
Water 11 02378 g003 550
Figure 3. Observed pressure versus simulated pressure (a) at P4 and (b) at P5 for CASE 1.
Figure 3. Observed pressure versus simulated pressure (a) at P4 and (b) at P5 for CASE 1.
Water 11 02378 g003
Water 11 02378 g004 550
Figure 4. Observed pressure versus simulated pressure at P6 for CASE 2 (with additional 30% NRW).
Figure 4. Observed pressure versus simulated pressure at P6 for CASE 2 (with additional 30% NRW).
Water 11 02378 g004
Water 11 02378 g005 550
Figure 5. Discrepancy Ratio (DR) for each case presented based on categorical values.
Figure 5. Discrepancy Ratio (DR) for each case presented based on categorical values.
Water 11 02378 g005
Table
Table 1. Hazen–Williams roughness coefficient for PVC pipes and NRW percentage for each case model simulation.
Table 1. Hazen–Williams roughness coefficient for PVC pipes and NRW percentage for each case model simulation.
Simulation30% NRWHazen–Williams Roughness Coefficient (for PVC Pipes)
CASE 1NO130
CASE 2YES130
CASE 3SELECTED ZONE(S)130
CASE 4NO140
CASE 5YES140
CASE 6SELECTED ZONE(S)140
CASE 7NO150
CASE 8YES150
CASE 9SELECTED ZONE(S)150
Table 2. Performance Indicators and Accuracy of Various Simulated Cases.
Table
MODEL30% NRWHazen-William CoefficientNash-Sutcliffe Efficiency Coefficient, NSECCoefficient of Determination, R2Mean Absolute Error, MAECorrelation Coefficient, rAccuracy (%)
P1P2P3P4P5P6
CASE 1NO1300.890.960.93−0.11−0.150.220.821.970.969
CASE 2YES1300.830.960.740.660.72−2.040.732.080.8881
CASE 3ONLY Z41300.90.960.960.40.30.080.841.740.9278
CASE 4NO1400.890.960.88−0.45−0.440.50.822.030.9077
CASE 5YES1400.830.960.890.570.52−1.090.761.980.8979
CASE 6ONLY Z41400.90.960.930.110.020.40.851.810.9275
CASE 7NO1500.890.960.81−0.78−0.720.670.822.080.9067
CASE 8YES1500.830.960.940.370.3−0.480.791.960.8975
CASE 9ONLY Z41500.90.960.88−0.2−0.260.60.851.880.9272
Table
LegendModel IndicatorNSEC / R2MAE (m)
Reject< 0.34> 10.0
Satisfactory 0.35–0.495.0–10.0
Acceptable0.50–0.653.1–5.0
Good0.66–0.791.5–3.1
Very Good0.80–1.00< 1.5

Share and Cite

MDPI and ACS Style

Abd Rahman, N.; Muhammad, N.S.; Abdullah, J.; Wan Mohtar, W.H.M. Model Performance Indicator of Aging Pipes in a Domestic Water Supply Distribution Network. Water 2019, 11, 2378. https://doi.org/10.3390/w11112378

AMA Style

Abd Rahman N, Muhammad NS, Abdullah J, Wan Mohtar WHM. Model Performance Indicator of Aging Pipes in a Domestic Water Supply Distribution Network. Water. 2019; 11(11):2378. https://doi.org/10.3390/w11112378

Chicago/Turabian Style

Abd Rahman, Norzaura, Nur Shazwani Muhammad, Jazuri Abdullah, and Wan Hanna Melini Wan Mohtar. 2019. "Model Performance Indicator of Aging Pipes in a Domestic Water Supply Distribution Network" Water 11, no. 11: 2378. https://doi.org/10.3390/w11112378

APA Style

Abd Rahman, N., Muhammad, N. S., Abdullah, J., & Wan Mohtar, W. H. M. (2019). Model Performance Indicator of Aging Pipes in a Domestic Water Supply Distribution Network. Water, 11(11), 2378. https://doi.org/10.3390/w11112378

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop