The Low-Impact Development Demand Index: A New Approach to Identifying Locations for LID
Abstract
:1. Introduction
1.1. Existing Geospatial Decision Models
1.2. Geospatial, Physically-Based Framework
2. Materials and Methods
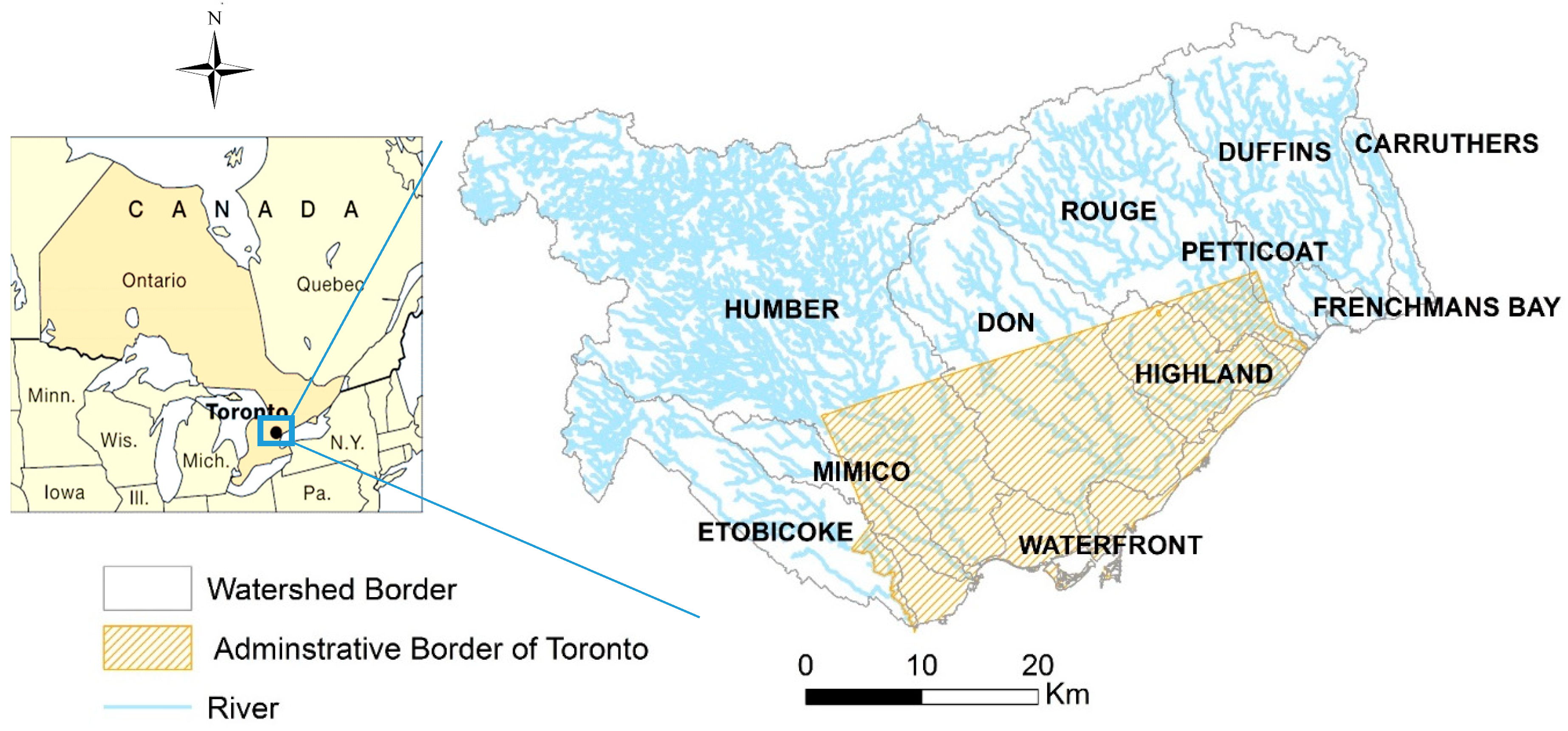
2.1. Study Area
2.2. Geospatial Data
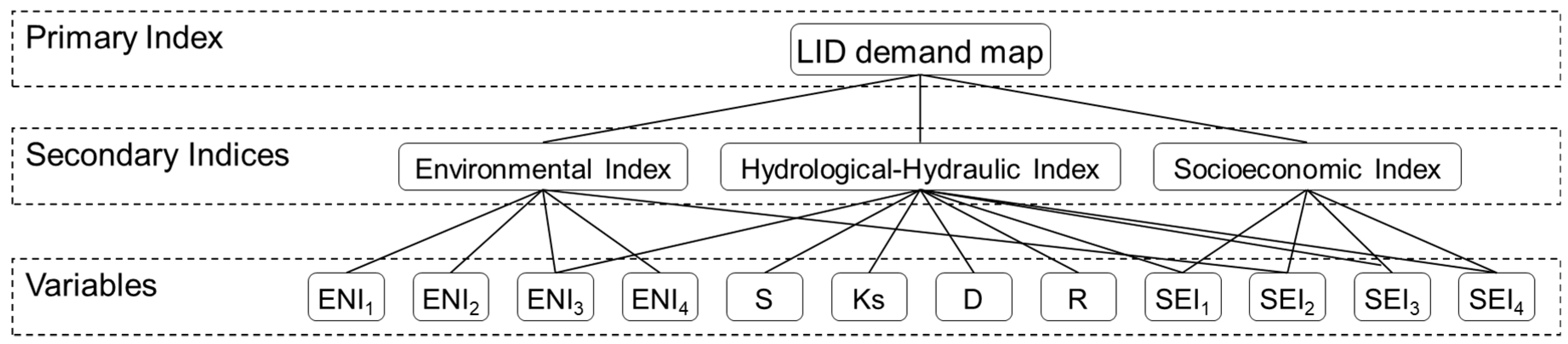
2.3. Hydrological-Hydraulic Index (HHI) Development
2.4. Environmental Index (ENI) Development
2.5. Socioeconomic Index (SEI) Development
2.6. LID Demand Index (LIDDI)
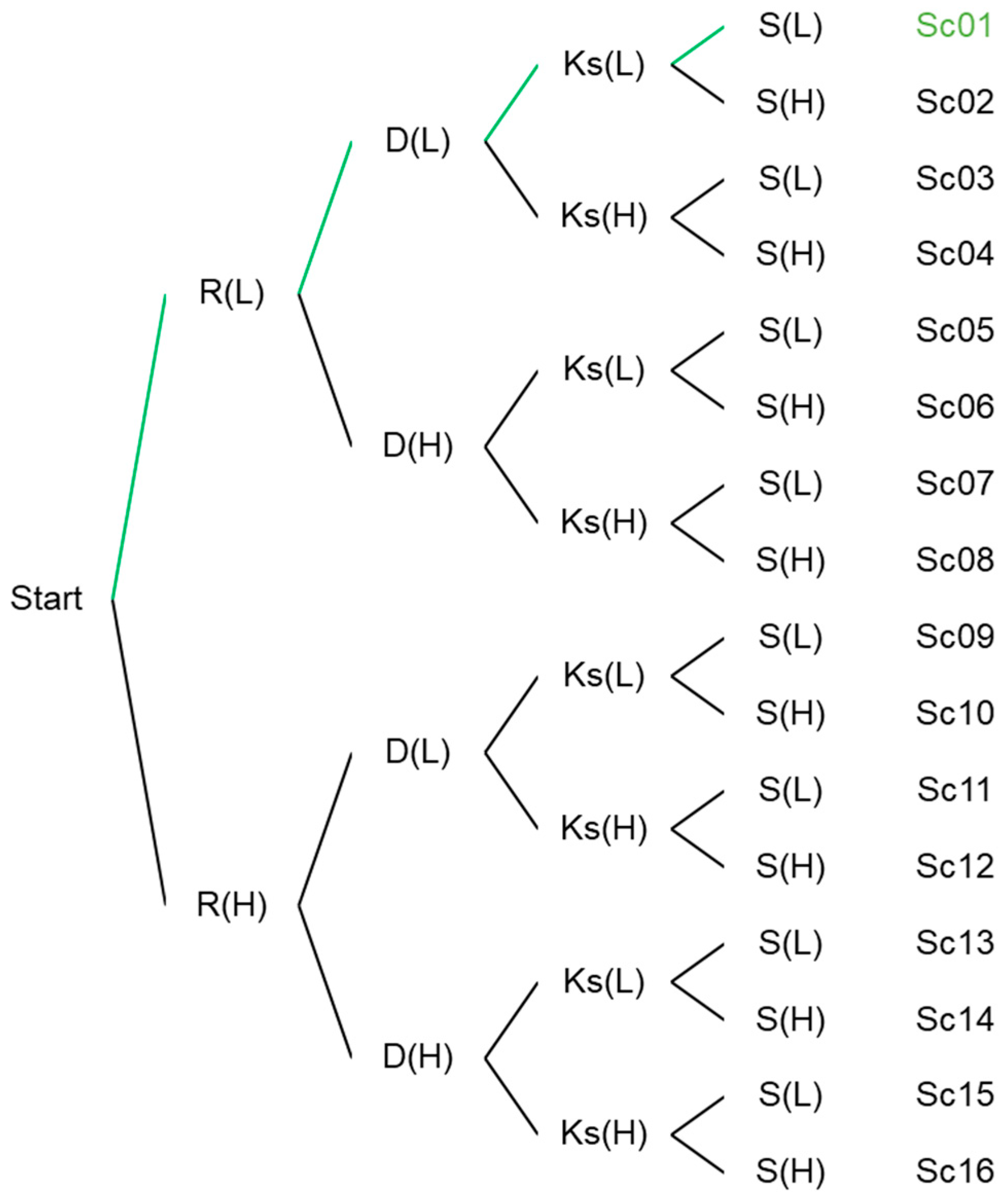
2.7. Adaptability of the Proposed Framework
3. Results and Discussion
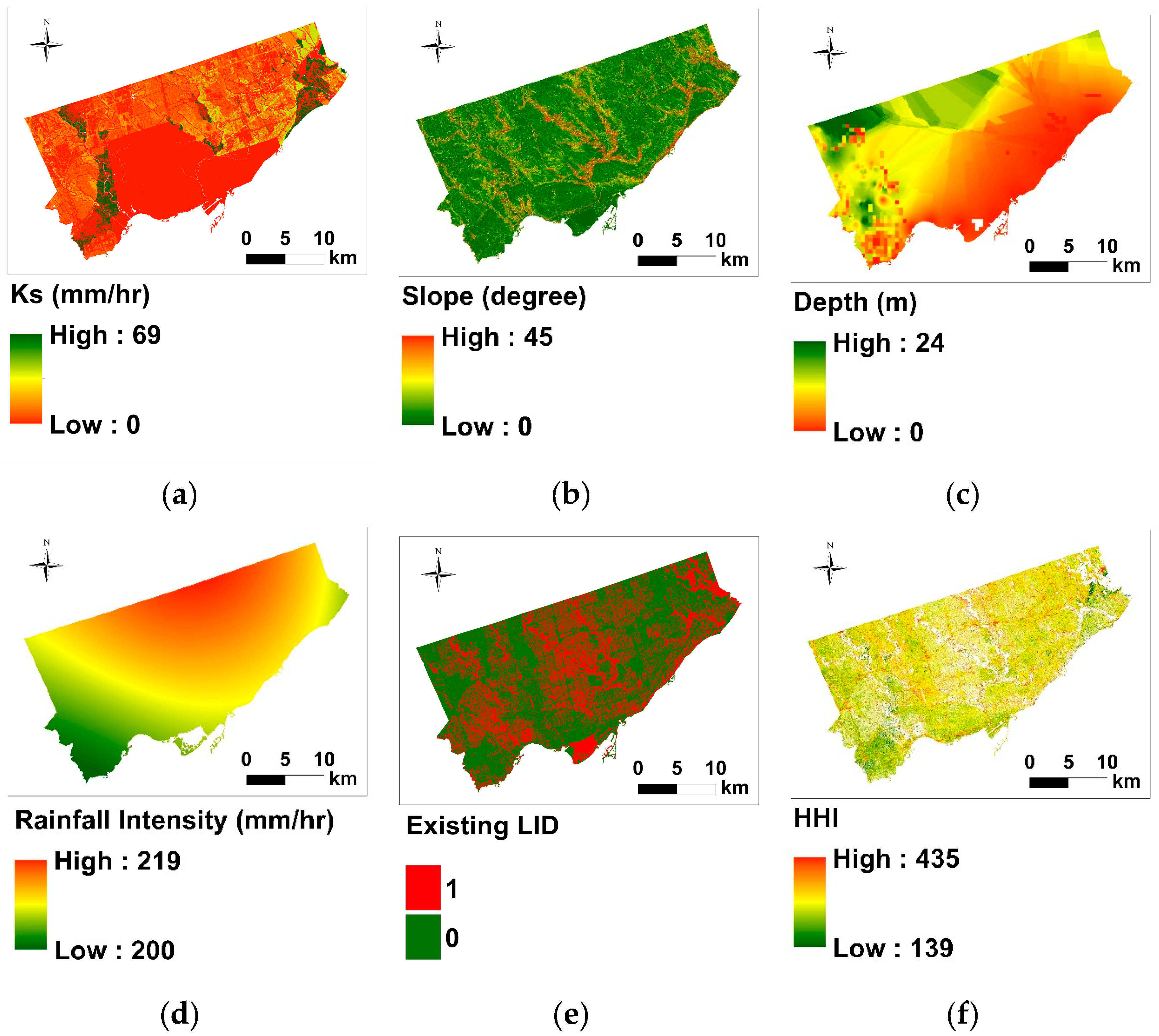
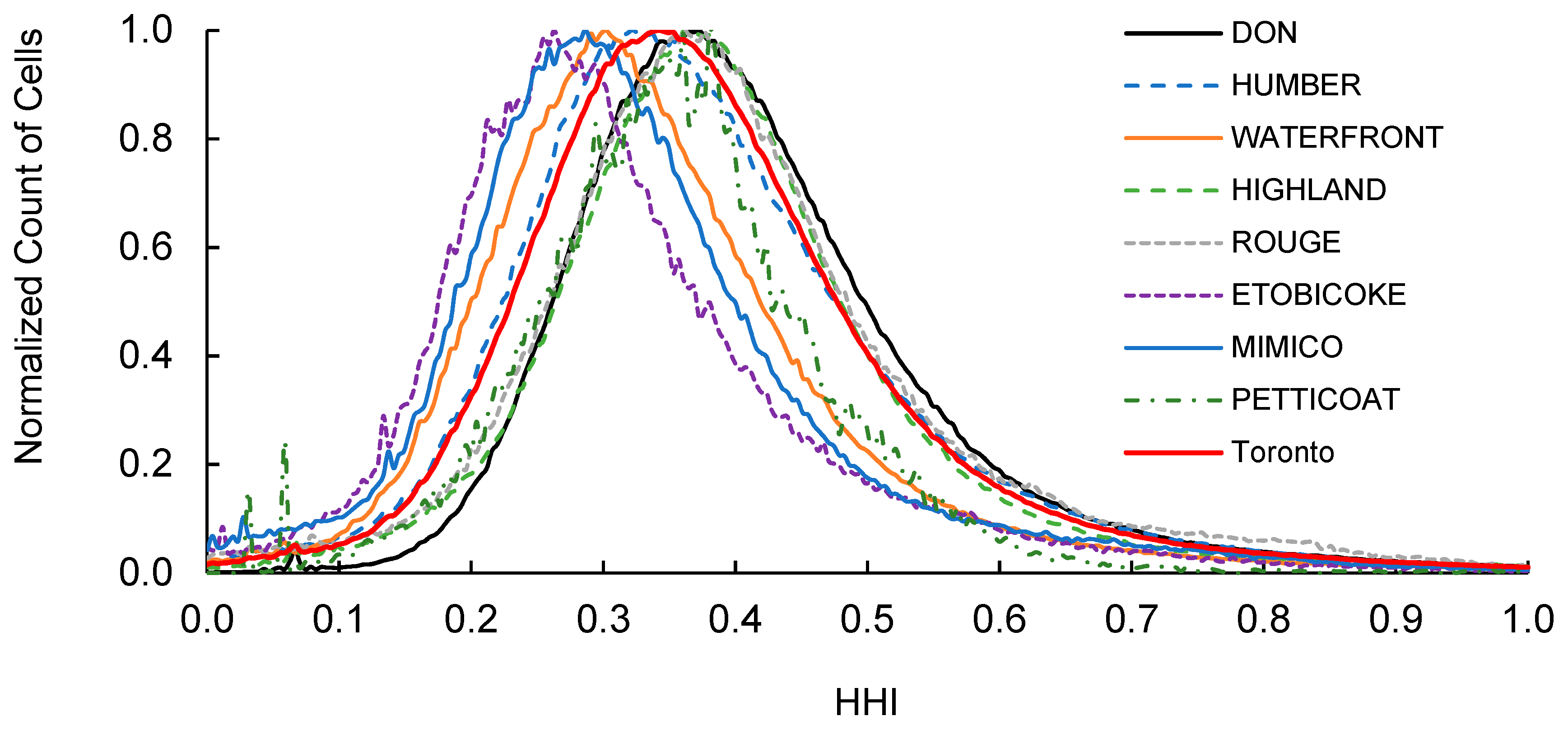
3.1. HHI Map
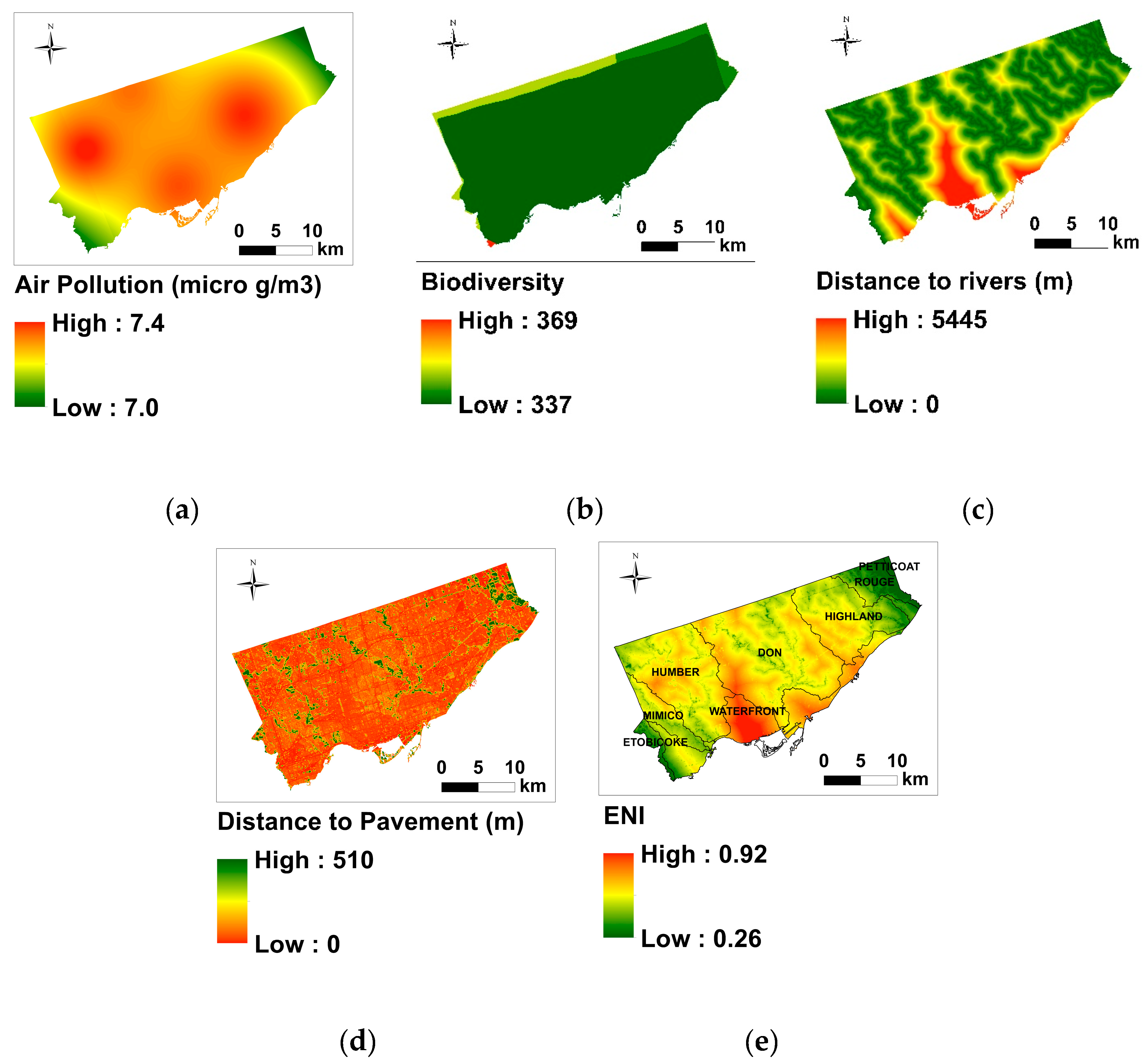
3.2. ENI Map
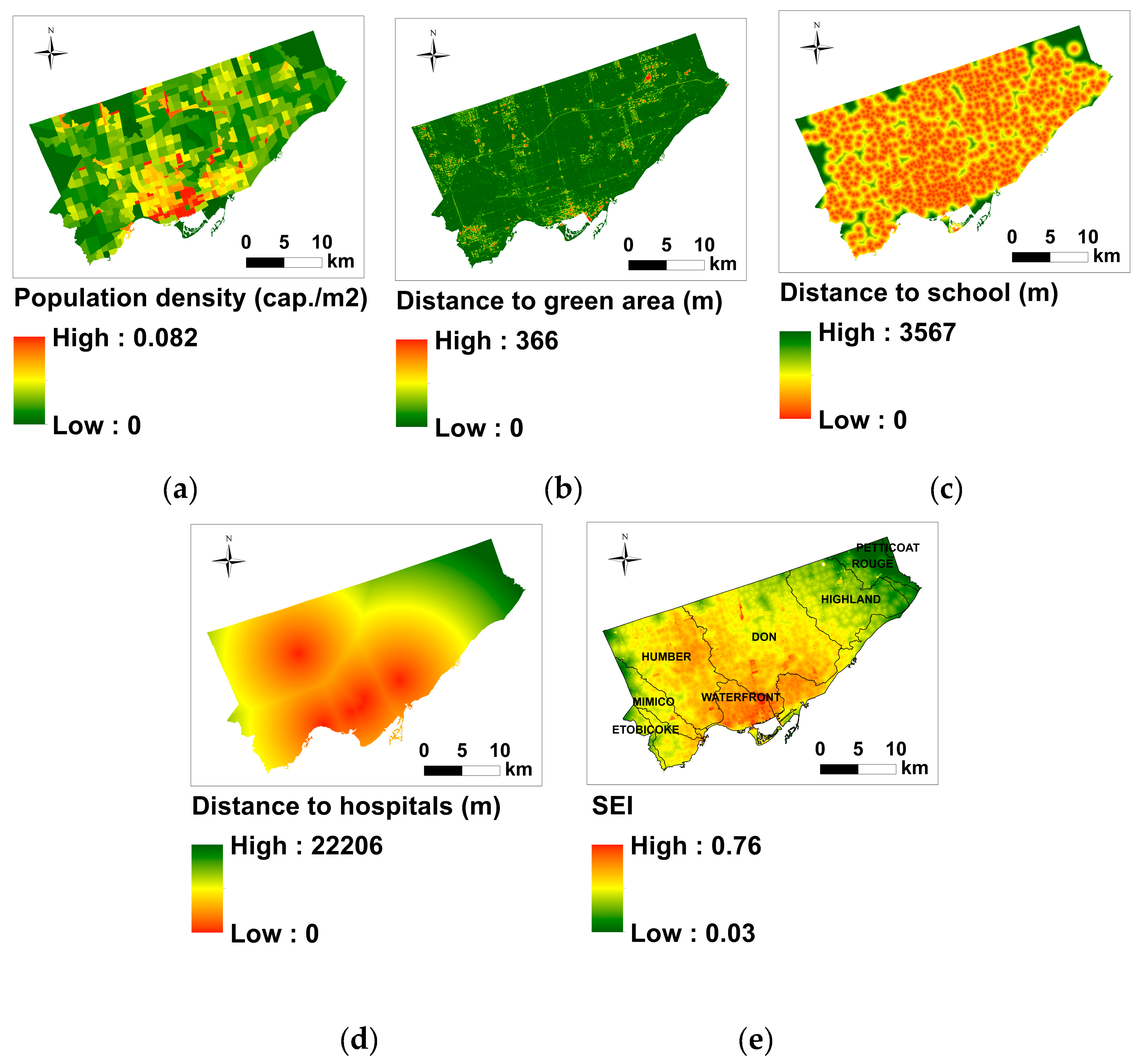
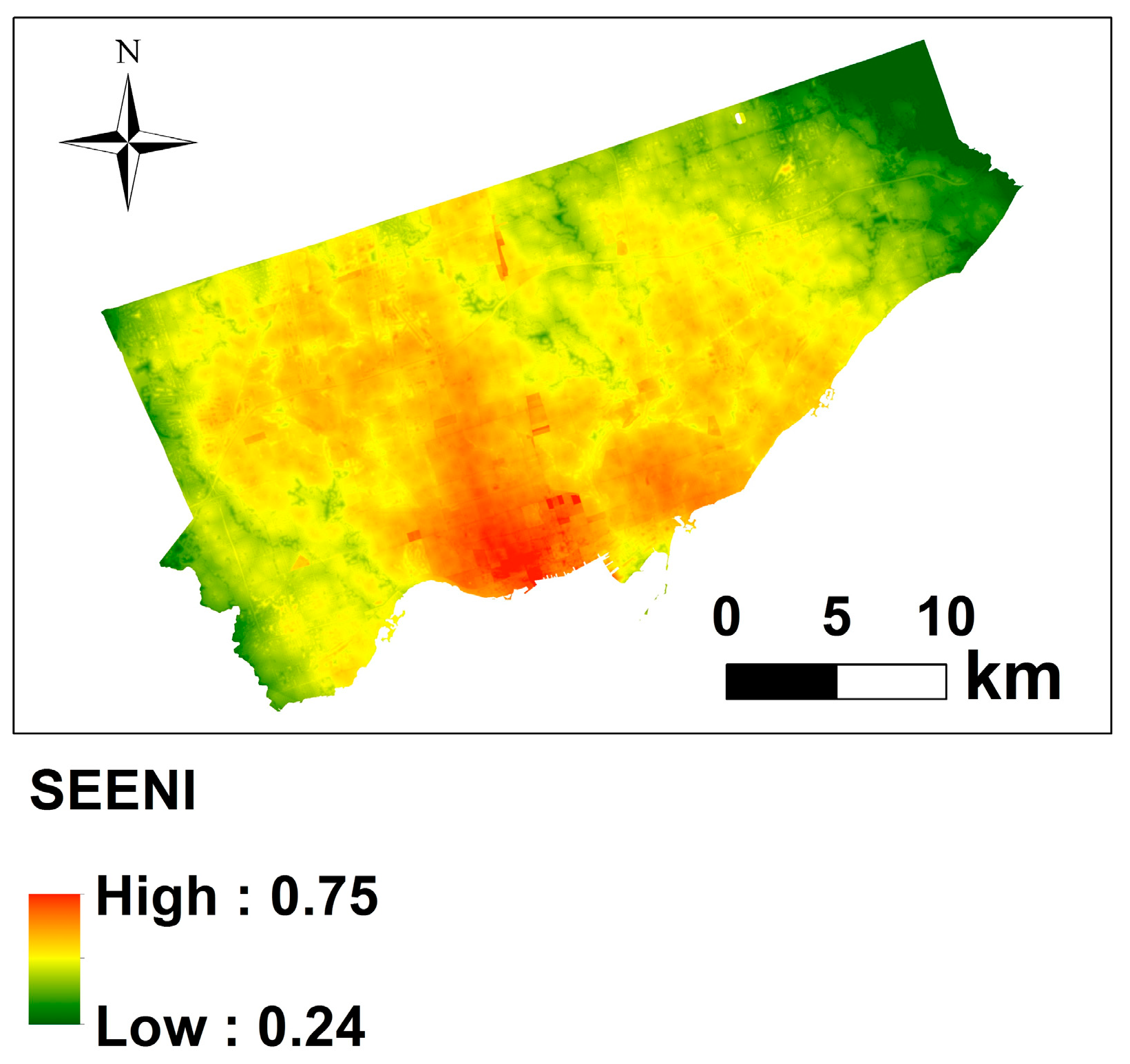
3.3. SEI Map
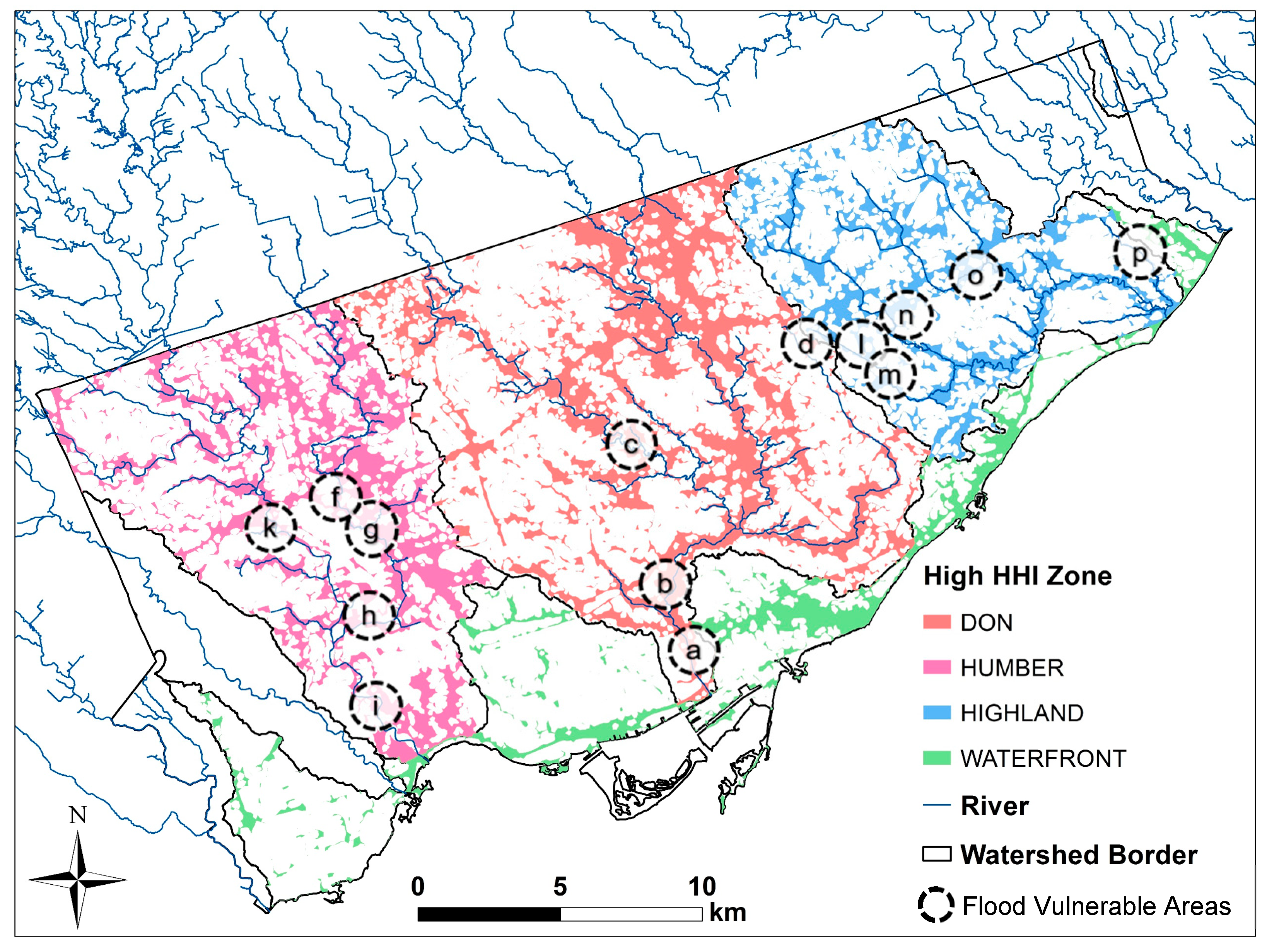
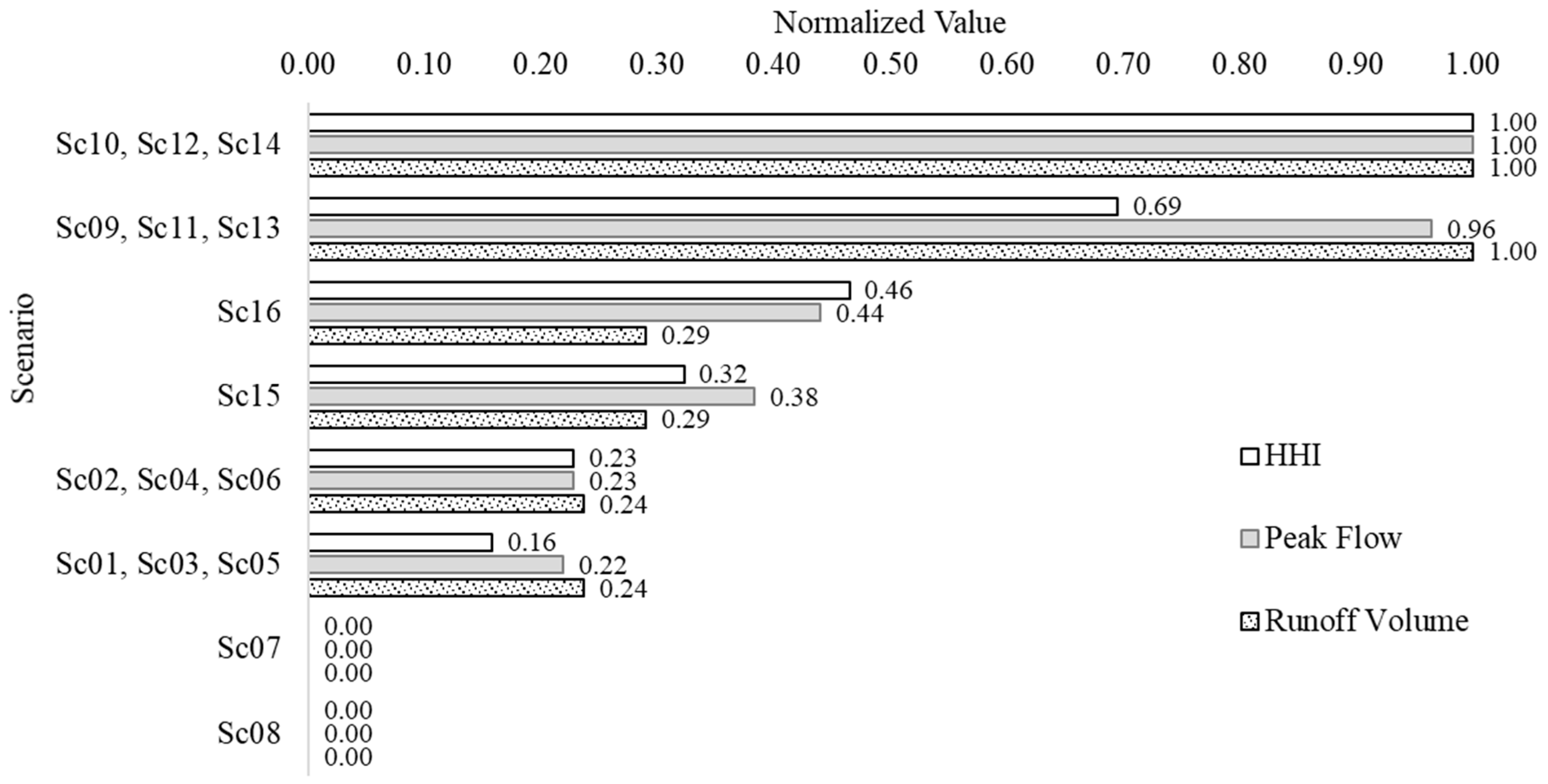
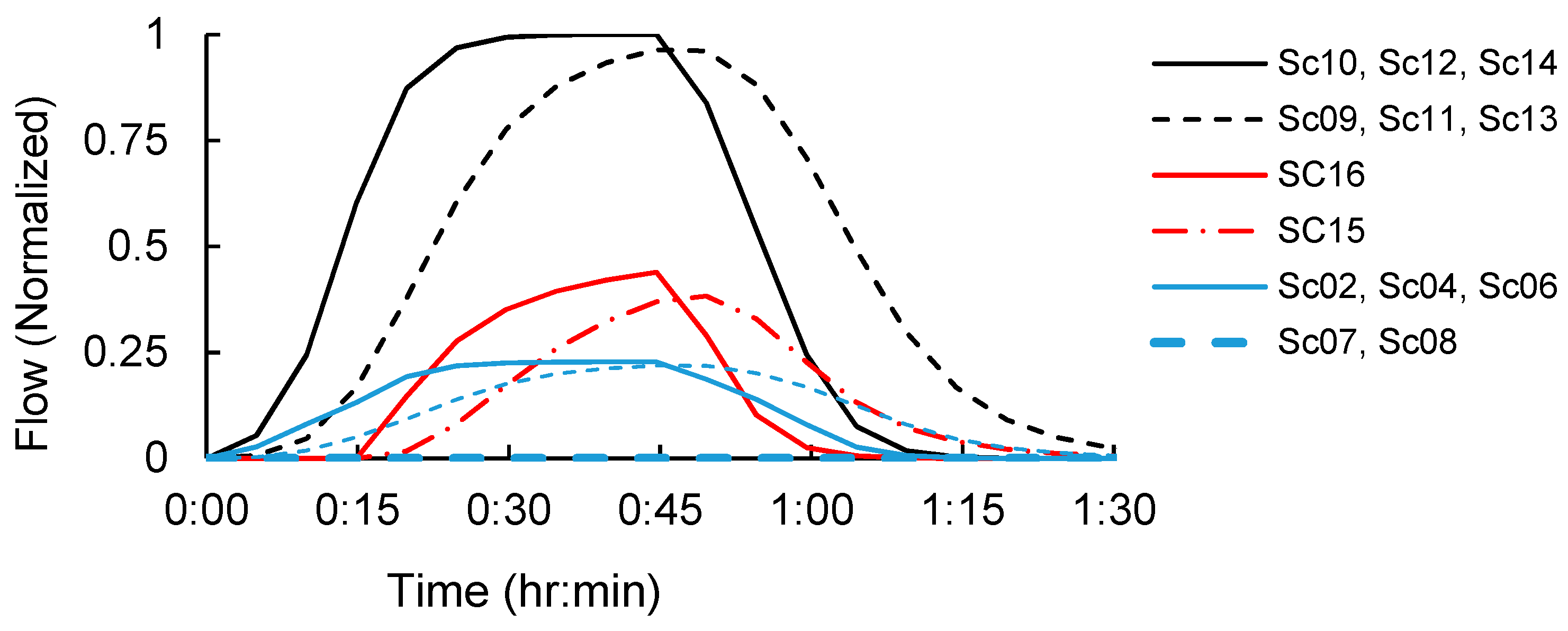
3.4. Validation of Indices
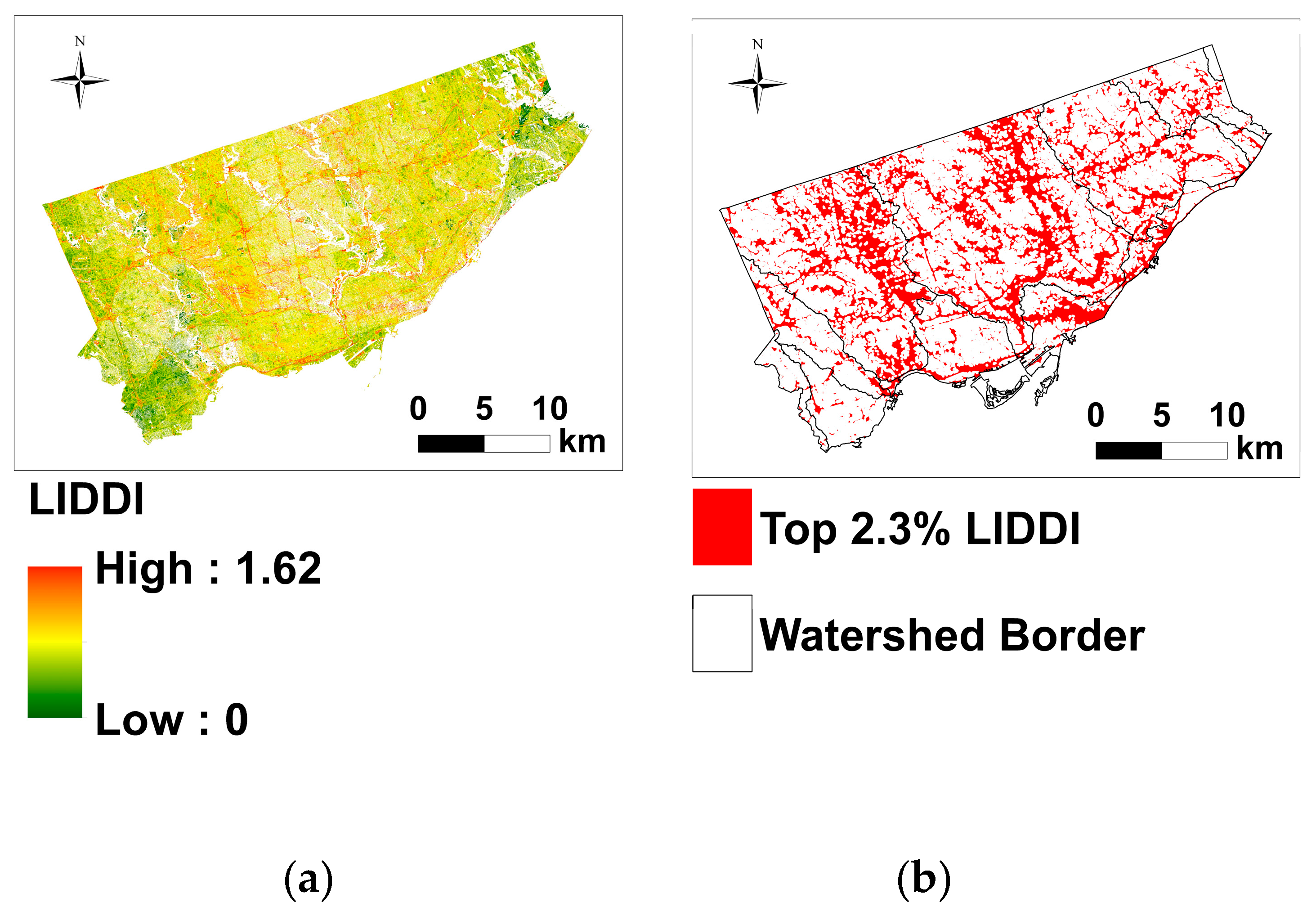
3.5. LIDDI Map
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Frantzeskaki, N.; Kabisch, N.; McPhearson, T. Advancing urban environmental governance: Understanding theories, practices and processes shaping urban sustainability and resilience. Environ. Sci. Policy 2016, 62, 1–6. [Google Scholar] [CrossRef]
- De Macedo, M.B.; do Lago, C.A.F.; Mendiondo, E.M. Stormwater volume reduction and water quality improvement by bioretention: Potentials and challenges for water security in a subtropical catchment. Sci. Total Environ. 2019, 647, 923–931. [Google Scholar] [CrossRef] [PubMed]
- Coffman, L.; Clar, M.; Weinstein, N. Overview of low impact development for stormwater management. In Proceedings of the 25th Annual Conference on Water Resources Planning and Management, Chicago, IL, USA, 7–10 June 1998; pp. 16–21. [Google Scholar]
- Fletcher, T.D.; Shuster, W.; Hunt, W.F.; Ashley, R.; Butler, D.; Arthur, S.; Trowsdale, S.; Barraud, S.; Semadeni-Davies, A.; Bertrand-Krajewski, J.-L.; et al. SUDS, LID, BMPs, WSUD and more—The Evolution and Application of Terminology Surrounding Urban Drainage. Urban Water J. 2015, 12, 525–542. [Google Scholar] [CrossRef]
- Prince George’s County Maryland. Low-Impact Development Design Strategies an Integrated Design Approach Low-Impact Development: An Integrated Design Approach; Department of Environmental Resources: Largo, MD, USA, 1999.
- Cheng, M.-S.; Coffman, L.S.; Clar, M.L. Low-Impact Development Hydrologic Analysis. In Urban Drainage Modeling: Proceedings of the Specialty Symposium of the World Water and Environmental Resources Congress, Orlando, FL, USA, 20-24 May 2001; American Society of Civil Engineers: Reston, VA, USA, 2001; pp. 659–681. [Google Scholar]
- Coffman, L.S. Low Impact Development: Smart Technology for Clean Water. In Proceedings of the Ninth International Conference on Urban Drainage, Portland, OR, USA, 8–13 September 2002; American Society for Civil Engineers: Reston, VA, USA, 2002; pp. 1–11. [Google Scholar]
- Khan, U.T.; Valeo, C.; Chu, A.; He, J. A Data Driven Approach to Bioretention Cell Performance: Prediction and Design. Water 2013, 5, 13–28. [Google Scholar] [CrossRef]
- Khan, U.T.; Valeo, C.; Chu, A.; van Duin, B. Bioretention Cell Efficacy In Cold Climates: Part 1—Hydrologic Performance. Can. J. Civ. Eng. 2012, 39, 1210–1221. [Google Scholar] [CrossRef]
- Khan, U.T.; Valeo, C.; Chu, A.; van Duin, B. Bioretention Cell Efficacy In Cold Climates: Part 2—Water Quality Performance. Can. J. Civ. Eng. 2012, 39, 1222–1233. [Google Scholar] [CrossRef]
- Ishaq, S.; Hewage, K.; Farooq, S.; Sadiq, R. State of provincial regulations and guidelines to promote low impact development (LID) alternatives across Canada: Content analysis and comparative assessment. J. Environ. Manag. 2019, 235, 389–402. [Google Scholar] [CrossRef]
- Elliott, A.H.; Trowsdale, S.A. A Review of Models for Low Impact Urban Stormwater Drainage. Environ. Model. Softw. 2007, 22, 394–405. [Google Scholar] [CrossRef]
- Coffman, L.S.; Goo, R.; Frederick, R. Low-Impact Development An Innovative Alternative Approach to Stormwater Management. In Proceedings of the 29th Annual Water Resources Planning and Management Conference, Tempe, AZ, USA, 6–9 June 1999; pp. 1–10. [Google Scholar]
- Vogel, J.R.; Moore, T.L.; Coffman, R.R.; Rodie, S.N.; Hutchinson, S.L.; McDonough, K.R.; McLemore, A.J.; McMaine, J.T. Critical Review of Technical Questions Facing Low Impact Development and Green Infrastructure: A Perspective from the Great Plains. Water Environ. Res. 2015, 87, 849–862. [Google Scholar] [CrossRef]
- Johns, C.; Shaheen, F.; Woodhouse, M. Green Infrastructure and Stormwater Management in Toronto: Policy Context and Instruments, Centre for Urban Research and Land Development; Centre for Urban Research and Land Development: Toronto, ON, Canada, 2018. [Google Scholar]
- Li, J.; Deng, C.; Li, Y.; Li, Y.; Song, J. Comprehensive Benefit Evaluation System for Low-Impact Development of Urban Stormwater Management Measures. Water Resour. Manag. 2017, 31, 4745–4758. [Google Scholar] [CrossRef]
- Mao, X.; Jia, H.; Yu, S.L. Assessing the ecological benefits of aggregate LID-BMPs through modelling. Ecol. Modell. 2017, 353, 139–149. [Google Scholar] [CrossRef]
- Schifman, L.A.; Prues, A.; Gilkey, K.; Shuster, W.D. Realizing the opportunities of black carbon in urban soils: Implications for water quality management with green infrastructure. Sci. Total Environ. 2018, 644, 1027–1035. [Google Scholar] [CrossRef] [PubMed]
- Xie, N.; Akin, M.; Shi, X. Permeable concrete pavements: A review of environmental benefits and durability. J. Clean. Prod. 2019, 210, 1605–1621. [Google Scholar] [CrossRef]
- Seo, M.; Jaber, F.; Srinivasan, R.; Jeong, J. Evaluating the Impact of Low Impact Development (LID) Practices on Water Quantity and Quality under Different Development Designs Using SWAT. Water 2017, 9, 193. [Google Scholar] [CrossRef]
- Capotorti, G.; Alós Ortí, M.M.; Copiz, R.; Fusaro, L.; Mollo, B.; Salvatori, E.; Zavattero, L. Biodiversity and ecosystem services in urban green infrastructure planning: A case study from the metropolitan area of Rome (Italy). Urban For. Urban Green. 2019, 37, 87–96. [Google Scholar] [CrossRef]
- Morakinyo, T.E.; Lam, Y.F.; Hao, S. Evaluating the role of green infrastructures on near-road pollutant dispersion and removal: Modelling and measurement. J. Environ. Manag. 2016, 182, 595–605. [Google Scholar] [CrossRef]
- Nordbo, A.; Järvi, L.; Haapanala, S.; Wood, C.R.; Vesala, T. Fraction of natural area as main predictor of net CO2 emissions from cities. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Chenoweth, J.; Anderson, A.R.; Kumar, P.; Hunt, W.F.; Chimbwandira, S.J.; Moore, T.L.C. The interrelationship of green infrastructure and natural capital. Land Use Policy 2018, 75, 137–144. [Google Scholar] [CrossRef]
- Rafael, S.; Vicente, B.; Rodrigues, V.; Miranda, A.I.; Borrego, C.; Lopes, M. Impacts of green infrastructures on aerodynamic flow and air quality in Porto’s urban area. Atmos. Environ. 2018, 190, 317–330. [Google Scholar] [CrossRef]
- Jayasooriya, V.M.; Ng, A.W.M.; Muthukumaran, S.; Perera, B.J.C. Urban Forestry & Urban Greening Green infrastructure practices for improvement of urban air quality. Urban For. Urban Green. 2017, 21, 34–47. [Google Scholar]
- Moore, T.L.C.; Hunt, W.F. Ecosystem service provision by stormwater wetlands and ponds—A means for evaluation? Water Res. 2012, 46, 6811–6823. [Google Scholar] [CrossRef] [PubMed]
- Hassall, C.; Anderson, S. Stormwater ponds can contain comparable biodiversity to unmanaged wetlands in urban areas. Hydrobiologia 2015, 745, 137–149. [Google Scholar] [CrossRef]
- Hassall, C. The ecology and biodiversity of urban ponds. Wiley Interdiscip. Rev. Water 2014, 1, 187–206. [Google Scholar] [CrossRef]
- Taylor, J.R.; Lovell, S.T. Urban home food gardens in the Global North: Research traditions and future directions. Agric. Hum. Values 2014, 31, 285–305. [Google Scholar] [CrossRef]
- Hostetler, M.; Allen, W.; Meurk, C. Landscape and Urban Planning Conserving urban biodiversity? Creating green infrastructure is only the first step. Landsc. Urban Plan. 2011, 100, 369–371. [Google Scholar] [CrossRef]
- Pinho, P.; Correia, O.; Lecoq, M.; Munzi, S.; Vasconcelos, S.; Gonçalves, P.; Rebelo, R.; Antunes, C.; Silva, P.; Freitas, C.; et al. Evaluating green infrastructure in urban environments using a multi-taxa and functional diversity approach. Environ. Res. 2016, 147, 601–610. [Google Scholar] [CrossRef]
- Ozturk, Z.C.; Dursun, S. Low Impact Development and Green Infrastructure. Sci. J. Environ. Sci. 2016, 5, 75–80. [Google Scholar]
- Winz, I.; Brierley, G.; Trowsdale, S. Dominant perspectives and the shape of urban stormwater futures. Urban Water J. 2011, 8, 337–349. [Google Scholar] [CrossRef]
- Russo, A.; Escobedo, F.J.; Cirella, G.T.; Zerbe, S. Edible green infrastructure: An approach and review of provisioning ecosystem services and disservices in urban environments. Agric. Ecosyst. Environ. 2017, 242, 53–66. [Google Scholar] [CrossRef]
- Kevern, J.T.; Asce, A.M. Green Building and Sustainable Infrastructure: Sustainability Education for Civil Engineers. J. Prof. Issues Eng. Educ. Pract. 2011, 137, 107–112. [Google Scholar] [CrossRef]
- Han, H.; Li, H.; Zhang, K. Urban Water Ecosystem Health Evaluation Based on the Improved Fuzzy Matter-Element Extension Assessment Model: Case Study from Zhengzhou City, China. Math. Probl. Eng. 2019, 2019, 7502342. [Google Scholar] [CrossRef]
- Markevych, I.; Schoierer, J.; Hartig, T.; Chudnovsky, A.; Hystad, P.; Dzhambov, A.M.; de Vries, S.; Triguero-Mas, M.; Brauer, M.; Nieuwenhuijsen, M.J.; et al. Exploring pathways linking greenspace to health: Theoretical and methodological guidance. Environ. Res. 2017, 158, 301–317. [Google Scholar] [CrossRef] [PubMed]
- Wood, L.; Hooper, P.; Foster, S.; Bull, F. Public green spaces and positive mental health—Investigating the relationship between access, quantity and types of parks and mental wellbeing. Health Place 2017, 48, 63–71. [Google Scholar] [CrossRef] [PubMed]
- United States Environmental Protection Agency (EPA) Terminology of Low Impact Development: Distinguishing LID from Other Techniques That Address Community Growth Issues. Available online: https://www.epa.gov/sites/production/files/2015-09/documents/bbfs2terms.pdf (accessed on 6 November 2019).
- Eckart, K.; McPhee, Z.; Bolisetti, T. Performance and implementation of low impact development—A review. Sci. Total Environ. 2017, 607–608, 413–432. [Google Scholar] [CrossRef]
- Kändler, N.; Annus, I.; Vassiljev, A.; Puust, R.; Kaur, K. Smart In-Line Storage Facilities in Urban Drainage Network. Proceedings 2018, 2, 631. [Google Scholar] [Green Version]
- Pochwat, K.; Iličić, K. A simplified dimensioning method for high-efficiency retention tanks. E3S Web Conf. VI International Conference of Science and Technology INFRAEKO 2018 Modern Cities. Infrastruct. Environ. 2018, 45, 1–8. [Google Scholar]
- Chang, C.L.; Lo, S.L.; Huang, S.M. Optimal strategies for best management practice placement in a synthetic watershed. Environ. Monit. Assess. 2009, 153, 359–364. [Google Scholar] [CrossRef]
- Ariza, S.L.J.; Martínez, J.A.; Muñoz, A.F.; Quijano, J.P.; Rodríguez, J.P.; Camacho, L.A.; Díaz-Granados, M. A Multicriteria Planning Framework to Locate and Select Sustainable Urban Drainage Systems (SUDS) in Consolidated Urban Areas. Sustainability 2019, 11, 2312. [Google Scholar] [CrossRef]
- Kuller, M.; Bach, P.M.; Roberts, S.; Browne, D.; Deletic, A. A planning-support tool for spatial suitability assessment of green urban stormwater infrastructure. Sci. Total Environ. 2019, 686, 856–868. [Google Scholar] [CrossRef]
- Kuller, M.; Bach, P.M.; Ramirez-Lovering, D.; Deletic, A. Framing water sensitive urban design as part of the urban form: A critical review of tools for best planning practice. Environ. Model. Softw. 2017, 96, 265–282. [Google Scholar] [CrossRef]
- Kaykhosravi, S.; Khan, U.; Jadidi, A.; Kaykhosravi, S.; Khan, U.T.; Jadidi, A. A Comprehensive Review of Low Impact Development Models for Research, Conceptual, Preliminary and Detailed Design Applications. Water 2018, 10, 1541. [Google Scholar] [CrossRef]
- Malczewski, J.; Rinner, C. Multicriteria Decision Analysis in Geographic Information Science; Springer: New York, NY, USA, 2015; ISBN 9783540747567. [Google Scholar]
- Zischg, J.; Zeisl, P.; Winkler, D.; Rauch, W.; Sitzenfrei, R. On the sensitivity of geospatial low impact development locations to the centralized sewer network. Water Sci. Technol. 2018, 77, 1851–1860. [Google Scholar] [CrossRef] [PubMed]
- Bach, P.M.; McCarthy, D.T.; Urich, C.; Sitzenfrei, R.; Kleidorfer, M.; Rauch, W.; Deletic, A. A planning algorithm for quantifying decentralised water management opportunities in urban environments. Water Sci. Technol. 2013, 68, 1857–1865. [Google Scholar] [CrossRef] [PubMed]
- Song, J.Y.; Chung, E. A Multi-Criteria Decision Analysis System for Prioritizing Sites and Types of Low Impact Development Practices: Case of Korea. Water 2017, 9, 291. [Google Scholar] [CrossRef]
- Ahmed, K.; Chung, E.-S.; Song, J.-Y.; Shahid, S. Effective Design and Planning Specification of Low Impact Development Practices Using Water Management Analysis Module (WMAM): Case of Malaysia. Water 2017, 9, 173. [Google Scholar] [CrossRef]
- Chung, E.S.; Hong, W.P.; Lee, K.S.; Burian, S.J. Integrated Use of a Continuous Simulation Model and Multi-Attribute Decision-Making for Ranking Urban Watershed Management Alternatives. Water Resour. Manag. 2010, 25, 641–659. [Google Scholar] [CrossRef]
- Lee, J.G.; Selvakumar, A.; Alvi, K.; Riverson, J.; Zhen, J.X.; Shoemaker, L.; Lai, F. A watershed-scale design optimization model for stormwater best management practices. Environ. Model. Softw. 2012, 37, 6–18. [Google Scholar] [CrossRef]
- Charlesworth, S.; Warwick, F.; Lashford, C. Decision-Making and Sustainable Drainage: Design and Scale. Sustainability 2016, 8, 782. [Google Scholar] [CrossRef]
- Jato-Espino, D.; Sillanpää, N.; Charlesworth, S.M.; Andrés-Doménech, I. Coupling GIS with Stormwater Modelling for the Location Prioritization and Hydrological Simulation of Permeable Pavements in Urban Catchments. Water 2016, 8, 451. [Google Scholar] [CrossRef]
- Yang, J.S.; Son, M.W.; Chung, E.S.; Kim, I.H. Prioritizing Feasible Locations for Permeable Pavement Using MODFLOW and Multi-criteria Decision Making Methods. Water Resour. Manag. 2015, 29, 4539–4555. [Google Scholar] [CrossRef]
- Lerer, S.; Arnbjerg-Nielsen, K.; Mikkelsen, P. A Mapping of Tools for Informing Water Sensitive Urban Design Planning Decisions—Questions, Aspects and Context Sensitivity. Water 2015, 7, 993–1012. [Google Scholar] [CrossRef]
- Martin-Miklea, C.J.; de Beurs, K.M.; Julianb, J.P.; Mayer, P.M. Identifying priority sites for low impact development (LID) in a mixed-use watershed. Landsc. Urban Plan. 2015, 140, 29–41. [Google Scholar] [CrossRef] [Green Version]
- Walter, M.T.; Walter, M.F.; Brooks, E.S.; Steenhuis, T.S.; Boll, J.; Weiler, K. Hydrologically Sensitive Areas: Variable Source Area Hydrology Implications for Water Quality Risk Assessment. J. Soil Water Conserv. 2000, 55, 277–284. [Google Scholar]
- Zhang, A.; Shi, H.; Li, T.; Fu, X. Analysis of the influence of rainfall spatial uncertainty on hydrological simulations using the bootstrap method. Atmosphere 2018, 9, 71. [Google Scholar] [CrossRef]
- Natural Resources Conservation Service. National Engineering Handbook Chapter 4 Storm Rainfall Depth; United States Department of Agriculture: Washington DC, USA, 2015.
- Zhang, K.; Chui, T.F.M. A Comprehensive Review of Spatial Allocation of LID-BMP-GI Practices: Strategies and Optimization Tools. Sci. Total Environ. 2018, 621, 915–929. [Google Scholar] [CrossRef]
- Bach, P.M.; Rauch, W.; Mikkelsen, P.S.; McCarthy, D.T.; Deletic, A. A critical review of integrated urban water modelling—Urban drainage and beyond. Environ. Model. Softw. 2014, 54, 88–107. [Google Scholar] [CrossRef]
- Nocco, M.A.; Rouse, S.E.; Balster, N.J. Vegetation type alters water and nitrogen budgets in a controlled, replicated experiment on residential-sized rain gardens planted with prairie, shrub, and turfgrass. Urban Ecosyst. 2016, 19, 1665–1691. [Google Scholar] [CrossRef]
- Toronto and Region Conservation Authority (TRCA) Low Impact Development. Available online: https://trca.ca/conservation/restoration/low-impact-development/ (accessed on 6 November 2019).
- Mein, R.G.; Larson, C.L. Modeling infiltration during a steady rain. Water Resour. Res. 1973, 9, 384–394. [Google Scholar] [CrossRef] [Green Version]
- McCuen, R.H.; Wong, S.L.; Rawls, W.J. Estimating urban time of concentration. J. Hydraul. Eng. 1984, 110, 887–904. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGrawHill: New York, NY, USA, 1988. [Google Scholar]
- European Environment Agency (EEA). Environmental Indicators: Typology and Overview; European Environment Agency: Copenhagen, Denmark, 1999. [Google Scholar]
- Matos, P.; Vieira, J.; Rocha, B.; Branquinho, C.; Pinho, P. Modeling the provision of air-quality regulation ecosystem service provided by urban green spaces using lichens as ecological indicators. Sci. Total Environ. 2019, 665, 521–530. [Google Scholar] [CrossRef]
- Buccolieri, R.; Jeanjean, A.P.R.; Gatto, E.; Leigh, R.J. The impact of trees on street ventilation, NOx and PM2.5 concentrations across heights in Marylebone Rd street canyon, central London. Sustain. Cities Soc. 2018, 41, 227–241. [Google Scholar] [CrossRef]
- Kyrö, K.; Brenneisen, S.; Kotze, D.J.; Szallies, A.; Gerner, M.; Lehvävirta, S. Local habitat characteristics have a stronger effect than the surrounding urban landscape on beetle communities on green roofs. Urban For. Urban Green. 2018, 29, 122–130. [Google Scholar] [CrossRef] [Green Version]
- Pei, N.; Wang, C.; Jin, J.; Jia, B.; Chen, B.; Qie, G.; Qiu, E.; Gu, L.; Sun, R.; Li, J.; et al. Long-term afforestation efforts increase bird species diversity in Beijing, China. Urban For. Urban Green. 2018, 29, 88–95. [Google Scholar] [CrossRef]
- Lucke, T.; Nichols, P.W.B. The pollution removal and stormwater reduction performance of street-side bioretention basins after ten years in operation. Sci. Total Environ. 2015, 536, 784–792. [Google Scholar] [CrossRef] [PubMed]
- Kluge, B.; Markert, A.; Facklam, M.; Sommer, H.; Kaiser, M.; Pallasch, M.; Wessolek, G. Metal accumulation and hydraulic performance of bioretention systems after long-term operation. J. Soils Sediments 2018, 18, 431–441. [Google Scholar] [CrossRef]
- Ma, Y.; He, W.; Zhao, H.; Zhao, J.; Wu, X.; Wu, W.; Li, X.; Yin, C. Influence of Low Impact Development practices on urban diffuse pollutant transport process at catchment scale. J. Clean. Prod. 2019, 213, 357–364. [Google Scholar] [CrossRef]
- Passeport, E.; Vidon, P.; Forshay, K.J.; Harris, L.; Kaushal, S.S.; Kellogg, D.Q.; Lazar, J.; Mayer, P.; Stander, E.K. Ecological Engineering Practices for the Reduction of Excess Nitrogen in Human-Influenced Landscapes: A Guide for Watershed Managers. Environ. Manag. 2013, 51, 392–413. [Google Scholar] [CrossRef]
- Weitman, D.; Weinberg, A.; Goo, R. Reducing stormwater costs through LID strategies and practices. In Proceedings of the Low Impact Development for Urban Ecosystem and Habitat Protection, Seattle, WA, USA, 16–19 November 2008. [Google Scholar]
- Shuster, W.D.; Gehring, R.; Gerken, J. Prospects for enhanced groundwater recharge via infiltration of urban storm water runoff: A case study. J. Soil Water Conserv. 2007, 62, 129–137. [Google Scholar]
- Deeb, M.; Groffman, P.M.; Joyner, J.L.; Lozefski, G.; Paltseva, A.; Lin, B.; Mania, K.; Cao, D.L.; McLaughlin, J.; Muth, T.; et al. Soil and microbial properties of green infrastructure stormwater management systems. Ecol. Eng. 2018, 125, 68–75. [Google Scholar] [CrossRef]
- McPhillips, L.; Walter, M.T. Hydrologic conditions drive denitrification and greenhouse gas emissions in stormwater detention basins. Ecol. Eng. 2015, 85, 67–75. [Google Scholar] [CrossRef] [Green Version]
- Hunt, W.F.; Davis, A.P.; Traver, R.G. Meeting Hydrologic and Water Quality Goals Through Targeted Bioretention Design. J. Environ. Eng. 2012, 138, 698–707. [Google Scholar] [CrossRef]
- Ballard, B.W.; Wilson, S.; Udale-Clarke, H.; Illman, S.; Scott, T.; Ashley, R.; Kellagher, R. The SUDS Manual; Constuction Industry Research and Informsation Association: London, UK, 2015. [Google Scholar]
- Meerow, S.; Newell, J.P. Spatial planning for multifunctional green infrastructure: Growing resilience in Detroit. Landsc. Urban Plan. 2017, 159, 62–75. [Google Scholar] [CrossRef]
- Shackleton, C.M.; Blair, A.; De Lacy, P.; Kaoma, H.; Mugwagwa, N.; Dalu, M.T.; Walton, W. How important is green infrastructure in small and medium-sized towns? Lessons from South Africa. Landsc. Urban Plan. 2018, 180, 273–281. [Google Scholar] [CrossRef]
- Kardan, O.; Gozdyra, P.; Misic, B.; Moola, F.; Palmer, L.J.; Paus, T.; Berman, M.G. Neighborhood greenspace and health in a large urban center. Sci. Rep. 2015, 5, 11610. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dadvand, P.; Poursafa, P.; Heshmat, R.; Motlagh, M.E.; Qorbani, M.; Basagaña, X.; Kelishadi, R. Use of green spaces and blood glucose in children; a population-based CASPIAN-V study. Environ. Pollut. 2018, 243, 1134–1140. [Google Scholar] [CrossRef]
- Kuo, M. How might contact with nature promote human health? Promising mechanisms and a possible central pathway. Front. Psychol. 2015, 6, 1093. [Google Scholar] [CrossRef]
- Scott, J.T.; Kilmer, R.P.; Wang, C.; Cook, J.R.; Haber, M.G. Natural environmental near schools: Potential benefits for socio-emotional and behavioural development in early childhood. Am. J. Community Psychol. 2018, 62, 419–432. [Google Scholar] [CrossRef]
- Leung, W.T.V.; Yee Tiffany Tam, T.; Pan, W.C.; Wu, C.-D.; Lung, S.-C.C.; Spengler, J.D. How is environmental greenness related to students’ academic performance in English and Mathematics? Landsc. Urban Plan. 2019, 181, 118–124. [Google Scholar] [CrossRef]
- Liu, G.C.; Wilson, J.S.; Qi, R.; Ying, J. Green neighborhoods, food retail and childhood overweight: Differences by population density. Am. J. Health Promot. 2007, 21, 317–325. [Google Scholar] [CrossRef]
- Kwak, D.; Kim, H.; Han, M. Runoff Control Potential for Design Types of Low Impact Development in Small Developing Area Using XPSWMM. Procedia Eng. 2016, 154, 1324–1332. [Google Scholar] [CrossRef] [Green Version]
- Kamenetzky, R.D. The Relationship Between the Analytic Hierarchy Process and the Additive Value Function. Decis. Sci. 1982, 13, 702–713. [Google Scholar] [CrossRef]
- Pereira, J.M.C.; Duckstein, L. A multiple criteria decision-making approach to gis-based land suitability evaluation. Int. J. Geogr. Inf. Syst. 1993, 7, 407–424. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers Hydrological Engineer Center. Available online: http://www.hec.usace.army.mil/software/hec-hms/features.aspx (accessed on 6 November 2019).
- Keller, G.; Sherar, J. Low-volume roads engineering: Best management practices field guide; United States Forest Service: Washington, DC, USA, 2005; Chapter 11; pp. 103–114.
- Muir, R.J. Flood Insurance in Canada. Available online: https://www.cityfloodmap.com/2013/12/flood-insurance-in-canada.html (accessed on 6 November 2019).
| ID | Data | Data Structure/Geometry | Data Source |
|---|---|---|---|
| 1 | Air pollution (PM2.5) | Vector/point | Ministry of Environment, Conservation and Parks |
| 2 | Bedrock layer | Vector/polygon | Ministry of Northern Development and Mines |
| 3 | Census tract boundaries 2016 | Vector/polygon | Statistics Canada |
| 4 | Demographics data-Census 2016 | Tabular data | Statistics Canada |
| 5 | Digital elevation model (DEM) | Raster/5 m × 5 m | Ontario Ministry of Natural Resources and Forestry-Provincial Mapping Unit |
| 6 | Ecozones of Ontario | Vector/polygon | Scholars Geoportal |
| 7 | Groundwater table | Vector/point | Groundwater Information Network (GIN) |
| 8 | Land cover | Raster/0.6 m × 0.6 m | City of Toronto |
| 9 | Toronto rivers | Vector/polyline | Toronto and Region Conservation Authority (TRCA) |
| 10 | Surficial geology and saturated hydraulic conductivity (Ks) | Vector/polygon | Government of Canada open data website |
| 11 | Toronto precipitation data | Vector/point | Government of Canada open data website |
| 12 | Educational institute | Vector/point | City of Toronto |
| 13 | Hospital | Vector/point | Google Earth |
| Cell # | HHI | SEENI | LIDDI | Rank |
|---|---|---|---|---|
| 1 | 0.9 | 1 | 1.8 | 1st |
| 2 | 0.9 | 0 | 0.9 | 2nd |
| 3 | 0 | 1 | 0 | 3rd |
| Variable | Low | High |
|---|---|---|
| R (mm/h) | 50 1 | 220 |
| D (mm) | 0 | 24000 2 |
| Ks (mm/h) | 0.3 | 117.8 |
| S (m/m) | 0.0001 | 0.15 3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaykhosravi, S.; Abogadil, K.; Khan, U.T.; Jadidi, M.A. The Low-Impact Development Demand Index: A New Approach to Identifying Locations for LID. Water 2019, 11, 2341. https://doi.org/10.3390/w11112341
Kaykhosravi S, Abogadil K, Khan UT, Jadidi MA. The Low-Impact Development Demand Index: A New Approach to Identifying Locations for LID. Water. 2019; 11(11):2341. https://doi.org/10.3390/w11112341
Chicago/Turabian StyleKaykhosravi, Sarah, Karen Abogadil, Usman T. Khan, and Mojgan A. Jadidi. 2019. "The Low-Impact Development Demand Index: A New Approach to Identifying Locations for LID" Water 11, no. 11: 2341. https://doi.org/10.3390/w11112341
APA StyleKaykhosravi, S., Abogadil, K., Khan, U. T., & Jadidi, M. A. (2019). The Low-Impact Development Demand Index: A New Approach to Identifying Locations for LID. Water, 11(11), 2341. https://doi.org/10.3390/w11112341






