Mathematical Reconstruction of Eroded Beach Ridges at the Ombrone River Delta
Abstract
:1. Introduction
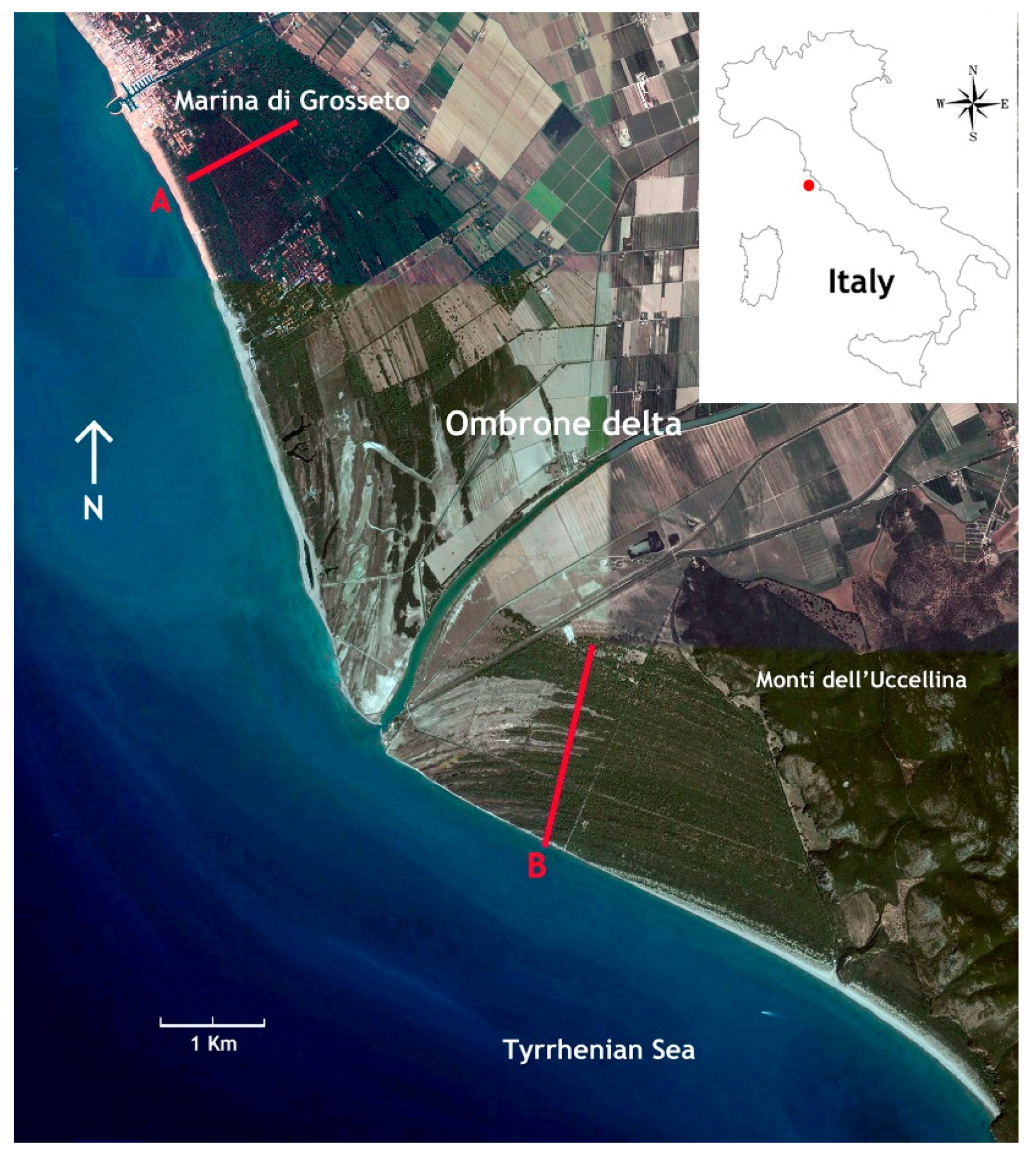
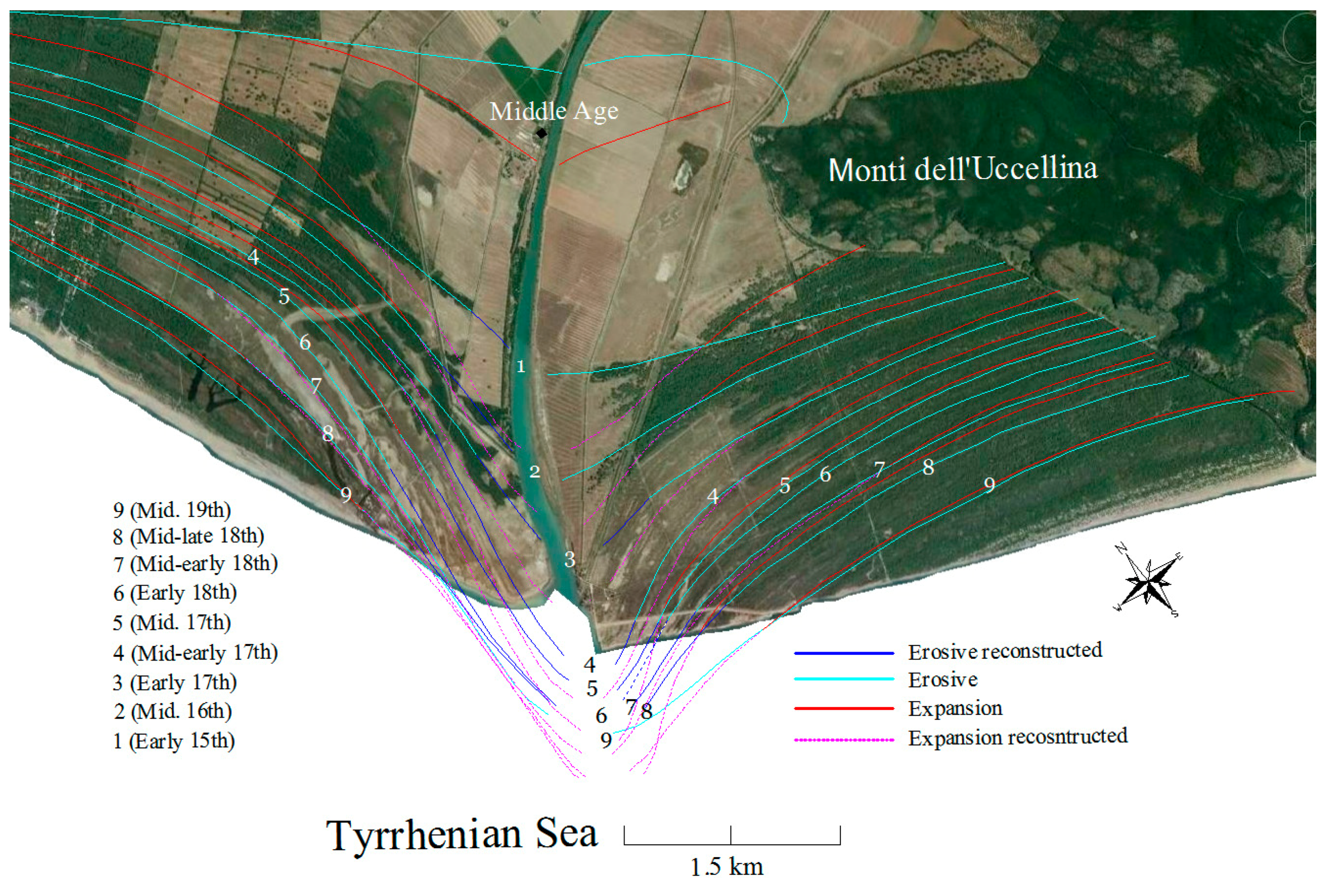
2. Study Area
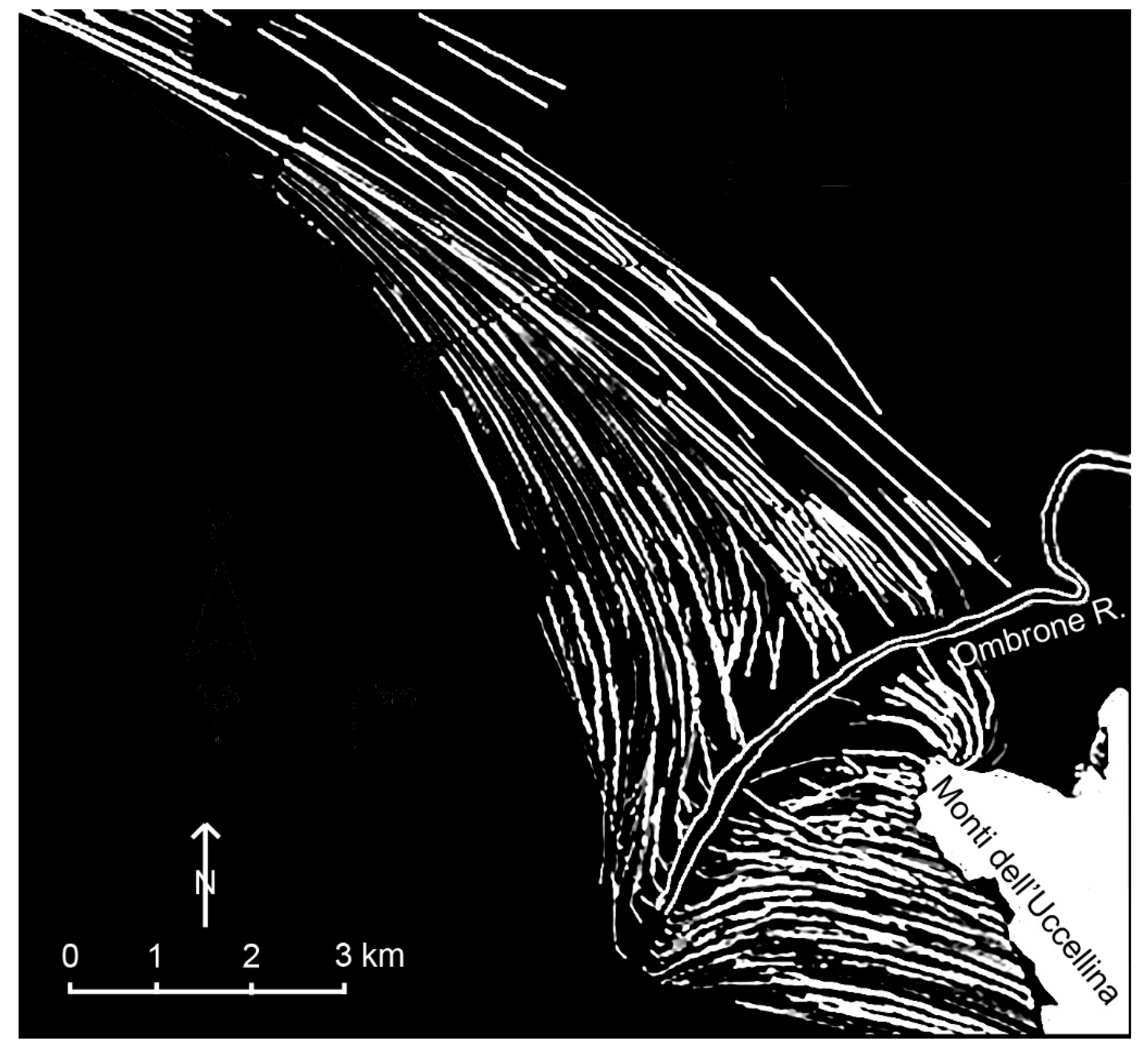
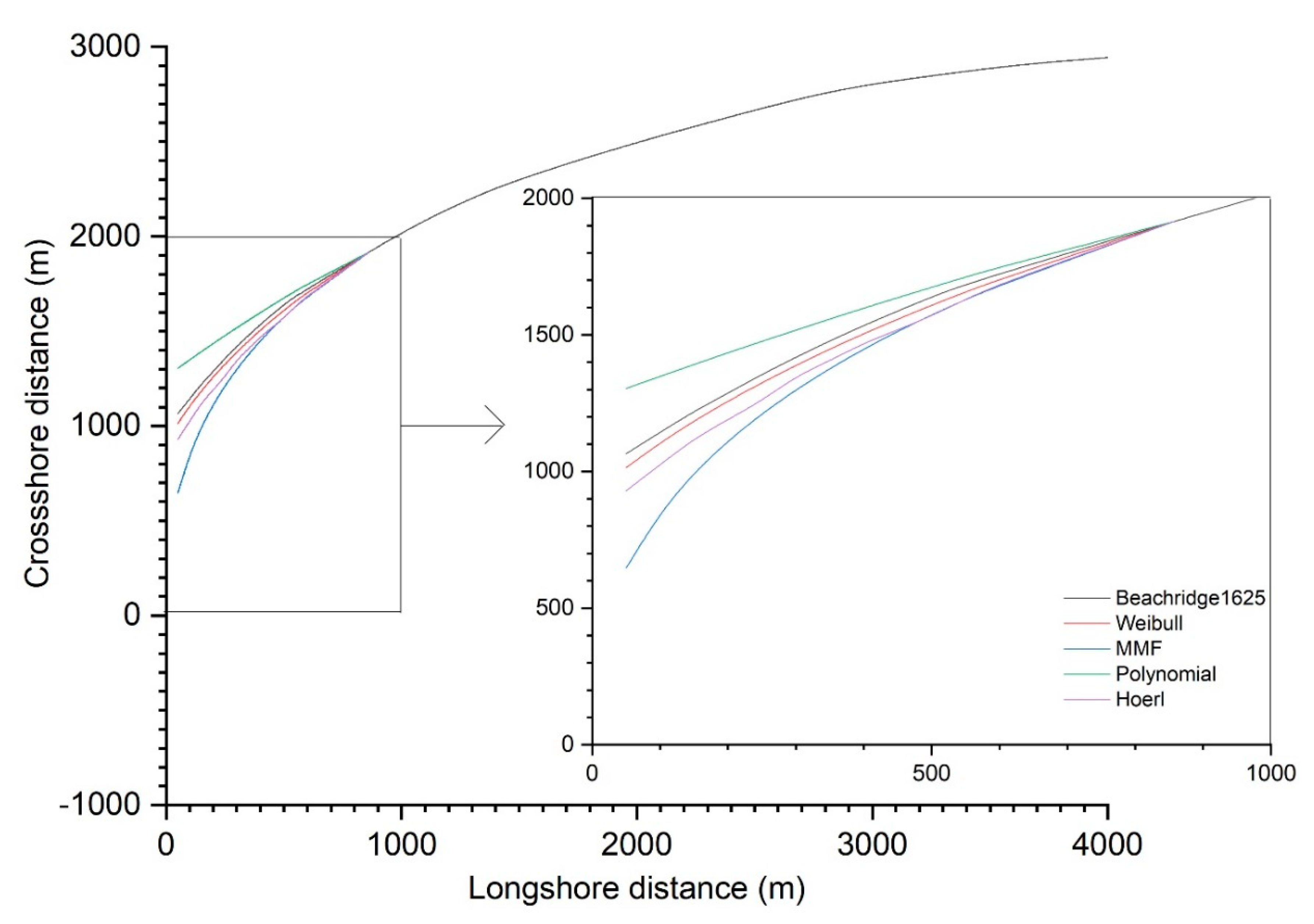
3. Material and Methods
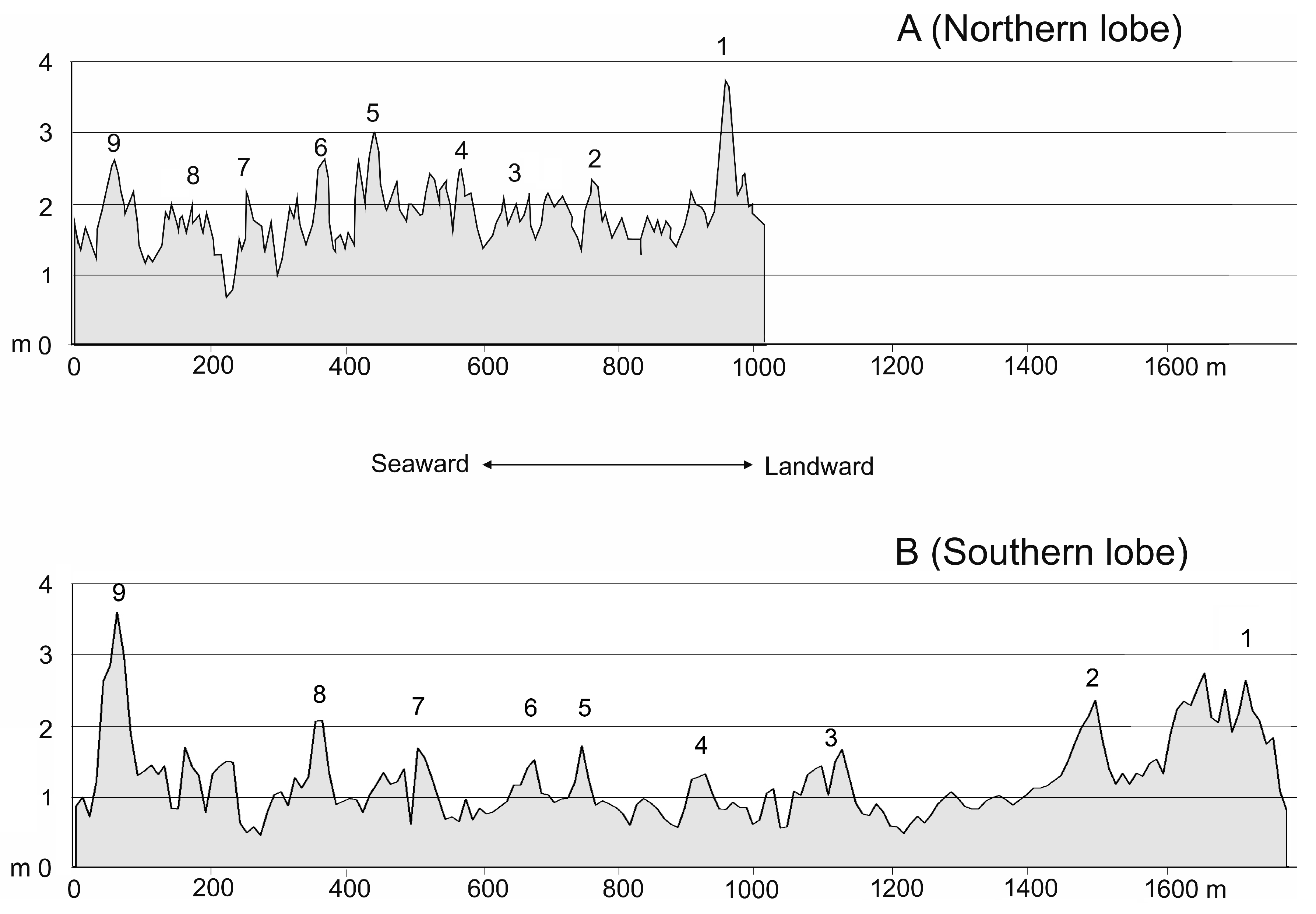
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Syvitski, J.P.; Milliman, J.D. Geology, geography and humans battle for dominance over the delivery of sediment to the coastal ocean. J. Geol. 2007, 115, 1–19. [Google Scholar] [CrossRef]
- Nienhuis, J.H.; Ashton, A.D.; Roos, P.C.; Hulscher, S.J.M.H.; Giosan, L. Wave reworking of abandoned deltas. Geophys. Res. Lett. 2013, 40, 5899–5903. [Google Scholar] [CrossRef] [Green Version]
- Wright, L.D.; Coleman, J.M. Variations in morphology of major river deltas as functions of ocean wave and river discharge regimes. AAPG Bull. 1973, 57, 370–398. [Google Scholar]
- Galloway, W.E. Process framework for describing the morphologic and stratigraphic evolution of deltaic depositional systems. In Deltas, Models for Exploration; Broussard, M.L., Ed.; Houston Geological Society: Houston, TX, USA, 1975; pp. 87–98. [Google Scholar]
- Van Maren, D.S.; Hoekstra, P. Cyclic development of a wave dominated delta. In Proceedings of the Coastal Sediments ’03, Clearwater Beach, FL, USA, 18–23 May 2013; p. 12. [Google Scholar]
- Bellotti, P.; Caputo, C.; Davoli, L.; Evangelista, S.; Valeri, P. Lineamenti morfologici e sedimentologici della piana deltizia del Fiume Ombrone (Toscana Meridionale). Boll. Soc. Geol. It. 1999, 118, 141–148. [Google Scholar]
- Otvos, E.G. Beach ridges–definition and significance. Geomorphology 2000, 32, 83–103. [Google Scholar] [CrossRef]
- Anthony, E.J. Beach ridge progradation in response to sediment supply examples from West Africa. Marine Geol. 1995, 129, 175–186. [Google Scholar] [CrossRef]
- Anthony, E.J. Wave influence in the construction, shaping and destruction of river deltas: A review. Marine Geol. 2015, 361, 53–78. [Google Scholar] [CrossRef]
- Vespremeanu-Stroe, A.; Preoteasa, L.; Zainescu, F.; Rotaru, S.; Croitoru, L.; Timar-Gabor, A. Formation of Danube delta beach ridge plains and signatures in morphology. Quat. Int. 2016, 415, 268–285. [Google Scholar] [CrossRef]
- Psuty, N.P. Spatial variation in coastal foredune development. In Coastal Dunes: Geomorphology, Ecology and Management; Balkema: Rotterdam, The Netherlands, 1992; pp. 3–13. [Google Scholar]
- Pranzini, E. Airborne LIDAR survey applied to the analysis of the historical evolution of the Arno River delta (Italy). J. Coast. Res. 2007, 400–409. [Google Scholar]
- Curray, J.R.; Emmel, F.J.; Crampton, P.J.S. Holocene history of a strand plain, Lagoonal Coast, Nayarit, Mexico. In Lagunas Costeras; Costonares, A.A., Phelger, F.B., Eds.; Un Simposio; Universidad Nacional Autonoma de Mexico: Mexico City, Mexico, 1967; p. 686. [Google Scholar]
- Stapor, F.W. Beach ridge and beach ridge coast. In Encyclopedia of Beaches and Coastal Environments; Schwartz, M.L., Ed.; Hutchinson Ross: Stroudsburg, PA, USA, 1982; pp. 160–161. [Google Scholar]
- Fairbridge, R.W.; Hillaire-Marcel, C. An 8000-yr palaeoclimatic record of the double-hale 45-yr solar cycle. Nature 1977, 268, 413–416. [Google Scholar] [CrossRef]
- Taylor, M.; Stone, G.W. Beach-bridges: A review. J. Coast. Res. 1996, 12, 612–621. [Google Scholar]
- Pranzini, E. Bilancio sedimentario ed evoluzione storica delle spiagge. Il Quaternario 1994, 7, 197–202. [Google Scholar]
- Syvitski, J.P.M.; Vörösmarty, C.J.; Kettner, A.J.; Green, P. Impact of humans on the flux of terrestrial sediment to the global coastal ocean. Science 2005, 308, 376–380. [Google Scholar] [CrossRef] [PubMed]
- Pranzini, E. Updrift river mouth migration on cuspate deltas: Two examples from the coast of Tuscany (Italy). Geomorphology 2001, 38, 125–132. [Google Scholar] [CrossRef]
- Komar, P.D. Computer model of delta growth due to sediment input rivers and longshore transport. Geol. Soc. Am. Bull. 1973, 84, 2217–2219. [Google Scholar] [CrossRef]
- Nienhuis, J.H.; Ashton, A.D.; Giosan, L. Littoral steering of deltaic channels. Earth Planet. Sci. Lett. 2016, 453, 204–214. [Google Scholar] [CrossRef] [Green Version]
- Pranzini, E. A model for cuspate delta erosion. In Proceedings of the 6th Sympoium on Coastal and Ocean Management/ASCE, Charleston, SC, USA, 11–14 July 1989; pp. 4345–4357. [Google Scholar]
- Ashton, A.D.; Giosan, L. Wave-angle control of delta evolution. Hydrol. Land Surf. Stud. 2011, 38, 4051–4056. [Google Scholar] [CrossRef]
- Aminti, P.; Pranzini, E. Variations in longshore sediment transport rates as a consequence of beach erosion in a cuspate delta. Proc. EUROCOAST Assoc. 1990, 130–134. [Google Scholar]
- Pike, R.J.; Evans, I.S.; Hengl, T. Geomorphometry: A brief guide. In Developments in Soil Science; Hengl, T., Reuter, H.I., Eds.; Geomorphometry—Concepts, Software, Applications; Elsevier: Amsterdam, The Netherlands, 2009; Volume 33, pp. 3–30. [Google Scholar]
- King, C.A.M. Geometrical forms in geomorphology. Int. J. Math. Educ. Sci. Technol. 2006, 2, 153–169. [Google Scholar] [CrossRef]
- Silvester, R.; Hsu, J.R.C. Coastal Stabilization. Innovative Concepts; PRT Prentice Hall: Upper Saddle River, NJ, USA, 1993; p. 578. [Google Scholar]
- Dean, R.G. Equilibrium beach profiles: U.S. Atlantic and Gulf coasts. In Ocean Engineering Report, 12; Department of Civil Engineering, University of Delaware: Newark, NJ, USA, 1977. [Google Scholar]
- Li, L.; Walstra, D.R.; Storms, J. The impact of wave-induced longshore transport on a delta-shoreface system. J. Sediment. Res. 2015, 85, 6–20. [Google Scholar]
- Meini, L.; Mucci, G.; Vittorini, S. Ricerche meteo marine sul litorale toscano: Centoventi anni di osservazioni metereologiche a Livorno (1857–1976). Boll. Soc. Geogl. It. 1979, VIII, 449–474. [Google Scholar]
- Aiello, E.; Bartolini, C.; Caputo, C.; D’Alessandro, L.; Fanucci, F.; Fierro, G.; Gnaccolini, M.; La Monica, G.B.; Lupia Palmieri, E.; Piccazzo, M.; et al. Il trasporto litoraneo lungo la costa toscana tra la foce del Fiume Magra ed i Monti dell’Uccellina. Boll. Soc. Geol. It. 1976, 94, 1519–1571. [Google Scholar]
- Aminti, P.L. Ricostruzione del clima ondoso della Toscana Meridionale sulla base di misure anemometriche. Bolettino Degli Ingegneri 1983, 4, 34–56. [Google Scholar]
- Salvioni, G. I movimenti del suolo nell’Italia centro-settentrionale. Bollettino di Geodesia e Scienze Affini 1957, 16, 325–366. [Google Scholar]
- Antonioli, F.; Silenzi, S. Variazioni relative del livello del mare e vulnerabilità delle pianure costiere italiane. Quaderni della Società Geologica Italiana 2007, 2, 1–29. [Google Scholar]
- Citter, C.; Arnoldus-Huyzendveld, A. Archeologia urbana a Grosseto, la città nel contesto geografico della bassa valle dell’Ombrone. Origine e sviluppo di una città medievale nella “Toscana delle città deboli”. In Le Ricerche 1997–2005; Edizioni all’Insegna del Giglio s.a.s: Fiorentino, Italy, 2007; pp. 41–60. [Google Scholar]
- Innocenti, L.; Pranzini, E. Geomorphological evolution and sedimentology of the Ombrone River Delta, Italy. J. Coast. Res. 1993, 9, 481–493. [Google Scholar]
- Bellotti, P.; Caputo, C.; Davoli, L.; Evangelista, S.; Garzanti, E.; Pugliese, F.; Valeri, P. Morpho-sedimentary characteristics and holocene evolution of the emergent part of the Ombrone River delta (southern Tuscany). Geomorphology 2004, 61, 71–90. [Google Scholar] [CrossRef]
- Barsanti, D.; Rombai, L. La Guerra delle Acque in Toscana; Edizioni Medicea: Firenze, Italy, 1986; p. 169. [Google Scholar]
- Mori, A. L’ evoluzione della costa grossetana dal Pliocene ad oggi. In Annuario 1932–1935 del Regio Liceo di Grosseto; La Maremmana: Grosseto, Italy, 1935; p. 21. [Google Scholar]
- Crist, E.P.; Cicone, R.C. A physically based transformation of thematic mapper data. IEEE Trans. Geosci. Remote Sens. 1984, GE-22, 256–263. [Google Scholar] [CrossRef]
- Pitty, A.F. The Nature of Geomorphology; Methuen & Co.: London, UK, 1982; p. 161. [Google Scholar]
- Luijendijk, A.; Hagenaars, G.; Ranasinghe, R.; Baart, F.; Donchyts, G.; Aarninkhof, S. The state of the world’s beaches. Nat. Sci. Rep. 2018, 8, 6641. [Google Scholar] [CrossRef]

| Year (ca.) | Evolution Type | Standard Error [m] for Four of the Best Different Fitting Models | |||
|---|---|---|---|---|---|
| MMF | Weibull. | Hoerl | 3rd Degree Polynomial | ||
| 1500 | ER | 5.1 | 3.2 | 4.0 | 3.3 |
| 1550 | PR | 14.4 | 16.6 | 16.4 | 22.2 |
| 1600 | ER | 16.6 | 12.6 | 14.5 | 19.2 |
| 1615 | PR | 7.0 | 11.4 | 15.8 | 27.5 |
| 1625 | ER | 14.3 | 12.8 | 16.8 | 23.9 |
| 1650 | ER | 12.5 | 8.2 | 7.2 | 16.3 |
| 1660 | PR | 5.5 | 9.3 | 12.3 | 18.9 |
| 1675 | ER | 16.6 | 10.0 | 11.9 | 12.6 |
| 1700 | ER | 15.2 | 7.1 | 9.4 | 8.4 |
| 1725 | ER | 13.4 | 8.5 | 10.2 | 18.2 |
| 1750 | PR | 9.3 | 12.1 | 21.2 | 16.2 |
| 1775 | ER | 18.8 | 14.7 | 19.6 | 32.7 |
| 1800 | ER | 16.4 | 11.5 | 13.1 | 9.5 |
| 1820 | ER | 16.5 | 5.6 | 18.7 | 21.1 |
| 1830 | PR | 6.4 | 14.9 | 15.5 | 23.8 |
| 1850 | ER | 29.7 | 13.2 | 20.7 | 11.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mammì, I.; Rossi, L.; Pranzini, E. Mathematical Reconstruction of Eroded Beach Ridges at the Ombrone River Delta. Water 2019, 11, 2281. https://doi.org/10.3390/w11112281
Mammì I, Rossi L, Pranzini E. Mathematical Reconstruction of Eroded Beach Ridges at the Ombrone River Delta. Water. 2019; 11(11):2281. https://doi.org/10.3390/w11112281
Chicago/Turabian StyleMammì, Irene, Lorenzo Rossi, and Enzo Pranzini. 2019. "Mathematical Reconstruction of Eroded Beach Ridges at the Ombrone River Delta" Water 11, no. 11: 2281. https://doi.org/10.3390/w11112281
APA StyleMammì, I., Rossi, L., & Pranzini, E. (2019). Mathematical Reconstruction of Eroded Beach Ridges at the Ombrone River Delta. Water, 11(11), 2281. https://doi.org/10.3390/w11112281





