Irrigation-Advisor—A Decision Support System for Irrigation of Vegetable Crops
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Model: Irrigation-Advisor
2.2. Input Data
2.3. Field Experiments for Model Testing
2.4. Model Evaluation and Statistical Analysis
3. Results
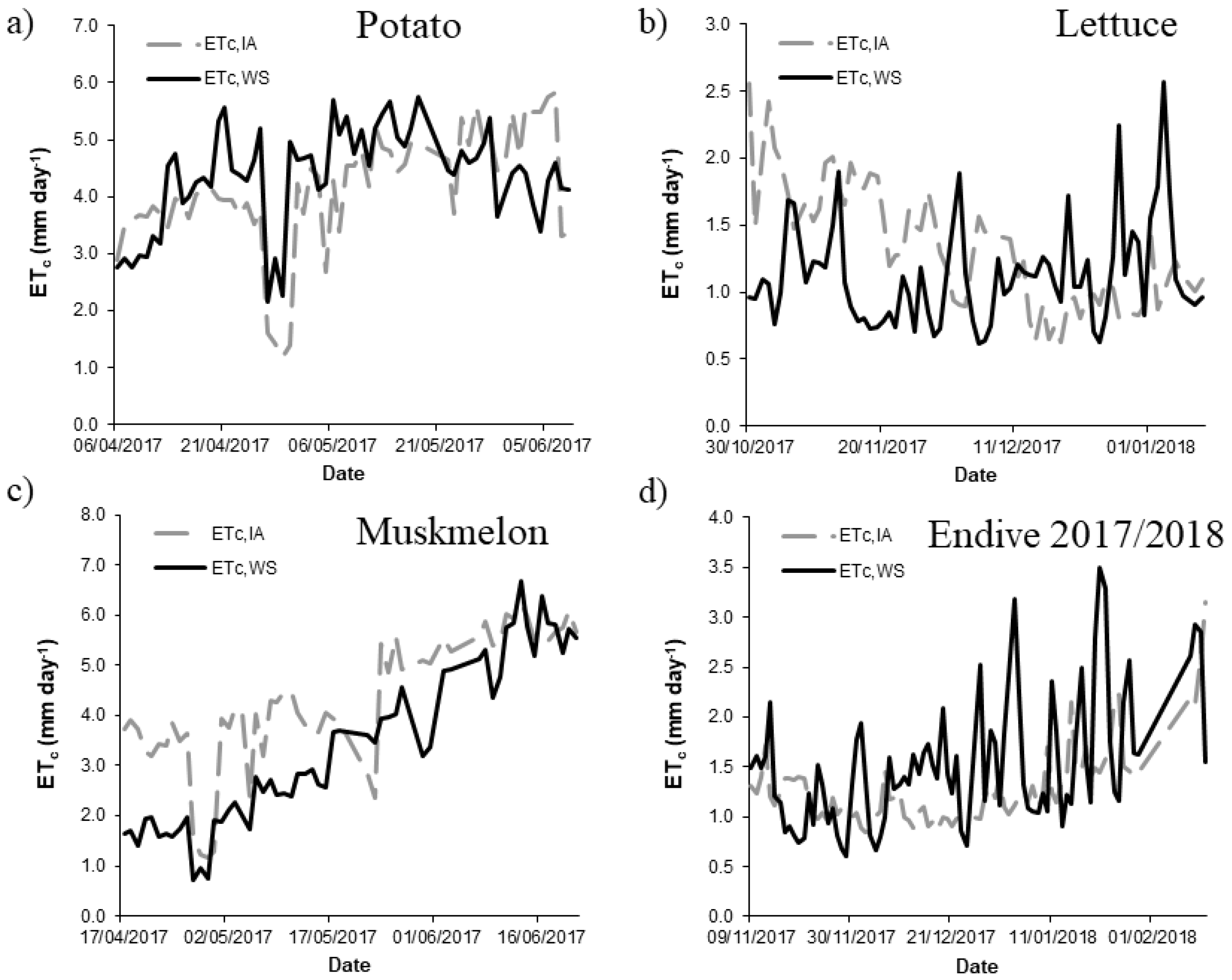
3.1. Model Evaluation
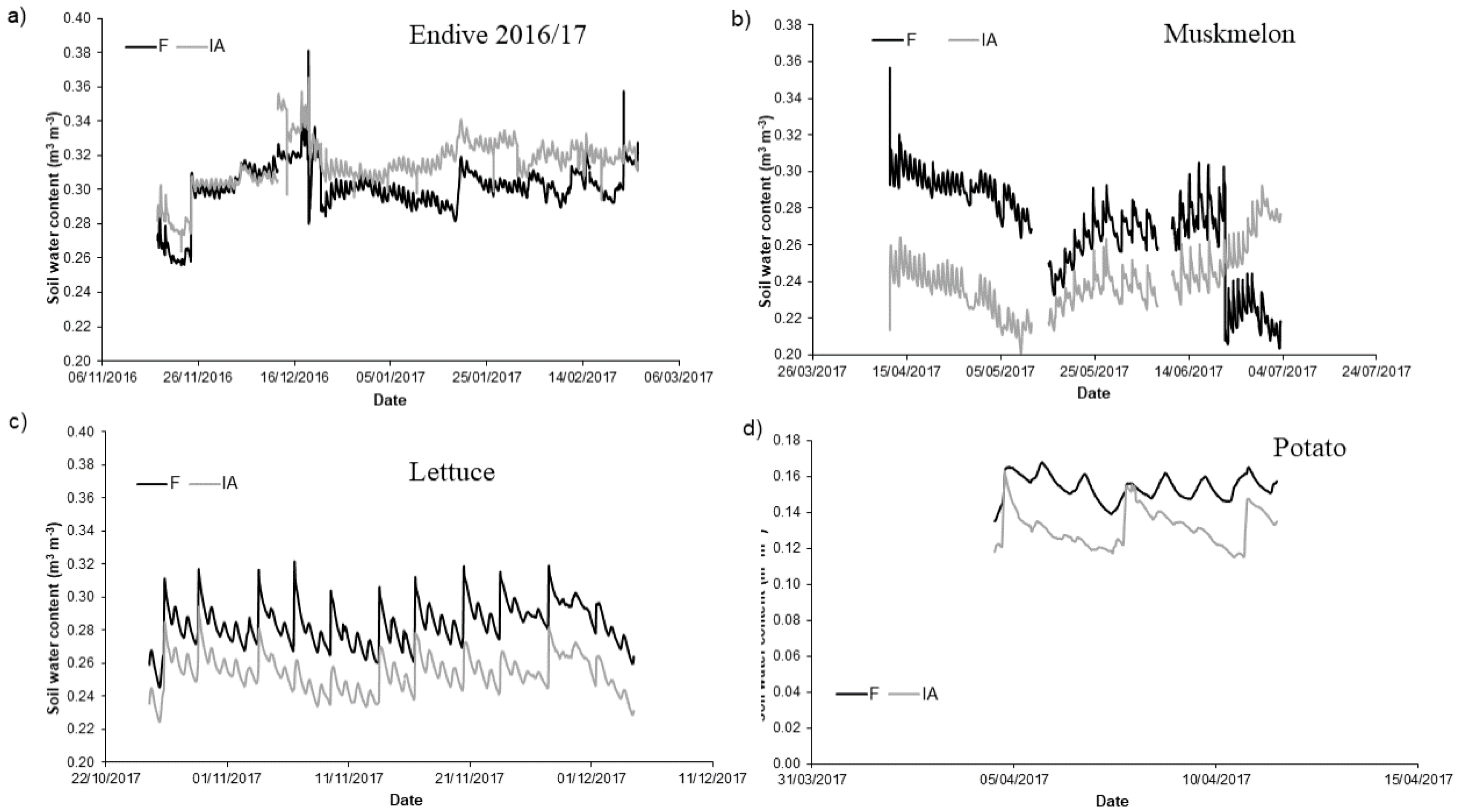
3.2. Field Experiments
4. Discussion
4.1. Model Evaluation: Advantages, Main Sources of Error and Limitations
4.2. Effects of Using the Current Irrigation-Advisor Version on Crop Yield
4.3. Future Improvements of the Model
5. Conclusions
6. Patents
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- FAO. Water for Sustainable Food and Agriculture. A Report for the G20 Presidency of Germany; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2017; p. 33. [Google Scholar]
- AQUASTAT. FAO’s Global Water Information System. Available online: http://www.fao.org/nr/aquastat (accessed on 25 February 2019).
- Turral, H.; Burke, J.; Faurès, J.M. Climate Change, Water and Food Security; Water Reports Nº 36; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2011; p. 200. [Google Scholar]
- Ventura, F.; Faber, B.A.; Bali, K.M.; Snyder, R.L.; Spano, D.; Duce, P.; Schulbach, K.F. Model for estimating evaporation and transpiration from row crops. J. Irrig. Drain. Engin. 2001, 127, 339–345. [Google Scholar] [CrossRef]
- Payero, J.O.; Irmak, S. Daily energy fluxes, evapotranspiration and crop coefficient of soybean. Agric. Water Manage. 2013, 129, 31–43. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop. Evapotranspiration–Guidelines for Computing Crop Water Requirements; Irrigation and Drainage Nº 56; FAO: Rome, Italy, 1998; p. 300. [Google Scholar]
- Giménez, L.; Paredes, P.; Pereira, L.S. Water use and yield of soybean under various irrigation regimes and severe water stress. Application of AquaCrop and SIMDualKc models. Water 2017, 9, 393. [Google Scholar] [CrossRef]
- Hong, M.; Zeng, W.; Ma, T.; Lei, G.; Zha, Y.; Fang, Y.; Wu, J.; Huang, J. Determination of growth stage-specific crop coefficients (Kc) of sunflowers (Helianthus anuus L.) under salt stress. Water 2017, 9, 2154. [Google Scholar] [CrossRef]
- Paredes, P.; D’agostino, D.; Assif, M.; Todorovic, M.; Pereira, L.S. Assessing potato transpiration, yield and water productivity under various water regimes and planting dates using the FAO dual Kc approach. Agric. Water Manag. 2018, 195, 11–22. [Google Scholar] [CrossRef]
- Dzikiti, S.; Volschenk, T.; Midgley, S.J.E.; Lötze, E.; Taylor, N.J.; Gush, M.B.; Ntshidi, Z.; Zirebwa, S.F.; Doko, Q.; Schmeisser, M.; et al. Estimating the water requirements of high yielding and young apple orchards in the winter rainfall areas of South Africa using a dual source evapotranspiration model. Agric. Water Manag. 2018, 20, 152–162. [Google Scholar] [CrossRef]
- Gharsallah, O.; Facchi, A.; Gandolfi, C. Comparison of six evapotranspiration models for a surface irrigated maize agro-ecosystem in Northern Italy. Agric. Water Manag. 2013, 130, 119–130. [Google Scholar] [CrossRef]
- Cammalleri, C.; Ciraolo, G.; Minacapilli, M.; Rallo, G. Evapotranspiration from an olive orchard using remote sensing-based dual crop coefficient approach. Water Resour. Manag. 2013, 27, 4877–4895. [Google Scholar] [CrossRef]
- Villalobos, F.J.; Testi, L.; Moreno-Pérez, M.F. Evaporation and canopy conductance of citrus orchards. Agric. Water Manag. 2009, 96, 565–573. [Google Scholar] [CrossRef]
- Abrisqueta, I.; Abrisqueta, J.M.; Tapia, L.M.; Munguía, J.P.; Conejero, W.; Vera, J.; Ruiz-Sánchez, M.C. Basal crop coefficients for early-season peach trees. Agric. Water Manag. 2013, 121, 158–163. [Google Scholar] [CrossRef]
- López-Urrea, R.; Montoro, A.; Trout, T.J. Consumptive water use and crop coefficients of irrigated sunflower. Irrig. Sci. 2014, 32, 99–109. [Google Scholar] [CrossRef]
- Ramírez-Cuesta, J.M.; Mirás-Avalos, J.M.; Rubio-Asensio, J.S.; Intrigliolo, D.S. A novel ArcGIS toolbox for estimating crop wate demands by integrating the dual crop coefficient approach with multi-satellite imagery. Water 2019, 11, 38. [Google Scholar] [CrossRef]
- Rallo, G.; González-Altozano, P.; Manzano-Juarez, J.; Provenzano, G. Using field measurements and FAO-56 model to assess the eco-physiological response of citrus orchards under regulated déficit irrigation. Agric. Water Manag. 2017, 180, 136–147. [Google Scholar] [CrossRef]
- Rana, G.; Katerji, N. Measurement and estimation of actual evapotranspiration in the field under Mediterranean climate: A review. Eur. J. Agron. 2000, 13, 125–153. [Google Scholar] [CrossRef]
- Soulis, K.X.; Elmaloglou, S. Optimum soil water content sensors placement for surface drip irrigation scheduling in layered soils. Comput. Electron. Agric. 2018, 152, 1–8. [Google Scholar] [CrossRef]
- Rana, G.; Katerji, N.; de Lorenz, F. Measurement and modelling of evapotranspiration of irrigated citrus orchard under Mediterranean conditions. Agric. For. Meteorol. 2005, 128, 199–209. [Google Scholar] [CrossRef]
- Moreno-Rivera, J.M.; Calera, A.; Osann, A. SPIDER–An Open GIS Application Use Case. In Proceedings of the Open GIS UK Conference, Nottingham, UK, 22 June 2009. [Google Scholar]
- Steduto, P.; Hsiao, T.C.; Raes, D.; Fereres, E. AquaCrop: The FAO crop model to simulate yield response to water. I. Concepts and underlying principles. Agron. J. 2009, 101, 426–437. [Google Scholar] [CrossRef]
- Verrelst, J.; Romjin, E.; Kooistra, L. Mapping vegetation density in heterogeneous river foodplain ecosystem using pointable CHRIS/PROBA data. Remote Sens. 2012, 4, 2866–2889. [Google Scholar] [CrossRef]
- Lorite, I.J.; García-Vila, M.; Santos, C.; Ruiz-Ramos, M.; Fereres, E. AquaData and AquaGIS: Two computer utilities for temporal and spatial simulations of water-limited yield with AquaCrop. Comp. Electron. Agric. 2013, 96, 227–237. [Google Scholar] [CrossRef] [Green Version]
- Gallardo, M.; Thompson, R.B.; Giménez, C.; Padilla, F.M.; Stöckle, C.O. Prototype decision support system based on the VegSyst simulation model to calculate crop N and water requirements for tomato under plastic cover. Irrig. Sci. 2014, 32, 237–253. [Google Scholar] [CrossRef]
- Giménez, C.; Thompson, R.B.; Prieto, M.H.; Suárez-Rey, E.; Padilla, F.M.; Gallardo, M. Adaptation of the VegSyst model to outdoor conditions for leafy vegetables and processing tomato. Agric. Syst. 2019, 171, 51–64. [Google Scholar] [CrossRef]
- Thysen, I.; Detlefsen, N.K. Online decision support for irrigation for farmers. Agric. Water Manag. 2006, 86, 269–276. [Google Scholar] [CrossRef]
- Navarro-Hellín, H.; Martínez-del-Rincón, J.; Domingo-Miguel, R.; Soto-Valles, F.; Torres-Sánchez, R. A decision support system for managing irrigation in agriculture. Comput. Electron. Agric. 2016, 124, 121–131. [Google Scholar] [CrossRef] [Green Version]
- Yang, G.; Liu, L.; Guo, P.; Li, M. A flexible decision support system for irrigation scheduling in an irrigation district in China. Agric. Water Manag. 2017, 179, 378–389. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Shen, Y.; Zhang, X.; Lei, Y. Web-based irrigation decision support system with limited inputs for farmers. Agric. Water Manag. 2018, 210, 279–285. [Google Scholar] [CrossRef]
- Ormsby, J.P.; Choudhury, B.J.; Owe, M. Vegetation spatial variability and its effect on vegetation indices. Int. J. Remote Sens. 1987, 8, 1301–1306. [Google Scholar] [CrossRef]
- Soundy, P.; Cantiffle, D.J.; Hochmuth, G.J.; Stoffella, P.J. Management of nitrogen and irrigation in lettuce transplant production affects transplant root and shoot development and subsequent crop yields. HortScience 2005, 40, 607–610. [Google Scholar] [CrossRef]
- USDA-SCS. Urban. Hydrology for Small Watersheds. Technical Release 55, 2nd ed.; United States Department of Agriculture, Soil Conservation Service: Washington, DC, USA, 1986; p. 164.
- Ritchie, J.T. Model for predicting evaporation from a row crop with incomplete cove. Water Resour. Res. 1972, 8, 1204–1213. [Google Scholar] [CrossRef]
- McEvoy, A.; Markvart, T.; Castaner, L. Practical Handbook of Photovoltaics: Fundamentals and Applications; Academic Press: Cambridge, MA, USA, 2012; p. 1268. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, Z.; Fan, J.; Zhou, D.; Tang, F. A meta-analysis of the canopy light extinction coefficient in terrestrial ecosystems. Front. Earth Sci. 2014, 8, 599–609. [Google Scholar] [CrossRef]
- Rana, G.; Katerji, N. Operational model for direct determination of evapotranspiration for well watered crops in Mediterranean region. Theor. Appl. Climatol. 2009, 97, 243–253. [Google Scholar] [CrossRef]
- Arya, S.P. Introduction to Micrometeorology, 2nd ed.; Academic Press: London, UK, 2001; p. 420. [Google Scholar] [CrossRef]
- Katerji, N.; Rana, G. FAO-56 methodology for determining water requirement of irrigated crops: Critical examination of the concepts, alternative proposals and validation in Mediterranean region. Theor. Appl. Climatol. 2014, 116, 515–536. [Google Scholar] [CrossRef]
- Ayers, R.S.; Westcot, D.W. Water Quality for Agriculture; Irrigation and Drainage Nº 29; FAO: Rome, Italy, 1985. [Google Scholar]
- Monge-Redondo, M.A. Diseño Agronómico e Hidráulico de Riegos Agrícolas a Presión; Agrícola: Madrid, Spain, 2018; p. 632. [Google Scholar]
- Saxton, K.E.; Rawls, W.J. Soil water characteristic estimates by texture and organic matter for hydrologic solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef]
- Ribalaygua, J.; Torres, L.; Pórtoles, J.; Monjo, R.; Gaitán, E.; Pino, M.R. Description and validation of a two-step analogue/regression downscaling method. Theor. Appl. Climatol. 2013, 114, 253–269. [Google Scholar] [CrossRef]
- Gaitán, E.; Monjo, R.; Pórtoles, J.; Pino-Otín, M.R. Projection of temperatures and heat and cold waves for Aragón (Spain) using a two-step statistical downscaling of CMIP5 model outputs. Sci. Tot. Environ. 2019, 650, 2778–2795. [Google Scholar] [CrossRef]
- Monjo, R.; Caselles, V.; Chust, G. Probabilistic correction of RCM precipitation in the Basque Country (Northern Spain). Theor. Appl. Climatol. 2014, 117, 317–329. [Google Scholar] [CrossRef]
- Escarabajal-Henajeros, D.; Molina-Martínez, J.M.; Fernández-Pacheco, D.G.; Cavas-Martínez, F.; García-Mateos, G. Digital photography applied to irrigation management of Little Gem lettuce. Agric. Water Manag. 2015, 151, 148–157. [Google Scholar] [CrossRef]
- Mousivand, A.; Menenti, M.; Gorte, B.; Verhoef, W. Multi-temporal, multi-sensor retrieval of terrestrial properties from spectral-directional radiometric data. Remote Sens. Environ. 2015, 158, 311–330. [Google Scholar] [CrossRef]
- González-Esquiva, J.M.; García-Mateos, G.; Escarabajal-Henajeros, D.; Hernández-Hernández, J.L.; Ruiz-Canales, A.; Molina-Martínez, J.M. A new model for water balance estimation on lettuce crops using effective diameter obtained with image analysis. Agric. Water Manag. 2017, 183, 116–122. [Google Scholar] [CrossRef]
- Tei, F.; Scaife, A.; Aikman, D.P. Growth of lettuce, onion, and red beet. 1. Growth analysis, light interception, and radiation use efficiency. Ann. Bot. 1996, 78, 633–643. [Google Scholar] [CrossRef]
- van Delden, A.; Pecio, A.; Haverkort, A.J. Temperature response of early foliar expansion of potato and wheat. Ann. Bot. 2000, 86, 355–369. [Google Scholar] [CrossRef]
- Harmanto Salokhe, V.M.; Babel, M.S.; Tantau, H.J. Water requirement of drip irrigated tomatoes grown in greenhouse in tropical environment. Agric. Water Environ. 2005, 71, 225–242. [Google Scholar] [CrossRef]
- Kuslu, Y.; Dursun, A.; Sahin, U.; Kiziloglu, F.M.; Turan, M. Short communication. Effect of deficit irrigation on curly lettuce grown under semiarid conditions. Span. J. Agric. Res. 2008, 6, 714–719. [Google Scholar] [CrossRef]
- Capra, A.; Consoli, S.; Russo, A.; Scicolone, B. Integrated agro-economic approach to deficit irrigation on lettuce crops in Sicily, Italy. J. Irrig. Drain. Eng. 2008, 134, 437–445. [Google Scholar] [CrossRef]
- Kirnak, H.; Taș, I.; Gökalp, Z.; Karaman, S. Effects of different irrigation levels on yield of lettuce grown in an unheated greenhouse. Curr. Trends Nat. Sci. 2016, 5, 145–151. [Google Scholar]
- Kargas, G.; Soulis, K.X. Performance analysis and calibration of a new low-cost capacitance soil moisture sensor. J. Irrig. Drain. Eng. 2012, 138, 632–641. [Google Scholar] [CrossRef]
- Visconti, F.; de Paz, J.M.; Martínez, D.; Molina, M.J. Laboratory and field assessment of the capacitance sensors Decagon 10HS and 5TE for estimating the water content of irrigated soils. Agric. Water Manag. 2014, 132, 111–119. [Google Scholar] [CrossRef]
- Yang, J.M.; Yang, J.Y.; Liu, S.; Hoogenboom, G. An evaluation of the statistical methods for testing the performance of crop models with observed data. Agric. Syst. 2014, 127, 81–89. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Antle, J.M.; Jones, J.W.; Rosenzweig, R. Next generation agricultural system models and knowledge products: Synthesis and strategy. Agric. Syst. 2017, 155, 179–185. [Google Scholar] [CrossRef]
- Azhar, A.H.; Perera, B.J.C. Evaluation of reference evapotranspiration estimation methods under southeast Australian conditions. J. Irrig. Drain. Eng. 2011, 137, 268–279. [Google Scholar] [CrossRef]
- Lorite, I.J.; Ramírez-Cuesta, J.M.; Cruz-Blanco, M.; Santos, C. Using weather forecast data for irrigation scheduling under semi-arid conditions. Irrig. Sci. 2015, 33, 411–427. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Khabba, S.; Simmoneaux, V.; Jarlan, L.; Ouldbba, A.; Rodríguez, J.C.; Allen, R. Assessment of reference evapotranspiration methods in semiarid regions: Can weather forecast data be used as alternate of ground meteorological parameters? J. Arid Environ. 2010, 74, 1587–1596. [Google Scholar] [CrossRef]
- Collins, J.M. Temperature variability over Africa. J. Clim. 2011, 24, 3649–3666. [Google Scholar] [CrossRef]
- Pedrero, F.; Kalavrouziotis, I.; Alarcón, J.J.; Koukoulakis, P.; Asano, T. Use of treated municipal wastewater in irrigated agriculture–Review of some practices in Spain and Greece. Agric. Water Manag. 2010, 97, 1233–1241. [Google Scholar] [CrossRef]
- Nicolás, E.; Alarcón, J.J.; Mounzer, O.; Pedrero, F.; Nortes, P.A.; Alcobendas, R.; Romero-Trigueros, C.; Bayona, J.M.; Maestre-Valero, J.F. Long-term physiological and agronomic responses of mandarin trees to irrigation with saline reclaimed water. Agric. Water Manag. 2016, 166, 1–8. [Google Scholar] [CrossRef]
- Cameira, M.R.; Mota, M. Nitrogen related diffuse pollution from horticulture production–Mitigation practices and assessment strategies. Horticulturae 2017, 3, 25. [Google Scholar] [CrossRef]
- Fereres, E.; Soriano, M.A. Deficit irrigation for reducing agricultural water use. J. Exp. Bot. 2007, 58, 147–159. [Google Scholar] [CrossRef]
- Fereres, E.; Orgaz, F.; González-Dugo, M.V. Reflections on food security under water scarcity. J. Exp. Bot. 2011, 62, 4079–4086. [Google Scholar] [CrossRef] [Green Version]
- Iglesias, A.; Garrote, L. Adaptation strategies for agricultural water management under climate change in Europe. Agric. Water Manag. 2015, 155, 113–124. [Google Scholar] [CrossRef] [Green Version]
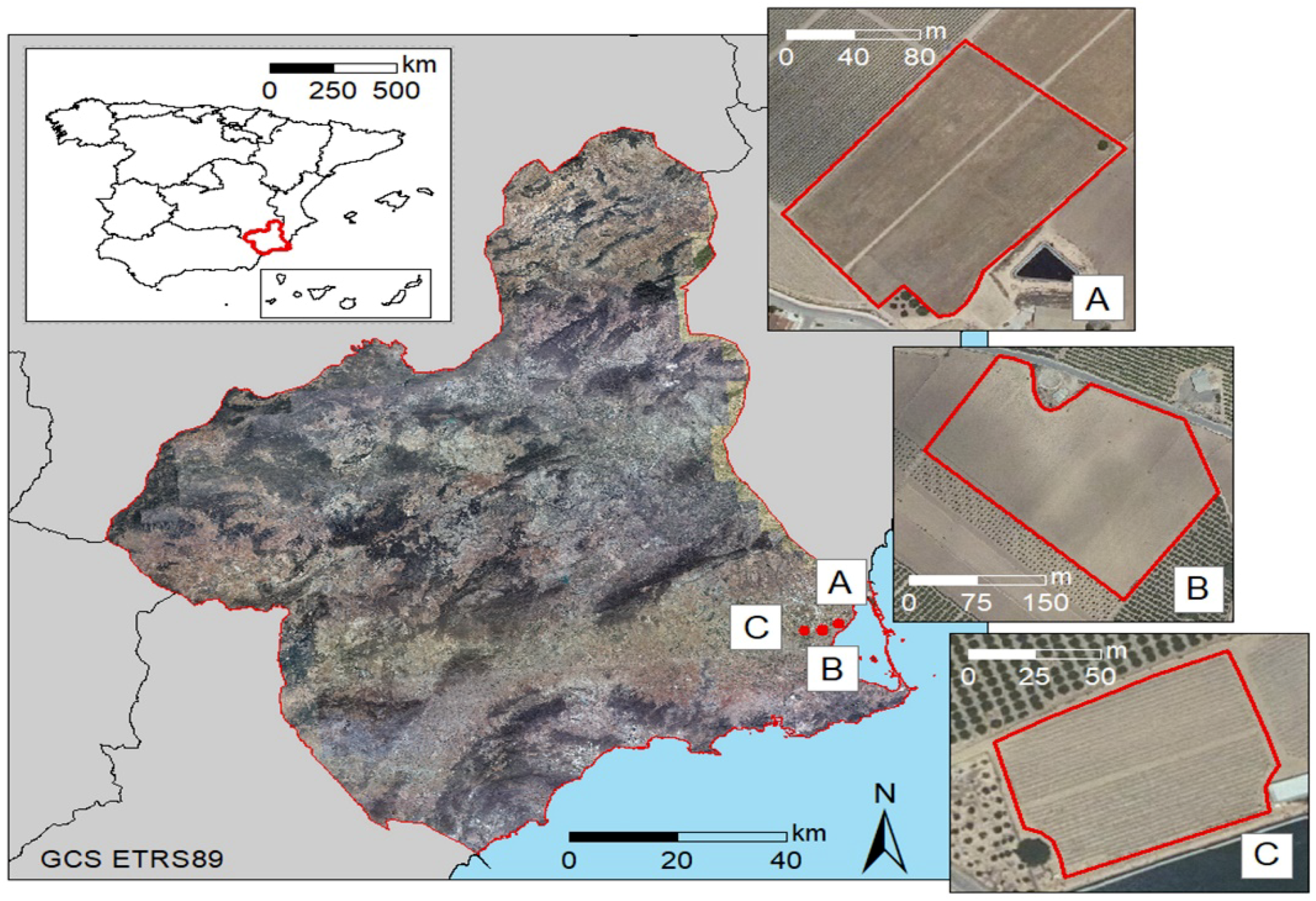

| Crop Species | Dates | Length of the Growing Cycle | Plantation Characteristics | Weather Variables over the Growing Season | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Planting | Harvest | Plant Density (plants m−2) | Density of Emitters (drippers m−2) | Flow (L h−1) | Electrical Conductivity of Irrigation Water(dS m−1) | Tair (°C) | RH (%) | P (mm) | ETo (mm) | ||
| Plot 1 | |||||||||||
| Potato | 14 January 2017 | 22 June 2017 | 160 | - | 3.3 | 1.7 | 3.15 | 16.2 | 66.0 | 124.3 | 565.2 |
| Plot 2 | |||||||||||
| Lettuce | 14 October 2017 | 09 January 2018 | 88 | 5.0 | 3.3 | 1.7 | 3.02 | 13.8 | 65.1 | 17.5 | 145.4 |
| Plot 3 | |||||||||||
| Endive | 07 November 2016 | 25 February 2017 | 111 | 5.0 | 5.0 | 1.7 | 2.74 | 12.1 | 73.9 | 385.8 | 145.4 |
| Muskmelon | 30 March 2017 | 01 July 2017 | 94 | 0.4 | 1.2 | 2.5 | 3.48 | 20.5 | 64.2 | 5.3 | 457.0 |
| Endive | 07 November 2017 | 17 February 2018 | 103 | 5.0 | 5.0 | 1.0 | 4.48 | 11.6 | 65.6 | 57.6 | 162.0 |
| Endive | 31 October 2018 | 04 February 2019 | 97 | 5.0 | 2.5 | 2.5 | 2.79 | 12.4 | 70.5 | 90.0 | 147.4 |
| Crop Species | Statistical Indicators | ||||
|---|---|---|---|---|---|
| ME (mm Day−1) | RMSE (mm Day−1) | NRMSE (%) | EF | Index of Agreement | |
| Comparison against ETc from weather station | |||||
| Potato 2017 | −0.85 | 1.22 | 27.89 | −1.03 | 0.75 |
| Muskmelon 2017 | 0.19 | 0.95 | 28.20 | 0.66 | 0.87 |
| Lettuce 2017–2018 | −0.20 | 0.58 | 51.36 | 0.76 | 0.79 |
| Endive 2017–2018 | −0.69 | 0.94 | 61.04 | −1.11 | 0.56 |
| Comparison against ETc from weather forecasts | |||||
| Potato 2017 | −1.04 | 1.32 | 28.99 | −0.50 | 0.79 |
| Muskmelon 2017 | 0.44 | 1.14 | 36.66 | 0.62 | 0.89 |
| Lettuce 2017–2018 | −1.12 | 1.53 | 74.53 | −2.25 | 0.69 |
| Endive 2017–2018 | −1.17 | 1.53 | 76.29 | −1.32 | 0.72 |
| Crop Species | Treatment | Irrigation Water Applied | Average Fruit/Plant Weight | Yield | Water Productivity |
|---|---|---|---|---|---|
| Plot 1 | |||||
| Potato 2017 | F vs. IA | 87.3 | 93.0 * | 93.5 * | 106.6 * |
| Plot 2 | |||||
| Lettuce 2017/2018 | F vs. IA | 131.2 | 118.2 * | 118.1 * | 90.1 * |
| Plot 3 | |||||
| Muskmelon 2017 | F vs. IA | 88.7 | 94.5 | 93.0 * | 104.9 * |
| Endive 2016/2017 | F vs. IA | 99.5 | 104.5 | 104.5 | 105.2 |
| F vs. IAs | 111.9 | 101.7 | 101.7 | 92.2 * | |
| Endive 2017/2018 | F vs. IA | 92.5 | 100.8 | 1007 | 100.8 |
| F vs. IAs | 109.7 | 98.1 | 98.1 | 98.3 | |
| F vs. IAd | 76.9 | 101.9 | 101.9 | 102.0 | |
| Endive 2018/2019 | F vs. IA | 99.2 | 91.2 | 91.3 | 92.0 |
| F vs. IAs | 119.4 | 92.5 | 92.5 | 77.5 * | |
| F vs. IAd | 86.4 | 93.8 | 93.9 | 108.5 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirás-Avalos, J.M.; Rubio-Asensio, J.S.; Ramírez-Cuesta, J.M.; Maestre-Valero, J.F.; Intrigliolo, D.S. Irrigation-Advisor—A Decision Support System for Irrigation of Vegetable Crops. Water 2019, 11, 2245. https://doi.org/10.3390/w11112245
Mirás-Avalos JM, Rubio-Asensio JS, Ramírez-Cuesta JM, Maestre-Valero JF, Intrigliolo DS. Irrigation-Advisor—A Decision Support System for Irrigation of Vegetable Crops. Water. 2019; 11(11):2245. https://doi.org/10.3390/w11112245
Chicago/Turabian StyleMirás-Avalos, José M., José S. Rubio-Asensio, Juan M. Ramírez-Cuesta, José F. Maestre-Valero, and Diego S. Intrigliolo. 2019. "Irrigation-Advisor—A Decision Support System for Irrigation of Vegetable Crops" Water 11, no. 11: 2245. https://doi.org/10.3390/w11112245
APA StyleMirás-Avalos, J. M., Rubio-Asensio, J. S., Ramírez-Cuesta, J. M., Maestre-Valero, J. F., & Intrigliolo, D. S. (2019). Irrigation-Advisor—A Decision Support System for Irrigation of Vegetable Crops. Water, 11(11), 2245. https://doi.org/10.3390/w11112245









