Abstract
The major aim of this work was to understand and estimate the evolution of the membrane selectivity of neutral solutes after the filtration of protein or amino acid solutions. Classical methodologies led to the estimation of the mean pore radius, different for each filtrated neutral solute. The use of pore size distribution from nitrogen adsorption/desorption experiments enabled a good description of hydraulic and selectivity performances. The modification of the membrane hydraulic properties after the successive filtration of protein solutions revealed that the decrease is quasi linear, the same for all the studied membranes and independent of prior tests. According to the experimental observations, an adsorption model was developed, considering a layer by layer adsorption in the larger pores of the membrane. The predictive obtained results are in good agreement with the experimental rejection rates, validating the assumptions.
1. Introduction
Membrane-based technology offers a reliable option in a growing market to the standard separation processes (especially in terms of power consumption, addition of chemical reagents, and operating convenience) [1]. Currently, membrane separation technology is widely used to separate, concentrate, and rectify solutions for various purposes (for example, waste treatment, water desalination, purification of pharmaceuticals) in many industrial sectors (food, medicine, waste decontamination, chemical, textile industries) [2,3,4,5]. Specifically, they are used for the separation of neutral solutes from aqueous solutions (proteins for food industry, vitamins, peptides, drugs in general for the medicine industry) [6,7].
Alternatively, neutral solute filtrations are mainly used for characterizing membranes (steric effect, cut-off). For this purpose, a transport model is used. For example, Schönherr et al. [8] filtrated raffinose to estimate the mean pore radius by using the Paganelli and Solomon model [9]. Schaerp et al. [10] used the Spiegler–Kedem equation [11] derived from irreversible thermodynamics to numerically approximate the experimental rejection curves of galactose–, maltose–, and raffinose–water solutions. The reflection coefficient is expressed by the steric hindrance pore model. Ito et al. [12] filtrated five dextran samples (molecular weights ranging from 10.5 kg mol−1 to 2000 kg mol−1) to investigate the modification of pore size as a function of the Ba2+ concentration. Velicangil and Howell [13] estimated the steric properties of ultrafiltration membranes by using the orifice model with rejection curves of three protein solutions (papain, Bovine Serum Albumin (BSA), and ovalbumin). In recent years, several works investigated the steric effect by using the Nernst–Planck model for uncharged solutes [14]. They studied the rejection rates of vitamin B12, raffinose, sucrose, and glucose and compared the estimated mean pore radius with the results from Atomic Force Microscopy (AFM). Significant differences were observed between the estimated mean pore radius, especially regarding pore size distribution estimated via AFM investigations. This methodology was used in many current works [15,16,17].
One major observation of these works is that results obtained with several molecules are different. Indeed, the filtration of different uncharged solutes leads to various estimations of mean pore radius. Another major problem, mainly related in the literature, is the adsorption of uncharged solutes in the membrane pore, and so, the partial clogging of the active layer. Proteins are indeed known to adsorb on various surfaces due to their high propensity of deformability and conformation modification, as demonstrated by Karlson et al. [18] and Norde [19]. Even if the amount of protein on hydrophobic substrates is generally high, the outer layer of membranes constituting of oxides can also absorb a non-negligible quantity of protein. Thereby, it reduces the apparent pore size and also modifies the surface properties of the active layer, as demonstrated by Huang et al. [20] and Ponche et al. [21].
For example, Robertson and Zydney [22] observed protein adsorption in ultrafiltration membrane pores, reducing the hydraulic permeability and increasing the selectivity. They estimated the decrease in pore size due to adsorption, a decrease compatible with a monolayer adsorption. A.M. Comerton et al. [23] studied the membrane adsorption of pharmaceutically active compounds. They observed that ultrafiltration (UF) membranes are more subject to adsorption than nanofiltration and reverse osmosis membranes. This phenomenon can be easily explained by the pore size of UF membranes. In most cases, the adsorption of uncharged solutes increases the membrane selectivity and decreases the hydraulic performances and, in some cases, can extend to complete pore clogging [24]. If studies referring to molecule adsorption in membrane pore are abundant [25], fewer studies deal with adsorption mechanisms in the pore, except the classical theoretical models (monolayer) [26] or for microfiltration membranes [27]. In any case, there has not been a study that dealt with the numerical estimation of solute rejection rate (predictive) by taking into account pore size distribution and pore adsorption.
In this study, the filtration of neutral solutes is performed with a ceramic ultrafiltration membrane to investigate size selectivity. To this end, the experimental pore size distribution estimated from nitrogen adsorption/desorption experiments is used as an input of the model. Adsorption phenomena are taken into account to understand the change in hydraulic performances and the membrane selectivity.
2. Materials and Methods
Experiments were performed with tubular ceramic membranes provided by TAMI Industries (Nyons, France). The active layer in TiO2 was deposited on the internal surface of an alumina macroporous tube (1 kDa, length = 25 cm, inner diameter = 8 mm). The TiO2 layer was observed by scanning electron microscopy (Philips XL30 First FEG, SEMTech Solutions, North Billerica, MA, USA) to estimate layer thickness.
Nitrogen gas adsorption–desorption isotherms were performed with a Micromeritics ASAP 2420 (Micrometrics, Ottawa, Canada, apparatus at T = 77 K. Prior to experiments, each sample (broken pieces of TiO2 membrane and alumina tube) was out gassed to a residual pressure lower than 0.8 Pa at 350 °C for 15 h. The micropore volume was calculated using the t-plot method. The cumulative volume and the pore size diameter (distribution) were calculated using the density functional theory method (DFT).
Filtration tests were performed in a laboratory pilot plant (stainless steel), previously described in literature [28]. The studied solution was stored in a 5 L tank and a volumetric pump provided solution circulation for tangential flow filtration (retentate). The flow was controlled by an analog flow rate sensor. The experiments were performed at 700 L/h, a value corresponding to a mean fluid velocity higher than 5 m/s to avoid concentration polarization at the surface of the active layer. After filtration, the permeate flow was sampled for analysis. Both retentate and permeate returned into the solution tank. The applied pressure was adjusted by a manual valve (4 to 12 bar) and was measured by two sensors upstream and downstream the membrane carter. A cooling unit maintained the fluid temperature at 25 °C. Between each filtration test, the experimental set-up was rinsed with demineralized water (conductivity < 0.1 µS/cm).
Before performing filtration tests, a conditioning step of the membrane was required. This step consisted of the filtration of pure water until hydraulic performances were in steady state.
Filtration tests of uncharged solute-water solution ware performed with vitamin B12 (Alfa Aesar, purity 98%), L-phenylalanine (Fluka, purity 99%), L-tyrosine (Fluka, purity 99%), and lysozyme (Sigma-Aldrich, from chicken egg white, activity > 70,000 U/mg). The concentrations of retentate (Cr) and permeate (Cp) samples were investigated by absorbance measurements with a UV-visible spectrophotometer (Lambda 35, Perkin Elmer Instrument). Information about the studied molecules are given in Table 1.

Table 1.
Information on the molecules used for experimental tests.
The observed rejection rate R was calculated using Equation (1):
Several tests of analytical measurement uncertainties were performed (repeated eight times). The maximal error was 1.9% for retentate and 2.9% for permeate samples. The rejection rate uncertainty was and, in all cases, was inferior to 4.8% (result for a rejection rate close to 0).
During the experimental tests, the hydraulic properties were monitored. To do this, between each experiment test, a pure water filtration test was performed. The permeate flux (Jv) was measured and plotted for different applied pressures (ΔP). The hydraulic permeability (Lp) was obtained from the slope of the linear curve via Equation (2):
Three series of tests were performed with the same membrane. Between each series the membrane was regenerated. The regeneration consisted of a hydrothermal treatment (five days in water at 105 °C) to recover its original hydraulic properties.
Filtration tests of neutral solutes were used to investigate size selectivity. Two models were studied: model A assumed a uniform one size distribution (average pore radius) and the second (model B) used an experimental size distribution determined from nitrogen adsorption/desorption experiment as an input.
In model A, the mean pore radius was estimated by numerically approximating rejection rates of the studied solutes. The equation used to approximate the experimental results was the solution of the mass balance (differential equation) in the membrane pore. The differential equation expressing solute mass balance is described by the Nernst–Planck approach for uncharged solutes [29,30], assuming uniform dispersed, one size cylindrical pores. This differential equation was solved with the equality of chemical potentials on both sides of the active layer [31] at the pore/solution interface. Starting from these assumptions, the rejection rate of an uncharged solute [32] can be calculated with Equation (3):
With the steric partitioning coefficient.
The second model (model B) implied that we had an experimental distribution of pore size. In this case, the permeation flow rate was assumed to be the sum of the flow rate of each pore (Equation (4)). The flow rate in the pore was calculated using Hagen Poiseuille’s law:
The rejection rate R was calculated using the Nernst–Planck approach for uncharged solutes (Equation (3)). The calculation was carried out for each pore size, summing all the contribution weighting by the pore number and the relative flow rate (Equation (5)) as follows:
3. Results
3.1. Experimental Results and Estimation of Steric Effect
Experimental tests were performed to understand the physical phenomena that act on the mass transfer mechanisms in a porous media. For this purpose, the monitoring of hydraulic and selectivity properties was required. Three series of tests were performed with the same membrane. Between each series of tests, the membrane was regenerated according to the protocol previously described in the Materials and Methods section. This regeneration aimed to recover the initial membrane properties. Table 2 provides experimental results obtained for three series in terms of maximal rejection rate (selectivity property) and hydraulic permeability (hydraulic performance). For each series, the results are in chronological order. These series were chosen as the first molecule filtrated was different (L-phenylalanine for series 1, vitamin B12 and Lysozyme for series 2, and L-Tyrosine for the last).

Table 2.
Filtration experiments (chronologic order) for the three series of tests.
The first experiments (left-hand column) were performed with a new membrane. After conditioning, the hydraulic permeability was 6.7 × 10−14 m3 m−2. The four studied molecules were filtrated one after another, from the smallest to the largest. The rejection rate increased as filtration tests were performed and, at the same time, the hydraulic permeability significantly decreased, suggesting that a part of the protein was adsorbed at the membrane surface (or in the pore), reducing mass transfer. Nevertheless, filtration of VB12 does not seem to modify the membrane hydraulic performances, and, thus, was chosen as the model solute to follow the membrane selectivity properties. The solute rejection rates obtained with the membrane still having its initial properties (i.e., membrane that had only filtrated water and vitamin B12 after regeneration) were 5% for L-phenylalanine (test 1 series 1), 5% for L-Tyrosine (test 1—series 3), 20% for Vitamin B12 (test 1 series 2), and 65% for Lysozyme (test 2—series 2). These rejection rates are in good agreement with the size of the studied molecules, but much lower than expected for a membrane with a cut-off of 1 kDa.
After these first experimental tests, the membrane permeability and the solute transmission decreased. This behavior was illustrated by the rejection rate of vitamin B12, which increased as protein or amino acid solutions were filtrated. For example, it increased from 20% to 90% after several filtration tests of lysozyme solutions (series 2), indicating that steric effect increased significantly. This can be explained by protein or amino acid adsorption at the membrane surface and or in the pore, thereby restricting the transfer of solute through the porous medium. These adsorption phenomena are not completely irreversible, since after the regeneration treatment the membrane recovered its initial properties.
The estimated mean pore radii are given in Table 2 for series 1 (from Equation (3)). The results (calculated average pore radii) corroborate previous observations. Indeed, the average pore radius decreased as protein filtration was performed. The results obtained with the different solutes show that this current model (model A) remains unsatisfactory for estimating steric effect because the results are dependent on the studied molecule. The average pore radius estimated with vitamin B12 was systematically lower than for lysozyme and L-phenylalanine. Bowen et al. [14] obtained the same results for the filtration of four uncharged solutes (vitamin B12, raffinose, sucrose, and glucose). Indeed, the estimated mean pore radius can vary by a ratio of 2:1. They also observed a modification of water permeability after filtration of each solute.
Additional tests were performed with mixtures of uncharged solutes (vitamin B12 and lysozyme) in water or salted water. These tests were performed following the tests of series 1.
The results (Table 3) show that the rejection rate of the solute was not modified by any another solute in the solution or by salt (NaCl—5 mM) in dilute solution. In the present case, it seems that the solutes in solution did not interact between them. However, in the literature, several studies [33,34,35] showed an increase in neutral solute transmission in saline solutions. This phenomenon is explained by a partial dehydratation of the molecule in the membrane pore, facilitating the transport through the membrane active layer. This behavior is specifically observed in nanofiltration. In the present study, the filtrated solutes, the porous material (membrane active layer), and the pore size were different, which could explain the observed differences.

Table 3.
Filtration tests of solute mixture.
Moreover, the difference in estimated mean pore radius according to the studied molecule was confirmed. There are two possible explanations. First, the one size cylindrical pore hypothesis is a poor and inadequate representation of the porous medium. Second, the solute interacts with the membrane surface according to the chemical groups of both the solute and the active layer (van der Waals forces or acid-base interactions). To investigate the first possibility, a pore size distribution was studied. To this end, nitrogen adsorption/desorption experiments were used to measure the porous volume according to the pore size.
Figure 1 shows the cumulative porous volume obtained during the nitrogen adsorption step according to pore size. This curve can be suitably approximated by a log-normal distribution. These results were substantiated by Scanning Electron Microscopy (SEM) investigations. Indeed, the SEM images (Figure 2c) show a top view of the active layer. The surface constituted sintered titania aggregates separated by nanometric cracks or channels. The larger ones, measuring about 4–10 nm, were of a lower amount than the smaller ones (less than 1 nm wide).
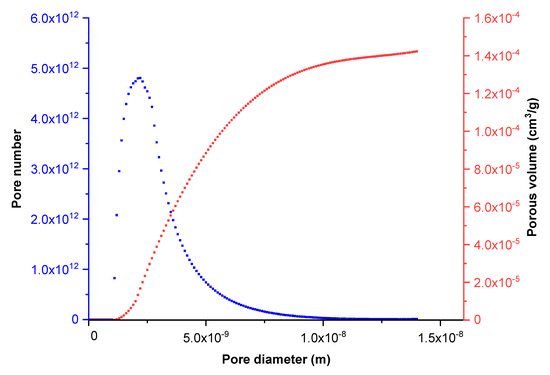
Figure 1.
Cumulative porous volume (red curve) versus pore diameter and pore size distribution (blue curve).

Figure 2.
SEM photographs of (a,b) cross section at different enlargements and (c) top view of the active layer.
From these experimental results, we assumed that the porous medium was constituted of cylindrical and unidirectional pores according to the previous size distribution (Figure 1) and calculated the pore number as a function of the pore size.
Assuming that the flow rate in each pore can be described by the Hagen–Poiseuille law, the permeation flux can be estimated with Equation (4). From these results, it is possible to estimate the active layer thickness by equaling the observed permeation flux with the flow rate calculated by Equation (4). For this purpose, the studied range of pore diameter (0–14 nm) was divided into sub-ranges of pore size from i = 0 to 1400. The active layer thickness was around 2.9 µm. Previous observations [28] performed by microscopy (SEM) showed that the active layer was about 1–2 µm thick. Figure 2a shows a cross section of the membrane obtained after breaking it. The different alumina layers (different porosities) are visible below the titania active layer (full grey layer). The apparent thickness (Figure 2c) of this layer is in agreement with previous investigation.
Calculations were performed for modelling selectivity performances of the new or regenerated membranes for the four studied molecules (i.e., for membranes, which have only been in contact with water). These calculated results were compared with the experimental observed rejection rates of the four studied solutes (Table 4). The results are very close to the experimental ones for the four studied molecules. This comparison indicates that taking into account pore size distribution provides a good way to estimate rejection rates of neutral solutes.

Table 4.
Experimental and calculated (pore size distribution) rejection rate of solutes (membrane with initial properties).
3.2. Hydraulic Performance Loss and Adsorption in the Pore
The hydraulic performances of the membranes decreased as filtration tests of neutral solutes were performed (except for Vitamin B12). At the same time, selectivity performances increased, indicating an increase in the steric effect limiting the mass transfer. As shown in Table 2 for the first series, the average pore radius (calculation relative to each filtrated molecule) decreased, step by step, until a minimum value. Four clogging/blocking mechanisms are classically reported in the literature: complete blocking (the filtrated molecule blocks the pore inlet), standard blocking (adsorption of the molecules in the pore), intermediate blocking (formation of a non-continuous layer, blocking partially the flow inlet), and a cake filtration. This last one often occurs in dead-end filtration. In our case, it can be ruled out owing to the tangential flow and associated shear stress. The intermediate blocking cannot explain both permeate flux decrease and selectivity increase. Indeed, to that end, non-continuous layers should preferentially grow, clogging the larger pore inlet only. The first mechanism, i.e., pore blocking, cannot be a plausible hypothesis, because during filtration of amino acids, the pores that clog should be the smallest, which would result in a decrease in rejection rate. So, the only plausible explanation is protein or amino acid adsorption in the larger pores, reducing the flow rate and increasing the selectivity. F. Wand et al. [36] observed that standard blocking occurred first during ultrafiltration of colloid–water solutions (dead-end filtration experiments). K. Katsoufidou et al. [37] observed a rapid irreversible membrane fouling during ultrafiltration of humic acid due to internal pore adsorption.
Figure 3 shows the hydraulic permeability of the membrane divided by the one obtained just before the first filtration test of lysozyme for series 1 and 3 (presented in Table 2). These results were compared with two test series performed in the same operating conditions with another membrane (series 4 and 5). The hydraulic permeability decreased as filtration tests were carried out (quasi linear behavior), indicating the same adsorption kinetics, regardless of the studied membrane and its past experiments. Assuming one size pore distribution, the hydraulic permeability was proportional to the fourth power of the pore radius (Poiseuille flow). In these conditions, the pore radius estimated by the filtration tests of a neutral solute should vary according to the fourth-root dependence of the number of tests.
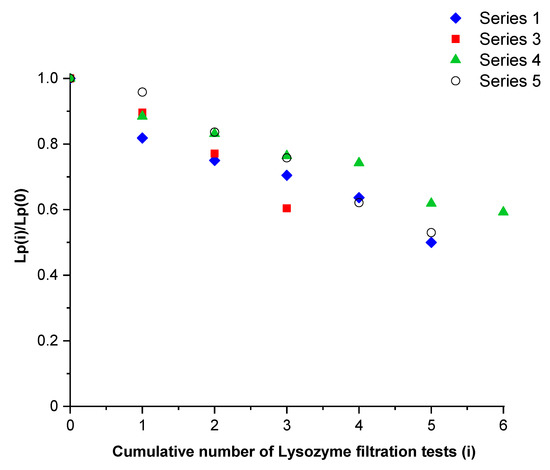
Figure 3.
Relative hydraulic permeability versus the number of filtration tests of lysozyme performed.
Figure 4 compares the estimated mean pore radius for vitamin B12 and Lysozyme filtration tests (series 1) with the mean pore radius calculated using a linear function of the fourth-root of the cumulative number of lysozyme test. For the two cases, the estimated pore radius can be approximated by .
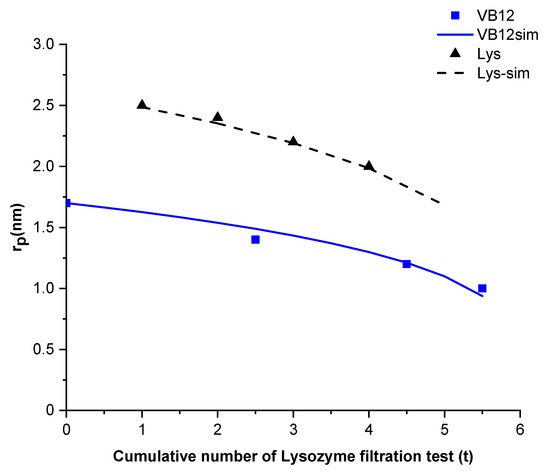
Figure 4.
Mean pore radius estimated from filtration experiments and calculation of neutral solute (series 1: Vitamin B12 and Lysozyme).
The same investigation with pore size distribution was not possible owing to the number of adjustable parameters (i.e., Np(i) and rp(i)).
Steric hindrance after protein adsorption is required in order to predict the selectivity performances of the membrane. Classical models of adsorption or adsorption kinetics do not provide information about flow restriction in pores.
In these conditions, to model these adsorption phenomena, we considered the adsorption of spherical molecules to be by uniform layers in the pore, reducing its radius of two stokes radius of the adsorbed molecule. This assumption is an arbitrary but required hypothesis for calculating the pore size distribution after molecule adsorption. The active layer thickness and the total number of pores were assumed to be unchanged (only their sizes can be modified). The calculation was carried out in all the pores with diameters twice larger than the molecule size. This procedure was numerically repeated until the calculated mass flow rate equaled the experimental permeation flux. When the equality of experimental and numerical hydraulic performances was reached, the model became predictive and capable of calculating the rejection rates of other filtrated molecules (i.e., Vitamin B12, L-Tyrosine, L-Phenylalanine, and Lysozyme).
Figure 5 shows the pore size distribution of the membrane after several filtration tests of lysozyme solution (series 1) compared to the initial one. This pore size distribution was obtained by equaling the experimental and calculated permeation fluxes. The results show that adsorption phenomena took place in the larger pores, partially clogging them and reducing their apparent diameters. Consequently, the pores with an initial size higher than 3.9 nm (corresponding to pores larger than adsorbed solute) completely disappeared and the pore quantity with a diameter in between the 1.8–2.8 nm range significantly increased.
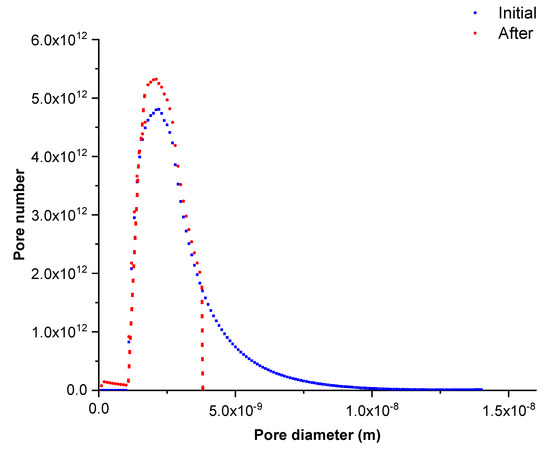
Figure 5.
Initial and calculated pore size distribution after lysozyme filtration tests (series 1).
To validate this modeling, rejection rates of the four filtrated molecules were calculated before and after lysozyme adsorption.
Experimental and calculated rejection rates of the studied molecules are given in Table 5 for the membrane before (initial properties) and after several filtration tests of lysozyme solutions. Taking into account that a pore size distribution provides a good description of membrane selectivity performances and its modification over time, from this new size distribution, the rejection rates of L-phenylalanine, L-Tyrosine, and Lysozyme increased and are in good agreement with the experimental results. Nevertheless, the rejection rate of vitamin B12 increased up to 60%, which is rather different regarding the experimental results (between 85% and 90%). These results are basically prior image and need to be further investigated and confirmed by other membranes and molecules.

Table 5.
Experimental and calculated rejection rates before and after lysozyme filtration.
4. Conclusions
In this work, filtration tests of four uncharged solutes were performed in order to investigate the steric exclusion effects. These tests were performed with new or regenerated membrane to investigate the pore size distribution and selectivity of the membrane regarding each solute. Taking into account a pore size distribution experimentally determined with nitrogen adsorption/desorption techniques made it possible to accurately describe the membrane selectivity performances. The simulated and experimental rejection rates of the four studied molecules are in good agreement for new membranes. Successive filtration tests showed that proteins and amino acids interact with the membrane (adsorption in the larger pore), reducing the hydraulic performances and increasing the selectivity. To describe this phenomenon, the pore size distribution was recalculated by considering molecule adsorption in the larger pore. In this way, the calculation was performed by equalizing experimental and numerical permeation flux. The simulated results provide a good perspective of trends in membrane selectivity for neutral solute filtration.
Author Contributions
Conceptualization, P.D. and A.P.; Methodology, S.M.M., P.D. and A.P.; Validation, S.M.M., P.D. and A.P.; Modelling P.D.; Investigation, S.M.M., P.D. and A.P.; Writing—Original Draft Preparation, S.M.M., P.D. and A.P.; Supervision, P.D. and A.P.
Funding
This research received no external funding
Conflicts of Interest
The authors declare no conflict of interest.
Glossary
| Cp | Permeate concentration of solute (mol m−3) |
| Cr | Solute concentration in the feed solution (mol m−3) |
| D∞ | Diffusion coefficient of solute at infinite dilution (m2 s−1) |
| Jv | Permeation flux (m3 m−2 s−1) |
| Kc | Hindrance factor for convection (dimensionless) Kc = 1 − 2.3λ + 1.154λ2 + 0.224λ3 |
| Kd | Hindrance factor for diffusion (dimensionless) Kd = (2 − φ)×(1 + 0.054λ − 0.988λ2 − 0.441λ3) |
| Lp | Hydraulic permeability (m3 m−2memb) |
| np(i) | Pore number with a size rp(i) |
| Q | Permeation flow rate (m3 s−1) |
| q(i) | Permeation flow rate in pores with a size rp(i) (m3 s−1) |
| r | Stokes radius of solute (m) |
| R | Observed rejection rate (dimensionless) |
| Rcalc | Calculated rejection rate |
| R(i) | Observed rejection rate of solute in pores with a size rp(i) (dimensionless) |
| rp | Average pore radius (m) |
| rp(i) | Pore radius |
| Sm | Membrane surface |
| t | Number of successive tests |
Greek Letters
| ΔP | Transmembrane pressure (Pa) |
| Δx | Active layer thickness (m) |
| λ | Radii ratio (dimensionless) λ = r/rp |
| μ | dynamic viscosity of the filtrated solution (Pa s) |
| φi | steric partition coefficient relative to pores with a size rp(i) (dimensionless) |
References
- Baker, R.W. Membrane Technology and Applications, 3rd ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Ho, W.S.W.; Sirkar, K.K. Membrane Handbook; Springer: New York, NY, USA, 1992. [Google Scholar]
- Li, N.N.; Fane, A.G.; Ho, W.S.W.; Matsuura, T. Advanced Membrane Technology and Applications; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Pabby, A.K.; Rizvi, S.S.H.; Requena, A.M.S. Handbook of Membrane Separations: Chemical, Pharmaceutical, Food and Biotechnological Applications, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Vandevivere, P.C.; Bianchi, R.; Verstraete, W. Review: Treatment and reuse of wastewater from the textile wet-processing industry: Review of emerging technology. J. Chem. Technol. Biotechnol. 1999, 72, 289–302. [Google Scholar] [CrossRef]
- Arise, A.K.; Alashi, A.M.; Nwachukwu, I.D.; Ijabadeniyi, O.A.; Aluko, R.E.; Amonsou, E.O. Antioxidant activities of bambara groundnut (Vigna subterranea) protein hydrolysates and their membrane ultrafiltration fractions. Food Funct. 2016, 5, 2431–2437. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Li, C.; Du, C.; Gao, J.; Zhao, K.X.; Shi, R.; Jiang, Y. Plasma protein binding monitoring of therapeutic drugs in patients using single set of hollow fiber centrifugal ultrafiltration. Bioanalysis 2017, 9, 579–592. [Google Scholar] [CrossRef] [PubMed]
- Schönherr, J. Water permeability of isolated cuticular membranes: The effect of pH and cations on diffusion, hydrodynamic permeability and size of polar pores in the cutin matrix. Planta 1976, 128, 113–126. [Google Scholar] [CrossRef]
- Paganelli, C.V.; Solomon, A.K. The rate of exchange of tritiated water across the human red cell membrane. J. Gen. Physiol. 1957, 41, 259–277. [Google Scholar] [CrossRef]
- Schaerp, J.; van der Bruggen, B.; Vandecasteerle, C.; Wilms, D. Influence of ion size and charge in nanofiltration. Sep. Purif. Technol. 1998, 14, 155–162. [Google Scholar] [CrossRef]
- Spiegler, K.S.; Kedem, O. Thermodynamics of hyperfiltration (reverse osmosis): Criteria for efficient membrane. Desalination 1966, 1, 311–326. [Google Scholar] [CrossRef]
- Ito, T.; Hioko, T.; Yamaguchi, T.; Shinbo, T.; Nakao, S.I.; Kimura, S. Development of a molecular recognition ion gating membrane and estimation of its pore size control. J. Am. Chem. Soc. 2002, 124, 7840–7846. [Google Scholar] [CrossRef]
- Velicangil, O.; Howell, J.A. Estimation of the properties of high-flux ultrafiltration membranes. J. Phys. Chem. 1980, 84, 2991–2992. [Google Scholar] [CrossRef]
- Bowen, W.R.; Mohammad, A.W.; Hilal, N. Characterisation of nanofiltration membranes for predictive purposes. Use of salts, uncharged solutes and atomic force microscopy. J. Memb. Sci. 1997, 126, 91–105. [Google Scholar] [CrossRef]
- Déon, S.; Lam, B.; Fievet, P. Application of a new dynamic transport model to predict the evolution of performances throughout the nanofiltration of single salt solutions in concentration and diafiltration modes. Water Res. 2018, 136, 22–33. [Google Scholar] [CrossRef] [PubMed]
- Dutournié, P.; Limousy, L.; Blel, W.; Déon, S.; Fievet, P. Understanding of ion transport in a Na-Mordenite membrane: Use of numerical modeling to estimate surface-solute interactions in the pore. Ind. Eng. Chem. Res. 2014, 53, 8221–8227. [Google Scholar] [CrossRef]
- Bandini, S.; Morelli, V. Mass transfer in 1812 spiral wound modules: Experimental study in dextrose-water nanofiltration. Sep. Pur. Technol. 2018, 199, 84–96. [Google Scholar] [CrossRef]
- Karlsson, M.; Ekeroth, J.; Elwing, H.; Carlsson, U. Reduction of irreversible protein adsorption on solid surfaces by protein engineering for increased stability. J. Biol. Chem. 2005, 280, 25558–25564. [Google Scholar] [CrossRef]
- Norde, W. Driving forces for protein adsorption at solid surfaces. Macromol. Symp. 1996, 103, 5–18. [Google Scholar] [CrossRef]
- Huang, T.; Anselme, K.; Sarrailh, S.; Ponche, A. High-performance liquid chromatography as a technique to determine protein adsorption onto hydrophilic/hydrophobic surfaces. Int. J. Pharm. 2016, 497, 54–61. [Google Scholar] [CrossRef]
- Ponche, A.; Ploux, L.; Anselme, K. Protein/Material Interfaces: Investigation on Model Surfaces. J. Adhes. Sci. Technol. 2010, 24, 2141–2164. [Google Scholar] [CrossRef]
- Robertson, B.C.; Zydney, A.L. Protein adsorption in asymmetric ultrafiltration membranes with highly constricted pores. J. Colloid Interface Sci. 1990, 134, 563–575. [Google Scholar] [CrossRef]
- Comerton, A.M.; Andrews, R.C.; Bagley, D.M.; Yang, P. Membrane adsorption of endocrine disrupting compounds and pharmaceutically active compounds. J. Membr. Sci. 2007, 303, 267–277. [Google Scholar] [CrossRef]
- Jepsen, K.L.; Bram, M.; Pedersen, S.; Yang, Z. Membrane fouling for produced water treatment: A review study from a process control perspective. Water 2018, 10, 847. [Google Scholar] [CrossRef]
- Bu, F.; Gao, B.; Yue, Q.; Liu, C.; Wang, W.; Shen, X. The Combination of Coagulation and Adsorption for Controlling Ultra-Filtration Membrane Fouling in Water Treatment. Water 2019, 11, 90. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, Y.; He, M.; Su, Y.; Zhao, X.; Elimelech, M.; Jiang, Z. Antifouling membranes for sustainable water purification: Strategies and mechanisms. Chem. Soc. Rev. 2016, 45, 5888–5924. [Google Scholar] [CrossRef] [PubMed]
- Tien, C.; Ramarao, B.V.; Yasarla, R. A blocking model of membrane filtration. Chem. Eng. Sci. 2014, 111, 421–431. [Google Scholar] [CrossRef]
- Dutournié, P.; Limousy, L.; Anquetil, J.; Déon, S. Modification of the selectivity properties of tubular ceramic membranes after alkaline treatment. Membranes 2017, 7, 65. [Google Scholar] [CrossRef]
- Bowen, W.R.; Welfoot, J.S.; Williams, P.M. Linearized transport model for nanofiltration: Development and assessment. AIChE J. 2002, 48, 760–773. [Google Scholar] [CrossRef]
- Déon, S.; Dutournié, P.; Limousy, L.; Bourseau, P. The two-dimensional pore and polarization transport model to describe mixtures separation by nanofiltration: Model validation. AIChE J. 2011, 57, 985–995. [Google Scholar] [CrossRef]
- Donnan, F.G. The theory of membrane equilibria. Chem. Rev. 1924, 1, 73–90. [Google Scholar] [CrossRef]
- Déon, S.; Dutournié, P.; Bourseau, P. Modelling nanofiltration with Nernst-Planck approach and polarization layer. AIChE J. 2007, 53, 1952–1969. [Google Scholar] [CrossRef]
- Bargeman, G.; Vollen broek, J.M.; Straatsma, J.; Schroën, C.G.P.H.; Boom, R.M. Nanofiltration of multi-component feeds. Interactions between neutral and charged components and their effect on retention. J. Membr. Sci. 2005, 247, 11–20. [Google Scholar] [CrossRef]
- Bellona, C.; Drewes, J.E.; Xu, P.; Amy, G. Factors affecting the rejection of organic solutes during NF/RO treatment—A literature review. Water Res. 2004, 38, 2795–2809. [Google Scholar] [CrossRef]
- Escoda, A.; Fievet, P.; Lakard, S.; Szymczyk, A.; Déon, S. Influence of salts on rejection of polyethyleneglycol by an NF organic membrane: Pore swelling and salting-out effects. J. Membr. Sci. 2010, 347, 174–182. [Google Scholar] [CrossRef]
- Wang, F.; Tarabara, V.V. Pore blocking mechanisms during early stages of membrane fouling by colloids. J. Colloid Interface Sci. 2008, 328, 464–469. [Google Scholar] [CrossRef] [PubMed]
- Katsoufidou, K.; Yiantsios, S.G.; Karabelas, A.J. A study of ultrafiltration membrane fouling bu humic acids and flux recovery by backwashing: Experiments and modelling. J. Membr. Sci. 2005, 266, 40–50. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).