Forecasting Groundwater Level for Soil Landslide Based on a Dynamic Model and Landslide Evolution Pattern
Abstract
1. Introduction
2. Theoretical Background
2.1. Quadratic Exponential Smoothing Model
2.2. Effect of Smoothness Parameter on the Forecasted Value
2.3. Clustering Analysis
- (1)
- Identify the nearest central point for each sample point Xi:
- (2)
- Calculate the means of the samples in each cluster. The mean vector will be the new center:
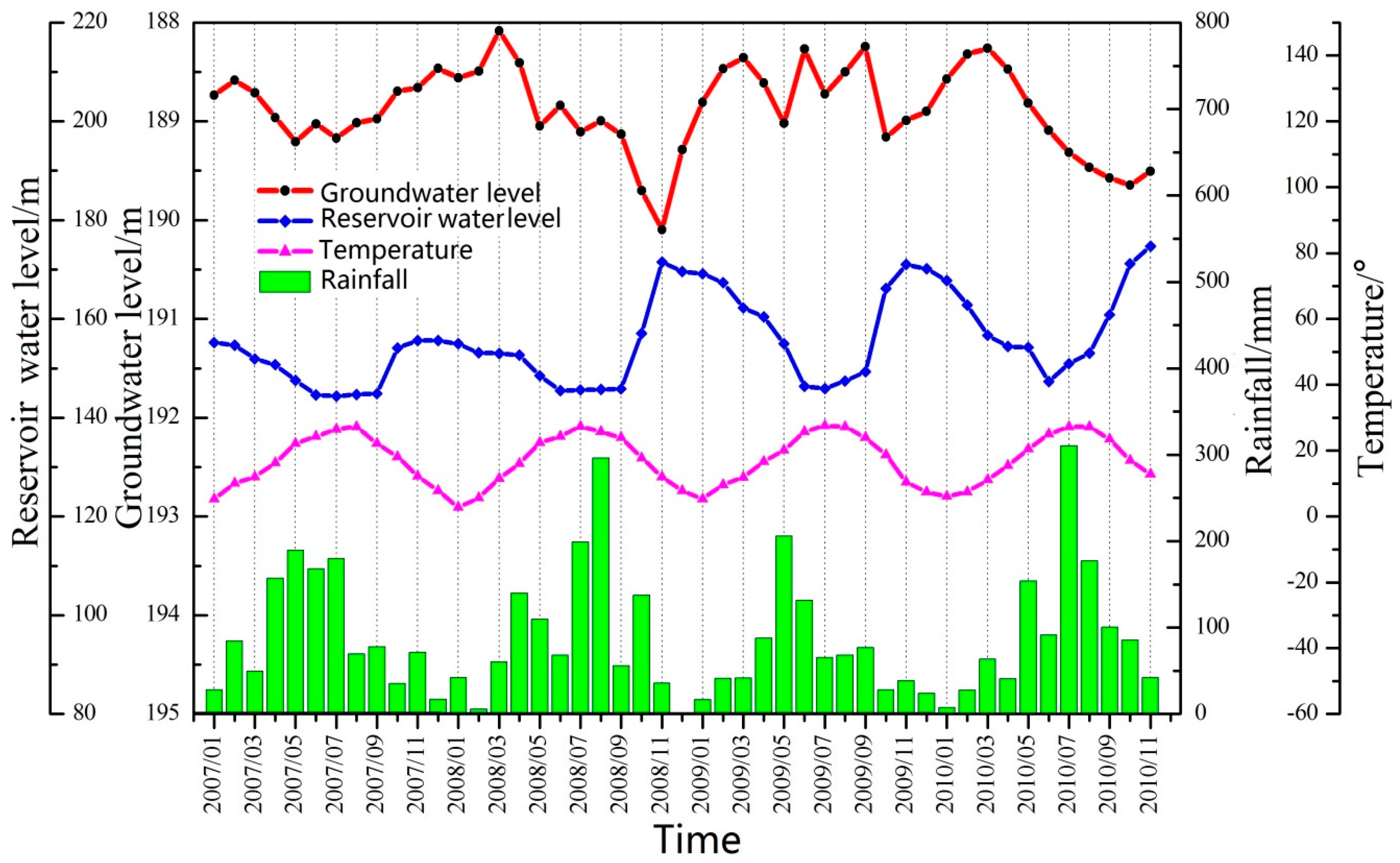
3. Characteristics of Groundwater Level in a Soil Landslide
4. Methods
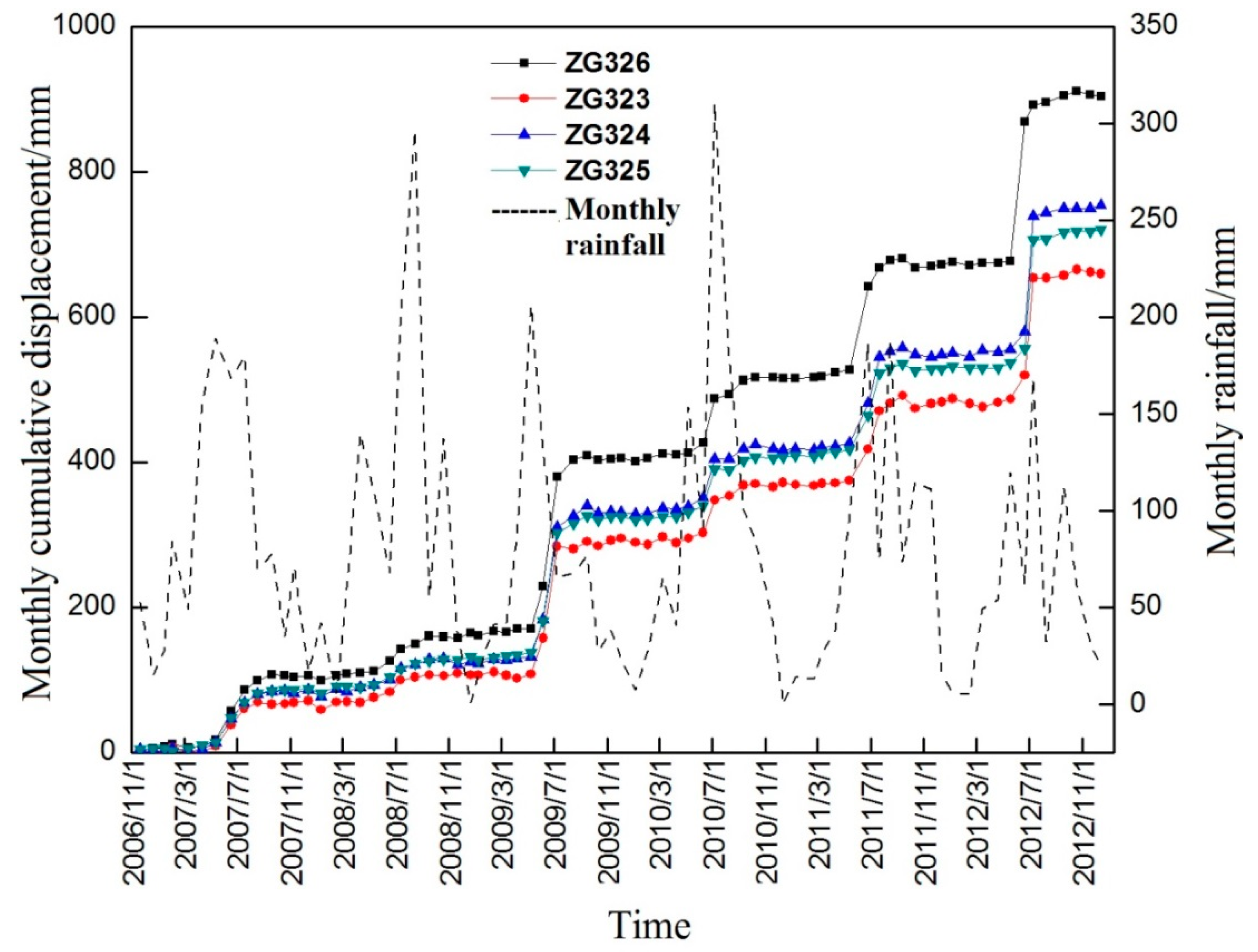
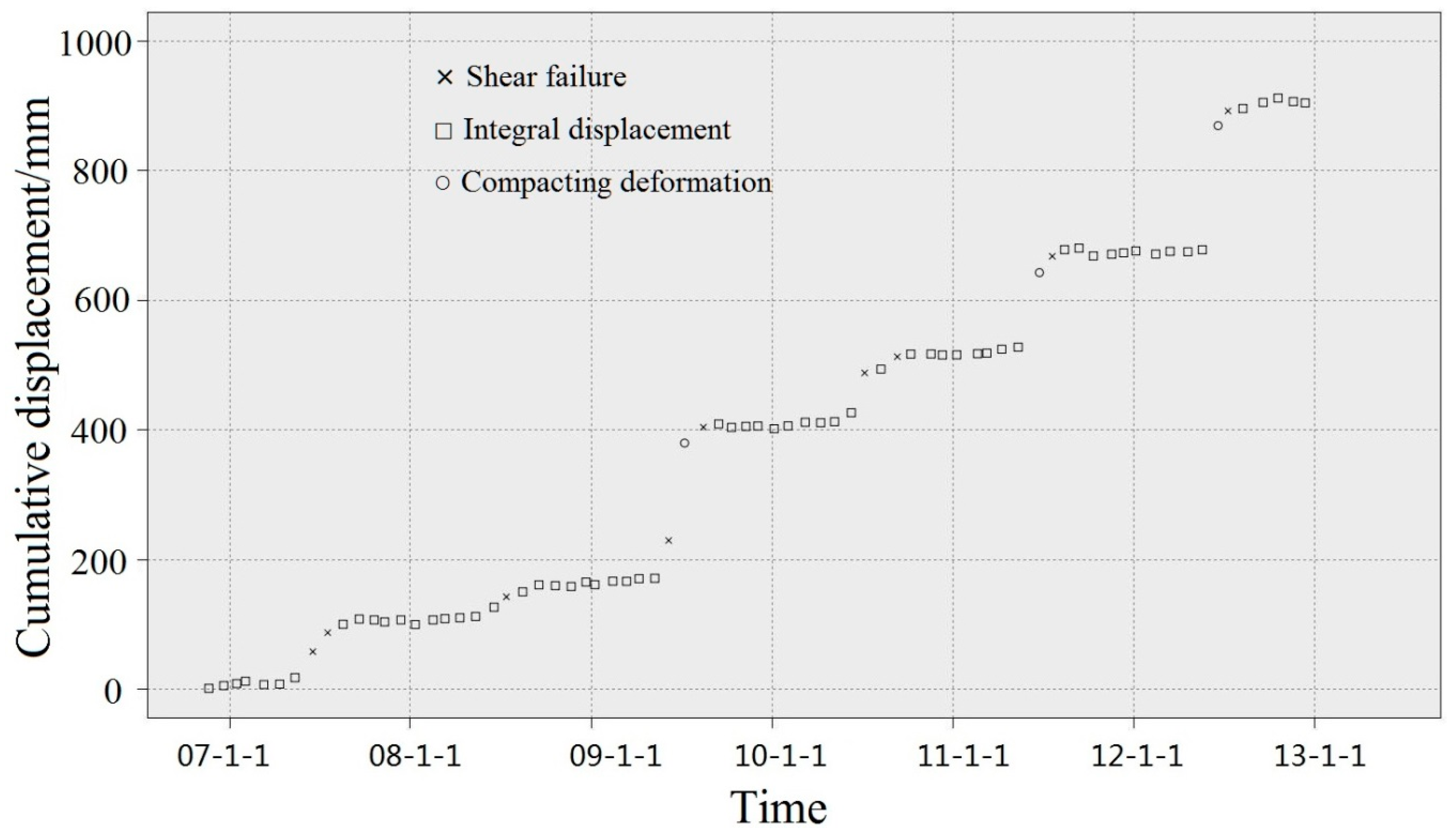
4.1. Division of Landslide Evolution
4.2. Establishment of the Dynamic Evaluation Factors
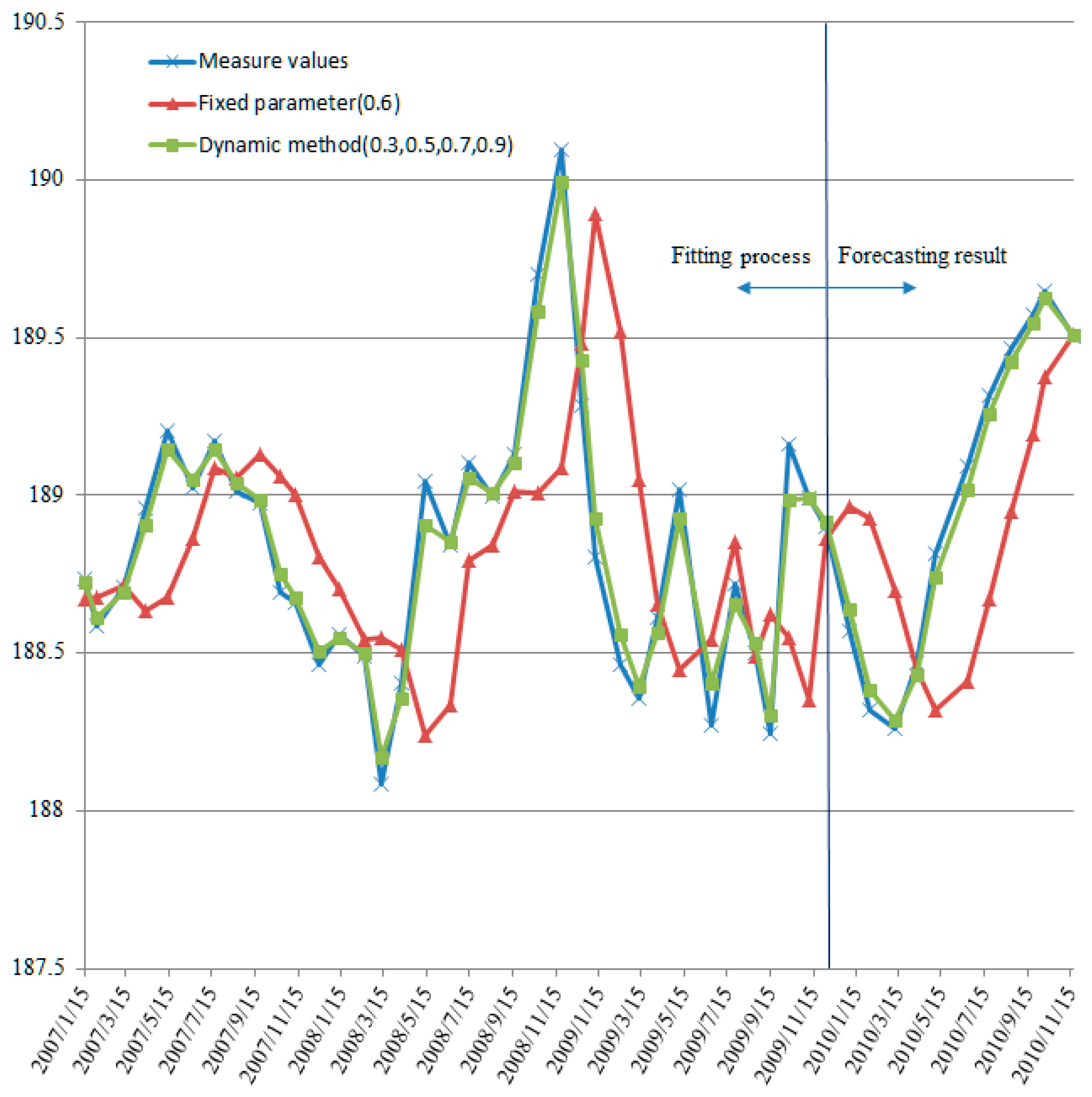
5. Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cojean, R.; Cai, Y.J. Analysis and modeling of slope stability in the Three-Gorges Dam reservoir (China)—The case of Huangtupo landslide. J. Mt. Sci. 2011, 8, 166–175. [Google Scholar] [CrossRef]
- Sun, G.; Zheng, H.; Tang, H.; Dai, F. Huangtupo landslide stability under water level fluctuations of the Three Gorges reservoir. Landslides 2016, 13, 1167–1179. [Google Scholar] [CrossRef]
- Gattinoni, P. Parametrical landslide modeling for the hydrogeological susceptibility assessment: From the Crati Valley to the Cavallerizzo landslide (Southern Italy). Nat. Hazards 2009, 50, 161–178. [Google Scholar] [CrossRef]
- Martins-Campina, B.; Huneau, F.; Fabre, R. The Eaux-Bonnes landslide (Western Pyrenees, France): Overview of possible triggering factors with emphasis on the role of groundwater. Environ. Geol. 2008, 55, 397–404. [Google Scholar] [CrossRef]
- Hong, Y.M.; Wan, S. Forecasting groundwater level fluctuations for rainfall-induced landslide. Nat. Hazards 2011, 57, 167–184. [Google Scholar] [CrossRef]
- Caris, J.; Van Asch, T. Geophysical, geotechnical and hydrological investigations of a small landslide in the French Alps. Eng. Geol. 1991, 31, 249–276. [Google Scholar] [CrossRef]
- Bredehoeft, J.D. The water budget myth revisited: Why hydrogeologists model. Ground Water 2002, 40, 340–345. [Google Scholar] [CrossRef]
- Corominas, J.; Moya, J.; Ledesma, A.; Lloret, A.; Gili, J.A. Prediction of ground displacements and velocities from groundwater level changes at the Vallcebre landslide (Eastern Pyrenees, Spain). Landslides 2005, 2, 83–96. [Google Scholar] [CrossRef]
- Cascini, L.; Calvello, M.; Grimaldi, G.M. Groundwater Modeling for the Analysis of Active Slow-Moving Landslides. J. Geotech. Geoenviron. Eng. 2010, 136, 1220–1230. [Google Scholar] [CrossRef]
- Sangrey, D.A.; Harrop-Williams, K.O.; Klaiber, J.A. Predicting Ground-Water Response to Precipitation. J. Geotech. Eng. 1984, 110, 957–975. [Google Scholar] [CrossRef]
- Iverson, R.M.; Major, J.J. Rainfall, ground-water flow, and seasonal movement at Minor Creek landslide, northwestern California: Physical interpretation of empirical relations. GSA Bull. 1987, 99, 579. [Google Scholar] [CrossRef]
- Cappa, F.; Guglielmi, Y.; Soukatchoff, V.M.; Mudry, J.; Bertrand, C.; Charmoille, A. Hydromechanical modeling of a large moving rock slope inferred from slope levelling coupled to spring long-term hydrochemical monitoring: Example of the La Clapière landslide (Southern Alps, France). J. Hydrol. 2009, 291, 67–90. [Google Scholar] [CrossRef]
- Vallet, A.; Bertrand, C.; Mudry, J.; Bogaard, T.; Fabbri, O.; Baudement, C.; Régent, B. Contribution of time-related environmental tracing combined with tracer tests for characterization of a groundwater conceptual model: A case study at the Séchilienne landslide, western Alps (France). Hydrogeol. J. 2015, 23, 1761–1779. [Google Scholar] [CrossRef]
- Chen, L.-H.; Chen, C.-T.; Pan, Y.-G. Groundwater Level Prediction Using SOM-RBFN Multisite Model. J. Hydrol. Eng. 2010, 15, 624–631. [Google Scholar] [CrossRef]
- Mohanty, S.; Jha, M.K.; Kumar, A.; Sudheer, K.P. Artificial Neural Network Modeling for Groundwater Level Forecasting in a River Island of Eastern India. Water Resour. Manag. 2010, 24, 1845–1865. [Google Scholar] [CrossRef]
- Zencich, S.J.; Froend, R.H.; Turner, J.V.; Gailitis, V. Influence of groundwater depth on the seasonal sources of water accessed by Banksia tree species on a shallow, sandy coastal aquifer. Oecologia 2002, 131, 8–19. [Google Scholar] [CrossRef]
- Gundogdu, K.S.; Guney, I. Spatial analyses of groundwater levels using universal kriging. J. Earth Syst. Sci. 2007, 116, 49–55. [Google Scholar] [CrossRef]
- Schmertmann, J.H. Estimating Slope Stability Reduction due to Rain Infiltration Mounding. J. Geotech. Geoenviron. Eng. 2006, 132, 1219–1228. [Google Scholar] [CrossRef]
- Ling, H.I.; Wu, M.-H.; Leshchinsky, D.; Leshchinsky, B. Centrifuge Modeling of Slope Instability. J. Geotech. Geoenviron. Eng. 2009, 135, 758–767. [Google Scholar] [CrossRef]
- Cho, S.E. Infiltration analysis to evaluate the surficial stability of two-layered slopes considering rainfall characteristics. Eng. Geol. 2009, 105, 32–43. [Google Scholar] [CrossRef]
- Baker, R. Inter-relations between experimental and computational aspects of slope stability analysis. Int. J. Numer. Anal. Methods Géoméch. 2003, 27, 379–401. [Google Scholar] [CrossRef]
- Jia, G.; Zhan, T.L.; Chen, Y.; Fredlund, D. Performance of a large-scale slope model subjected to rising and lowering water levels. Eng. Geol. 2009, 106, 92–103. [Google Scholar] [CrossRef]
- Wood, S.N.; Pya, N.; Säfken, B. Smoothing parameter and model selection for general smooth models. Publ. Am. Stat. Assoc. 2015, 111, 1548–1563. [Google Scholar] [CrossRef]
- Bermúdez, J.D.; Corberán-Vallet, A.; Vercher, E. Multivariate exponential smoothing: A Bayesian forecast approach based on simulation. Math. Comput. Simul. 2009, 79, 1761–1769. [Google Scholar] [CrossRef]
- Sbrana, G.; Silvestrini, A. Random switching exponential smoothing and inventory forecasting. Int. J. Prod. Econ. 2014, 156, 283–294. [Google Scholar] [CrossRef]
- Zhang, W.; Fan, J. Statistical estimation in varying coefficient models. Ann. Stat. 1999, 27, 1491–1518. [Google Scholar] [CrossRef]
- Kourentzes, N.; Petropoulos, F.; Trapero, J.R. Improving forecasting by estimating time series structural components across multiple frequencies. Int. J. Forecast. 2014, 30, 291–302. [Google Scholar] [CrossRef]
- Billah, B.; King, M.L.; Snyder, R.D.; Koehler, A.B. Exponential smoothing model selection for forecasting. Int. J. Forecast. 2006, 22, 239–247. [Google Scholar] [CrossRef]
- Yang, D.; Sharma, V.; Ye, Z.; Lim, L.I.; Zhao, L.; Aryaputera, A.W. Forecasting of global horizontal irradiance by exponential smoothing, using decompositions. Energy 2015, 81, 111–119. [Google Scholar] [CrossRef]
- Kang, S.H.; Sandberg, B.; Yip, A.M. A regularized k-means and multiphase scale segmentation. Inverse Probl. Imaging 2017, 5, 407–429. [Google Scholar] [CrossRef]
- Chen, K. On Coresets for k -Median and k -Means Clustering in Metric and Euclidean Spaces and Their Applications. SIAM J. Comput. 2009, 39, 923–947. [Google Scholar] [CrossRef]
- Chang, H.; Yeung, D.-Y.; Cheung, W.K. Relaxational metric adaptation and its application to semi-supervised clustering and content-based image retrieval. Pattern Recognit. 2006, 39, 1905–1917. [Google Scholar] [CrossRef]
- Har-Peled, S.; Kushal, A. Smaller Coresets for k-Median and k-Means Clustering. Discret. Comput. Geom. 2007, 37, 3–19. [Google Scholar] [CrossRef][Green Version]
- Peng, L.; Xu, S.; Hou, J.; Peng, J. Quantitative risk analysis for landslides: The case of the Three Gorges area, China. Landslides 2015, 12, 943–960. [Google Scholar] [CrossRef]
- Ilia, I.; Tsangaratos, P. Applying weight of evidence method and sensitivity analysis to produce a landslide susceptibility map. Landslides 2016, 13, 379–397. [Google Scholar] [CrossRef]
- Shrestha, H.K.; Yatabe, R.; Bhandary, N.P. Groundwater flow modeling for effective implementation of landslide stability enhancement measures—A case of landslide in Shikoku, Japan. Landslides 2008, 5, 281–290. [Google Scholar] [CrossRef]
- Tang, H.M.; Li, C.D.; Hu, X.L.; Su, A.; Wang, L.; Wu, Y.; Criss, R.; Xiong, C.; Li, Y. Evolution characteristics of the Huangtupo landslide based on in situ tunneling and monitoring. Landslides 2015, 12, 511–521. [Google Scholar] [CrossRef]
- Dai, F.; Lee, C. Frequency–volume relation and prediction of rainfall-induced landslides. Eng. Geol. 2001, 59, 253–266. [Google Scholar] [CrossRef]
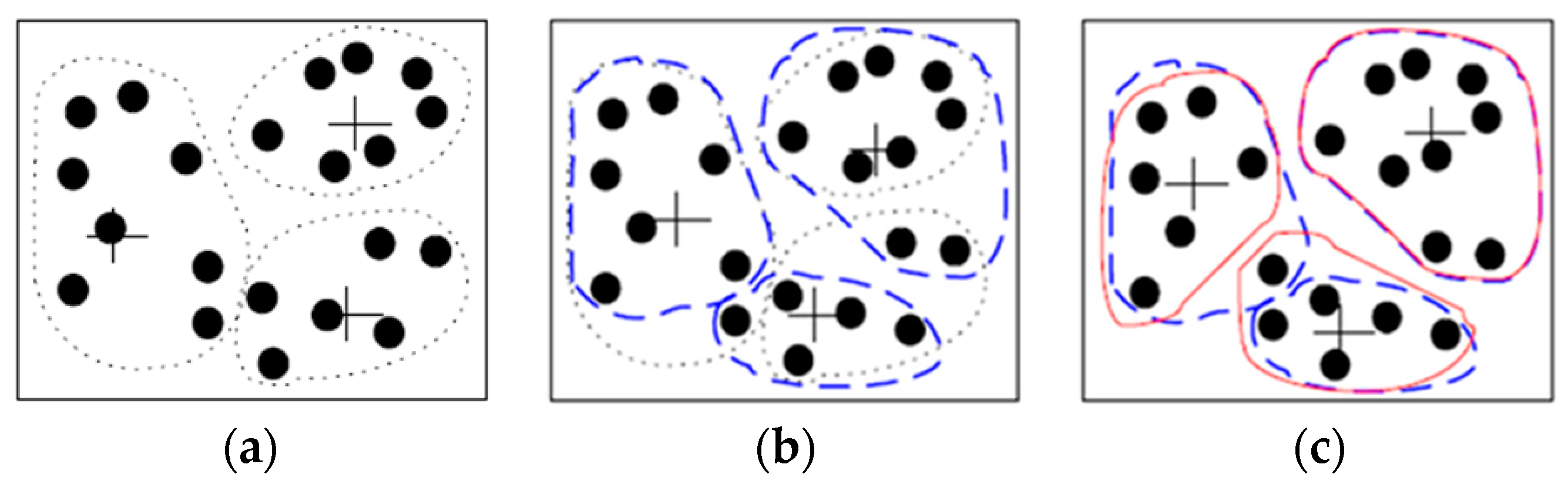
| C-1 | C-2 | C-3 | C-4 | C-5 | C-6 | |
|---|---|---|---|---|---|---|
| C-1 | 0 | |||||
| C-2 | 0.02 | 0 | ||||
| C-3 | 0.42 | 0.60 | 0 | |||
| C-4 | 0.70 | 0.31 | 0.71 | 0 | ||
| C-5 | 0.24 | 0.78 | 0.82 | 0.53 | 0 | |
| C-6 | 0.79 | 0.13 | 0.53 | 0.82 | 0.35 | 0 |
| Rainfall factor | Stage | Parameter |
|---|---|---|
| 3.5–62.1 | Compacting deformation | 0.3 |
| 62.1–124.1 | Integral displacement | 0.5 |
| 124.1–151.1 | Integral displacement | 0.7 |
| 151.1–316 | Shear failure compaction | 0.9 |
| Model | Mean Absolute Error | R |
|---|---|---|
| Dynamic Fixed | 0.053 0.363 | 0.929 0.327 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, G.; Chen, D.; Niu, R. Forecasting Groundwater Level for Soil Landslide Based on a Dynamic Model and Landslide Evolution Pattern. Water 2019, 11, 2163. https://doi.org/10.3390/w11102163
Duan G, Chen D, Niu R. Forecasting Groundwater Level for Soil Landslide Based on a Dynamic Model and Landslide Evolution Pattern. Water. 2019; 11(10):2163. https://doi.org/10.3390/w11102163
Chicago/Turabian StyleDuan, Gonghao, Deng Chen, and Ruiqing Niu. 2019. "Forecasting Groundwater Level for Soil Landslide Based on a Dynamic Model and Landslide Evolution Pattern" Water 11, no. 10: 2163. https://doi.org/10.3390/w11102163
APA StyleDuan, G., Chen, D., & Niu, R. (2019). Forecasting Groundwater Level for Soil Landslide Based on a Dynamic Model and Landslide Evolution Pattern. Water, 11(10), 2163. https://doi.org/10.3390/w11102163






