Changes of Annual Precipitation and Probability Distributions for Different Climate Types of the World

Abstract

Analysis of Spatio-temporal changes in precipitation (Pre) on the land surface of the earth was the focus of this study. Thiel-Sen median slopes and Modified Mann-Kendall (MMK) test were utilized to draw inferences. Majority of the regions were identified to show an increasing trend of annual precipitation except some of the low to mid-latitude regions in Northern hemisphere. The trends of wet-day frequency (Wet) were found in agreement with precipitation for most of the regions, but the inverse relationship was found for the subtropical regions of Northern hemisphere. These changes were examined for the world climate types based on Koppen-Gieger climate classes. Also, it was tried to find the probability distribution, which best describes the annual precipitation pattern in different climate types of the world among 21 commonly assumed probability distributions.

1. Introduction

Global warming is found to be responsible for the change in long term climate, which is termed as climate change. Many observed changes in climatic variables are found to be unprecedented before mid of 20th Century [1]. Climate change is found to be affecting the atmosphere, oceans, snow, and ice cover. Precipitation patterns across the globe have changed due to global warming [2,3]. Mishra et al. [4] reported the increase of heatwaves and a decrease in cold waves in the urban areas of the world. Warming of permafrost was also reported by Biskaborn et al. [5], which might further amplify global warming. Gudmundsson et al. [6] reported the significant changes in the mean and extreme values of streamflow across the globe.

Trend estimation is the primary exercise to understand the changes in climate. Trend estimation involves the computation of two characteristics of the time series, i.e., (i) trend direction and magnitude and (ii) significance of the trend. Sen slope estimate [7] has been widely used in climate studies to estimate the direction and magnitude as it is robust and insensitive to the outliers [8,9,10]. However, this method cannot be used to find the significance of the trends. So, Mann-Kendall (MK) test [11,12] is widely used for this purpose. The presence of serial correlation cannot be ruled out in the observed hydrometeorological data, but most of the researchers computed the significance of trend without considering the autocorrelation structure of the data [13,14,15,16,17]. Studies have found that the presence of positive serial correlation affects the ability of the MK test to correctly assess the significance of the trend [18]. The pre-whitening process has been used in different studies to remove the autocorrelation [19,20,21]. Bayazit et al. [22] argued that pre-whitening procedures are only useful when there is little to no trend. The pre-whitening results in the loss of some amount of existing trend [23]. MMK (Modified Mann-Kendall) test [24] is widely used to detect the significance of the trend in the presence of serial autocorrelation as this test considers the effect of serial correlation [25,26,27]. MMK and Sen Slope methods were adopted to find the significance of trends in this study.

The precipitation patterns are also not untouched by global warming. The world faced a high number of extreme weather conditions, including rare events of rainfall in the last decade [28]. The studies have found that the majority of lands may get stronger precipitation extremes than weaker [29]. Model simulations also suggest a net increase in global precipitation but the distribution may not be uniform [30]. Feng et al. [31] used high-resolution simulated data to study the global changes in the amount, intensity, and frequency of precipitation. They found an increase in precipitation except for latitude 15–40° N. The frequency of light and heavy precipitation was found to be increasing. Effect of climate change on precipitation has been studied largely on the regional scale than global scale [2,32,33]. Majority of these studies focused on finding the changes in climate extremes [25,34,35,36]. Raghvendra et al. [35] reported the increase in number and intensity of thunderstorm in the Congo Basin, Central Africa; however, the net rainfall was found to be decreased. Thomas and Nigam [37] reported the expansion of Sahara desert, South Africa, and warming trends of Southern regions than Northern regions. Choudhary et al. [36] detected a rapid decrease in monsoon rainfall in the wettest place on the earth, North-East India, in the last four decades. The changes in annual total precipitation directly affect the water budget of the regions and are crucial for maintaining adequate water resources. So, we limited our study to find the long-term changes in annual precipitation over the landmass of the earth.

Wet-day frequency is also an important parameter to assess the changes in precipitation patterns in the regions. It is defined by the number of rainy days at a particular location. This is a good parameter indicating the length of wet or dry spells. Change in the frequency of extreme events have been particularly reported in several studies [6,38,39]; however, the wet spells of moderate-intensity are equally crucial to maintain the water budget of the region. So, in this study, it was tried to find the relationship of changes in precipitation with a change in the number of wet days to estimate the patterns of extreme as well as moderate events and to check the probability of flooding or droughts in different parts of the world.

As global warming is not affecting every region of the world uniformly, in this study, it was tried to find the changes in precipitation patterns in different climate types of the world. Koppen-Geiger world map of climate type [40] is a widely adopted climate map to study different climate types [41,42,43]. The world climate is divided into five major climate types, i.e., Tropical, Arid, Temperate, Cold, and Polar, represented by A, B, C, D, and E letter, respectively, based on long monthly record (1901–2000) of temperature and precipitation. This classification is based on the combined effect of precipitation, temperature, seasonal variations, and extreme weather conditions. Kottek et al. [44] updated the Koppen climate type world map using gridded climate data from mid of 20th century. Peel et al. [45] used long term precipitation and temperature data set to update Koppen climate types. Beck et al. [46] also presented an updated climate type world map for the present day (1980–2016) and projected future (2071–2100). As it was required to identify the long term changes in different climate types of the world, the climate type map updated by Peel et al. [45] was considered in this study.

The trends show the behavior of the time series in the time domain, but global warming is not only affecting the precipitation patterns in the time domain but also in the frequency domain. In this study, it was tried to find the changes in the frequencies of the precipitation patterns in different locations using different probability distributions. The knowledge of correct probability distribution resembling the rainfall patterns is of the matter of eminent significance as the wrong estimation of design rainfall may lead to either lower/higher estimation, which in turn may cause the failure of hydraulic structures or an unnecessary increase in the cost. A good review of previous studies by Ye et al. [47] indicated that majority of the studies related to finding best-fit probability distribution were focused on daily time scale or extreme events [48,49,50]. The widely adopted probability distribution to represent the daily extreme rainfall patterns are Normal, Exponential, Log-Normal, Pearson, Log-Pearson (III), Weibull, Pareto, Generalized Gamma, Generalized Extreme Value (GEV), Logistic, Generalized Logistic, Wakebay, and Kappa. Only a few of the available studies are focused on finding global patterns of the best-fit probability distribution for precipitation. A review of available studies focusing on fitting probability distribution to daily extreme precipitations can be found in available literature [51,52,53]. It has been communicated that GEV III (Freshet distribution) can be best assumed to fit the daily extreme precipitation. However, it is known that the assumed best-fit probability distribution at different scale cannot be adopted to represent the frequency of precipitation at the annual scale. A study focused on finding a probability distribution function (PDF), which may represent global patterns of annual total precipitation, could not be found. The annual behavior of precipitation patterns is important to plan the water resources for the future. Extreme events do not generally affect the annual amount of rainfall, so even if the frequency of extreme events is found to be changing, the water availability for the year can be managed if the changes in annual precipitation are known. So, in this study, we tried to find the probability distribution, which can best define the annual precipitation across the globe. Here, 21 types of widely used probability distributions, which are assumed to be describing rainfall patterns by different researchers, were used in this study.

The objective of this study was to find the global-scale variations in annual precipitation (Pre) corresponding to changes in wet-day frequency (Wet) using high-resolution observed data. Changes in Pre with Wet might be useful to find the frequency of high or low precipitation events for a particular region. Changes in precipitation have not been analyzed for different climatic regions of the world earlier. We tried to find the relationship with increase/decrease in intensity of rainfall with the climate type of the region. Finally, the frequency distribution of annual precipitation patterns was also found out by fitting different PDFs.

The article is organized in five sections with the background described in Section 1. Study area, data used, and methodology are described in Section 2. Results are analyzed in Section 3 and discussed in Section 4, followed by conclusions in Section 5.

2. Materials and Methods

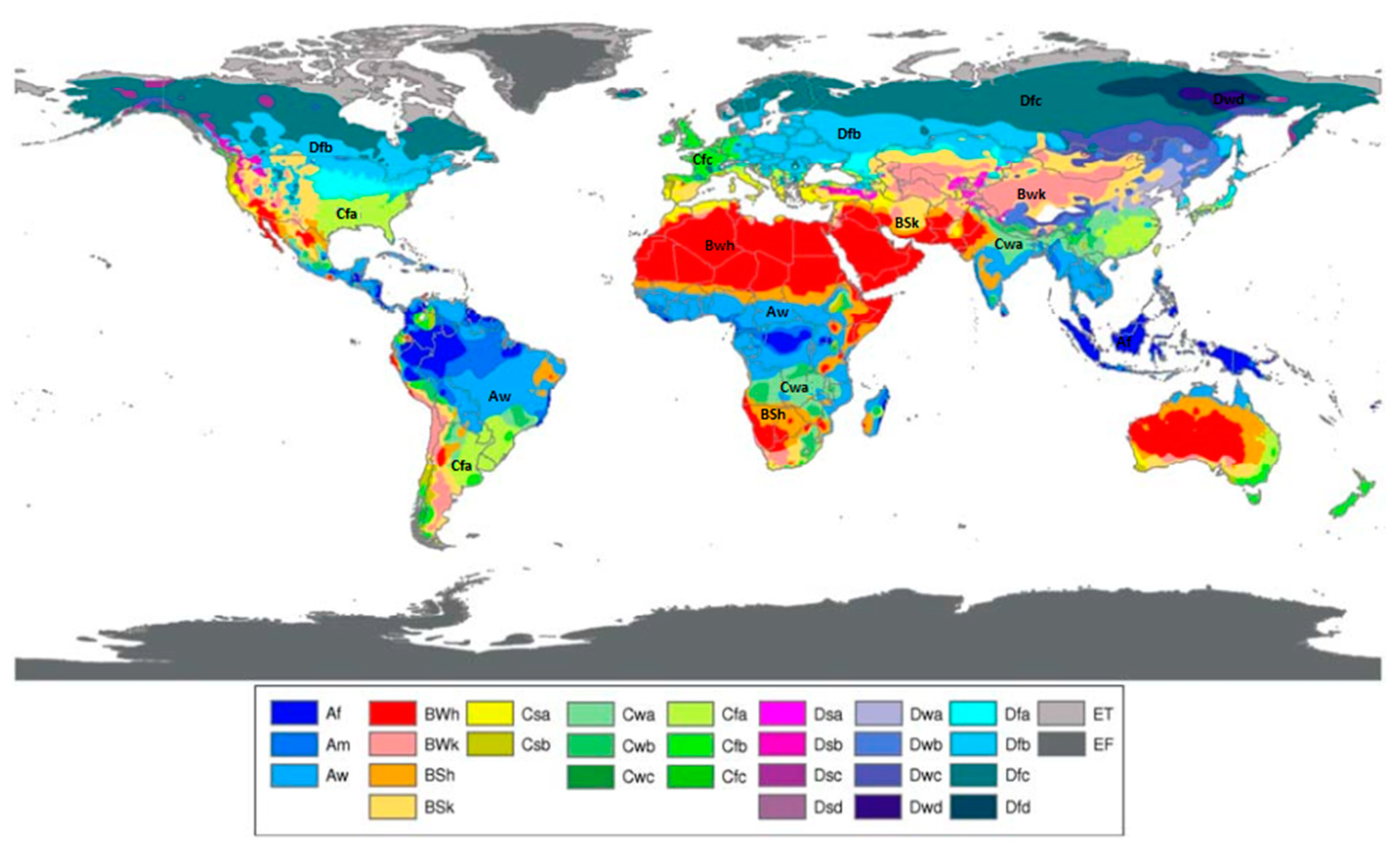
2.1. Study Area and Data

This study covered the entire landmass of the world, excluding Antarctica. Global high resolution gridded (0.5° longitude and 0.5° latitude) Pre and Wet data for years 1901 to 2016 provided by Climatic research unit (CRU) of East Anglia [54] were used in this study.

CRU provides monthly total values for these variables, which are derived from station data provided by the World Meteorological Organization (WMO) in collaboration with the US National Oceanographic and Atmospheric Administration (NOAA). Pre is the primary variable of the CRU dataset and is solely based on observed station data [55]. The half-degree grid cells were defined where at least one station data was available within 450 km from the center of the grid. Less interpolation was required for precipitation because of higher station density. Wet is the second variable of CRU dataset and is derived from Pre using the empirical formula given by New et al. [56]. Wet varies from zero to maximum number days in a month, as it counts the number of wet days in a month even if the amount of precipitation is less. The CRU data have been widely used in different hydrological and climate change impact studies [57,58,59,60]. CRU data was earlier compared with similar global datasets, i.e., University of Delaware (UDEL) (data provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA, from their Web site at https://www.esrl.noaa.gov/psd/) and Global Precipitation Climatology Center (GPCC) [61] and were found consistent.

2.2. Data Preparation and Methodology

The analysis of annual precipitation patterns of 116 years (1901–2016) for more than 57,000 locations (grid points) across the globe has been done. Several quality checks have already been adopted during data preparation by CRU, assuring good quality of data. However, it was observed that some of the grid points (even though having monthly data) of the same annual series were repeated for several years. The grid points, having such erroneous data, were not considered in this study. Monthly total ‘Pre’ and ‘Wet’ were converted to annual totals and used for further analysis. As previously discussed, autocorrelation highly influences the trend component, so the presence of autocorrelation was checked in the data.

Autocorrelation may be defined as cross-correlation of the time series with itself at defined time lag. The time lag by ‘k’ times represents the correlation of the series $x_1,x_2\dots x_{N-k}$ with the series $x_k,x_{k+1}\dots x_N$, where ‘N’ is the total number of data points in the time series. Autocorrelation (r) at lag k for the time series $x_1,x_2\dots x_N$ is given by

$$r_k=\frac{c_k}{{\sigma }^2}$$

(1)

here, $r_k$ is the autocorrelation at lag k, $c_k$ is the covariance at lag k,

$$c_k=\frac{1}{n}{\displaystyle \sum _{i=1}^{n-k}\left(x_i-\mu \right)}\left(x_{i+k}-\mu \right)$$

(2)

and $\mu ,{\sigma }^2$ are mean and variance, respectively.

Autocorrelation is said to be significant if it is out of the range of $\pm \frac{k}{\sqrt{N}}$, where k is the value of standard normal variate at a defined significance level, and N is sample size [62]. A significance level of 5% is adopted to check the significance of autocorrelation in this study.

The trends were estimated using non-parametric Sen’s Slope estimate. It is the most popular nonparametric technique for the estimation of a linear trend as it is robust and insensitive to outliers [63]. The parameter $T_i$ is computed as:

$$T_i=\frac{X_k-X_j}{k-j},i=1,2,3\dots N\mathrm{data}\mathrm{points}$$

(3)

where X_i and X_k are data at j and k times in time series $k>j$.

The $N$ values of $T_i$ are arranged in ascending order, and median of the slopes or Sen’s slope (β) is computed as

$$\beta =\{\begin{array}{cc}{T}_{\raisebox{1ex}{$(N+1)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\hfill & \mathrm{if}N\mathrm{is}\mathrm{odd}\hfill \\ \frac{T_{\raisebox{1ex}{$N$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+T_{\raisebox{1ex}{$(N+2)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{2}\hfill & \mathrm{if}N\mathrm{is}\mathrm{even}\hfill \end{array}$$

(4)

The positive or negative sign of β indicates rising and falling trend, respectively, and its value defines the magnitude of the trend. However, the significance of the trend cannot be directly known by this method. So, the MK test [11,12] is generally used to estimate the significance of the trend. The significance of trend is calculated using standard normal test static ‘Z_c’, which is compared with standard normal deviate ‘Z_s’ at defined significance level ‘α’. The null hypothesis H₀ of no trend is rejected if $\left|Z_c\right|>Z_{s|(1-\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.)}$.

$$Z_c{Z}_c=\{\begin{array}{cc}\frac{S-1}{\sqrt{Var(S)}},\hfill & \mathrm{if}S>0\hfill \\ 0,\hfill & \mathrm{if}S=0\hfill \\ \frac{S+1}{\sqrt{Var(S)}},\hfill & \mathrm{if}S<0\hfill \end{array}$$

(5)

where S is the MK test static.

$$S={\displaystyle \sum _{j=1}^{N-1}{\displaystyle \sum _{k=j+1}^{N}sgn(X_k-X_j)}}$$

(6)

here, N is the size of the series, and $X_j\mathrm{and}{X}_k$ are data at j and k times in time series $k>j$. $sgn(X_k-X_j)$ is the signum function which is 1, 0, −1 when $X_k<X_j,X_k=X_j,\mathrm{and}{X}_k>X_j$, respectively.

The variance of S is calculated as

$$Var(S)=\frac{N(N-1)(2N+5)-{\displaystyle \sum _{i=1}^m{t}_i(t_i+1)(2t_i+5)}}{18}$$

(7)

here, m is the number of tied groups, and $t_i$ is the number of ties of extent i. It has been found that the presence of serial correlational significantly affects the MK test static $Z_c$ [24]. They proposed Modified MMK test, which is suitable for autocorrelated data. They proposed to apply a correction factor $\frac{n}{n_s^{*}}$ to the variance of S

$$V^{*}\left(S\right)=Var\left(S\right)\frac{n}{n_s^{*}}=\frac{n\left(n-1\right)\left(2n+5\right)}{18}\times \frac{n}{n_s^{*}}$$

(8)

here, $n_s^{*}$ is the effective number of observations to be accounted for autocorrelation. The correction factor $\frac{n}{n_s^{*}}$ is computed as

$$\frac{n}{n_s^{*}}=1+\frac{2}{n\left(n-1\right)\left(n-2\right)}\times {\displaystyle \sum }_{k=1}^{n-1}\left(n-k\right)\left(n-k-1\right)\left(n-k-2\right)r_k$$

(9)

The probability distribution functions (PDF) considered in this study are described in Appendix A. Many statistical methods are available to find the parameters of probability distribution fitted to time series, i.e., least square method (LS), method of moments (Mo), maximum likelihood method (ML), generalized spacing estimator (GS), percentile estimator (PE), method of L-moments (LMo), etc. [64,65,66]. Distributions and their parameter estimation methods used in this study are given in

Table 1. Different Distributions and their parameter estimation methods used in this study.

Distribution Name	Parameter Estimation Method
Gamma	ML
Gamma_F	Mo
Gen. Extreme Value	LMo
Gen. Gamma	ML
Gen. Gamma_F	ML
Gen. Logistic	LMo
Gen. Pareto	LMo
Gumbel Max	Mo
Gumbel Min	Mo
Log-Logistic	ML
Log-Logistic_F	LS
Log-Pearson 3	Mo
Lognormal	Mo
Lognormal_F	Mo
Normal	ML
Pearson 5	ML
Pearson 5_F	ML
Pearson 6	ML
Pearson 6_F	ML
Weibull	ML
Weibull_F	LS

. Four methods, i.e., LS, ML, Mo, and LMo, were used to estimate the parameters of probability distributions. These methods are discussed in detail in Appendix B. Goodness of fit tests, i.e., Chi-Square (CS), Anderson–Darling (AD), and Kolmogorov–Smirnov (KS), were used to fit the probability distributions and are described in Appendix C.

All statistics and test values were produced from software EasyFit (available at http://www.mathwave.com/easyfit-distribution-fitting.html). EsayFit software was also used to apply Goodness of fit tests.

3. Results

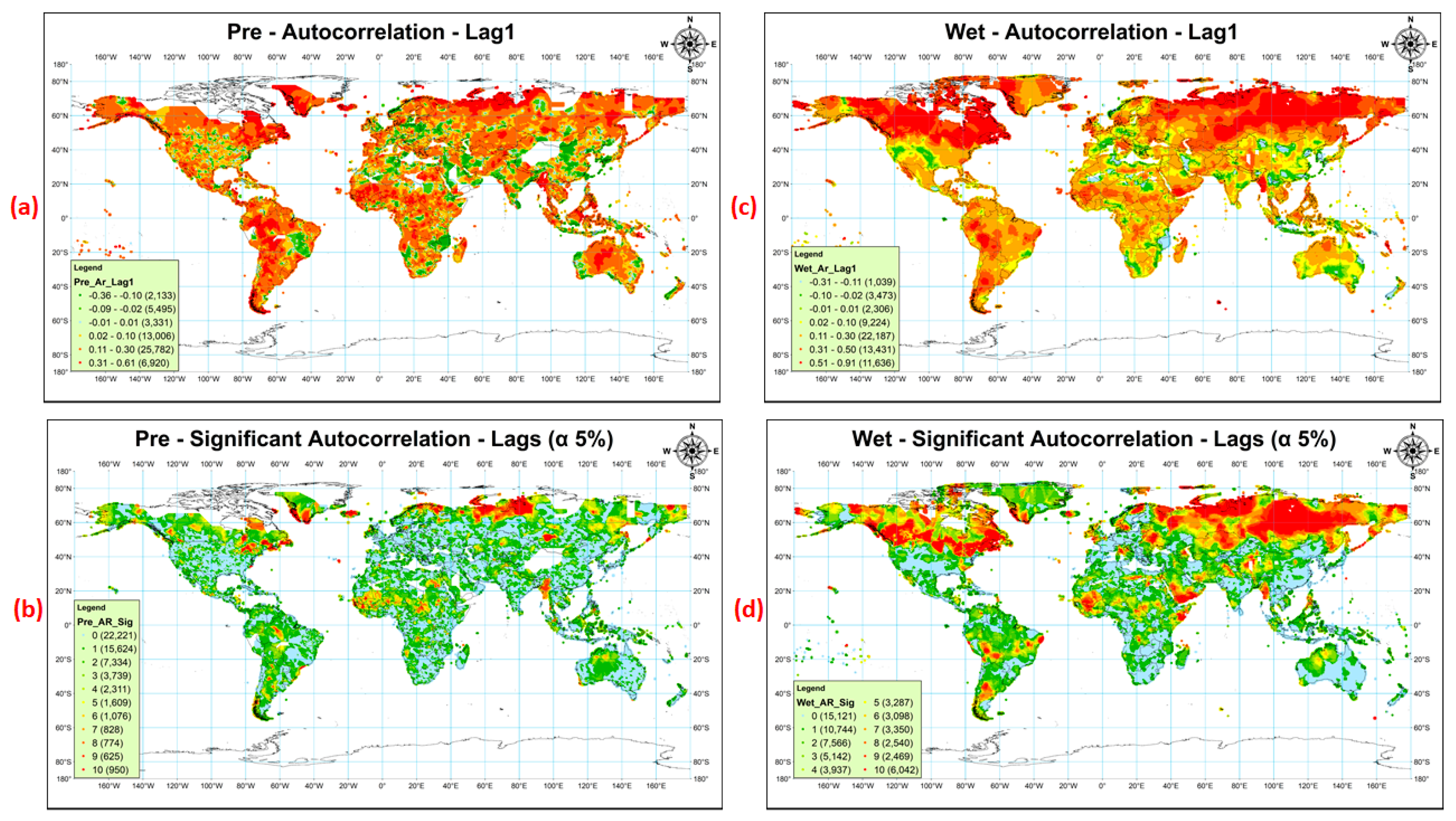
3.1. Serial Correlation

The lag1 autocorrelation, the significant autocorrelations up to lag10 at 5% significant level for Pre and Wet are shown in Figure 1a–d. Only a few of the regions showed significant negative autocorrelation. More than 60% of locations showed significant positive autocorrelation for precipitation, and out of them, almost 70% were found to be significantly autocorrelated up to lag2. Much more regions (>75%) indicated significant serial correlation for Wet data. Far Northern regions showed a higher order of serial correlation than the rest of the world.

So, it can be observed that the majority of the regions are not free from serial correlation. The autocorrelation indicates the persistence in the time series, so the positive serial correlation indicates that the precipitation is following the patterns of previous years in the succeeding years, that is, if the annual precipitation is decreasing, there is a higher probability of it to be decreasing in coming years as well and vice-versa [67,68]. However, this statement cannot be fully justified by observing only serial correlation, so the trends magnitude, direction, and significance were computed.

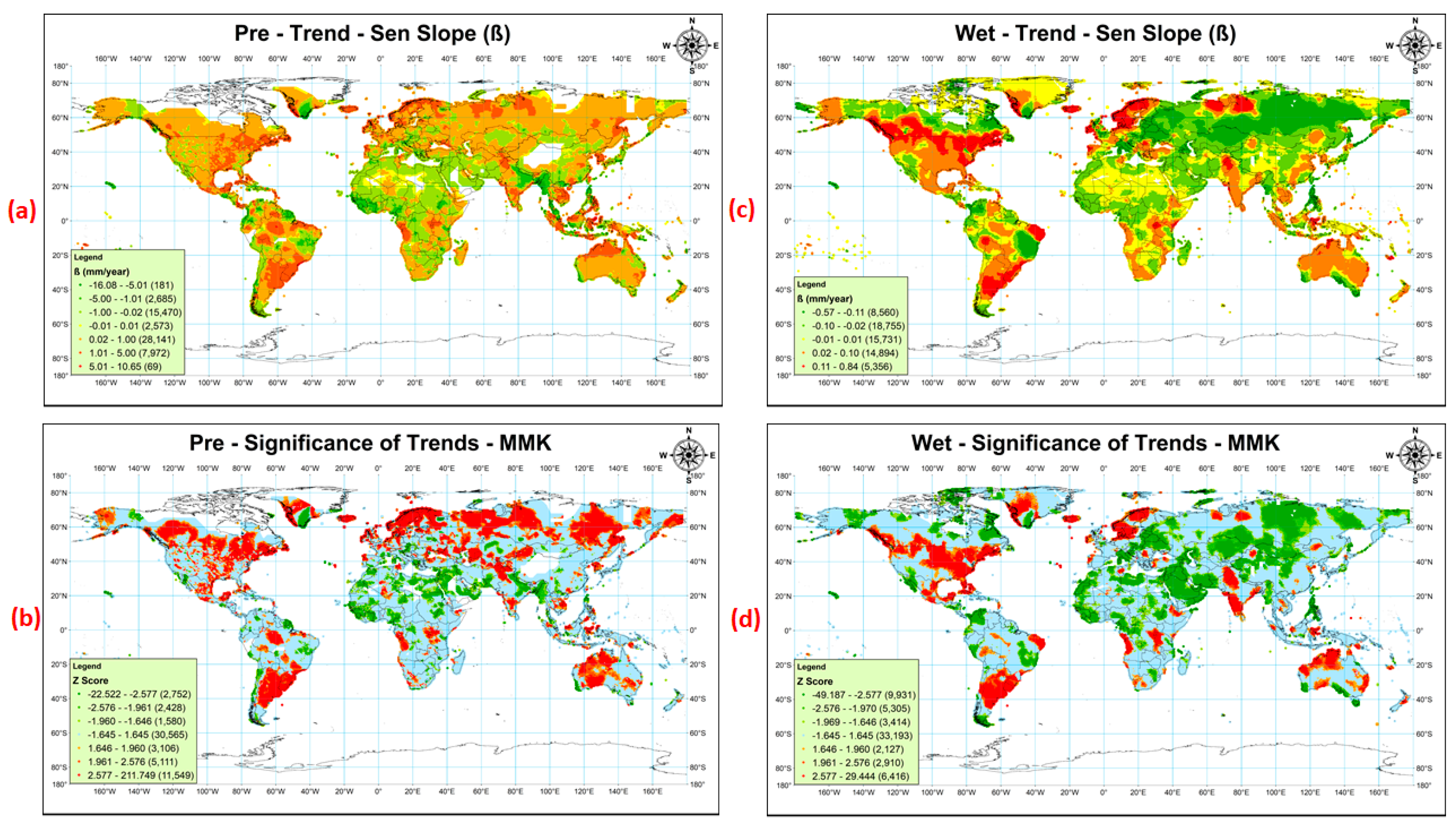
3.2. Trends

Instead of computing least-square-linear trend using simple linear regression, median slopes were calculated using Sen Slope method as the later one is robust to outliers. As it was found that the data was serially correlated and thus simple MK test could not be used to estimate the significance of the trends, so the MMK test was used which considers the autocorrelation effect on the significance of trends. The median slope ‘ß’ and Z score ‘Z_c’ of the MMK test are shown in Figure 2a–d. The value of |Z_c| more than or equal to 2.576, 1.96, and 1.645 indicated the significance level of trends at 1%, 5%, and 10%, respectively.

More than 46% of Pre data showed significant increasing or decreasing trends at 5% significance level, out of which high increasing trend of ~5–11 mm/year was found for ~68% regions. Significant decreasing trend, ~5–16mm/year, was detected for ~13% of entire Pre data. So, Pre was found to be increasing for the majority of the regions. Westra et al. [15] and Chou et al. [69] also indicated a significant increase in annual precipitation for more than two-thirds of the world stations.

Significant decreasing trends of Pre were found in the majority of the regions of world largest deserts, i.e., Sahara at Africa, Arabian at the Middle East, Thar at South Asia, Peruvian and Patagonian at South America, and Great Basin at North America. It might indicate a further decrease in the precipitation in the regions, which already were receiving less precipitation. Similar results for the world arid regions were found in the previous studies [70,71]. The regions of comparatively higher Pre, such as Northern and North-Eastern states of India—Bhutan and Myanmar, were found to be receiving lesser Pre, indicating a change in climate in these regions. However, on the contrary, the Pre was found to be significantly increased in the Great Sandy Simpson desert at Australia. Colder regions of the worlds like Russia, Europe, Central Asia, North America, and some Southern regions of South America were found to be experiencing significantly higher precipitation than past [72]. These results are similar to the model results, which identified the effect of anthropogenic activities on the increase in global mean precipitation at the regions near high latitudes and decrease in sub-tropical latitudes [73,74].

Increase or decrease in Pre alone cannot signify the extreme events until trends of the number of wet days are not closely analyzed with trends of precipitation. It was tried to find the relationship between the trends of Pre and Wet. The trends of Wet (ß_Wet) and the significance of these trends using MMK test are shown in Figure 2c,d, respectively. The significant trends of Wet were more or less similar to the Pre trends for the majority of the regions. The decreasing trend of Wet was found mostly in the regions of Africa, Asia, Russia, and Europe, and increasing trends were detected in some regions of North and South America, Australia, some parts of Europe, and some regions of South Asia. Lucero et al. [75] also found increasing wet days in Argentina (South America), but no change was detected in daily rainfall. However, opposite trends of Wet with Pre were found in the regions of North and East Asia. The Pre was found to be increasing, while the frequency of wet days was detected to be decreasing. This suggests the increase in high magnitude precipitation spells and decrease in the wet season.

The ratio of the trend of Pre to the trend of Wet shows the change in Pre with a unit change in Wet. Different possible combinations of Pre and Wet were made to analyze the results. These combinations were divided into two major sets, (i) Pre increasing and (ii) Pre decreasing. These major sets were further divided into four possible cases based on the magnitude and sign of ß_Pre/ß_Wet.

Case-1 −1 ≤ ß_Pre/ß_Wet ≤ 0

Case-2 0 ≤ ß_Pre/ß_Wet ≤ 1

Case-3 ß_Pre/ß_Wet < −1

Case-4 ß_Pre/ß_Wet > 1

Case-1 and 2 indicate that the magnitude of ß_Pre is lower than the magnitude of ß_Wet. As the trends of Wet were between −0.57 to 0.84 days/years, the trend of Pre lower than ß_Wet was found to be insignificant for most of the regions at 10% significance level, so these cases were not presented and discussed in this article. The variation of a trend in Pre with trends of Wet is shown in Figure 3a,b.

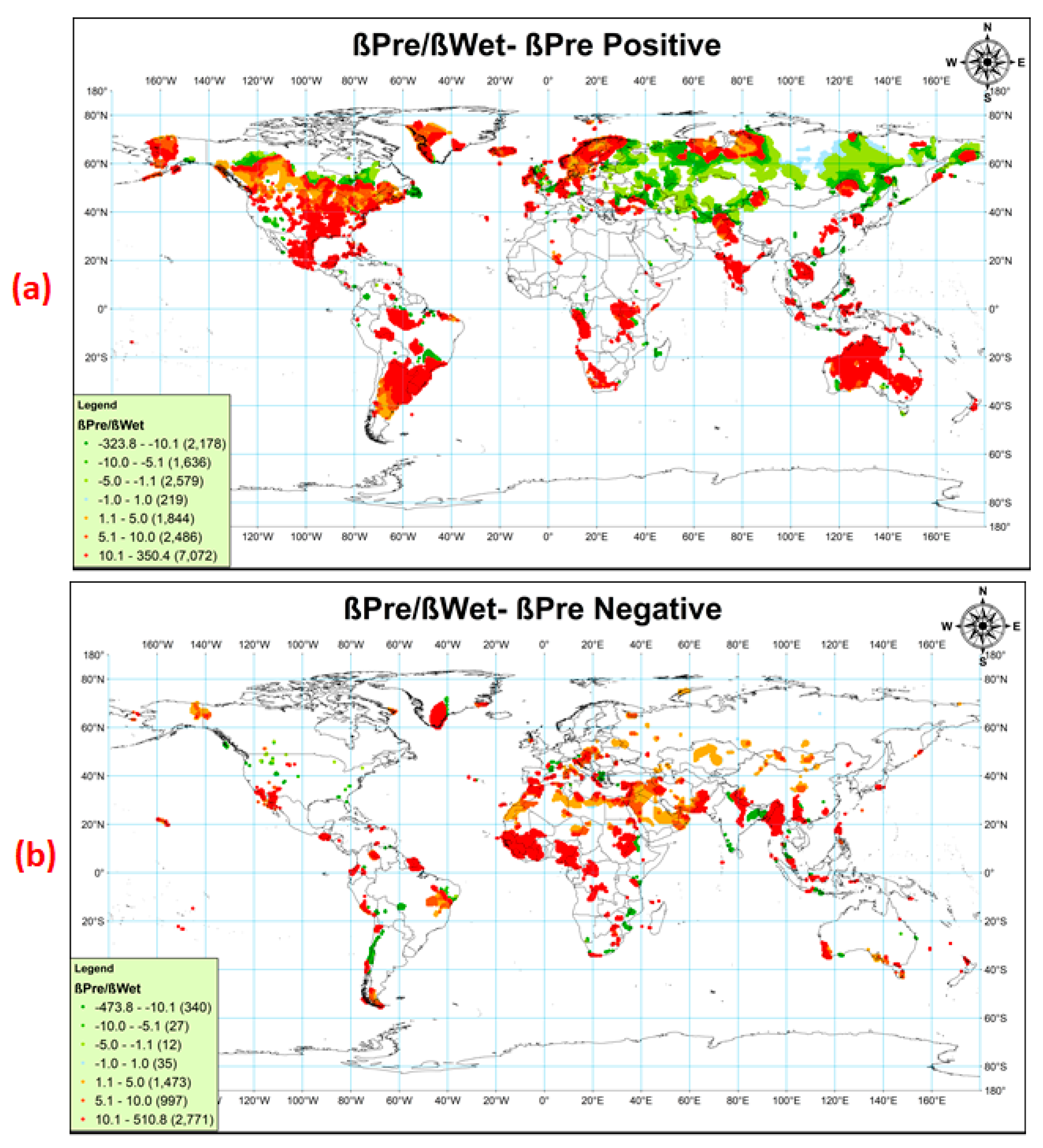
3.2.1. Pre Increasing (ß_Pre > 0)

The ratio of trends, i.e., ß_Pre/ß_Wet, is shown in Figure 3a. Case-3 and 4 are presented by shades of green and red color, respectively. The regions with dark green color represent a higher rate of increase in Pre and moderate rate of decrease in Wet, suggesting an increase in the high-intensity precipitation events. The regions with the high increasing trend with moderate or low increasing Wet are shown by dark red color, indicating moderate to the high intensity of precipitation events. Most of the regions of Russia, Central Asia, and Southern Canada were found to be experiencing a higher intensity of Pre events and longer duration of the dry season.

3.2.2. Pre Decreasing (ß_Pre < 0)

The ratio of trends, ß_Pre/ß_Wet, for the regions, which indicated a decrease in Pre at significance level ≤10%, is shown in Figure 3b. Regions showing a high decrease in precipitation with low to moderate increase in wet-day frequency are shown by dark green color. These regions indicate a slightly higher number of wet spells with low intensity of rainfall. The regions represented by dark red color denotes a high decrease in precipitation with low to moderate decrease in the number of wet days, indicating drier season and wet season with lesser precipitation. These climatic conditions may impose drought-like situations. Some regions of South-East Asia, i.e., Myanmar, North India, Afghanistan, East and Central Africa, and some coastal regions of Australia, North and South America were found to be receiving a much lesser amount of precipitation with lesser number of wet spells.

It was also tried to find the relationship between Pre trends in different climates of the world. Different climate types of the world [45] are shown in Figure 4.

The falling trend of Pre for climate class ‘BWh’ (represents Arid ‘B’, desert ‘W’, and hot climate ‘h’ type) at 10% significance level was detected except for Australia where an increase in Pre was detected. This climate type represents the deserts having much lesser Pre, so the regions of North Africa, Middle East, and South Asia have started receiving lesser precipitation, and the chances of drought events might get an increase. However, the dry regions of Australia were found to be receiving higher precipitation. The first letter ‘D’ of the climate class was defined by a cold climate with a temperature of the hottest month ≥10 °C and the temperature of the coldest month ≤0 °C. The second letter ‘f’ represent regions without dry seasons and the third letter a, b, c, d represents hot, warm, cold summer and very cold winter respectively. More than 70% of cold climate type regions without dry seasons, i.e., ‘Dfa’, ‘Dfb’, ‘Dfc’, and ‘Dfd’, showed increasing Pre trends at 1% significance level. So, the cold regions started to be receiving comparatively higher precipitation. The first letter ‘C’ of climate type represents temperate climate, which was defined by the temperature of the hottest month ≥18 °C and the temperature of the coldest month between 0 °C–18 °C. Decreasing trends in the Pre were found for temperate regions, which receives comparatively lesser rainfall than other temperate regions, i.e., climate type ‘Cwa’ (‘w’ for dry winter and ‘a’ for hot summer). Tropical climate type was represented by the first letter ‘A’ and defined by coldest month temperature ≥18 °C. Decreasing trends of Pre were found at a 5% significance level for most of the Tropical Savannah regions characterized by ‘Aw’, which receives comparatively lesser dry season rainfall.

Generally, it has been found that the regions with high magnitude of increasing trends are more prone to high-intensity precipitation spells and the regions with high magnitude of decreasing trends are highly susceptible to receive much lesser precipitation and longer dry seasons. These findings are fulfilling the criteria of rainfall intensification defined by [34], which refers to the more extreme climate of longer dry spells and more extreme rainfall.

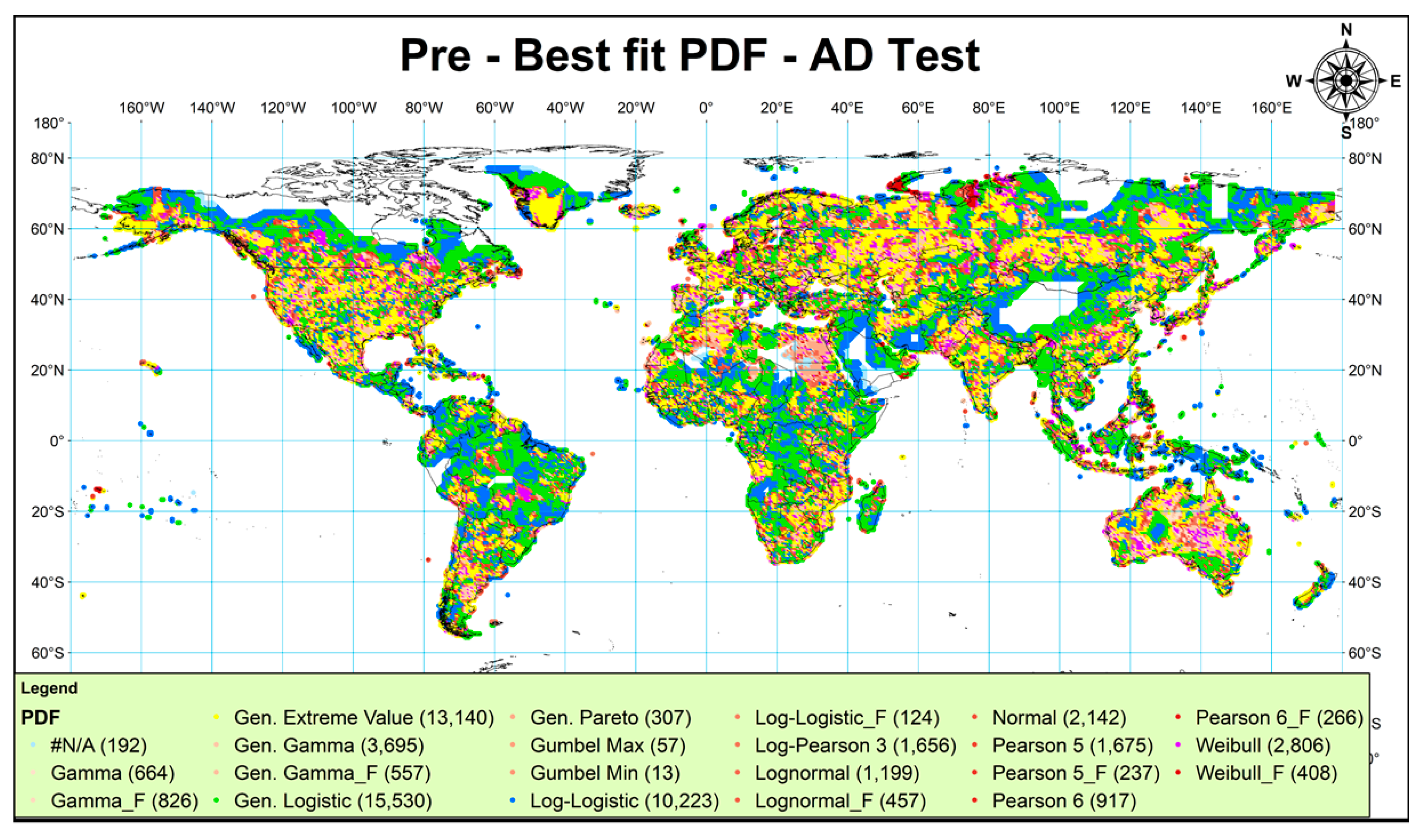
3.3. Best-Fit Distribution

Three most popular goodness of fit (GoF) tests, i.e., AD, KS, and CS test, were applied to find the best-fit probability distributions. A significance level of 5% was adopted in this study for GoF tests. AD test is considered to be best a suitable GoF test because it gives more weights to the tails of the distribution [76]. CS test is not considered to be high power GoF test [77]. A summary of the percentage of precipitation data best fitted for a particular probability distribution is given in

Table 2. Percentage distribution of best-fit probability distribution with different tests.

Distribution	AD	KS	CS
Gamma	1.2%	2.3%	2.6%
Gamma_F	1.4%	2.4%	3.1%
GEV	23.0%	14.7%	6.8%
Gen. Gamma	6.5%	5.6%	4.7%
Gen. Gamma_F	1.0%	2.3%	3.0%
Gen. Logistic	27.2%	16.3%	10.3%
Gen. Pareto	0.5%	1.7%	0.2%
Gumbel Max	0.1%	1.6%	5.2%
Gumbel Min	0.0%	0.2%	1.8%
Log-Logistic	17.9%	20.3%	10.7%
Log-Logistic_F	0.2%	2.8%	6.7%
Log-Pearson 3	2.9%	2.9%	3.0%
Lognormal	2.1%	2.3%	2.1%
Lognormal_F	0.8%	2.7%	4.0%
Normal	3.8%	4.1%	6.7%
Pearson 5	2.9%	2.8%	2.4%
Pearson 5_F	0.4%	1.7%	4.7%
Pearson 6	1.6%	1.9%	2.1%
Pearson 6_F	0.5%	1.3%	2.3%
Weibull	4.9%	5.2%	4.6%
Weibull_F	0.7%	4.3%	7.4%
#N/A	0.3%	0.5%	5.6%

. Best-fit probability distributions for annual precipitation data for the landmass of the world is shown in Figure 5.

Almost entire Madagascar was found to be best fitted with Log-Logistic (LL) distribution. GEV, Generalized-Logistic (GL), and LL distributions were best fitted to more than 68% regions of the world for precipitation data. GEV distribution was mostly best fitted in regions of North America, Russia, Europe, India, and Eastern China. Most of the regions of Northern and Eastern Russia, Mongolia, Northern and Central China, Bangladesh, Indonesia, Middle East, Madagascar, Central Africa, Northern South and North America, and Northern Greenland showed more similarity with GL and LL distributions.

The best-fit distributions for different regions showed significant changes in precipitation patterns that might be divided into two groups.

3.3.1. Regions with Significant Decreases in Annual Precipitation

Pre patterns for the arid lands of North Africa showed similarity with GEV and GL distributions. The regions of the Middle East showed agreement with the GL and LL distributions. GL distribution was found to be the best fit for eastern regions of India and Myanmar. Regions of Greenland and South America showing significant decreasing trend were found to follow the frequency of GEV distribution.

3.3.2. Regions with Significant Increases in Annual Precipitation

Most of the mid to high latitude regions showed significant increasing trends in annual Pre. These regions were found to be the best fit with GEV and Generalized Gamma (GG) distributions. High latitude regions of Southern hemisphere were found to be showing similarity with GEV, GG, and LL distributions.

4. Discussion

The hydrological cycle is changing due to climate change at a global scale, and the precipitation is one of the most vulnerable hydrometeorological variable [78]. In this study, a net increase in total annual precipitation for the last century was observed in more than two-third landmasses of the world, supporting the findings of other previous studies [15,69]. However, large variations in the seasonal patterns were observed, including shifting of monsoon season [79], increase in the frequency of extreme events, i.e., floods, droughts, etc. [28,80]. The present study also indicated a decrease in moderate precipitation events and an increase in extreme precipitation with a decreasing number of rainfall events, leading to the long spell of dry summers and short spell of the high rainfall season. However, the inference of “dry become drier and wet become wetter” [73,81] could not be justified in the present study, as some arid regions showed an increase in the precipitation events (arid regions in Australia), while others showed an increase in the desert land, supporting the findings of Greve et al. [82].

As long-term prediction of rainfall data is not feasible deterministically, the assumed probability distribution functions are fitted to find the magnitude and/or frequency of precipitation [83]. The prediction of precipitation is required for efficient water-resource management and to optimize the infrastructure designs. A wide range of PDF was adopted, in this study, to find the distribution which might best describe the precipitation. GEV, LL, and GL PDFs were best fitted to more than two-thirds of the locations, indicating that these distributions might be adopted for annual rainfall predictions rather than general events. Similar studies also indicate that the GEV distribution may be the best choice for the representation of precipitation [84]. It is recommended to find the best-fit distribution among a variety of PDFs to predict the rainfall at a local scale. The findings of this study are limited to only annual total precipitation, which may differ if the temporal scale is changed, such as daily, seasonal, extreme events, etc.

5. Conclusions

The present study assessed the changes in annual Pre patterns and found the simple probability model that could best describe the annual Pre patterns in different Koppen-Giger world climate types across the globe. Based on this study, the following can be inferred:

• The relationship of the trends of Pre with Wet showed an increase in the intensity of Pre and longer duration of dry seasons for most of the cold regions in mid to high latitude regions.
• Drought-like conditions, i.e., low-intensity wet spells and long dry spells, were found to be prevailing in the arid and semi-arid regions of the world.
• The best-fit probability distribution for the regions showing significant decrease or increase (at a 5% significance level) in annual Pre indicated that GL and GEV distributions were two competent models followed by LL distribution.
• Widely considered probability distributions by different climatologists, i.e., Gamma, Log-Normal, Extreme Value and 3, and Generalized Pareto distributions, were best fitted to less than 1% (individually) of global regions, while Normal and Log-Pearson 3 distributions best fitted to 2–5% regions only. So, the authors conclude that instead of simply assuming the probability distribution for statistical analysis and forecasting long-term precipitation at any location of the world, either a wide range of PDFs should be fitted to data to find the best-fit PDF or simply the results of this study may be referred.

This study may be helpful for not only the researchers but also planners to predict the annual behavior of precipitation patterns across the globe, and this could help in designing the economic infrastructure and saving lives.