Statistical Analysis of Bed Load Transport over an Armored Bed Layer with Cluster Microforms
Abstract
1. Introduction
2. Theoretical Backgrounds
3. Experimental Techniques and Methodology
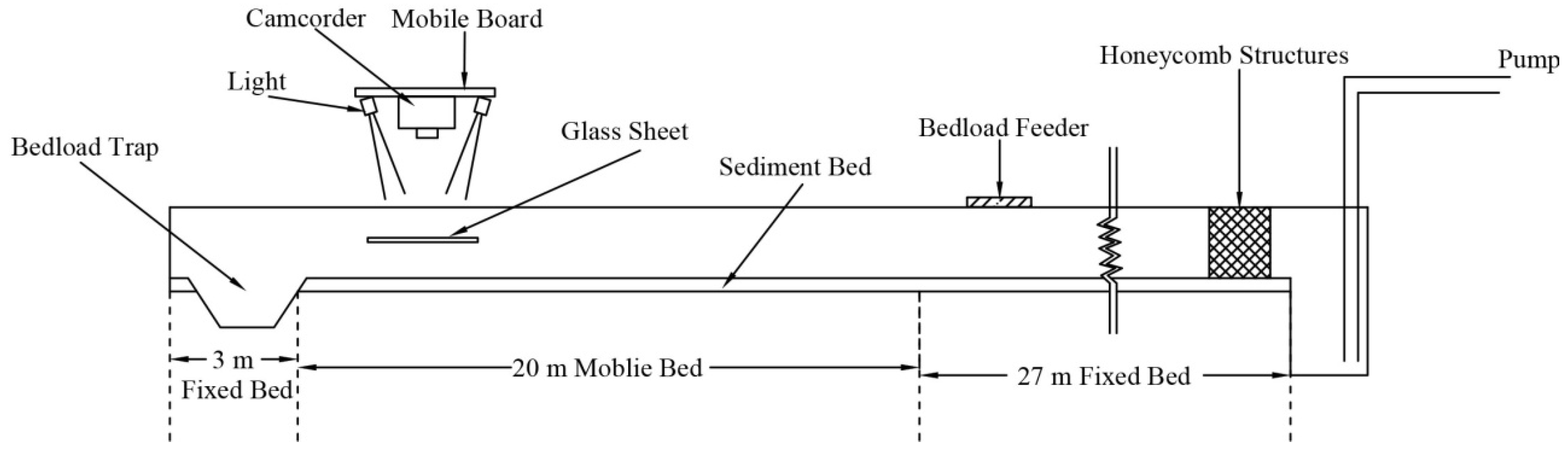
3.1. Experimental Setup
3.2. Image Processing
4. Experimental Results
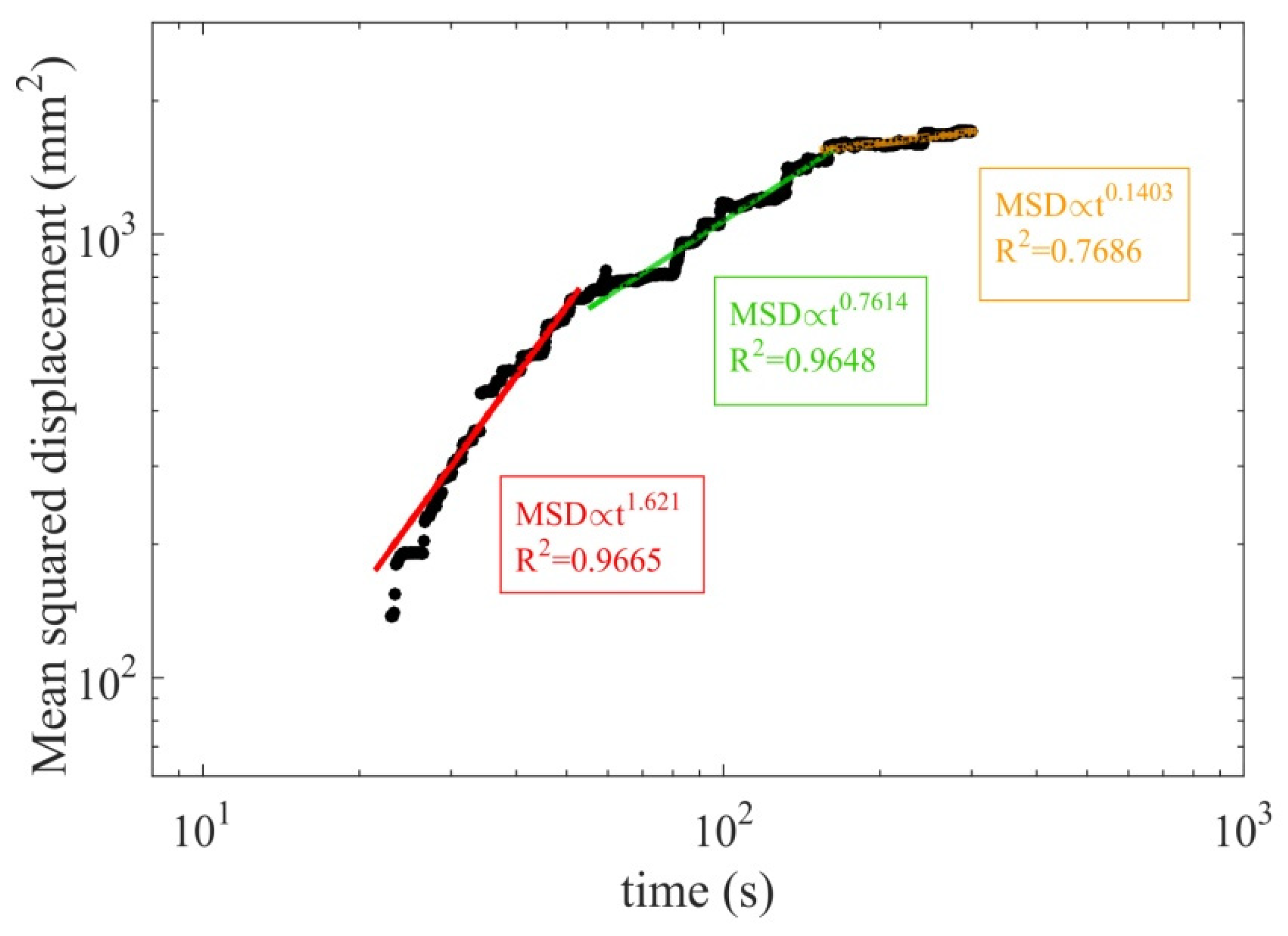
4.1. MSD Growth and Particle Diffusion Regimes
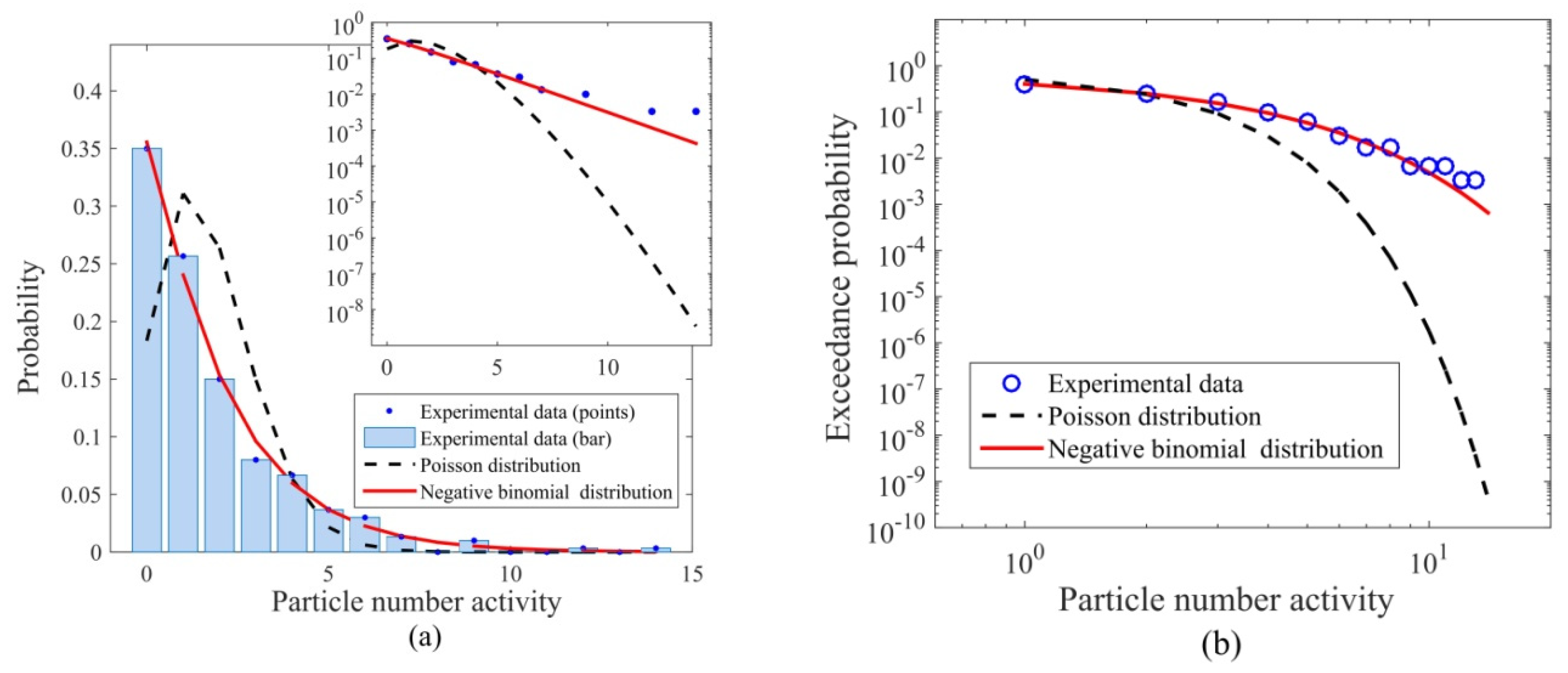
4.2. Particle Number Activity
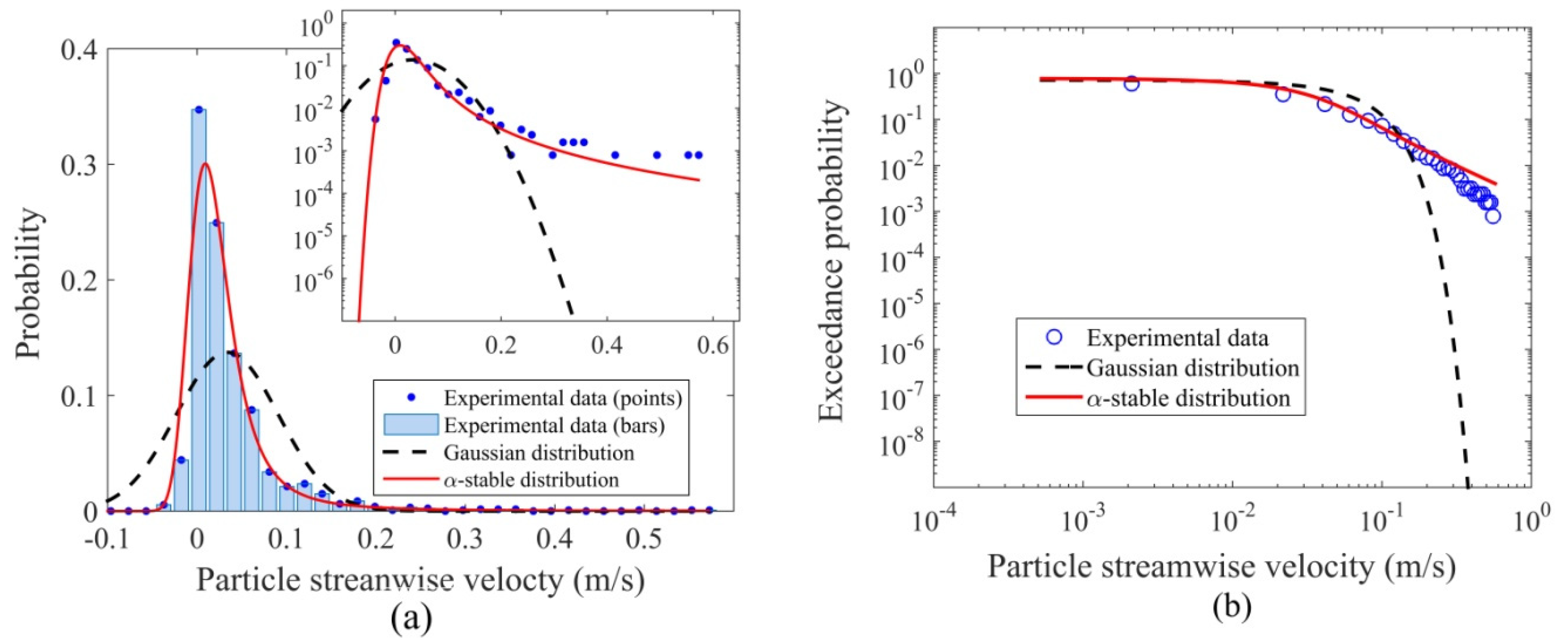
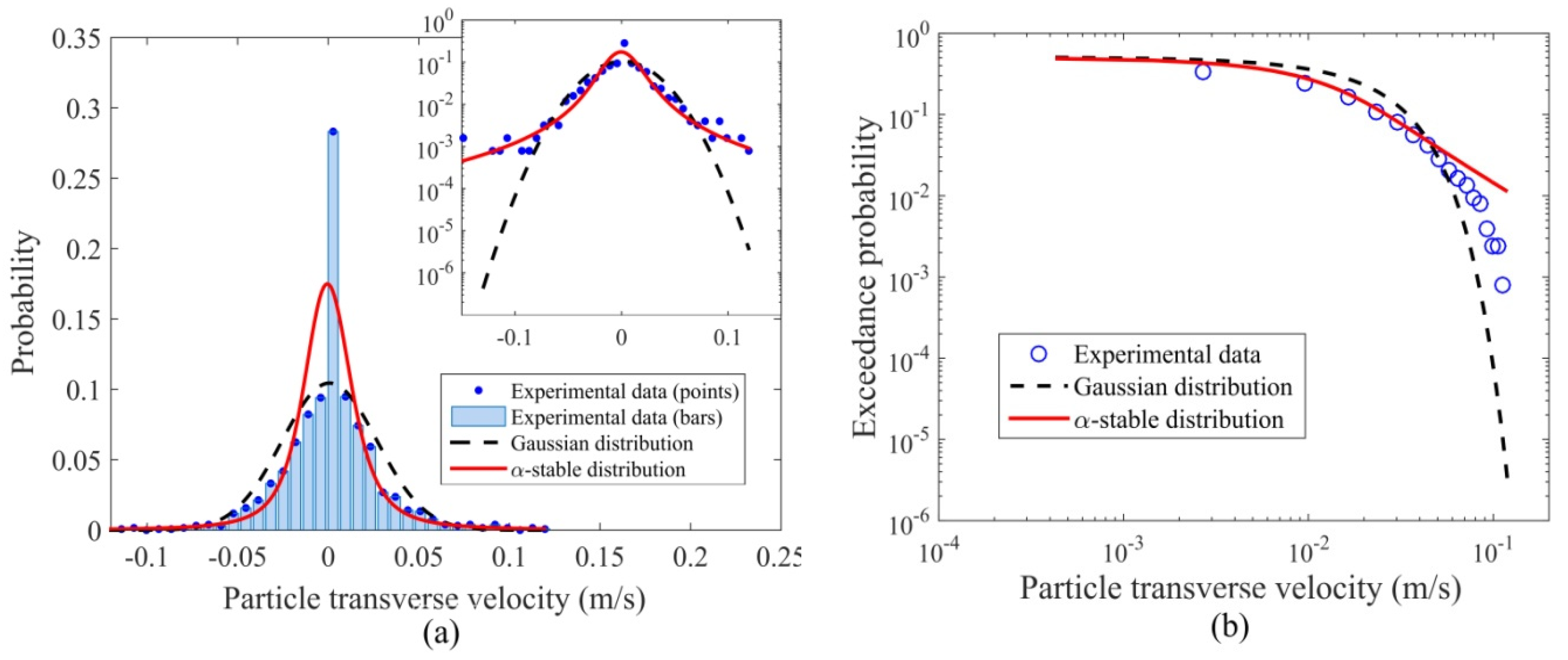
4.3. Particle Velocity
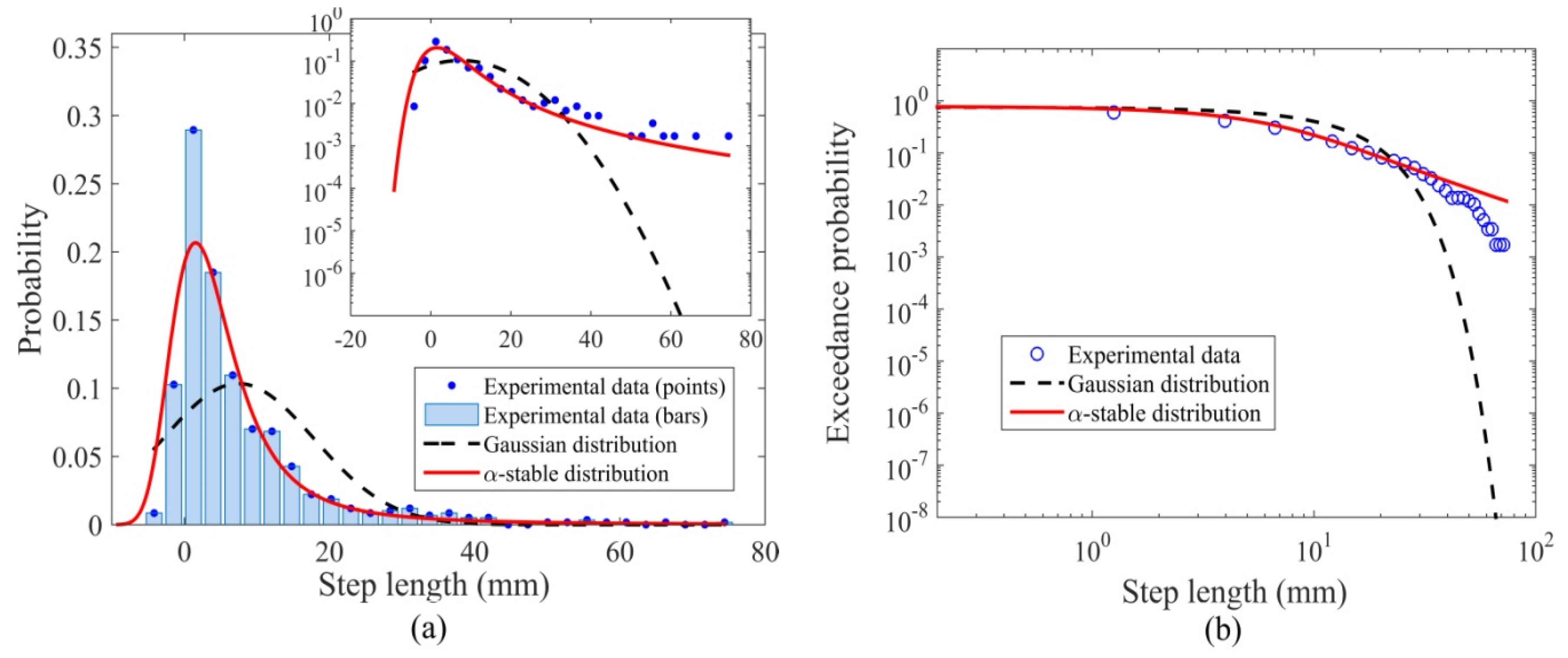
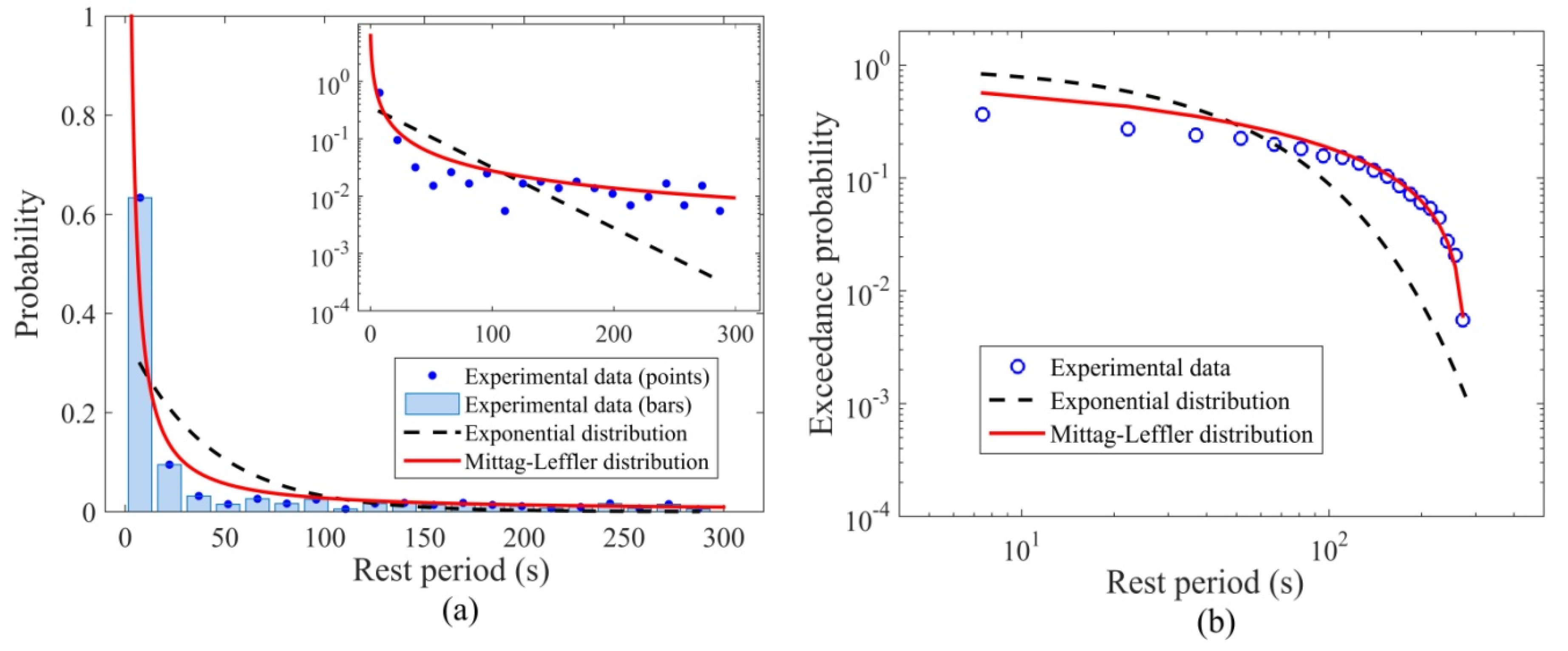
4.4. Particle Step Length and Rest Period
5. Discussion
5.1. Comparison with Previous Experiments
5.2. Particle Diffusion Regime and Particle Motion Statistics
5.3. Limitations of the Present Study
6. Conclusions
- The scaling growth of the MSD with time showed that the particle diffusion regimes in this experiment varied at different time scales: the particle diffusion regime was superdiffusive at small time scales (T < 50 s), but became subdiffusive at larger time scales.
- The particle number activity followed a negative binomial distribution, which is consistent with the theoretical solution derived in Ancey et al. [22] by accounting for the collective entrainment processes. The power-law tails in the probability distributions of both the streamwise and transverse particle velocities indicated a significant amount of fast-travelling particles, whereas the negative tail in the streamwise particle velocity distribution indicated a noticeable amount of grains occasionally moved in the upstream direction, which has rarely been considered in previous experiments. This may be explained by the particle clusters over dual impact on bed load transport exerted by the armored bed layers: some particles are accelerated in the preferential paths between particle clusters, while others were obstructed by the clusters to produce negative streamwise particle velocities. The distributions of the transverse particle velocity, the step length and the rest period all displayed heavy tails that were well described by the α-stable and M-L distributions. Nonetheless, the effect of the armored bed layer with cluster microforms on the distributions of these parameters needs to be confirmed with more experimental data.
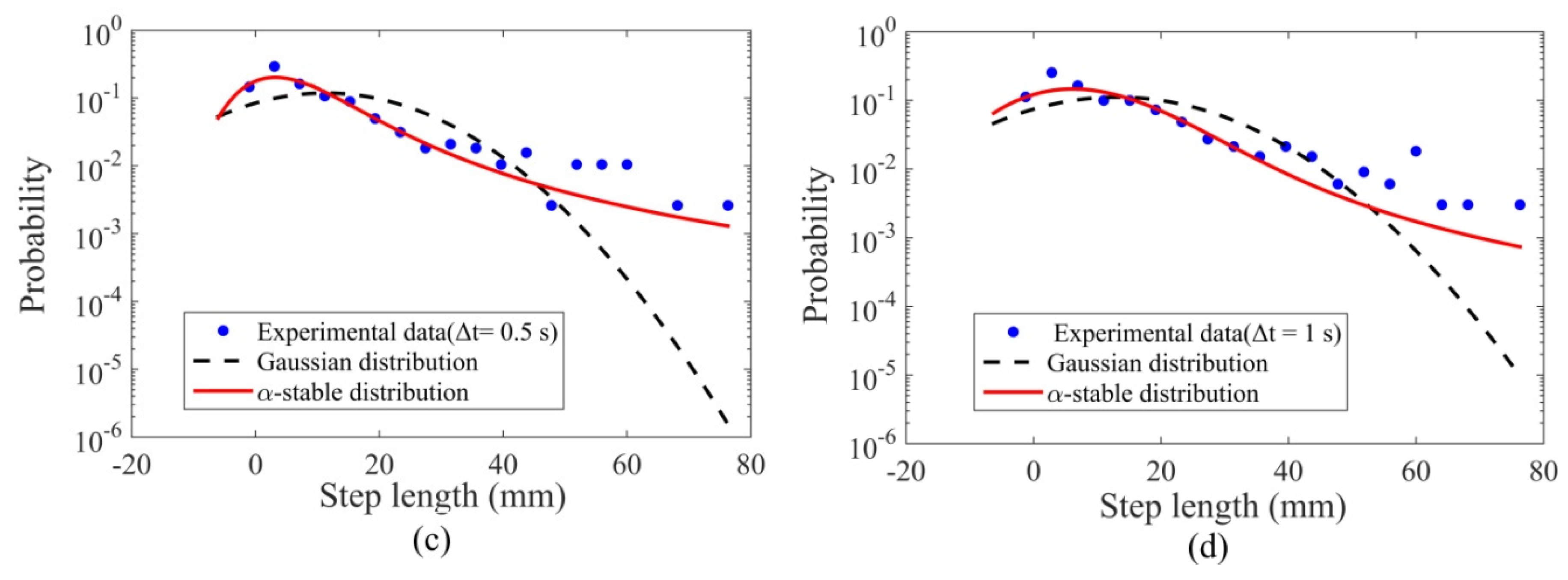
- The particle transport regime may be scale-dependent, i.e., the transport process may exhibit different diffusion regimes on different timescales. Meanwhile, the shapes of the distribution tails of the bed load motion parameters varied as observation time scale increases. We propose that the heavy tails in the distributions of the bed load motion parameters were associated with small time scales and may average out over longer observation periods. Nonetheless, the time scales associated with the transition of particle diffusion regimes and those with the changes in the statistical characteristics of bed load particle motions were different. Further investigation is needed in unraveling their connections.
Author Contributions
Funding
Conflicts of Interest
References
- Papanicolaou, A.N.; Strom, K.; Schuyler, A.; Talebbeydokhti, N. The role of sediment specific gravity and availability on cluster evolution. Earth Surf. Process. Landf. 2003, 28, 69–86. [Google Scholar] [CrossRef]
- Strom, K.; Papanicolaou, A.N.; Evangelopoulos, N.; Odeh, M. Microforms in Gravel Bed Rivers: Formation, Disintegration, and Effects on Bedload Transport. J. Hydraul. Eng. 2004, 130, 554–567. [Google Scholar] [CrossRef]
- Sun, H.; Chen, D.; Zhang, Y.; Chen, L. Understanding partial bed-load transport: Experiments and stochastic model analysis. J. Hydrol. 2015, 521, 196–204. [Google Scholar] [CrossRef]
- Strom, K.; Papanicolaou, A.N. Morphological characterization of cluster microforms. Sedimentology 2008, 55, 137–153. [Google Scholar] [CrossRef]
- Carrivick, J.L.; Jones, R.; Keevil, G. Experimental insights on geomorphological processes within dam break outburst floods. J. Hydrol. 2011, 408, 153–163. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.S.Y.; Jia, Y. Nonuniform sediment transport in alluvial rivers. J. Hydraul. Res. 2000, 38, 427–434. [Google Scholar] [CrossRef]
- Wilcock, P.R.; Crowe, J.C. Surface-based transport model for mixed-size sediment. J. Hydraul. Eng. 2003, 129, 120–128. [Google Scholar] [CrossRef]
- Barry, J.J. A general power equation for predicting bed load transport rates in gravel bed rivers. Water Resour. Res. 2004, 40, 2709–2710. [Google Scholar] [CrossRef]
- Ancey, C.; Böhm, T.; Jodeau, M.; Frey, P. Statistical description of sediment transport experiments. Phys. Rev. 2006, 74, 011302. [Google Scholar] [CrossRef]
- Lajeunesse, E.; Malverti, L.; Charru, F. Bed load transport in turbulent flow at the grain scale: Experiments and modeling. J. Geophys. Res. Earth Surf. 2010, 115, F04001. [Google Scholar] [CrossRef]
- Martin, R.L.; Jerolmack, D.J.; Schumer, R. The physical basis for anomalous diffusion in bed load transport. J. Geophys. Res. Earth Surf. 2012, 117, F01018. [Google Scholar] [CrossRef]
- Heyman, J.; Bohorquez, P.; Ancey, C. Entrainment, motion, and deposition of coarse particles transported by water over a sloping mobile bed. J. Geophys. Res. Earth Surf. 2016, 121, 1931–1952. [Google Scholar] [CrossRef]
- Roseberry, J.C.; Schmeeckle, M.W.; Furbish, D.J. A probabilistic description of the bed load sediment flux: 2. Particle activity and motions. J. Geophys. Res. Earth Surf. 2012, 117, F03032. [Google Scholar] [CrossRef]
- Fathel, S.L.; Furbish, D.J.; Schmeeckle, M.W. Experimental evidence of statistical ensemble behavior in bed load sediment transport. J. Geophys. Res. Earth Surf. 2015, 120, 2298–2317. [Google Scholar] [CrossRef]
- Fan, N.; Singh, A.; Guala, M.; Foufoula-Georgiou, E.; Wu, B. Exploring a semimechanistic episodic Langevin model for bed load transport: Emergence of normal and anomalous advection and diffusion regimes. Water Resour. Res. 2016, 52, 2789–2801. [Google Scholar] [CrossRef]
- Furbish, D.J.; Schmeeckle, M.W.; Schumer, R.; Fathel, S.L. Probability distributions of bed load particle velocities, accelerations, hop distances, and travel times informed by Jaynes’s principle of maximum entropy. J. Geophys. Res.Earth Surf. 2016, 121, 1373–1390. [Google Scholar] [CrossRef]
- Shim, J.; Duan, J.G. Experimental study of bed-load transport using particle motion tracking. Int. J. Sediment Res. 2017, 32, 73–81. [Google Scholar] [CrossRef]
- Lee, H.; Lin, Y.; You, J. On three-dimensional continuous saltating process of ediment particles near the channel bed. J. Hydraul. Res. 2006, 44, 374–389. [Google Scholar] [CrossRef]
- Furbish, D.J.; Schmeeckle, M.W. A probabilistic derivation of the exponential-like distribution of bed load particle velocities. Water Resour. Res. 2013, 49, 1537–1551. [Google Scholar] [CrossRef]
- Fan, N.N.; Zhong, D.Y.; Wu, B.S.; Foufoula-Georgiou, E.; Guala, M. A mechanistic-stochastic formulation of bed load particle motions: From individual particle forces to the Fokker-Planck equation under low transport rates. J. Geophys. Res. Earth Surf. 2014, 119, 464–482. [Google Scholar] [CrossRef]
- Houssais, M.; Lajeunesse, E. Bedload transport of a bimodal sediment bed. J. Geophys. Res. Earth Surf. 2012, 117, F04015. [Google Scholar] [CrossRef]
- Ancey, C.; Davison, A.C.; Bohm, T.; Jodeau, M.; Frey, P. Entrainment and motion of coarse particles in a shallow water stream down a steep slope. J. Fluid Mech. 2008, 595, 83–114. [Google Scholar] [CrossRef]
- Hubbell, D.W.; Sayre, W.W. Sand transport studies with radioactive tracers. J. Hydraul. Eng. Div. 1964, 90, 39–68. [Google Scholar]
- Schmidt, K.H.; Ergenzinger, P. Bedload Entrainment, Travel Lengths, Step Lengths, Rest Periods - Studied with Passive (Iron, Magnetic) and Active (Radio) Tracer Techniques. Earth Surf. Processes Landf. 1992, 17, 147–165. [Google Scholar] [CrossRef]
- Habersack, H.M. Radio-tracking gravel particles in a large braided river in New Zealand: A field test of the stochastic theory of bed load transport proposed by Einstein. Hydrol. Process. 2001, 15, 377–391. [Google Scholar] [CrossRef]
- Ganti, V.; Meerschaert, M.; Foufoula-Georgiou, E.; Viparelli, E.; Parker, G. Normal and anomalous dispersion of gravel tracers in rivers. J. Geophys. Res. Earth Surf. 2010, 115, 2156–2202. [Google Scholar] [CrossRef]
- McNamara, J.P.; Borden, C. Observations on the movement of coarse gravel using implanted motion-sensing radio transmitters. Hydrol. Process. 2004, 18, 1871–1884. [Google Scholar] [CrossRef]
- Voepel, H.; Schumer, R.; Hassan, M.A. Sediment residence time distributions: Theory and application from bed elevation measurements. J. Geophys. Res. Earth Surf. 2013, 118, 2557–2567. [Google Scholar] [CrossRef]
- Hill, K.M.; DellAngelo, L.; Meerschaert, M.M. Heavy-tailed travel distance in gravel bed transport: An exploratory enquiry. J. Geophys. Res. Earth Surf. 2010, 115, F00A14. [Google Scholar] [CrossRef]
- Wittenberg, L.; Newson, M.D. Particle clusters in gravel-bed rivers: An experimental morphological approach to bed material transport and stability concepts. Earth Surf. Process. Landf. 2005, 30, 1351–1368. [Google Scholar] [CrossRef]
- Billi, P. A note on cluster bedform behaviour in a gravel-bed river. Catena 1988, 15, 473–481. [Google Scholar] [CrossRef]
- Bouchaud, J.P.; Georges, A. Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications. Phys. Rep. 1990, 195, 127–293. [Google Scholar] [CrossRef]
- Blom, A.; Parker, G.; Ribberink, J.S.; De Vriend, H.J. Vertical sorting and the morphodynamics of bed-form-dominated rivers: An equilibrium sorting model. J. Geophys. Res. Earth Surf. 2006, 111, F01006. [Google Scholar] [CrossRef]
- Chien, N.; Wan, Z. Mechanics of Sediment Transport; ASCE Press: Reston, VA, USA, 1999. [Google Scholar]
- Schumer, R.; Meerschaert, M.M.; Baeumer, B. Fractional advection-dispersion equations for modeling transport at the Earth surface. J. Geophys. Res. Earth Surf. 2009, 114, F00A07. [Google Scholar] [CrossRef]
- Weeks, E.R.; Urbach, J.S.; Swinney, H.L. Anomalous diffusion in asymmetric random walks with a quasi-geostrophic flow example. Physica D 1996, 97, 291–310. [Google Scholar] [CrossRef]
- Pelosi, A.; Parker, G.; Schumer, R.; Ma, H.B. Exner-Based Master Equation for transport and dispersion of river pebble tracers: Derivation, asymptotic forms, and quantification of nonlocal vertical dispersion. J. Geophys. Res. Earth Surf. 2014, 119, 1818–1832. [Google Scholar] [CrossRef]
- Furbish, D.J.; Haff, P.K.; Roseberry, J.C.; Schmeeckle, M.W. A probabilistic description of the bed load sediment flux: 1. Theory. J. Geophys. Res. Earth Surf. 2012, 117, F03031. [Google Scholar] [CrossRef]
- Nikora, V.; Habersack, H.; Huber, T.; McEwan, I. On bed particle diffusion in gravel bed flows under weak bed load transport. Water Resour. Res. 2002, 38, 17-1–17-9. [Google Scholar] [CrossRef]
- Lin, F.; Bao, J. Environment-dependent continuous time random walk. Chin.Phys. B 2011, 20, 040502. [Google Scholar] [CrossRef]
- Ancey, C.; Heyman, J. A microstructural approach to bed load transport: mean behaviour and fluctuations of particle transport rates. J. Fluid Mech. 2014, 744, 129–168. [Google Scholar] [CrossRef]
- Bradley, D.N.; Tucker, G.E.; Benson, D.A. Fractional dispersion in a sand bed river. J. Geophys. Res. Earth Surf. 2010, 115, F00A09. [Google Scholar] [CrossRef]
- Huang, H.; Fiedler, H.; Wang, J. Limitation and improvement of PIV. Exp. Fluids 1993, 15, 168–174. [Google Scholar] [CrossRef]
- Gharahjeh, S.; Aydin, I. Application of video imagery techniques for low cost measurement of water surface velocity in open channels. Flow Meas. Instrum. 2016, 51, 79–94. [Google Scholar] [CrossRef]
- Fan, N.; Xie, Y.; Nie, R. Bed load transport for a mixture of particle sizes: Downstream sorting rather than anomalous diffusion. J. Hydrol. 2017, 553, 26–34. [Google Scholar] [CrossRef]
- Nakagawa, H. Sand bed instability due to bedload motion. J. Hydraul. Div. 1980, 106, 2029–2051. [Google Scholar]
- Malmon, D.V.; Dunne, T.; Reneau, S.L. Stochastic Theory of Particle Trajectories through Alluvial Valley Floors. J. Geol. 2003, 111, 525–542. [Google Scholar] [CrossRef]
- Brayshaw, A.C.; Frostick, L.E.; Reid, I. The hydrodynamics of particle clusters and sediment entrapment in coarse alluvial channels. Sedimentology 1983, 30, 137–143. [Google Scholar] [CrossRef]
- Singh, A.; Fienberg, K.; Jerolmack, D.J.; Marr, J.; Foufoula-Georgiou, E. Experimental evidence for statistical scaling and intermittency in sediment transport rates. J. Geophys. Res. Earth Surf. 2009, 114, F01025. [Google Scholar]
- Phillips, C.B.; Martin, R.L.; Jerolmack, D.J. Impulse framework for unsteady flows reveals superdiffusive bed load transport. Geophys. Res. Lett. 2013, 40, 1328–1333. [Google Scholar] [CrossRef]
- Bialik, R.J.; Karpiński, M. On the effect of the window size on the assessment of particle diffusion. J. Hydraul. Res. 2018, 56, 560–566. [Google Scholar] [CrossRef]


| Size Group | Median Size (mm) | Size Range (mm) | Weight Fraction (%) |
|---|---|---|---|
| 1 | 0.45 | 0.25–0.8 | 10 |
| 2 | 1.0 | 0.6–1.25 | 15 |
| 3 | 3.0 | 1.0–5.0 | 25 |
| 4 | 7.0 | 5.0–10.0 | 25 |
| 5 | 17.0 | 15.0–20.0 | 25 |
| Q (L/s) | H (cm) | Fr | Re | Θ | U* (m/s) |
|---|---|---|---|---|---|
| 130 | 16.1 | 0.64 | 9.8 × 104 | 0.13 | 0.08 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Zhang, S.; Chen, D. Statistical Analysis of Bed Load Transport over an Armored Bed Layer with Cluster Microforms. Water 2019, 11, 2082. https://doi.org/10.3390/w11102082
Zhu Z, Zhang S, Chen D. Statistical Analysis of Bed Load Transport over an Armored Bed Layer with Cluster Microforms. Water. 2019; 11(10):2082. https://doi.org/10.3390/w11102082
Chicago/Turabian StyleZhu, Zhenhui, Shiyan Zhang, and Dong Chen. 2019. "Statistical Analysis of Bed Load Transport over an Armored Bed Layer with Cluster Microforms" Water 11, no. 10: 2082. https://doi.org/10.3390/w11102082
APA StyleZhu, Z., Zhang, S., & Chen, D. (2019). Statistical Analysis of Bed Load Transport over an Armored Bed Layer with Cluster Microforms. Water, 11(10), 2082. https://doi.org/10.3390/w11102082





