1. Introduction
Flows around a wall-mounted circular cylinder appear in a large number of technical and environmental applications, such as river flows past bridge piers and pile foundations [
1,
2,
3]. When the natural wall-bounded flow encounters a vertical cylinder, horseshoe vortices (HVs) are formed in the junction region between the bed and the cylinder [
4,
5,
6]. The HVs are a system of necklace structures wrapping around the front and flanks of the cylinder. Depending on the regime of the approaching flow at the location of the cylinder, the horseshoe vortex (HV) system appears as a laminar or turbulent system, respectively [
7]. The turbulent HV system oscillates randomly in front of the cylinder, inducing highly elevated means and fluctuations in bed shear stress [
8]. Therefore, a full understanding of the evolution of the turbulent HV system is necessary for understanding, predicting, and controlling the initial stage of the local scour in front of cylinders.
Due to the highly dynamical nature of the turbulent HV system, many investigations have focused on interpreting its underlying dynamics with models of low complexity [
9,
10,
11,
12,
13].
The evolution of the instantaneous turbulent HV system, however, has received less attention, partly due to its complexity manifesting as aperiodic interactions and variations in number, position, size, and strength. Dargahi [
14] made one of the earliest descriptions on the evolutionary process of the turbulent HV system based on experimental observations conducted with flow visualization method. Results showed the HV closest to the cylinder oscillates upstream and downstream along the bed. When the HV moves downstream toward the cylinder, it approaches the bed, and its cross-section area and circulation strength decreases. Latter, Agui and Andreopoulos [
15] visualized the flow structures around a circular cylinder for cylinder Reynolds numbers, Re
D, of 1.0 × 10
5 and 2.2 × 10
5. They observed that the flow field upstream of the cylinder is always dominated by a much more stable and larger primary HV (PHV). They also concluded the PHV wanders mostly in the streamwise direction under the action of large-scale structures in the incoming flow.
More detailed descriptions on the evolution of the turbulent HV system were not available until eddy-resolving numerical simulations were applied. Kirkil et al. [
16] performed one of the earliest large eddy simulations (LES) on flow around a circular cylinder at a Reynolds number of 18.000. They found the junction region is not always dominated by a large relatively stable PHV. The PHV can generate through growing of a small vortex or merging of several vortices with the same rotation sense. Moreover, some of the vortices are separated from the attached boundary layer on the upstream cylinder face instead of the upstream separation region. During its lifetime, the PHV gains or loses vorticity due to interaction with co-rotating or counter-rotating vortices, respectively. In some cases, the PHV was split or practically destroyed. Later, Paik et al. [
10] carried out detached eddy simulations (DES) for flow around a wing mounted on a flat bed at Re
D = 1.15 × 10
5. They found the flow is dominated by a coherent PHV. However, for flows around a circular cylinder with lower Reynolds number, the DESs carried out by Escauriaza and Sotiropoulos [
11] showed some differences on the evolution of the turbulent HV system. For the flow at Re
D = 39,000, the system was found to be dominated by two primary horseshoe vortices (PHVs). These two HVs move upstream and downstream, respectively. On the other hand, the HV system at Re
D = 20,000 is composed of four or five PHVs at all times, which move only in the downstream direction.
Recently, Kirkil and Constantinescu [
17] adopted the LES and DES approaches to study flows around a circular cylinder with Re
D = 16,000 and 500,000, respectively. In both cases, the turbulent HV system was found to dominate by one PHV. The main mechanism for increasing the coherence of PHV is the merging and extraction of vorticity of the same sign from vortices originating in either the down-flow or the separation region. Meanwhile, the core of the PHV is larger when it is located away from the cylinder.
Quantitative experimental studies on the evolution of the turbulent HV system upstream of a circular cylinder were reported recently by several groups. Apsilidis et al. [
12] reported the influence of cylinder Reynolds number on the dynamics of the turbulent HV system by using time-resolved PIV. For the case with Re
D = 29,000, the flow upstream of the cylinder is not dominated by a PHV sometimes. However, the flows upstream of the cylinder with Re
D = 47,000 and 123,000 are always dominated by a PHV. The PHV can maintain its coherence by merging vortices originating in the incoming flow, the down-flow along the cylinder face, or the upstream separation region. Schanderl et al. [
18] obtained the flow fields in front of a circular cylinder on a flat bed with Re
D = 39,000 by using PIV. The turbulent HV system was found to be dominated by a PHV.
The PHV undergoes relatively large streamwise displacements, and the closer to the cylinder it locates the more coherent it would be. Recently, Li et al. [
19] observed part of the evolutionary process of turbulent HV in front of a circular cylinder with Re
D = 9400 and 13,500 by using time-resolved PIV. The strength and size of the PHV were found to decrease gradually when it retreats back to the cylinder.
To summarize, despite many valuable contributions by using flow visualization methods, eddy-resolving simulations, and quantitative measurements, the evolutionary process of the turbulent HV system is far to be well understood. On one hand, existing observations based on different methods, especially numerical simulations, have shown some discordances. On the other hand, many existing investigations on the evolution of turbulent HV system have been based merely on the observations of instantaneous velocity fields, which is insufficient for building a statistically reliable description on the evolutionary process of the turbulent HV system. Therefore, the present study uses quantitative and statistical methods to investigate the evolution of the turbulent HV system. It expands upon the previously published work by Chen et al [
13]. Especially, relationships between the various features of the PHV dominating the turbulent HV system during its evolution were investigated. Meanwhile, the underlying mechanisms responsible for the generation, disappearance, large-scale streamwise movements, and strength variations of the PHV were re-investigated.
2. Datasets and Methodology
2.1. Datasets
Three experimental datasets were used for the present investigation. The experiments were carried out in a recirculating tilting water flume that was 20 m long and 0.3 m wide.
Figure 1 shows two diagrams and a photograph of the experimental setup. A circular cylinder with a diameter of 3.2 cm was mounted vertically on the flat bed of the flume. The length of the cylinder is larger than the water depth to avoid submergence. The distance between the axis of the cylinder and the entrance of the flume is 12 m to ensure a fully developed turbulent open channel flow. The cylinder Reynolds number Re
D, defined with the diameter of the cylinder,
D, and the bulk mean velocity,
Um, was 8600, 10,200, and 13,900, respectively. The detailed flow characteristics for each experimental case are summarized in
Table 1. For the sake of distinction, each case is named by its cylinder Reynolds number preceded by the letter “C”. According to the results of Wei et al. [
7], the HV systems in the minimum and maximum Re
D cases considered here are intermittently and fully turbulent, respectively. The 2D instantaneous velocity fields in the symmetry plane upstream of the cylinder were measured using a time-resolved PIV system. For each flow condition, two or three sequences of continuous velocity fields were measured with a frequency larger than 500 Hz. The total numbers of velocity fields for each case are 21,000, 21,000, and 24,000, respectively. More details about the experimental setup, PIV system, and the validation of the experiment data can be found in Chen et al. [
13].
As shown in
Figure 1, the origin of the coordinate system used to describe the results is defined to lie at the center of the cylinder on its bottom surface. The
x axis is oriented along the main flow and parallel to the flume bed. The
y axis is normal to the bed and coincides with the central axis of the cylinder. The transverse
z axis is normal to the side walls of the flume. The instantaneous velocity components in the
x,
y, and
z directions are denoted by
U,
V, and
W, respectively.
2.2. Vortex Identification and Characterization Methods
The turbulent HVs are usually identified as closed or spiral streamlines. However, this method fails when the convection velocity of a vortex becomes non-ignorable [
20]. Meanwhile, quantitative features of vortices can hardly be read out from the streamline patterns. Therefore, a number of recent investigations used kinematics implied by the velocity gradient tensor as the indicators of HVs. For instance, Paik et al. [
10], Kirkil and Constantinescu [
17], and Apsilidis et al. [
12] adopted the Q criterion to visualize vortices within the HV system.
The present investigation uses the swirling strength criterion to identify HVs. The criterion adopts the imaginary part of the eigenvalues of the velocity gradient tensor (termed swirling strength and denoted by
λci) as the vortex indicator [
21]. When
λci is non-zero at a point, the local streamline around the point is swirling, and the strength of the local swirling motion is represented by its value. For real vortices in turbulent flows, the strength of swirling motion shows maximum value at the center and decreases monotonously along the radius. Therefore, vortices are detected as non-zero clusters around the peaks of
λci [
22]. Since the imaginary part of the eigenvalues is always positive, we define
Λci =
λci∙sign(
ωz) to distinguish between vortices rotating in the clockwise and counterclockwise sense, where
ωz is the spanwise vorticity. The peak position of each cluster of
Λci indicates the center of each vortex, and the peak value,
Λv, denotes the coherence of each vortex.
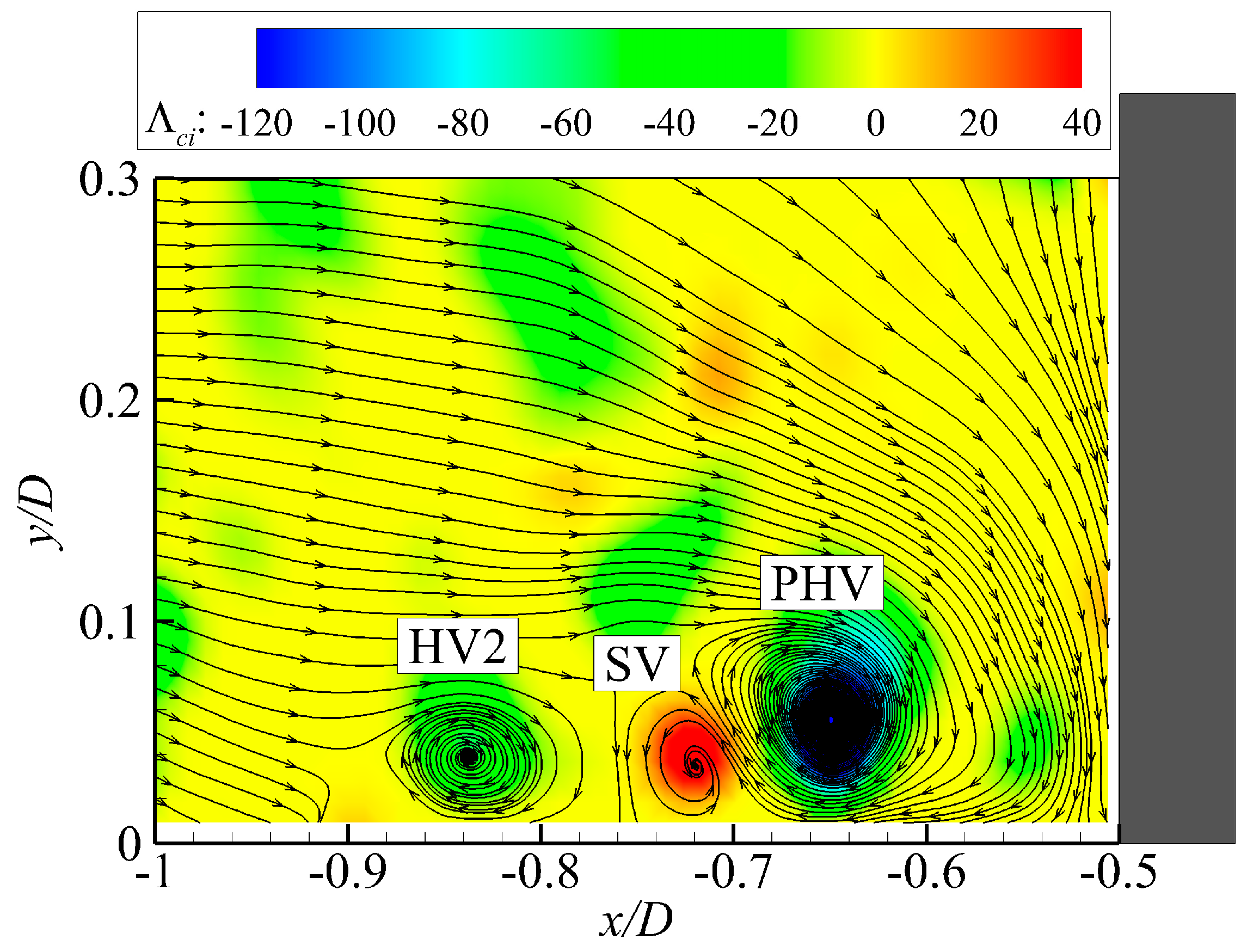
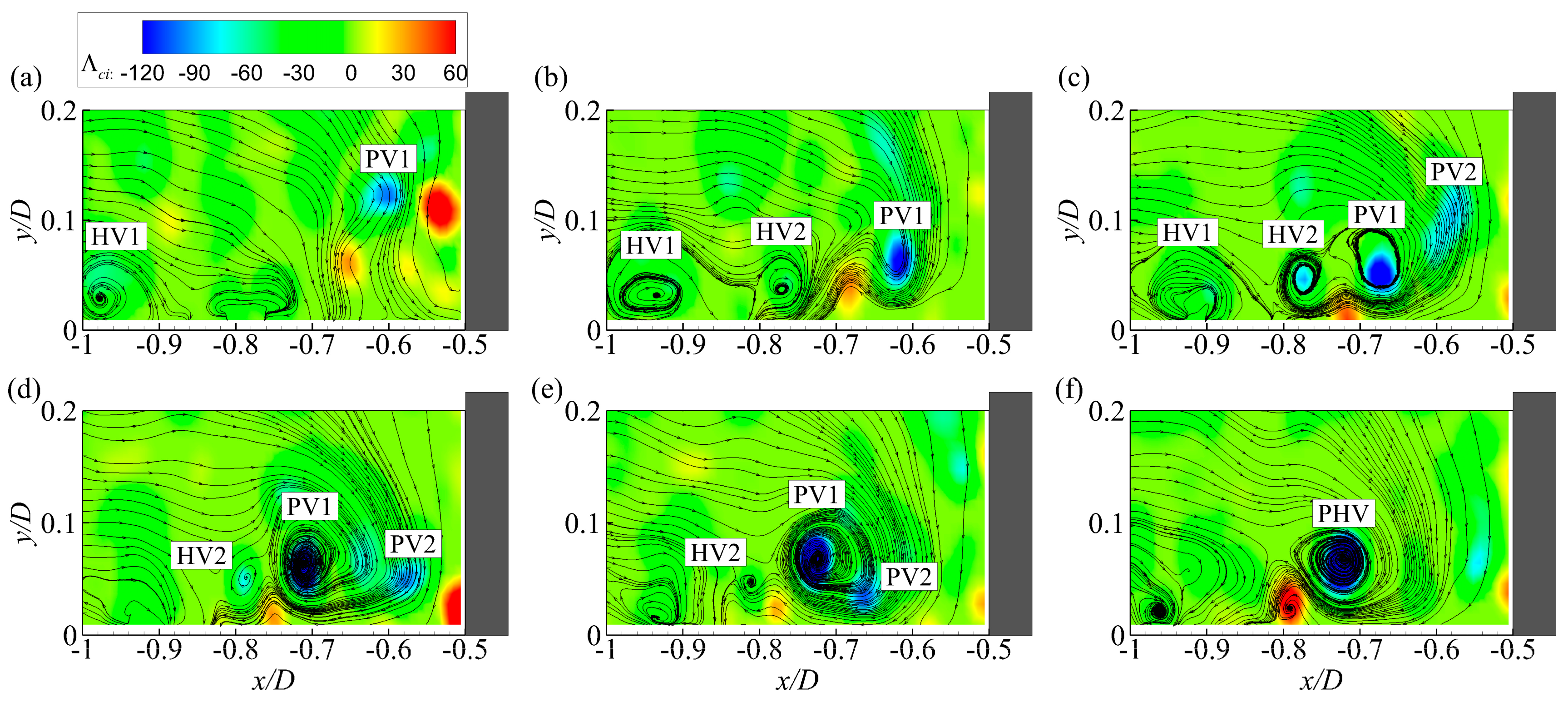
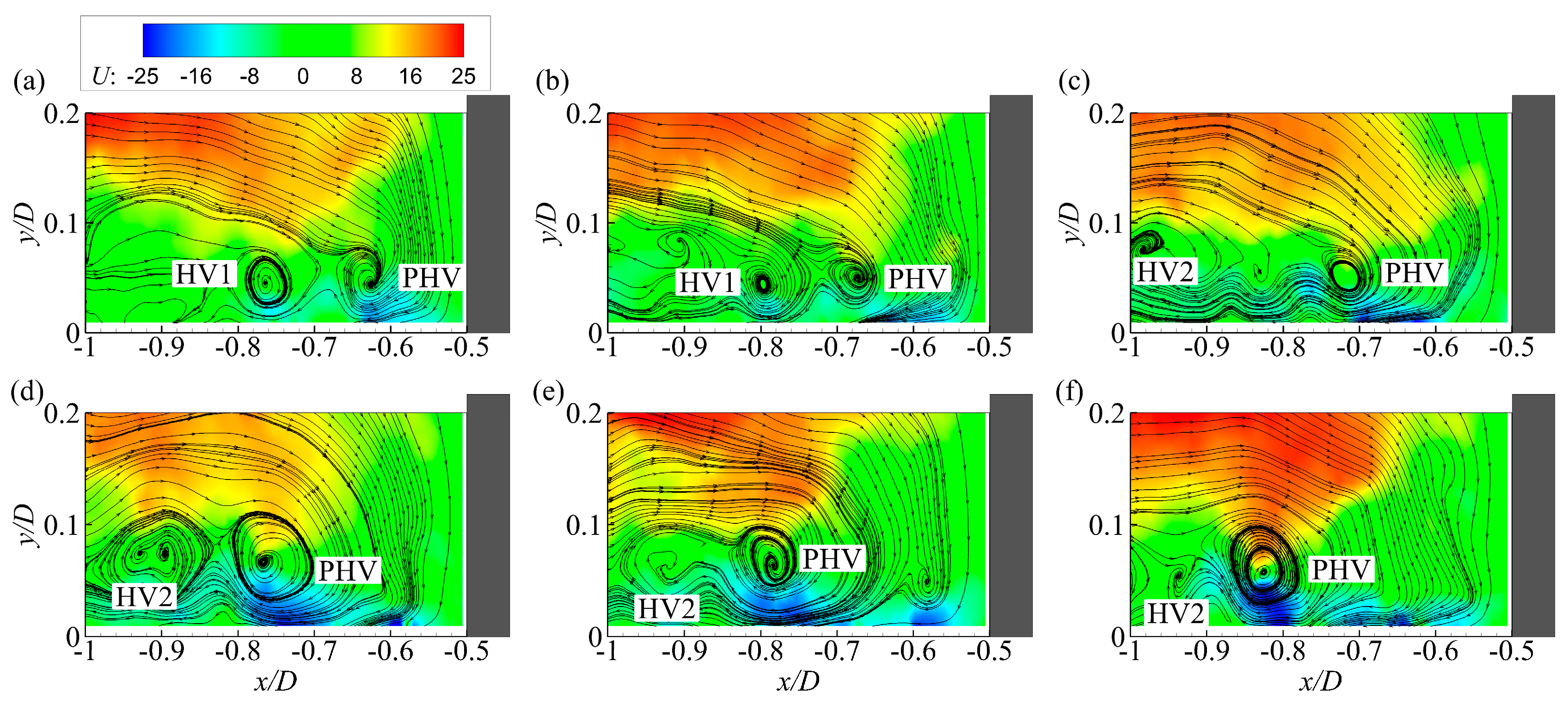
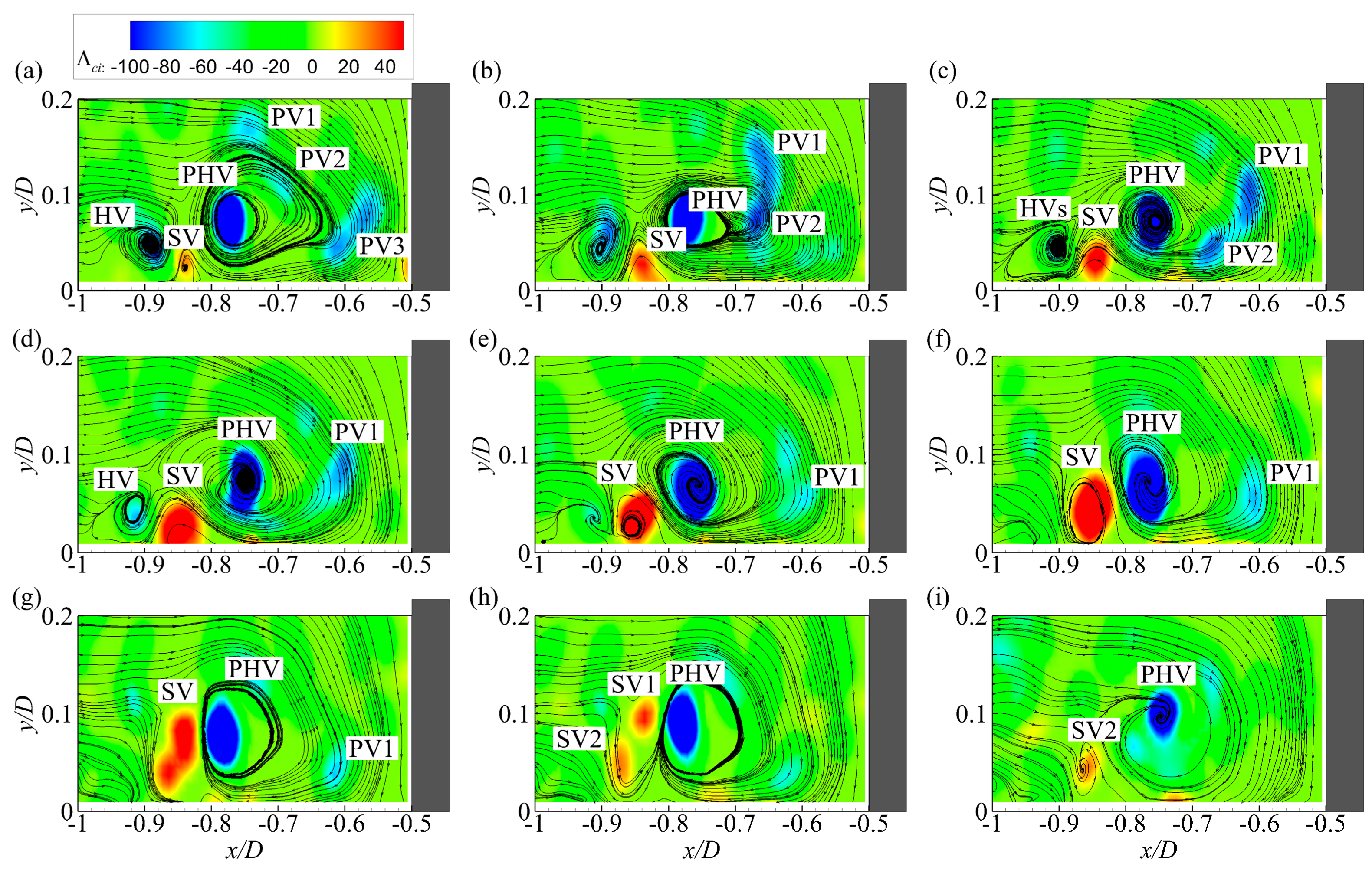
Figure 2 presents the streamlines and contours of
Λci in an instantaneous velocity field in front of the cylinder for case C8600. According to the streamline patterns, two HVs and one secondary vortex (SV) are observed in the junction region. The swirling strength criterion correctly identifies these vortices.
The swirling strength criterion can determine the center and coherence of each vortex, but methods are still required to determine their core size and circulation strength. Traditionally, two categories of methods were widely used. The first kind of methods define the boundary of a vortex as an isoline of vortex indicators, of which the value equals to a given threshold [
22]. The circulation strength of the vortex is then calculated by integrating the vorticity within the vortex core. These methods are simple and intuitive, but the results depend on the selected threshold. The second kind of methods extract the features of a vortex by fitting the local velocity field with a standard vortex model [
23]. By properly selecting the model, results of this kind of method would be more objective. However, it is computationally intense and may lose its superiority in treating instantaneous vortices.
We adopted a revised version of the threshold method to determine the size and circulation strength of instantaneous HVs. Instead of selecting a universal and constant threshold for all vortices, we defined the threshold for each vortex based on its own coherence as
where
Λv is the swirling strength at the center of each vortex. The threshold is selected based on the following relation holding for a standard Oseen vortex [
24]
2.3. Vortex Tracking Method
In order to quantitatively investigate the evolution of turbulent HV system, vortices comprising the system should be tracked. However, as shown in
Figure 2, the instantaneous turbulent HV system is usually composed of more than one vortex with different size and strength, making it impractical to track all these vortices. According to existing investigations, most of the time the turbulent HV system is dominated by a primary vortex which relates tightly with the dynamics of the system. Therefore, only the PHV is selected as the representative vortex in the turbulent HV system and tracked. Nevertheless, one difficulty still exists, as no clear and universal definition for the PHV is available even though it is commonly used. In a laminar HV system, the PHV is typically the standing HV closest to the cylinder base [
7]. For the turbulent HV system, however, the most coherent HV seems a more intuitively accepted definition for the PHV. Therefore, we chose the HV with the highest peak of
Λci in a given velocity field as the PHV.
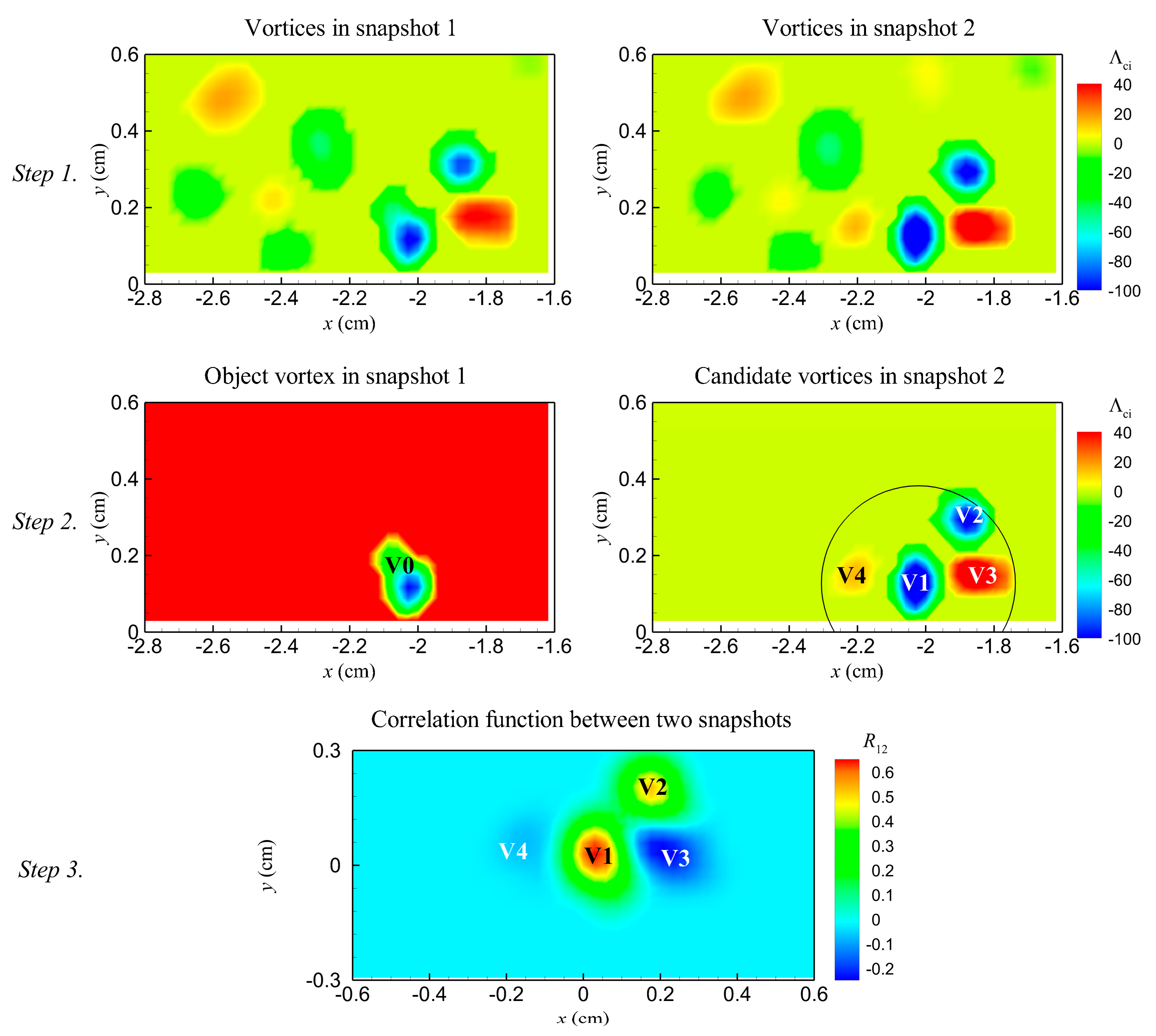
To track a PHV in successive velocity fields, we treated the spatial distribution of
Λci within its vortex core as the gray-level intensity of a particle image. Following some basic ideas of the particle tracking velocimetry technique, the method for tracking vortex contains the following steps, as illustrated in
Figure 3.
Step 1. Vortices in all instantaneous velocity fields of a sequence are identified with the swirling strength criterion. The core of each vortex is represented by the contours of swirling strength within its boundary, defined by Equation (1).
Step 2. The PHV in the first snapshot (V0) is selected as the tracking object and candidates of this vortex in the next snapshot (V1–V4) are determined by a displacement threshold (denoted by a circle). The threshold is defined as
where
Vc is the convective velocity of the vortex V0 defined as the instantaneous velocity at its center; Δ
t is the time interval between two successive velocity fields;
Rv is the radius of the vortex V0. The introduction of
Rv is based on the observation that the center of HV can vary dramatically within its core.
Step 3. Counterpart of the object vortex in the second snapshot is detected by a cross-correlation analysis. The cross-correlation analysis is performed between the swirling strength distribution of snapshot one and that of snapshot two. In the resulted correlation map, the maximum peak represents the correlation coefficient between the object vortex and its counterpart, and its coordinate represents the displacement of the object vortex during Δt.
After obtaining the displacement of the object vortex, the position of its counterpart in the second snapshot (V1) is determined. The detected counterpart is defined as the new object vortex in the next step.
Step 4. Steps 2 and 3 are conducted repeatedly until the correlation coefficient between the object vortex and its counterpart is smaller than 0.5. The threshold of 0.5 has been selected based on pre-conducted sensitive analysis. Such a circumstance means that the old PHV disappears. Then a new PHV is defined in the next snapshot and the tracking process restarts.
Step 5. The tracking results for each velocity field sequence are double checked manually to avoid possible mismatch. The image of streamlines and contours of Λci in each instantaneous velocity field is converted into a frame of a video animation. By replaying the videos, incorrect tracking results are identified and revised. Meanwhile, the videos are used to assist analyzing the evolution behaviors of the PHV.
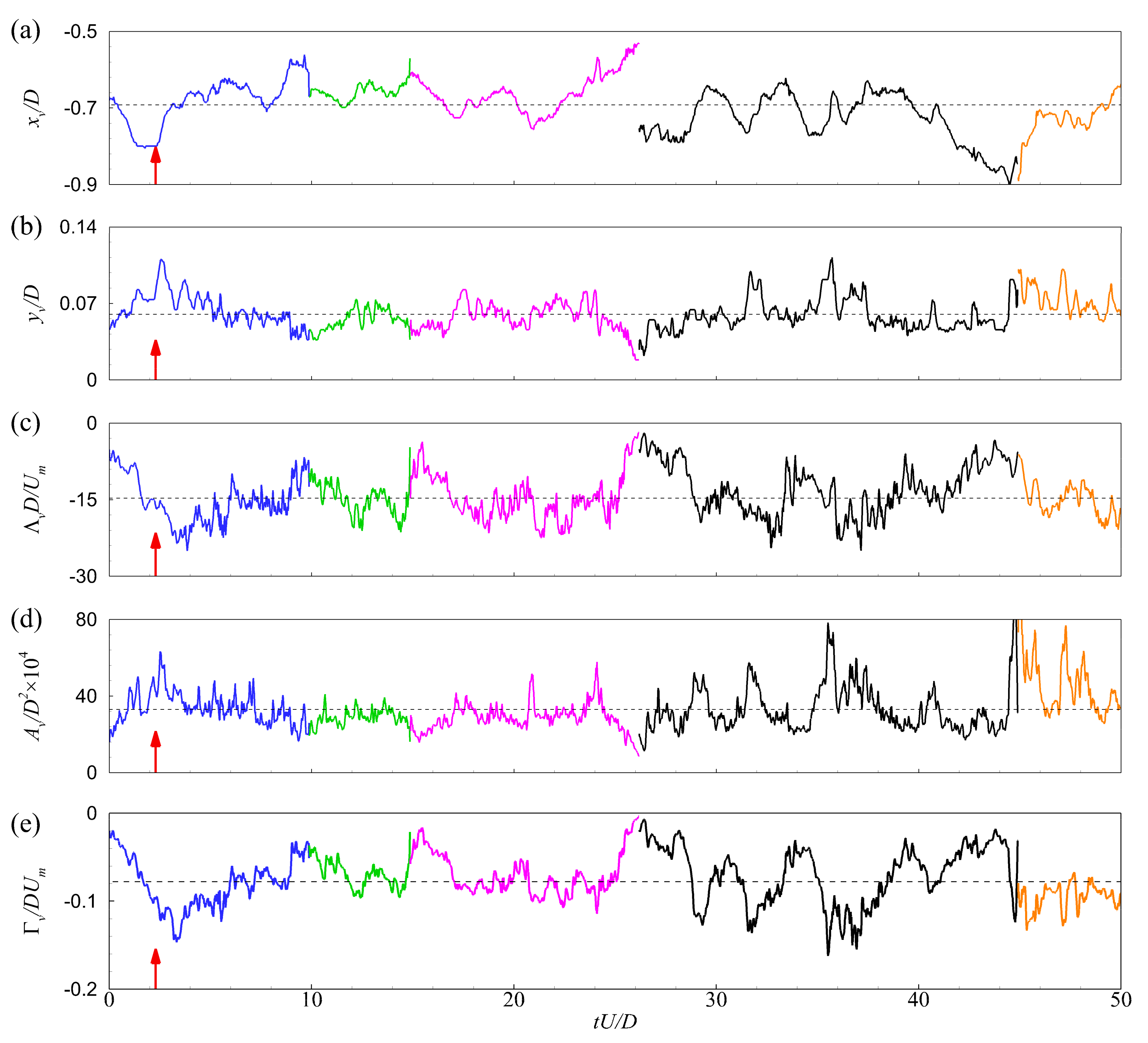
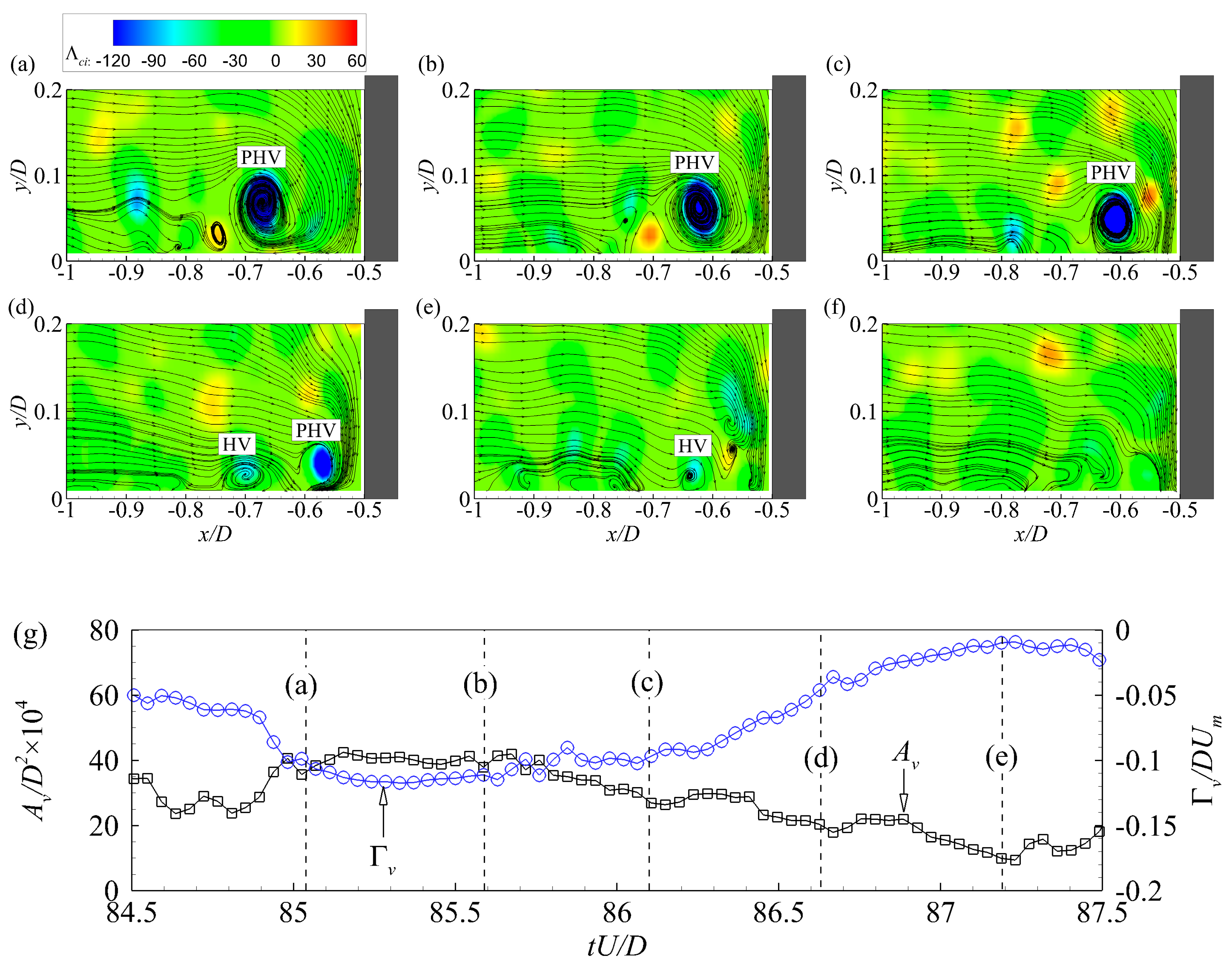
Figure 4 presents the time histories of the streamwise position,
xv, vertical position,
yv, coherence,
Λv, core area,
Av, and circulation strength,
Γv, of several PHVs that appeared one after another in case C13900. A color change on the time histories indicates the disappearance of an old PHV and the generation of a new PHV. The horizontal dashed line indicates the time-averaged value of the corresponding feature.
Figure 4a,b reveal the aperiodic oscillation, both streamwise and vertical, of the PHV. The streamwise position of the PHV changes from −0.91
D to −0.53
D with a mean value of about −0.7
D. The vertical position lies in the range of 0.02
D to 0.13
D, with a mean value of about 0.06
D. The instantaneous and mean positions of the PHV obtained by vortex tracking are in accordance with previous observations [
12,
18,
25]. These agreements validate the reasonableness of the current definition of PHV and the reliability of the tracking results. In
Figure 4c–e, the size, coherence, and circulation strength of the PHV also show chaotic variations with time. These features indicate that the investigated HV system is fully turbulent, at least in the case of C13900. The mean diameter and circulation strength are 0.033
D and −0.08
DUm, respectively.
2.4. Correlation Analysis Between the Features of PHV
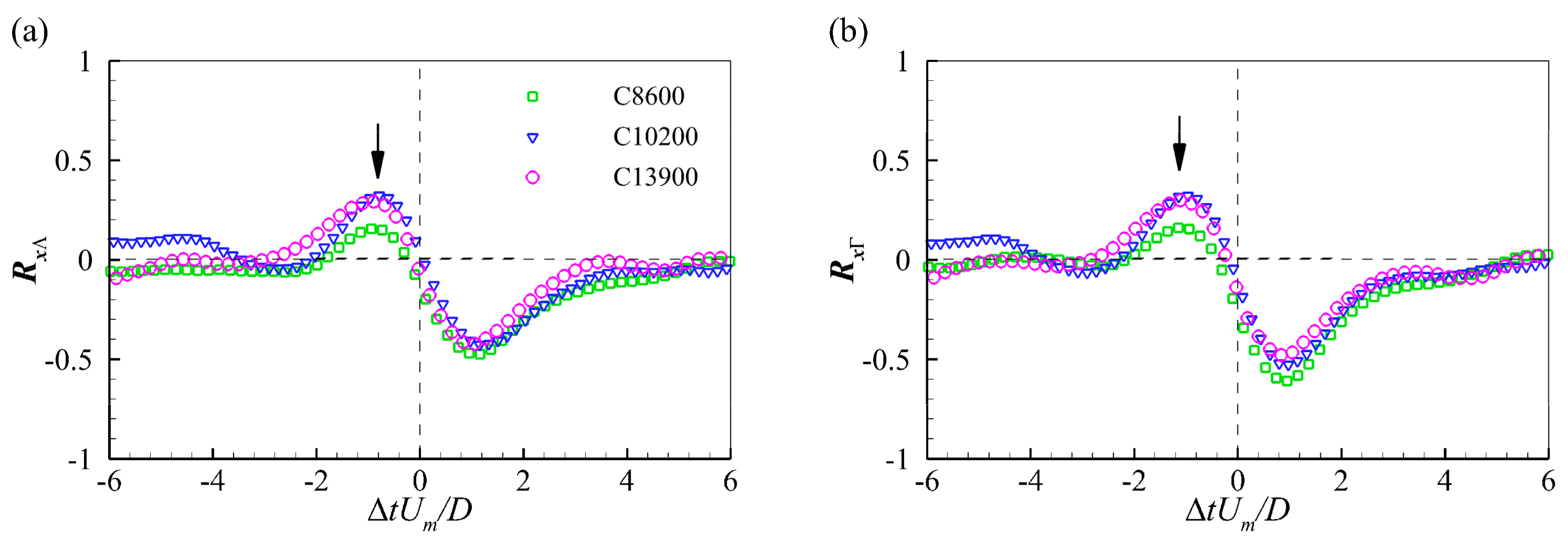
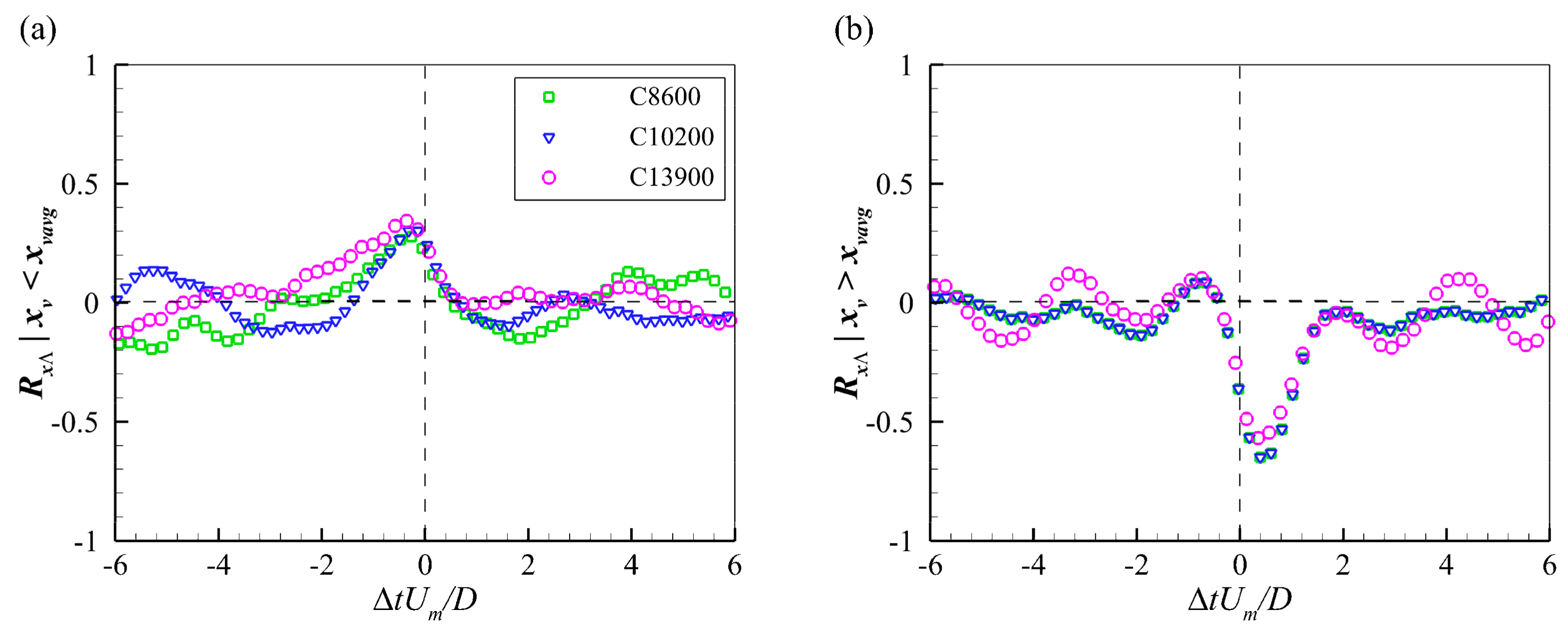
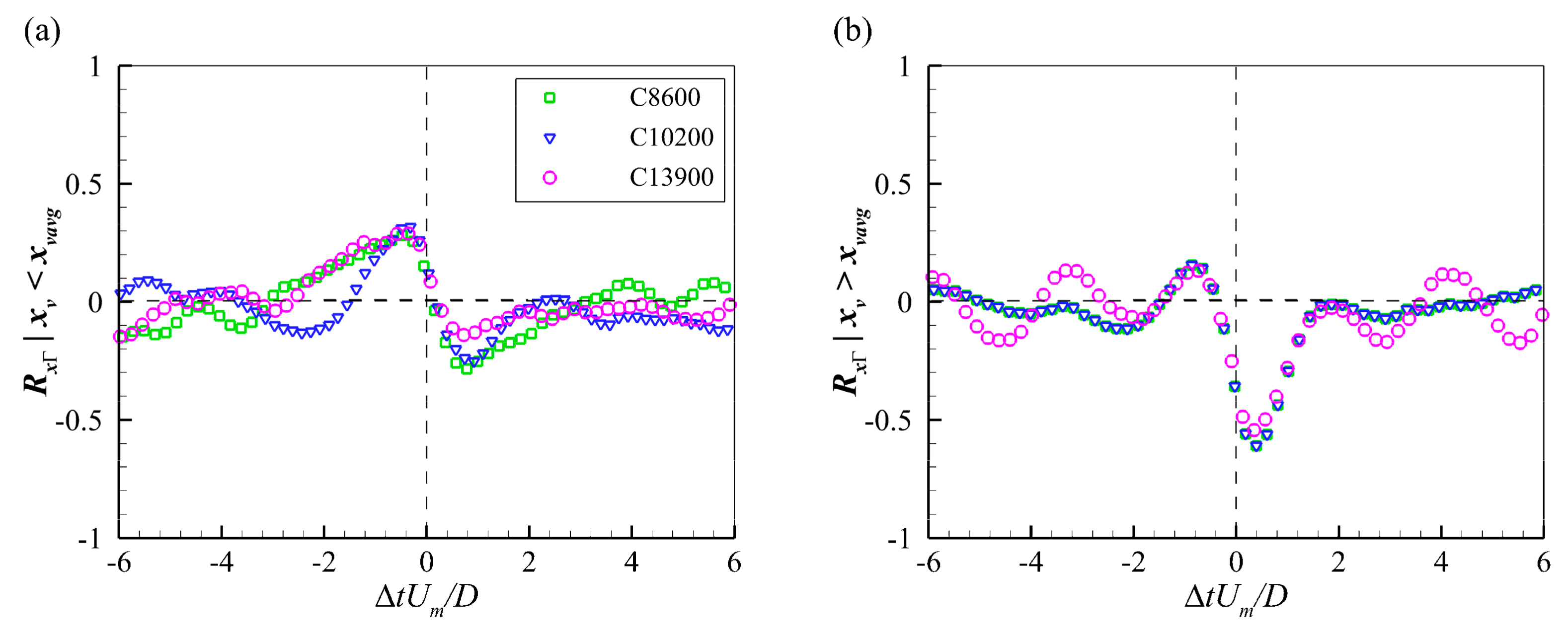
Despite their chaotic variations, a scrutiny of
Figure 4 reveals that the variations of different features are quasi-synchronous with each other. For example, the moment indicated by the arrows corresponds to local minima in the streamwise position, coherence, and circulations strength, and local maxima in the vertical position and core area, respectively. To explore the inter-relationships among these features, temporal cross-correlation analyses were conducted between the streamwise position and the other features of the PHV. As an example, the temporal cross-correlation function between the streamwise and vertical positions is calculated as follows:
Here, N is the sample number of velocity fields and the overbar represents time-averaging. For the sake of interpretation, absolute value of the coherence (swirling strength) and the circulation strength, which were negative by definition, were used to calculate the correlation functions.
4. Conclusions
The evolution of the turbulent HV system around a circular cylinder mounted on the flat bed of an open channel was investigated quantitatively and statistically with time-resolve PIV measurements. The cylinder Reynolds numbers of the flows were 8600, 10.600, and 13.600, respectively. Among vortices comprising the turbulent HV system, the PHV was selected as the representative vortex, and was tracked continuously in successive velocity fields with a novel method to obtain the time histories of its position, size, coherence, and circulation strength. These histories were cross-correlated to investigate the evolution trends of the PHV. Meanwhile, mechanisms underlying the evolutionary process of the turbulent HV system were re-investigated and enriched by using the time-resolved instantaneous velocity fields.
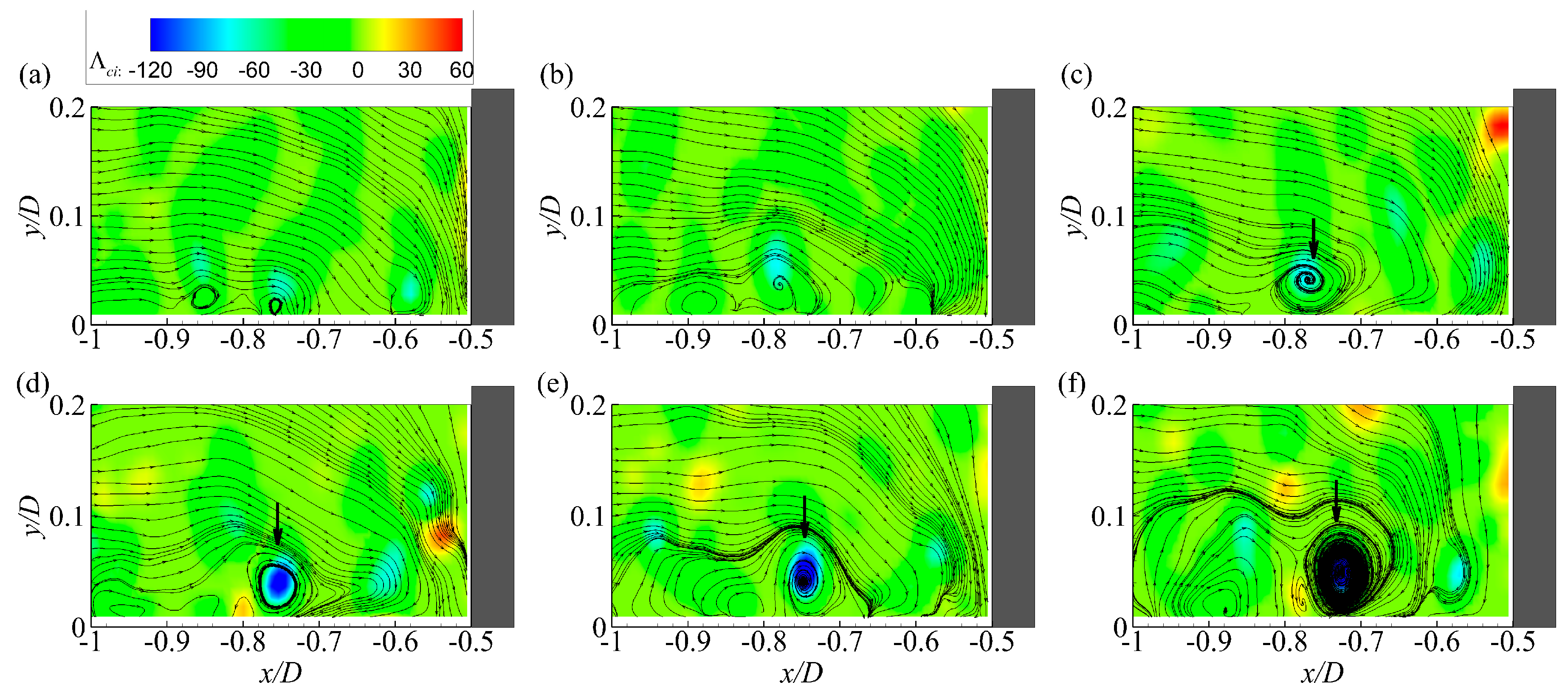
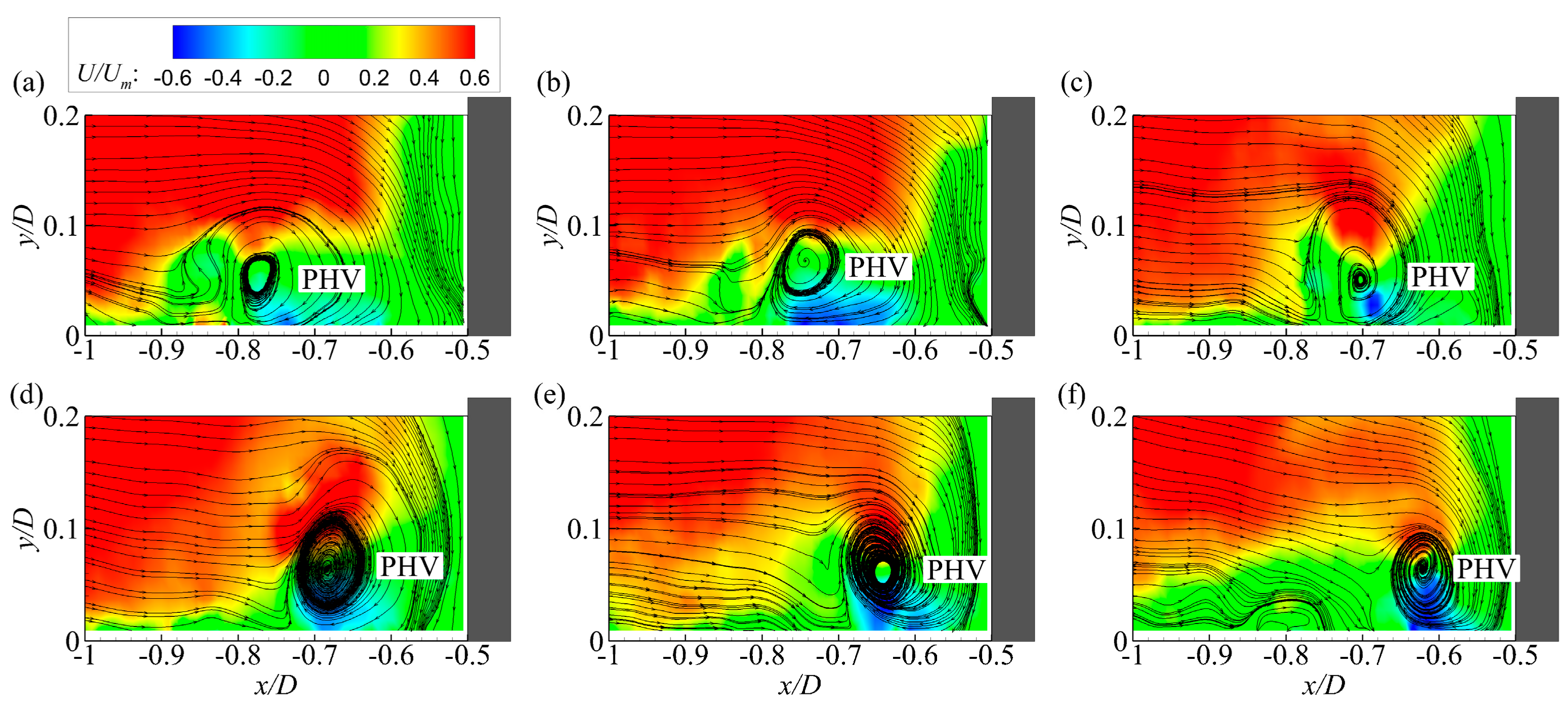
The PHV undergoes a complete evolutionary process composed of generation, life, and disappearance stages. The generation of the PHV originates either from the growth of a HV shedding from the separation region or the merging of several vortices from the incoming flow or the down-flow. The dissipation of the PHV takes place mainly in the region very close to the cylinder due to the enhanced interactions with counter-rotating vortices and the bed. The mean lifespan of the PHV is estimated to be about 5.0D/Um. During its lifetime, the PHV undergoes large-amplitude streamwise oscillation due to the action of large-scale and high-momentum structures from the incoming flow. Meanwhile, the size and strength of the PHV varies dramatically due to frequent interactions with vortices and the bed. The interaction of the PHV with secondary vortices lifted off the wall is responsible for triggering the zero-flow mode. However, such interactions neither have preferential locations nor always result in the downstream movement of the PHV. These mechanisms imply that the evolution of the turbulent HV can be controlled indirectly through manipulating coherent structures in the incoming flow and the down-flow.
The statistical relationships between the features of the PHV during its evolutionary process were obtained. When a PHV moves downstream from the separation region toward the cylinder, it approaches the bed and decreases in size. Its coherence first increases slightly and then decreases quickly. Consequently, the circulation strength of the PHV shows no tendency variation and decreases dramatically in the region upstream and downstream of its time-averaged position, respectively. The opposite is true when the PHV moves upstream from the region very close to the cylinder. The change trends of the vertical position, size, and circulation strength can correctly interpret and predict the spatial distribution of the time-averaged bed shear stress in front of a vertical cylinder.