Numerical Study of Sulfonamide Occurrence and Transport at the Near-Shore Area of Laizhou Bay
Abstract
:1. Introduction
2. Governing Equations
2.1. Shallow Water Equations
2.2. Depth-Averaged Advection–Diffusion Equation
3. Lattice Boltzmann Model
3.1. LBM for Shallow Water Equations
3.2. LBM for Depth-Averaged Advection–Diffusion Equation
4. Numerical Study
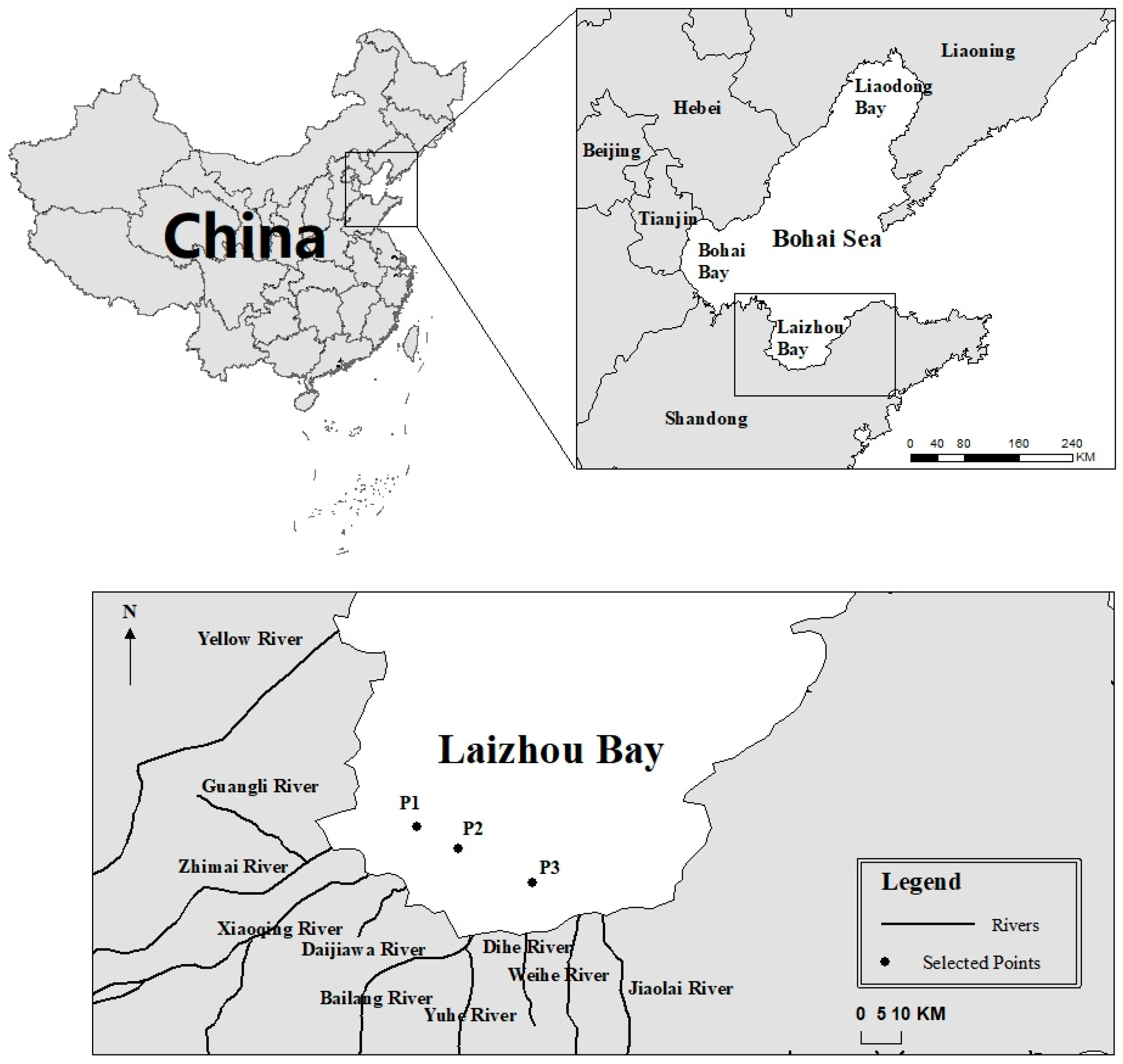
4.1. Research Area
4.2. Acquisition of the Data
4.3. Boundary Conditions
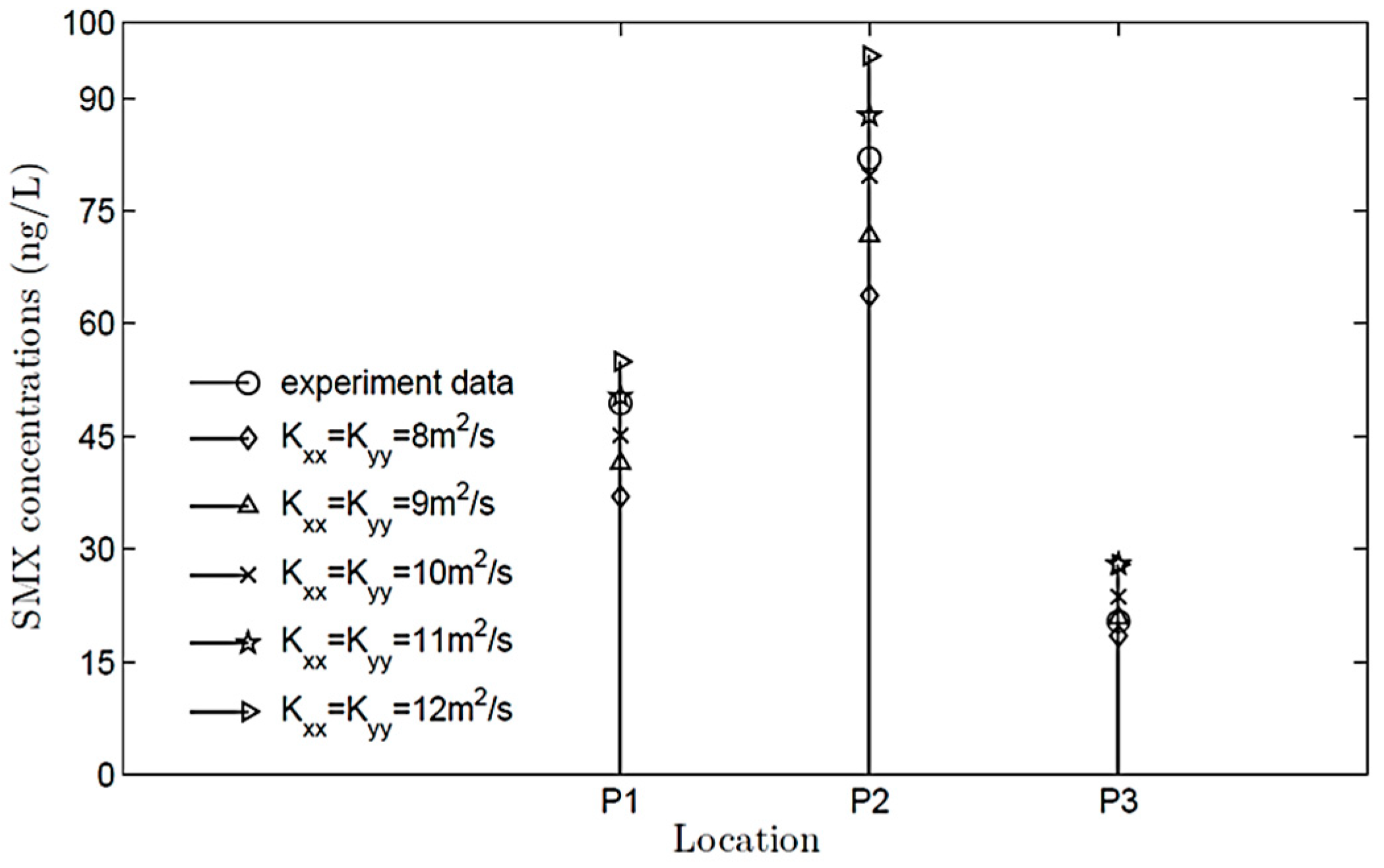
4.4. Parameter Setting and Sensitivity Analysis
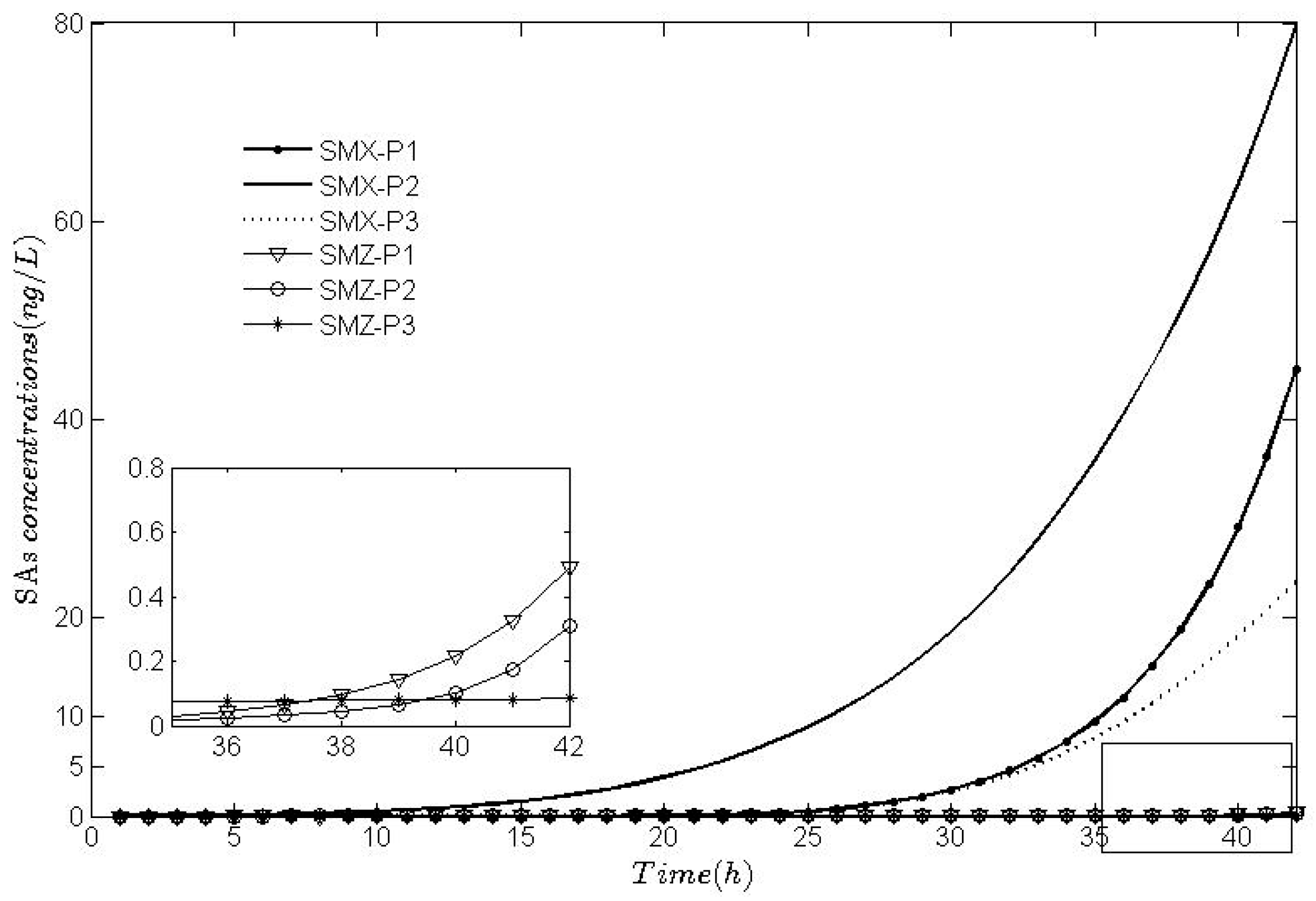
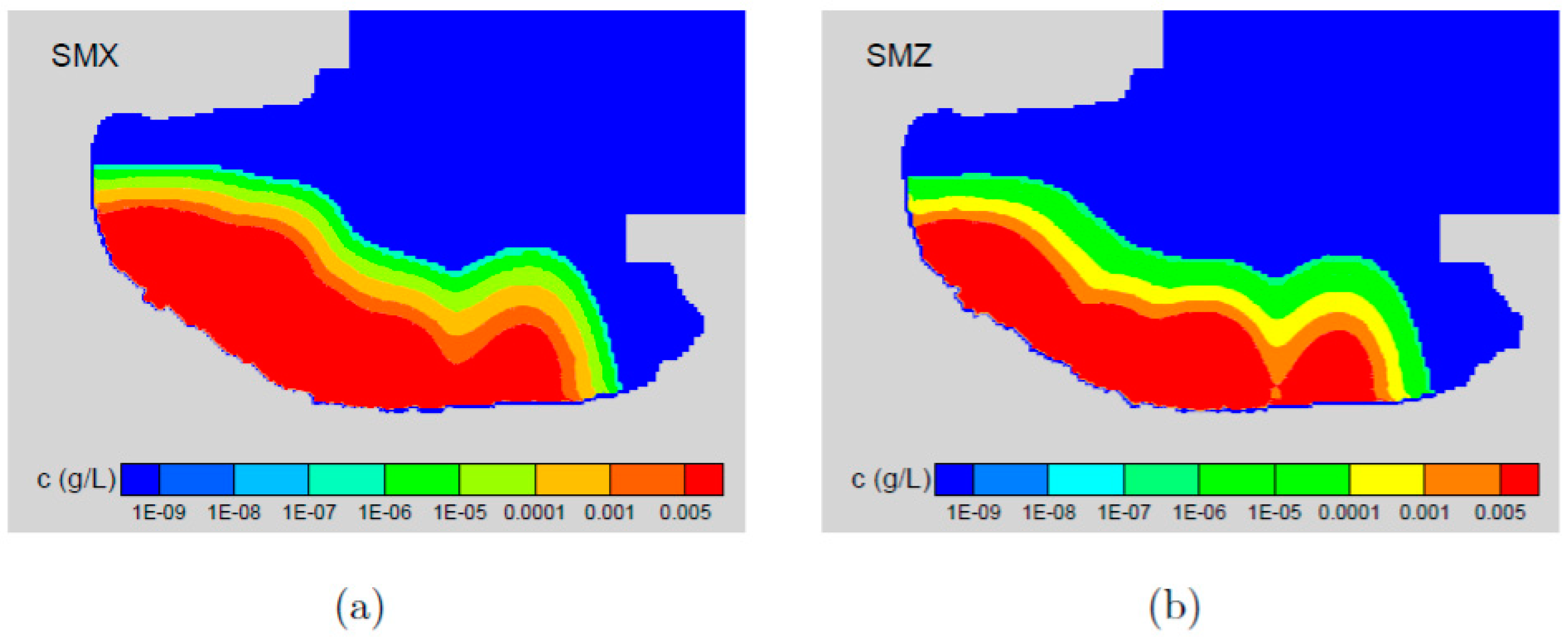
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sapkota, A.; Sapkota, A.R.; Kucharski, M.; Burke, J.; McKenzie, S.; Walker, P.; Lawrence, R. Aquaculture practices and potential human health risks: Current knowledge and future priorities. Environ. Int. 2008, 34, 1215–1226. [Google Scholar] [CrossRef] [PubMed]
- McEwen, S.A.; Fedorka-Cray, P.J. Antimicrobial use and resistance in animals. Clin. Infect. Dis. 2002, 34 (Suppl. 3), S93–S106. [Google Scholar] [CrossRef]
- Kümmerer, K. Antibiotics in the aquatic environment—A review–part II. Chemosphere 2009, 75, 435–441. [Google Scholar] [CrossRef] [PubMed]
- Saxena, S.; Rangasamy, R.; Krishnan, A.; Singh, D.; Uke, S.; Malekadi, P.; Sengar, A.; Mohamed, D.; Gupta, A. Simultaneous determination of multi-residue and multi-class antibiotics in aquaculture shrimps by UPLC-MS/MS. Food Chem. 2018, 260, 336–343. [Google Scholar] [CrossRef] [PubMed]
- Cabello, F.C. Heavy use of prophylactic antibiotics in aquaculture: A growing problem for human and animal health and for the environment. Environ. Microbiol. 2006, 8, 1137–1144. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Wang, N.; Wang, B.; Zhao, Q.; Fang, H.; Fu, C.; Tang, C.; Jiang, F.; Zhou, Y.; Chen, Y.; et al. Antibiotics in drinking water in Shanghai and their contribution to antibiotic exposure of school children. Environ. Sci. Technol. 2016, 50, 2692–2699. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Bekele, T.G.; Zhao, H.; Cai, X.; Chen, J. Bioaccumulation and tissue distribution of antibiotics in wild marine fish from Laizhou Bay, North China. Sci. Total Environ. 2018, 631, 1398–1405. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, G.; Zheng, Q.; Tang, J.; Chen, Y.; Xu, W.; Zou, Y.; Chen, X. Occurrence and risks of antibiotics in the Laizhou Bay, China: Impacts of river discharge. Ecotox. Environ. Saf. 2012, 80, 208–215. [Google Scholar] [CrossRef]
- Du, J.; Zhao, H.; Chen, J. Simultaneous determination of 23-antibiotics in mariculture water using solid-phase extraction and high performance liquid chromatography-tandem mass spectrometry. Chin. J. Chromatogr. 2015, 33, 348–353. [Google Scholar] [CrossRef]
- Liu, S.; Zhao, H.; Lehmler, H.J.; Cai, X.; Chen, J. Antibiotic pollution in marine food webs in Laizhou Bay, North China: Trophodynamics and human exposure implication. Environ. Sci. Technol. 2017, 51, 2392–2400. [Google Scholar] [CrossRef]
- Grizzetti, B.; Bouraoui, F.; Granlund, K.; Rekolainen, S.; Bidoglio, G. Modelling diffuse emission and retention of nutrients in the Vantaanjoki watershed (Finland) using the SWAT model. Ecol. Model. 2003, 169, 25–38. [Google Scholar] [CrossRef]
- Chi, J.; Yang, Q. Effects of Potamogeton crispus L. on the fate of phthalic acid esters in an aquatic microcosm. Water Res. 2012, 46, 2570–2578. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Jing, L.; Teng, Y.; Wang, J. Multimedia fate modeling and risk assessment of antibiotics in a water-scarce megacity. J. Hazard. Mater. 2018, 348, 75–83. [Google Scholar] [CrossRef] [PubMed]
- Frisch, U.; Hasslacher, B.; Pomeau, Y. Lattice-gas automata for the Navier-Stokes equation. Phys. Rev. Lett. 1986, 56, 1505. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Zhou, J.G.; Li, M.; Zhao, Y. Multi-block lattice Boltzmann simulations of solute transport in shallow water flows. Adv. Water Resour. 2013, 58, 24–40. [Google Scholar] [CrossRef]
- Zhou, J.G.; Liu, H. Determination of bed elevation in the enhanced lattice Boltzmann method for the shallow-water equations. Phys. Rev. E 2013, 88, 023302. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Liu, H.; Peng, Y.; Xing, L. Lattice Boltzmann method for rain-induced overland flow. J. Hydrol. 2018, 562, 789–795. [Google Scholar] [CrossRef]
- Zhou, J. Lattice Boltzmann Methods for Shallow Water Flows; Springer: Berlin, Germany, 2004. [Google Scholar]
- Liu, H.; Zhang, J.; Wang, H.; Ding, Y.; Yi, Y. Numerical modeling of the tidal wave run-up and the eelgrass habitat at the Laizhou Bay. Ecol. Model. 2017, 360, 378–386. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, J.G. Lattice Boltzmann approach to simulating a wetting–drying front in shallow flows. J. Fluid Mech. 2014, 743, 32–59. [Google Scholar] [CrossRef]
- Andreozzi, R.; Raffaele, M.; Nicklas, P. Pharmaceuticals in STP effluents and their solar photodegradation in aquatic environment. Chemosphere 2003, 50, 1319–1330. [Google Scholar] [CrossRef]
- Minh, T.; Leung, H.; Loi, I.; Chan, W.; So, M.; Mao, J.; Choi, D.; Lam, J.; Zheng, G.; Martin, M.; et al. Antibiotics in the Hong Kong metropolitan area: Ubiquitous distribution and fate in Victoria Harbour. Mar. Pollut. Bull. 2009, 58, 1052–1062. [Google Scholar] [CrossRef] [PubMed]
- Zou, S.; Xu, W.; Zhang, R.; Tang, J.; Chen, Y.; Zhang, G. Occurrence and distribution of antibiotics in coastal water of the Bohai Bay, China: Impacts of river discharge and aquaculture activities. Environ. Pollut. 2011, 159, 2913–2920. [Google Scholar] [CrossRef] [PubMed]

| Estuary | Location | SMX | SMZ |
|---|---|---|---|
| Xiaoqing river | 119°00.157’ E, 37°17.210’ N | 92.9 | 23.4 |
| Guangli river | 118°56.841’ E, 37°21.437’ N | 83.5 | 15.2 |
| Bailang river | 119°12.557’ E, 37°11.154’ N | 194 | 15.7 |
| Dihe river | 119°19.205’ E, 37°07.753’ N | 31.3 | 108 |
| Yuhe river | 119°17.180’ E, 37°07.787’ N | 10.4 | 3.5 |
| Zhimai river | 118°56.841’ E, 37°21.437’ N | 9.9 | 5.8 |
| Jiaolai river | 119°35.177’ E, 37°06.866’ N | 3.5 | 2.8 |
| Weihe river | 119°29.528’ E, 37°07.219’ N | 0.68 | 0.29 |
| Dajiawa river | 119°03.886’ E, 37°14.964’ N | 527 | 0.9 |
| Location | SA | Simulation Results | Experimental Data | Fractional Errors |
|---|---|---|---|---|
| P1 | SMX | 45.127 | 49.4 | 9.47% |
| SMZ | 0.489 | 0.56 | 14.48% | |
| P2 | SMX | 79.693 | 82.0 | 2.89% |
| SMZ | 0.309 | 0.34 | 10.13% | |
| P3 | SMX | 23.671 | 20.4 | −13.82% |
| SMZ | 0.087 | Undetected | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, L.; Liu, H.; Guo, W.; Ding, Y.; Ru, Z.; Tu, G.; Wu, X. Numerical Study of Sulfonamide Occurrence and Transport at the Near-Shore Area of Laizhou Bay. Water 2019, 11, 2065. https://doi.org/10.3390/w11102065
Xing L, Liu H, Guo W, Ding Y, Ru Z, Tu G, Wu X. Numerical Study of Sulfonamide Occurrence and Transport at the Near-Shore Area of Laizhou Bay. Water. 2019; 11(10):2065. https://doi.org/10.3390/w11102065
Chicago/Turabian StyleXing, Liming, Haifei Liu, Wenxian Guo, Yu Ding, Zhiming Ru, Gangqin Tu, and Xuerong Wu. 2019. "Numerical Study of Sulfonamide Occurrence and Transport at the Near-Shore Area of Laizhou Bay" Water 11, no. 10: 2065. https://doi.org/10.3390/w11102065
APA StyleXing, L., Liu, H., Guo, W., Ding, Y., Ru, Z., Tu, G., & Wu, X. (2019). Numerical Study of Sulfonamide Occurrence and Transport at the Near-Shore Area of Laizhou Bay. Water, 11(10), 2065. https://doi.org/10.3390/w11102065







