Prediction of Suspended Sediment Load Using Data-Driven Models

Abstract

Estimation of suspended sediments carried by natural rivers is essential for projects related to water resource planning and management. This study proposes a dynamic evolving neural fuzzy inference system (DENFIS) as an alternative tool to estimate the suspended sediment load based on previous values of streamflow and sediment. Several input scenarios of daily streamflow and suspended sediment load measured at two locations of China—Guangyuan and Beibei—were tried to assess the ability of this new method and its results were compared with those of the other two common methods, adaptive neural fuzzy inference system with fuzzy c-means clustering (ANFIS-FCM) and multivariate adaptive regression splines (MARS) based on three commonly utilized statistical indices, root mean square error (RMSE), mean absolute error (MAE), and Nash–Sutcliffe efficiency (NSE). The data period covers 01/04/2007–12/31/2015 for the both stations. A comparison of the methods indicated that the DENFIS-based models improved the accuracy of the ANFIS-FCM and MARS-based models with respect to RMSE by 33% (32%) and 31% (36%) for the Guangyuan (Beibei) station, respectively. The NSE accuracy for ANFIS-FCM and MARS-based models were increased by 4% (36%) and 15% (19%) using DENFIS for the Guangyuan (Beibei) station, respectively. It was found that the suspended sediment load can be accurately estimated by DENFIS-based models using only previous streamflow data.

1. Introduction

The suspended sediments comprising primarily of fine sand, silt and clay (with mean size < 63 µm) are washed down to the streams and rivers from upland and transported downstream. In time, under certain conditions, such as reducing flow velocity and momentum, the sediments could, therefore, be transiently accumulated in the channel or river bottom and under the most common hydraulic systems; the sediment is entrained and remobilized back into the outer flow. Where the velocity is slow and the submerged weight of particles becomes influential, the sediment is settled and deposited. In addition, sediments can also be deposited in reservoirs under quiescent condition by the action of gravity. Thus, this reduces their storage capacities. The sedimentation problem also chokes and interferes with the normal hydrological system of river flow. Mobilization of sediments on land might cause surface (sheet), gully and rill types of erosion in the upland catchment. In addition, massive land movement, such as slumps, landslides, and mudflows, are also probable if deforestation and land clearance are not done sustainably [1]. Therefore, it is of important to develop an accurate prediction model for sediment transport.

In fact, linear model has been extended to be able to capture the non-linear interrelationship in the data pattern which is the most common challenges in engineering application and more specifically sediment transport. Such improvement has been developed by introducing polynomial regression terms. For example, the Multivariate Adaptive Regression Splines (MARS) has been developed as high dimensional data modelling to provide proper procedure to detect the non-linear interrelationship in the input-output data patterns [2,3]. MARS is considered as non-parametric regression method that could be used to identify the mapping between the desired parameter and a group of predictor parameters aided by the splines to detect the non-linearity in the data patterns. Piecewise cubic or linear splines to identify the local fit are used by MARS and it develops an adaptive procedure to architect the optimal model. It has been proved that the MARS model could be successfully applied for different cross-disciplinary fields, especially in hydrological applications [4,5,6,7,8,9,10].

Due to the ability of the artificial neural network (ANN) methods to mimic the interrelationship for a particular input-output pattern, these methods have been applied in several hydrological phenomena. In addition, according to Mustafa et al. [11], these methods have a strong ability to capture the internal features and characteristics even those experienced highly non-linear behaviour. The ANNs based-models have been effectively implemented in several hydrological modelling including runoff prediction, rainfall forecasting and water quality prediction [12,13,14]. In this context, the utilization of the ANN methods is widened to be applied for predicting the sediment transport [15,16,17,18]. In most of these researches, the consequences of the river streamflow and the suspended sediment load have been used and made available as input while the future value of the sediment load is considered as the desired output. Different pre-processing analyses have been carried out before implementing the model such as normalization, sensitivity analysis and statistical analysis including the correlation and cross correlation to select the most effective pattern of the input variables to achieve the best model performance [19]. In addition, comprehensive analysis has been carried out for the selection of the best training algorithms including gradient decent (GD), conjugate gradient (CG) and Levenberg–Marquardt (LM) [20,21,22]. However, most of these models experienced a few drawbacks related to slow convergence, over-fitting and trapping in local optima using classical optimization methods. In addition, in a few cases, there is a need to pre-processing the data before using in order to identify the most sensitive input variables to achieve better prediction accuracy for the sediment load value.

Furthermore, more recently, by Jang [23], a new learning procedure with a new architecture, namely, Adaptive Neural Fuzzy Inference System (ANFIS) has been developed. The main idea behind the ANFIS method is to overcome the drawback of the ANN method so from each particular input-output pair, it could generate a suitable membership functions (MFs) and, hence, the learning algorithm of the ANN could be processed to build up a set of fuzzy IF-THEN rules for such pair. ANFIS motivates the hydrologists to replace the classical ANN methods to apply for several complex non-linear hydrological phenomena such as water level, rainfall and streamflow [24,25,26,27,28,29].

Kisi’s research study in 2005 is considered as one of the most primitive study on developing ANFIS model for predicting the sediment transport in river and compared the results with the classical ANN model for the same case study [30]. The analyses of the results were also extended to include the comparison with sediment rating curve and multi-linear regression model. The major outcome from this study concluded that the ANFIS method outperformed the other methods and achieved relatively accurate prediction of the sediment load. Similarly, Lohani et al. [25] examined the ability of the ANFIS model against the classical ANN methods for predicting the concentration of the sediment in the rivers. Basically, in this study, the input pattern was slightly different than the previous study by Kisi [30], as the input included not only the sediment concentration and streamflow but also include the water level. It has been concluded that the ANFIS method has more ability to detect the non-linear behaviour of the input-output pattern and achieves a remarkable improvement of the prediction accuracy over the classical ANN model. Furthermore, the ANFIS method showed outstanding performance over the ANN model for the ability to predict the sediment load even with considerable difference between the streamflow and water level compared to the ANN methods [31,32,33,34]. As a result, it could be concluded that the ANFIS could be able to detect and effectively map the highly non-linear pattern between the input and the output for the sediment load and enhanced the prediction accuracy compared with the classical ANN, however, ANFIS, in a few cases, experienced instability training process while generating the appropriate fuzzy rules [35,36,37]. In addition, the ANFIS still needs several trial-and-error procedures to adjust and achieve the best value of internal parameters. In the same time, it is relatively difficult to integrate the ANFIS structure with advanced optimization algorithm in order to adapt the selection of such internal parameters. Therefore, there is a need to develop a proper dynamical structure that able to self-adapting the fuzzy rules to be able to detect the new feature of the new input-output pattern without losing the training stability.

In fact, within ANFIS modelling, one of the following methods, namely, subtractive clustering (SC), grid partitioning (GP), and fuzzy c-means (FCM) for the measured input-output data could be used to perform in order to identify the fuzzy modelling of ANFIS to generate the fuzzy rule. In general, for fuzzy modelling, the clustering of the data is an accessible procedure where the clusters attained from the data pattern of the input-output utilizing particular clustering algorithm are considered as a base for generating the fuzzy rule. The procedure for fuzzy identifications utilizing clustering is first to find the clusters in the space of the available data and, hence, it uses the cluster centres to compute the consequent and the premise parts of the fuzzy rules. As a result of this procedure, the clustering accuracy defines the superiority of the rule base of the fuzzy inference system (FIS) and, consequently, the overall accomplishment of the fuzzy model’s results. Finally, Bezdek et al. [38] proposed the FCM clustering method and has been enhanced by Zhang and Chen [39], which is considered as one of the most effective methods for data clustering. One of the most advantage of the FCM is the improvement of computing the measurement of the distance between the point of the data input-output pattern during the clustering and hence more precise cluster centres. Therefore, FCM could be used to develop better rule base for ANFIS based on better defined partitioning for the data which could lead to overall enhancement for ANFIS-FCM’s output and the prediction accuracy [40].

In order to overcome the drawbacks of the classical ANFIS method, in this study, the new advanced version of ANFIS, namely, the dynamic evolving neuro-fuzzy inference system (DENFIS) is proposed [41]. The proposed DENFIS is almost comparable to ANFIS method up to certain extends. The main idea behind the structure of DENFIS method over the ANFIS method is that the DENFIS method, after the completion of the learning phase, the fuzzy inference system computes the desired output based on m fuzzy rules which are dynamically formed after the learning phase. The suitableness of the DENFIS for effectively predicting the sediment transport is that the DENFIS progresses throughout an incremental change in the data pattern. In addition, DENFIS could accommodate and learn the new pattern of the input data that might include a new feature or new classes. In fact, the most advantage of the DENFIS over the classical ANFIS is that unlimited number of the new fuzzy rule could be generated and updated during the training session of the model procedure using DENFIS method. From the modelling process of the DENFIS method, it could be expected that the DENFIS method could be successfully applied to mimic dynamic pattern and accommodate the complexity experienced in the sediment transport sequences and has a strong potential to outperform the performance achieved using the classical ANN and ANFIS methods.

In general, the data used for modelling play essential role on the successfulness of the model performance. The size of the data and the time increment scale of the data are considered as the main features in the used data to relatively assure that the proposed model could achieve acceptable performance. First, the size of the data is important for modelling as it provides the model with the necessary information to predict the desired output. Therefore, the bigger the size of the data the more the patterns of the interrelationship between the input parameters and the desired output will be trained by the model and, hence, it is expected that the model will achieve acceptable performance. Second, the time increment scale, and more specifically for sediment transport, there are several time increment scales for the data that could be used hourly, daily, weekly and monthly. Although the model could be developed using any time increment scale of the data, the model development depends only on the availability the time increment scale of the used data. However, the availability of the data with smaller time increment scale (hourly or daily) is more promising and effective to achieve satisfactory model performance. This is due to the fact that for the data with small time increment scale, it is expected that the dynamic and the nonlinearity in the desired output will be insignificant as well. As a result, it will be relatively affluent for the model to detect such nonlinearity and less interrelationship and achieve adequate performance.

The aim of this study is to investigate the potential of utilizing the DENFIS model to predict the sediment load in river streamflow. Real sediment load and river streamflow data at two locations of China, Guangyuan and Beibei have been utilized to examine and explore the suitability of the proposed DENFIS model. The main purpose of using two different case studies is to verify the effectiveness of the proposed DENFIS model. In addition, different scenarios for the modelling input-output architecture have been adapted in order to achieve the optimal prediction accuracy for the sediment load. Finally, in order to evaluate the performance between the proposed DENFIS model and the other machine learning methods, comprehensive comparative analysis has been carried out.

2. Materials and Methods

2.1. Study Basin and Data

For the present study, Jialing River, with a drainage area of 160,000 km², the second largest tributary of the Yangtze River and one of the most important flood and sediment sources for the Three Gorges Reservoir, China was selected as a case study. The Qu River and Fu River are the two main tributaries of Jialing River basin from left and right banks, respectively. The upstream section of the basin rivers has very deep valleys with mountainous terrain, whereas the lower section has flat river beds. The Jialing River elevation varies from 126 m to 5024 m with mean annual rainfall of 935 mm and mean annual temperature of 16 °C.

In the present research work, two stations on Jialing River basin, namely, Guangyuan and Beibei, were selected for estimation of daily suspended sediment (see Figure 1). These two stations were selected due to their geographical location in the basin to analyse the overall sediment phenomena in the basin. It can be observed from Figure 2 that Guangyuan Station is located in the upper section of the Jialing River whereas Beibei Station is located downstream of the Jialing River basin. The daily streamflow and sediment data applied in the present study covering the duration of 2007–2015 were obtained from Hydrological Yearbooks of the People’s Republic of China. Figure 1 illustrates the time variations plot of daily sediment load of two stations during the study period. The measurement of the suspended sediment load includes sampling to determine the silt content and measuring the discharge. The main procedure of sample treatment is to determine the sample volume and the weight of dry sediment; then proceed to calculate the silt content. The silt content of the treated sample was calculated by the following formula:

$$C_s=\frac{W_s}{V}\times 1000$$

(1)

where $C_s$ is the observed silt content, kg/m³, g/L; $W_s$ is the weight of dry sediment in a sample, g; V is the volume of the sample, mL.

After determining the silt content, the suspended sediment load was calculated using the formula:

$$S_s=\left[C_{s{m}_1}{q}_0+\frac{1}{2}\left(C_{s{m}_1}+C_{s{m}_2}\right)q_1+\cdots +\frac{1}{2}\left(C_{s{m}_{n-1}}+C_{s{m}_n}\right)q_{n-1}+C_{s{m}_n}{q}_n\right]$$

(2)

where $Q_s$ is the suspended sediment discharge, kg/s; $C_{s{m}_1}$, $C_{s{m}_2},\dots ,C_{s{m}_n}$ are the mean silt contents of various sampling verticals, kg/m³; $q_0,q_1,\dots ,q_n$ are the partial discharges within various pairs of adjacent sampling verticals, m³/s.

Data for the period from 01/04/2007–12/31/2013 (2554 daily values) were used for training period and remaining data 01/01/2014–12/31/2015 (730 daily values) were used for testing. The brief statistics of the used discharge and sediment data are tabulated in

Table 1. The statistical parameters of the applied data.

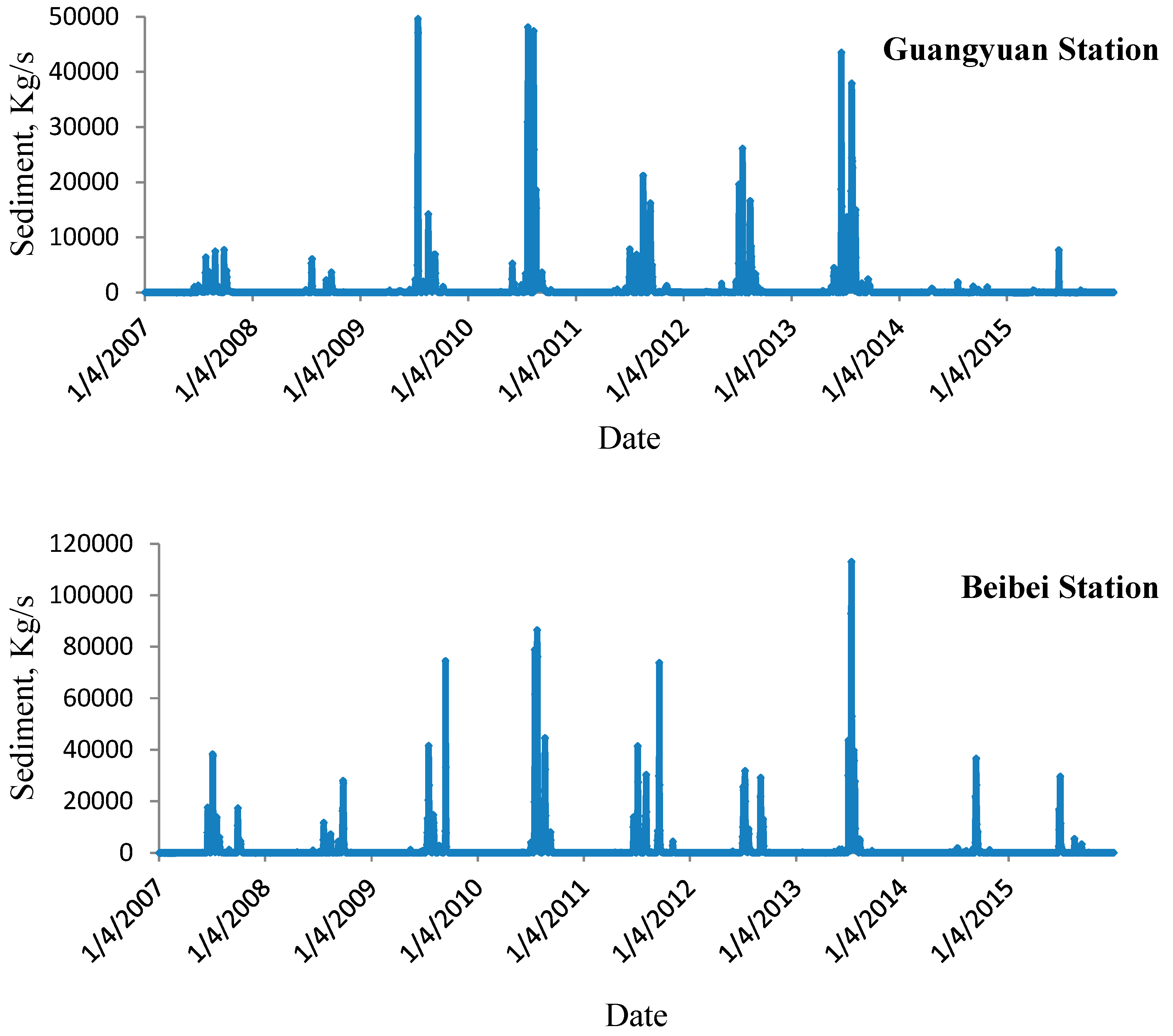
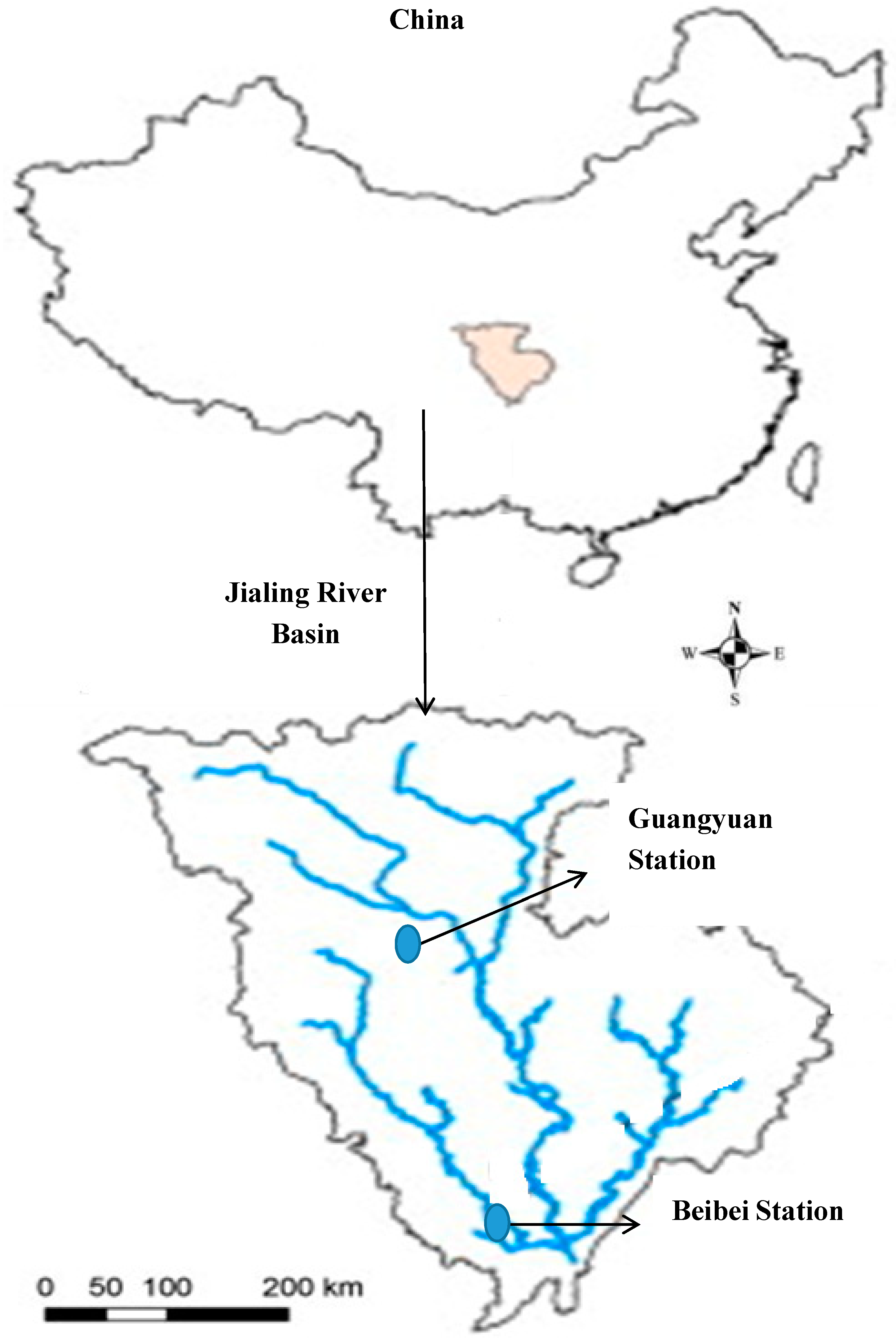
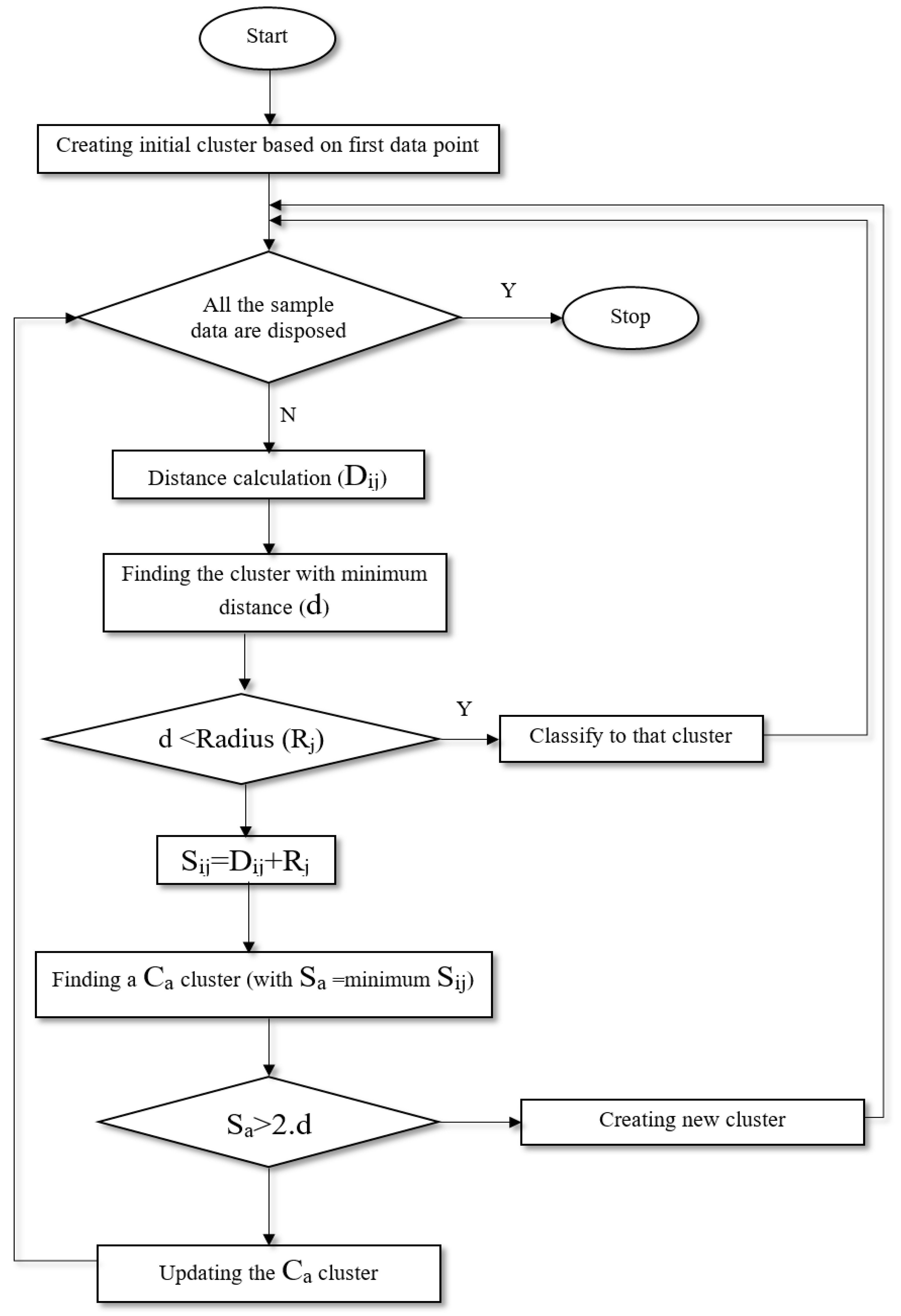
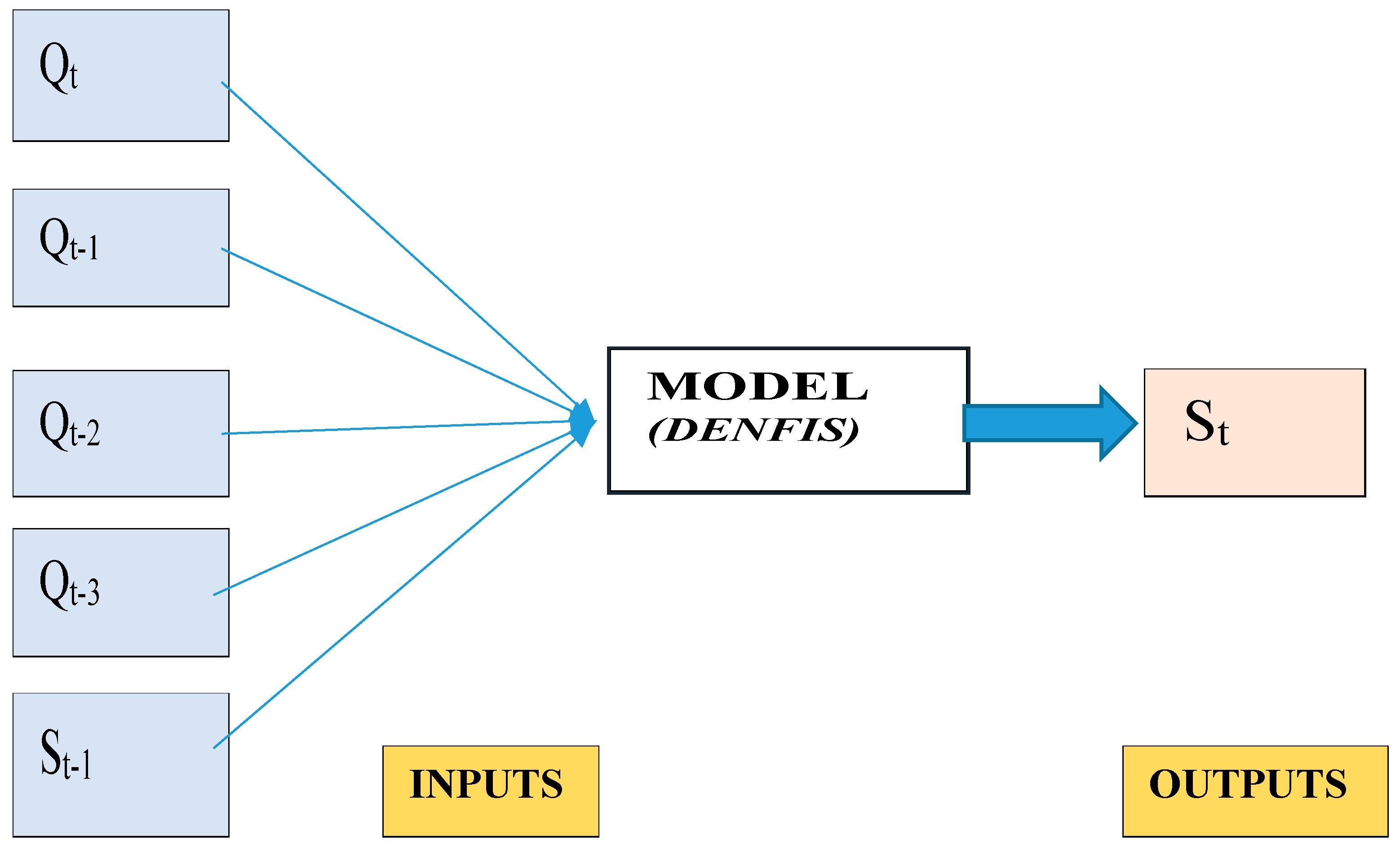
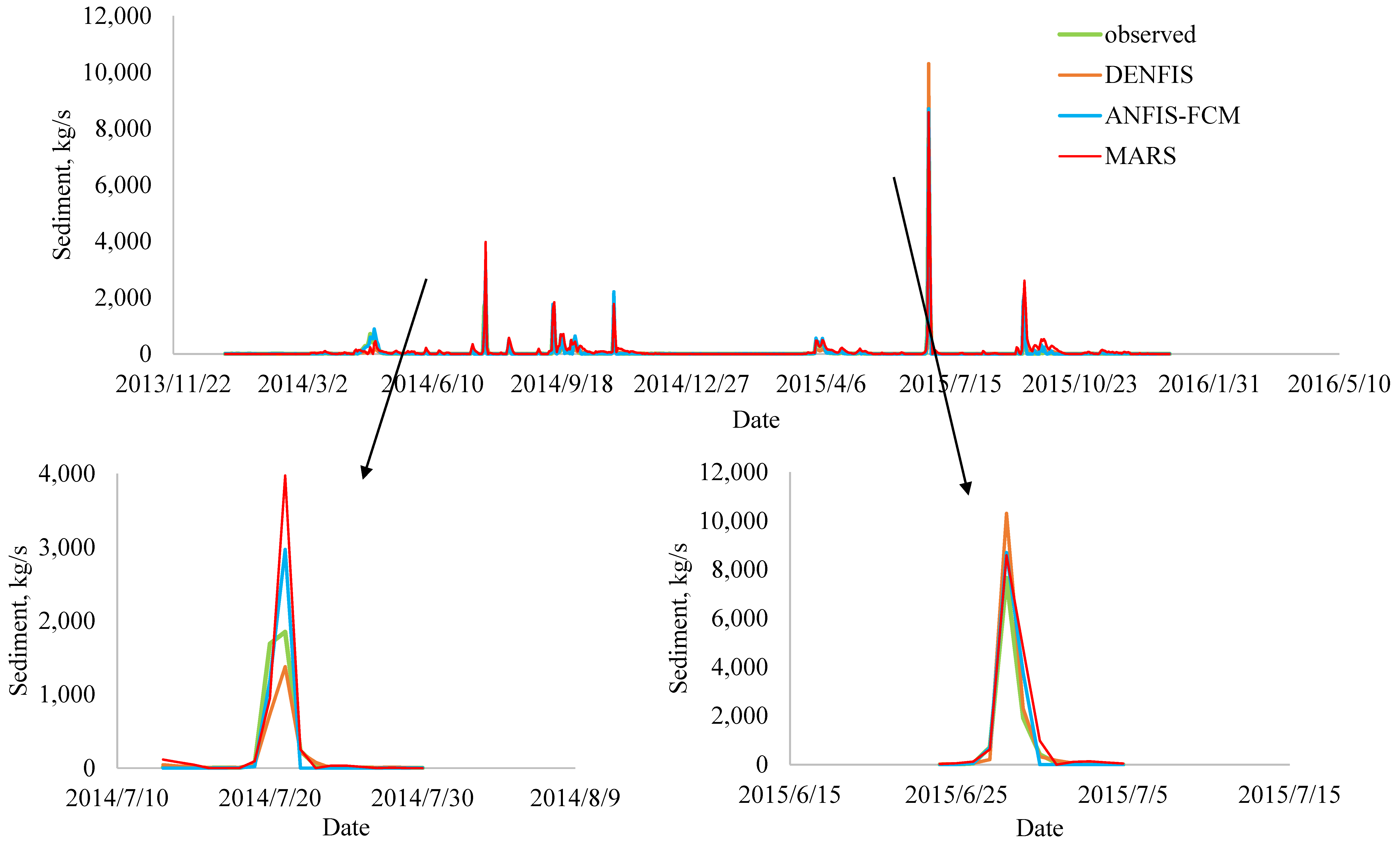
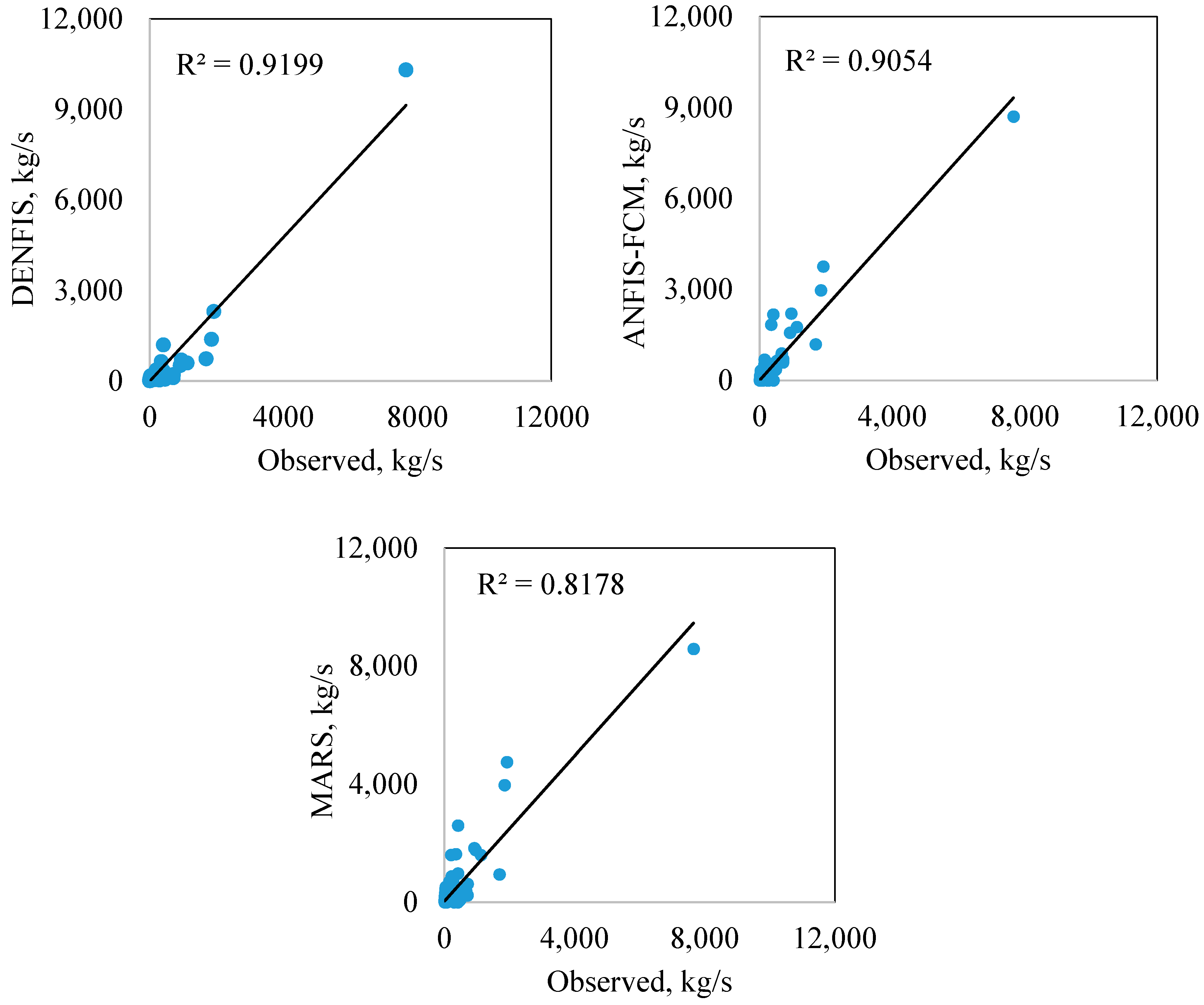
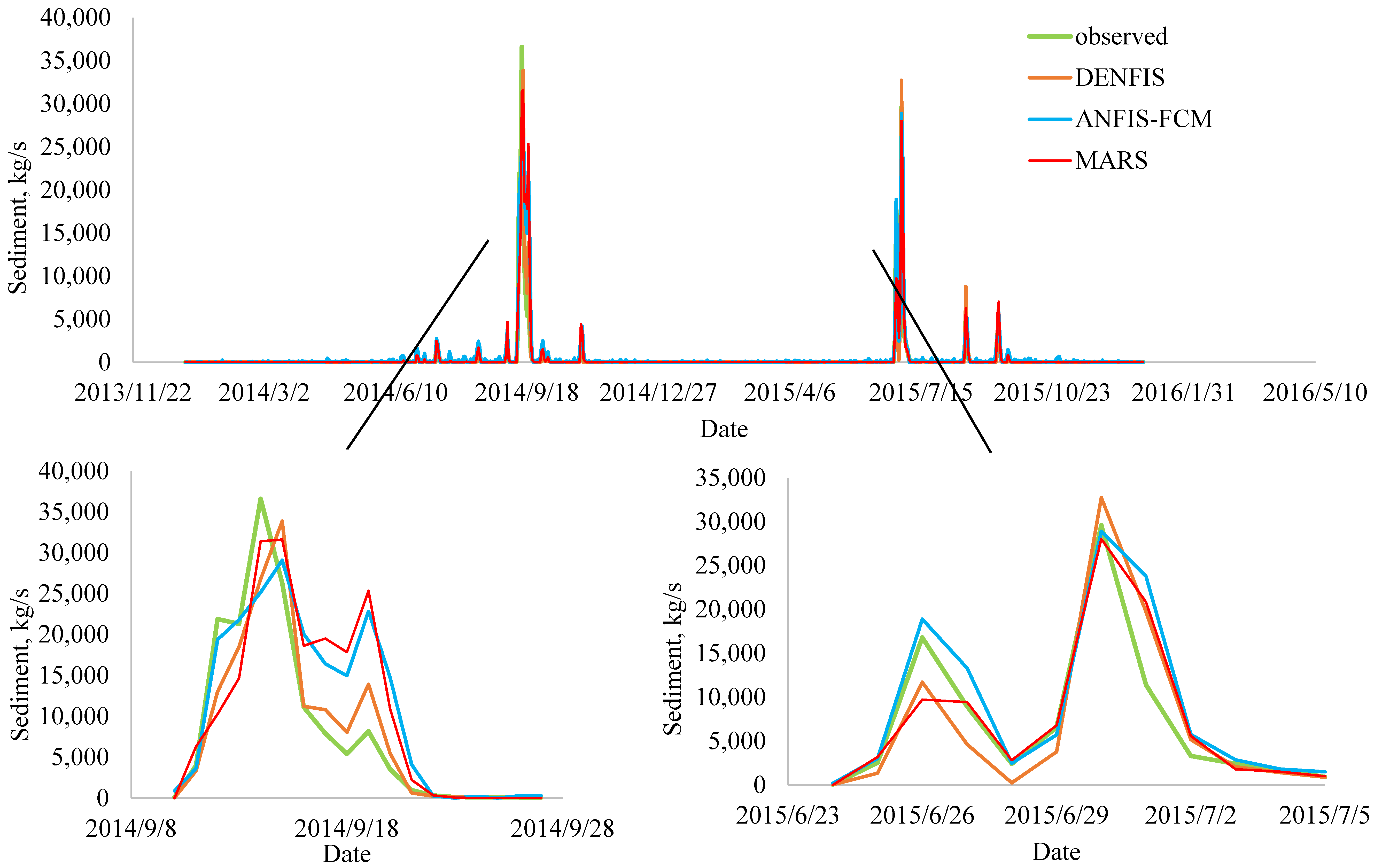
Statistical Parameters	Guangyuan Station			Beibei Station
	Whole Data	Training Data	Testing Data	Whole Data	Training Data	Testing Data
Streamflow (m3/s)
xmean	175.1	198.3	93.9	2136	2231	1805
xmin	4.5	4.5	10.8	105	105	281
xmax	6290	6290	1890	34,700	34,700	20,800
Csx	6.84	6.26	7.06	4.32	4.15	4.77
Sx	336	372	126	3230	3427	2388
$\frac{x_{max}}{x_{mean}}$	36	32	20	16	16	12
Cv (Sx/xmean)	1.92	1.88	1.34	1.51	1.54	1.32
Sediment (kg/s)
xmean	431.9	541	49.9	971	1139	381
xmin	0.349	0.91	0.349	0.105	0.105	1.69
xmax	49,600	49,600	7660	113,000	113,000	36,600
Csx	12.1	10.7	19.2	10.5	9.73	9.96
Sx	2673	3018	321	5681	6287	2533
$\frac{x_{max}}{x_{mean}}$	115	91.7	154	116	99	96
Cv (Sx/xmean)	6.19	5.58	6.44	5.85	5.52	6.65

. In the table, xmean, xmin, xmax, Csx, Sx, Cv (Sx/xmean) are the mean, minimum, maximum, skewness, standard deviation and variation coefficient, respectively. It is seen from Table 1 that sediment data have highly positive skewed distribution for the both stations. On the other hand, both sediment data have considerably high xmax/xmean ratios. All these indicate the complexity of the investigated phenomenon (sediment modelling). The range of training period covers the range of test period and this implies that the models will not face with the extrapolation difficulties as also reported in literature [42,43].

2.2. Used Methods

In this section, the basic principles and development of the general structure related to three proposed machine learning (ML) models used in this article are presented for sediment transport modelling. In this regard, the three methods used in this work can be divided into two main groups: (1) methods based on the creation of an ML system relying on fuzzy rules and clustering; (2) those based on the creation of an ML with respect to piecewise linear regression rules.

Comparing the results of the two fuzzy logic-based methods in the first group provides the possibility of evaluating the applicability of a dynamic evolving system in improving the prediction of a complex phenomenon such as sediment transport. Afterwards, an appropriate platform is made for challenging fuzzy logic-based and clustering methods with the function of different ML methods, such as MARS, relying on the comparison of the results of the methods of the first and second groups.

Hence, first, the ANFIS-FCM method which uses (fuzzy c-means clustering) FCM method to generate the fuzzy inference system (FIS) is introduced and described. Subsequently, the dynamic evolving neural-fuzzy inference system (DENFIS) model which uses the evolving clustering method (ECM) for clustering fuzzy rules is described. It is worth noting that this method has been able to indicate very suitable performance in modelling complex problems [44,45]. Eventually, the MARS method, which is capable of generating an efficient model with the capability of modelling non-linear and complex problems using the concepts of linear regression, is described.

Correlation analysis (cross-correlation, autocorrelation and partial autocorrelation) is commonly used in the literature for determination of maximum lag of input scenario and combination of input variables. The main deficiency of this method is that it cannot determine the non-linear relationship between the input and output. Therefore, in the present study, a different strategy was followed. We tried different input scenarios using each ML method and thus, nonlinear relationships between input and output were identified by examining the test accuracy of input combinations.

2.2.1. Adaptive Neuro-Fuzzy Inference System with Fuzzy C-Means Clustering (ANFIS-FCM)

Since the advent of ANFIS, many studies have been carried out on modelling and simulation problems in hydrology and most of these studies indicate much higher capability of this network than other commonly used methods such as ANN [46,47,48]. ANFIS is a hybrid system composed of feed-forward ANN and FIS which basically relies on the crisp inputs and their fuzzification by membership functions. By applying the inference mechanism and antecedent (premise) part of IF-THEN rule, and their relationship with the consequent part in the neurons of network, the general structure of ANFIS in the form of five layers of a network is constructed. The learning algorithm of ANFIS is a hybrid algorithm, which is usually performed through the least square estimator for consequent parameters and gradient descent for the section of premise parameters.

Since the function and architecture of ANFIS are noted in many related articles, its function is not explained here to prevent repetition. For understanding the details of this method, interested readers are referred to the related papers [49,50,51]. ANFIS can be made by partitioning the input-output data to the rules and using the methods such as FCM. In other words, generating ANFIS structure using other FIS generation methods such as grid partition (ANFIS-GP) and sub-clustering (ANFIS-SC) is also possible. However, given the confirmation of the suitable function of ANFIS-FCM method in many hydrological problems, the application of this approach was considered in this paper [50]. In the FCM method, each piece of data has the possibility of belonging to two or more clusters with regard to a specified degree. This algorithm is based on minimization of the following objective function (F) which is the weighted sum of squared errors in clusters:

$$F={\displaystyle \sum _{i=1}^N\sum _{j=1}^C}{u}_{ij}^m{\parallel x_i-c_j\parallel }^2,1\le m<\infty$$

(3)

where N denotes the number of data samples, c stands for the number of clusters, m is a number greater than unity, u_ij represents the degree of membership of x_i in the cluster j where x_i denotes the ith measured data, $c_j$ is the centre of the jth cluster, and $\Vert \Vert$ is the norm distance between the ith measured data and the jth cluster centre.

$$\parallel x_i-c_j\parallel =\frac{{\left(\sum {\left|x_i-c_j\right|}^2\right)}^{1/2}}{q^{1/2}}$$

(4)

where q explains the dimension of problem. Values for the degree of membership and cluster centre can be obtained considering the following equations:

$$u_{ij}=\frac{1}{{\sum }_{k=1}^C{\left(\frac{\parallel x_i-c_j\parallel }{\parallel x_i-c_j\parallel }\right)}^{1/\left(m-1\right)}}$$

(5)

$$c_j=\frac{{\sum }_{i=1}^N{u}_{ij}{}^m{x}_i}{{\sum }_{i=1}^N{u}_{ij}{}^m}$$

(6)

where k stands for an iteration step. Fuzzy partitioning works based on an optimization of the objective function in Equation (3) through an iterative process and by updating membership u_ij and cluster centres $c_j$. The iteration process continues as long as reaching to a predetermined threshold value:

$$ma{x}_{ij}\left(u_{ij}{}^{k+1}-u_{ij}{}^k\right)<\epsilon$$

(7)

DENFIS, which was first presented by Kasabov and Song [41], is a FIS model that uses clustering procedure for online and offline learning. In this method, first, FIS is generated given the clustering of the data and with respect to evolving clustering method (ECM). ECM can be considered as a powerful and efficient algorithm in handling highly noisy data. This algorithm is based on maximum distance-based clustering and is used for partitioning the input space in DENFIS to determine the fuzzy rules. Generally, depending on the problem conditions, this algorithm is designed for two modes of online and offline learning systems.

In the online model of DENFIS, the linear function is generated in the consequent parts and is updated through the least square estimator learning process. Additionally, there is the possibility of updating fuzzy rules as new training data in the system. Additionally, in the DENFIS offline, the aspect related to the dynamic evolving can be replaced with a complex learning algorithm in order to achieve high precision [41,52].

At the beginning of the online DENFIS learning process, the number of M clusters is generated by executing the ECM on the input vector of the initial data (n).

Then, for each cluster, the closest points are determined. The distance determination is generally defined with respect to general Euclidean distance. Therefore, assuming the consideration of the centre of a cluster (c) and position of example point (x), the distance between them (Dij) can be calculated using Equation (4). The general trend of determining the point for each cluster is in accordance with the concept of the maximum distance between each point and the cluster centre, and its comparison with a threshold value (d) [53].

If the calculated distance is less than the threshold, then no cluster will be created or updated and the existing cluster will be known as classified, otherwise the algorithm will proceed to the next step for finding decision parameters to create/update new cluster(s). Afterwards, the summation value (Sij) for each cluster distance (Dij) and the cluster’s radius (Rj) is calculated. Having the summation values, the cluster with the minimum amount of Sij (Sa) is identified as the Ca cluster. Considering the Ca cluster, if Sa > 2.d (d = the given threshold), a new cluster will be formed and the algorithm will return to its initial step. Otherwise, the Ca cluster will be updated with its new radius equal to Sa/2. The flowchart of the ECM algorithm is shown in Figure 3.

In the next step, the fuzzy rules are separately explained for each cluster. It should be noted that in both online and offline DENFIS modes, the Takagi-Sugeno fuzzy inference system (TS-FIS) is used for the model establishment. In other words, after deriving the clusters, TS-FIS is generated for each of the clusters. Then, the generated fuzzy rules are optimized using the back-propagation method. Therefore, for each simulation or prediction stage, the most important rules are dynamically selected.

Accordingly, assuming m fuzzy rules with two membership functions, the rules can be written as follows:

$$IF\left(x_{1}is{R}_{11}AND{x}_{2}is{R}_{12}\right)THEN\left(f_1=\left({\alpha }_{1}x+{\beta }_{1}y+{\gamma }_1\right)\right)\dots \dots \dots \dots .IF\left(x_{1}is{R}_{m1}AND{x}_{2}is{R}_{m2}\right)THEN\left(f_m=\left({\alpha }_{m}x+{\beta }_{m}y+{\gamma }_m\right)\right)$$

(8)

where R denotes the fuzzy sets with membership functions, in the antecedent parts of the TS-FIS. In the consequent parts of the TS-FIS, the crisp function (f) is employed to determine the consequent variable. Here, f is a polynomial function in the input variables x and y with linear coefficients of $\alpha$, $\beta$ and $\gamma$ as the constant. It should be noted that in both online and offline DENFIS modes, by default, all fuzzy membership functions are considered triangular.

2.2.2. Multivariate Adaptive Regression Splines (MARS)

As proposed by Friedman in 1991 [54], MARS is known as a non-parametric modelling method, which is capable of revealing non-linear patterns hidden in complex and high-dimensional data. The principles of the MARS function lie in establishing a relationship between input and output data through a series of coefficients and basic functions with respect to the regression technique [55,56]. In contrast to many ML methods, in the MARS method, only that group of input data which are correlated with the output data is selected to generate a model. Hence, MARS is capable of generating a simple, flexible, and robust model, which is also optimal in terms of computational cost. In this model, the available data are separated to a different number of regions with respect to knots, so that each of the regions has its own regression form. In other words, the basis of the research method in MARS is to generate the piecewise linear basis functions. The general shape of basis function (BF) can be expressed as follows:

$$\left[max\left(0,x-k\right)\right]OR\left[max\left(0,k-x\right)\right]$$

(9)

where x refers to the predictor variable and k explains threshold value in knots. The general formulation of MARS with the combination of BFs can be expressed as follows:

$$\begin{array}{c}y=f\left(x\right)+error\\ f\left(x\right)={\beta }_0+{\beta }_{m}B{F}_m\left(x\right)\end{array}$$

(10)

where y is a dependent variable that is estimated by function f(x) and are the tuning coefficients of the function. The MARS modelling is based on both forward and backward phases. The BFs are generated in the forward stepwise phase. After generating basis functions, the generalized cross validation criterion (GCV) is applied in order to determine the most appropriate node points and BFs. To put it simply, in the backward phase of the model, the number of basis functions is reduced and this continues until the lowest value of GCV is achieved. In this study, MATLAB software is used for application of these models [57,58,59]. In this study, genfis3 command which is included under Fuzzy Logic Toolbox in MATLAB was used for ANFIS-FCM simulation. For the DENFIS model simulation, a MATLAB code provided by the Kasabov and Song [41] was used. For MARS model, a MATLAB toolbox, ARESLab, was used. Detailed information about the MARS algorithm is given in [54].

2.2.3. The Evaluation Metrics Used for Model Comparison

The models’ performances were assessed using the following statistics:

$$MAE=\frac{1}{N}{\sum }_{i=1}^N|S_{io}-S_{ic}|$$

(11)

$$RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(\left(S_{io}\right)-\left(S_{ic}\right)\right)}^2}$$

(12)

$$NSE=1-\frac{{\sum }_{t=1}^N{\left(S_{io}-S_{ic}\right)}^2}{{\sum }_{t=1}^N{\left(S_{ic}-\overline{S_{ic}}\right)}^2}-\infty \le NSE\le 1$$

(13)

where MAE is the mean absolute error, RMSE is the root mean square error, NSE is the Nash–Sutcliffe efficiency, N refers to data quantity, $S_{io}$ is the observed sediment, $S_{ic}$ is the calculated sediment and $\overline{S_{ic}}$ is the average calculated sediment.

3. Results and Discussion

In the presented study, the ability of the dynamic evolving neural fuzzy inference system was investigated in modelling the suspended sediment load and its exactness was evaluated by comparing with adaptive neural fuzzy inference system with fuzzy c means clustering and multivariate adaptive regression splines. For each method, several input scenarios, including previous discharge and sediment loads (see

Table 2. The training and test statistics of the DENFIS, ANFIS-FCM and MARS models using different combinations of sediment and streamflow for daily suspended sediment prediction, Guangyuan Station.

Models	Scenario	Model Inputs	Model Parameters	Training Period			Test Period
				RMSE	MAE	NSE	RMSE	MAE	NSE
	S1	Qt,	0.05	1968	356	0.575	217	37.9	0.541
	S2	Qt, Qt−1	0.14	1797	366	0.646	164	35.7	0.739
	S3	Qt, Qt−1, Qt−2	0.11	2257	409	0.515	146	34.1	0.793
DENFIS	S4	Qt, Qt−1, Qt−2, Qt−3	0.13	2167	418	0.832	134	32.2	0.861
	S5	Qt, Qt−1, Qt−2, Qt−3, St−1	0.12	1986	353	0.567	168	22.4	0.726
	S6	Qt, Qt−1, Qt−2, Qt−3, St−1, St−2	0.11	2137	403	0.499	187	23.6	0.661
	S7	Qt, Qt−1, Qt−2, Qt−3, St−1, St−2, St−3	0.11	2340	435	0.399	228	29.4	0.495
	S1	Qt,	5,100	1828	373	0.633	294	69.4	0.164
	S2	Qt, Qt−1	6,10	1787	367	0.650	270	55.9	0.293
ANFIS-FCM	S3	Qt, Qt−1, Qt−2	4,100	1803	372	0.643	295	59.9	0.157
	S4	Qt, Qt−1, St−1	8,90	1322	243	0.808	318	46.5	0.020
	S5	Qt, Qt−1, St−1, St−2	8,70	1266	228	0.824	199	33.4	0.826
	S6	Qt, Qt−1, St−1, St−2, St−3	8,80	1807	363	0.642	258	52.1	0.353
	S1	Qt,	-	1760	372	0.660	327	65.0	−0.036
	S2	Qt, Qt−1	-	1758	376	0.661	368	80.3	−0.316
MARS	S3	Qt, St−1	-	1578	337	0.727	239	64.5	0.446
	S4	Qt, St−1, St−2	-	1614	343	0.714	195	62.4	0.631
	S5	Qt, St−1, St−2, St−3	-	1595	343	0.721	254	60.9	0.372

), were applied. First, previous discharge values were used as inputs. Previous discharge values were added to the model input one by one until a satisfactory accuracy in the test stage was obtained. After obtaining optimal discharge inputs, previous sediment values were merged with the optimal discharge input one by one until a satisfactory accuracy in the test stage was obtained.

Table 2 sums up the training and test accuracies of the DENFIS, ANFIS-FCM and MARS methods with respect to various input scenarios for Guangyuan Station. As an example, the structure of the DENFIS-based model based on scenario 5 is schematically shown in Figure 4. Qt-1 and St-1 refer the streamflow and sediment of one previous day and vice versa. Optimal model parameters are also provided in the fourth column of the table for the DENFIS and ANFIS-FCM-based models. In the MARS method, there is no control parameter. For the DENFIS-based models, various distance threshold values were tried (between 0 and 1). For the ANFIS-FCM-based models, various numbers of clusters and iterations were used. In Table 2, for example, 5100 indicate five clusters indicating five Gaussian membership functions for each input and iteration number.

As observed from the table where overall performances are indicated, each method has different accuracies for different input scenarios and their best models have different inputs. The best DENFIS-based model was developed utilizing input scenario 4 (S4) involving Qt, Qt-1, Qt-2, Qt-3 inputs while the best ANFIS-FCM-based and MARS-based models have the S5 (Qt, Qt-1, St-1, St-2) and S4 (Qt, St-1, St-2) inputs. The reason of this might be the fact that each method has different learning mechanisms and/or assumptions and system behaviour with respect to different input scenarios is also different to each other. Among the employed methods, DENFIS has the highest overall accuracy in the test stage. It is notable that ANFIS-FCM and MARS have similar accuracies in modelling the suspended sediment at Guangyuan Station. The other important issue which should be mentioned here are the input scenarios used for the best models. The best DENFIS-based model uses only previous streamflow data as input and this practically very important because measuring sediment is very difficult while the other two methods-based models use both streamflow and sediment inputs. The DENFIS-based model with S5 has improved the RMSE accuracy of ANFIS-FCM and MARS by 33% and 31%, respectively. Time variation graphs of the observed and estimated suspended sediment by the best DENFIS, ANFIS-FCM and MARS in the test period of Guangyuan Station are illustrated in Figure 5. This figure also includes two detailed graphs derived from the main graph. In the first graph, the DENFIS underestimates the observed peak while the ANFIS-FCM and MARS overestimate. However, the estimates of the DENFIS-based model are closer to the observed one compared to the other models. In the second graph, it is observed that all the models overestimate the observed peak and ANFIS-FCM and MARS are closer compared to DENFIS. Figure 6 gives the scatter graphs of the best model of each method. It is clear that the DENFIS-based model has the least scattered estimates with the highest R² value.

The overall suspended sediment estimation accuracies of the three applied methods are compared in

Table 3. The training and test statistics of the DENFIS, ANFIS-FCM and MARS models using different combinations of sediment and streamflow for daily suspended sediment prediction, Beibei Station.

Models	Scenario	Model Inputs	Model Parameters	Training Period			Test Period
				RMSE	MAE	NSE	RMSE	MAE	NSE
	S1	Qt,	0.01	4014	663	0.593	1546	229	0.628
	S2	Qt, Qt−1	0.17	3779	656	0.639	1417	233	0.687
	S3	Qt, Qt−1, Qt−2	0.02	4158	711	0.563	1177	204	0.784
DENFIS	S4	Qt, Qt−1, Qt−2, Qt−3	0.06	4302	732	0.532	1024	169	0.837
	S5	Qt, Qt−1, Qt−2, Qt−3, St−1	0.15	4325	753	0.527	1153	184	0.793
	S6	Qt, Qt−1, Qt−2, Qt−3, St−1, St−2	0.05	3936	663	0.609	797	134	0.901
	S7	Qt, Qt−1, Qt−2, Qt−3, St−1, St−2, St−3	0.06	4237	752	0.547	884	149	0.878
	S1	Qt,	8,20	3802	656	0.635	1214	228	0.770
	S2	Qt, Qt−1	8,10	3707	663	0.653	1235	224	0.762
ANFIS-FCM	S3	Qt, Qt−1, Qt−2	4,80	3742	657	0.646	1171	257	0.786
	S4	Qt, Qt−1, Qt−2, Qt−3	5,30	4084	801	0.579	1864	328	0.459
	S5	Qt, St−1	8,20	3685	620	0.657	1312	215	0.732
	S6	Qt, St−1, St−2	6,60	3332	606	0.720	1616	229	0.784
	S7	Qt, St−1, St−2, St−3	5,50	4410	871	0.509	2772	407	−0.197
	S1	Qt,	-	3646	631	0.664	1423	284	0.685
	S2	Qt, Qt−1	-	3596	629	0.673	1509	271	0.645
MARS	S3	Qt, St−1	-	3089	518	0.759	1252	213	0.756
	S4	Qt, St−1, St−2	-	2945	523	0.781	1362	229	0.711
	S5	Qt, St−1, St−2, St−3	-	2905	520	0.787	1397	234	0.696

for Beibei Station. In contrast to previous station, the best DENFIS-based model was obtained from the 6th scenario (Qt, Qt-1, Qt-2, Qt-3, St-1, St-2) while the S3 scenarios (Qt, Qt-1, Qt-2, Qt-3 and Qt, St-1) provided the best accuracies for the best ANFIS-FCM and MARS-based models. It should be noted that there is a slight difference between S1 and S3 scenarios for the ANFIS-FCM model. In addition, the MAE value of the S1 scenario is lower than that of the S3 scenario. For this reason, previous sediment values were merged with S1. At this station DENFIS also outperformed the other two methods with respect to RMSE, MAE and NSE criteria. MARS showed the worst accuracy in estimating suspended sediment of Beibei Station. The DENFIS-based model with S6 input improved the RMSE (MAE) accuracy of the best ANFIS-FCM and MARS-based models by 32% (48%) and 36% (37%), respectively. Figure 7 compares the observed and estimated suspended sediment by the best DENFIS, ANFIS-FCM and MARS in the test period of Beibei Station in the form of hydrograph. It is apparent from the detail graphs that the DENFIS is able to follow the observed sediment values closer than those of the other two methods. The scatter graphs given in Figure 8 also confirm that the DENFIS-based model is superior over the ANFIS-FCM and MARS-based models and it has less scattered estimates with higher R2 than those of the others.

The peak estimation accuracies of the three employed methods are compared in

Table 4. The comparison of DENFIS, ANFIS-FCM and MARS peak-estimates for the test period, Guangyuan Station.

Date	Peaks > 900 kg/s				Relative Error
		DENFIS kg/s	ANFIS-FCM kg/s	MARS kg/s	DENFIS %	ANFIS-FCM %	MARS %
7 July 2014	1690	733.37	1191.2	946.26	−56.6	−29.5	−44.0
21 July 2014	1850	1376.5	2970.8	3977.1	−25.6	60.6	115.0
11 September 2014	1120	590.73	1764.6	1600.9	−47.3	57.6	42.9
12 September 2014	917	511.98	1573.3	1839.7	−44.2	71.6	100.6
28 June 2015	7660	10,309	8704.3	8585.3	34.6	13.6	12.1
29 June 2015	1920	2302.3	3756.8	4758.9	19.9	95.7	147.9
		Total (Absolute) =			228	329	462

and

Table 5. The comparison of DENFIS, ANFIS-FCM and MARS peak-estimates for the test period, Beibei Station.

Date	Peaks > 11,000 kg/s				Relative Error
		DENFIS kg/s	ANFIS-FCM kg/s	MARS kg/s	DENFIS %	ANFIS-FCM %	MARS %
12 September 2014	21,900	13,021	19,377	10,258	−40.5	−11.5	−53.2
13 September 2014	21,300	18,516	21,817	14,659	−13.1	2.4	−31.2
14 September 2014	36,600	26,760	25,166	31,414	−26.9	−31.2	−14.2
15 September 2014	26,300	33,871	29,084	31,615	28.8	10.6	20.2
16 September 2014	11,100	11,219	20,040	18,622	1.1	80.5	67.8
26 June 2015	16,800	11,704	18,896	9720.9	−30.3	12.5	−42.1
30 June 2015	29,600	32,742	28,895	28,031	10.6	−2.4	−5.3
1 July 2015	11,400	19,727	23,768	20,847	73.1	108.5	82.9
		Total (Absolute) =			224	260	317

for the Guangyuan and Beibei stations, respectively. It is apparent from Table 4 that the DENFIS-based model generally has better accuracy in catching peak sediment values compared to ANFIS-FCM and MARS-based models (see the absolute total of relative error). Detailed graphs (Figure 4) correspond to the 2nd and 5th peaks given in this table. According to Table 4, for example, DENFIS computed the observed sediment peak, 1690 kg/s as 733.37 kg/s with an underestimation of 56.6% while the ANFIS-FCM and MARS resulted in 1191.20 kg/s and 946.26 kg/s with underestimations of 29.5% and 44%, respectively. The DENFIS-based model with an absolute total error of 224 has superior accuracy in estimating peak sediments of Beibei Station compared to the ANFIS-FCM (260) and MARS-based (317) DENFIS-based model. Detailed graphs (Figure 7) correspond to the 3rd and 7th peaks given in Table 5. In both stations, MARS has the worst accuracy. It should be noted here that the DENFIS-based models can simulate peak sediment loads more successfully on average. For some storm events, ANFIS-FCM and MARS-based models perform superior to the DENFIS-based model in estimating peak sediment loads (see the 1st and 5th peaks of Guangyuan Station and the 4th and 7th peaks of Beibei Station). It is clear from Table 2, Table 3, Table 4 and Table 5 that the accuracies of the models are worse for Guangyuan Station compared to Beibei. This might be due to the fact that testing data of first station have more skewed distribution and $\frac{x_{\max }}{x_{\mathrm{mean}}}$ ratio compared to 2nd one.

4. Conclusions

The ability of the dynamic evolving neural fuzzy inference system was investigated in modelling the suspended sediment load employing several input scenarios including previous values of streamflow and sediment. The results were compared with the adaptive neural fuzzy inference system with fuzzy c means clustering and multivariate adaptive regression splines and the following conclusions were reached after the application:

Three methods were applied the data of two stations—Guangyuan and Beibei—and DENFIS-based models provided the best performance in both stations while the worst estimates belonged to MARS-based models.

It was concluded that the DENFIS-based models can accurately model the suspended sediment load based only on previous streamflow data.

By applying DENFIS-based models, the prediction accuracy of RMSE, MAE and NSE of the ANFIS-FCM-based models were improved by 33%, 4% and 4%, respectively, for Guangyuan Station while the corresponding values were 32%, 48% and 15% for Beibei Station, respectively. Similarly, in the case of MARS-based models, the application of DENFIS-based models improved the prediction accuracy of RMSE, MAE and NSE by 31%, 48% and 36%, respectively, for Guangyuan Station while the corresponding values were 36%, 37% and 19% for the Beibei Station.

Overall, the DENFIS-based models were found to be more successful in simulating the peak sediment values on average compared to the other two models. In some storm events, however, the ANFIS-FCM and MARS-based models provided better accuracy compared the DENFIS-based models.

The DENFIS method can be thought as a better alternative to ANFIS-FCM and MARS in estimating suspended sediment in the study region. This method may be further explored by using more data from different regions of the world to reach more robust conclusions.