4.1. Trends Test
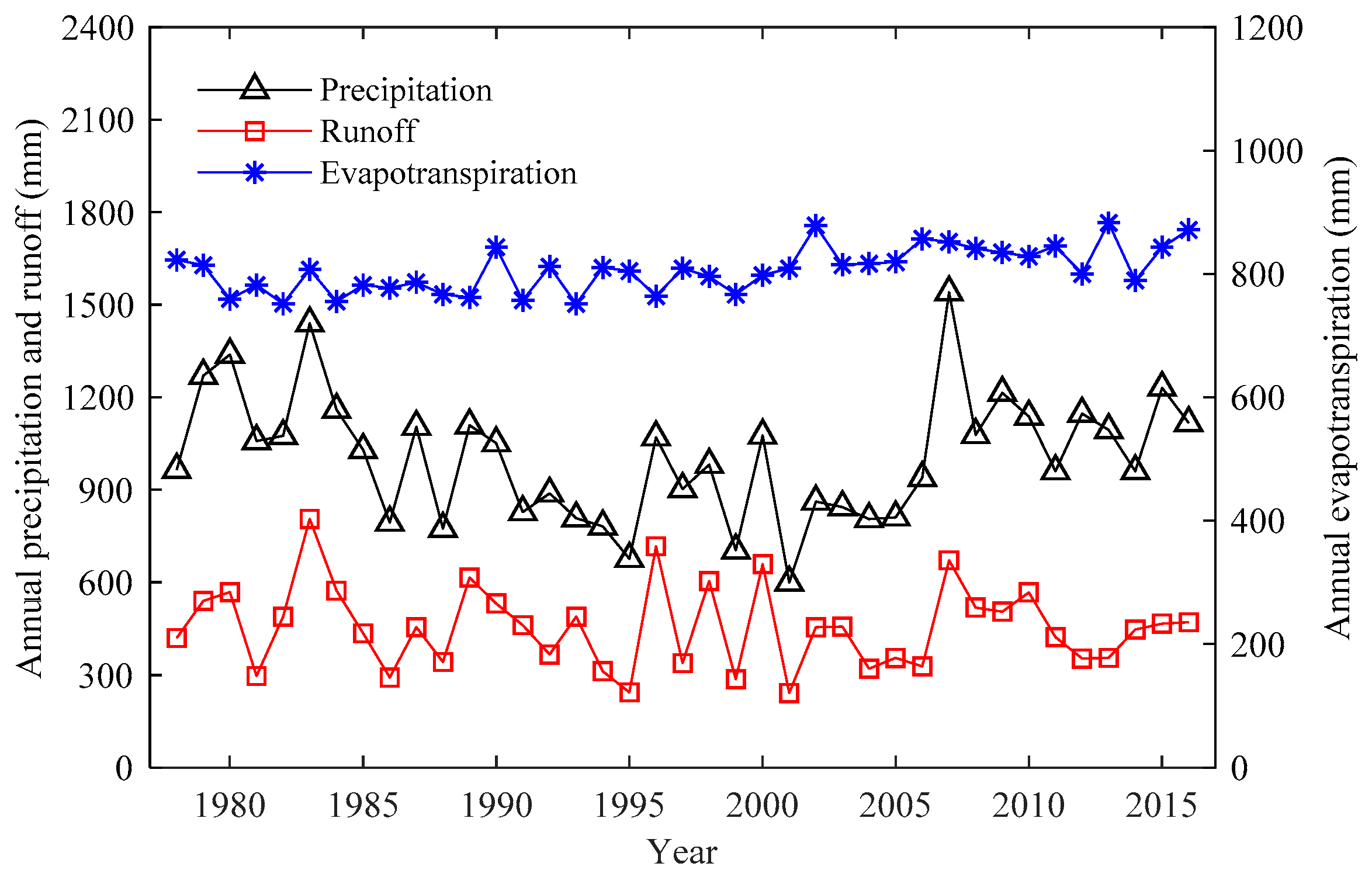
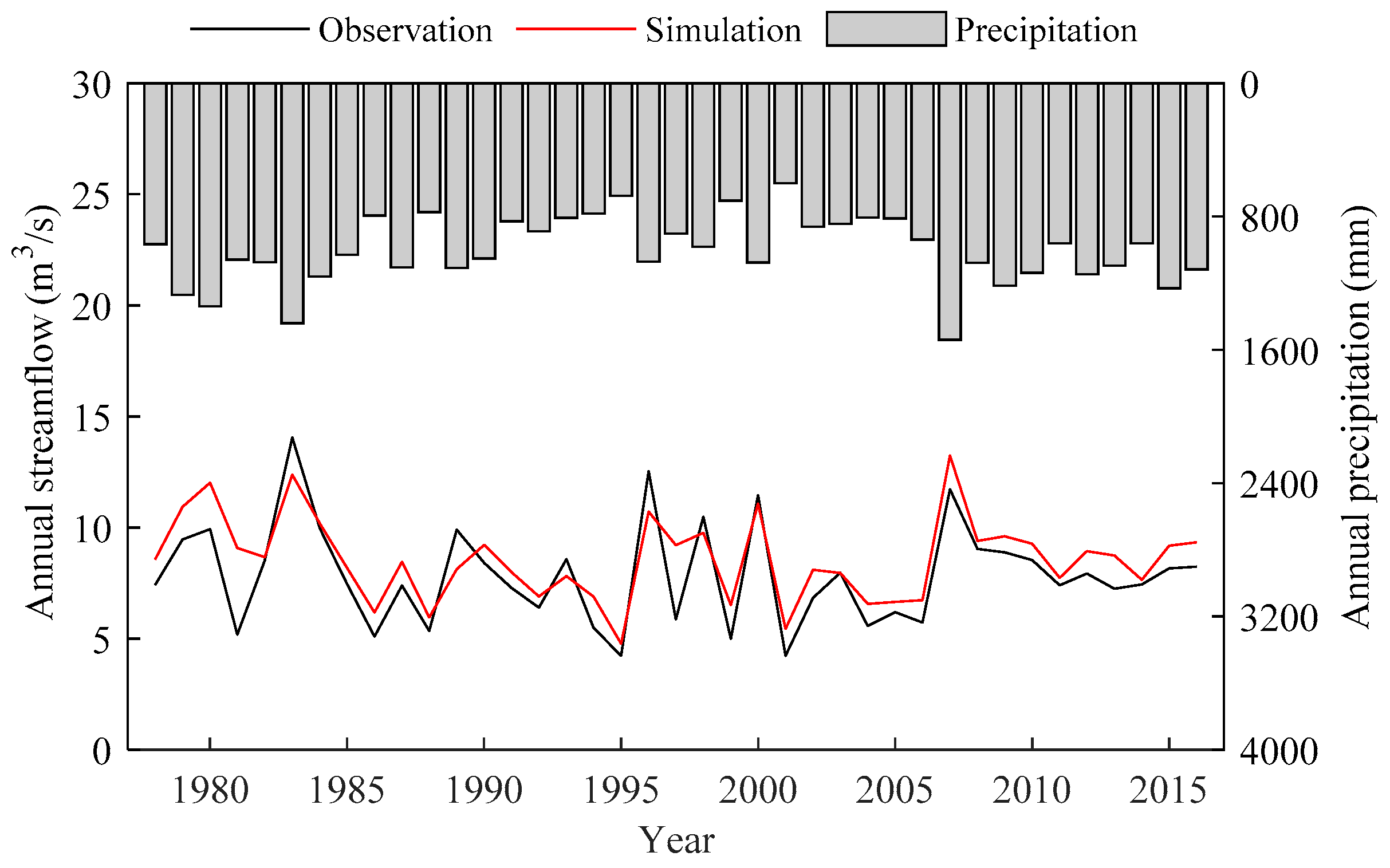
The annual precipitation, runoff and evapotranspiration of the upper areas of TFM dam are shown in
Figure 2. The annual runoff declines at the rate of −1.1 mm/year. The lower values of annual runoff are in 1995 (243.2 mm) and 2001 (241.2 mm). The highest runoff occurs in 1983, which is up to 805.7 mm. Furthermore, the remarkably continuous dry years from 1985 to 2006 are found. The decreasing rate of annual precipitation is −0.5 mm/year between 1978 and 2016. The maximum annual precipitation occurs in 2007, achieving 1540.4 mm and the second highest is in 1983 (1440.3 mm). The annual evapotranspiration significantly increases at the rate of 1.96 mm/year. The maximum annual evapotranspiration occurs in 2013, achieving 882.7 mm and the second highest is in 2002 (878.4 mm). However, compared with the corresponding annual runoff data in 2007 and 1983, the annual runoff in 2007 (675.9 mm) is significantly smaller than that in 1983 (805.7 mm). Even though the annual evapotranspiration in 2007 (852.0 mm) is larger than that in 1983 (807.1 mm), the increasing rate of annual evapotranspiration (5.3%) is significantly smaller that of annual runoff (19.2%). That is to say, the more precipitation occurs in 2007 than that in 1983 but on the contrary, less runoff produces in 2007. The runoff coefficient (0.44) in 2007 is significantly smaller than that (0.56) in 1983. Therefore, it implies that the runoff in 2007 is remarkably affected by other factors.
The decadal of mean annual precipitation, runoff and runoff coefficient are then shown in
Table 1. During the period of 1978–2009, the values of distance to mean in runoff data are consistent with that in precipitation data, however, during the period the 2010 to 2016, the value is opposite. This phenomenon indicates that the relationship between precipitation and runoff is weaker, in other words, the same precipitation produces less runoff. Furthermore, the runoff coefficient (0.41) is the smallest in this period (
Table 1).
The change in trend and magnitude of annual runoff, precipitation, evapotranspiration and runoff coefficient are listed in
Table 2. The results showed that only the Z value (3.79) in annual evapotranspiration is larger than the threshold of Z
1−a/2 (i.e., Z
1−a/2=±1.96 at a=5% significance level), indicating that the increasing trend of annual evapotranspiration is significant. However, the decreasing trend of annual runoff, precipitation and runoff coefficient are all not significant because of the Z values of −0.44, −0.17 and −0.82 for the whole period (1978–2016), respectively. The trend magnitude of annual runoff coefficient is larger than that of both annual precipitation and runoff and the change rate of annual precipitation is much weaker than that of annual runoff.
4.2. Change Point Analysis
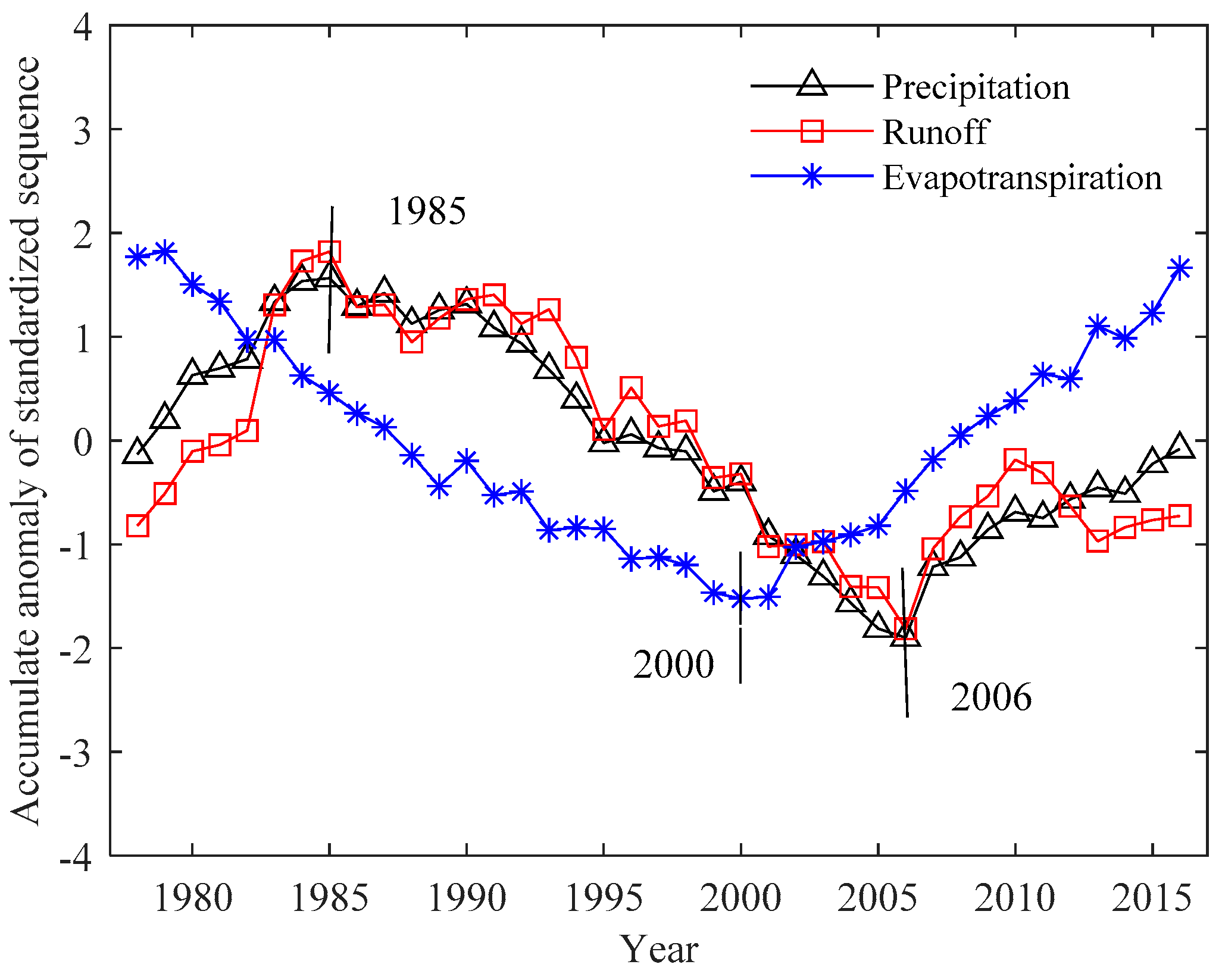
The accumulate anomaly curve of the annual runoff data series for the whole period of 1978–2016 is displayed in
Figure 3. The highest value of the accumulative anomaly curve of runoff is in 1985 and the lowest value is in 2006 and second higher in 2010, second lower in 2013. There is a rising trend and decreasing trend before and after 1985, respectively and there is also an upward and downward trend before and after 2006. Furthermore, the accumulative anomaly curves of annual precipitation and evapotranspiration are also calculated and presented in
Figure 3. There are two significant change points in 1985 and 2006 in annual precipitation data, which are the same as that of the annual runoff data. However, there is only one change point in annual evapotranspiration data (2000). According to the research by Dey and Mishra, (2017) [
18], the change points of runoff should be in the interval of that of precipitation and evapotranspiration. Therefore, the change points (1985 and 2006) were selected as the final change points for the total 39 years.
In the upper reach of TFM dam, the variation of runoff before 1985 had been majorly impacted by the variation of precipitation, due to in this period there were few human activities. Since the year of 1985, human activities have gradually intensified and influenced the variation of runoff to some extent. To determine the contributions of climate change and human interactions to variation of annual runoff, the period of 1978–1984 is considered the reference period Ta, the other two change periods (i.e., Tb (1985–2005) and Tc (2006–2016)) are treated as measurement periods.
Based on the change points of annul runoff time series, the mean annual values of runoff, precipitation and evapotranspiration data in the three periods are listed in
Table 3 and graphically displayed in
Figure 4. Due to the lack of observed evapotranspiration data, two data sources are included in this paper. The evapotranspiration data were obtained from GLEAM, however. due to the area of the study basin is smaller, the evapotranspiration map only includes a small percentage of GLEAM map. The other method is that the mean annual evapotranspiration in every period was calculated using the Equation (11). In this equation, the fraction of forest cover (f) is the most important parameter. In this study, the mean fraction of forest cover for the baseline period Ta (1978–1984) is obtained from the land use map in 1980 (0.886). For the change period Tb (1985–2005), mean fraction of forest cover is calculated based on the two land use maps (1995 and 2000), which is the mean of the values of two forest coverages. A fraction of the forest cover of the land use map 2008 is used for the change period Tc (2006–2016), respectively. The mean fraction of forest cover in every period is listed in
Table 3 and the calculated value of mean annual evapotranspiration in every period is also shown in
Table 3.
Based on the GLEAM evapotranspiration and compared with the baseline period Ta, the mean annual of precipitation during the change period Tb, decreases by 25.8% (1186.8 mm in Ta vs. 881.1 mm in Tb) and evapotranspiration increases by 1.5% (784.7 mm in Ta vs. 796.4 mm in Tb), while that of runoff decreases by 19% (532.7 mm in Ta vs. 431.7 mm in Tb). The mean annual of precipitation during the change period Tc reduces by 4.9% (1186.8 mm in Ta vs. 1129.2 mm in Tc) and evapotranspiration increases by 7.1% (840.5 mm in Ta vs. 784.7 mm in Tc), whereas that of runoff reduces by 12.4% (532.7 mm in Ta vs. 466.8 mm in Tc).
However, based on the evapotranspiration calculated by Equation (11) and compared with the baseline period Ta, the mean annual evapotranspiration decreases by 18.7% (919.5 mm in Ta vs. 747.7 mm in Tb). The mean annual evapotranspiration reduces by 3.3% (919.5 mm in Ta vs. 889.2 mm in Tc).
Generally speaking, it could be seen that the change rate annual runoff in change period Tc is larger that the sum of that of precipitation and evapotranspiration, indicating human activities in this period is intensive and might be the most important influencing factor of the decline in runoff.
Furthermore, the mean runoff coefficients are 0.45 (532.7 mm/1186.8 mm) in the reference period Ta, 0.49 (431.7 mm /881.1 mm) in the the change period Tb and 0.41 (466.8 mm/1129.2 mm) in the change period Tc, respectively. Therefore, the value of runoff coefficient during the period Tc is the minimum compared with other two periods, indicating that the correlation beween precipitation and runoff is weakest, in other words, runoff variation might be less influenced by precipitation in this period Tc.
4.3. SCRAQ Method
4.3.1. Relationships between Year and Precipitation and between Year and Runoff
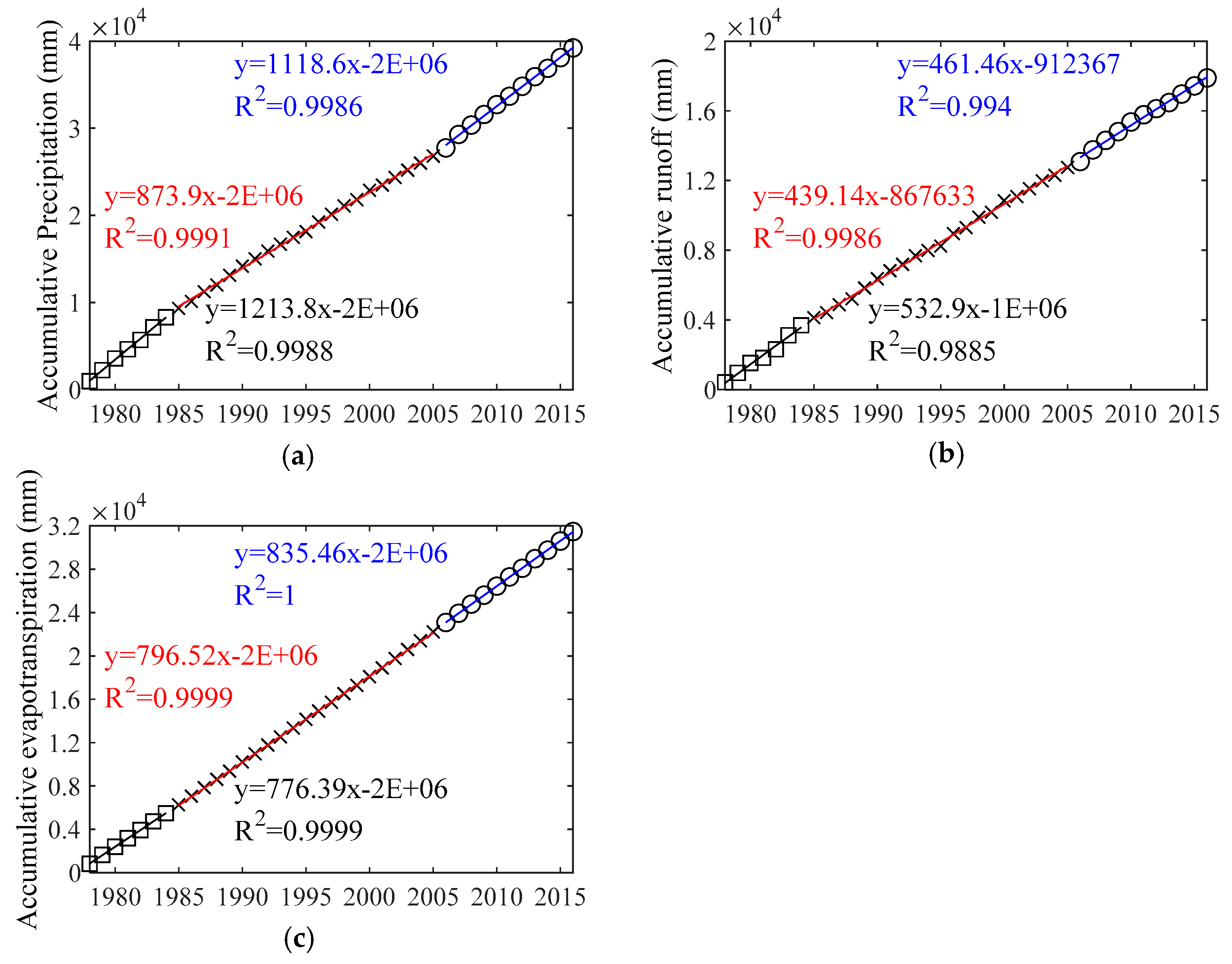
The scatter distributions, fitted lines by linear regression between accumulative runoff and year, accumulative precipitation and year and accumulative evapotranspiration and year, for the every period (Ta: 1978–1984, Tb: 1985–2005 and Tc: 2006–2016) are graphically displayed in
Figure 5. It could be seen that the correlation coefficients of R
2 values are all high for the three periods, even exceeding 0.98. At the same time, the confidence levels of P values are less than 0.0001. Therefore, correlation of accumulative streamflow and year is good in every period. The parameters of slope extracted for every period are also listed in
Table 4.
4.3.2. Quantification of the Impacts of Climate Change and Human Interactions
Based on the parameters shown in
Table 3 and
Table 4, the results of contribution rates of precipitation, evapotranspiration and human activities to the runoff variation are listed in
Table 5. It could be seen that the impact of precipitation to the variation of runoff is positive, while that of evapotranspiration is negative (
Table 5).
When the period Ta (1978–1984) is treated as reference period, the contributions of precipitation on the runoff variation for the period Tb (1985–2006) and Tc (2006–2016) are 159% and 58.5%, respectively.
When the evapotranspiration data were obtained from GLEAM, the contributions on the runoff variation for the periods Tb and Tc are 13.9% and 56.7%, respectively. Hence, the contribution of climate variabilities (precipitation plus evapotranspiration) to runoff changes are 173% and 115.2%, respectively. Therefore, in the change period Tb and Tc, the climate change is the main driving factor. However, the climate change is less influenced in the change period Tc, implying the contribution of anthropogenic activities gradually increase.
When the evapotranspiration data were calculated using the Equation (11), it can be seen that the contribution of evapotranspiration to the runoff variation for the measurement periods Tb and Tc are −98.6% and −37.8%, respectively. In the whole, the contributions of climate change (precipitation plus evapotranspiration) to runoff variation are 60.5% and 20.7%, respectively. Therefore, the contribution of anthropogenic activities to the variation in runoff are 39.5% and 79.3%, respectively.
In general, in the change period Tb, the climate change is the main driving factor, whereas, in the change period Tc, the human activities are increasing, which can be the dominant influencing factor.