Multi-Objective Operation of Cascade Hydropower Reservoirs Using TOPSIS and Gravitational Search Algorithm with Opposition Learning and Mutation
Abstract
1. Introduction
2. Enhanced Gravitational Search Algorithm (EGSA)
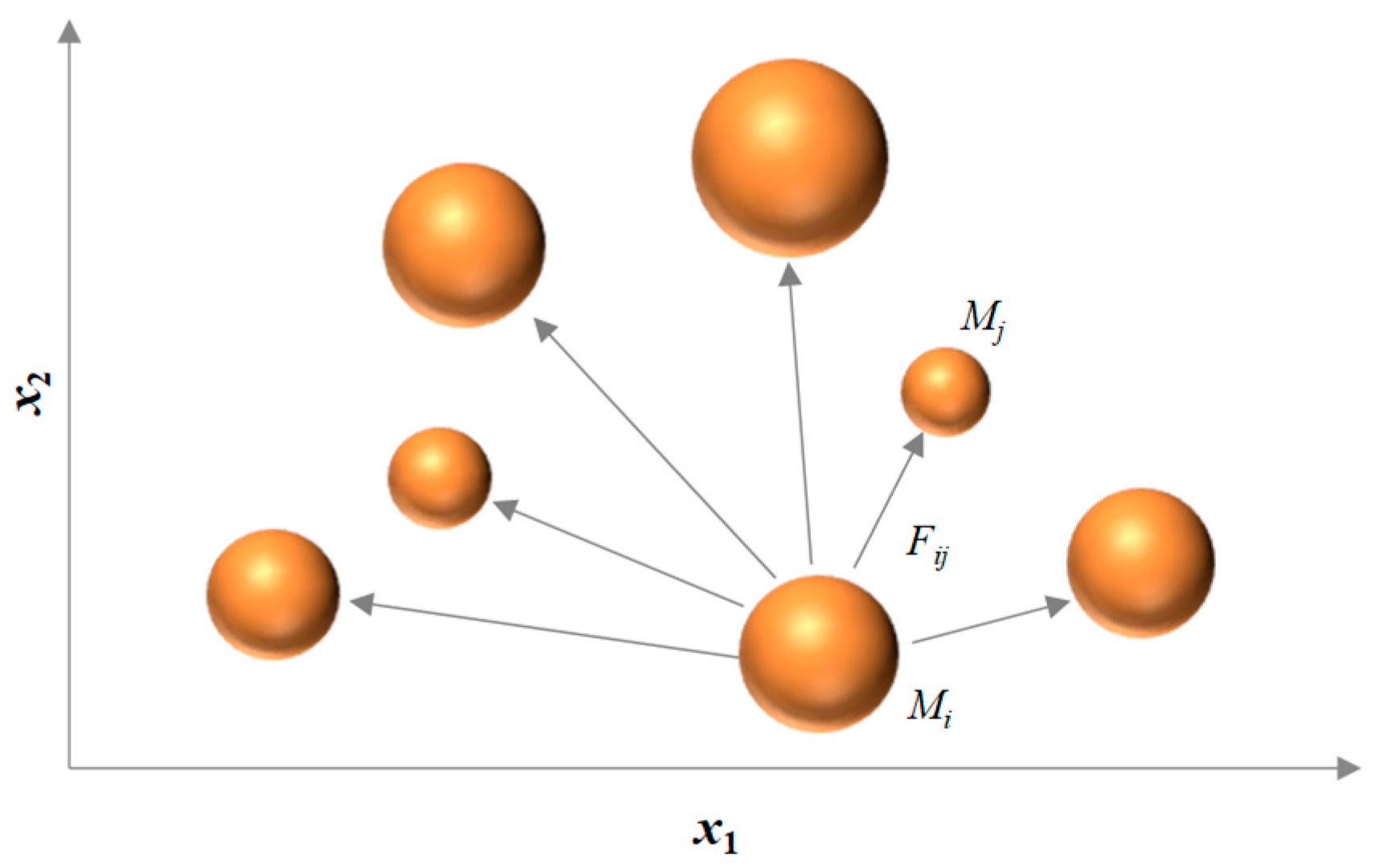
2.1. Gravitational Search Algorithm (GSA)
2.2. Opposition Learning Strategy to Improve the Convergence Speed of the Swarm
2.3. Partial Mutation Strategy to Enhance the Individual Diversity
2.4. Elastic-Ball Modification Strategy to Promote Solution Feasibility
2.5. Execution Procedure of the Proposed EGSA Method
- Step 1: Set the values of the computational parameters and then randomly generate the initial swarm in the problem space.
- Step 2: Calculate the fitness values of all the agents in the current population, and then update the personal best-known of each agent and the global best-known agent of the swarm.
- Step 3: Calculate the correlated variables (like the gravitational coefficient, mass, and acceleration) to update the velocity and position values of all the agents.
- Step 4: Execute the opposition learning strategy to increase the convergence speed of the swarm.
- Step 5: Execute the partial mutation search strategy to enhance the individual diversity.
- Step 6: Execute the elastic-ball modification strategy to promote the solution feasibility.
- Step 7: Repeat Step 2–6 until the stopping criterion is met, and then the global optimal position is regarded as the final solution of the optimization problem.
3. Numerical Experiments to Verify the Performance of the EGSA Method
3.1. Benchmark Functions
3.2. Parameters Settings
3.3. Comparison with Other Evolutionary Algorithms in Small-Scale Problems
3.3.1. Result Comparison in Multiple Runs
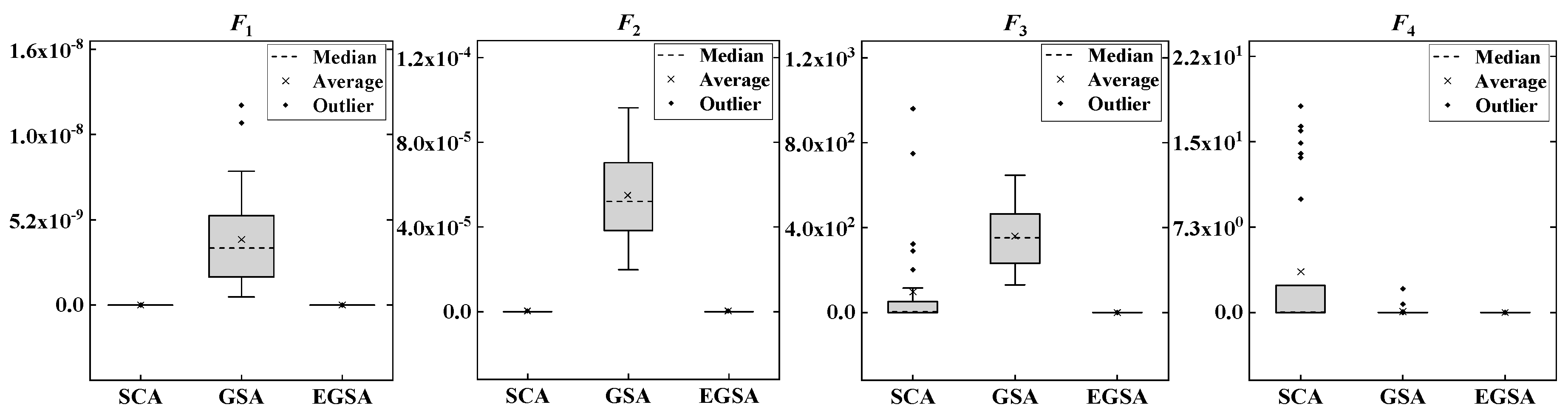
3.3.2. Box and Whisker Test
3.3.3. Wilcoxon Nonparametric Test
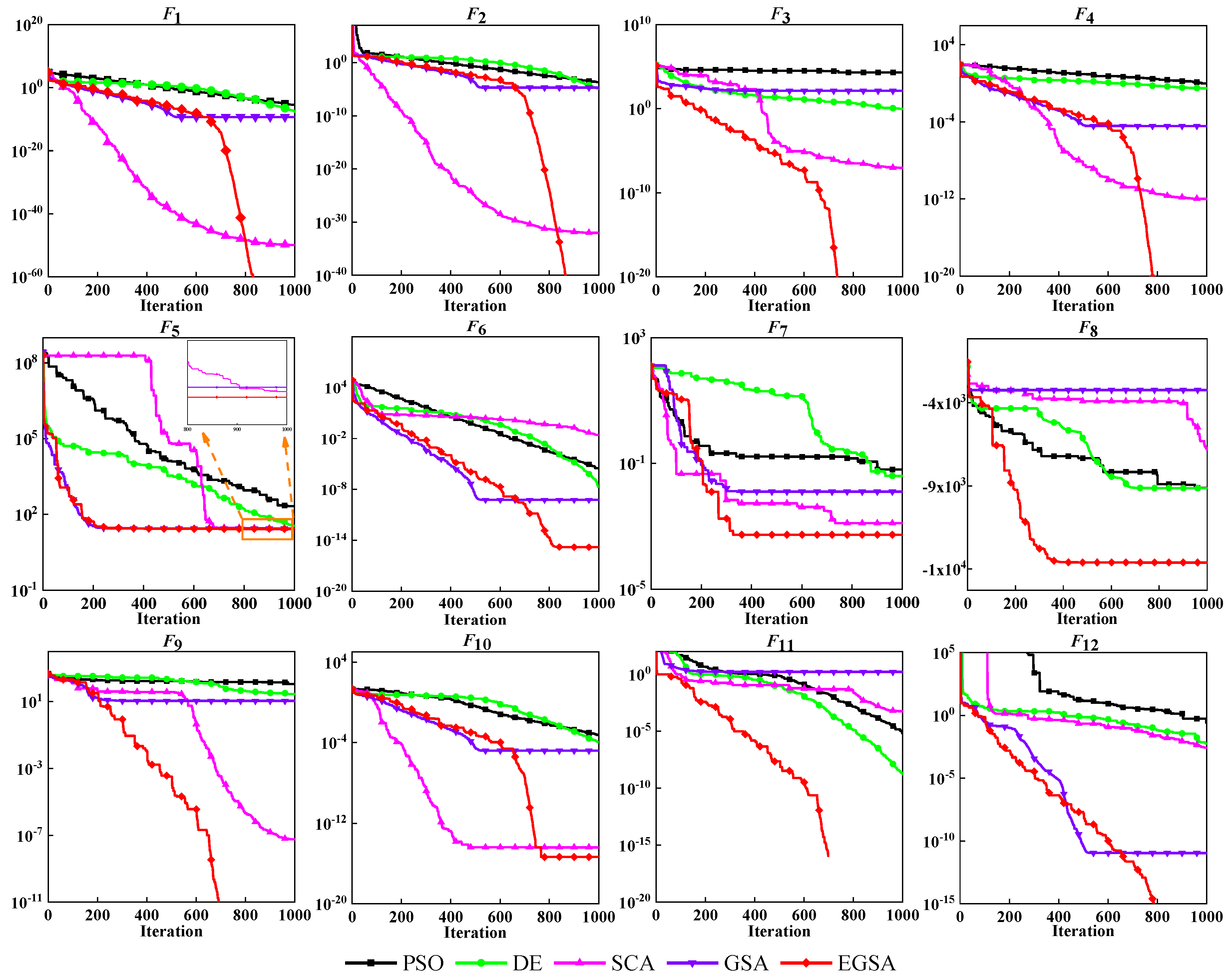
3.3.4. Convergence Analysis
4. EGSA for the Multi-Objective Operation of Cascade Hydropower Reservoirs
4.1. Mathematical Model
4.1.1. Objective Functions
4.1.2. Physical Constraints
4.2. Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS)
4.3. Details of EGSA for Multi-Objective Operation of Cascade Hydropower Reservoirs
4.3.1. Individual Structure and Swarm Initialization
4.3.2. Heuristic Constraint Handling Method
4.3.3. Calculation of the Modified Objective Values
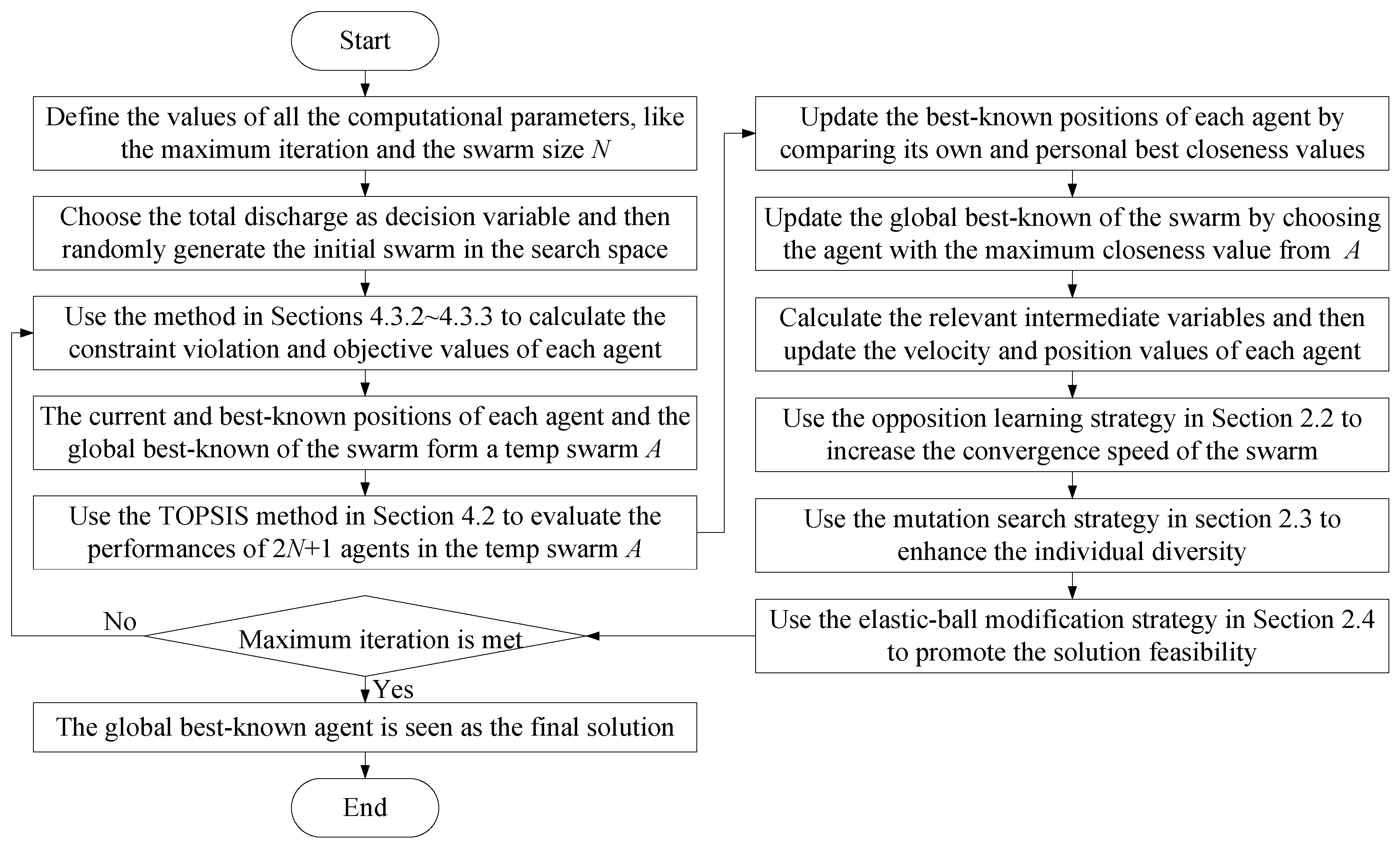
4.3.4. Execution Procedures of the EGSA Method for the Target Problem
5. Case Studies
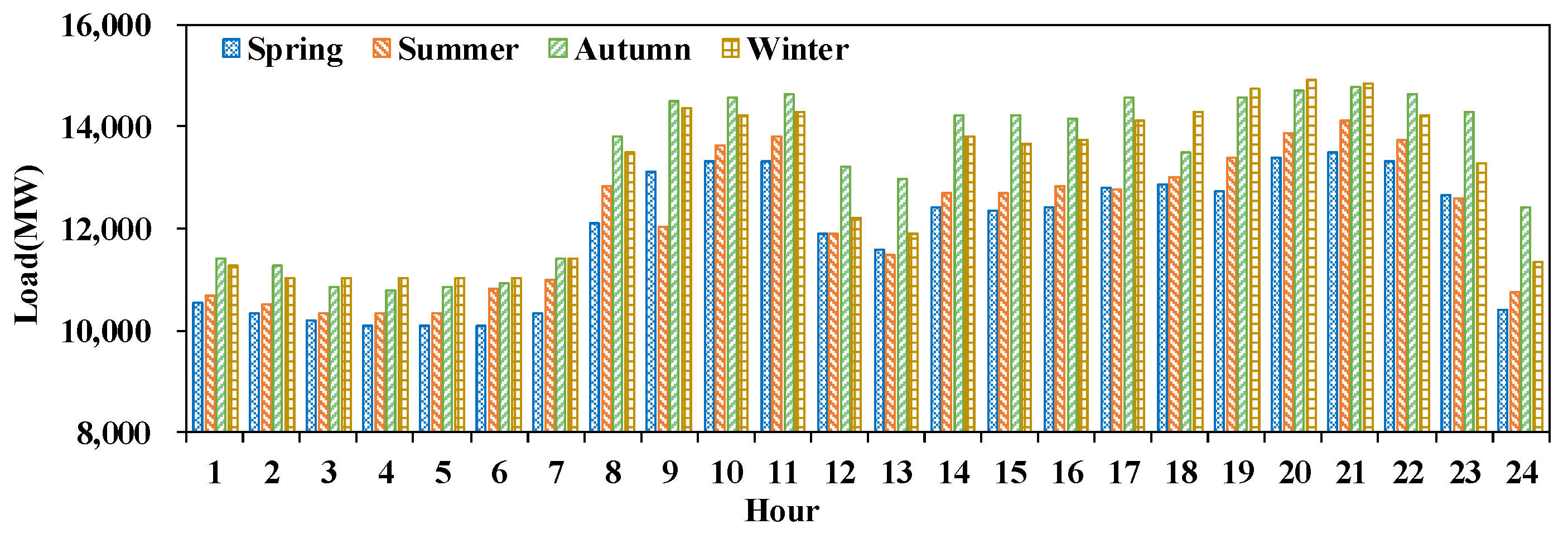
5.1. Engineering Background
5.2. Case Study 1: Power Generation of Cascade Hydropower Reservoirs
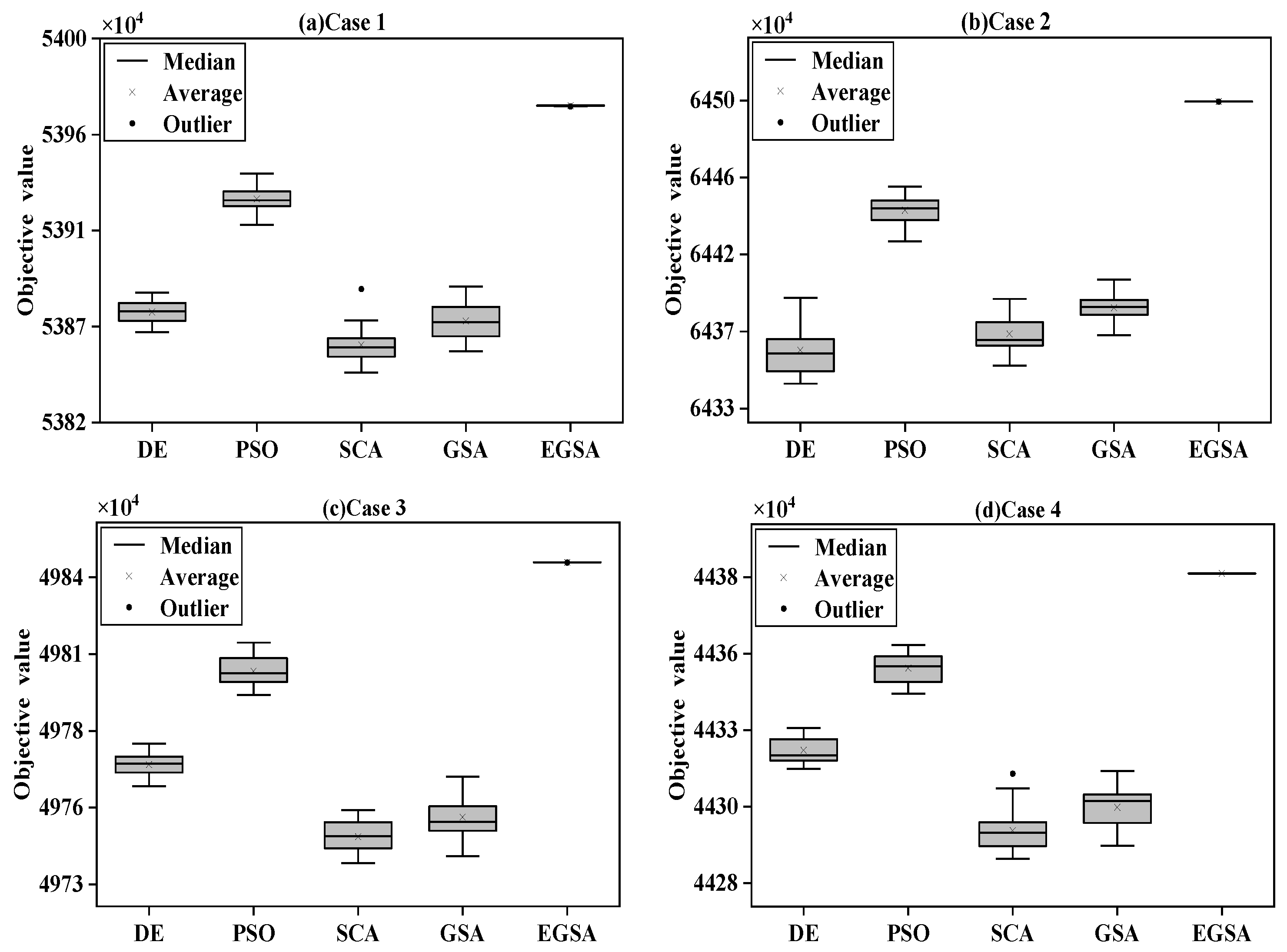
5.2.1. Robustness Testing of Different Evolutionary Algorithms
5.2.2. Comparison of the Optimal Results Obtained by Different Evolutionary Algorithms
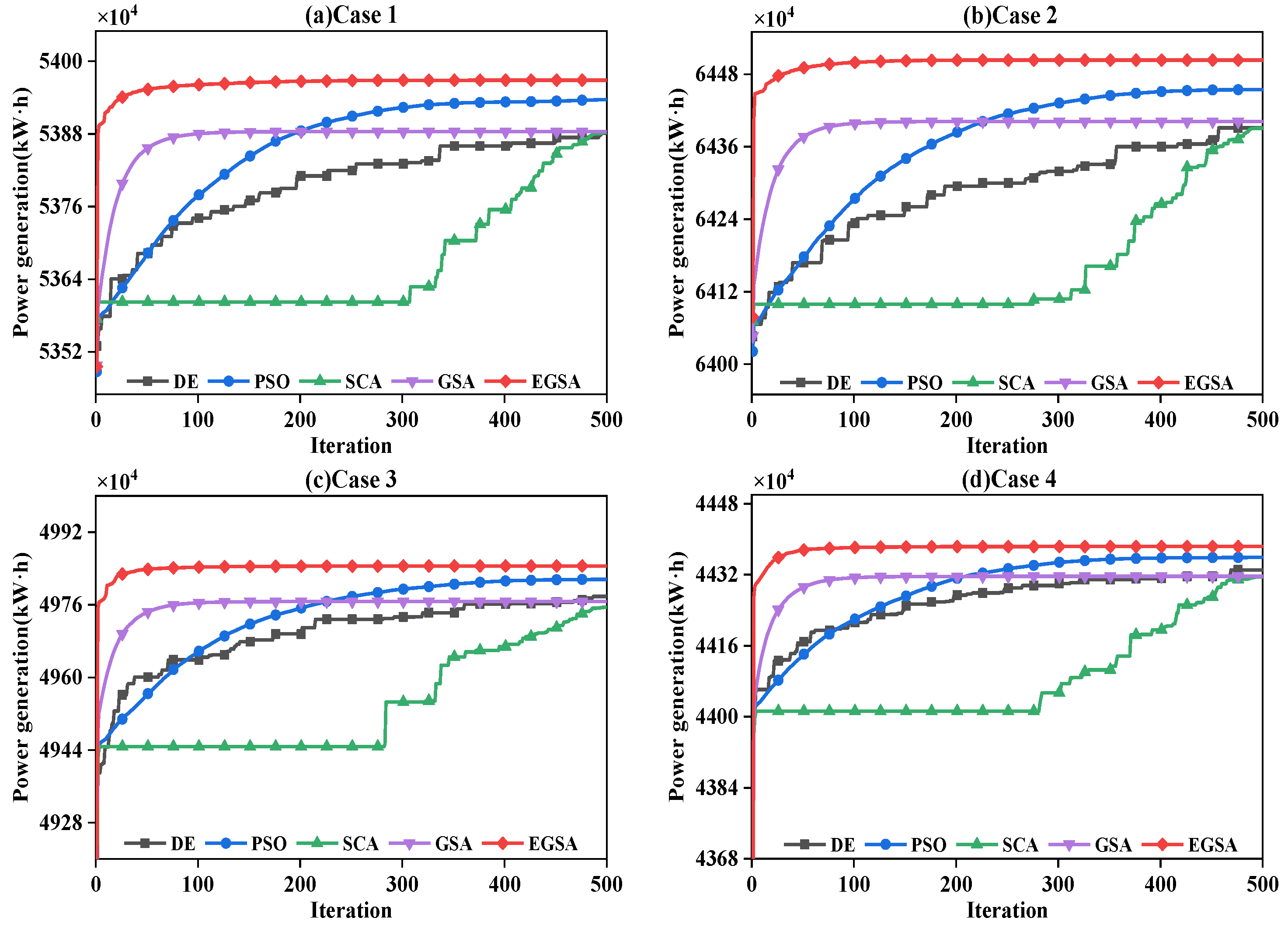
5.2.3. Convergence Analysis of Different Evolutionary Algorithms
5.3. Case Study 2: Peak Operation of Cascade Hydropower Reservoirs
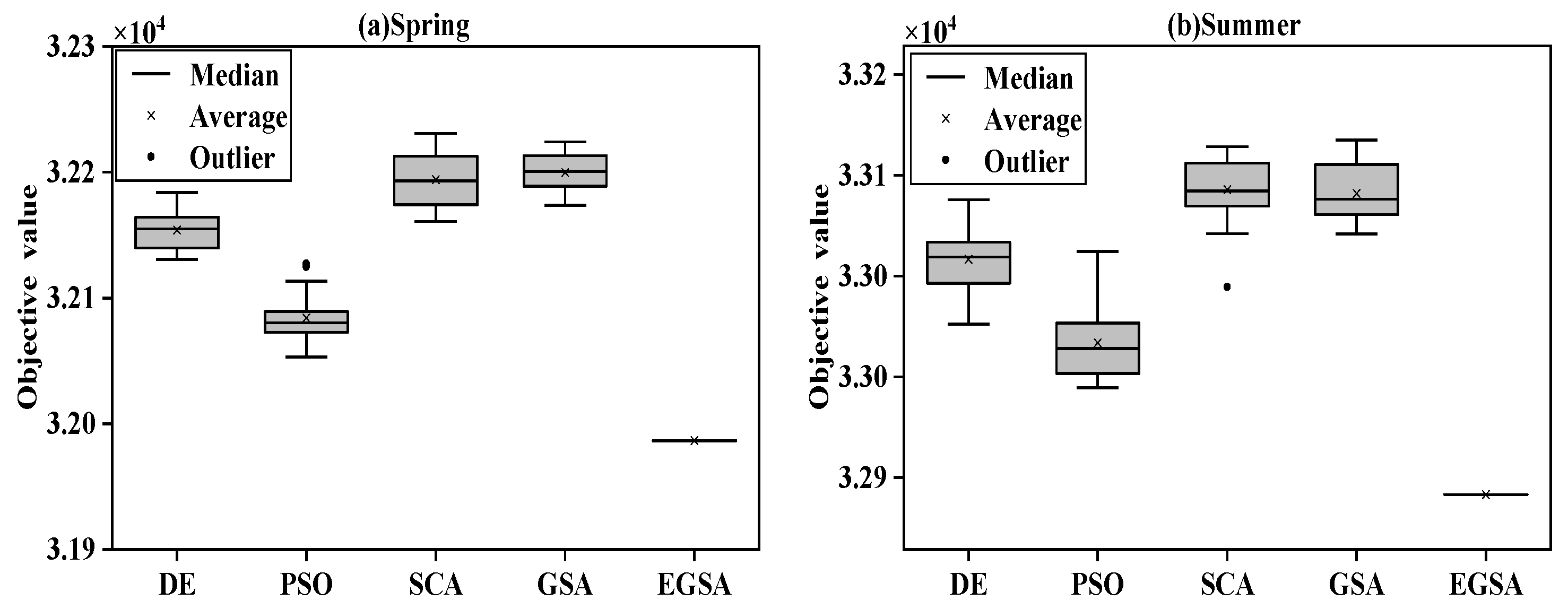
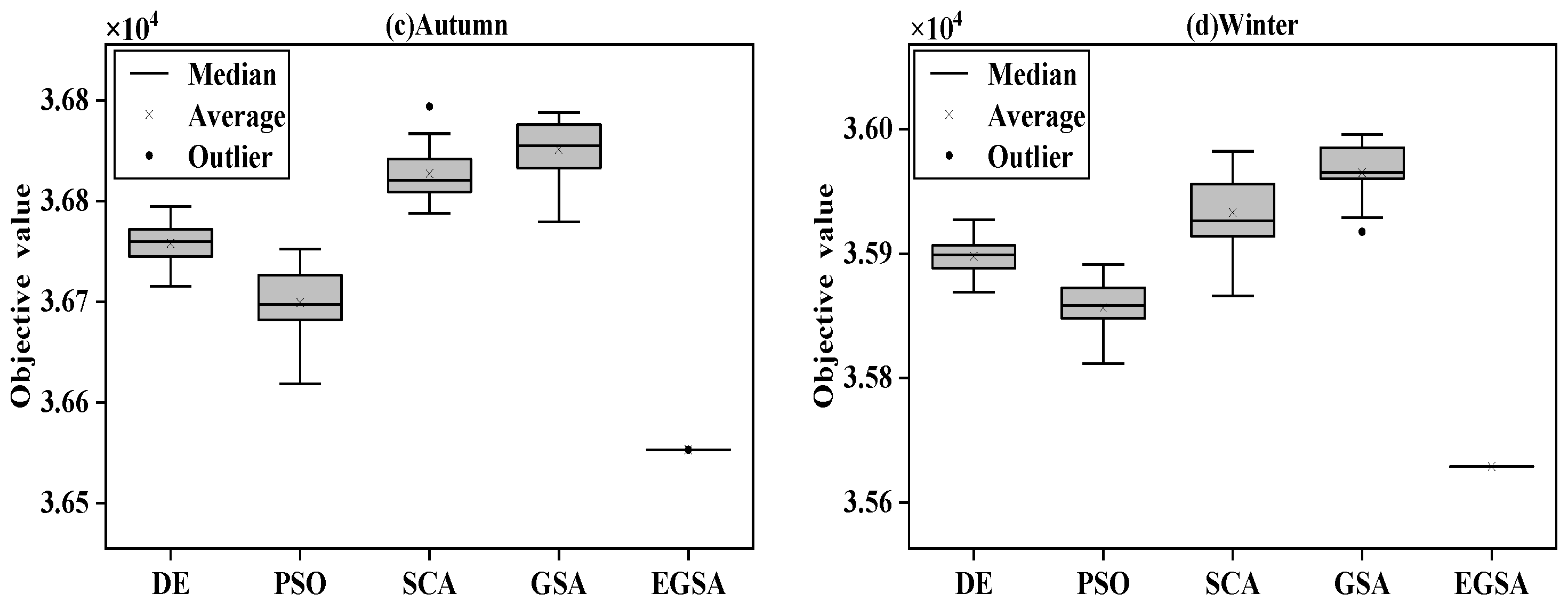
5.3.1. Robustness Testing of Different Evolutionary Algorithms
5.3.2. Comparison of the Optimal Results Obtained by Different Evolutionary Algorithms
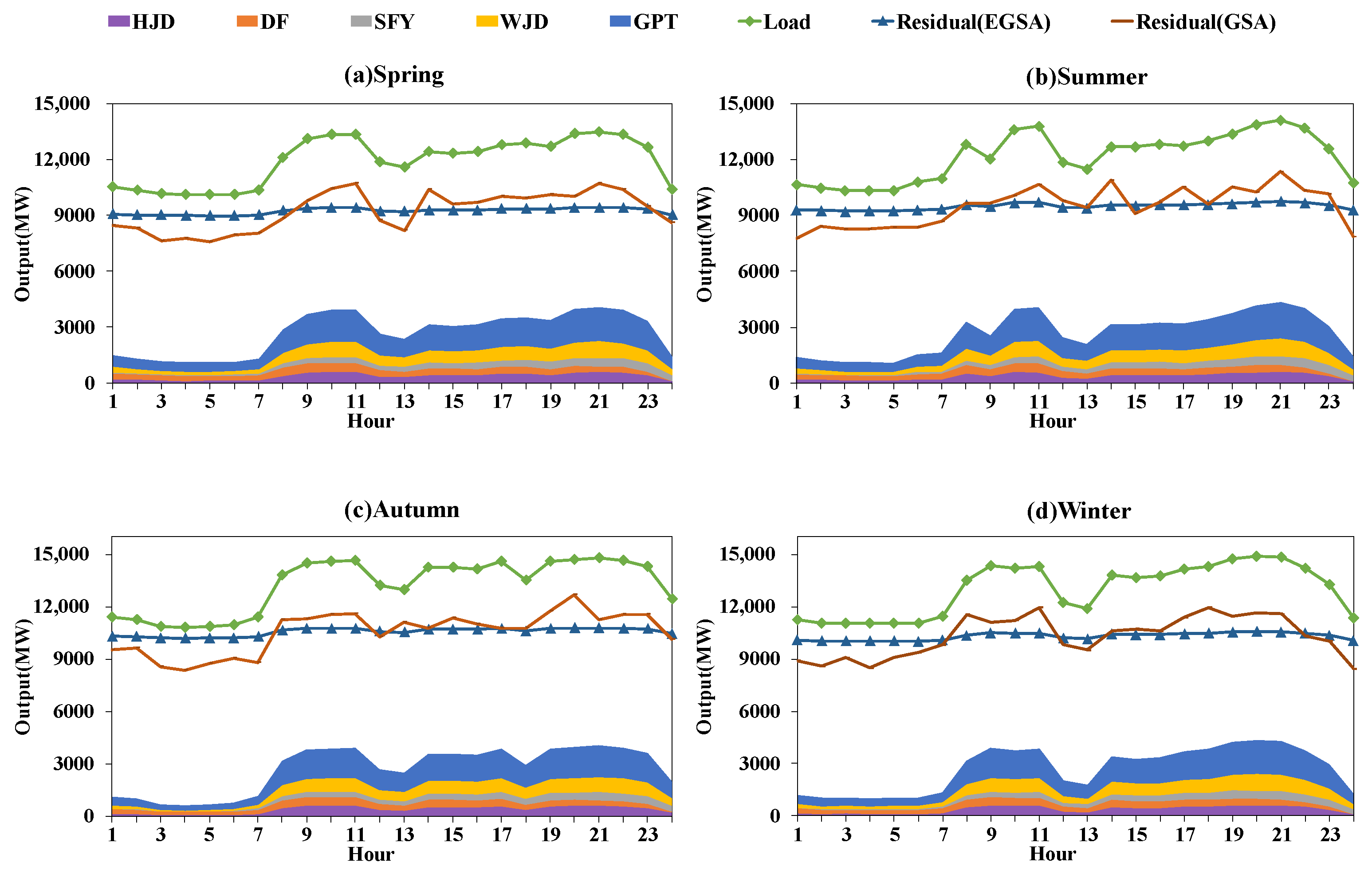
5.3.3. Rationality Analysis of the Best Results Obtained by the Different Evolutionary Algorithms
5.4. Case Study 3: Mutli-Objective Operation of Cascade Hydropower Reservoirs
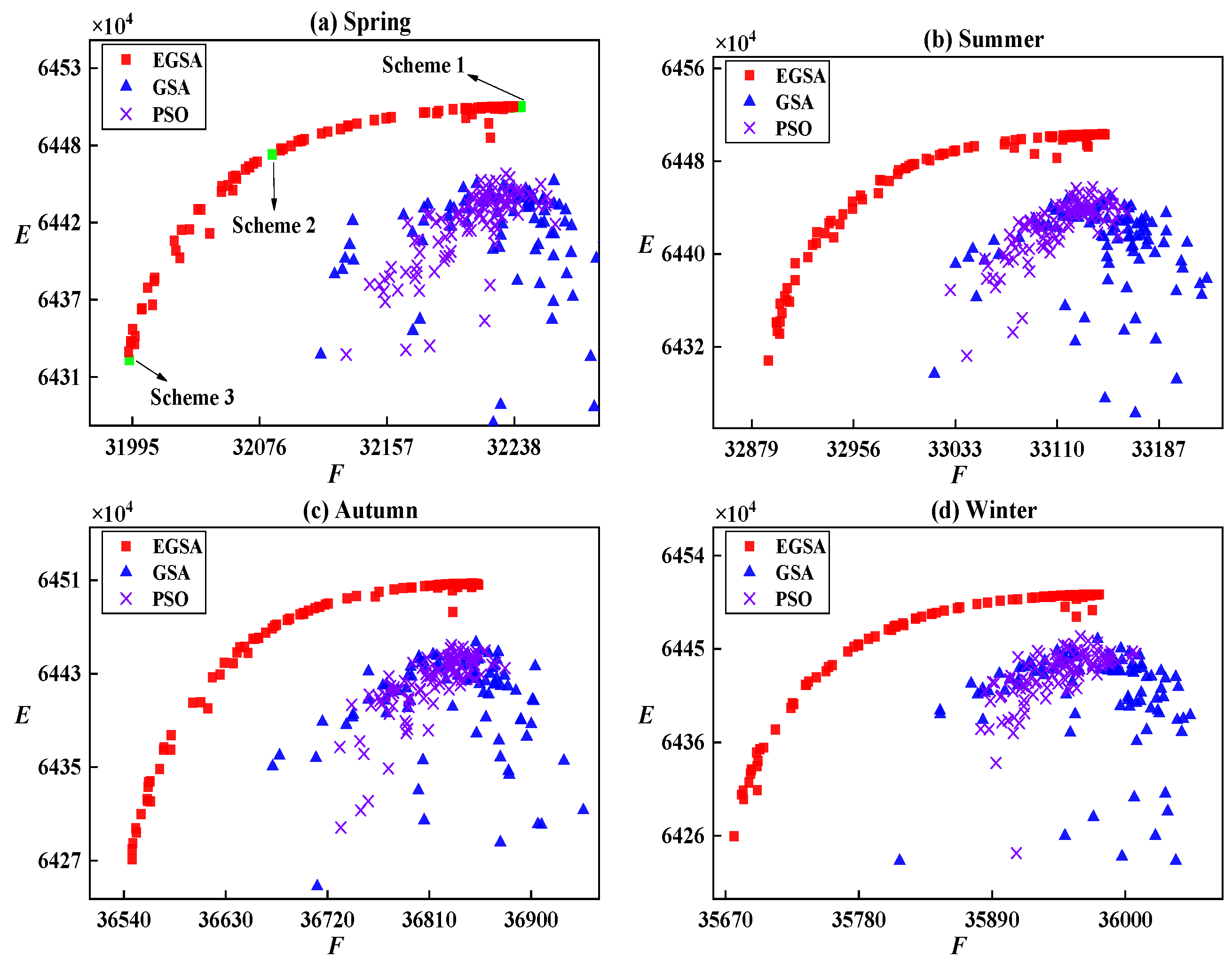
5.4.1. Comparative Analysis of the Optimal Results Obtained by the Different Methods with 100 Weights
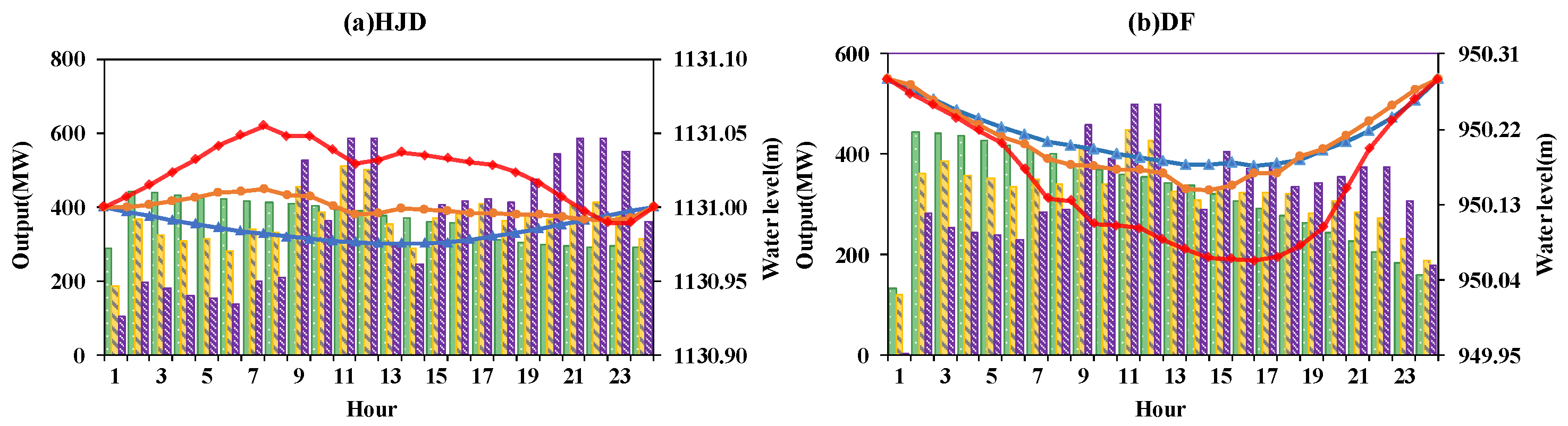
5.4.2. Rationality Analysis of the Best Results Obtained by the Different Evolutionary Algorithms
6. Conclusions
- (1)
- Due to the loss of the population diversity, the conventional GSA method suffered from severe premature convergence shortcomings. The proposed method based on the three modified strategies (opposite learning strategy, partial mutation strategy and elastic-ball modification strategy) could effectively improve the convergence speed, swarm diversity, and solution feasibility of the standard GSA method, respectively.
- (2)
- For the original complex multi-objective optimization problem, balancing power generation and peak operation requirements, the famous TOPSIS method was used to transform it into the relatively simple single-objective problem, which could help make an obvious reduction in the modeling difficulty of the multi-objective decision.
- (3)
- There was a competitive relationship between the generation benefit of the hydropower enterprise and the peak operation of the power system. In other words, an increasing value of one objective would obviously reduce another objective value. Thus, it was necessary for operators to carefully determine the scheduling schemes so as to effectively balance the practical requirements of power generation enterprises and power grid companies.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chang, J.; Li, Y.; Yuan, M.; Wang, Y. Efficiency evaluation of hydropower station operation: A case study of Longyangxia station in the Yellow River, China. Energy 2017, 135, 23–31. [Google Scholar] [CrossRef]
- Feng, M.; Liu, P.; Guo, S.; Gui, Z.; Zhang, X.; Zhang, W.; Xiong, L. Identifying changing patterns of reservoir operating rules under various inflow alteration scenarios. Adv. Water Resour. 2017, 104, 23–36. [Google Scholar] [CrossRef]
- Liu, P.; Li, L.; Chen, G.; Rheinheimer, D.E. Parameter uncertainty analysis of reservoir operating rules based on implicit stochastic optimization. J. Hydrol. 2014, 514, 102–113. [Google Scholar] [CrossRef]
- Zhao, T.; Zhao, J.; Yang, D. Improved dynamic programming for hydropower reservoir operation. J. Water Res. Plan. Manag. 2014, 140, 365–374. [Google Scholar] [CrossRef]
- Liu, S.; Feng, Z.K.; Niu, W.J.; Zhang, H.R.; Song, Z.G. Peak operation problem solving for hydropower reservoirs by elite-guide sine cosine algorithm with Gaussian local search and random mutation. Energies 2019, 12, 2189. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T. China’s large-scale hydropower system: Operation characteristics, modeling challenge and dimensionality reduction possibilities. Renew. Energy 2019, 136, 805–818. [Google Scholar] [CrossRef]
- Bai, T.; Wu, L.; Chang, J.X.; Huang, Q. Multi-Objective Optimal Operation Model of Cascade Reservoirs and Its Application on Water and Sediment Regulation. Water Resour. Manag. 2015, 29, 2751–2770. [Google Scholar] [CrossRef]
- Guo, X.Y.; Ma, C.; Tang, Z.B. Multi-timescale joint optimal dispatch model considering environmental flow requirements for a dewatered river channel: Case study of Jinping cascade hydropower stations. J. Water Res. Plan. Manag. 2018, 144, 05018014. [Google Scholar] [CrossRef]
- Liu, P.; Nguyen, T.D.; Cai, X.; Jiang, X. Finding multiple optimal solutions to optimal load distribution problem in hydropower plant. Energies 2012, 5, 1413–1432. [Google Scholar] [CrossRef]
- Chang, J.; Wang, X.; Li, Y.; Wang, Y.; Zhang, H. Hydropower plant operation rules optimization response to climate change. Energy 2018, 160, 886–897. [Google Scholar] [CrossRef]
- Guo, S.; Chen, J.; Li, Y.; Liu, P.; Li, T. Joint operation of the multi-reservoir system of the Three Gorges and the Qingjiang cascade reservoirs. Energies 2011, 4, 1036–1050. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, Z.; Ji, C.; Sun, P. Contrastive analysis of three parallel modes in multi-dimensional dynamic programming and its application in cascade reservoirs operation. J. Hydrol. 2015, 529, 22–34. [Google Scholar] [CrossRef]
- Reddy, S.; Abhyankar, A.R.; Bijwe, P.R. Reactive power price clearing using multi-objective optimization. Energy 2011, 36, 3579–3589. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Wang, S.; Cheng, C.T.; Jiang, Z.Q.; Qin, H.; Liu, Y. Developing a successive linear programming model for head-sensitive hydropower system operation considering power shortage aspect. Energy 2018, 155, 252–261. [Google Scholar] [CrossRef]
- Catalao, J.P.S.; Mariano, S.J.P.S.; Mendes, V.M.F.; Ferreira, L.A.F.M. Scheduling of head-sensitive cascaded hydro systems: A nonlinear approach. IEEE Trans. Power Syst. 2009, 24, 337–346. [Google Scholar] [CrossRef]
- Jiang, Z.; Wang, C.; Liu, Y.; Feng, Z.; Ji, C.; Zhang, H. Study on the raw water allocation and optimization in shenzhen city, China. Water 2019, 11, 1426. [Google Scholar] [CrossRef]
- Jiang, Z.; Ji, C.; Qin, H.; Feng, Z. Multi-stage progressive optimality algorithm and its application in energy storage operation chart optimization of cascade reservoirs. Energy 2018, 148, 309–323. [Google Scholar] [CrossRef]
- Huang, G.H.; He, L.; Zeng, G.M.; Lu, H.W. Identification of optimal urban solid waste flow schemes under impacts of energy prices. Environ. Eng. Sci. 2008, 25, 685–695. [Google Scholar] [CrossRef]
- Ren, G.; Cao, Y.; Wen, S.; Huang, T.; Zeng, Z. A modified Elman neural network with a new learning rate scheme. Neurocomputing 2018, 286, 11–18. [Google Scholar] [CrossRef]
- Xie, X.; Wen, S.; Zeng, Z.; Huang, T. Memristor-based circuit implementation of pulse-coupled neural network with dynamical threshold generators. Neurocomputing 2018, 284, 10–16. [Google Scholar] [CrossRef]
- Wen, S.; Xie, X.; Yan, Z.; Huang, T.; Zeng, Z. General memristor with applications in multilayer neural networks. Neural Netw. 2018, 103, 142–149. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Gao, X.; Sellars, S.L.; Sorooshian, S. Improving the multi-objective evolutionary optimization algorithm for hydropower reservoir operations in the California Oroville-Thermalito complex. Environ. Model. Softw. 2015, 69, 262–279. [Google Scholar] [CrossRef]
- Xu, B.; Zhong, P.A.; Du, B.; Chen, J.; Liu, W.; Li, J.; Guo, L.; Zhao, Y. Analysis of a stochastic programming model for optimal hydropower system operation under a deregulated electricity market by considering forecasting uncertainty. Water 2018, 10, 885. [Google Scholar] [CrossRef]
- Zhao, T.; Zhao, J. Improved multiple-objective dynamic programming model for reservoir operation optimization. J. Hydroinform. 2014, 16, 1142–1157. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T. Optimizing electrical power production of hydropower system by uniform progressive optimality algorithm based on two-stage search mechanism and uniform design. J. Clean. Prod. 2018, 190, 432–442. [Google Scholar] [CrossRef]
- Catalão, J.P.S.; Mariano, S.J.P.S.; Mendes, V.M.F.; Ferreira, L.A.F.M. Nonlinear optimization method for short-term hydro scheduling considering head-dependency. Eur. Trans. Electr. Power 2010, 20, 172–183. [Google Scholar] [CrossRef]
- Jia, B.; Zhong, P.; Wan, X.; Xu, B.; Chen, J. Decomposition-coordination model of reservoir group and flood storage basin for real-time flood control operation. Hydrol. Res. 2015, 46, 11–25. [Google Scholar] [CrossRef]
- Dong, M.; Wen, S.; Zeng, Z.; Yan, Z.; Huang, T. Sparse fully convolutional network for face labeling. Neurocomputing 2019, 331, 465–472. [Google Scholar] [CrossRef]
- Li, Z.; Dong, M.; Wen, S.; Hu, X.; Zhou, P.; Zeng, Z. CLU-CNNs: Object detection for medical images. Neurocomputing 2019, 350, 53–59. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, S.; Guo, Z.; Huang, T.; Wen, S. Synchronization of memristive neural networks with leakage delay and parameters mismatch via event-triggered control. Neural Netw. 2019, 119, 178–189. [Google Scholar] [CrossRef]
- Zheng, F. Comparing the real-time searching behavior of four differential-evolution variants applied to water-distribution-network design optimization. J. Water Res. Plan. Manag. 2015, 141, 04015016. [Google Scholar] [CrossRef]
- Yang, T.; Asanjan, A.A.; Faridzad, M.; Hayatbini, N.; Gao, X.; Sorooshian, S. An enhanced artificial neural network with a shuffled complex evolutionary global optimization with principal component analysis. Inf. Sci. 2017, 418–419, 302–316. [Google Scholar] [CrossRef]
- Wan, W.; Guo, X.; Lei, X.; Jiang, Y.; Wang, H. A Novel Optimization Method for Multi-Reservoir Operation Policy Derivation in Complex Inter-Basin Water Transfer System. Water Resour. Manag. 2018, 32, 31–51. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T. Optimization of hydropower reservoirs operation balancing generation benefit and ecological requirement with parallel multi-objective genetic algorithm. Energy 2018, 153, 706–718. [Google Scholar] [CrossRef]
- Zheng, F.; Zecchin, A.C.; Maier, H.R.; Simpson, A.R. Comparison of the searching behavior of NSGA-II, SAMODE, and borg MOEAs applied to water distribution system design problems. J. Water Res. Plan. Manag. 2016, 142, 04016017. [Google Scholar] [CrossRef]
- Salkuti, S.R. Short-term electrical load forecasting using hybrid ANN–DE and wavelet transforms approach. Electr. Eng. 2018, 100, 2755–2763. [Google Scholar] [CrossRef]
- Chang, J.X.; Bai, T.; Huang, Q.; Yang, D.W. Optimization of Water Resources Utilization by PSO-GA. Water Resour. Manag. 2013, 27, 3525–3540. [Google Scholar] [CrossRef]
- Ji, Y.; Lei, X.; Cai, S.; Wang, X. Hedging rules for water supply reservoir based on the model of simulation and optimization. Water 2016, 8, 249. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Z.; Wang, X.; Lei, X.; Liu, P.; Feng, M.; Khu, S.T.; Wang, H. A novel method for deriving reservoir operating rules based on flood classification-aggregation-decomposition. J. Hydrol. 2019, 568, 722–734. [Google Scholar] [CrossRef]
- Niu, W.J.; Feng, Z.K.; Cheng, C.T.; Wu, X.Y. A parallel multi-objective particle swarm optimization for cascade hydropower reservoir operation in southwest China. Appl. Soft Comput. J. 2018, 70, 562–575. [Google Scholar] [CrossRef]
- Ming, B.; Chang, J.X.; Huang, Q.; Wang, Y.M.; Huang, S.Z. Optimal Operation of Multi-Reservoir System Based-On Cuckoo Search Algorithm. Water Resour. Manag. 2015, 29, 5671–5687. [Google Scholar] [CrossRef]
- Reddy, S.S.; Panigrahi, B.K.; Debchoudhury, S.; Kundu, R.; Mukherjee, R. Short-term hydro-thermal scheduling using CMA-ES with directed target to best perturbation scheme. Int. J. Bio-Inspired Comput. 2015, 7, 195–208. [Google Scholar] [CrossRef]
- Salkuti, S.R. Short-term optimal hydro-thermal scheduling using clustered adaptive teaching learning based optimization. Int. J. Electr. Comput. Eng. 2019, 9, 3359–3365. [Google Scholar]
- Niu, W.; Feng, Z.; Cheng, C.; Zhou, J. Forecasting daily runoff by extreme learning machine based on quantum-behaved particle swarm optimization. J. Hydrol. Eng. 2018, 23, 04018002. [Google Scholar] [CrossRef]
- Zheng, F.; Zecchin, A.C.; Simpson, A.R. Self-adaptive differential evolution algorithm applied to water distribution system optimization. J. Comput. Civ. Eng. 2013, 27, 148–158. [Google Scholar] [CrossRef]
- Zheng, F.; Simpson, A.R.; Zecchin, A.C. A combined NLP-differential evolution algorithm approach for the optimization of looped water distribution systems. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T. Multi-objective quantum-behaved particle swarm optimization for economic environmental hydrothermal energy system scheduling. Energy 2017, 131, 165–178. [Google Scholar] [CrossRef]
- Bai, T.; Kan, Y.B.; Chang, J.X.; Huang, Q.; Chang, F.J. Fusing feasible search space into PSO for multi-objective cascade reservoir optimization. Appl. Soft Comput. J. 2017, 51, 328–340. [Google Scholar] [CrossRef]
- Rezaei, F.; Safavi, H.R.; Mirchi, A.; Madani, K. f-MOPSO: An alternative multi-objective PSO algorithm for conjunctive water use management. J. Hydro-Environ. Res. 2017, 14, 1–18. [Google Scholar] [CrossRef]
- Reddy, S.S.; Bijwe, P.R. Multi-Objective Optimal Power Flow Using Efficient Evolutionary Algorithm. Int. J. Emerg. Electr. Power Syst. 2017, 18. [Google Scholar] [CrossRef]
- Ji, B.; Yuan, X.; Yuan, Y.; Lei, X.; Fernando, T.; Iu, H.H.C. Exact and heuristic methods for optimizing lock-quay system in inland waterway. Eur. J. Oper. Res. 2019, 277, 740–755. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. Adaptive gbest-guided gravitational search algorithm. Neural Comput. Appl. 2014, 25, 1569–1584. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Niu, W.J.; Feng, Z.K.; Zeng, M.; Feng, B.F.; Min, Y.W.; Cheng, C.T.; Zhou, J.Z. Forecasting reservoir monthly runoff via ensemble empirical mode decomposition and extreme learning machine optimized by an improved gravitational search algorithm. Appl. Soft Comput. J. 2019, 82, 105589. [Google Scholar] [CrossRef]
- Tian, H.; Yuan, X.; Ji, B.; Chen, Z. Multi-objective optimization of short-term hydrothermal scheduling using non-dominated sorting gravitational search algorithm with chaotic mutation. Energy Convers. Manag. 2014, 81, 504–519. [Google Scholar] [CrossRef]
- Mahootchi, M.; Tizhoosh, H.R.; Ponnambalam, K. Oppositional extension of reinforcement learning techniques. Inf. Sci. 2014, 275, 101–114. [Google Scholar] [CrossRef]
- Mahdavi, S.; Rahnamayan, S.; Deb, K. Opposition based learning: A literature review. Swarm Evol. Comput. 2018, 39, 1–23. [Google Scholar] [CrossRef]
- Ewees, A.A.; Abd Elaziz, M.; Houssein, E.H. Improved grasshopper optimization algorithm using opposition-based learning. Expert Syst. Appl. 2018, 112, 156–172. [Google Scholar] [CrossRef]
- Xia, Y.; Feng, Z.; Niu, W.; Qin, H.; Jiang, Z.; Zhou, J. Simplex quantum-behaved particle swarm optimization algorithm with application to ecological operation of cascade hydropower reservoirs. Appl. Soft Comput. 2019, 84, 105715. [Google Scholar] [CrossRef]
- Chen, Z.; Yuan, X.; Tian, H.; Ji, B. Improved gravitational search algorithm for parameter identification of water turbine regulation system. Energy Convers. Manag. 2014, 78, 306–315. [Google Scholar] [CrossRef]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Yang, X.; Deb, S. Cuckoo Search via Lévy Flights; IEEE: Piscataway, NJ, USA, 2009; pp. 210–214. [Google Scholar]
- Walton, S.; Hassan, O.; Morgan, K.; Brown, M.R. Modified cuckoo search: A new gradient free optimisation algorithm. Chaos Solitons Fractals 2011, 44, 710–718. [Google Scholar] [CrossRef]
- Shareef, H.; Ibrahim, A.A.; Mutlag, A.H. Lightning search algorithm. Appl. Soft Comput. 2015, 36, 315–333. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly Algorithm in Engineering Optimization; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Hua, Z.; Ma, C.; Lian, J.; Pang, X.; Yang, W. Optimal capacity allocation of multiple solar trackers and storage capacity for utility-scale photovoltaic plants considering output characteristics and complementary demand. Appl. Energy 2019, 238, 721–733. [Google Scholar] [CrossRef]
- Reddy, S.S.; Bijwe, P.R.; Abhyankar, A.R. Optimal dynamic emergency reserve activation using spinning, hydro and demand-side reserves. Front. Energy 2016, 10, 409–423. [Google Scholar] [CrossRef]
- Reddy, S.S.; Bijwe, P.R. Real time economic dispatch considering renewable energy resources. Renew. Energy 2015, 83, 1215–1226. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Zhang, R.; Wang, S.; Cheng, C.T. Operation rule derivation of hydropower reservoir by k-means clustering method and extreme learning machine based on particle swarm optimization. J. Hydrol. 2019, 576, 229–238. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T.; Wu, X.Y. Optimization of hydropower system operation by uniform dynamic programming for dimensionality reduction. Energy 2017, 134, 718–730. [Google Scholar] [CrossRef]
- Zhang, C.; Ding, W.; Li, Y.; Meng, F.; Fu, G. Cost-Benefit Framework for Optimal Design of Water Transfer Systems. J. Water Res. Plan. Manag. 2019, 145, 04019007. [Google Scholar] [CrossRef]
- Li, H.; Chen, D.; Arzaghi, E.; Abbassi, R.; Xu, B.; Patelli, E.; Tolo, S. Safety assessment of hydro-generating units using experiments and grey-entropy correlation analysis. Energy 2018, 165, 222–234. [Google Scholar] [CrossRef]
- Chen, D.; Liu, S.; Ma, X. Modeling, nonlinear dynamical analysis of a novel power system with random wind power and it’s control. Energy 2013, 53, 139–146. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, D.; Ma, X. Nonlinear predictive control of a hydropower system model. Entropy-Switz 2015, 17, 6129–6149. [Google Scholar] [CrossRef]
- Feng, Z.; Niu, W.; Wang, W.; Zhou, J.; Cheng, C. A mixed integer linear programming model for unit commitment of thermal plants with peak shaving operation aspect in regional power grid lack of flexible hydropower energy. Energy 2019, 175, 618–629. [Google Scholar] [CrossRef]
- Feng, Z.; Niu, W.; Wang, S.; Cheng, C.; Song, Z. Mixed integer linear programming model for peak operation of gas-fired generating units with disjoint-prohibited operating zones. Energies 2019, 12, 2179. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T.; Zhou, J.Z. Peak shaving operation of hydro-thermal-nuclear plants serving multiple power grids by linear programming. Energy 2017, 135, 210–219. [Google Scholar] [CrossRef]
- Niu, W.J.; Feng, Z.K.; Feng, B.F.; Min, Y.W.; Cheng, C.T.; Zhou, J.Z. Comparison of multiple linear regression, artificial neural network, extreme learning machine, and support vector machine in deriving operation rule of hydropower reservoir. Water 2019, 11, 88. [Google Scholar] [CrossRef]
- Ma, C.; Lian, J.; Wang, J. Short-term optimal operation of Three-gorge and Gezhouba cascade hydropower stations in non-flood season with operation rules from data mining. Energy Convers. Manag. 2013, 65, 616–627. [Google Scholar] [CrossRef]
- Jiang, Z.; Liu, P.; Ji, C.; Zhang, H.; Chen, Y. Ecological flow considered multi-objective sorage energy operation chart optimization of large-scale mixed reservoirs. J. Hydrol. 2019, 577, 123949. [Google Scholar] [CrossRef]
- Lian, J.; Yao, Y.; Ma, C.; Guo, Q. Reservoir operation rules for controlling algal blooms in a tributary to the impoundment of three Gorges Dam. Water 2014, 6, 3200–3223. [Google Scholar] [CrossRef]
- Fu, W.; Wang, K.; Zhang, C.; Tan, J. A hybrid approach for measuring the vibrational trend of hydroelectric unit with enhanced multi-scale chaotic series analysis and optimized least squares support vector machine. Trans. Inst. Meas. Control 2019, 41, 4436–4449. [Google Scholar] [CrossRef]



| Function | D | Range | fmin |
|---|---|---|---|
| 30 | [−100,100] | 0 | |
| 30 | [−10,10] | 0 | |
| 30 | [−100,100] | 0 | |
| 30 | [−100,100] | 0 | |
| 30 | [−30,30] | 0 | |
| 30 | [−100,100] | 0 | |
| 30 | [−1.28,1.28] | 0 | |
| 30 | [−500,500] | −418.9 × D | |
| 30 | [−5.12,5.12] | 0 | |
| 30 | [−32,32] | 0 | |
| 30 | [−600,600] | 0 | |
| 30 | [−50,50] | 0 |
| Function | Item | CS | MCS | LSA | GWO | FA | WOA | ALO | DE | PSO | SCA | GSA | EGSA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Ave. | 9.06 × 101 | 1.01 × 100 | 4.81 × 10−8 | 6.59 × 10−28 | 1.20 × 10−2 | 1.41 × 10−30 | 2.59 × 10−10 | 7.80 × 10−6 | 4.58 × 10−7 | 2.87 × 10−35 | 4.00 × 10−9 | 6.96 × 10−134 |
| Std. | 2.62 × 101 | 2.72 × 10−1 | 3.40 × 10−7 | 6.34 × 10−5 | 4.30 × 10−3 | 4.91 × 10−30 | 1.65 × 10−10 | 3.14 × 10−6 | 3.51 × 10−7 | 1.26 × 10−34 | 2.92 × 10−9 | 3.70 × 10−133 | |
| F2 | Ave. | 9.70 × 100 | 1.81 × 10−1 | 3.68 × 10−2 | 7.18 × 10−17 | 3.73 × 10−1 | 1.06 × 10−21 | 1.84 × 10−6 | 3.73 × 10−4 | 1.19 × 10−4 | 2.21 × 10−27 | 5.48 × 10−5 | 5.21 × 10−69 |
| Std. | 1.98 × 100 | 3.31 × 10−2 | 1.56 × 10−1 | 2.90 × 10−2 | 1.01 × 10−1 | 2.39 × 10−21 | 6.58 × 10−7 | 9.05 × 10−5 | 8.03 × 10−5 | 6.99 × 10−27 | 2.24 × 10−5 | 2.09 × 10−68 | |
| F3 | Ave. | 3.84 × 103 | 4.62 × 102 | 4.32 × 101 | 3.29 × 10−6 | 1.81 × 103 | 5.39 × 10−7 | 6.06 × 10−10 | 2.94 × 104 | 2.33 × 100 | 9.74 × 101 | 3.61 × 102 | 4.30 × 10−119 |
| Std. | 7.24 × 102 | 1.23 × 102 | 2.99 × 101 | 7.91 × 101 | 6.60 × 102 | 2.93 × 10−6 | 6.34 × 10−10 | 4.13 × 103 | 1.14 × 100 | 2.24 × 102 | 1.45 × 102 | 2.29 × 10−118 | |
| F4 | Ave. | 7.23 × 100 | 1.73 × 100 | 1.49 × 100 | 5.61 × 10−7 | 7.67 × 10−2 | 7.26 × 10−2 | 1.36 × 10−8 | 1.43 × 100 | 5.35 × 10−1 | 2.66 × 100 | 9.48 × 10−2 | 5.58 × 10−70 |
| Std. | 6.76 × 10−1 | 5.12 × 10−1 | 1.30 × 100 | 1.32 × 100 | 1.46 × 10−2 | 3.97 × 10−1 | 1.81 × 10−9 | 3.21 × 10−1 | 1.33 × 10−1 | 4.16 × 100 | 3.92 × 10−1 | 2.12 × 10−69 | |
| F5 | Ave. | 4.98 × 100 | 5.81 × 101 | 6.43 × 101 | 2.68 × 101 | 1.28 × 102 | 2.79 × 101 | 3.47 × 10−1 | 4.45 × 102 | 1.64 × 102 | 2.74 × 101 | 3.45 × 101 | 2.69 × 101 |
| Std. | 1.75 × 100 | 3.31 × 101 | 4.38 × 101 | 6.99 × 101 | 2.79 × 102 | 7.64 × 10−1 | 1.10 × 10−1 | 1.55 × 102 | 1.55 × 102 | 3.85 × 10−1 | 3.65 × 101 | 9.72 × 10−2 | |
| F6 | Ave. | 4.31 × 104 | 4.44 × 103 | 3.34 × 100 | 8.17 × 10−1 | 0 | 3.12 × 100 | 2.56 × 10−10 | 7.94 × 10−6 | 9.29 × 10−7 | 5.30 × 10−2 | 4.99 × 10−9 | 8.23 × 10−15 |
| Std. | 7.21 × 103 | 7.52 × 102 | 2.09 × 100 | 1.26 × 10−4 | 0 | 5.32 × 10−1 | 1.09 × 10−10 | 3.39 × 10−6 | 1.93 × 10−6 | 4.98 × 10−2 | 3.74 × 10−9 | 4.61 × 10−15 | |
| F7 | Ave. | 2.46 × 10−2 | 9.10 × 10−3 | 2.41 × 10−2 | 2.21 × 10−3 | 3.52 × 10−2 | 1.43 × 10−3 | 4.29 × 10−3 | 1.35 × 10−1 | 3.55 × 100 | 7.48 × 10−3 | 3.05 × 10−2 | 4.76 × 10−4 |
| Std. | 7.90 × 10−3 | 2.20 × 10−3 | 5.72 × 10−3 | 1.00 × 10−1 | 2.40 × 10−2 | 1.15 × 10−3 | 5.09 × 10−3 | 2.93 × 10−2 | 4.79 × 100 | 6.96 × 10−3 | 1.59 × 10−2 | 2.32 × 10−4 | |
| F8 | Ave. | −8.98 × 103 | −9.80 × 103 | −8.00 × 103 | −6.12 × 103 | −5.90 × 103 | −5.08 × 103 | −1.61 × 103 | −7.95 × 103 | −6.39 × 103 | −5.66 × 103 | −2.75 × 103 | −1.19 × 104 |
| Std. | 1.98 × 102 | 5.31 × 102 | 6.69 × 102 | 4.09 × 103 | 6.56 × 102 | 6.96 × 102 | 3.14 × 102 | 3.33 × 102 | 1.29 × 103 | 3.52 × 102 | 4.00 × 102 | 3.13 × 102 | |
| F9 | Ave. | 2.94 × 102 | 1.35 × 102 | 6.28 × 101 | 3.11 × 10−1 | 2.63 × 101 | 0 | 7.71 × 10−6 | 1.32 × 102 | 7.87 × 101 | 1.87 × 10−9 | 1.67 × 101 | 0 |
| Std. | 1.43 × 101 | 2.16 × 101 | 1.49 × 101 | 4.74 × 101 | 9.15 × 100 | 0 | 8.45 × 10−6 | 8.78 × 100 | 2.91 × 101 | 1.02 × 10−8 | 3.82 × 100 | 0 | |
| F10 | Ave. | 1.93 × 101 | 1.21 × 101 | 2.69 × 100 | 1.06 × 10−13 | 5.12 × 10−2 | 7.40 × 100 | 3.73 × 10−15 | 1.37 × 10−3 | 5.99 × 10−4 | 1.34 × 101 | 3.25 × 10−5 | 3.64 × 10−15 |
| Std. | 3.50 × 10−1 | 7.52 × 10−1 | 9.11 × 10−1 | 7.78 × 10−2 | 1.37 × 10−2 | 9.90 × 100 | 1.50 × 10−15 | 8.85 × 10−4 | 5.43 × 10−4 | 9.64 × 100 | 1.10 × 10−5 | 1.08 × 10−15 | |
| F11 | Ave. | 2.12 × 102 | 8.32 × 100 | 7.24 × 10−3 | 4.49 × 10−3 | 5.84 × 10−3 | 2.89 × 10−4 | 1.86 × 10−2 | 3.36 × 10−3 | 6.98 × 10−3 | 1.86 × 10−5 | 4.34 × 100 | 0 |
| Std. | 3.97 × 101 | 1.54 × 100 | 6.70 × 10−3 | 6.66 × 10−3 | 1.43 × 10−3 | 1.59 × 10−3 | 9.55 × 10−3 | 1.06 × 10−2 | 8.16 × 10−3 | 1.02 × 10−4 | 1.66 × 100 | 0 | |
| F12 | Ave. | 1.47 × 100 | 1.38 × 10−1 | 3.58 × 10−1 | 5.34 × 10−2 | 2.40 × 10−4 | 3.40 × 10−1 | 9.74 × 10−12 | 6.87 × 10−1 | 2.01 × 10−2 | 8.52 × 10−3 | 9.59 × 10−2 | 5.30 × 10−17 |
| Std. | 3.61 × 10−1 | 2.86 × 10−1 | 7.44 × 10−1 | 2.07 × 10−2 | 1.00 × 10−4 | 2.15 × 10−1 | 9.33 × 10−12 | 3.05 × 10−1 | 2.26 × 10−2 | 4.69 × 10−3 | 1.75 × 10−1 | 1.92 × 10−17 |
| Function | EGSA–CS | EGSA–MCS | EGSA–LSA | EGSA–GWO | EGSA–FA | EGSA–WOA | EGSA–ALO | EGSA–DE | EGSA–PSO | EGSA–SCA | EGSA–GSA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA |
| F2 | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA |
| F3 | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA |
| F4 | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA |
| F5 | CS | EGSA | EGSA | GWO | EGSA | EGSA | ALO | EGSA | EGSA | EGSA | EGSA |
| F6 | EGSA | EGSA | EGSA | EGSA | FA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA |
| F7 | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA |
| F8 | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA |
| F9 | EGSA | EGSA | EGSA | EGSA | EGSA | Tie | EGSA | EGSA | EGSA | EGSA | EGSA |
| F10 | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA |
| F11 | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA |
| F12 | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA | EGSA |
| W/T/L | 11/0/1 | 12/0/0 | 12/0/0 | 11/0/1 | 11/0/1 | 11/1/0 | 11/0/1 | 12/0/0 | 12/0/0 | 12/0/0 | 12/0/0 |
| Item | EGSA–CS | EGSA–MCS | EGSA–LSA | EGSA–GWO | EGSA–FA | EGSA–WOA | EGSA–ALO | EGSA–DE | EGSA–PSO | EGSA–SCA | EGSA–GSA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| R+ | 72 | 78 | 78 | 70 | 77 | 77.5 | 67 | 78 | 78 | 78 | 78 |
| R− | 6 | 0 | 0 | 8 | 1 | 0.5 | 11 | 0 | 0 | 0 | 0 |
| p-value | 6.84 × 10−3 | 4.88 × 10−4 | 4.88 × 10−4 | 1.22 × 10−2 | 9.77 × 10−4 | 9.77 × 10−4 | 2.69 × 10−2 | 4.88 × 10−4 | 4.88 × 10−4 | 4.88 × 10−4 | 4.88 × 10−4 |
| Significant | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Case | Method | Best | Worst | Average | Standard Deviation | Range |
|---|---|---|---|---|---|---|
| Case 1 | DE | 5388.10 | 5386.25 | 5387.19 | 0.56 | 1.85 |
| PSO | 5393.67 | 5391.27 | 5392.49 | 0.57 | 2.40 | |
| SCA | 5388.26 | 5384.34 | 5385.65 | 0.89 | 3.92 | |
| GSA | 5388.37 | 5385.34 | 5386.76 | 0.88 | 3.03 | |
| EGSA | 5396.87 | 5396.81 | 5396.86 | 0.02 | 0.06 | |
| Case 2 | DE | 6439.12 | 6434.22 | 6436.14 | 1.43 | 4.90 |
| PSO | 6445.48 | 6442.35 | 6444.12 | 0.79 | 3.13 | |
| SCA | 6439.06 | 6435.25 | 6437.07 | 1.03 | 3.81 | |
| GSA | 6440.17 | 6437.00 | 6438.55 | 0.79 | 3.17 | |
| EGSA | 6450.34 | 6450.33 | 6450.33 | 0.01 | 0.01 | |
| Case3 | DE | 4977.94 | 4976.38 | 4977.17 | 0.40 | 1.56 |
| PSO | 4981.62 | 4979.71 | 4980.58 | 0.55 | 1.91 | |
| SCA | 4975.51 | 4973.58 | 4974.54 | 0.58 | 1.93 | |
| GSA | 4976.74 | 4973.83 | 4975.25 | 0.71 | 2.91 | |
| EGSA | 4984.56 | 4984.54 | 4984.55 | 0.01 | 0.02 | |
| Case4 | DE | 4433.08 | 4431.68 | 4432.32 | 0.44 | 1.40 |
| PSO | 4435.89 | 4434.23 | 4435.11 | 0.49 | 1.66 | |
| SCA | 4431.51 | 4428.62 | 4429.58 | 0.70 | 2.89 | |
| GSA | 4431.61 | 4429.07 | 4430.37 | 0.64 | 2.54 | |
| EGSA | 4438.33 | 4438.32 | 4438.33 | 0.01 | 0.01 |
| Runoff | Method | HJD | DF | SFY | WJD | GPT | Sum |
|---|---|---|---|---|---|---|---|
| Case 1 | DE | 726.73 | 646.19 | 527.41 | 1106.65 | 2381.12 | 5388.10 |
| PSO | 728.66 | 647.76 | 526.51 | 1107.99 | 2382.75 | 5393.67 | |
| SCA | 727.92 | 644.60 | 527.68 | 1106.77 | 2381.29 | 5388.26 | |
| GSA | 728.35 | 647.35 | 526.77 | 1107.15 | 2378.75 | 5388.37 | |
| EGSA | 728.84 | 646.94 | 530.33 | 1108.10 | 2382.66 | 5396.87 | |
| Case 2 | DE | 869.46 | 770.94 | 632.25 | 1322.47 | 2844.00 | 6439.12 |
| PSO | 871.70 | 774.09 | 627.59 | 1325.38 | 2846.72 | 6445.48 | |
| SCA | 871.15 | 771.70 | 628.34 | 1322.76 | 2845.11 | 6439.06 | |
| GSA | 871.48 | 774.01 | 627.42 | 1324.03 | 2843.23 | 6440.17 | |
| EGSA | 871.58 | 773.17 | 633.84 | 1324.91 | 2846.84 | 6450.34 | |
| Case 3 | DE | 234.57 | 400.46 | 461.27 | 1052.33 | 2829.31 | 4977.94 |
| PSO | 235.21 | 402.56 | 459.19 | 1054.13 | 2830.53 | 4981.62 | |
| SCA | 233.99 | 401.01 | 459.94 | 1052.01 | 2828.56 | 4975.51 | |
| GSA | 235.02 | 402.45 | 457.71 | 1053.20 | 2828.36 | 4976.74 | |
| EGSA | 235.50 | 401.67 | 462.62 | 1054.23 | 2830.54 | 4984.56 | |
| Case 4 | DE | 208.46 | 355.81 | 411.02 | 936.99 | 2520.8 | 4433.08 |
| PSO | 208.58 | 358.21 | 409.24 | 938.46 | 2521.4 | 4435.89 | |
| SCA | 208.26 | 356.74 | 409.21 | 937.08 | 2520.22 | 4431.51 | |
| GSA | 208.82 | 357.66 | 408.43 | 937.47 | 2519.23 | 4431.61 | |
| EGSA | 209.13 | 357.35 | 411.88 | 938.51 | 2521.46 | 4438.33 |
| Season | Item | Best | Worst | Average | Standard Deviation | Range |
|---|---|---|---|---|---|---|
| Spring | DE | 32,130.69 | 32,183.80 | 32,153.90 | 16.22 | 53.11 |
| PSO | 32,052.91 | 32,127.22 | 32,084.17 | 20.24 | 74.31 | |
| SCA | 32,160.67 | 32,230.89 | 32,194.00 | 22.32 | 70.22 | |
| GSA | 32,173.70 | 32,224.22 | 32,199.76 | 14.41 | 50.52 | |
| EGSA | 31,986.47 | 31,986.62 | 31,986.53 | 0.04 | 0.15 | |
| Summer | DE | 33,006.63 | 33,093.05 | 33,051.56 | 23.51 | 86.42 |
| PSO | 32,962.41 | 33,057.03 | 32,993.63 | 22.72 | 94.62 | |
| SCA | 33,032.40 | 33,129.77 | 33,100.08 | 24.05 | 97.37 | |
| GSA | 33,069.24 | 33,134.56 | 33,097.29 | 19.83 | 65.32 | |
| EGSA | 32,888.05 | 32,888.16 | 32,888.10 | 0.03 | 0.11 | |
| Autumn | DE | 36,681.47 | 36,752.01 | 36,719.49 | 17.51 | 70.54 |
| PSO | 36,595.43 | 36,714.71 | 36,667.14 | 30.32 | 119.28 | |
| SCA | 36,745.91 | 36,840.43 | 36,781.14 | 24.73 | 94.52 | |
| GSA | 36,738.72 | 36,835.34 | 36,802.57 | 27.25 | 96.62 | |
| EGSA | 36,536.95 | 36,537.06 | 36,537.00 | 0.03 | 0.11 | |
| Winter | DE | 35,825.89 | 35,890.14 | 35,857.52 | 14.79 | 64.25 |
| PSO | 35,762.63 | 35,850.26 | 35,811.97 | 23.97 | 87.63 | |
| SCA | 35,822.72 | 35,950.51 | 35,896.25 | 32.32 | 127.79 | |
| GSA | 35,879.31 | 35,965.39 | 35,931.63 | 22.63 | 86.08 | |
| EGSA | 35,671.70 | 35,671.80 | 35,671.74 | 0.03 | 0.10 |
| Season | Method | Item | Peak | Valley | Peak-valley | Average | Standard Deviation |
|---|---|---|---|---|---|---|---|
| Spring | Original | 13,477.93 | 10,101.60 | 3376.33 | 11,910.93 | 1281.95 | |
| DE | Optimization | 10,952.90 | 7716.77 | 3236.13 | 9242.92 | 789.32 | |
| Reduction | 2525.03 | 2384.83 | 140.20 | 2668.01 | 492.63 | ||
| PSO | Optimization | 10,050.98 | 8169.90 | 1881.08 | 9231.64 | 640.11 | |
| Reduction | 3426.95 | 1931.7 | 1495.25 | 2679.29 | 641.84 | ||
| SCA | Optimization | 10,752.18 | 7809.30 | 2942.88 | 9239.61 | 926.13 | |
| Reduction | 2725.75 | 2292.3 | 433.45 | 2671.32 | 355.82 | ||
| GSA | Optimization | 10,737.30 | 7592.29 | 3145.01 | 9229.75 | 1058.60 | |
| Reduction | 2740.63 | 2509.31 | 231.32 | 2681.18 | 223.35 | ||
| EGSA | Optimization | 9428.01 | 8987.22 | 440.79 | 9232.28 | 165.13 | |
| Reduction | 4049.92 | 1114.38 | 2935.54 | 2678.65 | 1116.82 | ||
| Summer | Original | 14,119.78 | 10,342.98 | 3776.80 | 12,170.94 | 1302.21 | |
| DE | Optimization | 11,151.13 | 8535.00 | 2616.13 | 9505.54 | 670.54 | |
| Reduction | 2968.65 | 1807.98 | 1160.67 | 2665.40 | 631.67 | ||
| PSO | Optimization | 10,610.47 | 8392.24 | 2218.23 | 9492.57 | 673.27 | |
| Reduction | 3509.31 | 1950.74 | 1558.57 | 2678.37 | 628.94 | ||
| SCA | Optimization | 10,749.92 | 7591.09 | 3158.83 | 9500.12 | 839.87 | |
| Reduction | 3369.86 | 2751.89 | 617.97 | 2670.82 | 462.34 | ||
| GSA | Optimization | 11,379.10 | 7774.71 | 3604.39 | 9493.04 | 1028.32 | |
| Reduction | 2740.68 | 2568.27 | 172.41 | 2677.90 | 273.89 | ||
| EGSA | Optimization | 9759.71 | 9234.99 | 524.72 | 9492.46 | 172.66 | |
| Reduction | 4360.07 | 1107.99 | 3252.08 | 2678.48 | 1129.55 | ||
| Autumn | Original | 14,773.84 | 10,786.00 | 3987.84 | 13,220.16 | 1528.83 | |
| DE | Optimization | 12,615.24 | 8928.53 | 3686.71 | 10,553.86 | 880.28 | |
| Reduction | 2158.6 | 1857.5 | 301.1 | 2666.3 | 648.6 | ||
| PSO | Optimization | 11,234.24 | 9366.35 | 1867.89 | 10,547.10 | 613.62 | |
| Reduction | 3539.6 | 1419.65 | 2119.95 | 2673.06 | 915.21 | ||
| SCA | Optimization | 11,891.57 | 8142.23 | 3749.34 | 10,552.90 | 1099.32 | |
| Reduction | 2882.27 | 2643.77 | 238.50 | 2667.26 | 429.51 | ||
| GSA | Optimization | 12,649.33 | 8347.14 | 4302.19 | 10,541.04 | 1193.12 | |
| Reduction | 2124.51 | 2438.86 | −314.35 | 2679.12 | 335.71 | ||
| EGSA | Optimization | 10,760.16 | 10,182.25 | 577.91 | 10,545.07 | 221.99 | |
| Reduction | 4013.68 | 603.75 | 3409.93 | 2675.09 | 1306.84 | ||
| Winter | Original | 14,913.26 | 11,028.24 | 3885.02 | 12,971.28 | 1489.76 | |
| DE | Optimization | 11,709.53 | 8772.72 | 2936.81 | 10,303.38 | 955.49 | |
| Reduction | 3203.73 | 2255.52 | 948.21 | 2667.90 | 534.27 | ||
| PSO | Optimization | 11,884.52 | 8637.32 | 3247.20 | 10,293.13 | 970.91 | |
| Reduction | 3028.74 | 2390.92 | 637.82 | 2678.15 | 518.85 | ||
| SCA | Optimization | 12,391.09 | 8667.77 | 3723.32 | 10,301.54 | 1052.86 | |
| Reduction | 2522.17 | 2360.47 | 161.70 | 2669.74 | 436.90 | ||
| GSA | Optimization | 11,946.42 | 8414.17 | 3532.25 | 10,293.50 | 1174.01 | |
| Reduction | 2966.84 | 2614.07 | 352.77 | 2677.78 | 315.75 | ||
| EGSA | Optimization | 10,568.93 | 10,012.57 | 556.36 | 10,295.50 | 208.98 | |
| Reduction | 4344.33 | 1015.67 | 3328.66 | 2675.78 | 1280.78 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Z.-k.; Liu, S.; Niu, W.-j.; Jiang, Z.-q.; Luo, B.; Miao, S.-m. Multi-Objective Operation of Cascade Hydropower Reservoirs Using TOPSIS and Gravitational Search Algorithm with Opposition Learning and Mutation. Water 2019, 11, 2040. https://doi.org/10.3390/w11102040
Feng Z-k, Liu S, Niu W-j, Jiang Z-q, Luo B, Miao S-m. Multi-Objective Operation of Cascade Hydropower Reservoirs Using TOPSIS and Gravitational Search Algorithm with Opposition Learning and Mutation. Water. 2019; 11(10):2040. https://doi.org/10.3390/w11102040
Chicago/Turabian StyleFeng, Zhong-kai, Shuai Liu, Wen-jing Niu, Zhi-qiang Jiang, Bin Luo, and Shu-min Miao. 2019. "Multi-Objective Operation of Cascade Hydropower Reservoirs Using TOPSIS and Gravitational Search Algorithm with Opposition Learning and Mutation" Water 11, no. 10: 2040. https://doi.org/10.3390/w11102040
APA StyleFeng, Z.-k., Liu, S., Niu, W.-j., Jiang, Z.-q., Luo, B., & Miao, S.-m. (2019). Multi-Objective Operation of Cascade Hydropower Reservoirs Using TOPSIS and Gravitational Search Algorithm with Opposition Learning and Mutation. Water, 11(10), 2040. https://doi.org/10.3390/w11102040





