A Stochastic Approach for the Analysis of Long Dry Spells with Different Threshold Values in Southern Italy
Abstract
1. Introduction
2. Materials and Methods
3. Application
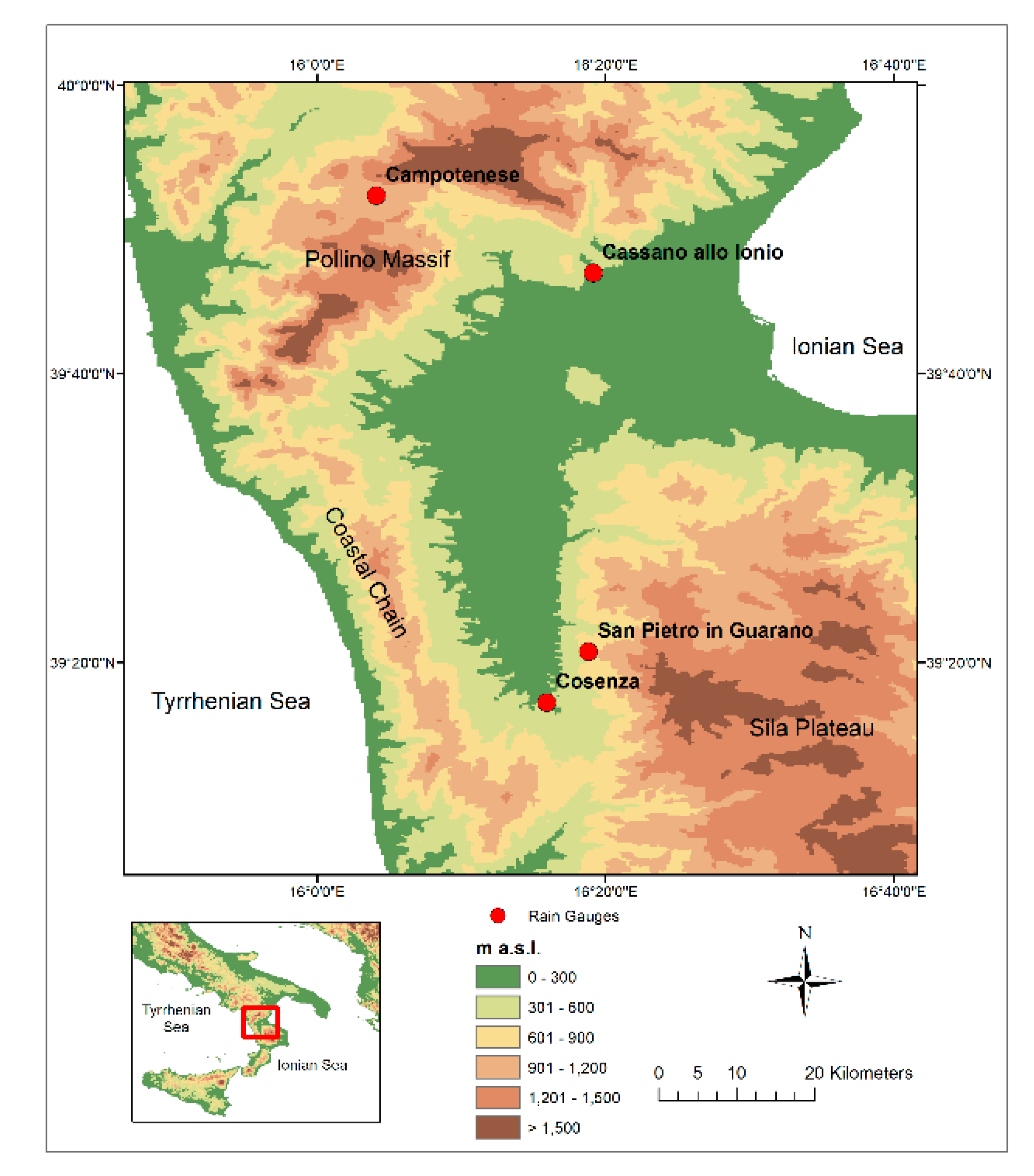
3.1. Study Area and Data Base
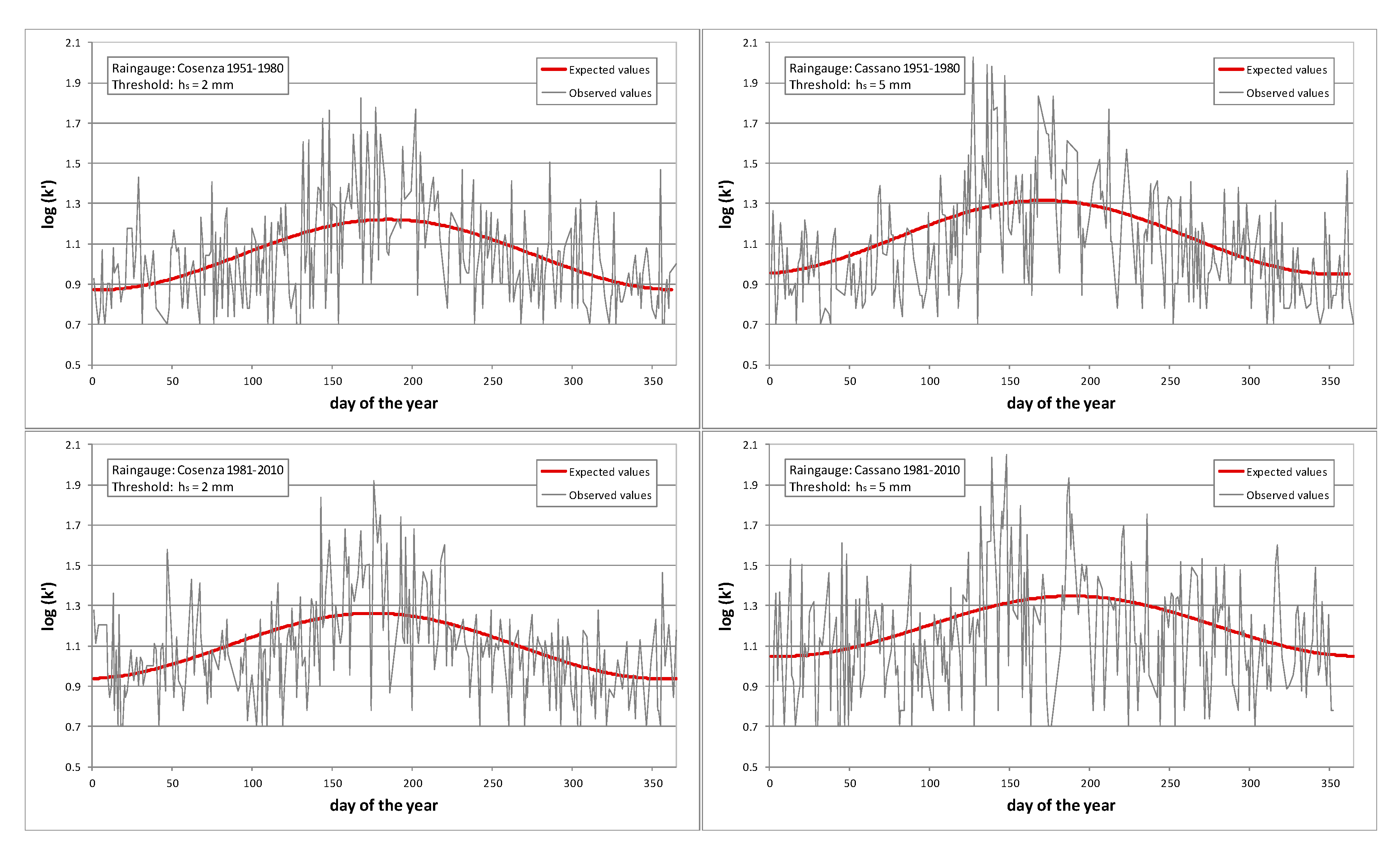
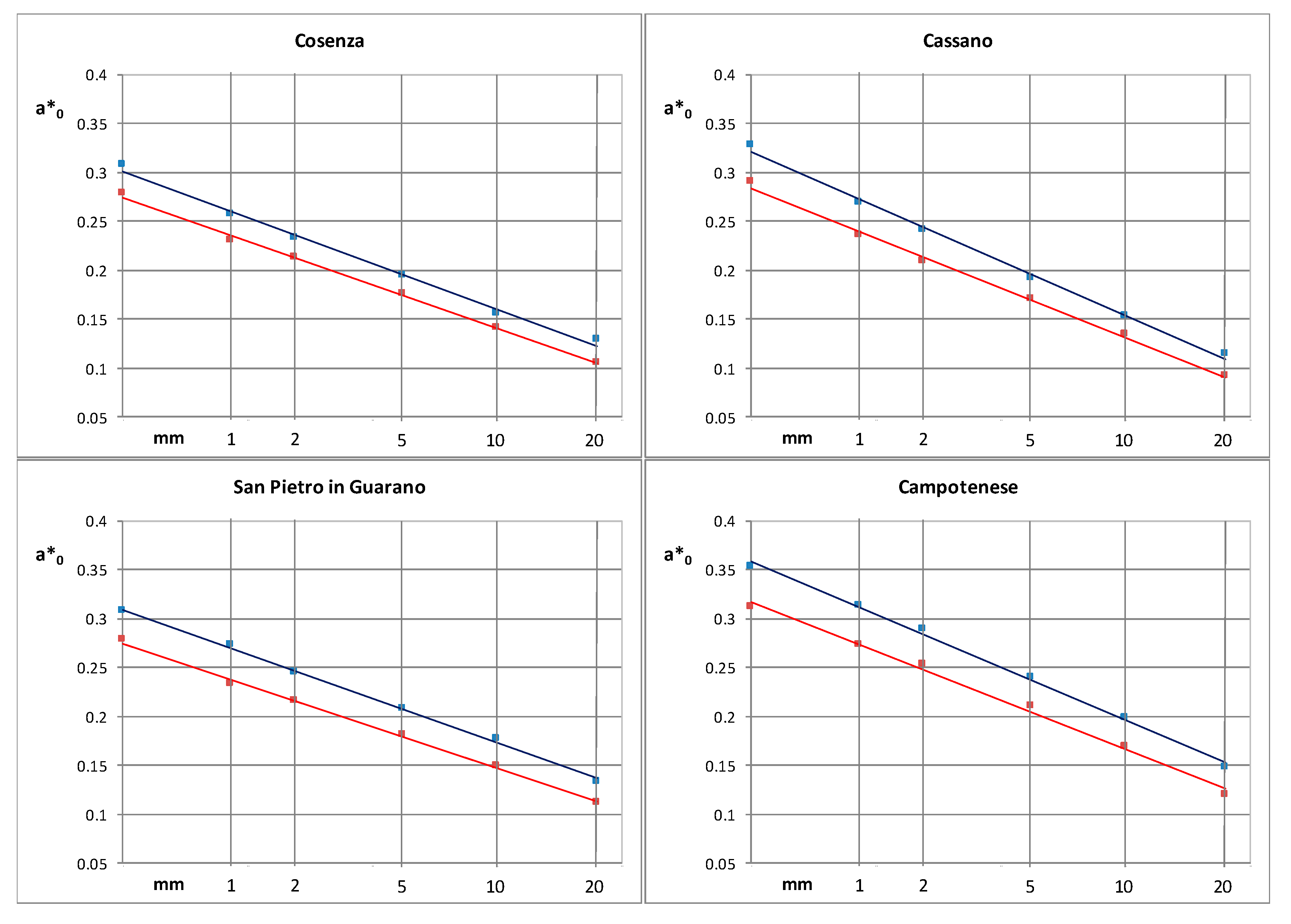
3.2. Intensity Function Modelled through Truncated Fourier Series
3.3. Test on the Statistical Significance of the Variation of Dry Spells between the Two Periods
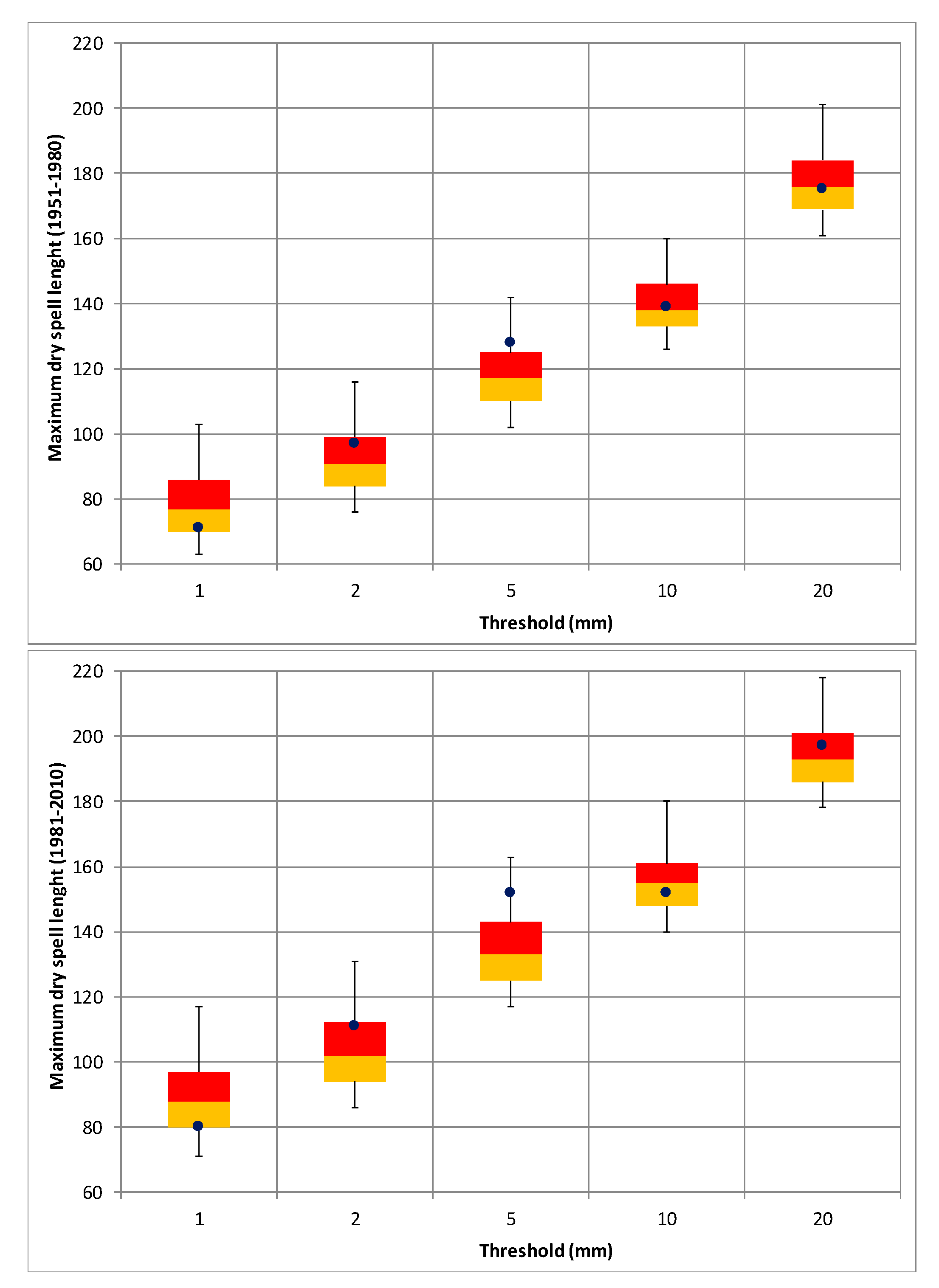
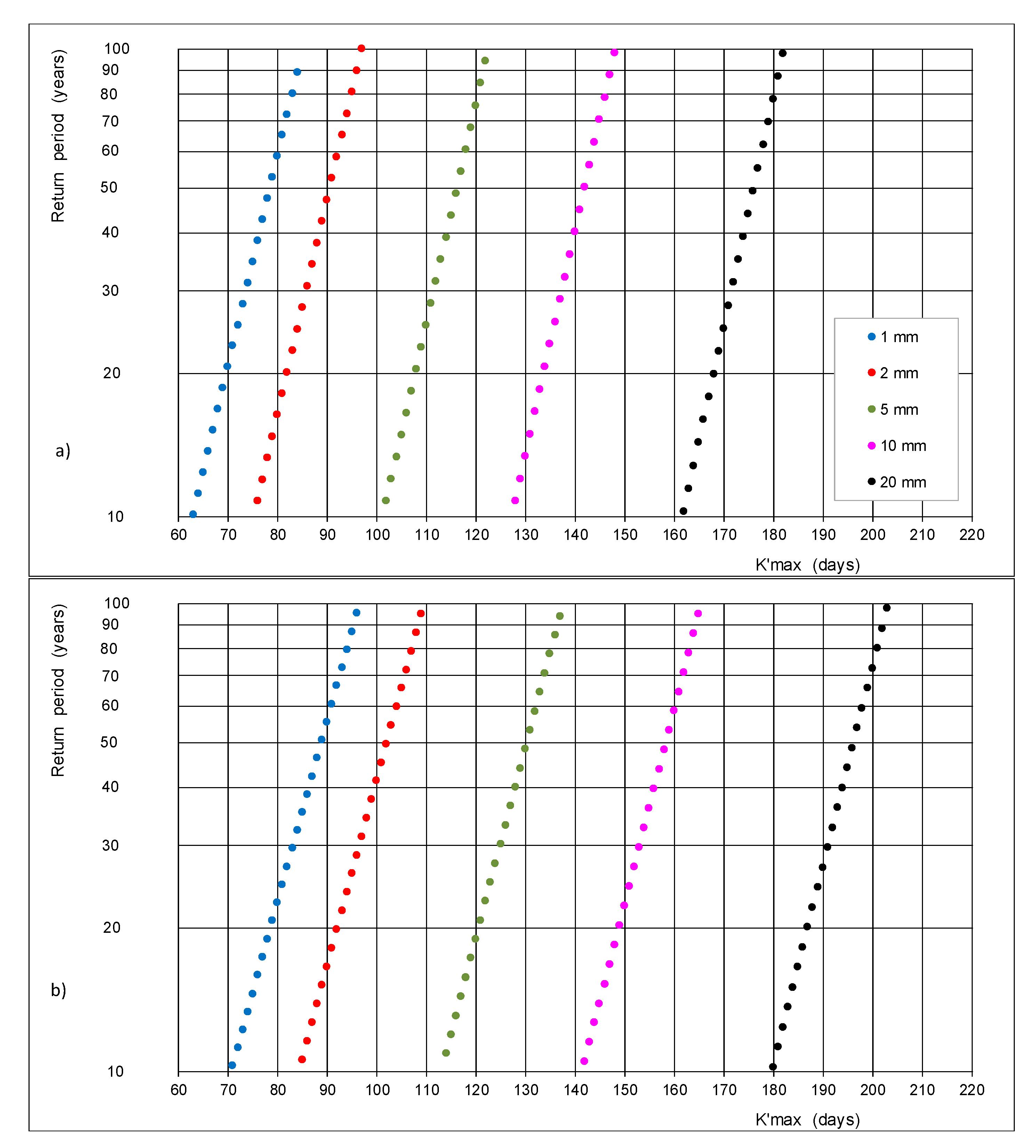
3.4. Occurrence Probability of Long Dry Spells
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- IPCC. Summary for Policymakers; Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Cindrić, K.; Prtenjak, M.T.; Herceg-Bulić, I.; Mihajlović, D.; Pasarić, Z. Analysis of the extraordinary 2011/2012 drought in Croatia. Theor. Appl. Climatol. 2016, 123, 503–522. [Google Scholar] [CrossRef]
- Caloiero, T.; Veltri, S. Drought Assessment in the Sardinia Region (Italy) During 1922–2011 Using the Standardized Precipitation Index. Pure Appl. Geophys. 2019, 176, 925–935. [Google Scholar] [CrossRef]
- Merino, A.; López, L.; Hermida, L.; Sánchez, J.L.; García-Ortega, E.; Gascón, E.; Fernández-González, S. Identification of drought phases in a 110-year record from Western Mediterranean basin: Trends, anomalies and periodicity analysis for Iberian Peninsula. Glob. Planet. Chang. 2015, 133, 96–108. [Google Scholar] [CrossRef]
- Wellstein, C.; Poschlod, P.; Gohlke, A.; Chelli, S.; Campetella, G.; Rosbakh, S.; Canullo, R.; Kreyling, J.; Jentsch, A.; Beierkuhnlein, C. Effects of extreme drought on specific leaf area of grassland species: A meta-analysis of experimental studies in temperate and sub-Mediterranean systems. Glob. Chang. Biol. 2017, 23, 2473–2481. [Google Scholar] [CrossRef] [PubMed]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Sirangelo, B. Occurrence Probabilities of Wet and Dry Periods in Southern Italy through the SPI Evaluated on Synthetic Monthly Precipitation Series. Water 2018, 10, 336. [Google Scholar] [CrossRef]
- González-Hidalgo, J.C.; Vicente-Serrano, S.M.; Peña-Angulo, D.; Salinas, C.; Tomas-Burguera, M.; Beguería, S. High-resolution spatio-temporal analyses of drought episodes in the western Mediterranean basin (Spanish mainland, Iberian Peninsula). Acta Geophys. 2018, 66, 381–392. [Google Scholar] [CrossRef]
- Bonaccorso, B.; Cancelliere, A.; Rossi, G. Probabilistic forecasting of drought class transitions in Sicily (Italy) using Standardized Precipitation Index and North Atlantic Oscillation Index. J. Hydrol. 2015, 526, 136–150. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Sirangelo, B. Analysis of Dry Spells in Southern Italy (Calabria). Water 2015, 7, 3009–3023. [Google Scholar] [CrossRef]
- Maccioni, P.; Kossida, M.; Brocca, L.; Moramarco, T. Assessment of the Drought Hazard in the Tiber River Basin in Central Italy and a Comparison of New and Commonly Used Meteorological Indicators. J. Hydrol. Eng. 2015, 20, 05014029. [Google Scholar] [CrossRef]
- Buttafuoco, G.; Caloiero, T.; Ricca, N.; Guagliardi, I. Assessment of drought and its uncertainty in a southern Italy area (Calabria region). Measurement 2018, 113, 205–210. [Google Scholar] [CrossRef]
- Chiogna, G.; Skrobanek, P.; Narany, T.S.; Ludwig, R.; Stumpp, C. Effects of the 2017 drought on isotopic and geochemical gradients in the Adige catchment, Italy. Sci. Total Environ. 2018, 645, 924–936. [Google Scholar] [CrossRef] [PubMed]
- Colangelo, M.; Camarero, J.J.; Borghetti, M.; Gentilesca, T.; Oliva, J.; Redondo, M.A.; Ripullone, F. Drought and Phytophthora Are Associated with the Decline of Oak Species in Southern Italy. Front. Plant Sci. 2018, 9, 1595. [Google Scholar] [CrossRef] [PubMed]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Sirangelo, B. An Analysis of the Occurrence Probabilities of Wet and Dry Periods through a Stochastic Monthly Rainfall Model. Water 2016, 8, 39. [Google Scholar] [CrossRef]
- Marini, G.; Fontana, N.; Mishra, A.K. Investigating drought in Apulia region, Italy using SPI and RDI. Theor. Appl. Climatol. 2018. [Google Scholar] [CrossRef]
- Nagarajan, R. Drought Assessment; Springer: New Delhi, India, 2009. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería-Portugués, S. Estimating extreme dry-spell risk in the middle Ebro valley (Northeastern Spain): A comparative analysis of partial duration series with a general Pareto distribution, annual maxima series with a Gumbel distribution. Int. J. Climatol. 2003, 23, 1103–1118. [Google Scholar] [CrossRef]
- Cindrić, K.; Pasarić, Z. Modelling Dry Spells by Extreme Value Distribution with Bayesian Inference. Pure Appl. Geophys. 2018, 175, 3891–3908. [Google Scholar] [CrossRef]
- Kutiel, H. The multimodality of the rainfall course in Israel, as reflected by the distribution of dry spells. Meteorol. Atmos. Phys. 1985, 36, 15–27. [Google Scholar] [CrossRef]
- Nastos, P.T.; Zerefos, C.S. Spatial and temporal variability of consecutive dry and wet days in Greece. Atmos. Res. 2009, 94, 616–628. [Google Scholar] [CrossRef]
- Anagnostopoulou, C.H.R.; Maheras, P.; Karacostas, T.; Vafiadis, M. Spatial and temporal analysis of dry spells in Greece. Theor. Appl. Climatol. 2003, 74, 77–91. [Google Scholar] [CrossRef]
- Di Giuseppe, E.; Vento, D.; Epifani, C.; Esposito, S. Analysis of dry and wet spells from 1870 to 2000 in four Italian sites. Geophys. Res. Abstr. 2005, 7, 07712. [Google Scholar]
- Tolika, K.; Maheras, P. Spatial and temporal characteristics of wet spells in Greece. Theor. Appl. Climatol. 2005, 81, 71–85. [Google Scholar] [CrossRef]
- Deni, S.M.; Jemain, A.A.; Ibrahim, K. The best probability models for dry and wet spells in Peninsular Malaysia during monsoon seasons. Int. J. Climatol. 2010, 30, 1194–1205. [Google Scholar] [CrossRef]
- Li, X.; Meshgi, A.; Babovic, V. Spatio-temporal variation of wet and dry spell characteristics of tropical precipitation in Singapore and its association with ENSO. Int. J. Climatol. 2016, 36, 4831–4846. [Google Scholar] [CrossRef]
- Singh, N.; Ranade, A. The wet and dry spells across India during 1951–2007. J. Hydrometeorol. 2010, 11, 26–45. [Google Scholar] [CrossRef]
- Ye, H. Changes in duration of dry and wet spells associated with air temperatures in Russia. Environ. Res. Lett. 2018, 13, 034036. [Google Scholar] [CrossRef]
- Hussain, M.S.; Lee, S. Long-term variability and changes of the precipitation regime in Pakistan. Asia Pac. J. Atmos. Sci. 2014, 50, 271–282. [Google Scholar] [CrossRef]
- Usman, M.T.; Reason, C.J.C. Dry spell frequencies and their variability over southern Africa. Clim. Res. 2004, 26, 199–211. [Google Scholar] [CrossRef]
- Raymond, F.; Drobinski, P.; Ullmann, A.; Camberlin, P. Extreme dry spells over the Mediterranean Basin during the wet season: Assessment of HyMeX/Med-CORDEX regional climate simulations (1979–2009). Int. J. Climatol. 2018, 38, 3090–3105. [Google Scholar] [CrossRef]
- Schmidli, J.; Frei, C. Trends of heavy precipitation and wet and dry spells in Switzerland during the 20th century. Int. J. Climatol. 2005, 25, 753–771. [Google Scholar] [CrossRef]
- Pérez-Sánchez, J.; Senent-Aparicio, J. Analysis of meteorological droughts and dry spells in semiarid regions: A comparative analysis of probability distribution functions in the Segura Basin (SE Spain). Theor. Appl. Climatol. 2018, 133, 1061–1074. [Google Scholar] [CrossRef]
- Zolina, O.; Simmer, C.; Belyaev, K.; Sergey, K.; Gulev, S.; Koltermann, P. Changes in the duration of European wet and dry spells during the last 60 years. J. Clim. 2013, 26, 2022–2047. [Google Scholar] [CrossRef]
- Gupta, V.; Duckstein, L. Droughts as extreme distributions from a point rainfall process. Water Resour. Res. 1975, 11, 221–228. [Google Scholar] [CrossRef]
- Gregory, J.M.; Wigley, T.M.L.; Jones, P.D. Application of Markov models to area-average daily precipitation series and interannual variability in seasonal totals. Clim. Dyn. 1993, 8, 299–310. [Google Scholar] [CrossRef]
- Lana, X.; Fernandez Mills, G.; Burgueño, A. Daily precipitation maxima in Catalonia (NE Spain): Expected values and their spatial distribution. Int. J. Climatol. 1995, 15, 341–354. [Google Scholar] [CrossRef]
- Chapman, T. Stochastic models for daily rainfall in the Western Pacific. Math. Comput. Simul. 1997, 43, 351–358. [Google Scholar] [CrossRef]
- Chapman, T. Stochastic models of daily rainfall: The impact of adjoining wet days on the distribution of rainfall amounts. Environ. Model. Softw. 1998, 13, 317–324. [Google Scholar] [CrossRef]
- Lana, X.; Burgueñom, A. Daily dry–wet behaviour in Catalonia (NE Spain) from the viewpoint of Markov chains. Int. J. Climatol. 1998, 18, 793–815. [Google Scholar] [CrossRef]
- Xu, Z.; Schumann, A.; Brass, C.; Li, J.; Ho, K. Chain dependent Markov correlation pulse model for daily stream flow generation. Adv. Water. Resour. 2001, 24, 551–564. [Google Scholar] [CrossRef]
- Cancelliere, A.; Salas, J.D. Drought length properties for periodic stochastic hydrologic data. Water Resour. Res. 2004, 40, W02503. [Google Scholar] [CrossRef]
- Cindrić, K.; Pasarić, Z.; Gajić-Čapka, M. Spatial and temporal analysis of dry spells in Croatia. Theor. Appl. Climatol. 2010, 102, 171–184. [Google Scholar] [CrossRef]
- Ochola, W.O.; Kerkides, P. A Markov chain simulation model for predicting critical wet and dry spells in Kenya: Analysing rainfall events in the Kano Plains. Irrig. Drain. 2003, 52, 327–342. [Google Scholar] [CrossRef]
- Sirangelo, B.; Caloiero, T.; Coscarelli, R.; Ferrari, E. A stochastic model for the analysis of the temporal change of dry spells. Stoch. Environ. Res. Risk. Assess. 2015, 29, 143–155. [Google Scholar] [CrossRef]
- Sirangelo, B.; Caloiero, T.; Coscarelli, R.; Ferrari, E. Stochastic analysis of long dry spells in Calabria (Southern Italy). Theor. Appl. Climatol. 2017, 127, 711–724. [Google Scholar] [CrossRef]
- Parzen, E. Stochastic Processes; Holden-Day Series in Probability and Statistics; Holden-Day: San Francisco, CA, USA, 1962. [Google Scholar]
- Cinlair, E. Introduction to Stochastic Processes; Prentice Hall: Englewood Cliffs, NJ, USA, 1975. [Google Scholar]
- Gullà, G.; Caloiero, T.; Coscarelli, R.; Petrucci, O. A proposal for a methodological approach to the characterisation of Widespread Landslide Events: An application to Southern Italy. Nat. Hazards Earth Syst. Sci. 2012, 12, 165–173. [Google Scholar] [CrossRef]
- Buttafuoco, G.; Caloiero, T.; Coscarelli, R. Analyses of Drought Events in Calabria (Southern Italy) Using Standardized Precipitation Index. Water Resour. Manag. 2015, 29, 557–573. [Google Scholar] [CrossRef]
- Coscarelli, R.; Caloiero, T.; Ferrari, E.; Sirangelo, B. Detection and analysis of drought events in Calabria (southern Italy). Ital. J. Eng. Geol. Environ. 2018, 1, 13–25. [Google Scholar]
- Serra, C.; Martínez, M.D.; Lana, X.; Burgueño, A. European dry spells distributions, years 1951–2000. Theor. Appl. Climatol. 2013, 114, 531–551. [Google Scholar] [CrossRef]
- Yevjevich, V. An Objective Approach to Definitions and Investigations of Continental Hydrologic Droughts; Hydrol Papers 23; Colorado State University Publication: Fort Collins, CO, USA, 1957. [Google Scholar]
| Rain Gauge | Latitude | Longitude | Altitude (m a.s.l.) | Proximity to Sea Side (km) | % Missing Data | Mean Annual Rainfall (mm) | Mean Dry Spell Length (days) |
|---|---|---|---|---|---|---|---|
| Cosenza | 39°46’56” | 16°19’08” | 251 | 14.452 | 1.4 | 1014.6 | 6.9 |
| Cassano allo Jonio | 39°17’11” | 16°15’55” | 242 | 18.257 | 1.9 | 734.2 | 6.7 |
| San Pietro in Guarano | 39°20’42” | 16°18’48” | 660 | 23.435 | 1.1 | 992.9 | 6.5 |
| Campotenese | 39°52’19” | 16°04’05” | 965 | 23.672 | 0.2 | 1465.3 | 5.7 |
| Threshold | Rain Gauges | 1951–1980 | 1981–2010 | ||||
|---|---|---|---|---|---|---|---|
| hs = 1 mm | Cosenza | 0.2568 | 0.0521 | 0.0237 | 0.2308 | 0.0533 | 0.0190 |
| Cassano allo Ionio | 0.2692 | 0.0499 | 0.0160 | 0.2359 | 0.0401 | 0.0136 | |
| San Pietro in Guarano | 0.2734 | 0.0597 | 0.0253 | 0.2332 | 0.0557 | 0.0232 | |
| Campotenese | 0.3124 | 0.0528 | 0.0147 | 0.2730 | 0.0551 | 0.0123 | |
| hs = 2 mm | Cosenza | 0.2333 | 0.0495 | 0.0224 | 0.2133 | 0.0497 | 0.0177 |
| Cassano allo Ionio | 0.2409 | 0.0452 | 0.0148 | 0.2092 | 0.0385 | 0.0120 | |
| San Pietro in Guarano | 0.2456 | 0.0514 | 0.0247 | 0.2156 | 0.0495 | 0.0200 | |
| Campotenese | 0.2895 | 0.0455 | 0.0130 | 0.2524 | 0.0477 | 0.0114 | |
| hs = 5 mm | Cosenza | 0.1949 | 0.0407 | 0.0177 | 0.1762 | 0.0401 | 0.0133 |
| Cassano allo Ionio | 0.1923 | 0.0409 | 0.0109 | 0.1708 | 0.0257 | 0.0112 | |
| San Pietro in Guarano | 0.2073 | 0.0408 | 0.0216 | 0.1816 | 0.0409 | 0.0166 | |
| Campotenese | 0.2403 | 0.0341 | 0.0110 | 0.2103 | 0.0355 | 0.0102 | |
| hs = 10 mm | Cosenza | 0.1560 | 0.0373 | 0.0166 | 0.1417 | 0.0367 | 0.0092 |
| Cassano allo Ionio | 0.1532 | 0.0389 | 0.0100 | 0.1344 | 0.0235 | 0.0101 | |
| San Pietro in Guarano | 0.1775 | 0.0390 | 0.0191 | 0.1496 | 0.0387 | 0.0151 | |
| Campotenese | 0.1987 | 0.0300 | 0.0105 | 0.1693 | 0.0227 | 0.0098 | |
| hs = 20 mm | Cosenza | 0.1296 | 0.0292 | 0.0130 | 0.1059 | 0.0267 | 0.0066 |
| Cassano allo Ionio | 0.1151 | 0.0324 | 0.0066 | 0.0924 | 0.0158 | 0.0088 | |
| San Pietro in Guarano | 0.1333 | 0.0317 | 0.0138 | 0.1120 | 0.0318 | 0.0127 | |
| Campotenese | 0.1427 | 0.0222 | 0.0086 | 0.1212 | 0.0102 | 0.0089 | |
| Rain Gauge | ||||
|---|---|---|---|---|
| Cosenza | 18.34 | 18.28 | 0.954 | Rejected |
| Cassano allo Jonio | 19.45 | 18.90 | 0.968 | Rejected |
| San Pietro in Guarano | 17.72 | 17.43 | 0.961 | Rejected |
| Campotenese | 16.32 | 15.44 | 0.982 | Rejected |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sirangelo, B.; Caloiero, T.; Coscarelli, R.; Ferrari, E. A Stochastic Approach for the Analysis of Long Dry Spells with Different Threshold Values in Southern Italy. Water 2019, 11, 2026. https://doi.org/10.3390/w11102026
Sirangelo B, Caloiero T, Coscarelli R, Ferrari E. A Stochastic Approach for the Analysis of Long Dry Spells with Different Threshold Values in Southern Italy. Water. 2019; 11(10):2026. https://doi.org/10.3390/w11102026
Chicago/Turabian StyleSirangelo, Beniamino, Tommaso Caloiero, Roberto Coscarelli, and Ennio Ferrari. 2019. "A Stochastic Approach for the Analysis of Long Dry Spells with Different Threshold Values in Southern Italy" Water 11, no. 10: 2026. https://doi.org/10.3390/w11102026
APA StyleSirangelo, B., Caloiero, T., Coscarelli, R., & Ferrari, E. (2019). A Stochastic Approach for the Analysis of Long Dry Spells with Different Threshold Values in Southern Italy. Water, 11(10), 2026. https://doi.org/10.3390/w11102026





