Abstract
Water resources are threatened by many pollution sources. The harmful effects of pollution can be evaluated through biological indicators capable of tracing problems in life forms caused by the contaminants discharged into the streams. In the present study, the effects on stream water quality of landscape configuration, season, and distance from contaminant emissions of diffuse and point sources were accessed through the evaluation of a Portuguese macroinvertebrate index (IPtIN) in 12 observation points distributed within the studied area (Ave River Basin, Portugal). Partial least-squares path models (PLS-PMs) were used to set up cause–effect relationships between this index, various metrics adapted to forest, agriculture, and artificial areas, and the aforementioned emissions, considering 13 distances from the contaminant sources ranging from 100 m to 56 km. The PLS-PM models were applied to summer and winter data to explore seasonality effects. The results of PLS-PM exposed significant scale and seasonal effects. The harmful effects of artificial areas were visible for distances larger than 10 km. The impact of agriculture was also distance related, but in summer this influence was more evident. The forested areas could hold onto contamination mainly in the winter periods. The impact of diffuse contaminant emissions was stronger during summer, when accessed on a short distance. The impact of effluent discharges was small, compared to the influence of landscape metrics, and had a limited statistical significance. Overall, the PLS-PM results evidenced significant cause–effect relationships between land use metrics and stream water quality at 10 km or larger scales, regardless of the season. This result is valid for the studied catchment, but transposition to other similar catchments needs to be carefully verified given the limited, though available, number of observation points.
1. Introduction
The growing population and demographic expansion threaten hydric resources, not only by inducing stressful water demands but also because of the continuous surge of pollution sources. The response to anthropogenic pressures relies on proper management that should always stand on environmental research. The risks to water quality are well known by experts, but continuous research should be applied since the world is in constant change [1,2]. Effluent discharges are an undeniable threat. The potential contamination by wastewaters is frequently reduced in urban and industrial areas where treatment stations are efficient, but in many regions proper treatment is not applied [3]. In those situations, surface waters are directly contaminated by bacteria [4], nutrient loads [5,6,7], heavy metals [8,9] and even microplastics [10]. The runoff transports herbicides and pesticides from agriculture [11] and high organic loads from livestock [7] to surface waters. The presence of forested areas or riparian vegetation can create a barrier that retains such flow of contaminants [12,13]. Wildfires are another threat to water quality [14,15], not only because they can destroy the aforementioned barriers [16], but also because soil erosion increases [17], and ash-derived contaminants are leached towards the streams [18]. Another factor that can affect water quality is land occupation planning. When land use is not conformed to land capability (natural use), land use conflict is generated [19], which amplifies soil losses [20] and accelerates other phenomena that cause water deterioration [21]. Land use type and configuration are other key aspects that have been studied by many authors in the context of water quality changes [22]. Relevant conclusions achieved in these studies are that landscapes retain nutrients [23]; a high edge density is an indicator of high anthropogenic activity [24]; as Shannon’s diversity index (SHDI) increases, the water quality decreases [25]; and aggregated urban land uses are more suited to preserve surface water quality [24], among others.
The effects of landscape metrics on water quality are commonly accessed by Spearman or Pearson correlation coefficients and, when predictions are involved, through multiple linear regression analyses [26]. When these matters are studied, the authors are aware that the spatial resolution of land cover maps can affect the results [23,27]. But another critical aspect that is questioned by many authors is the spatial extent for statistical sampling [28]. This can vary from circular buffers, riparian extents, or catchments [29,30]. For proper management of river basins or even urban planning, it is essential to use an appropriate scale. By comparing different studies, some inconsistencies can be detected regarding the option for a suitable scale. Some authors infer that the use of entire watersheds provides better results [28,31,32,33,34], but other working groups argue that a riparian scale is more suitable [35,36,37]. These inconsistent results can be attributed to differences between study designs and study areas [38], but other factors such as stream order [28], season [39], and topology [34,39] can also play prominent roles.
Water quality research requires the use of statistical or process-based models [40]. The first type has the advantage to access the relationships between the pertinent variables, while in mechanistic models, the interactions are already determined by chemical, biological, and physical processes, which makes them preferable for prediction purposes [41].
An example of a statistical method is the multivariate method called partial least-squares path modeling (PLS-PM). The first steps of PLS-PM have been given in social sciences [42]. Nowadays, this method is being practiced in many studies in diverse research areas, namely the environment [43,44,45,46], geology [47], flood effects [48], and ecological conservation [49], among others. The authors have adopted this technique because it can exhibit cause–effect relations straightforwardly using a graphical interface. The present work continues a sequence of studies developed by this research team, who has been studying the quality of water in the Ave River Basin (Portugal) through multivariate statistics. In the first study, three PLS regression models were tested in a row to explain the pollution of surface waters and the resulting impacts on ecological integrity [50]. In a second study, an identical dataset was used in PLS-PM [51] to trace the difference of cause–effect relations between an anthropogenic (Ave River) and a rural (Sabor River) basin. Since the results were promising in both studies, in a third study they were used to predict the ecological status of the Ave River Basin in the near future [52]. The aim in the present work was to take another step forward and explore the influence of landscape metrics and contaminant emissions on ecological integrity, as well as the impact of season and scale on the results.
2. Materials and Methods
2.1. Study Area
The Ave River Basin is located in the northern region of Portugal (Figure 1A), occupying an area of approximately 1322 km2. The main water course extends for 100 km, the most important tributary catchments are the Este (247 km2) and Vizela (323 km2) rivers. The altitude ranges from 0 m along the Atlantic coast to 1254 m at the Cabreira mountains, where the catchment headwaters are located. This river basin is surrounded to the west the by the Atlantic Ocean, to the south by the Leça River Basin, to the east by the Douro River Basin, and to the north by the Cávado River Basin. The group of three river basins, Ave, Leça and Cávado, belong to the same management unit, namely hydrographic region number 2 [53].
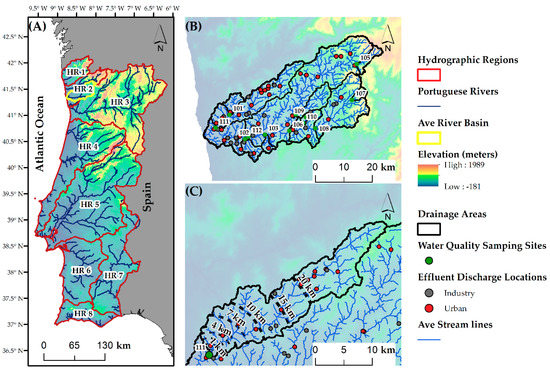
Figure 1.
(A) Map of Portugal with the distribution of hydrographic regions. (B) Ave River Basin and sampling sites. (C) Drainage area of sampling site 111 and intersection of buffer limits with the drainage area.
In the second half of the 20th century, the Ave River Basin was heavily contaminated by untreated domestic and industrial effluents, being tagged as “Europe’s Great Sewer”. Following the construction of public wastewater treatment plants in the 90s, water quality increased, but some microbial contamination persisted related to improper functioning of some domestic plants. The heavy pollution of Ave comprised high concentrations of heavy metals in sediments and freshwater, especially in the Este, Selho, and Vizela rivers [9,54]. This condition improved after public investment in the wastewater treatment plants [55,56]. The abundant and persistent nutrient and metal contamination deteriorated the river’s ecological status at the central area and lowlands of the Ave River Basin [57,58] where industrial areas have been settled on the river banks for years. Besides the effluents from domestic and industrial origins, contributions from agriculture and livestock production have also been reported as significant causes of water quality and ecological deterioration [59,60,61].
2.2. Workflow
The purpose of the present study was to show how the cause–effect relationships between ecological integrity and pollution sources/indicators changed with the season and distance from contaminant sources. Ecological integrity was assessed through the measurement of a macroinvertebrate index (IPtIN; see Equation (1) below) in 12 sampling sites along the Ave River Basin (Figure 1B) during the winter and summer seasons of 2017. For these sites, the entire upstream drainage area was delineated and then sectioned at predefined distances from the sampling site (Figure 1C). Subsequent to catchment delineation and sectioning, land use and contaminant emission data were prepared for each section to be used in PLS-PM models. Two separate models were defined based on IPtIN values determined in winter and summer, respectively. The purpose was to explore how the effects of anthropogenic pressures could change as a function of season and scale. Figure 2 displays the adopted workflow, summarized in 6 steps.
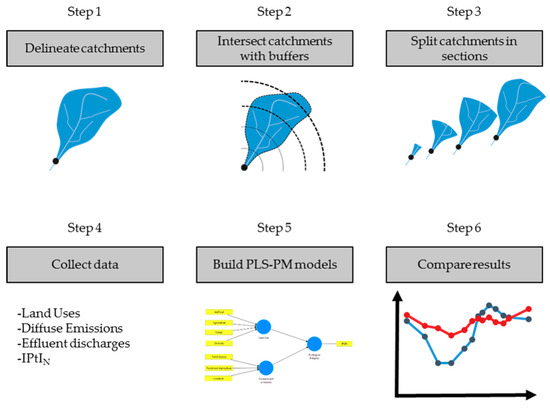
Figure 2.
Workflow distributed in six steps.
For the delineation of drainage areas and drainage networks (Step 1), ArcMap [62] and its embedded module ArcHydro [63] were used. These computer packages are the key technical elements used in environmental studies with a strong spatial incidence [64,65,66,67,68,69,70,71]. As an input, a digital elevation model with a pixel resolution of 25 m was used. To design each drainage area, the tool “Batch Watershed Delineation” was used, followed by previous procedures [72]. For each sampling site, the “Buffer” ArcMap tool was used to create a circular area, while the created buffers extended for 100, 250, 500, 1000, 2000, 3000, 4000, 5000, 7000, 10,000, 15,000, 20,000, and 56,000 m (Step 2). Each drainage area intersected with the respective buffer in order to create drainage sections (Step 3). The collected spatial data (Table 1) were processed and applied in the PLS-PM models (Step 4). The land uses and discharge emissions were collected using the ArcMap “Intersect” tool. A total of 26 PLS-PM models were created, one for each season and distance combination. The algorithm was executed in SmartPLS software [73]. PLS-PM analysis was the chosen method because it could establish cause–effect relationships for the studied latent variables, which were termed “Land Use”, “Contaminant Emissions”, and “Ecological Integrity”. Formative models were chosen because these have prediction capabilities and, at the same time, establish the wanted cause–effect relationships [74]. The 26 model outputs were measured with weights, path coefficients, and R-squared values. The outputs were compiled and compared using graphics designed in Excel [75] (Step 6).

Table 1.
Data sources.
2.3. Dataset
In this study, a group of variables was gathered (Table 1) that could be connected to the variation of IPtIN. The actual data are provided as Supplementary Material. The elevation model was used for the delineation of drainage areas. The effluent discharge points values were provided by the Agência Portuguesa do Ambiente (APA; in English, Portuguese Environmental Agency) in the form of shapefiles. Each point contained was attached to information on the total discharge of nitrogen, phosphorous, and chemical and biological oxygen demands, expressed in released kilograms during the year of 2016. The discharge of nitrogen and phosphorous from livestock production, agriculture, and forestry were also provided by the APA in the form of shapefiles. Each polygon was a catchment containing the released kilograms of nutrients during the year of 2016. The most recent Portuguese land use map refers to 2015 (COS 2015) and is available at the Portuguese Territory Planning website. This map was obtained in the form of a shapefile, containing the land use or occupation from each zone. The land use types were assembled into 4 categories: agriculture, artificial surfaces, forest, and seminatural areas and water bodies. For the calculation of IPtIN, samples were collected in situ during the summer and winter of 2017. After laboratory analyses, the index was calculated for the twelve locations.
For each drainage section, the discharging values of BOD (biochemical oxygen demand), COD (chemical oxygen demand), N, and P were summed and then divided by the drainage area, creating four variables representing the discharge of each type of nutrient and oxygen demand. For diffuse discharges, the total release discharge of N and P in the drainage sections was calculated and then divided by the respective area, resulting in 4 variables: the releases of N and P from livestock and forest/agriculture. For each section, landscape metrics were calculated using a python toolbox embedded in ArcMap [76]. A total of 17 metrics were calculated for all the drainage sections (Table 2).

Table 2.
IPtIN values and classification for the twelve measurement sites for winter and summer of 2017. An identification color was linked to each class that shades the corresponding cells: red—Very Poor, orange—Poor, yellow—Moderate, green—Excellent. The shades were added to the table for illustration and prompt interpretation of the quality classes.
The north invertebrate Portuguese index (IPtIN) is widely used to evaluate the ecological status of stream waters in northern Portugal [77]. The IPtIN index reflects the abundance and diversity of benthic invertebrates that are sensitive to all forms of pollution [77,78,79].
For the measurement of this indicator, organism samples were collected from 12 surface water locations, illustrated in Figure 1C. For each site, the organisms were classified and counted, and then Equation (1) was used to calculate the IPtIN score. The equation is complex since it uses a variety of parameters, namely, the number of taxonomic groups present in the sample (N° taxa); the number of families that belong to Ephemeroptera, Plecoptera, and Trichoptera orders (EPT); Pioleu index or evenness [80,81]; biological monitoring working party index divided by the number of families included in this index (IASPT) [82]; and the sum of individuals belonging to Heptageniidae, Ephemeridae, Brachycentridae, Goeridae, Odontoceridae, Limnephilidae, Polycentropodidae, Athericidae, Dixidae, Dolichopodidae, Empididae, and Stratiomyidae families (Sel.ETD):
IPtIN = N° Taxa × 0.25 + EPT × 0.15 + Evenness × 0.1 + (IASPT − 2) × 0.3 + Log (Sel.ETD + 1) × 0.2.
Among all possible variables that could be used in this study, only 8 were chosen for the PLS-PM models. The purpose was to reach low variance inflation factors (VIFs), and hence statistical significance, making a note that variables of the same domain can be strongly correlated in raising the VIFs. To represent the effluent discharges, the released annual flow divided by the drainage area was used, naming this variable as “Point Source”. For diffuse contamination, the discharges of nitrogen from livestock, forestry, and agriculture were used, naming these variables as “Livestock” and “Forest and Agriculture”, respectively. The chosen landscape metrics were Shannon’s diversity, the edge density of forest and seminatural areas, the number of patches of artificial surfaces that were connected at a distance of 500 m, and the percentage of “agricultural areas” that were connected at a distance of 500 m. The land use variables were named as “Diversity”, “Forest”, “Artificial” and “Agriculture”, respectively. The Portuguese index of macroinvertebrates was also used, named as “IPtIN” for the PLS-PM models, as an evaluator of biodiversity as well as water quality.
3. Results
3.1. Spatial Data
Figure 3 illustrates the spatial distribution of pressures in the Ave River Basin. Figure 3A depicts the land use map of 2015. It can be noted that 50% was occupied by the dominant land use, forest and seminatural areas. Agricultural areas occupied 30% of the river basin, 20% was artificial surfaces, and less than 0.5% was water bodies. The values of discharged nitrogen from livestock, forest, and agricultural areas in the river basin catchments can be seen in Figure 3B,D. The scattered effluent discharge sites are represented in Figure 3C. Among a total of 60 locations, 24 were discharge sites of industrial treatment plants, while 36 were from domestic sewage treatment plants.
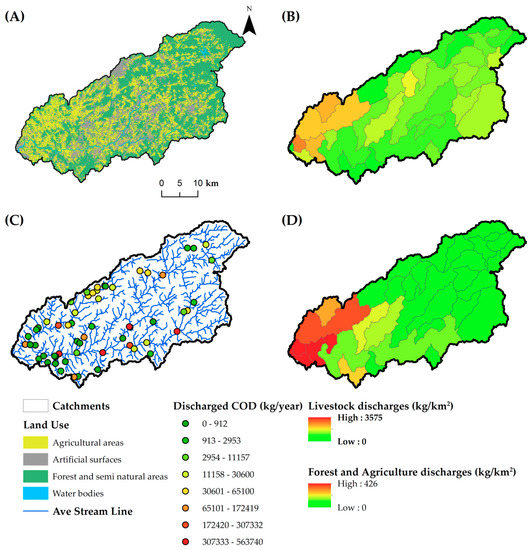
Figure 3.
Spatial distribution of pressure data used in the partial least-squares path models (PLS-PMs). (A) Land Uses. (B) Forest and agriculture discharges of nitrogen. (C) Effluent discharge locations. (D) Livestock discharges of nitrogen.
The twelve river sites where the IPtIN was measured are represented in Figure 1, numbered from 101 to 112. Table 2 depicts the IPtIN values and respective classification. During the winter of 2017, the ecological status was classified as “Excellent” in two sites, “Moderate” in 4, “Poor” for another 4 sites, and “Very Poor” in 2. Overall, the values increased from winter to summer, as none of the sites was classified as “Very Poor” in summer, 6 were classified as “Poor”, 3 as “Moderate”, and 3 as “Excellent”. In the locations 103, 105, 111, 112, 107, and 108, the classification changes were minimal. Besides, in site 111 the classification changed from “Moderate” to “Poor” because the IPtIN value was very close to the class threshold. In site 106 the classification changed from “Poor” to “Moderate”, but in sites 109, 110, 103, and 104 the decrease in ecological status was startling because there was a significant decrease in IPtIN and subsequent classification of a less-rich class. For site 101 there was a significant increase, from “Poor” to the maximum class “Excellent”. These changes of values were dependent upon seasonal effects but also on the pressures in surface waters.
3.2. Interpretation of a PLS-PM Example Model
The output models of SmartPLS were all similar to the one represented, as an example, in Figure 4. Each measured variable (MV) is represented as a yellow rectangle, and latent variables (LVs) as blue circles. Inside the LVs preceding other LVs, the R-squared value is portrayed. In the example model, only “Ecological Integrity” has an R-squared value, since this is the only variable that has a measured score (calculated by the sum of the product of MVs with the own weight) and a predicted score (calculated by the sum of the product between the LVs). In a PLS-PM model, weights and path coefficients are determined through an iterative process, termed the path algorithm [83], with the purpose to maximize the R-squared value.
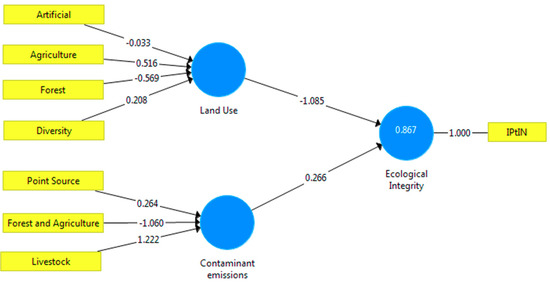
Figure 4.
PLS-PM example model.
Several PLS-PM models were built and analyzed in this study. In order to exemplify how these models can be interpreted, a PLS-PM model is demonstrated in Figure 4, where the data were gathered for the drainage sections within a distance of 4 km and IPtIN values measured during the winter of 2017.
Each LV was formed by one or more MVs. For the present case study, an LV “Land Use” was created and composed of 4 MVs, namely “Diversity”, “Forest”, “Agriculture”, and “Artificial”. The LV “Contaminant Emissions” was composed of three MVs pertaining to different types of contaminant flows: “Point Source”, “Livestock”, and “Forest and Agriculture”. “Ecological Integrity” was formed by a single MV, which is the IPtIN. This LV accumulated the effects of the other LVs that were pressures in surface waters, which is why “Contaminant Emissions” and “Land Use” were connected to “Ecological Integrity”. The PLS-PM model was divided into two sub-models, inner and outer. The equations of the measured scores of each LV were calculated according to Equations (2)–(4) for “Land Use”, “Contaminant Emissions”, and “Ecological Integrity”, respectively, and are the equations that composed the outer models. The inner model was composed of relations between latent variables, which, in this case, is solely expressed by Equation (5).
To interpret the example model, the weights and path coefficients should be analyzed simultaneously, which can be viewed in Equation (6), where the combination of Equations (2)–(5) is made. For example, the MV “Diversity” has a positive weight (0.208), so it increases the LV “Land Use”, while the same applies to “Agriculture” (0.561). Conversely, “Forest” and “Artificial” have negative weights, namely −0.569 and −0.033, and therefore decrease “Land Use”. But since the path coefficient of “Land Use” in “Ecological Integrity” is negative (−1.085), “Diversity” and “Agriculture” are variables that decrease “Ecological Integrity” because the product of the weight and path coefficient is negative: −0.226 and −0.560, respectively. On the other hand, “Forest” and “Artificial Areas” increase “Ecological Integrity”, since the product between the path coefficient and weight is positive, respectively 0.617 and 0.036. Equation (6) expresses the total effect of each pressure in “Ecological Integrity”. The results of this study were based on the analysis of the product between the path coefficients and weights (termed pcw) for the studied 26 models.
3.3. Results of All PLS-PM Models
As shown in Table 2, the IPtIN values were collected during two seasons, winter and summer. For this reason, the 26 PLS-PM models were divided into two groups, winter (2017) and summer (2017), and traced as two dot arrays colored as blue and red, respectively, in Figure 5. For each model in the respective group, the pressure values were used as input data, gathered from the 13 drainage sections and the IPtIN values collected in winter or summer. Figure 5 portrays the results of the PLS-PM models. Each graphic describes the pcw of a measured variable in all models (y axis). The x axis represents the logarithm of the buffer distance for the respective model. For the distances of 100, 250, 500, 1000, 2000, 3000, 4000, 5000, 7000, 10,000, 15,000, 20,000, and 56,000 meters, the log10 scores were 2, 2.4, 2.7, 3, 3.3, 3.5, 3.6, 3.7, 3.8, 4, 4.2, 4.3, and 4.7, respectively. The purpose of the plots was to illustrate the effects of the pressures in “Ecological Integrity” (“IPtIN”).
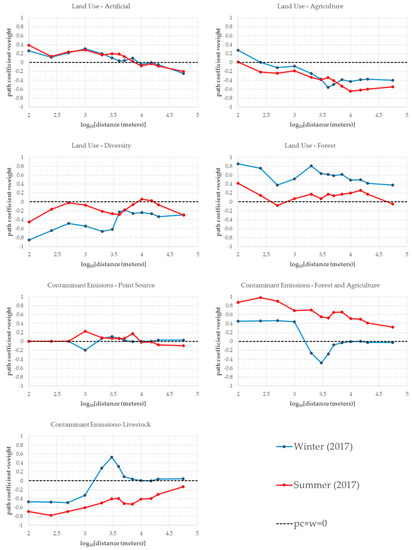
Figure 5.
PLS-PM results.
The effect of “Artificial” was independent of the season since the variations with distance were practically identical for both winter and summer. For distances shorter than 10 km, the effect was positive, but for longer distances the effect became negative. The strongest positive effects were detected for a distance of 100 m in summer (pcw = 0.386) and for 1000 m in winter (pcw = 0.310). The strongest negative effects were detected for the maximum distance (56 km) (i.e., for the entire drainage areas) either in winter (pcw= −0.247) or summer (pcw= −0.201).
For “Agriculture” it was seen that for both winter and summer periods, the effect was practically identical, but the summer line was below the winter line for a majority of buffer distances (only between 3 km and 5 km is the red line above the blue). The effect of agriculture was practically null for a distance of 100 m in summer (pcw = 0.008). For the same distance, it was positive during winter (pcw = 0.276) and practically null for a distance of 250 m (pcw = 0.01). For longer distances, the effect was negative, which indicated that agriculture decreased water quality. Peak values were found for distances of 4 km in winter (pcw = −0.560) and 10 km in summer (pcw = −0.648), but for distances larger than 10 km, the changes were minimal. The results lead to the conclusion that, for the Ave River basin, agriculture is a threat to water quality, while the impact seems to be stronger during the summer period.
Peak values of “Diversity” were detected for the minimum distance, 100 m, either in winter (pcw = −0.856) or in summer (pcw = −0.456). The effect was always negative for winter periods, and stronger in this season for almost all distances, except between 4 and 5 km. For the summer period, the effect was close to zero, but still negative; only distances of 500 m, 10, and 15 km were close to zero, since the pcw values were −0.024, 0.059, and 0.026, respectively. For the longest distance (56 km), the effect was practically the same for winter (pcw = −0.290) and summer (pcw = −0.298). The results provide evidence that the impact of “Diversity” is a threat in winter.
The effect of “Forest” was essentially positive. For the winter period, the effect was positive for all distances, and always higher than in summer, where the effect was negative but close to zero for the distances 500 m (pcw = −0.080) and 56 km (pcw = −0.049). Peak values occurred on the shortest scale, 100 m. In winter the pcw was 0.853, and in summer it was 0.419. As the buffer distances increased, the effects changed irregularly (drop and rise), but from an overall view, values were always between 0.853 and 0.374 during winter. It can be said that globally (for winter and summer), “Forest” favors water quality.
The variable that had less effects along all distances and seasons was “Point Source”. For this variable and the models that comprehended distances between 100 to 500 m, the attributed weight was 0, since for short distances there were no discharge points. Even so, compared to all the other variables, it had less impact because the pcw values were contained in a short range that varied from −0.198 to 0.226. For winter, negative values were found in 1 km (pcw = −0.198) and 7 km (pcw = −0.006), while in summer the negative values were observed for distances longer than 7 km. This indicates that the effect of effluent discharges only decreased IPtIN values during the summer period when long distances were analyzed, but with minimal impact.
The discharges of nitrogen from diffuse pressures were represented by the variables “Forest and Agriculture” and “Livestock”. When both graphics were compared, it was seen that there was an inverse relationship between these two variables for all models in both seasons. When the effect “Forest and Agriculture” increased, “Livestock” decreases. For the summer period, the effect of “Livestock” was always negative, while the effect of “Forest and Agriculture” was always positive. These effects were stronger over shorter distances, since maximum values for “Forest and Agriculture” and minimum values for “Livestock” appeared over the short distances. But as the distance increased, both effects approached zero. The variations of both variables were minimal for short distances (≤1 km), positive for “Forest and Agriculture”, and negative for “Livestock”. At the distances 2, 3, and 4 km, the effect became positive for “Livestock” and negative for “Forest and Agriculture”, with a peak at 4 km. For distances longer than 4 km, the effect tended to zero.
The analysis of the pcw variations for the 7 measured variables for all the models is crucial to comprehend the cause–effect relationship changes as function of season and distance. But the analysis of the R-squared values (Figure 6) reveals the models’ capacity to explain IPtIN variations.
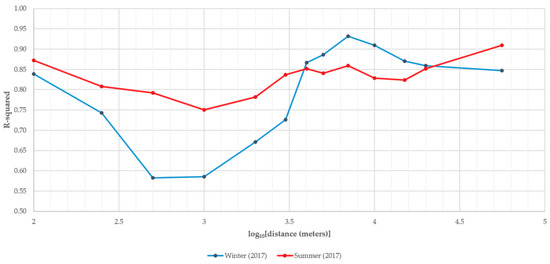
Figure 6.
PLS-PM R-squared values.
The calculated R-squared values of summer varied less than the winter counterparts. The range of values varied from 0.75 (1 km) to 0.91 (56 km) in summer, while in winter they ranged from 0.58 (500 m) to 0.93 (7 km). For the winter period, for distances comprehended between 250 m and 3 km, the model’s explicability was below 0.75, but the in winter models that comprehended distances between 4 to 20 km, the values were higher than in the corresponding summer models.
In order to assure that the models had no multicollinearity, it was ensured that all the VIF values were below 5 (please see Supplementary Material). The significance of weights and path coefficients was accessed through bootstrapping. By approaching the traditional threshold for statistical significance, p values larger than 0.05 were achieved for the weights (please see Supplementary Material). On the other hand, it was verified that the path coefficients of “Land Use” were significant, characterized by p values lower than 0.05 for long distances (Figure 7).
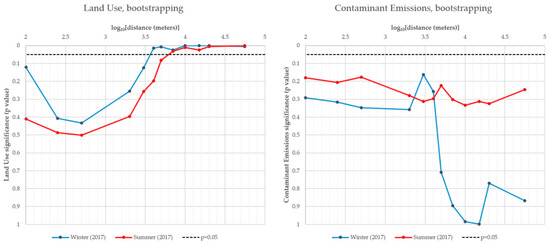
Figure 7.
PLS-PM significance of path coefficients.
The significance of land uses seemed to follow a sigmoid pattern. For the summer period, statistical significance (p < 0.05) was achieved for distances larger than 5 km, but for the winter period, significance was achieved for distances larger than 3 km. When it comes to “Contaminant emissions” none of the models achieved statistical significance. For the summer period, p values increased with distance. For winter, p values seemed not to change for distances below 2 km, increased to 0.124 at 3 km, and then dropped consistently until a distance of 15 km. For 20 and 56 km, there was a notable loss of statistical significance.
4. Discussion
Before analyzing the results, some expectations regarding the effect of the variables are outlined. It was expected that all pressures had a negative impact on ecological integrity, while “Forest” was expected to have a positive effect. This was expected because in catchments with a high presence of forested areas, good water quality can be found [84]. It was also thought that the measured variables that belonged to the latent variable “Contaminant Emissions” would have a higher effect than “Land Use”. This was because the discharges of COD from point sources and nitrogen from livestock, agriculture, and forestry represented the mass flow of contaminants that were transported to surface water, while land use metrics were only indicators of possible pollution. In terms of season and scale, no expectations were anticipated because authors already recognized in different studies that different conclusions can be achieved [34].
The positive effect of “Artificial” for distances below 10 km is hard to explain. By studying the impact of land uses on biological integrity, a positive response was found in urbanized areas [31] by accessing a riparian scale. Another author [85] compared the effects of land uses in the same Index, of Biotic Integrity (IBI) and noted that, in a riparian range, the impacts of urban activity were positively correlated to this index, but for the watershed scale, the outcome was negative, which is in concordance with the present study. This might happen because, at a short range, the impacts of urban presence may be hard to capture, compared to an extended scale. Possibly, urbanized areas only affect water quality when their predominance occurs over a long range.
The agricultural land uses are revealed as a threat to Ave River Basin. For distances larger than 200 m, the effect was negative and increased in scale for both winter and summer seasons. This can reflect that agriculture only affects water quality when the predominance is on a long scale, as there is a high accumulation of contaminants. Likewise, other studies revealed a negative impact over a long scale [24,34,39,86].
The edge density of forested areas “Forest” was the variable that had an expected impact on winter and summer (except at the distances of 56 km and 500 m, where the effects were null and negative, respectively). Many authors have concluded that the effect of forestry improves water quality. Positive impacts are found with biotic indexes [31,32], and negative correlations or effects with contaminant concentrations are found [23,24,25,28,39,86,87] independently of scale, season, and study area, or even accessed metric.
In light of the previously mentioned reasons, it was not expected that the effect of “Land use” would be greater than “Contaminant Emissions”. It was noticed that in the winter period, the measured variables that belonged to “Land Use” were the ones with stronger effects (except in the model of the scale 500 m, where livestock had the strongest impact). But, in the summer period, the contaminant emissions from “Forest and Agriculture” and “Livestock” were the variables with the highest pcw. Only at a scale higher than 7 km did the effect of agricultural land use overlap contaminant emissions.
When it comes to significance, the path coefficient of “Land Use” achieved statistical significance in both seasons at a long scale, while “Contaminant emissions” did not. This leads to the conclusion that, in concordance with other authors, the effect of land use should be accessed on a long scale, also called a complete watershed. Both diffuse and point-source discharges have temporal changes [7,88,89,90]. To access the seasonal effects of contaminant emissions, it is important to trace the temporal changes in the contaminant flow, just like it was done in other studies [91]. In the present study, the point source flow of COD and diffuse discharge resulting from livestock production, forested, and agricultural activities was in the form of annual flow. In fact, it is quite hard to access the released contamination on shorter temporal scales for a whole river basin. But, if the data of point and diffuse sources from APA were monthly, or even seasonal, it is believed that the significance of “Contaminant Emissions” would be higher in the model and could possibly reveal higher effects than landscape metrics. In previous studies where the Ave River Basin water quality was assessed, it was noted that point-source pressures [51] and livestock production [52] were major threats to water quality. But, in those studies, landscape metrics were not used in such a detailed form, only the percentage of catchments occupied by agricultural and artificial areas were used. During summer, the contribution of underground water to river discharge increased due to the lack of rainfall [92]. In the presented models this is shown because contaminant emissions from agriculture, forest, and livestock effects were indeed larger in summer periods than in winter. During winter, the runoff effect was higher due to strong rainfalls, which explains why variables related to land use metrics had a stronger impact in winter rather than in summer.
Another important aspect is that when formative PLS-PM models are adopted, the number of explaining variables cannot be large because of the shortcomings of variance inflation. One technique to reduce variance inflation is by restraining the number of variables [93]. For this reason, the effects of other land use metrics were not accessed in this study, only the edge density of forested areas, Shannon’s diversity index, and connectance metrics of agricultural and artificial surfaces. However, this study succeeded in demonstrating the seasonal and scale effects in the interaction between various pollution sources and ecological integrity. The low sample size (n = 12) was a limitation. As a consequence, the weights were not significant. Despite this, it was still possible to achieve significance for the path coefficient “Land Use” latent variable. So, it is recommended to use larger sample sizes in similar and future studies. Since the weights were not significant, the tested models may not be suited for prediction purposes. At any rate, the presented study indicates that, in terms of prediction in the Ave River Basin, longer scales should be adopted, considering the consistent high R-squared values and significance of land use variables observed at these scales.
For proper river basin management, landscape metric variables should always be assessed, as it is quite easy to calculate them using computer packages such as FRAGSTATS [94] or the ArcGIS toolbox [76]. In terms of landscape management, when the consequences of anthropogenic pressures for water quality are to be assessed, the exercise should always be applied to various scales. This is recommended because this study concluded that the sense (positive or negative) of an impact can change with scale.
The most limiting factor in this study was probably the small number of sampling points used to assess the IPtIN, just 12. However, these few samples allowed us to provisionally expose the significant role (p < 0.05) of land use metrics for a satisfactory (R2 ≈ 0.85) explanation of water quality (IPtIN) in the long range (>4 km from the contaminant sources). This result is noteworthy. It can be (and was) argued that more samples would render the possibility to reveal the influence of other anthropogenic pressures, eventually hidden in this study by the sample’s coarse resolution. Nevertheless, it would not be a surprise if the results obtained in this study were replicated with a finer resolution, as contaminant emissions are subject to larger inter annual variations than are land uses, and, hence, they could eventually be inefficient in the studied period. A larger sample would probably capture fine-resolution effects, for example, related to point-source contaminant emissions, but is not certain that would change the general outcomes and conclusions taken from this study. The main goals were achieved, which were to explore the influence of anthropogenic pressures on water quality as function of scale and season using a novel statistical method. The 26 PLS-PM models implemented in a predefined sequence were capable of identifying the most important variables and distances from contaminant sources that controlled water quality in the Ave River Basin in the studied period. The model results may not be directly used in management initiatives without prior verification using a larger sample, but they suggested how scale and season can affect the conclusions about cause–effect relationships involving anthropogenic pressures and water quality. In that context, the outcomes from this study provided interesting clues for managers of water quality at catchment scale, which are inherently an important scientific result.
5. Conclusions
This study has shown to be effective in demonstrating seasonal and scale impacts in the interplay between the effect of landscape metrics and contamination sources on water quality. This analysis plays an important role for decision makers to take into account that territory planning is intrinsically linked to water quality. As it was found in this study, the effect of metrics can be greater than contamination sources. From a statistical point of view, this study showed that the use of a long scale is preferable, since it obtained higher coefficients of determination in both winter and summer, but also high statistical significance for the latent variable “Land Use”. Even so, it is advised that when water quality studies are carried out, effects should always be analyzed not at a long scale but also at a short scale. This is because each river basin is unique and reveals natural and anthropogenic interactions that are different in each river basin. So, in other locations, stronger effects can be found at shorter scales. In terms of water quality improvement, besides the constant monitoring and reduction of pollution sources, it is pointed out that the presence of forested areas improves the ecological integrity, not in total area but in terms of edge density. As far as agricultural areas are concerned for ecological integrity, strategic relocations can also be a key strategy in order to decrease connectance. While in urban areas, these hardly can be changed, given the enormous costs that such processes can entail.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4441/11/10/2025/s1, The supplementary materials comprise an Excel file with base data and results of PLS-PM models.
Author Contributions
Conceptualization, A.C.P.F.; methodology, A.C.P.F. and F.A.L.P.; software, A.C.P.F.; validation, F.A.L.P.; formal analysis, L.F.S.F.; investigation, A.C.P.F.; resources, L.F.S.F. and R.M.V.C.; data curation, A.C.P.F., F.A.L.P., L.F.S.F. and R.M.V.C.; writing—original draft preparation, A.C.P.F.; writing—review and editing, F.A.L.P.; visualization, A.C.P.F.; supervision, F.A.L.P. and L.F.S.F.; project administration, R.M.V.C.; funding acquisition, R.M.V.C.
Funding
This research was funded by the INTERACT project “Integrated Research in Environment, Agro-Chain and Technology”, no. NORTE-01-0145-FEDER-000017, in the line of research entitled BEST “Bio-economy and Sustainability”, and co-financed by the European Regional Development Fund (ERDF) through NORTE 2020 (the North Regional Operational Program 2014/2020). For authors at the CITAB research centre, this research was further financed by the FEDER/COMPETE/POCI—Operational Competitiveness and Internationalization Programme under Project POCI-01-0145-FEDER-006958, and by National Funds of FCT—Portuguese Foundation for Science and Technology under the project UID/AGR/04033/2019. For the author in the CQVR, this research was additionally supported by National Funds of FCT—Portuguese Foundation for Science and Technology under the project UID/QUI/00616/2019.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript or in the decision to publish the results.
References
- Vorosmarty, C.J.; Green, P.; Salisbury, J.; Lammers, R.B. Global Water Resources: Vulnerability from Climate Change and Population Growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef] [PubMed]
- Delpla, I.; Jung, A.-V.; Baures, E.; Clement, M.; Thomas, O. Impacts of climate change on surface water quality in relation to drinking water production. Environ. Int. 2009, 35, 1225–1233. [Google Scholar] [CrossRef] [PubMed]
- Muga, H.E.; Mihelcic, J.R. Sustainability of wastewater treatment technologies. J. Environ. Manag. 2008, 88, 437–447. [Google Scholar] [CrossRef] [PubMed]
- Wright, J.; Gundry, S.; Conroy, R. Household drinking water in developing countries: A systematic review of microbiological contamination between source and point-of-use. Trop. Med. Int. Health 2004, 9, 106–117. [Google Scholar] [CrossRef] [PubMed]
- Hayet, C.; Saida, B.A.; Youssef, T.; Hédi, S. Study of biodegradability for municipal and industrial Tunisian wastewater by respirometric technique and batch reactor test. Sustain. Environ. Res. 2016, 26, 55–62. [Google Scholar] [CrossRef][Green Version]
- Serrano-Grijalva, L.; Sánchez-Carrillo, S.; Angeler, D.G.; Sánchez-Andrés, R.; Álvarez-Cobelas, M. Effects of shrimp-farm effluents on the food web structure in subtropical coastal lagoons. J. Exp. Mar. Biol. Ecol. 2011, 402, 65–74. [Google Scholar] [CrossRef]
- Grizzetti, B.; Bouraoui, F.; De Marsily, G. Assessing nitrogen pressures on European surface water. Glob. Biogeochem. Cycles 2008, 22. [Google Scholar] [CrossRef]
- Sheoran, A.S.; Sheoran, V. Heavy metal removal mechanism of acid mine drainage in wetlands: A critical review. Miner. Eng. 2006, 19, 105–116. [Google Scholar] [CrossRef]
- Soares, H.M.V.; Boaventura, R.A.; Machado, A.A.S.; Esteves da Silva, J.C. Sediments as monitors of heavy metal contamination in the Ave river basin (Portugal): Multivariate analysis of data. Environ. Pollut. 1999, 105, 311–323. [Google Scholar] [CrossRef]
- Murphy, F.; Ewins, C.; Carbonnier, F.; Quinn, B. Wastewater Treatment Works (WwTW) as a Source of Microplastics in the Aquatic Environment. Environ. Sci. Technol. 2016, 50, 5800–5808. [Google Scholar] [CrossRef]
- Ayers, R.S.; Westcot, D.W. Water Quality for Agriculture; FAO United Nations: Rome, Italy, 1985. [Google Scholar]
- Nilsson, C.; Svedmark, M. Basic Principles and Ecological Consequences of Changing Water Regimes: Riparian Plant Communities. Environ. Manag. 2002, 30, 468–480. [Google Scholar] [CrossRef]
- Merritt, R.W.; Walker, E.D.; Small, P.L.C.; Wallace, J.R.; Johnson, P.D.R.; Benbow, M.E.; Boakye, D.A. Ecology and transmission of Buruli ulcer disease: A systematic review. PLoS Negl. Trop. Dis. 2010, 4, e911. [Google Scholar] [CrossRef] [PubMed]
- Santos, R.M.B.; Sanches Fernandes, L.F.; Varandas, S.G.P.; Pereira, M.G.; Sousa, R.; Teixeira, A.; Lopes-Lima, M.; Cortes, R.M.V.; Pacheco, F.A.L. Impacts of climate change and land-use scenarios on Margaritifera margaritifera, an environmental indicator and endangered species. Sci. Total Environ. 2015, 511, 477–488. [Google Scholar] [CrossRef] [PubMed]
- Townsend, S.A.; Douglas, M.M. The effect of a wildfire on stream water quality and catchment water yield in a tropical savanna excluded from fire for 10 years (Kakadu National Park, North Australia). Water Res. 2004, 38, 3051–3058. [Google Scholar] [CrossRef]
- Arkle, R.S.; Pilliod, D.S. Prescribed fires as ecological surrogates for wildfires: A stream and riparian perspective. For. Ecol. Manag. 2010, 259, 893–903. [Google Scholar] [CrossRef]
- Smith, H.G.; Sheridan, G.J.; Lane, P.N.J.; Nyman, P.; Haydon, S. Wildfire effects on water quality in forest catchments: A review with implications for water supply. J. Hydrol. 2011, 396, 170–192. [Google Scholar] [CrossRef]
- Santos, R.M.B.; Sanches Fernandes, L.F.; Pereira, M.G.; Cortes, R.M.V.; Pacheco, F.A.L. A framework model for investigating the export of phosphorus to surface waters in forested watersheds: Implications to management. Sci. Total Environ. 2015, 536, 295–305. [Google Scholar] [CrossRef]
- Júnior, R.; Galbiatti, J.A.; Pissarra, T.C.; Martins Filho, M. Diagnóstico do Conflito de Uso e Ocupação do Solo na Bacia do Rio Uberaba. Glob. Sci. Technol. 2013, 6, 40–52. [Google Scholar] [CrossRef]
- Pacheco, F.A.L.; Varandas, S.G.P.; Sanches Fernandes, L.F.; Valle Junior, R.F. Soil losses in rural watersheds with environmental land use conflicts. Sci. Total Environ. 2014, 485–486, 110–120. [Google Scholar] [CrossRef]
- Pacheco, F.A.L.; Sanches Fernandes, L.F. Environmental land use conflicts in catchments: A major cause of amplified nitrate in river water. Sci. Total Environ. 2016, 548–549, 173–188. [Google Scholar] [CrossRef]
- McGarigal, K. Landscape Pattern Metrics. In Wiley StatsRef: Statistics Reference Online; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Uuemaa, E.; Roosaare, J.; Mander, Ü. Scale dependence of landscape metrics and their indicatory value for nutrient and organic matter losses from catchments. Ecol. Indic. 2005, 5, 350–369. [Google Scholar] [CrossRef]
- Lee, S.-W.; Hwang, S.-J.; Lee, S.-B.; Hwang, H.-S.; Sung, H.-C. Landscape ecological approach to the relationships of land use patterns in watersheds to water quality characteristics. Landsc. Urban Plan. 2009, 92, 80–89. [Google Scholar] [CrossRef]
- Łowicki, D. Prediction of flowing water pollution on the basis of landscape metrics as a tool supporting delimitation of Nitrate Vulnerable Zones. Ecol. Indic. 2012, 23, 27–33. [Google Scholar] [CrossRef]
- Wu, M.Y.; Xue, L.; Jin, W.B.; Xiong, Q.X.; Ai, T.C.; Li, B.L. Modelling the Linkage Between Landscape Metrics and Water Quality Indices of Hydrological Units in Sihu Basin, Hubei Province, China: An Allometric Model. Procedia Environ. Sci. 2012, 13, 2131–2145. [Google Scholar] [CrossRef][Green Version]
- Wu, J.; Shen, W.; Sun, W.; Tueller, P.T. Empirical patterns of the effects of changing scale on landscape metrics. Landsc. Ecol. 2002, 17, 761–782. [Google Scholar] [CrossRef]
- Ding, J.; Jiang, Y.; Liu, Q.; Hou, Z.; Liao, J.; Fu, L.; Peng, Q. Influences of the land use pattern on water quality in low-order streams of the Dongjiang River basin, China: A multi-scale analysis. Sci. Total Environ. 2016, 551–552, 205–216. [Google Scholar] [CrossRef] [PubMed]
- Morley, S.A.; Karr, J.R. Assessing and restoring the health of urban streams in the Puget Sound Basin. Conserv. Biol. 2002, 16, 1498–1509. [Google Scholar] [CrossRef]
- Allan, J.D.; Erickson, D.L.; Fay, J. The influence of catchment land use on stream integrity across multiple spatial scales. Freshw. Biol. 1997, 37, 149–161. [Google Scholar] [CrossRef]
- Roth, N.E.; Allan, J.D.; Erickson, D.L. Landscape influences on stream biotic integrity assessed at multiple spatial scales. Landsc. Ecol. 1996, 11, 141–156. [Google Scholar] [CrossRef]
- Potter, K.M.; Cubbage, F.W.; Schaberg, R.H. Multiple-scale landscape predictors of benthic macroinvertebrate community structure in North Carolina. Landsc. Urban Plan. 2005, 71, 77–90. [Google Scholar] [CrossRef]
- Hunsaker, C.T.; Levine, D.A. Hierarchical Approaches to the Study of Water Quality in Rivers. Bioscience 1995, 45, 193–203. [Google Scholar] [CrossRef]
- Zhang, J.; Li, S.; Dong, R.; Jiang, C.; Ni, M. Influences of land use metrics at multi-spatial scales on seasonal water quality: A case study of river systems in the Three Gorges Reservoir Area, China. J. Clean. Prod. 2019, 206, 76–85. [Google Scholar] [CrossRef]
- Johnson, L.B.; Richards, C.; Host, G.E.; Arthur, J.W. Landscape influences on water chemistry in Midwestern stream ecosystems. Freshw. Biol. 1997, 37, 193–208. [Google Scholar] [CrossRef]
- Dodds, W.K.; Oakes, R.M. Headwater influences on downstream water quality. Environ. Manag. 2008, 41, 367–377. [Google Scholar] [CrossRef] [PubMed]
- Tran, C.P.; Bode, R.W.; Smith, A.J.; Kleppel, G.S. Land-use proximity as a basis for assessing stream water quality in New York State (USA). Ecol. Indic. 2010, 10, 727–733. [Google Scholar] [CrossRef]
- Schiff, R.; Benoit, G. Effects of impervious cover at multiple spatial scales on coastal watershed streams. J. Am. Water Resour. Assoc. 2007, 43, 712–730. [Google Scholar] [CrossRef]
- Yu, S.; Xu, Z.; Wu, W.; Zuo, D. Effect of land use types on stream water quality under seasonal variation and topographic characteristics in the Wei River basin, China. Ecol. Indic. 2016, 60, 202–212. [Google Scholar] [CrossRef]
- Thakur, A.K. Model: Mechanistic vs Empirical. In New Trends in Pharmacokinetics; Springer: Boston, MA, USA, 1991; pp. 41–51. [Google Scholar]
- Loucks, D.P.; van Beek, E. Water Quality Modelling and Prediction. In Water Resources Systems Planning and Management; UNESKO: Paris, France, 2005. [Google Scholar]
- Astrachan, C.B.; Patel, V.K.; Wanzenried, G. A comparative study of CB-SEM and PLS-SEM for theory development in family firm research. J. Fam. Bus. Strategy 2014, 5, 116–128. [Google Scholar] [CrossRef]
- Gorai, A.K.; Tuluri, F.; Tchounwou, P.B. Development of PLS–path model for understanding the role of precursors on ground level ozone concentration in Gulfport, Mississippi, USA. Atmos. Pollut. Res. 2015, 6, 389–397. [Google Scholar] [CrossRef]
- Chenini, I.; Khmiri, S. Evaluation of ground water quality using multiple linear regression and structural equation modeling. Int. J. Environ. Sci. Technol. 2009, 6, 509–519. [Google Scholar] [CrossRef]
- Levêque, J.G.; Burns, R.C. A Structural Equation Modeling approach to water quality perceptions. J. Environ. Manag. 2017, 197, 440–447. [Google Scholar] [CrossRef] [PubMed]
- Nugroho, A.R.; Masduqi, A. Structural equation modelling as instrument for water pollution factor analysis. In Proceedings of the 4th International Conference Advances in Applied Science and Environmental Technology—ASET 2016, Bangkok, Thailand, 7–8 May 2016. [Google Scholar]
- Martins, L.; Pereira, A.; Oliveira, A.; Fernandes, A.; Sanches Fernandes, L.F.; Pacheco, F.A.L. An assessment of groundwater contamination risk with radon based on clustering and structural models. Water 2019, 11, 1107. [Google Scholar] [CrossRef]
- Salgado Terêncio, D.P.; Sanches Fernandes, L.F.; Vitor Cortes, R.M.; Moura, J.P.; Leal Pacheco, F.A. Can Land Cover Changes Mitigate Large Floods? A Reflection Based on Partial Least Squares-Path Modeling. Water 2019, 11, 684. [Google Scholar] [CrossRef]
- Garcês, A.; Pires, I.; Pacheco, F.A.L.; Sanches Fernandes, L.F.; Soeiro, V.; Lóio, S.; Prada, J.; Cortes, R.; Queiroga, F.L. Preservation of wild bird species in northern Portugal—Effects of anthropogenic pressures in wild bird populations (2008–2017). Sci. Total Environ. 2019, 650, 2996–3006. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, A.R.L.; Sanches Fernandes, L.F.; Cortes, R.M.V.; Pacheco, F.A.L. Assessing anthropogenic impacts on riverine ecosystems using nested partial least squares regression. Sci. Total Environ. 2017, 583, 466–477. [Google Scholar] [CrossRef] [PubMed]
- Sanches Fernandes, L.F.; Fernandes, A.C.P.; Ferreira, A.R.L.; Cortes, R.M.V.; Pacheco, F.A.L. A partial least squares—Path modeling analysis for the understanding of biodiversity loss in rural and urban watersheds in Portugal. Sci. Total Environ. 2018, 626, 1069–1085. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, A.C.P.; Sanches Fernandes, L.F.; Moura, J.P.; Cortes, R.M.V.; Pacheco, F.A.L. A structural equation model to predict macroinvertebrate-based ecological status in catchments influenced by anthropogenic pressures. Sci. Total Environ. 2019, 681, 242–257. [Google Scholar] [CrossRef]
- APA—ARH-Norte. Plano de Gestão da Região Hidrográfica do Cávado, Ave e Leça (RH2). Relatório Base 1o Ciclo Parte 1—Enquadramento e Aspectos Gerais; Agência Portuguesa do Ambiente: Porto, Portugal, 2012. [Google Scholar]
- Gonçalves, E.P.R.; Boaventura, R.A.R.; Mouvet, C. Sediments and aquatic mosses as pollution indicators for heavy metals in the Ave river basin (Portugal). Sci. Total Environ. 1992, 114, 7–24. [Google Scholar] [CrossRef]
- Alves, C.; Boaventura, R.; Soares, H. Evaluation of Heavy Metals Pollution Loadings in the Sediments of the Ave River Basin (Portugal). Soil Sediment. Contam. 2009, 18, 603–618. [Google Scholar] [CrossRef]
- Peixoto, F.P.; Carrola, J.; Coimbra, A.M.; Teixeira, P.; Coelho, L.; Conceição, I.; Oliveira, M.M.; Fontaínhas-Fernandes, A.; Fernandes, C. Oxidative stress responses and histological hepatic alterations in barbel, Barbus bocagei, from Vizela River, Portugal. Rev. Int. Contam. Ambient. 2013, 29, 29–38. [Google Scholar]
- Pascoal, C.; Pinho, M.; Cássio, F.; Gomes, P. Assessing structural and functional ecosystem condition using leaf breakdown: Studies on a polluted river. Freshw. Biol. 2003, 48, 2033–2044. [Google Scholar] [CrossRef]
- Pascoal, C.; Cássio, F.; Marvanová, L. Anthropogenic stress may affect aquatic hyphomycete diversity more than leaf decomposition in a low-order stream. Arch. Hydrobiol. 2005, 162, 481–496. [Google Scholar] [CrossRef]
- Dunck, B.; Lima-Fernandes, E.; Cássio, F.; Cunha, A.; Rodrigues, L.; Pascoal, C. Responses of primary production, leaf litter decomposition and associated communities to stream eutrophication. Environ. Pollut. 2015, 202, 32–40. [Google Scholar] [CrossRef] [PubMed]
- Pinto, D.; Fernandes, A.; Fernandes, R.; Mendes, I.; Pereira, S.; Vinha, A.; Herdeiro, T.; Santos, E.; Machado, M. Determination of heavy metals and other indicators in waters, soils and medicinal plants from Ave valley, in Portugal, and its correlation to urban and industrial pollution. Sci. Microb. Pathog. Commun. Curr. Res. Technol. Adv. 2011, 303–309. [Google Scholar]
- Ribeiro, C.M.R.; Maia, A.S.; Ribeiro, A.R.; Couto, C.; Almeida, A.A.; Santos, M.; Tiritan, M.E. Anthropogenic pressure in a Portuguese river: Endocrine-disrupting compounds, trace elements and nutrients. J. Environ. Sci. Health Part. A 2016, 51, 1043–1052. [Google Scholar] [CrossRef]
- Environmental Systems Resource Institute. ArcMap 10.2.; ESRI: Redlands, CA, USA, 2014. [Google Scholar]
- Maidment, D.R. Arc Hydro: GIS for Water Resources; ESRI Inc.: Redlands, CA, USA, 2002. [Google Scholar]
- Santos, R.M.B.; Sanches Fernandes, L.F.; Cortes, R.M.V.; Varandas, S.G.P.; Jesus, J.J.B.; Pacheco, F.A.L. Integrative assessment of river damming impacts on aquatic fauna in a Portuguese reservoir. Sci. Total Environ. 2017, 601, 1108–1118. [Google Scholar] [CrossRef]
- Fonseca, A.R.; Sanches Fernandes, L.F.; Fontainhas-Fernandes, A.; Monteiro, S.M.; Pacheco, F.A.L. The impact of freshwater metal concentrations on the severity of histopathological changes in fish gills: A statistical perspective. Sci. Total Environ. 2017, 599, 217–226. [Google Scholar] [CrossRef] [PubMed]
- Pacheco, F.A.L. Regional groundwater flow in hard rocks. Sci. Total Environ. 2015, 506, 182–195. [Google Scholar] [CrossRef] [PubMed]
- Pacheco, F.A.L.; Sousa Oliveira, A.; Van Der Weijden, A.J.; Van Der Weijden, C.H. Weathering, biomass production and groundwater chemistry in an area of dominant anthropogenic influence, the Chaves-Vila Pouca de Aguiar region, north of Portugal. Water Air Soil Pollut. 1999, 115, 481–512. [Google Scholar] [CrossRef]
- Pacheco, F.A.L.; Landim, P.M.B. Two-Way Regionalized Classification of Multivariate Datasets and its Application to the Assessment of Hydrodynamic Dispersion. Math. Geol. 2005, 37, 393–417. [Google Scholar] [CrossRef]
- Pacheco, F.A.L.; Landim, P.M.B.; Szocs, T. Anthropogenic impacts on mineral weathering: A statistical perspective. Appl. Geochem. 2013, 36, 34–48. [Google Scholar] [CrossRef]
- Valle Junior, R.F.; Varandas, S.G.P.; Sanches Fernandes, L.F.; Pacheco, F.A.L. Multi Criteria Analysis for the monitoring of aquifer vulnerability: A scientific tool in environmental policy. Environ. Sci. Policy 2015, 48, 250–264. [Google Scholar] [CrossRef]
- Valera, C.A.; Pissarra, T.C.T.; Martins Filho, M.V.; Valle Junior, R.F.; Sanches Fernandes, L.F.; Pacheco, F.A.L. A legal framework with scientific basis for applying the ‘polluter pays principle’ to soil conservation in rural watersheds in Brazil. Land Use Policy 2017, 66, 61–71. [Google Scholar] [CrossRef]
- Environmental Systems Resource Institute. ArcHydro Tools for ArcGIS 10—Tutorial; ESRI: Redlands, CA, USA, 2012. [Google Scholar]
- Ring, C.M.; Wende, S.; Will, A. Smart PLS. Hamburg, Germany. 2005. Available online: http//www.smartpls.de (accessed on 1 May 2019).
- Hair, J.F., Jr.; Sarstedt, M.; Hopkins, L.; Kuppelwieser, V.G. Partial least squares structural equation modeling (PLS-SEM). Eur. Bus. Rev. 2014, 26, 106–121. [Google Scholar] [CrossRef]
- Schindler, U.; Klinner, K.; Nestler, W. Microsoft® Excel—Grundlagen der Makroprogrammierung; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Adamczyk, J.; Tiede, D. ZonalMetrics—A Python toolbox for zonal landscape structure analysis. Comput. Geosci. 2017, 99, 91–99. [Google Scholar] [CrossRef]
- APA Critérios de Classificação do Estado das Massas de Água—Rios e Albufeiras. Available online: https://www.apambiente.pt/dqa/criterios-classificacao.html (accessed on 22 June 2019).
- UKTAG (UKTechnical Advisory Group on the WaterFramework Directive). Technical Report on Groundwater Hazardous Substances. 2016. Available online: https://www.wfduk.org (accessed on 22 June 2019).
- European Commission. Monitoring under the Water Framework Directive. In Common Implementation Strategy for the Water Framework Directive (2000/60/EC); European Commission: Brussels, Belgium, 2003. [Google Scholar]
- Pielou, E.C. The measurement of diversity in different types of biological collections. J. Theor. Biol. 1966, 13, 131–144. [Google Scholar] [CrossRef]
- Jost, L. The Relation between Evenness and Diversity. Diversity 2010, 2, 207–232. [Google Scholar] [CrossRef]
- Devís-Devís, J.; Villamón-Herrera, M. A scientific field searching visibility. International Workshop on Physical Activity and Sport Sciences Quality Journals. Proc. Prof. Inf. 2008, 17, 242–246. [Google Scholar]
- Ketchen, D.J. A Primer on Partial Least Squares Structural Equation Modeling. Long Range Plan. 2013, 46, 184–185. [Google Scholar] [CrossRef]
- Neary, D.G.; Ice, G.G.; Jackson, C.R. Linkages between forest soils and water quality and quantity. For. Ecol. Manag. 2009, 258, 2269–2281. [Google Scholar] [CrossRef]
- Snyder, C.D.; Young, J.A.; Villella, R.; Lemarié, D.P. Influences of upland and riparian land use patterns on stream biotic integrity. Landsc. Ecol. 2003, 18, 647–664. [Google Scholar] [CrossRef]
- Sliva, L.; Dudley Williams, D. Buffer Zone versus Whole Catchment Approaches to Studying Land Use Impact on River Water Quality. Water Res. 2001, 35, 3462–3472. [Google Scholar] [CrossRef]
- Bu, H.; Meng, W.; Zhang, Y.; Wan, J. Relationships between land use patterns and water quality in the Taizi River basin, China. Ecol. Indic. 2014, 41, 187–197. [Google Scholar] [CrossRef]
- Grizzetti, B.; Bouraoui, F.; de Marsily, G.; Bidoglio, G. A statistical method for source apportionment of riverine nitrogen loads. J. Hydrol. 2005, 304, 302–315. [Google Scholar] [CrossRef]
- Bowes, M.J.; Smith, J.T.; Jarvie, H.P.; Neal, C.; Barden, R. Changes in point and diffuse source phosphorus inputs to the River Frome (Dorset, UK) from 1966 to 2006. Sci. Total Environ. 2009, 407, 1954–1966. [Google Scholar] [CrossRef]
- Heathwaite, A.L.; Dils, R.M.; Liu, S.; Carvalho, L.; Brazier, R.E.; Pope, L.; Hughes, M.; Phillips, G.; May, L. A tiered risk-based approach for predicting diffuse and point source phosphorus losses in agricultural areas. Sci. Total Environ. 2005, 344, 225–239. [Google Scholar] [CrossRef] [PubMed]
- Spieles, D.J.; Mitsch, W.J. The effects of season and hydrologic and chemical loading on nitrate retention in constructed wetlands: A comparison of low- and high-nutrient riverine systems. Ecol. Eng. 1999, 14, 77–91. [Google Scholar] [CrossRef]
- Jones, J.P.; Sudicky, E.A.; Brookfield, A.E.; Park, Y.-J. An assessment of the tracer-based approach to quantifying groundwater contributions to streamflow. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Coltman, T.; Devinney, T.M.; Midgley, D.F.; Venaik, S. Formative versus reflective measurement models: Two applications of formative measurement. J. Bus. Res. 2008, 61, 1250–1262. [Google Scholar] [CrossRef]
- McGarigal, K.; Marks, B.J. FRAGSTATS: Spatial Pattern Analysis Program for Quantifying Landscape Structure; U.S. Department Agriculture Forest Service/Pacific Northwest Research Station: Washington, DC, USA, 1995.
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).