Comparison of Multiple Linear Regression, Artificial Neural Network, Extreme Learning Machine, and Support Vector Machine in Deriving Operation Rule of Hydropower Reservoir
Abstract
1. Introduction
2. Deterministic Hydropower Reservoir Operation to Produce Dataset
2.1. Objective Function
2.2. Operation Constraints
2.3. Optimization Methods
3. Brief Introductions of the Adopted Methods
3.1. Multiple Linear Regression (MLR)
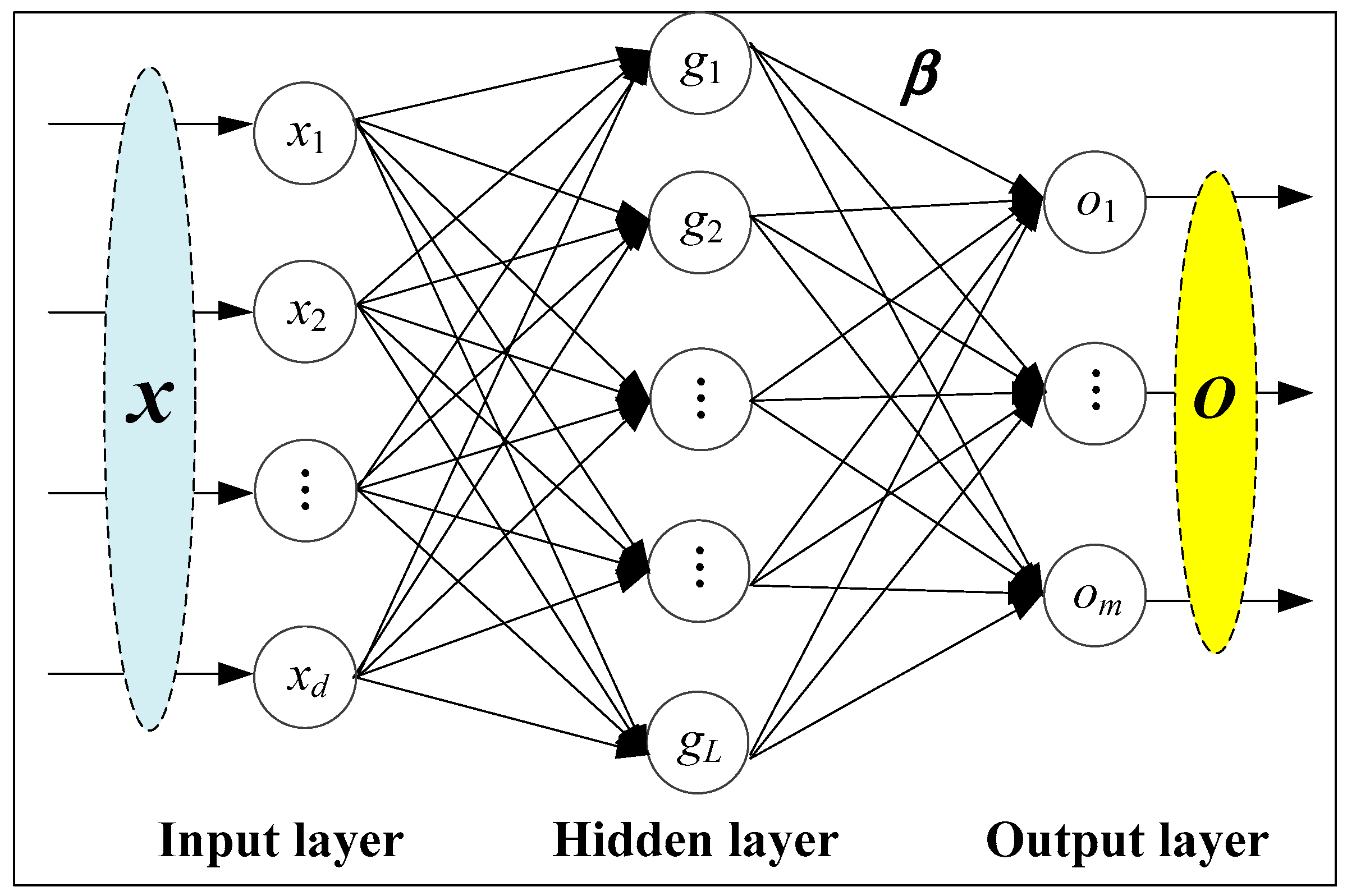
3.2. Artificial Neural Network (ANN)
3.3. Extreme Learning Machine (ELM)
- Step 1:
- Define the amount of hidden neurons and the activation function of each neuron.
- Step 2:
- Produce the input-hidden weights as well as the hidden biases.
- Step 3:
- Use all the data samples to obtain the output matrix of the hidden layer.
- Step 4:
- Choose the suitable method to calculate the hidden-output weights.
- Step 5:
- Use the optimized ELM network to produce the simulated output for new samples.
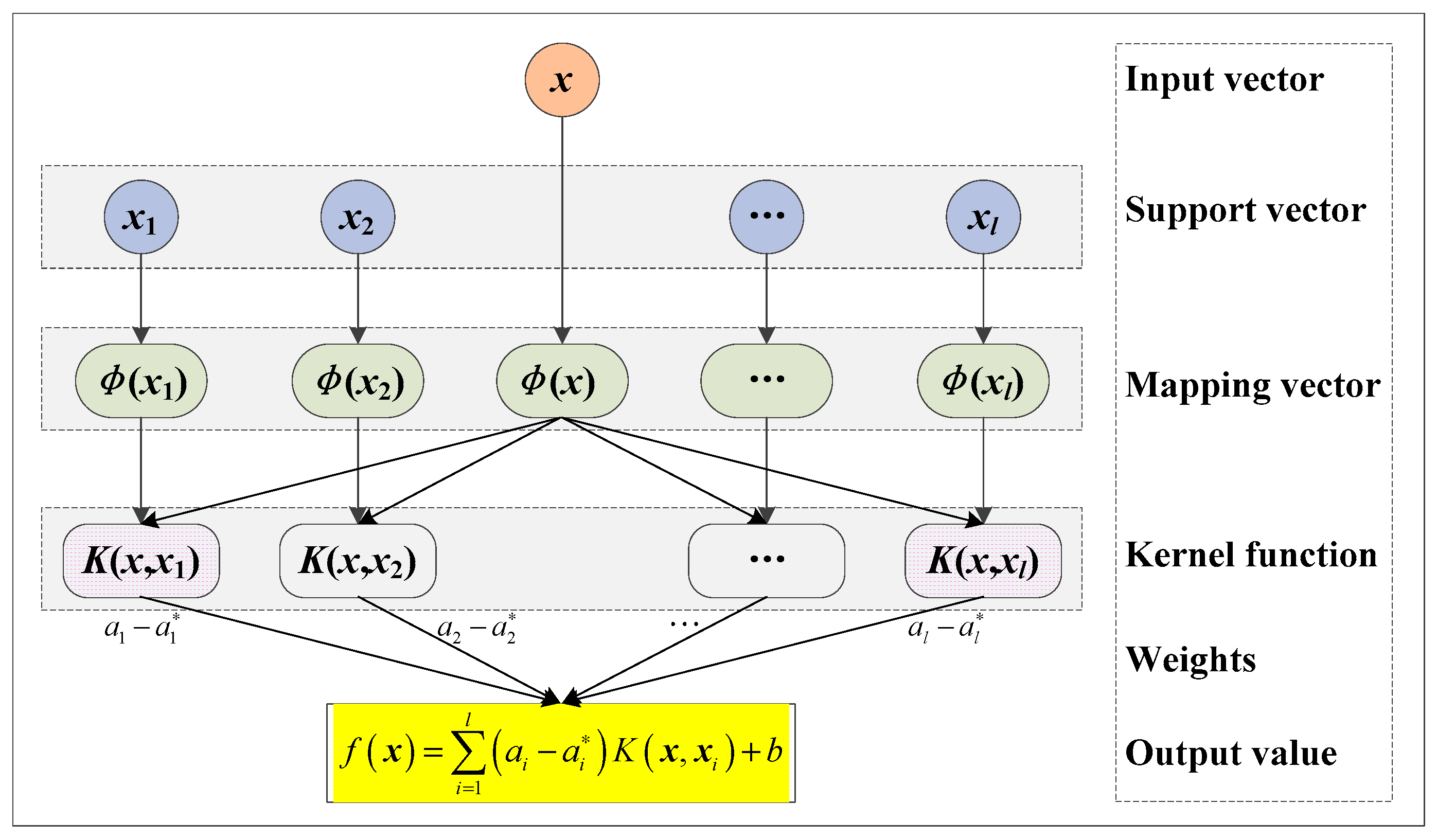
3.4. Support Vector Machine (SVM)
4. Experimental Results
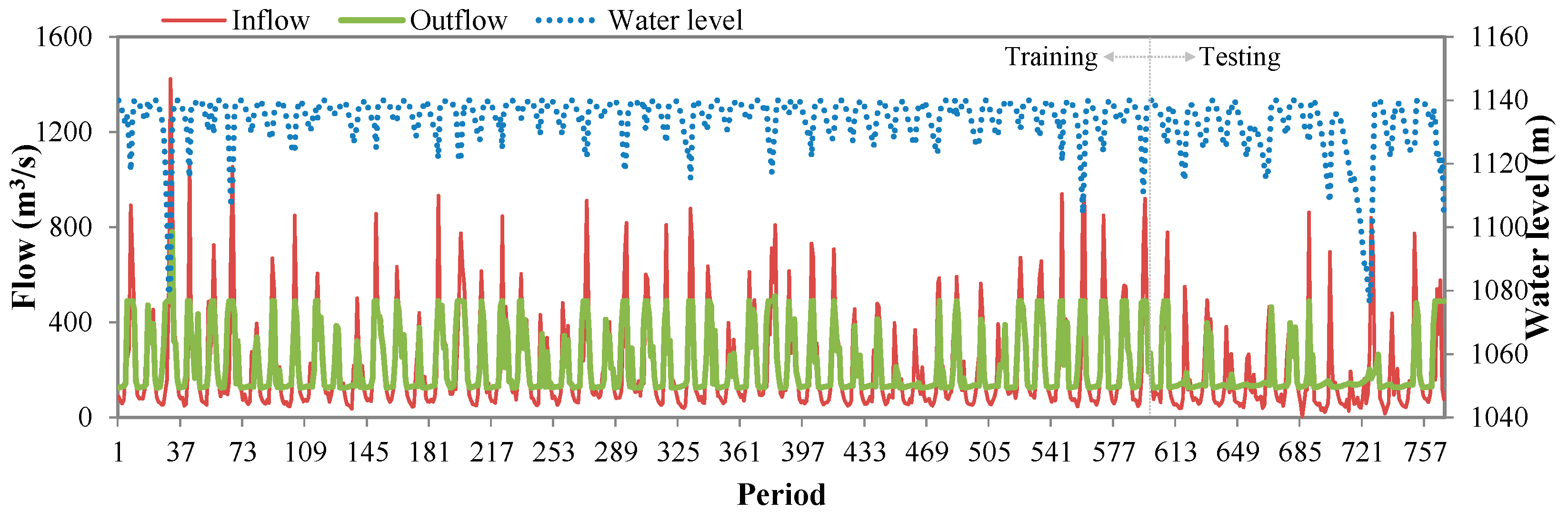
4.1. Study Area and Dataset
4.2. Performance Criterion
4.3. Model Development
4.3.1. MLR Model Development
4.3.2. ANN Model Development
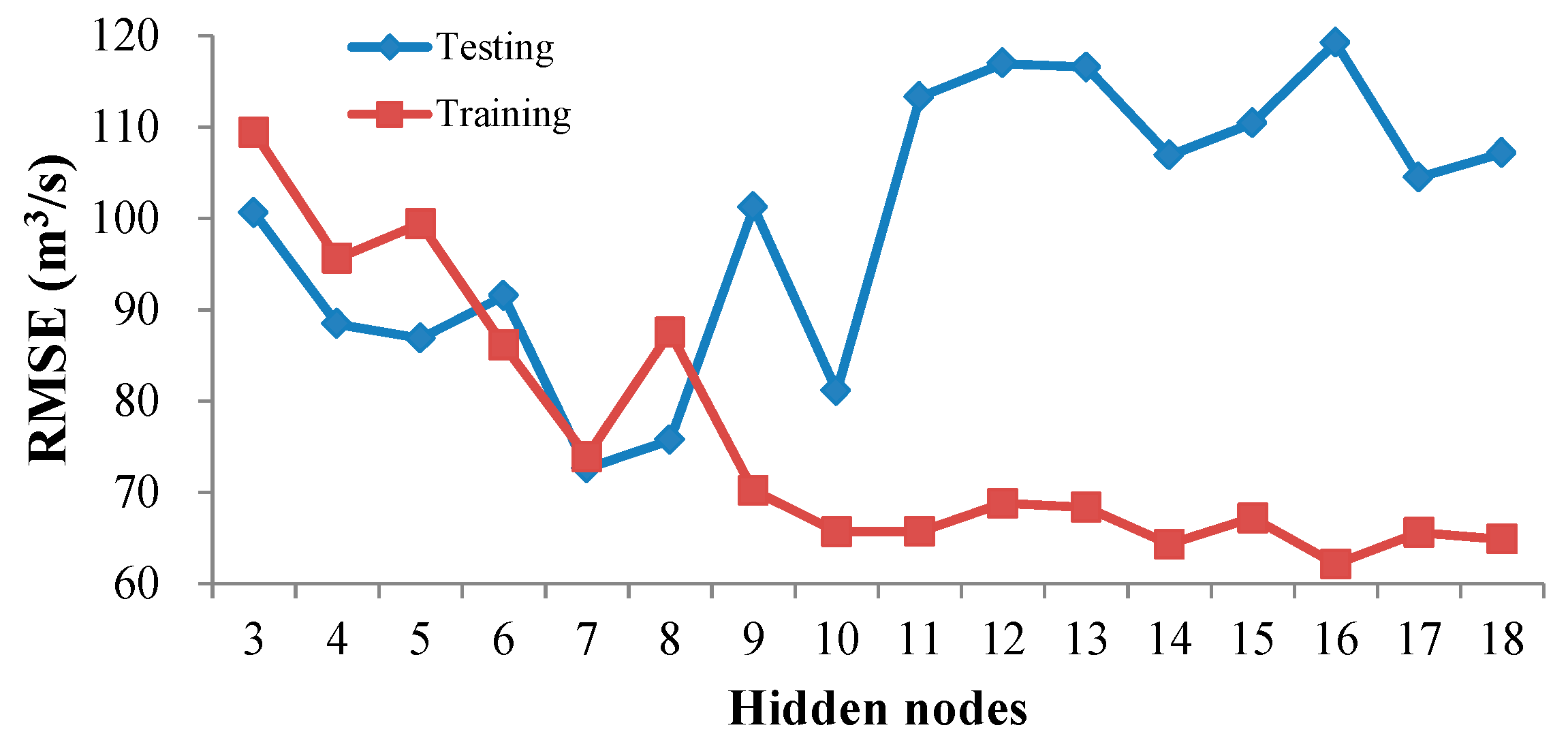
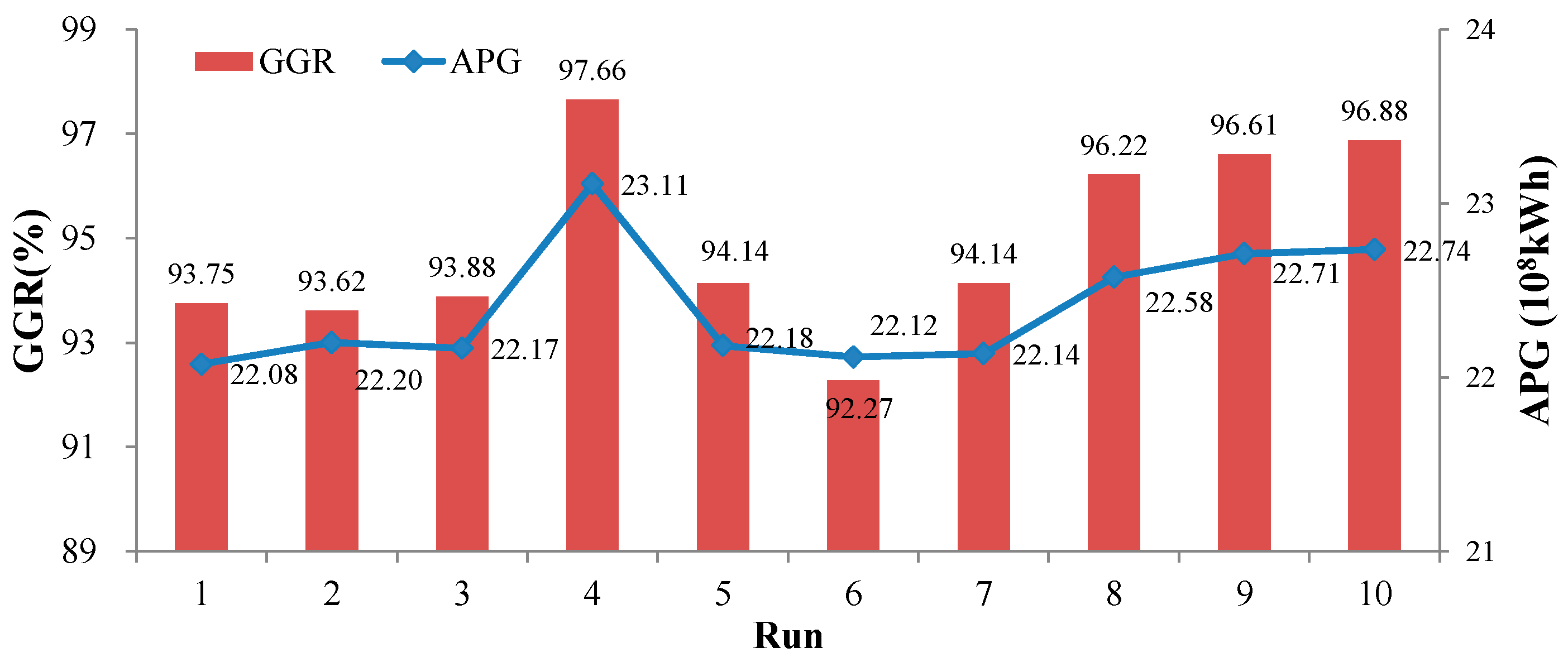
4.3.3. ELM Model Development
4.3.4. SVM Model Development
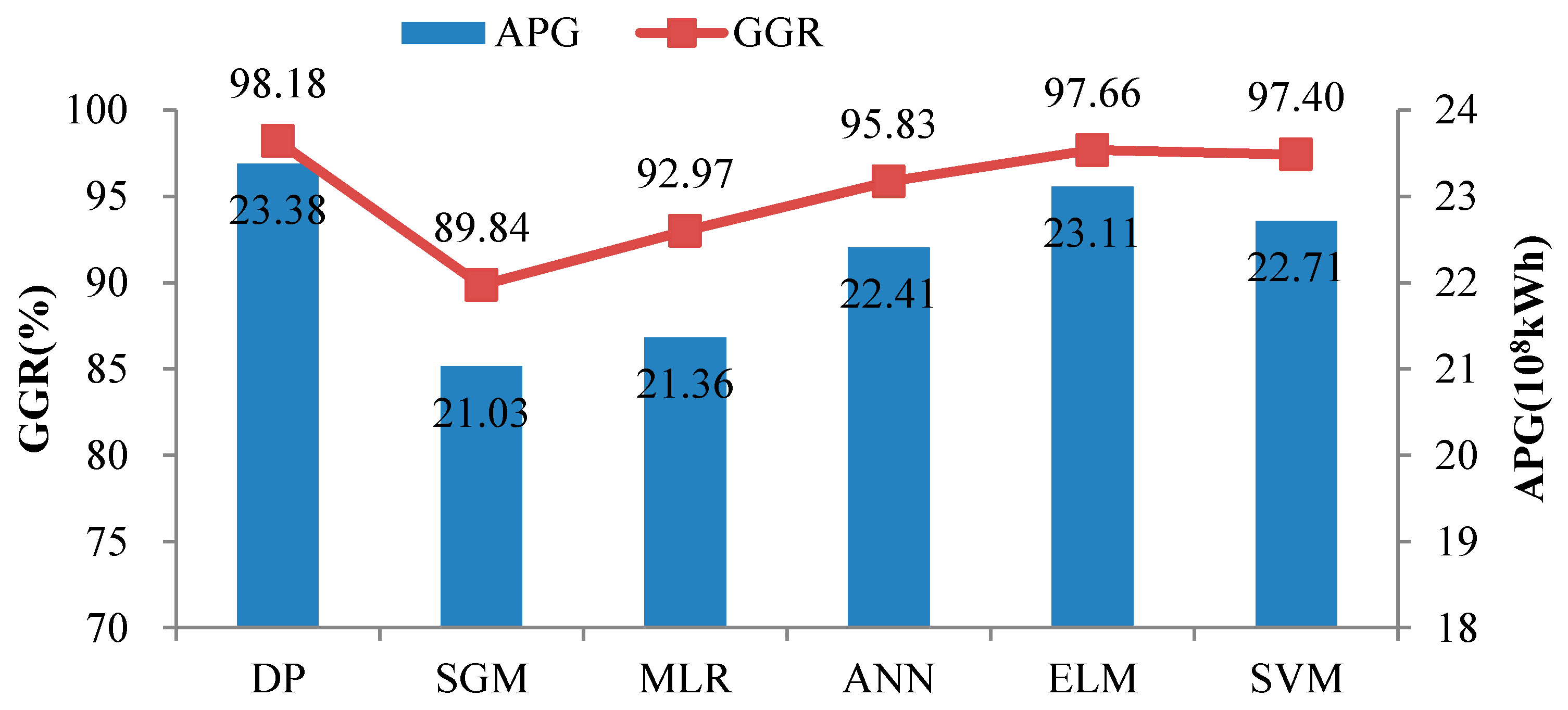
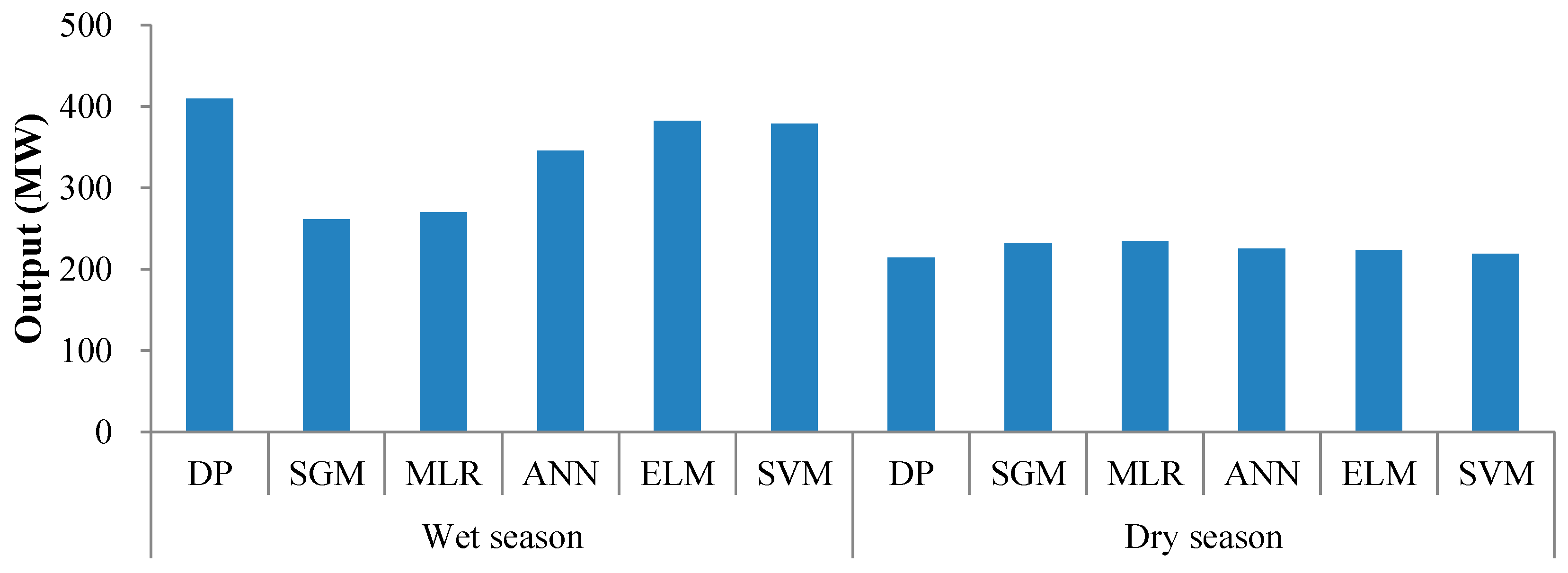
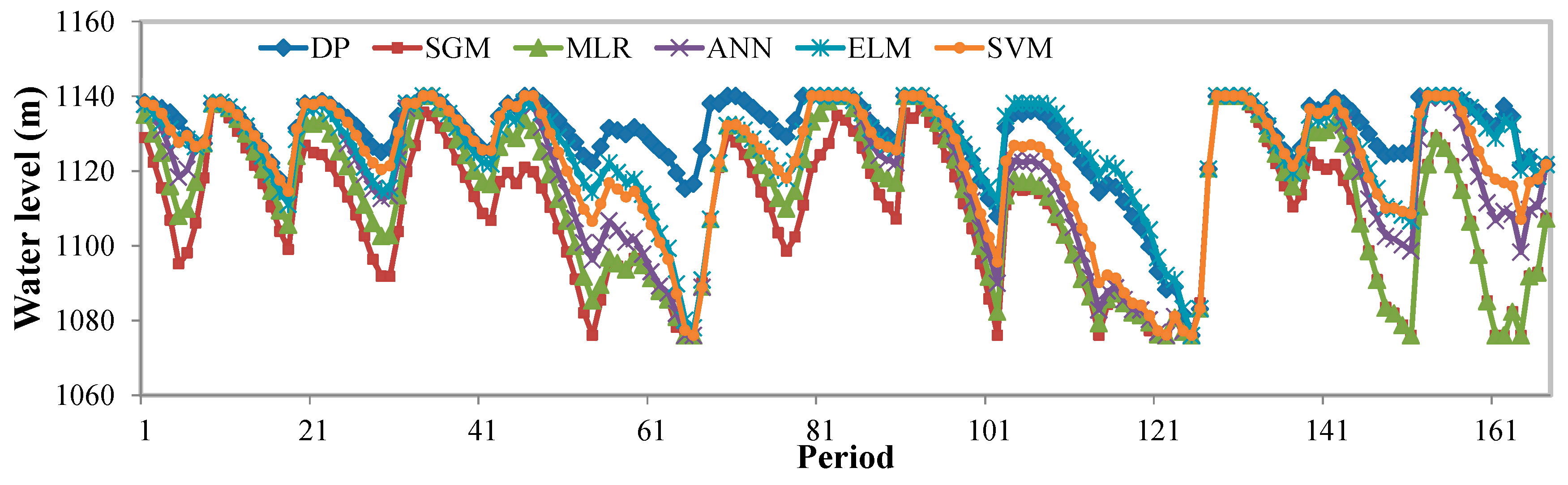
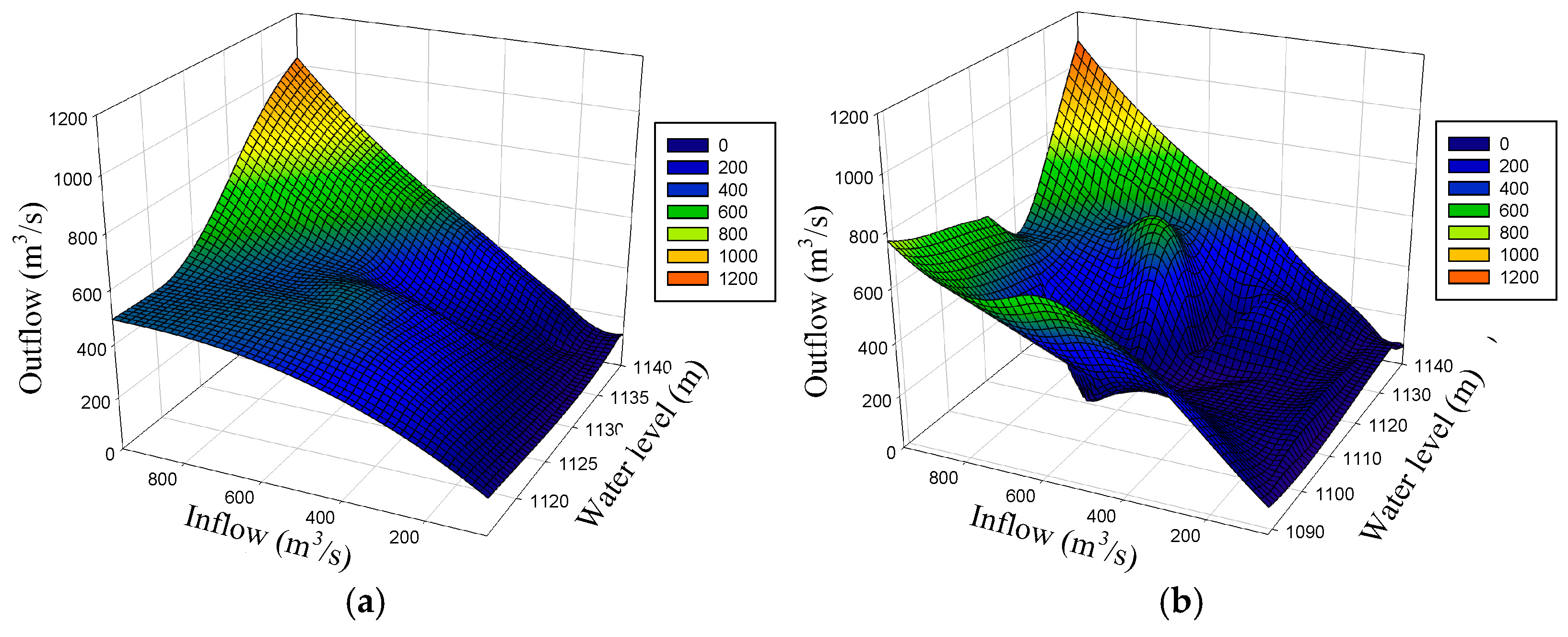
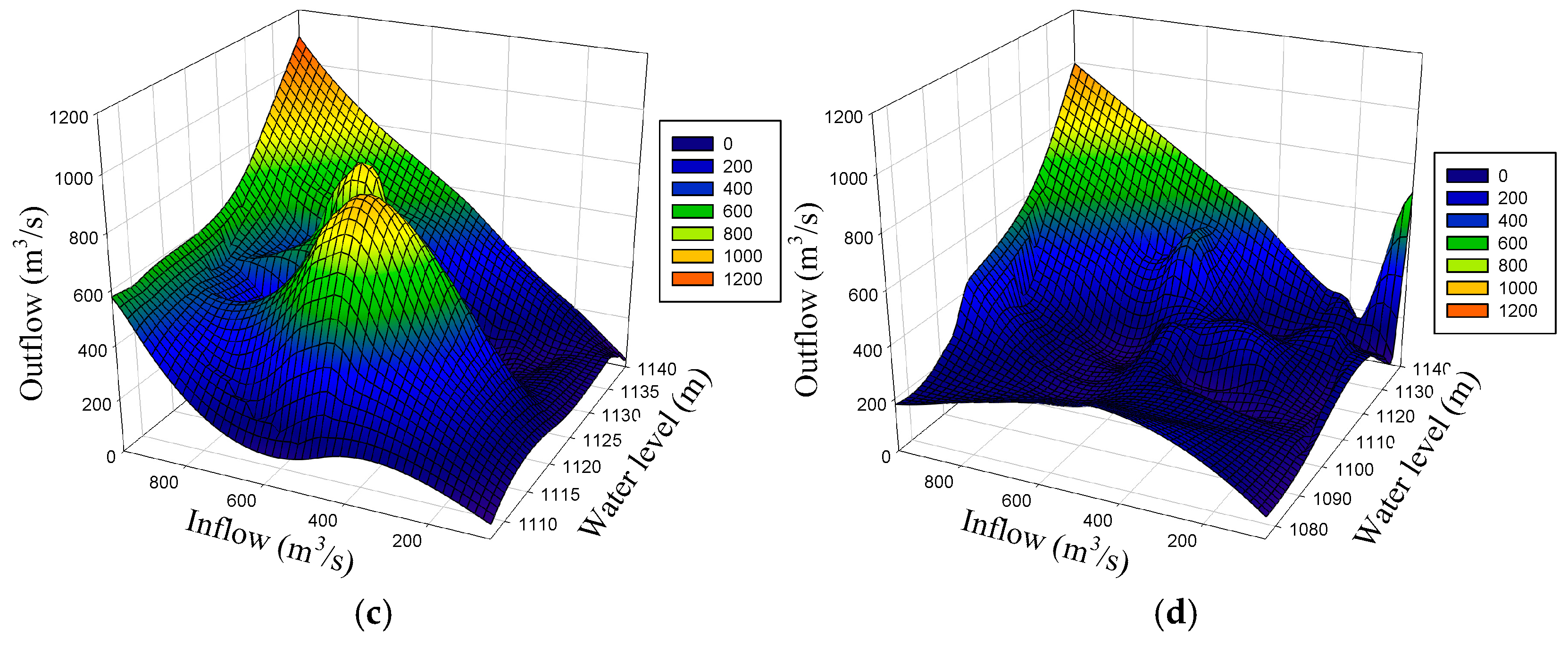
4.4. Comparison and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Feng, Z.K.; Niu, W.J.; Cheng, C.T.; Liao, S.L. Hydropower system operation optimization by discrete differential dynamic programming based on orthogonal experiment design. Energy 2017, 126, 720–732. [Google Scholar] [CrossRef]
- Ming, B.; Chang, J.X.; Huang, Q.; Wang, Y.M.; Huang, S.Z. Optimal operation of Multi-Reservoir system Based-On cuckoo search algorithm. Water Resour. Manag. 2015, 29, 5671–5687. [Google Scholar] [CrossRef]
- Madani, K. Game theory and water resources. J. Hydrol. 2010, 381, 225–238. [Google Scholar] [CrossRef]
- Niu, W.J.; Feng, Z.K.; Cheng, C.T.; Wu, X.Y. A parallel multi-objective particle swarm optimization for cascade hydropower reservoir operation in southwest china. Appl. Soft Comput. 2018, 70, 562–575. [Google Scholar] [CrossRef]
- Madani, K.; Lund, J.R.; Krone, R.B. Innovative modelling for Califomian high hydro. Int. Water Power Dam Constr. 2012, 64, 34–36. [Google Scholar]
- Zhang, Y.; Jiang, Z.; Ji, C.; Sun, P. Contrastive analysis of three parallel modes in multi-dimensional dynamic programming and its application in cascade reservoirs operation. J. Hydrol. 2015, 529, 22–34. [Google Scholar] [CrossRef]
- Li, X.; Wei, J.; Li, T.; Wang, G.; Yeh, W.W.G. A parallel dynamic programming algorithm for multi-reservoir system optimization. Adv. Water Resour. 2014, 67, 1–15. [Google Scholar] [CrossRef]
- Liu, P.; Li, L.; Chen, G.; Rheinheimer, D.E. Parameter uncertainty analysis of reservoir operating rules based on implicit stochastic optimization. J. Hydrol. 2014, 514, 102–113. [Google Scholar] [CrossRef]
- Liu, P.; Guo, S.; Xu, X.; Chen, J. Derivation of Aggregation-Based joint operating rule curves for cascade hydropower reservoirs. Water Resour. Manag. 2011, 25, 3177–3200. [Google Scholar] [CrossRef]
- Ji, C.M.; Zhou, T.; Huang, H.T. Operating rules derivation of Jinsha reservoirs system with parameter calibrated support vector regression. Water Resour. Manag. 2014, 28, 2435–2451. [Google Scholar] [CrossRef]
- Yang, G.; Guo, S.; Liu, P.; Li, L.; Liu, Z. Multiobjective cascade reservoir operation rules and uncertainty analysis based on PA-DDS algorithm. J. Water Res. Plan. Man. 2017, 143, 04017025. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, S.L.; Yang, G.; Hong, X.J.; Hu, T. Optimal early refill rules for Danjiangkou Reservoir. Water Sci. Eng. 2014, 7, 403–419. [Google Scholar]
- Ma, C.; Lian, J.; Wang, J. Short-term optimal operation of Three-gorge and Gezhouba cascade hydropower stations in non-flood season with operation rules from data mining. Energ. Convers. Manag. 2013, 65, 616–627. [Google Scholar] [CrossRef]
- Chau, K.W. Particle swarm optimization training algorithm for ANNs in stage prediction of Shing Mun River. J. Hydrol. 2006, 329, 363–367. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W.; Li, Y.S. River stage prediction based on a distributed support vector regression. J. Hydrol. 2008, 358, 96–111. [Google Scholar] [CrossRef]
- Cheng, C.; Niu, W.; Feng, Z.; Shen, J.; Chau, K. Daily reservoir runoff forecasting method using artificial neural network based on quantum-behaved particle swarm optimization. Water 2015, 7, 4232–4246. [Google Scholar] [CrossRef]
- Wang, T.; Yang, K.; Guo, Y. Application of artificial neural networks to forecasting ice conditions of the yellow river in the inner Mongolia reach. J. Hydrol. Eng. 2008, 13, 811–816. [Google Scholar]
- Wang, W.C.; Chau, K.W.; Cheng, C.T.; Qiu, L. A comparison of performance of several artificial intelligence methods for forecasting monthly discharge time series. J. Hydrol. 2009, 374, 294–306. [Google Scholar] [CrossRef]
- Choudhury, P.; Roy, P. Forecasting concurrent flows in a river system using ANNs. J. Hydrol. Eng. 2015, 20, 06014012. [Google Scholar] [CrossRef]
- Cheng, C.T.; Feng, Z.K.; Niu, W.J.; Liao, S.L. Heuristic methods for reservoir monthly inflow forecasting: A case study of Xinfengjiang Reservoir in Pearl river, China. Water 2015, 7, 4477–4495. [Google Scholar] [CrossRef]
- Li, B.; Cheng, C. Monthly discharge forecasting using wavelet neural networks with extreme learning machine. Sci. China Technol. Sci. 2014, 57, 2441–2452. [Google Scholar] [CrossRef]
- Niu, W.; Feng, Z.; Cheng, C.; Zhou, J. Forecasting daily runoff by extreme learning machine based on quantum-behaved particle swarm optimization. J. Hydrol. Eng. 2018, 23, 04018002. [Google Scholar] [CrossRef]
- Lu, X.; Zou, H.; Zhou, H.; Xie, L.; Huang, G.B. Robust extreme learning machine with its application to indoor positioning. IEEE Trans. Cybern. 2016, 46, 194–205. [Google Scholar] [CrossRef] [PubMed]
- Zong, W.; Huang, G.B.; Chen, Y. Weighted extreme learning machine for imbalance learning. Neurocomputing 2013, 101, 229–242. [Google Scholar] [CrossRef]
- Taormina, R.; Chau, K.W.; Sivakumar, B. Neural network river forecasting through baseflow separation and binary-coded swarm optimization. J. Hydrol. 2015, 529, 1788–1797. [Google Scholar] [CrossRef]
- Taormina, R.; Chau, K.W. Data-driven input variable selection for rainfall-runoff modeling using binary-coded particle swarm optimization and Extreme Learning Machines. J. Hydrol. 2015, 529, 1617–1632. [Google Scholar] [CrossRef]
- Li, C.; Xiao, Z.; Xia, X.; Zou, W.; Zhang, C. A hybrid model based on synchronous optimisation for multi-step short-term wind speed forecasting. Appl. Energy 2018, 215, 131–144. [Google Scholar] [CrossRef]
- Zhu, S.; Zhou, J.; Ye, L.; Meng, C. Streamflow estimation by support vector machine coupled with different methods of time series decomposition in the upper reaches of Yangtze River, China. Environ. Earth Sci. 2016, 75, 531. [Google Scholar] [CrossRef]
- Lin, J.Y.; Cheng, C.T.; Chau, K.W. Using support vector machines for long-term discharge prediction. Hydrol. Sci. J. 2006, 51, 599–612. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, P.; Wang, C.; Qian, J.; Hou, J. Combined monthly inflow forecasting and multiobjective ecological reservoir operations model: Case study of the Three Gorges Reservoir. J. Water Res. Plan. Manag. 2017, 143, 05017004. [Google Scholar] [CrossRef]
- Kang, F.; Li, J. Artificial bee colony algorithm optimized support vector regression for system reliability analysis of slopes. J. Comput. Civ. Eng. 2016, 30, 04015040. [Google Scholar] [CrossRef]
- Wang, W.C.; Xu, D.M.; Chau, K.W.; Chen, S. Improved annual rainfall-runoff forecasting using PSO-SVM model based on EEMD. J. Hydroinform. 2013, 15, 1377–1390. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T.; Lund, J.R. Optimizing hydropower reservoirs operation via an orthogonal progressive optimality algorithm. J. Water Resour. Plan. Manag. 2018, 144, 4018001. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T.; Wu, X.Y. Peak operation of hydropower system with parallel technique and progressive optimality algorithm. Int. J. Electr. Power Energy Syst. 2018, 94, 267–275. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T.; Wu, X.Y. Optimization of large-scale hydropower system peak operation with hybrid dynamic programming and domain knowledge. J. Clean. Prod. 2018, 171, 390–402. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T. Optimizing electrical power production of hydropower system by uniform progressive optimality algorithm based on two-stage search mechanism and uniform design. J. Clean. Prod. 2018, 190, 432–442. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T.; Wu, X.Y. Optimization of hydropower system operation by uniform dynamic programming for dimensionality reduction. Energy 2017, 134, 718–730. [Google Scholar] [CrossRef]
- Chang, J.; Wang, X.; Li, Y.; Wang, Y.; Zhang, H. Hydropower plant operation rules optimization response to climate change. Energy 2018, 160, 886–897. [Google Scholar] [CrossRef]
- Wang, S.; Huang, G.H.; He, L. Development of a clusterwise-linear-regression-based forecasting system for characterizing DNAPL dissolution behaviors in porous media. Sci. Total Environ. 2012, 433, 141–150. [Google Scholar] [CrossRef]
- Chau, K.W.; Wu, C.L.; Li, Y.S. Comparison of several flood forecasting models in Yangtze River. J. Hydrol. Eng. 2005, 10, 485–491. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, S.Z.; Chang, J.X.; Huang, Q.; Chen, Y.T. Monthly streamflow prediction using modified EMD-based support vector machine. J. Hydrol. 2014, 511, 764–775. [Google Scholar]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T. Optimization of hydropower reservoirs operation balancing generation benefit and ecological requirement with parallel multi-objective genetic algorithm. Energy 2018, 153, 706–718. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T. Optimal allocation of hydropower and hybrid electricity injected from inter-regional transmission lines among multiple receiving-end power grids in china. Energy 2018, 162, 444–452. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Wang, S.; Cheng, C.T.; Jiang, Z.Q.; Qin, H.; Liu, Y. Developing a successive linear programming model for head-sensitive hydropower system operation considering power shortage aspect. Energy 2018, 155, 252–261. [Google Scholar] [CrossRef]
- Chang, J.; Meng, X.; Wang, Z.; Wang, X.; Huang, Q. Optimized cascade reservoir operation considering ice flood control and power generation. J. Hydrol. 2014, 519, 1042–1051. [Google Scholar] [CrossRef]
- Niu, W.J.; Feng, Z.K.; Cheng, C.T. Optimization of variable-head hydropower system operation considering power shortage aspect with quadratic programming and successive approximation. Energy 2018, 143, 1020–1028. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T.; Zhou, J.Z. Peak shaving operation of hydro-thermal-nuclear plants serving multiple power grids by linear programming. Energy 2017, 135, 210–219. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Zhou, J.Z.; Cheng, C.T.; Qin, H.; Jiang, Z.Q. Parallel multi-objective genetic algorithm for short-term economic environmental hydrothermal scheduling. Energies 2017, 10, 163. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2012, 42, 513–529. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T. Multi-objective quantum-behaved particle swarm optimization for economic environmental hydrothermal energy system scheduling. Energy 2017, 131, 165–178. [Google Scholar] [CrossRef]
- Chang, J.; Wang, Y.; Istanbulluoglu, E.; Bai, T.; Huang, Q.; Yang, D.; Huang, S. Impact of climate change and human activities on runoff in the Weihe River Basin, China. Quat. Int. 2015, 380–381, 169–179. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Zhou, J.Z.; Cheng, C.T.; Zhang, Y.C. Scheduling of short-term hydrothermal energy system by parallel multi-objective differential evolution. Appl. Soft Comput. 2017, 61, 58–71. [Google Scholar] [CrossRef]
- Zimmer, C.A.; Heathcote, I.W.; Whiteley, H.R.; Schroter, H. Low-Impact-Development practices for stormwater: Implications for urban hydrology. Can. Water Resour. J. 2007, 32, 193–212. [Google Scholar] [CrossRef]
- Abu-Zreig, M.; Rudra, R.P.; Lalonde, M.N.; Whiteley, H.R.; Kaushik, N.K. Experimental investigation of runoff reduction and sediment removal by vegetated filter strips. Hydrol. Process. 2004, 18, 2029–2037. [Google Scholar] [CrossRef]
| Coefficient | Month | |||||
|---|---|---|---|---|---|---|
| 1 | 3 | 5 | 7 | 9 | 11 | |
| a | 740.9 | 966.6 | −205.9 | −7001.2 | 2698.6 | 6297.8 |
| b | −0.54 | −0.73 | 0.30 | 6.30 | −2.34 | −5.49 |
| c | −0.04 | 0.02 | 0.58 | 0.50 | 0.73 | 0.84 |
| Method | DP | SGM | MLR | ANN | ELM | SVM |
|---|---|---|---|---|---|---|
| APG (108 kWh) | 23.38 | 21.03 | 21.36 | 22.41 | 23.11 | 22.71 |
| Gap (%) | - | −10.05 | −8.64 | −4.15 | −1.15 | −2.87 |
| GGR (%) | 98.18 | 89.84 | 92.97 | 95.83 | 97.66 | 97.40 |
| Gap (%) | - | −8.49 | −5.31 | −2.39 | −0.53 | −0.79 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, W.-J.; Feng, Z.-K.; Feng, B.-F.; Min, Y.-W.; Cheng, C.-T.; Zhou, J.-Z. Comparison of Multiple Linear Regression, Artificial Neural Network, Extreme Learning Machine, and Support Vector Machine in Deriving Operation Rule of Hydropower Reservoir. Water 2019, 11, 88. https://doi.org/10.3390/w11010088
Niu W-J, Feng Z-K, Feng B-F, Min Y-W, Cheng C-T, Zhou J-Z. Comparison of Multiple Linear Regression, Artificial Neural Network, Extreme Learning Machine, and Support Vector Machine in Deriving Operation Rule of Hydropower Reservoir. Water. 2019; 11(1):88. https://doi.org/10.3390/w11010088
Chicago/Turabian StyleNiu, Wen-Jing, Zhong-Kai Feng, Bao-Fei Feng, Yao-Wu Min, Chun-Tian Cheng, and Jian-Zhong Zhou. 2019. "Comparison of Multiple Linear Regression, Artificial Neural Network, Extreme Learning Machine, and Support Vector Machine in Deriving Operation Rule of Hydropower Reservoir" Water 11, no. 1: 88. https://doi.org/10.3390/w11010088
APA StyleNiu, W.-J., Feng, Z.-K., Feng, B.-F., Min, Y.-W., Cheng, C.-T., & Zhou, J.-Z. (2019). Comparison of Multiple Linear Regression, Artificial Neural Network, Extreme Learning Machine, and Support Vector Machine in Deriving Operation Rule of Hydropower Reservoir. Water, 11(1), 88. https://doi.org/10.3390/w11010088






