Modeling Pesticide and Sediment Transport in the Malewa River Basin (Kenya) Using SWAT
Abstract
:1. Introduction
2. Materials and Methods
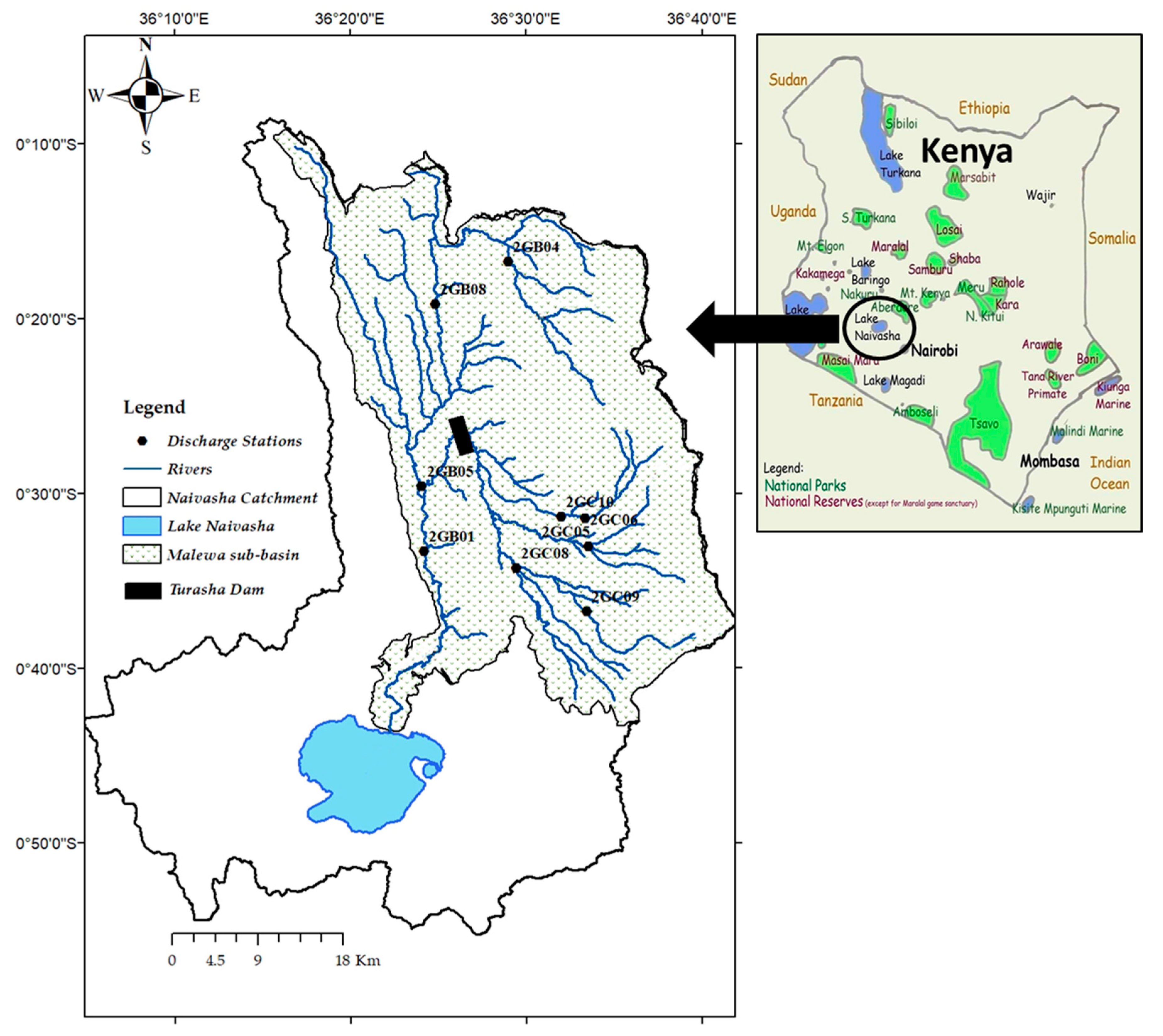
2.1. Study Area
2.2. Data Procurement
2.3. Model Setup
2.4. Model Sensitivity Analysis, Calibration and Validation
3. Results
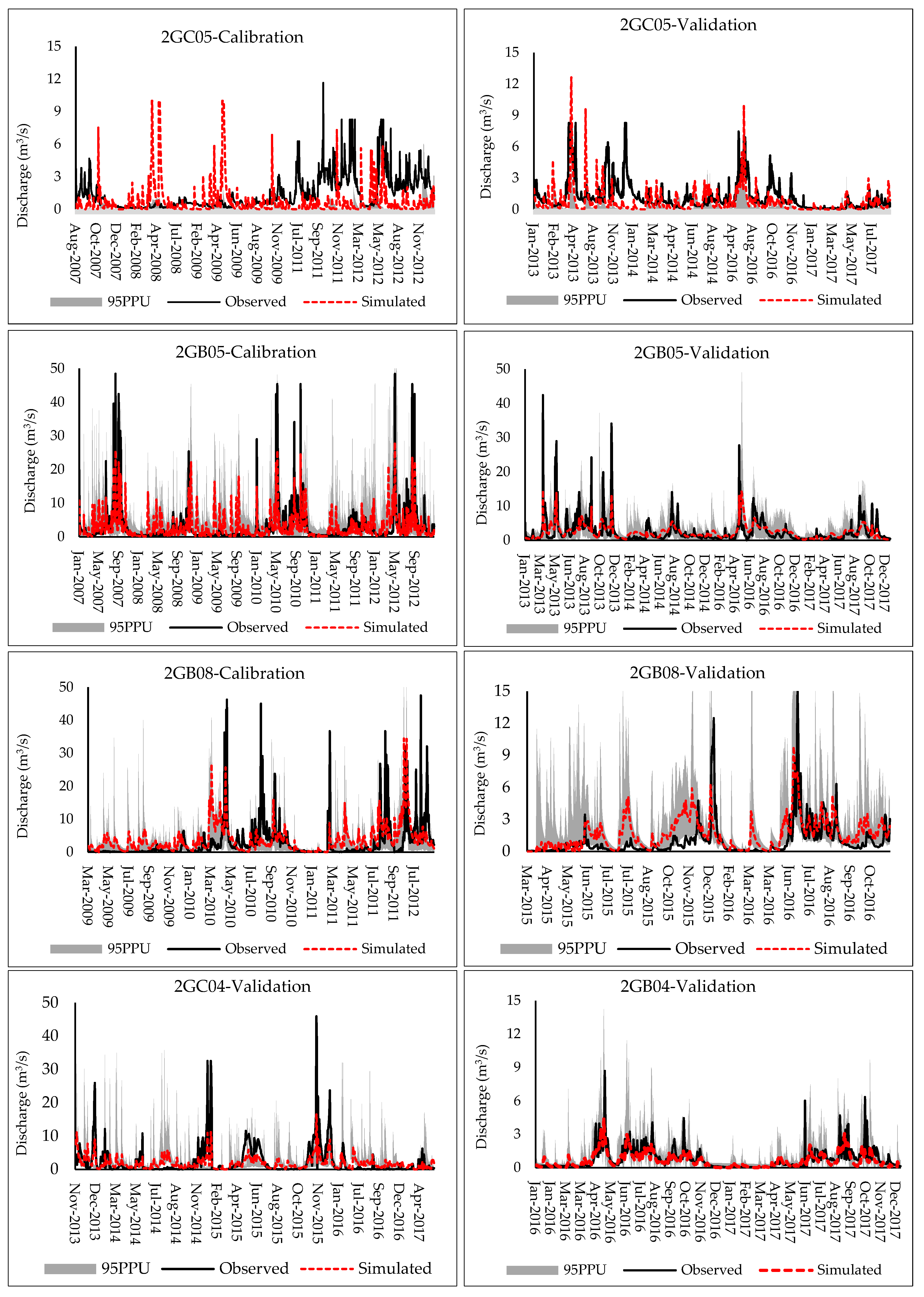
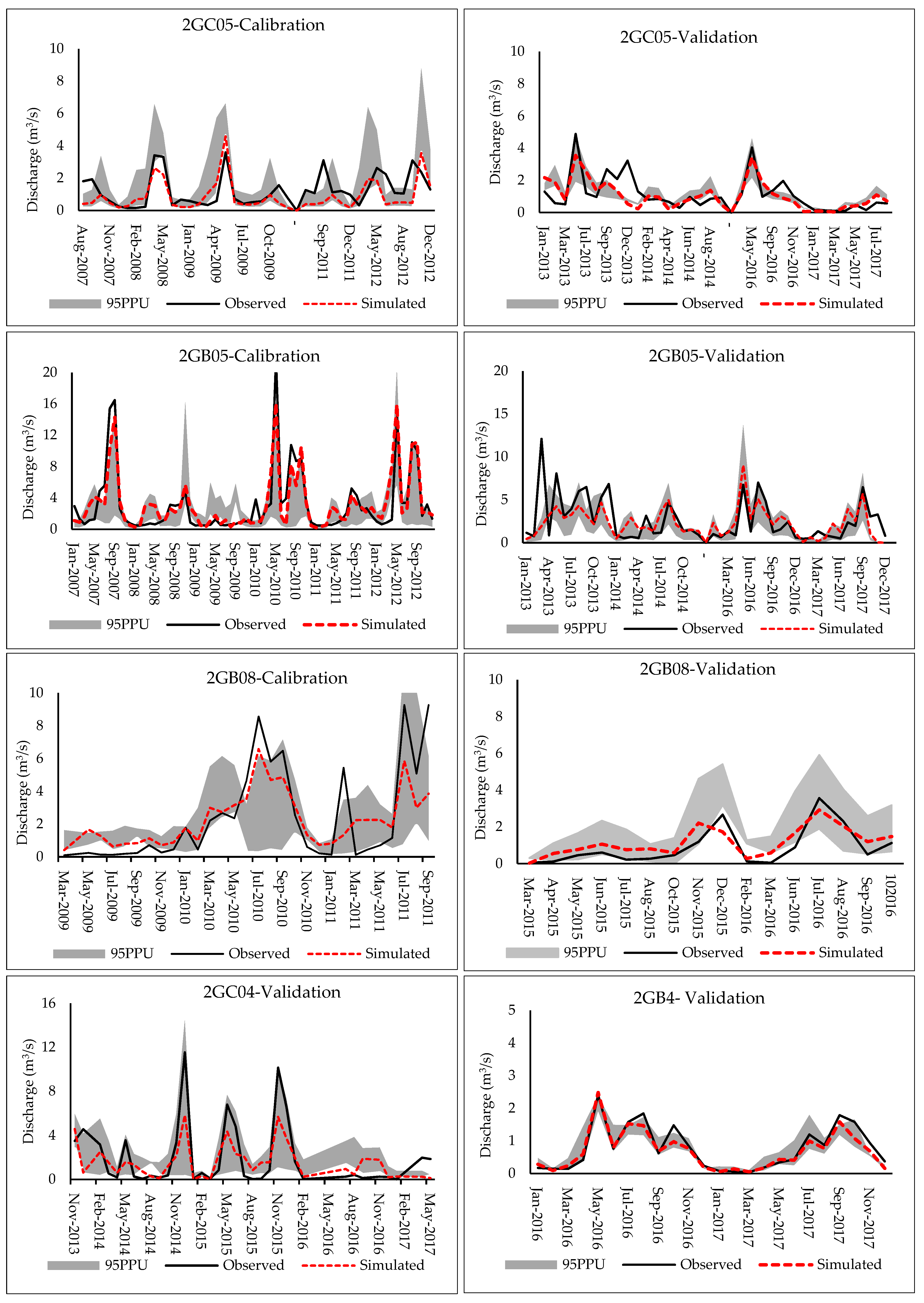
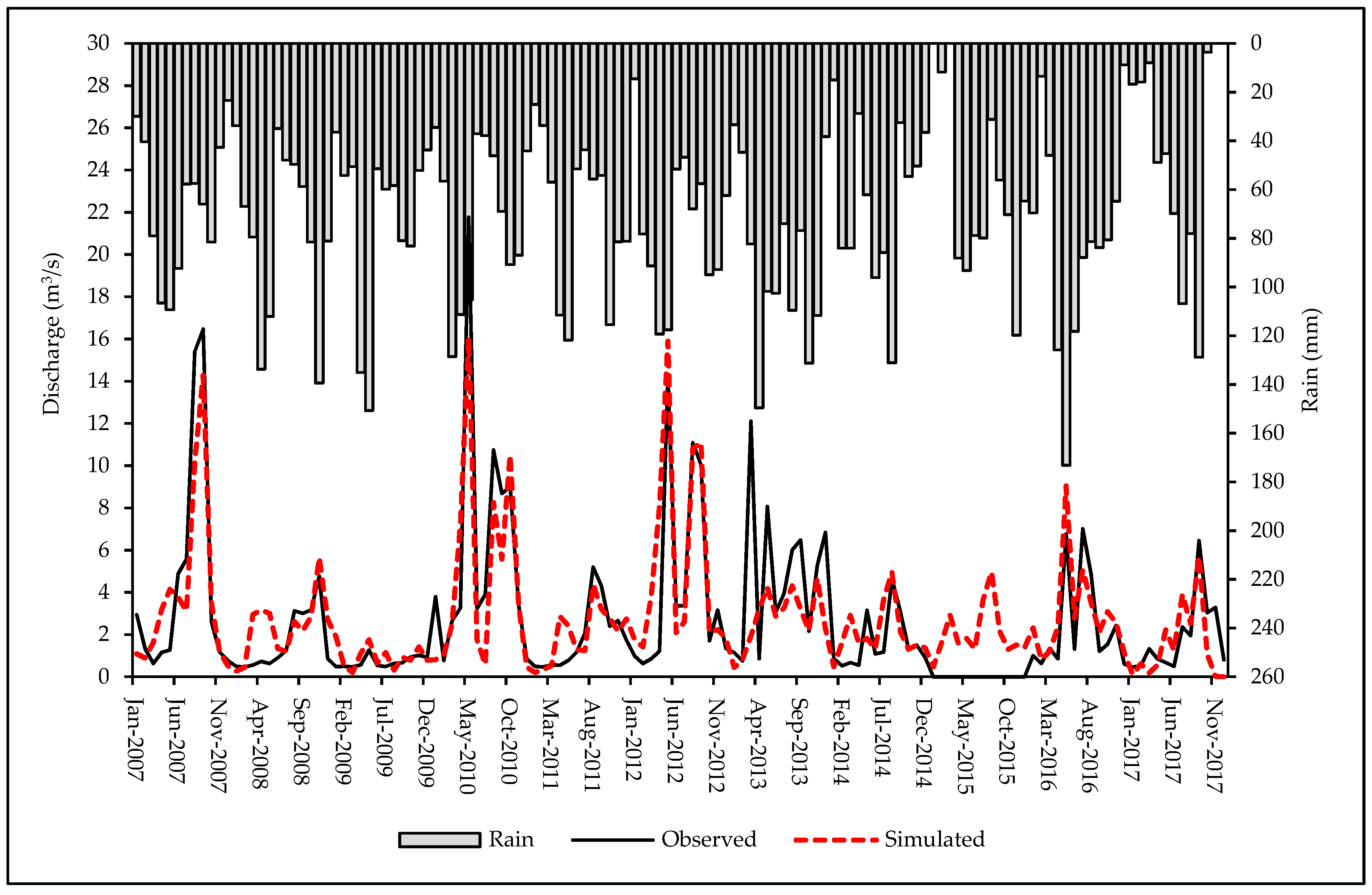
3.1. Discharge Simulation
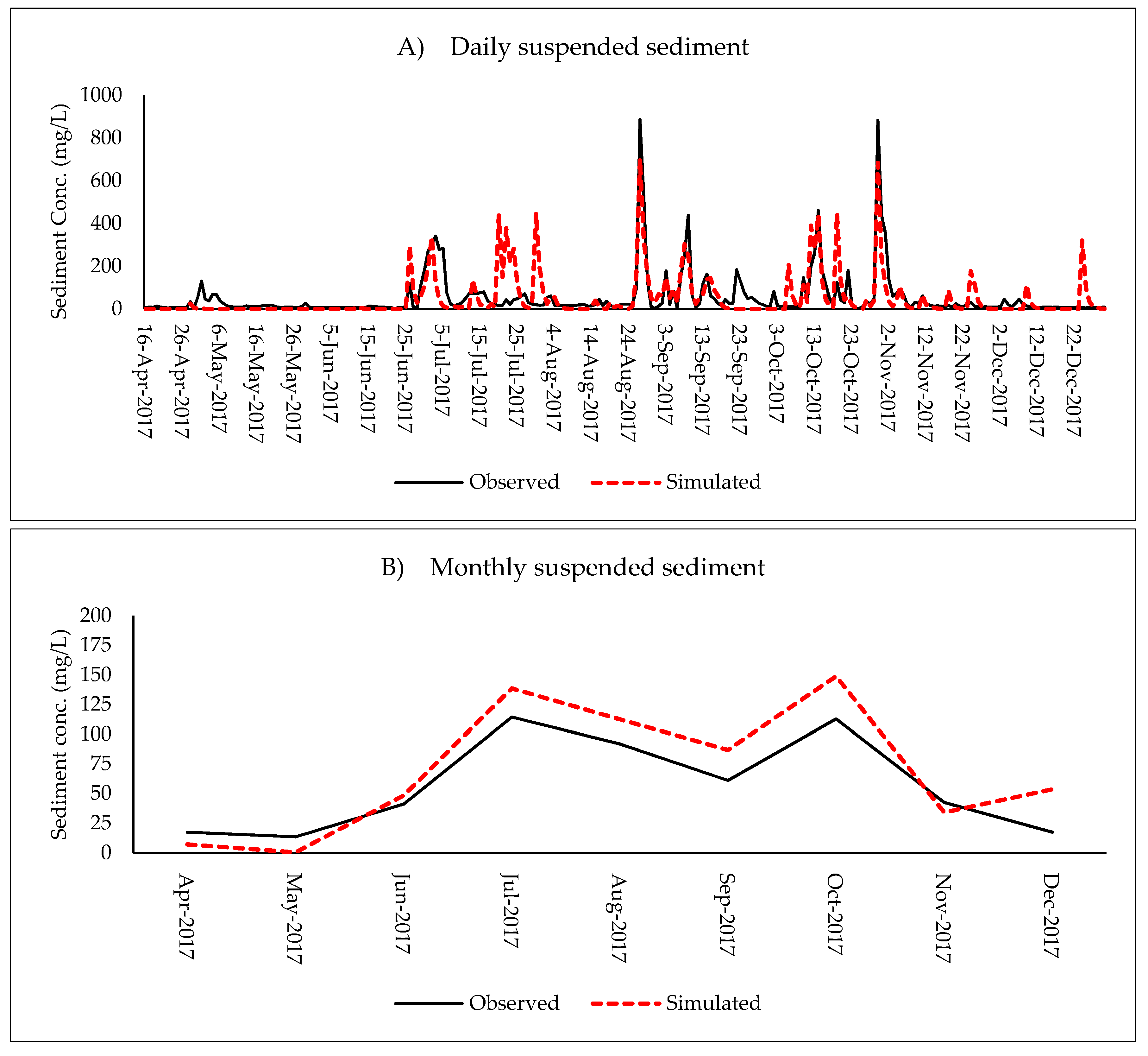
3.2. Suspended Sediment Tranpsort Simulation
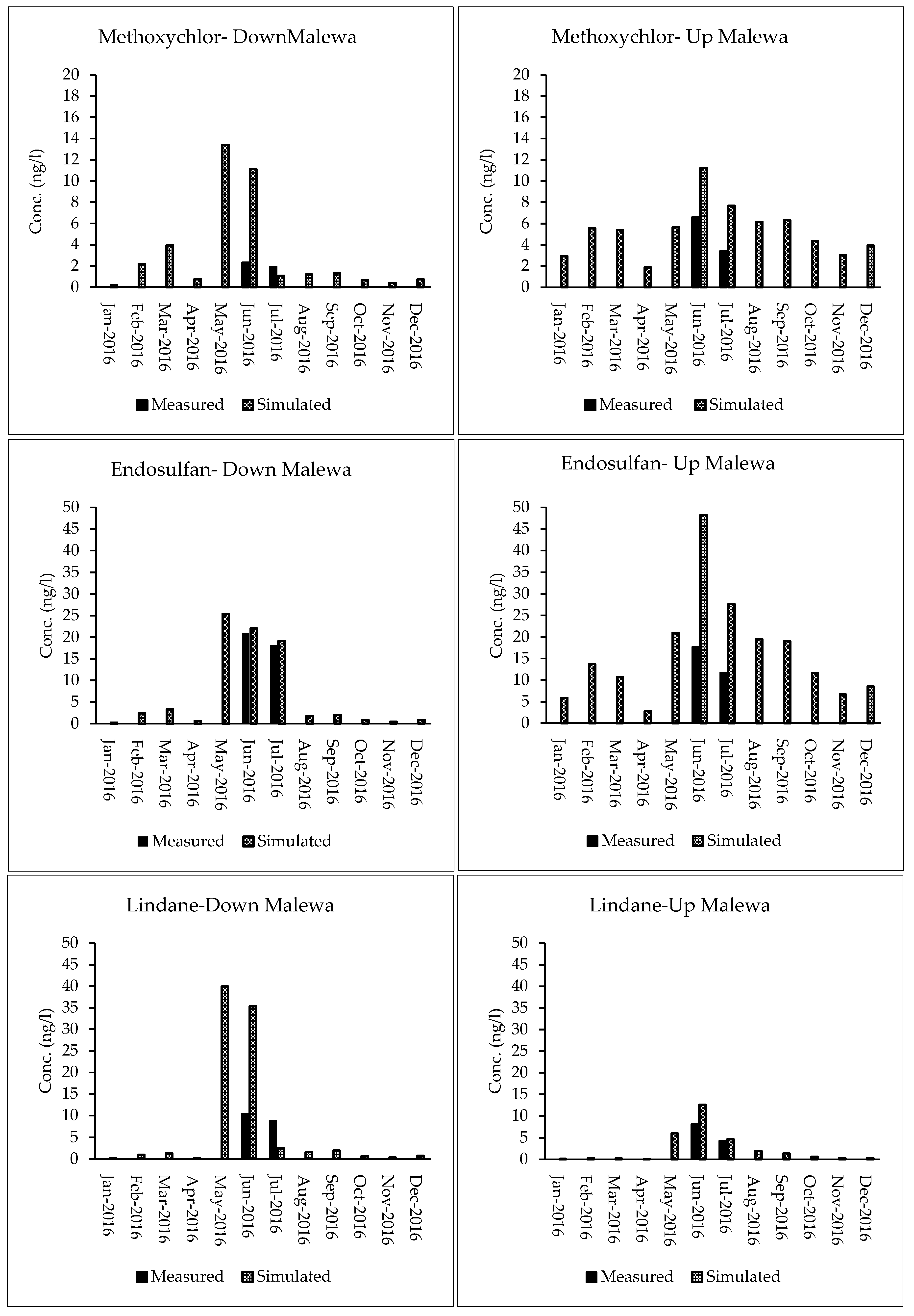
3.3. Pesticides Transport Simulation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Harper, D.M.; Morrison, E.H.J.; Macharia, M.M.; Mavuti, K.M.; Upton, C. Lake naivasha, kenya: Ecology, society and future. Freshw. Rev. 2011, 4, 89–114. [Google Scholar] [CrossRef]
- Warren, N.; Allan, I.J.; Carter, J.E.; House, W.A.; Parker, A. Pesticides and other micro-organic contaminants in freshwater sedimentary environments—A review. Appl. Geochem. 2003, 18, 159–194. [Google Scholar] [CrossRef]
- Vigiak, O.; Malago, A.; Bouraoui, F.; Vanmaercke, M.; Obreja, F.; Poesen, J.; Habersack, H.; Feher, J.; Groselj, S. Modelling sediment fluxes in the danube river basin with SWAT. Sci. Total Environ. 2017, 599–600, 992–1012. [Google Scholar] [CrossRef]
- Panuwet, P.; Siriwong, W.; Prapamontol, T.; Ryan, P.B.; Fiedler, N.; Robson, M.G.; Barr, D.B. Agricultural pesticide management in thailand: Situation and population health risk. Environ. Sci. Policy 2012, 17, 72–81. [Google Scholar] [CrossRef] [PubMed]
- Odongo, V.O.; Onyando, J.O.; Mutua, B.M.; van Oel, P.R.; Becht, R. Sensitivity analysis and calibration of the modified universal soil loss equation (musle) for the upper malewa catchment, kenya. Int. J. Sediment Res. 2013, 28, 368–383. [Google Scholar] [CrossRef]
- Chen, H.; Luo, Y.; Potter, C.; Moran, P.J.; Grieneisen, M.L.; Zhang, M. Modeling pesticide diuron loading from the san joaquin watershed into the sacramento-san joaquin delta using SWAT. Water Res. 2017, 121, 374–385. [Google Scholar] [CrossRef] [PubMed]
- Ben Salah, N.C.; Abida, H. Runoff and sediment yield modeling using SWAT model: Case of wadi hatab basin, central tunisia. Arab. J. Geosci. 2016, 9, 579. [Google Scholar] [CrossRef]
- Borah, D.K.; Bera, M. Watershed-scale hydrologic and nonpoint-source pollution models: Review of applications. Am. Soc. Agric. Eng. 2004, 47, 789–803. [Google Scholar] [CrossRef]
- Scopel, C. SWAT: Soil & Water Assessment Tool. ArcGIS Blog. Available online: https://www.esri.com/arcgis-blog/products/product/water/swat-soil-water-assessment-tool/ (accessed on 15 February 2018).
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Bannwarth, M.A.; Sangchan, W.; Hugenschmidt, C.; Lamers, M.; Ingwersen, J.; Ziegler, A.D.; Streck, T. Pesticide transport simulation in a tropical catchment by SWAT. Environ. Pollut. 2014, 191, 70–79. [Google Scholar] [CrossRef]
- Dutta, S.; Sen, D. Application of SWAT model for predicting soil erosion and sediment yield. Sustain. Water Res. Manag. 2017, 4, 447–468. [Google Scholar] [CrossRef]
- Ligaray, M.; Kim, M.; Baek, S.; Ra, J.-S.; Chun, J.; Park, Y.; Boithias, L.; Ribolzi, O.; Chon, K.; Cho, K. Modeling the fate and transport of malathion in the Pagsanjan-Lumban basin, Philippines. Water 2017, 9, 451. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, X.; Liu, X.; Ficklin, D.; Zhang, M. Dynamic modeling of organophosphate pesticide load in surface water in the northern San Joaquin Valley watershed of California. Environ. Pollut. 2008, 156, 1171–1181. [Google Scholar] [CrossRef] [PubMed]
- Mahzari, S.; Kiani, F.; Azimi, M.; Khormali, F. Using SWAT model to determine runoff, sediment yield and nitrate loss in gorganrood watershed, Iran. Ecopersia 2016, 4, 1359–1377. [Google Scholar] [CrossRef]
- Folle, S.M. SWAT Modeling of Sediment, Nutrients and Pesticides in the Le-Sueur River Watershed, South-Central Minnesota. Ph.D. Dissertation, Uniersity of Minesota, Minneapolis, MN, USA, 2010. [Google Scholar]
- Parker, R.; Arnold, J.G.; Barrett, M.; Burns, L.; Carrubba, L.; Neitsch, S.L.; Snyder, N.J.; Srinivasan, R. Evaluation of three watershed-scale pesticide environmental transportat and fate models. J. Am. Water Res. Assoc. 2007, 43, 1424–1443. [Google Scholar] [CrossRef]
- Winchell, M.F.; Peranginangin, N.; Srinivasan, R.; Chen, W. Soil and water assessment tool model predictions of annual maximum pesticide concentrations in high vulnerability watersheds. Integr. Environ. Assess. Manag. 2018, 14, 358–368. [Google Scholar] [CrossRef] [PubMed]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, P.S.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration and validation. Am. Soc. Agric. Biol. Eng. 2012, 55, 1491–1508. [Google Scholar]
- Wang, W.; Neuman, S.P.; Yao, T.; Wierenga, P.J. Simulation of large-scale field infiltration experiments using a hierarchy of models based on public, generic, and site data. Vadose Zone J. 2003, 2, 297–312. [Google Scholar] [CrossRef]
- Xu, T.Z. Water Quality Assessment and Pesticide Fate Modeling in the Lake Naivasha Area, Kenya. Master’s Thesis, University of Twente, Enschede, The Netherlands, 1999. [Google Scholar]
- Becht, R.; Odada, E.; Higgins, S. Lake Naivasha experience and lessons learned brief. Int. Water Learn. Exch. Res. Net 2010, 2, 277–298. [Google Scholar]
- Meins, F.M. Evaluation of Spatial Scale Alternatives for Hydrological Modelling of the Lake Naivasha Basin, Kenya. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2013. [Google Scholar]
- Odongo, V.O.; Mulatu, D.W.; Muthoni, F.K.; van Oel, P.R.; Meins, F.M.; van der Tol, C.; Skidmore, A.K.; Groen, T.A.; Becht, R.; Onyando, J.O.; et al. Coupling socio-economic factors and eco-hydrological processes using a cascade-modeling approach. J. Hydrol. 2014, 518, 49–59. [Google Scholar] [CrossRef]
- Gitahi, S.M.; Harper, D.M.; Muchiri, S.M.; Tole, M.P.; Ng’ang’a, R.N. Organochlorine and organophosphorus pesticide concentrations in water, sediment, and selected organisms in Lake Naivasha (Kenya). Hydrobiologia 2002, 488, 123–128. [Google Scholar] [CrossRef]
- Abbasi, Y.; Mannaerts, C.M. Evaluating organochlorine pesticide residues in the aquatic environment of the lake naivasha river basin using passive sampling techniques. Environ. Monit. Assess. 2018, 190, 349. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil & Water Assessment Tool, Theoretical Documentation; Technical Report No. 406; Texas A&M University: Texas, TX, USA, 2011. [Google Scholar]
- Zettam, A.; Taleb, A.; Sauvage, S.; Boithias, L.; Belaidi, N.; Sánchez-Pérez, J. Modelling hydrology and sediment transport in a semi-arid and anthropized catchment using the SWAT model: The case of the Tafna river (northwest Algeria). Water 2017, 9, 216. [Google Scholar] [CrossRef]
- MCkay, M.D.; Beckma, R.J.; Conover, W.J. A comparision of three methods for selelcting valuses of input variables in the analysis of output from a computer code. Am. Stat. Assoc. Am. Soc. Qual. 2000, 42, 55–61. [Google Scholar]
- Abbaspour, K.C. SWAT-CUP: SWAT Calibration and Uncertainty Programs—A User Manual; Swiss Federal Institute of Aquatic Science and Technology, Eawag: Dübendorf, Switzerland, 2015. [Google Scholar]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Am. Soc. Agric. Biol. Eng. 2015, 58, 1763–1785. [Google Scholar]
- Malone, R.W.; Yagow, G.; Baffaut, C.; Gitau, M.W.; Qi, Z.; Amatya, D.M.; Parajuli, P.B.; Bonta, J.V.; Green, T.R. Parameterization guidelines and considerations for hydrologic models. Am. Soc. Agric. Biol. Eng. 2015, 58, 1681–1703. [Google Scholar]
- Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R.; Haney, E.B.; Neitsch, S.L. Soil & Water Assessment Tool Input-Output Documentation; TR-439; Texas Water Resources Institute: Texas, TX, USA, 2013. [Google Scholar]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2004, 524, 733–752. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, W.; Yu, Z.; Lung, I.; Gharabaghi, B. Estimating sediment yield from upland and channel erosion at awatershed scale using SWAT. Water Res. Manag. 2015, 29, 1399–1412. [Google Scholar] [CrossRef]
- Spruill, C.A.; Workman, S.R.; Taraba, J.L. Simulation of daily stream discharge from small watersheds using the SWAT model. Am. Soc. Agric. Biol. Eng. 2000, 1, 1431–1439. [Google Scholar] [CrossRef]
- Dasa, S.K.; Nga, A.W.M.; Perera, B.J.C. Sensitivity analysis of SWAT model in the yarra river catchment. In Proceedings of the 20th International Congress on Modelling and Simulation, Adelaide, Australia, 1–6 December 2013. [Google Scholar]
- Traum, J.A.; Phillips, S.P.; Bennett, G.L.; Zamora, C.; Metzger, L.F. Documentation of a Groundwater Flow Model (SJRRPGW) for the San Joaquin River Restoration Program Study Area, California; Scientific Investigations Report 2014-5148; United States Geological Survey (USGS): Reston, VA, USA, 2014.
- Qiu, L.; Zheng, F.; Yin, R. SWAT-based runoff and sediment simulation in a small watershed, the loessial hilly-gullied region of china: Capabilities and challenges. Int. J. Sediment Res. 2012, 27, 226–234. [Google Scholar] [CrossRef]
- Asres, M.T.; Awulachew, S.B. SWAT based runoff and sediment yield modelling: A case study of the gumera watershed in the blue nile basin. Ecohydrol. Hydrobiol. 2010, 10, 191–199. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Gong, Y.W.; Li, Y.H.; Hong, Q.; Xu, L.; Liu, R.M. A comparison of wepp and SWAT for modeling soil erosion of the Zhangjiachong watershed in the Three Gorges Reservoir area. Agric. Water Manag. 2009, 96, 1435–1442. [Google Scholar] [CrossRef]
- Renschler, C.S.; Mannaerts, C.M.; Diekkruger, B. Evaluating spatial and temporal variability in soil erosion risk—Rainfall erosivity and soil loss ratios in Andalusia, Spain. Catena 1999, 34, 209–225. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Luo, Y.; Zhang, M. Watershed modelling of hydrology and water quality in the Sacramento River watershed, California. Hydrol. Process. 2013, 27, 236–250. [Google Scholar] [CrossRef]
- Kannan, N.; White, S.M.; Worrall, F.; Whelan, M.J. Pesticide modelling for a small catchment using SWAT-2000. J. Environ. Sci. Health B 2006, 41, 1049–1070. [Google Scholar] [CrossRef] [PubMed]
- Agency for Toxic Substances and Disease Registry (ATSDR). Toxicological Profile for Methoxychlor; U.S. Department of Health and Human Services Public Health Service: Atlanta, GA, USA, 2002.
- Stockholm Convention on Persistent Organic Pollutants (pops), Text and Annexes; The Secretariat of the Stockholm Convention on Persistent Organic Pollutants: Geneva, Switzerland, 2009.
- Agency for Toxic Substances and Disease Registry (ATSDR). Toxicological Profile for Hexachlorocyclohexane; U.S. Department of Health and Human Services Public Health Service: Atlanta, GA, USA, 2005.
- Weber, J.; Halsall, C.J.; Muir, D.; Teixeira, C.; Small, J.; Solomon, K.; Hermanson, M.; Hung, H.; Bidleman, T. Endosulfan, a global pesticide: A review of its fate in the environment and occurrence in the arctic. Sci. Total Environ. 2010, 408, 2966–2984. [Google Scholar] [CrossRef] [PubMed]
- National Center for Biotechnology Information. Pubchem Compound Database; cid=3224. Available online: https://pubchem.Ncbi.Nlm.Nih.Gov/compound/3224 (accessed on 8 December 2018).
- Doppler, T.; Camenzuli, L.; Hirzel, G.; Krauss, M.; Lück, A.; Stamm, C. Spatial variability of herbicide mobilisation and transport at catchment scale: Insights from a field experiment. Hydrol. Earth Syst. Sci. 2012, 16, 1947–1967. [Google Scholar] [CrossRef]
- Schuol, J.; Abbaspour, K.C.; Srinivasan, R.; Yang, H. Estimation of freshwater availability in the west African sub-continent using the SWAT hydrologic model. J. Hydrol. 2008, 352, 30–49. [Google Scholar] [CrossRef]
| Parameter (Unit) | SWAT Code | Min Value | Max Value | Fitted Value | Rank |
|---|---|---|---|---|---|
| SCS runoff curve (-) | CN2 | 35 | 95 | [79–93] * | 1 |
| Base flow alpha factor (day) | ALPHA_BF | 0.15 | 0.50 | [0.15–0.38] | 4 |
| Groundwater delay (day) | GW_DELAY | 0 | 500 | 10.90 | 11 |
| Threshold depth outflow from shallow aquifer (mm) | GWQMN | 1 | 500 | 35.43 | 10 |
| Threshold depth of water in the shallow aquifer (mm) | REVAPMN | 0 | 1000 | 599 | 6 |
| Soil available water storage capacity (mm H2O/mm soil) | SOL_AWC | 0 | 1 | [0.1–0.3] | 7 |
| Soil conductivity (mm/h) | SOL_K | 0 | 200 | [4–41] | 2 |
| Soil evaporation compensation coefficient (-) | ESCO | 0 | 1 | 0.46 | 9 |
| Manning’s value for overland flow (-) | OV_N | 0.01 | 30 | [0.01–3.79] | 15 |
| Manning’s value for the main channel | CH_N2 | 0.1 | 0.5 | 0.21 | 14 |
| Main channel hydraulic conductivity (mm/h) | CH_K2 | 0.01 | 173 | [1–122.92] | 13 |
| Deep aquifer percolation fraction (-) | RCHRG_DP | 0 | 1 | 0.15 | 5 |
| Transmission losses from channel to deep aquifer fraction | TRNSRCH | 0 | 1 | 0.18 | 3 |
| Soil depth of layers (mm) | SOL_Z | 0 | 2000 | [380–1153] | 16 |
| Groundwater “revap” coefficient | GW_REVAP | 0.02 | 0.40 | 0.2 | 8 |
| Surface runoff lag coefficient | SURLAG | 0 | 4 | [0.3–2] | 12 |
| Daily/Monthly | Station | P-Factor | R-Factor | R2 | NSE | |PBIAS|(%) | R2 Rating | NSE Rating | PBIAS Rating |
|---|---|---|---|---|---|---|---|---|---|
| Daily | Discharge and Sediment calibration Discharge | ||||||||
| 2GB05 | 0.44 | 0.79 | 0.61 | 0.47 | 12.93 | *Sat. | *Unsat. | Sat. | |
| 2GB08 | 0.27 | 0.75 | 0.56 | 0.42 | 36.56 | Unsat. | Unsat. | Unsat. | |
| 2GC05 | 0.43 | 1.05 | 0.05 | −1.20 | 50.52 | Unsat. | Unsat. | Unsat. | |
| Sediment | |||||||||
| 2GB04 | 0. 60 | 1.10 | 0.51 | 0.44 | 19.00 | Sat. | Unsat. | Sat. | |
| Discharge validation | |||||||||
| 2GB05 | 0.84 | 0.81 | 0.45 | 0.42 | 12.24 | Unsat. | Unsat. | Sat. | |
| 2GB08 | 0.63 | 1.16 | 0.28 | 0.02 | 66.09 | Unsat. | Unsat. | Unsat. | |
| 2GC05 | 0.58 | 1.48 | 0.32 | −0.08 | 49.56 | Unsat. | Unsat. | Unsat. | |
| 2GC04 | 0.77 | 2.49 | 0.60 | 0.46 | 17.96 | Unsat. | Unsat. | Unsat. | |
| 2GB04 | 0.78 | 1.59 | 0.57 | 0.52 | 10.05 | Unsat. | Sat. | Sat. | |
| Monthly | Discharge and Sediment calibration Discharge | ||||||||
| 2GB05 | 0.37 | 0.55 | 0.86 | 0.64 | 12.93 | *V. good | Sat. | Sat. | |
| 2GB08 | 0.26 | 0.67 | 0.81 | 0.51 | 36.56 | Good | Sat. | Unsat. | |
| 2GC05 | 0.44 | 0.84 | 0.72 | 0.59 | 8.80 | Sat. | Sat. | Good | |
| Sediment | |||||||||
| 2GB04 | 0.96 | 1.19 | 0.60 | 0.70 | 19.00 | Sat. | Good | Sat. | |
| Pesticides | |||||||||
| Up Malewa | - | - | 0.34 | 0.74 | 16.15 | Sat. | Good | Good | |
| Down Malewa | - | - | 0.30 | 0.36 | 25.85 | Sat. | Sat. | Sat. | |
| Discharge validation | |||||||||
| 2GB05 | 0.76 | 0.79 | 0.62 | 0.61 | 12.24 | Sat. | Sat. | Sat. | |
| 2GB08 | 0.61 | 1.13 | 0.60 | 0.53 | 66.09 | Sat. | Sat. | Unsat. | |
| 2GC05 | 0.58 | 1.29 | 0.53 | 0.35 | 49.56 | Unsat. | Unsat. | Unsat. | |
| 2GC04 | 0.74 | 1.19 | 0.97 | 0.52 | 17.96 | V. good | Sat. | Unsat. | |
| 2GB04 | 0.76 | 1.60 | 0.84 | 0.80 | 10.05 | Good | Good | Sat. | |
| Parameter (Unit) | SWAT Code | Min Value | Max Value | Fitted Value | Rank |
|---|---|---|---|---|---|
| USLE soil erodibility factor | USLE-K | 0 | 0.7 | 0.025 | 1 |
| USLE equation support practice factor | USLE_P | 0 | 1 | [0.036–0.9] ** | 2 |
| Sediment calculation Linear parameter * | SPCON | 0 | 1 | 0.025 | 3 |
| Sediment calculation Exponent parameter * | SPEXP | 0.1 | 2 | 0.25 | 6 |
| Channel cover | CH_COV | 0 | 1 | 0.5 | 4 |
| Channel erodibility | CH_EROD | 0.05 | 0.9 | 0.5 | 5 |
| Pesticide | Range | SKOC (mL/g) | WOF | HLIFE_F (Day) | HLIFE_S (Day) | WSOL (mg/L) | AP_EF |
|---|---|---|---|---|---|---|---|
| Lindane | Initial Value | 1100 | 0.05 | 2.5 | 400 | 7.3 | 0.75 |
| Fitted Value | 1500 | 0.05 | 5 | 90 | 7.3 | 0.35 | |
| Endosulfan | Initial Value | 12,400 | 0.05 | 3 | 50 | 0.32 | 0.75 |
| Fitted Value | 15,000 | 0.15 | 10 | 70 | 0.30 | 0.50 | |
| Methoxychlor | Initial Value | 80,000 | 0.05 | 6 | 120 | 0.1 | 0.75 |
| Fitted Value | 87,000 | 0.10 | 8 | 90 | 0.01 | 0.45 | |
| Rank | 5 | 4 | 3 | 2 | 6 | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbasi, Y.; Mannaerts, C.M.; Makau, W. Modeling Pesticide and Sediment Transport in the Malewa River Basin (Kenya) Using SWAT. Water 2019, 11, 87. https://doi.org/10.3390/w11010087
Abbasi Y, Mannaerts CM, Makau W. Modeling Pesticide and Sediment Transport in the Malewa River Basin (Kenya) Using SWAT. Water. 2019; 11(1):87. https://doi.org/10.3390/w11010087
Chicago/Turabian StyleAbbasi, Yasser, Chris M. Mannaerts, and William Makau. 2019. "Modeling Pesticide and Sediment Transport in the Malewa River Basin (Kenya) Using SWAT" Water 11, no. 1: 87. https://doi.org/10.3390/w11010087
APA StyleAbbasi, Y., Mannaerts, C. M., & Makau, W. (2019). Modeling Pesticide and Sediment Transport in the Malewa River Basin (Kenya) Using SWAT. Water, 11(1), 87. https://doi.org/10.3390/w11010087





