5.1. The First Case at Nanjing Station
According to the flood records of Nanjing station in the lower reaches of the Yangtze River from 1951 to 2005, the flood samples are as shown in
Table 4 [
8,
26]. There are 10 floods, with data on the flood peak level, the number of days that the flood level was over 9 m, the flood discharge in DaTong station, the flood volume from May to September, and the synthetic index of discharge and time, where the final index is the composite value of the flood discharge and its duration according to References [
8,
26].
On the basis of the Chinese National Standard for Hydrological Forecasting, which was implemented on January 1, 2009, and according to the flood recurrence periods of less than 5 years, 5–20 years, 20–50 years, and more than 50 years, the floods are divided into four grades, i.e., small floods, common floods, large floods, and catastrophic floods. Considering the fact that the flood samples in this paper are at least common floods, the aim of the first study is to divide the flood records into three classes; in other words, the floods are also clustered into catastrophic floods, large floods, and common floods, also denoted as I, II, and III.
Hence, in this case study, FCI-CW and IGWO are applied to flood classification at Nanjing Station.
The parameters employed for FCI-CW are set as follows: the number of flood samples, indices, and clusters is
,
, and
, respectively. According to an analysis of the historical flood characteristics of Nanjing station and the influence of various indices on the flood intensity [
8], the subjective weight by the Delphi method [
35,
36] is
. Meanwhile, according to the projection pursuit method [
35,
36], the objective weight is
.
The parameters employed for IGWO are set as follows: population size ; maximum evolution generation .
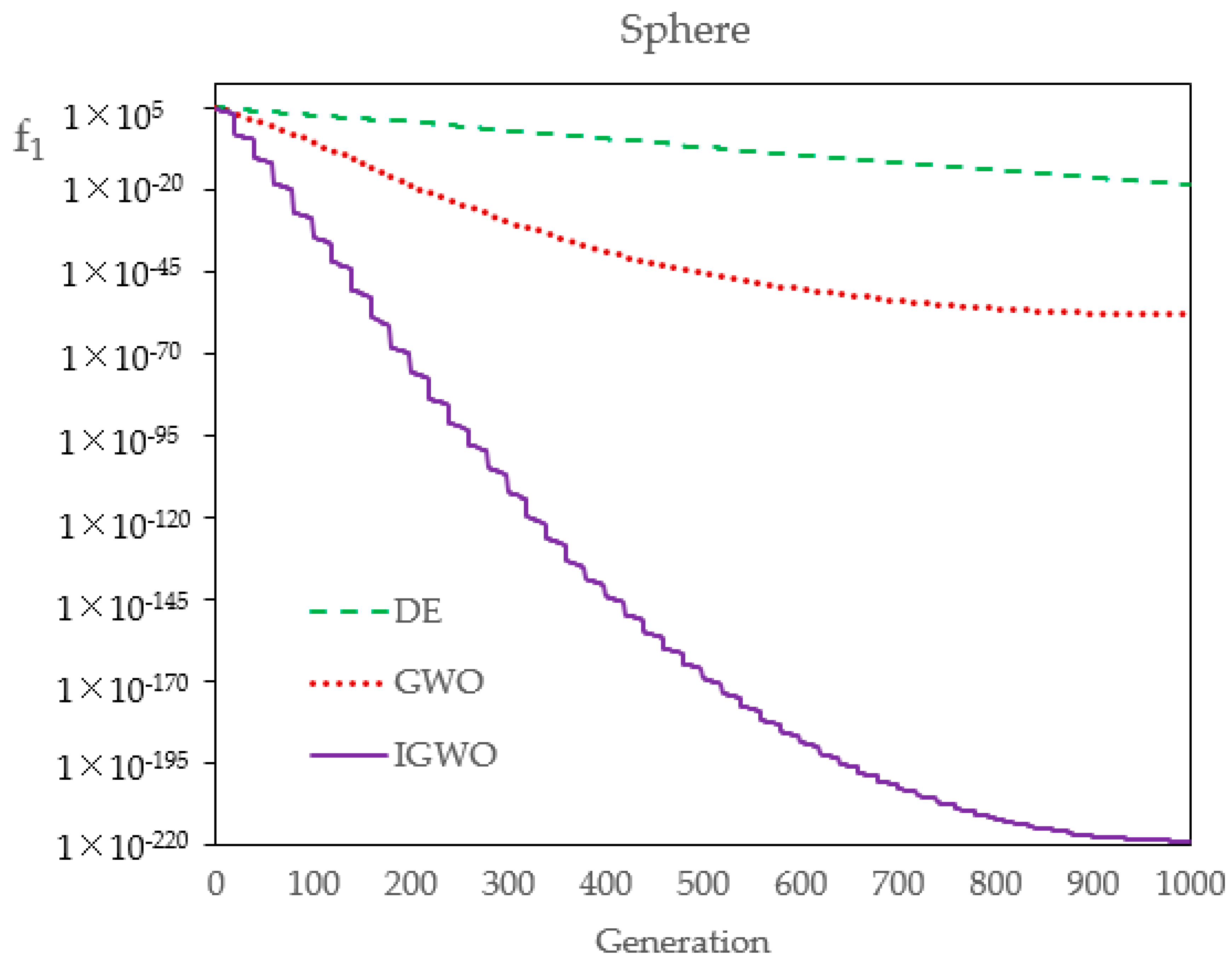
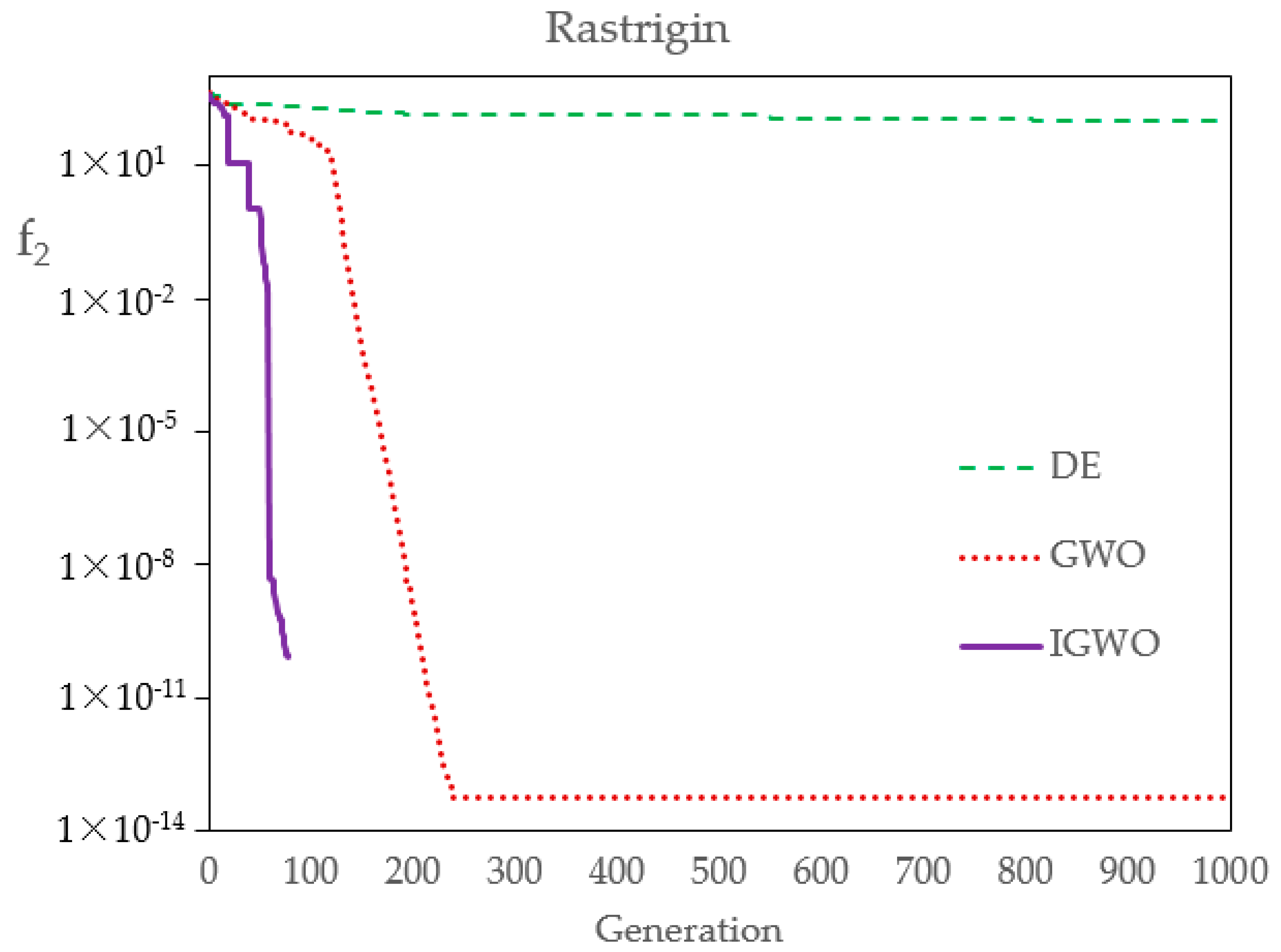
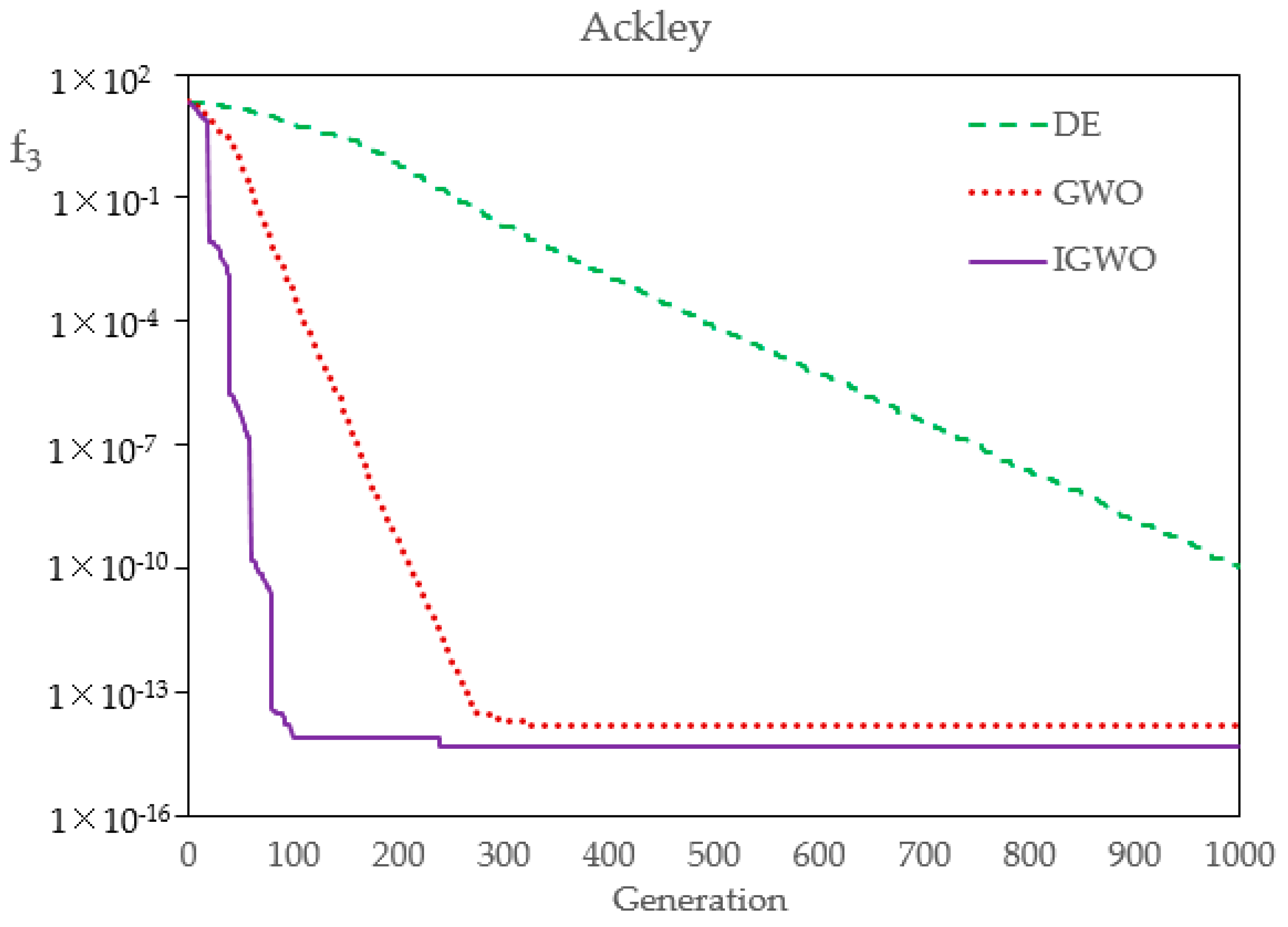
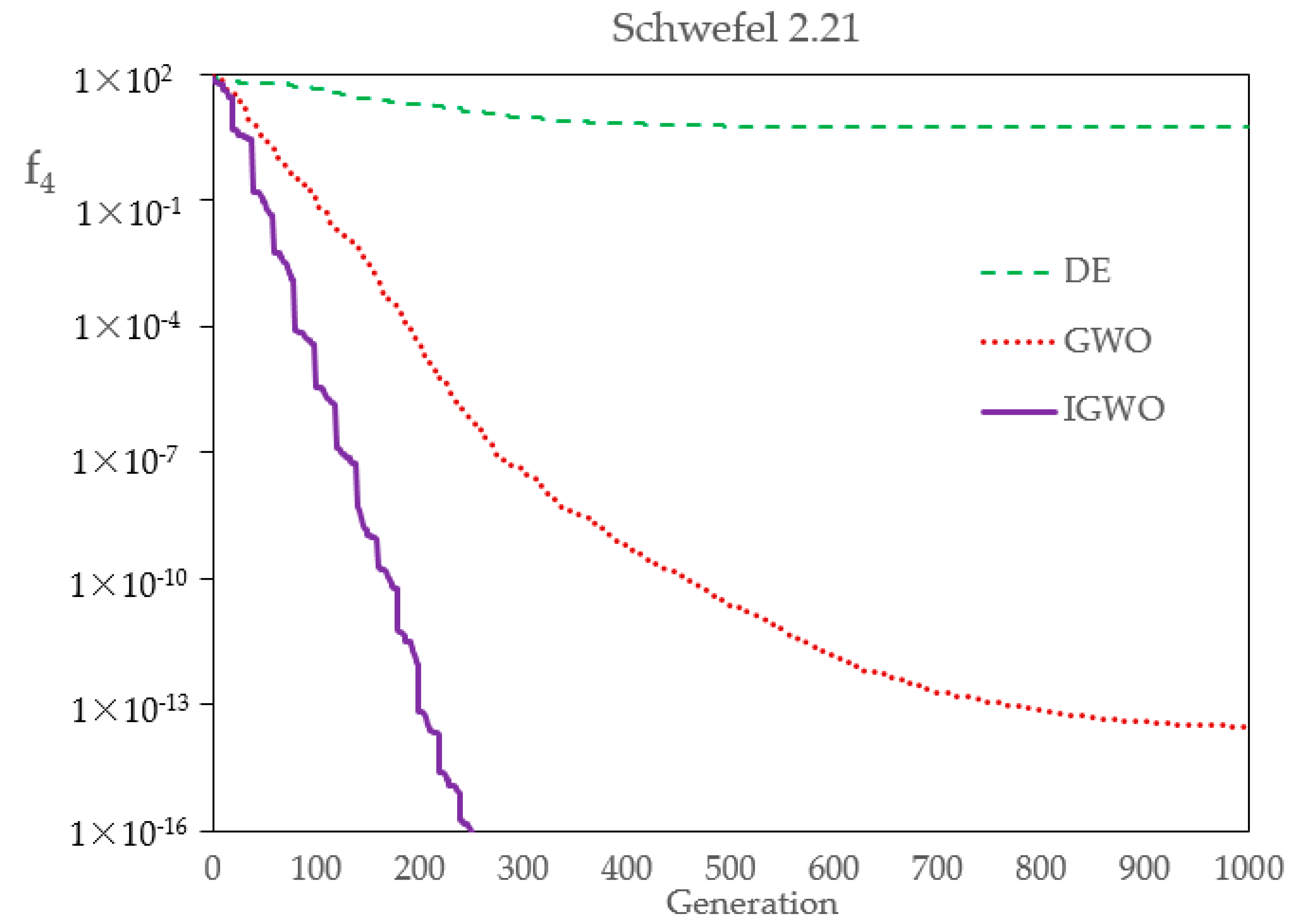
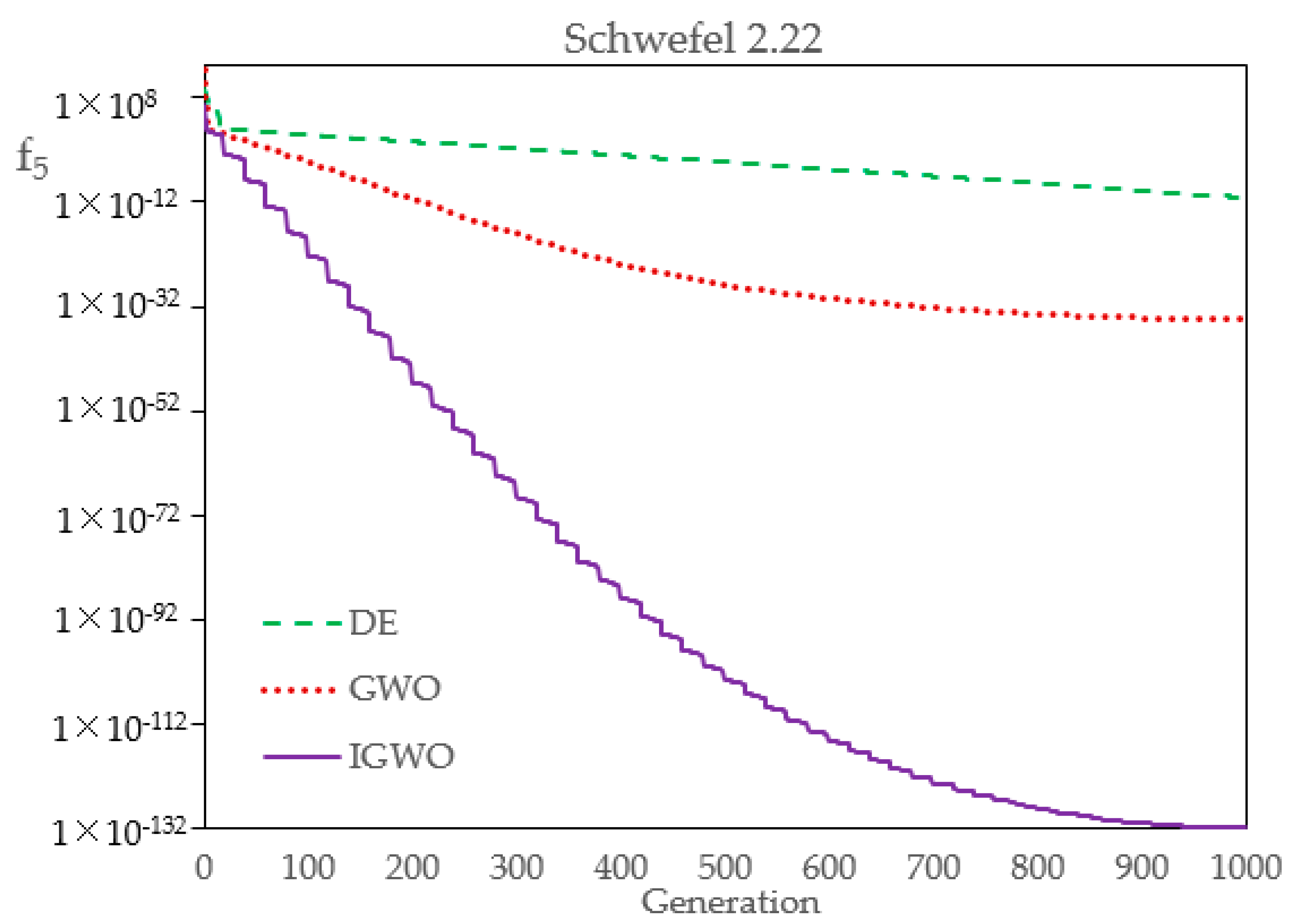
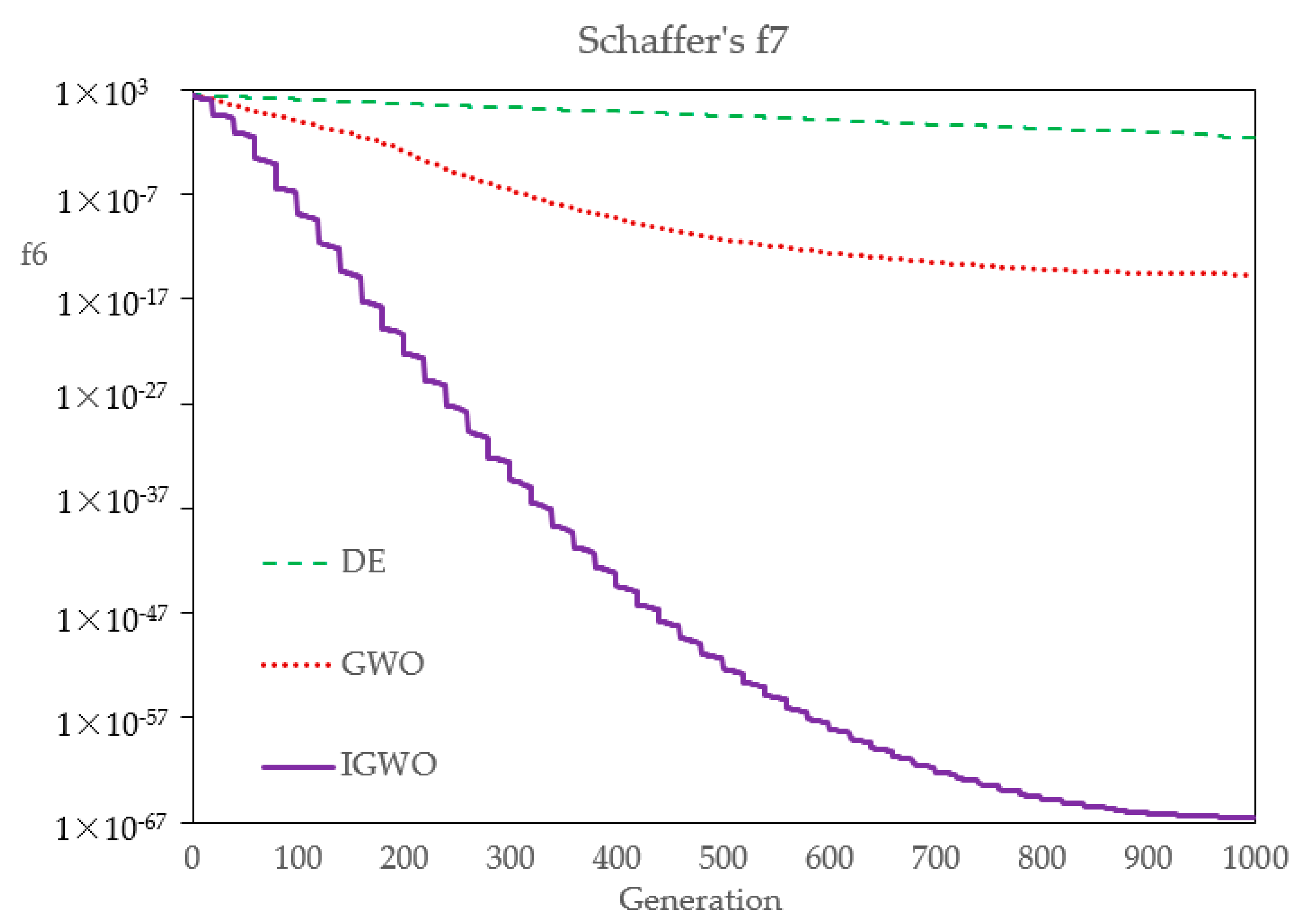
Firstly, in order to compare the optimization performance of DE, GWO, and IGWO,
Table 5 shows their statistical results over 30 runs. The results show that the three kinds of evolutionary algorithms have different precisions, to a certain extent. The standard deviation and average value of IGWO are both the smallest, and can basically achieve the same optimal solution every time, which indicates that, compared with DE and GWO, IGWO has better robustness and higher convergence precision. Of course, the number of flood samples in this case study is very small, which leads to a classification effect at an order of magnitude. If the number of samples and the index dimension increases, the optimization effect of IGWO will be more obvious and effective.
In this case study, the minimum objective function value is 2.023083 × 10−2, and the optimal search result of IGWO was output to obtain the optimal fuzzy class center matrix and the optimal sensitivity coefficient shown in Equations (36) and (37), respectively. Afterwards, the index weight matrix was calculated as , which was combined with the subjective weight and the objective weight by using to obtain the best optimal value of GEWD.
Finally, the optimal fuzzy clustering matrix
was achieved as shown in Equation (39).
According to the clustering results in Equation (39), we can conclude that there was a huge flood disaster in 1954 and 1998; there was a medium flood disaster in 1983, 1995, and 1996; and there was a small flood disaster in 1969, 1973, 1980, 1991, and 1992, as shown in
Table 6. This sorting result is identical to that obtained with the optimal curve projection dynamic cluster method (OC-PDC) [
23], variable fuzzy set theory (VFS) [
8], the fuzzy clustering iteration model with a chaotic differential evolution algorithm (FCI-CDE) [
26], and the weighted fuzzy kernel-clustering algorithm with an adaptive differential evolution algorithm (WFKCA-ADE) [
27], which demonstrates that the proposed methodology for flood classification is reasonable and reliable.
Moreover, VFS only considers the subjective weight; however, there is unavoidable factual evidence, which means that an objective weight is also needed to describe the distribution characteristics of flood samples. Moreover, the index weight is coded as a search-variable representation in FCI-CDE [
26], and its optimal fitness, i.e., the GEWD, is 1.277551 × 10
−2, which is less than the optimal value 2.020046 × 10
−2 by the proposed method. However, its optimal weight vector, denoted as
= (0.0908, 0.6267, 0.1141, 0.0801, 0.0883), is just the “mathematical weight” in the sense of sample data calculation, which indicates that the importance of the second index is much larger than the sum of the other four indices. This is contrary to the decision-maker’s subjective cognition and the actual situation, so it is necessary to reasonably modify the weight results.
Furthermore, the effect of the sensitivity coefficient on the classification results using FCI-CW and IGWO was evaluated, as shown in
Table 7. Here, the sensitivity coefficients were chosen to be different values, such as 0, 0.2, 0.4, 0.45, 0.5, 0.55, 0.6, 0.8, and 1. In other words, when β = 0 in Equation (17), it means that only the objective weight was employed, and the FCI-CW was degraded into a fuzzy clustering iteration model with objective weight (FCI-OW); when β = 1 in Equation (17), it means that only the subjective weight was employed, and the FCI-CW was degraded into a fuzzy clustering iteration model with subjective weight (FCI-SW); and when β = 0.5 in Equation (17), it is the traditional parameter selection using the additive synthesis method. According to
Table 7, when β was calculated as 5.595729 × 10
−1, the GEWD was the smallest of all, which indicates that the proposed methodology to calculate the fuzzy class center matrix and the sensitivity coefficient for flood classification is reasonable. This renders it superior to the conventional methods, since only considering subjectivity or objectivity, or just setting β = 0.5, lacks a powerful mathematical basis.
Finally, we also calculate the GEWD for the combined weights that were obtained by the multiplicative synthesis method shown in Equation (15) and the minimum relative entropy method shown in Equation (16). Their GEWDs are 1.019555 and 1.020171, respectively, which are larger than the adopted combined weight method, i.e., the additive synthesis method with a sensitivity coefficient.
5.2. The Second Case of Yichang Station
According to the flood records of Yichang station, which is the representative hydrological station for the Three Gorges Reservoir in the middle reaches of the Yangtze River, the flood samples are as shown in
Table 8 [
8]. There are 12 floods, with data on the flood peak level, the flood peak discharge, three-day floods, seven-day floods, and fifteen-day floods. The aim of the study is to divide the flood records into three classes, also denoted as I, II, and III, similarly to the first case.
In this study, FCI-CW and IGWO are applied to flood classification at Yichang station. The parameters employed for FCI-CW are set as follows: the number of flood samples, indices, and clusters is
,
, and
, respectively. According to an analysis of the historical flood characteristics of Yichang station and the influence of various indices on the flood intensity, the subjective weight by the Delphi method [
36] is
. Meanwhile, according to the projection pursuit method [
24], the objective weight is
. The parameters employed for IGWO are set as follows: population size
; maximum evolution generation
.
Firstly, in order to compare the optimization performance of DE, GWO, and IGWO,
Table 9 shows their statistical results over 30 runs. The results show that the three kinds of evolutionary algorithm have different precisions, to a certain extent. The standard deviation and the average value of IGWO are both the smallest, and can basically achieve the same optimal solution every time, which indicates that, compared with DE and GWO, IGWO has better robustness and higher convergence precision.
In this case study, the minimum objective function value is 2.644227 × 10
−2, and the optimal search result of IGWO was output to obtain the optimal fuzzy class center matrix
and the optimal sensitivity coefficient
shown in Equations (40) and (41), respectively. Afterwards, the index weight matrix was calculated as
, which was combined with the subjective weight and the objective weight. Finally, the optimal fuzzy clustering matrix
was achieved as shown in Equation (43).
Moreover, according to the clustering results in Equation (43), we can conclude that there was a huge flood disaster in 1931, 1954, 1981, and 1998; there was a medium flood disaster in 1935, 1958, 1966, 1974, 1980, 1982, and 1996; and there was a small flood disaster in 1969, as shown in
Table 10. This sorting result is identical to that obtained with VFS [
8], which demonstrates that the proposed methodology for flood classification is reasonable and reliable.
Finally, the effect of the sensitivity coefficient on the classification results using FCI-CW and IGWO was evaluated, as shown in
Table 11. Here, the sensitivity coefficients were chosen to be different values, such as 0, 0.2, 0.4, 0.45, 0.5, 0.55, 0.6, 0.8, and 1. According to
Table 11, When β was calculated as 6.027070 × 10
−1, the GEWD was the smallest of all, which indicates that the proposed methodology is reasonable. This renders it superior to the conventional methods, since only considering subjectivity or objectivity, or just setting β = 0.5, lacks a powerful mathematical basis.
Therefore, the simulation and analysis results of the second case are identical with those of the first case, and illustrate that it is necessary to adopt the sensitivity coefficient to effectively and comprehensively consider subjectivity and objectivity in classification problems.