Hydrogeological Parameter Determination in the Southern Catchments of Taiwan by Flow Recession Method
Abstract
1. Introduction
2. Study Area
3. Methodology
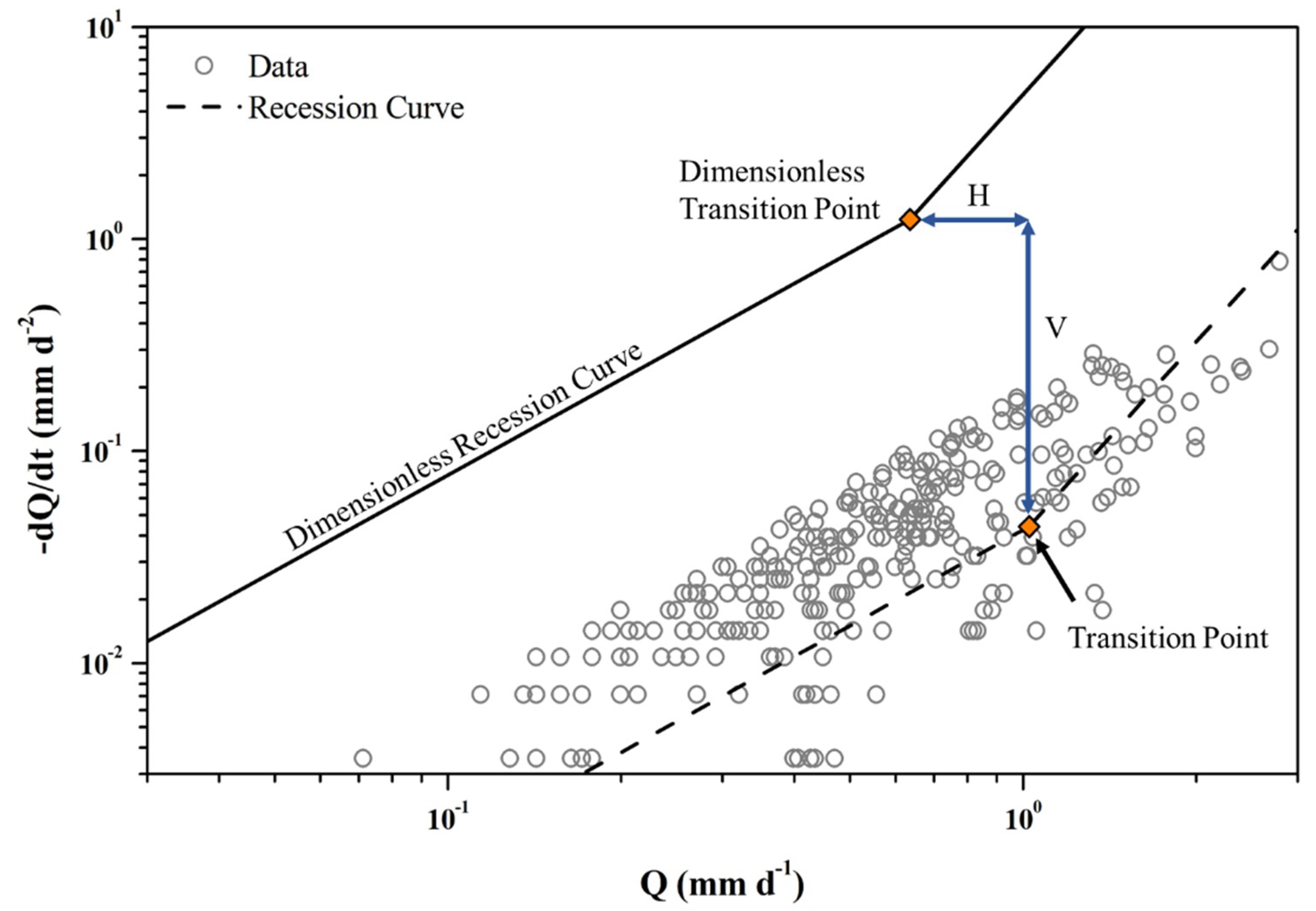
3.1. Low-Flow Recession Analysis Method
- (1)
- First transition point: The intersection of the lower envelope lines of the short-term flow regime (b = 3) and long-term flow regime (b = 1.5) were defined through the application of the methodology proposed by Brutsaert and Nieber [12]. The envelope lines were placed such that 10% of the data points lay below the lines to reduce the influence of evapotranspiration.
- (2)
- Second transition point: The intersection of the linear regression line on the plot of dQ/dt vs. Q and the lower envelope for b = 3.
- (3)
- Third transition point: The intersection of the upper envelope for b = 1 and the highest log (Q) value among the data points.
3.2. Selection Criteria for Recession Flow Data
- (1)
- Eliminate all data points with positive and zero values of dQ/dt.
- (2)
- Eliminate two data points before dQ/dt becomes positive or zero, and three data points after the last positive and zero dQ/dt.
- (3)
- Eliminate four data points after major events, with major events defined based on the discharge duration curve [36].
- (4)
- Eliminate anomalous points in the data series.
- (5)
- Eliminate data points corresponding to days with daily rainfall >0 and several days after rainfall.
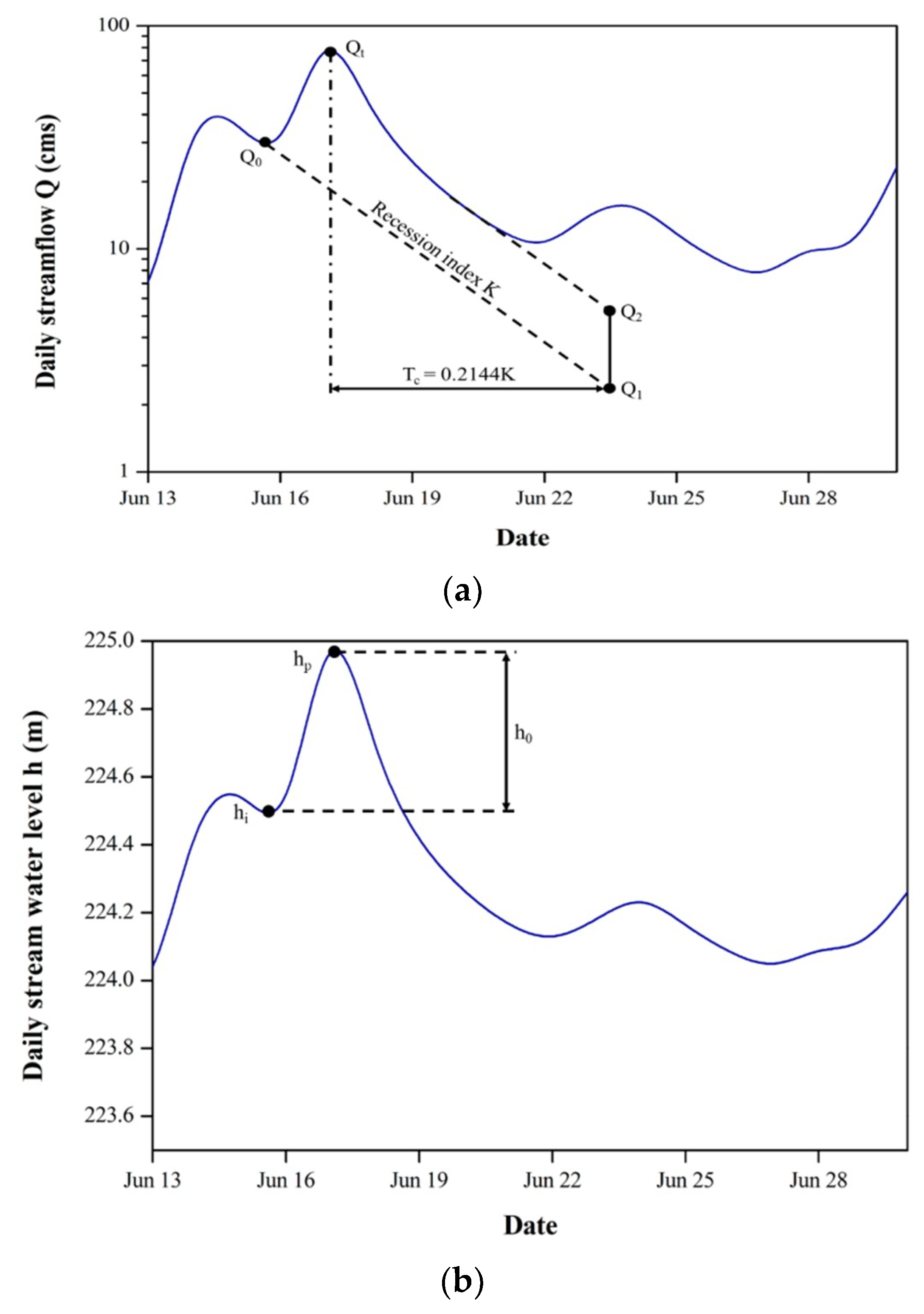
3.3. Recession-Curve-Displacement Method
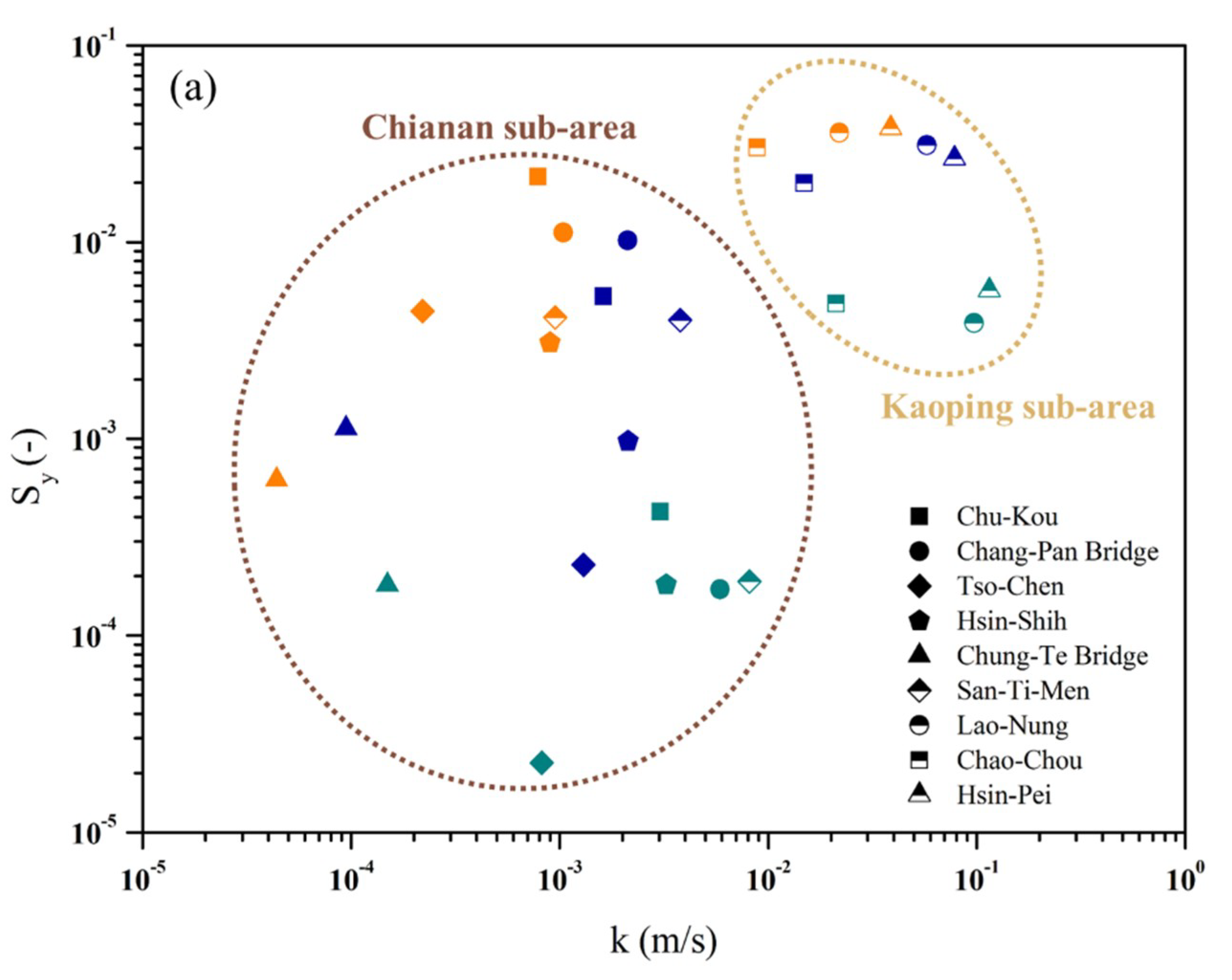
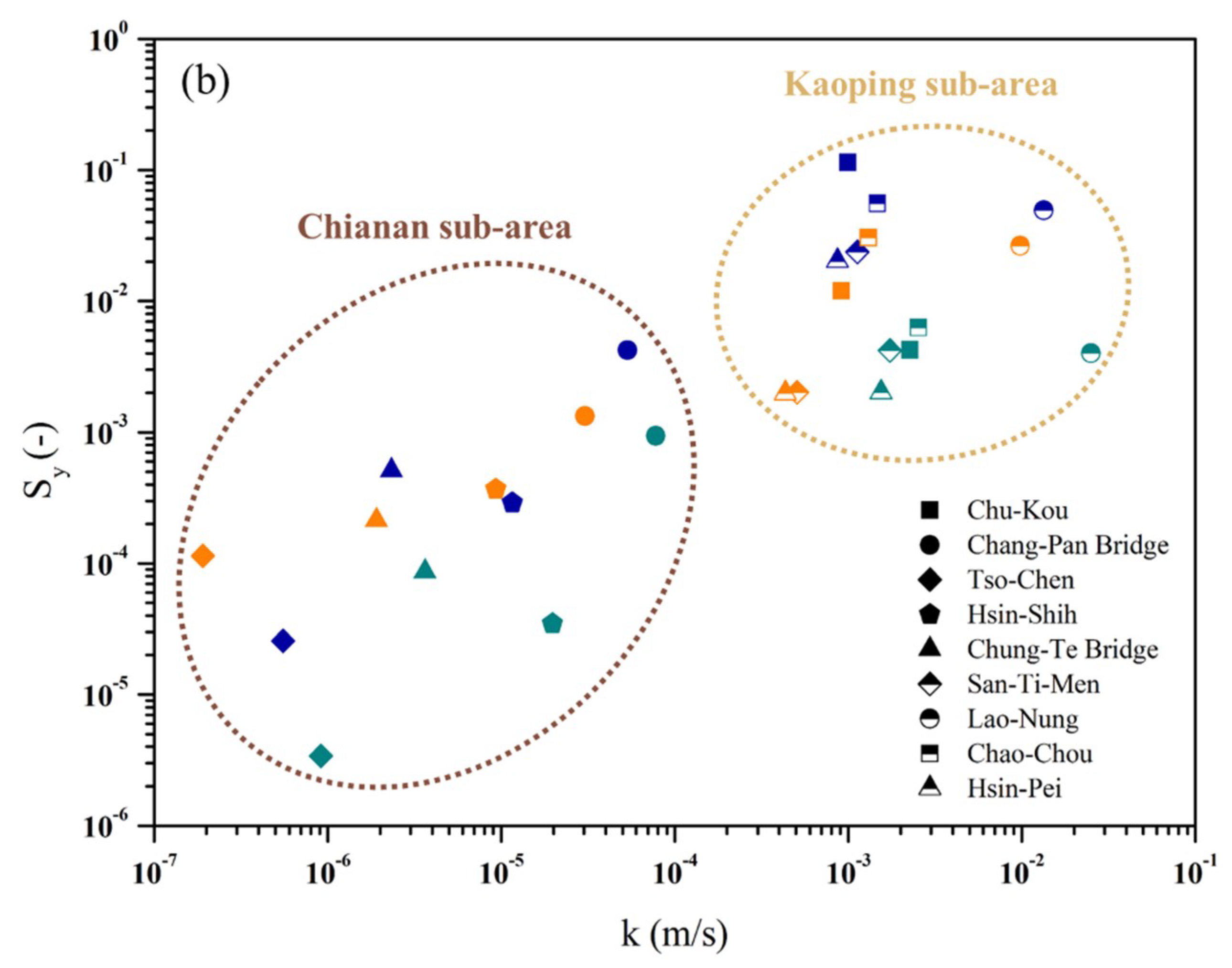
4. Results and Discussion
4.1. Low-Flow Recession Analysis
4.2. Estimation of Hydrogeological Parameters
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alley, W.; Healy, R.; LaBaugh, J.; Reilly, T. Hydrology—Flow and storage in groundwater systems. Science 2002, 296, 1985–1990. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.Y.; Singh, V.P. Review on regional water resources assessment models under stationary and changing climate. Water Resour. Manag. 2004, 18, 591–612. [Google Scholar] [CrossRef]
- Conama, D. Estudio de la Variabilidad Climática en Chile Para el Siglo XXI; Departamento de Geofısica, Universidad de Chile: Santiago, Chile, 2006. [Google Scholar]
- Berghuijs, W.R.; Hartmann, A.; Woods, R.A. Streamflow sensitivity to water storage changes across Europe. Geophys. Res. Lett. 2016, 43, 1980–1987. [Google Scholar] [CrossRef]
- Staudinger, M.; Stoelzle, M.; Seeger, S.; Seibert, J.; Weiler, M.; Stahl, K. Catchment water storage variation with elevation. Hydrol. Process. 2017, 31, 2000–2015. [Google Scholar] [CrossRef]
- Lin, K.T.; Yeh, H.F. Baseflow recession characterization and groundwater storage trends in northern Taiwan. Hydrol. Res. 2017. [Google Scholar] [CrossRef]
- Oyarzún, R.; Godoy, R.; Núñez, J.; Fairley, J.P.; Oyarzún, J.; Maturana, H.; Freixas, G. Recession flow analysis as a suitable tool for hydrogeological parameter determination in steep, arid basins. J. Arid Environ. 2014, 105, 1–11. [Google Scholar] [CrossRef]
- Vannier, O.; Braud, I.; Anquetin, S. Regional estimation of catchment—Scale soil properties by means of streamflow recession analysis for use in distributed hydrological models. Hydrol. Process. 2014, 28, 6276–6291. [Google Scholar] [CrossRef]
- Arumí, J.L.; Maureira, H.; Souvignet, M.; Pérez, C.; Rivera, D.; Oyarzún, R. Where does the water go? Understanding geohydrological behaviour of Andean catchments in south-central Chile. Hydrol. Sci. J. 2016, 61, 844–855. [Google Scholar] [CrossRef]
- Senkondo, W.; Tuwa, J.; Koutsouris, A.; Lyon, S.W. Estimating Aquifer Transmissivity Using the Recession-Curve-Displacement Method in Tanzania’s Kilombero Valley. Water 2017, 9, 948. [Google Scholar] [CrossRef]
- Smakhtin, V.U. Low flow hydrology: A review. J. Hydrol. 2001, 240, 147–186. [Google Scholar] [CrossRef]
- Brutsaert, W.; Nieber, J.L. Regionalized drought flow hydrographs from a mature glaciated plateau. Water Resour. Res. 1977, 13, 637–643. [Google Scholar] [CrossRef]
- Roques, C.; Rupp, D.E.; Selker, J.S. Improved streamflow recession parameter estimation with attention to calculation of −dQ/dt. Adv. Water Resour. 2017, 108, 29–43. [Google Scholar] [CrossRef]
- Mendoza, G.F.; Steenhuis, T.S.; Walter, M.T.; Parlange, J.Y. Estimating basin-wide hydraulic parameters of a semi-arid mountainous watershed by recession-flow analysis. J. Hydrol. 2003, 279, 57–69. [Google Scholar] [CrossRef]
- Dewandel, B.; Lachassagne, P.; Bakalowicz, M.; Weng, P.H.; Al-Malki, A. Evaluation of aquifer thickness by analysing recession hydrographs. Application to the Oman ophiolite hard-rock aquifer. J. Hydrol. 2003, 274, 248–269. [Google Scholar] [CrossRef]
- Brutsaert, W. Long-term groundwater storage trends estimated from streamflow records: Climatic perspective. Water Resour. Res. 2008, 44, W02409. [Google Scholar] [CrossRef]
- Sawaske, S.R.; Freyberg, D.L. An analysis of trends in baseflow recession and low-flows in rain-dominated coastal streams of the pacific coast. J. Hydrol. 2014, 519, 599–610. [Google Scholar] [CrossRef]
- Stoelzle, M.; Stahl, K.; Weiler, M. As simple as possible? Drought recognition based on streamflow recession. In Proceedings of the 10th International Conference on Hydroinformatics, Hamburg, Germany, 14–18 July 2012; pp. 1–8. [Google Scholar]
- Stoelzle, M.; Stahl, K.; Morhard, A.; Weiler, M. Streamflow sensitivity to drought scenarios in catchments with different geology. Geophys. Res. Lett. 2014, 41, 6174–6183. [Google Scholar] [CrossRef]
- Van Dijk, A.I.J.M. Climate and terrain factors explaining streamflow response and recession in Australian catchments. Hydrol. Earth Syst. Sci. 2010, 14, 159–169. [Google Scholar] [CrossRef]
- Beck, H.E.; Dijk, A.I.; Miralles, D.G.; Jeu, R.A.; McVicar, T.R.; Schellekens, J. Global patterns in base flow index and recession based on streamflow observations from 3394 catchments. Water Resour. Res. 2013, 49, 7843–7863. [Google Scholar] [CrossRef]
- Rorabough, M.I. Estimating changes in bank storage and grounwater contribution to streamflow. Int. Assoc. Sci. Hydrol. Publ. 1964, 63, 432–441. [Google Scholar]
- Abo, R.K.; Merkel, B.J. Investigation of the potential surface–groundwater relationship using automated base-flow separation techniques and recession curve analysis in Al Zerba region of Aleppo, Syria. Arab. J. Geosci. 2015, 8, 10543–10563. [Google Scholar] [CrossRef]
- Rutledge, A.T. Computer Programs for Describing the Recession of Ground-Water Discharge and for Estimating mean Ground-Water Recharge and Discharge from Streamflow Record; U.S. Geological Survey, U.S.G.S. Earth Science Information Center, Open-File Reports Section: Reston, VA, USA, 1993.
- Zhang, L.; Brutsaert, W.; Crosbie, R.; Potter, N. Long-term annual groundwater storage trends in Australian catchments. Adv. Water Resour. 2014, 74, 156–165. [Google Scholar] [CrossRef]
- Water Resources Agency. Hydrological Year Book; Water Resources Agency: Taipei, Taiwan, 2017. (In Chinese) [Google Scholar]
- Water Resources Agency. The Third Stage Management Project of Climate Change Impacts and Adaptation on Water Environment (3/5); Water Resources Agency: Taipei, Taiwan, 2016. (In Chinese) [Google Scholar]
- Water Resources Agency. Assessment of Groundwater Potential Exploiting Zones and Groundwater Yields in Kaoping and Chianan Watersheds (2/2); Water Resources Agency: Taipei, Taiwan, 2017. (In Chinese) [Google Scholar]
- Central Geological Survey. Hydrogeology Investigation and Groundwater Resource Assessment for Taiwan-Groundwater Recharge Estimation amd Model Simulation Pingtung Plain; Central Geological Survey: Taipei, Taiwan, 2012. (In Chinese) [Google Scholar]
- Boussinesq, J. Essai sur la théorie des eaux courantes. Imprimerie Nationale: Paris, France, 1877.
- Bogaart, P.W.; Van Der Velde, Y.; Lyon, S.W.; Dekker, S.C. Streamflow recession patterns can help unravel the role of climate and humans in landscape co-evolution. Hydrol. Earth Syst. Sci. 2016, 20, 1413–1432. [Google Scholar] [CrossRef]
- Rupp, D.E.; Selker, J.S. On the use of the Boussinesq equation for interpreting recession hydrographs from sloping aquifers. Water Resour. Res. 2006, 42, W12421. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Y.D.; Hickel, K.; Shao, Q. Analysis of low-flow characteristics for catchments in Dongjiang Basin, China. Hydrogeol. J. 2009, 17, 631–640. [Google Scholar] [CrossRef]
- Szilagyi, J. Vadose zone influences on aquifer parameter estimates of saturated-zone hydraulic theory. J. Hydrol. 2004, 286, 78–86. [Google Scholar] [CrossRef]
- Parlange, J.Y.; Stagnitti, F.; Heilig, A.; Szilagyi, J.; Parlange, M.B.; Steenhuis, T.S.; Hogarth, W.L.; Barry, D.A.; Li, L. Sudden drawdown and drainage of a horizontal aquifer. Water Resour. Res. 2001, 37, 2097–2101. [Google Scholar] [CrossRef]
- Kingsford, R.T.; Thomas, R.F. Environmental Flows on the Paroo and Warrego Rivers; National Parks & Wildlife Service: New South Wales, Australia, 2000. [Google Scholar]
- Troch, P.A.; Mancini, M.; Paniconi, C.; Wood, E.F. Evaluation of a distributed catchment scale water balance model. Water Resour. Res. 1993, 29, 1805–1817. [Google Scholar] [CrossRef]
- Rorabaugh, M.I.; Simons, W.D. Exploration of Methods of Relating Ground Water to Surface Water, Columbia River Basin-Second Phase: U.S. Geol. Survey (USGS) Open-File Report; US Geological Survey: Reston, VA, USA, 1966. [Google Scholar]
- Bevans, H.E. Estimating Stream-Aquifer Interactions in Coal Areas of Eastern Kansas by Using Streamflow Records; US Geological Survey Water Supply Paper; US Geological Survey: Reston, VA, USA, 1986; pp. 51–64.
- Barnes, B.S. The structure of discharge-recession curves. Eos Trans. Am. Geophys. Union 1939, 20, 721–725. [Google Scholar] [CrossRef]
- Anderson, M.G.; Burt, T.P. Interpretation of recession flow. J. Hydrol. 1980, 46, 89–101. [Google Scholar] [CrossRef]
- Lyon, S.W.; Koutsouris, A.; Scheibler, F.; Jarsjö, J.; Mbanguka, R.; Tumbo, M.; Robert, K.K.; Sharma, A.N.; van der Velde, Y. Interpreting characteristic drainage timescale variability across Kilombero Valley, Tanzania. Hydrol. Process. 2015, 29, 1912–1924. [Google Scholar] [CrossRef]
- Shaw, S.B.; McHardy, T.M.; Riha, S.J. Evaluating the influence of watershed moisture storage on variations in base flow recession rates during prolonged rain-free periods in medium-sized catchments in New York and Illinois, USA. Water Resour. Res. 2013, 49, 6022–6028. [Google Scholar] [CrossRef]
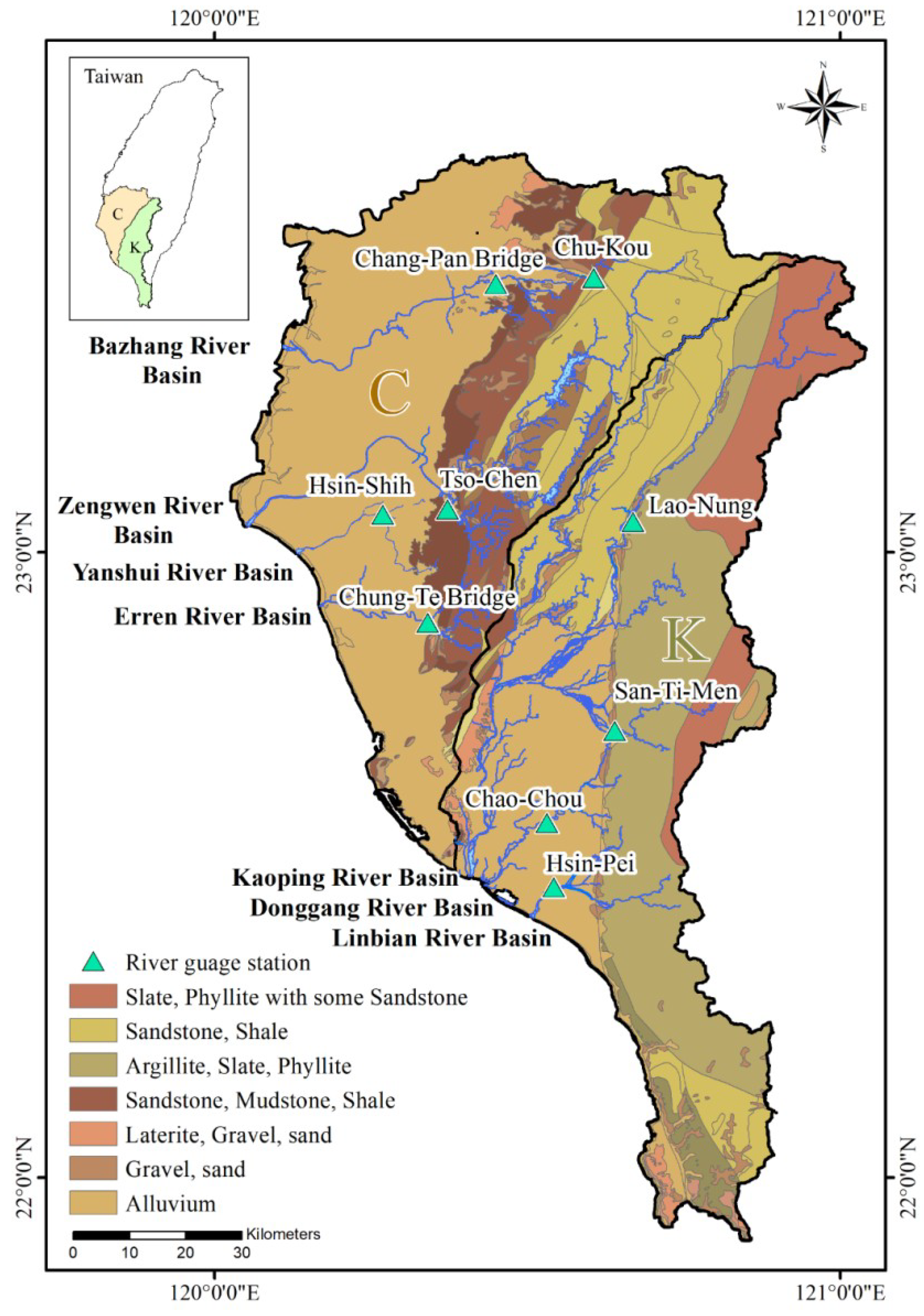
| Basin | Station | Area (km2) | X-Coordinate (TWD67 a) | Y-Coordinate (TWD67 a) | Record Years |
|---|---|---|---|---|---|
| Bazhang River | Chu-Kou | 83.1 | 209,775.8 | 2,592,901.4 | 1967–2017 |
| Chang-Pan Bridge | 101.1 | 193,794.3 | 2,591,889.4 | 1970–2017 | |
| Zengwen River | Tso-Chen | 121.3 | 186,554.1 | 2,551,818.6 | 1971–2017 |
| Yanshui River | Hsin-Shih | 146.5 | 175,903.5 | 2,550,924.6 | 1973–2017 |
| Erren River | Chung-Te Bridge | 139.6 | 183,217.2 | 2,531,714.6 | 1982–2017 |
| Kaoping River | Lao-Nung | 812.0 | 216,098.8 | 2,549,698.6 | 1959–2008 |
| San-Ti-Men | 408.5 | 213,804.4 | 2,512,457.7 | 1964–2017 | |
| Donggang River | Chao-Chou | 175.3 | 203,071.1 | 2,496,579.8 | 1965–2017 |
| Linbian River | Hsin-Pei | 309.9 | 203,708 | 2,484,782.9 | 1962–2013 |
| Station | K | |
|---|---|---|
| Dry Season | Wet Season | |
| Chu-Kou | 117.65 | 57.80 |
| Chang-Pan Bridge | 50 | 30.30 |
| Tso-Chen | 51.81 | 31.45 |
| Hsin-Shih | 39.53 | 37.45 |
| Chung-Te Bridge | 29.94 | 31.25 |
| Lao-Nung | 70.42 | 55.56 |
| San-Ti-Men | 93.76 | 29.85 |
| Chao-Chou | 131.58 | 58.82 |
| Hsin-Pei | 40.16 | 34.97 |
| Chu-Kou | 69.43 | 40.83 |
| Chianan Sub-Area | |||
| Hydrogeological Parameters | Pumping Test | Dry Season | Wet Season |
| T (m2/min) | 2.63 × 10−1–4.40 × 10−3 | 100–10−2 | 100–10−2 |
| k (m/s) | 10−4–10−6 | 10−3–10−5 | 10−4–10−6 |
| Sy (-) | 10−2 | 10−2–10−4 | 10−1–10−5 |
| Kaoping Sub-Area | |||
| Hydrogeological Parameters | Pumping Test | Dry Season | Wet Season |
| T (m/min) | 3.00 × 10−5–1.51 × 101 | 100–101 | 100 |
| k (m/s) | 10−3–10−5 | 10−2–10−3 | 10−2–10−3 |
| Sy (-) | 10−1–10−5 | 10−2–10−3 | 10−2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.-C.; Yeh, H.-F. Hydrogeological Parameter Determination in the Southern Catchments of Taiwan by Flow Recession Method. Water 2019, 11, 7. https://doi.org/10.3390/w11010007
Huang C-C, Yeh H-F. Hydrogeological Parameter Determination in the Southern Catchments of Taiwan by Flow Recession Method. Water. 2019; 11(1):7. https://doi.org/10.3390/w11010007
Chicago/Turabian StyleHuang, Chia-Chi, and Hsin-Fu Yeh. 2019. "Hydrogeological Parameter Determination in the Southern Catchments of Taiwan by Flow Recession Method" Water 11, no. 1: 7. https://doi.org/10.3390/w11010007
APA StyleHuang, C.-C., & Yeh, H.-F. (2019). Hydrogeological Parameter Determination in the Southern Catchments of Taiwan by Flow Recession Method. Water, 11(1), 7. https://doi.org/10.3390/w11010007






