Numerical Study of the Velocity Decay of Offset Jet in a Narrow and Deep Pool
Abstract
1. Introduction
2. Numerical Simulation
2.1. Mathematical Model
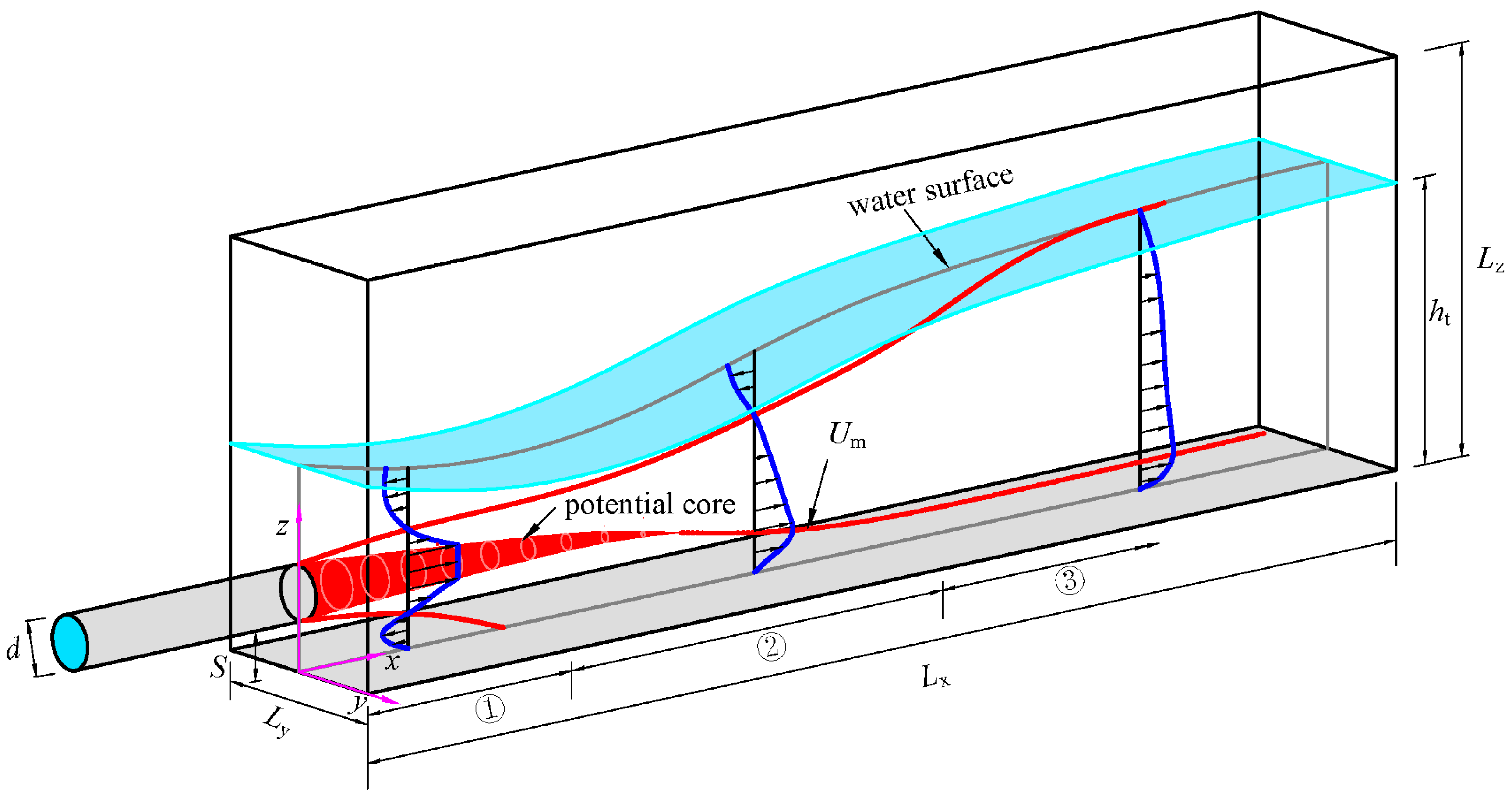
2.2. Simulation Setup
2.3. Initial Conditions and Boundary Conditions
- Inflow boundary: the inlet was treated as an inlet velocity boundary with the velocity was set as 5 m/s;
- Outflow boundary: pressure outlet boundary was selected at the outlet, the depth of tailwater was fixed at 0.55 m with the help of user-defined function (UDF);
- Free surface: pressure inlet was employed, and its value was the standard atmospheric pressure, the operating pressure and density were selected as 101,325 Pa and 1.225 kg/m3, respectively.
- Wall boundary: for the parameters investigated in this study, the data near the wall was ineffective. No slip boundary condition is considered for velocity. To avoid the fine mesh required to resolve the viscous sub-layer near the boundary, so standard wall function method has been used.
2.4. Numerical Discretizations
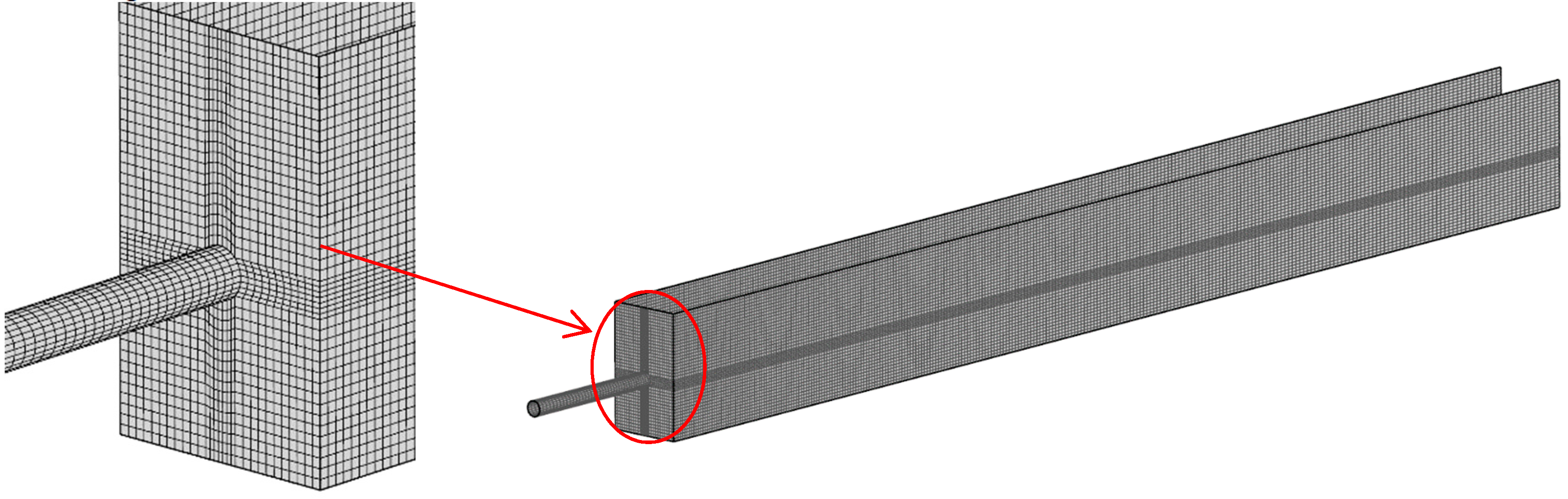
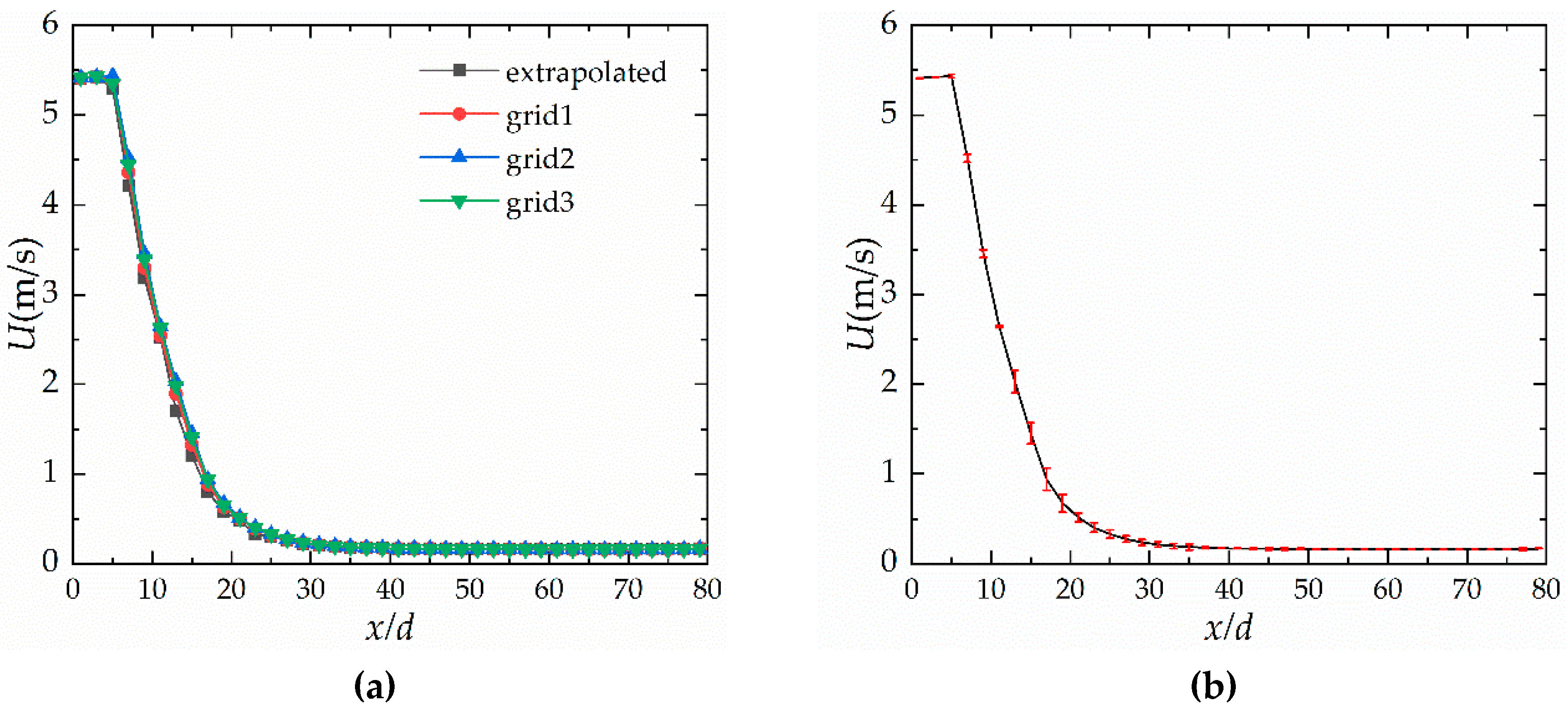
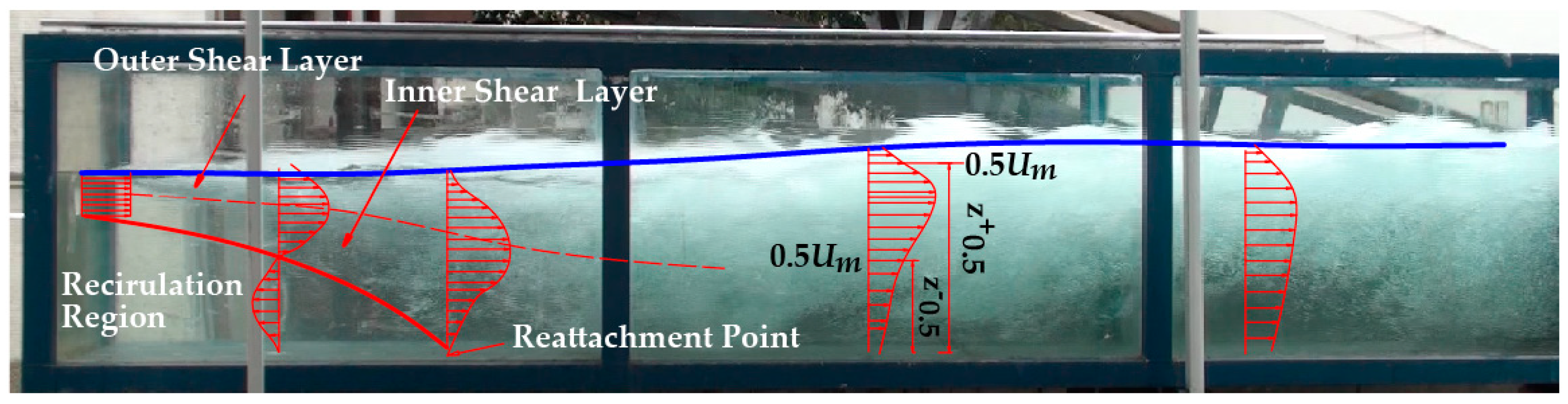
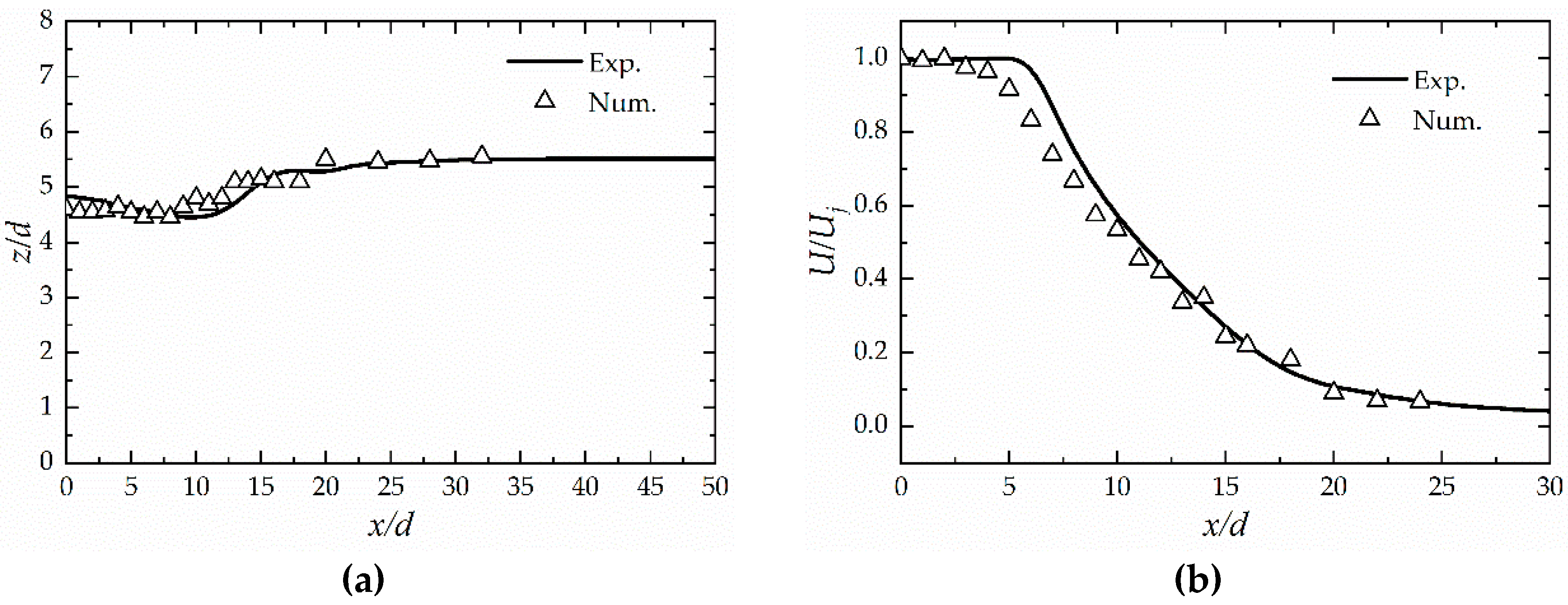
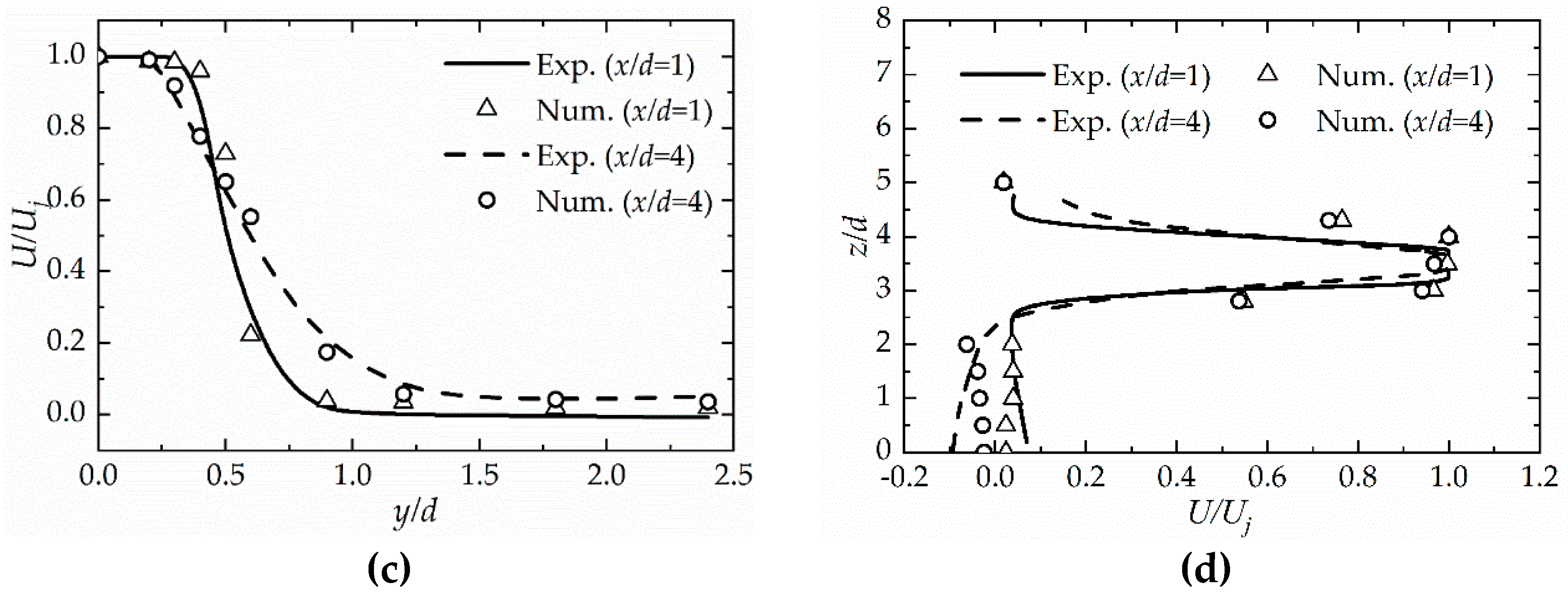
2.5. Grids Sensitivity and Model Validation
3. Results and Analysis
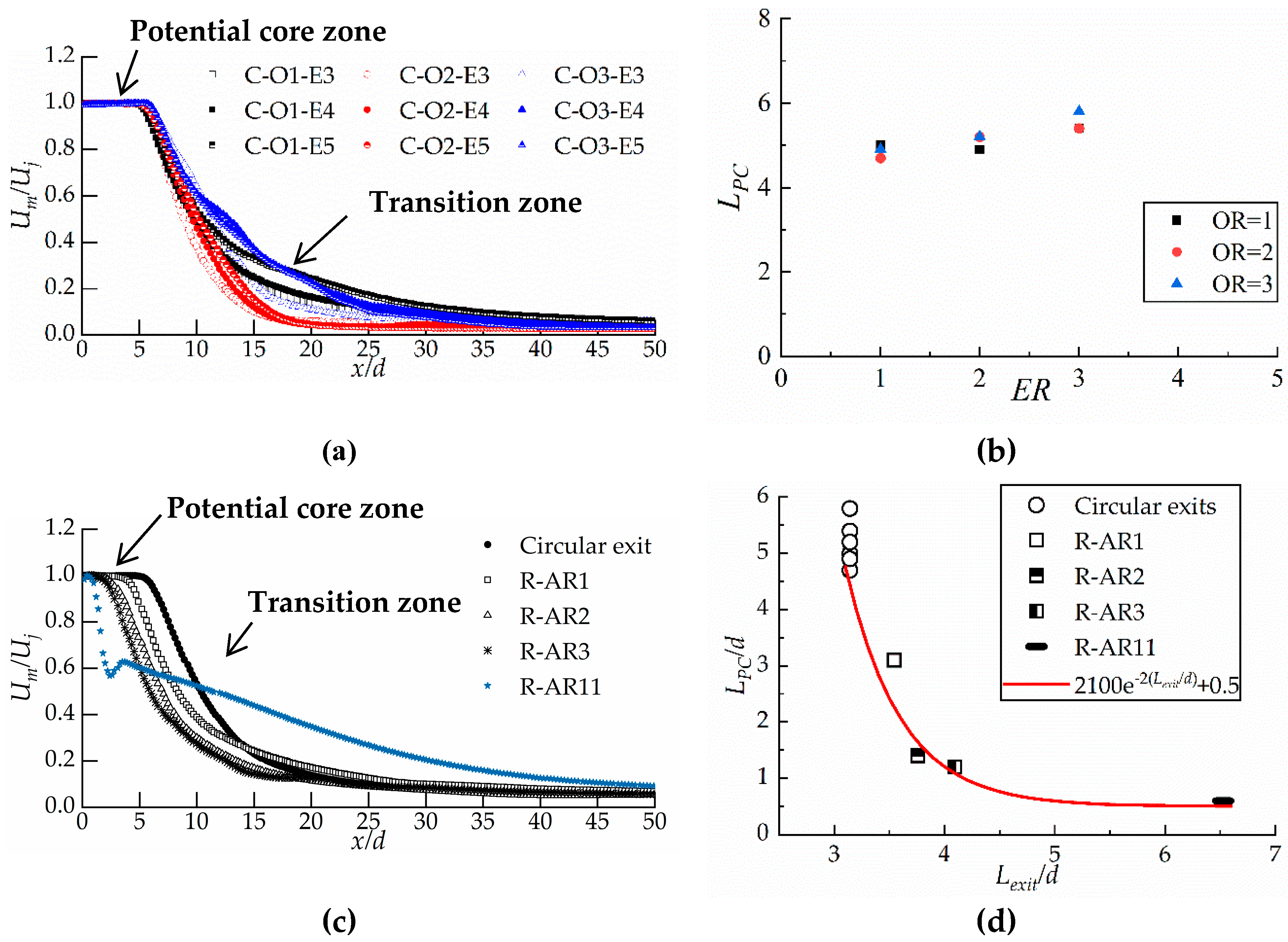
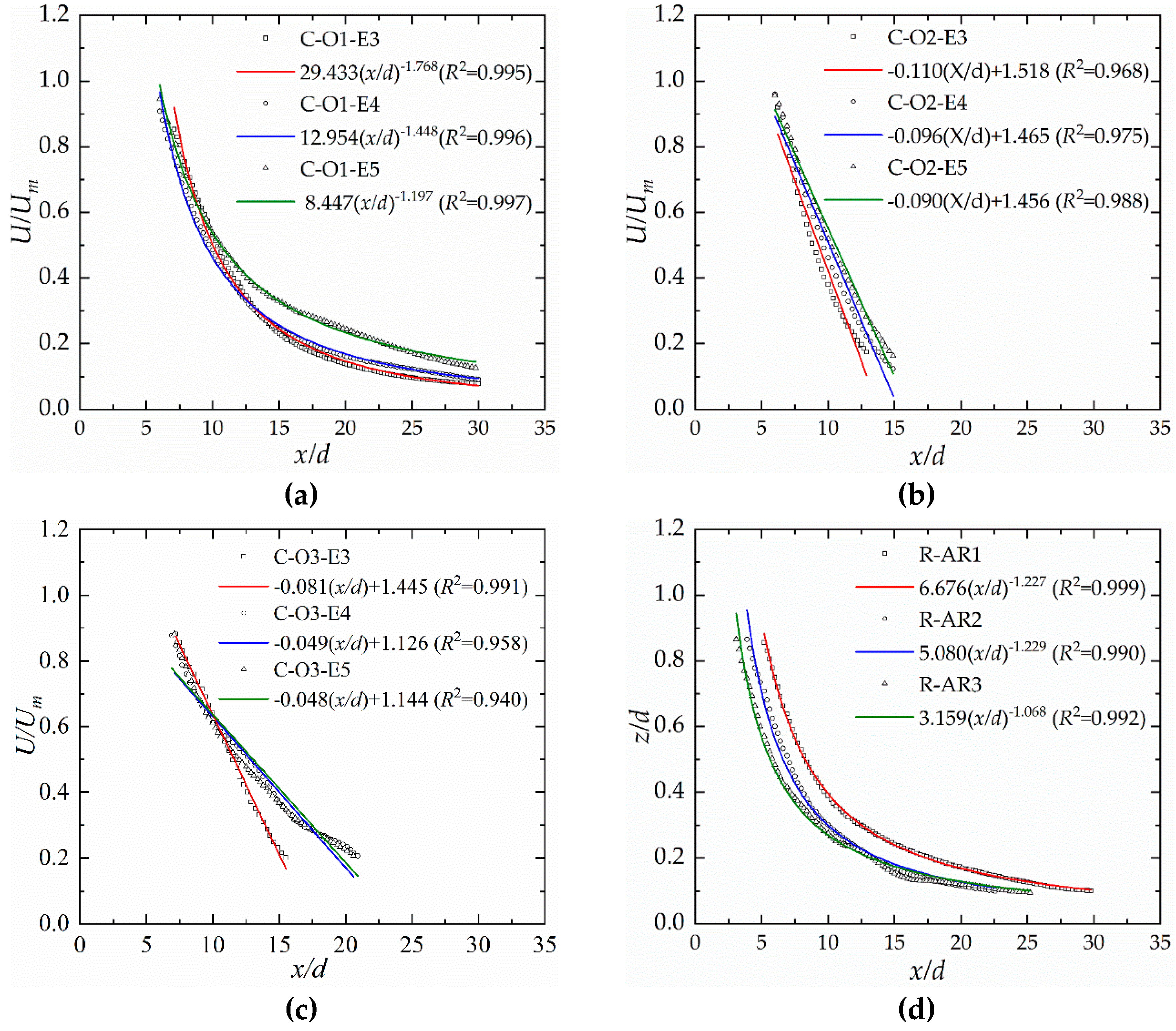
3.1. Velocity Attenuation
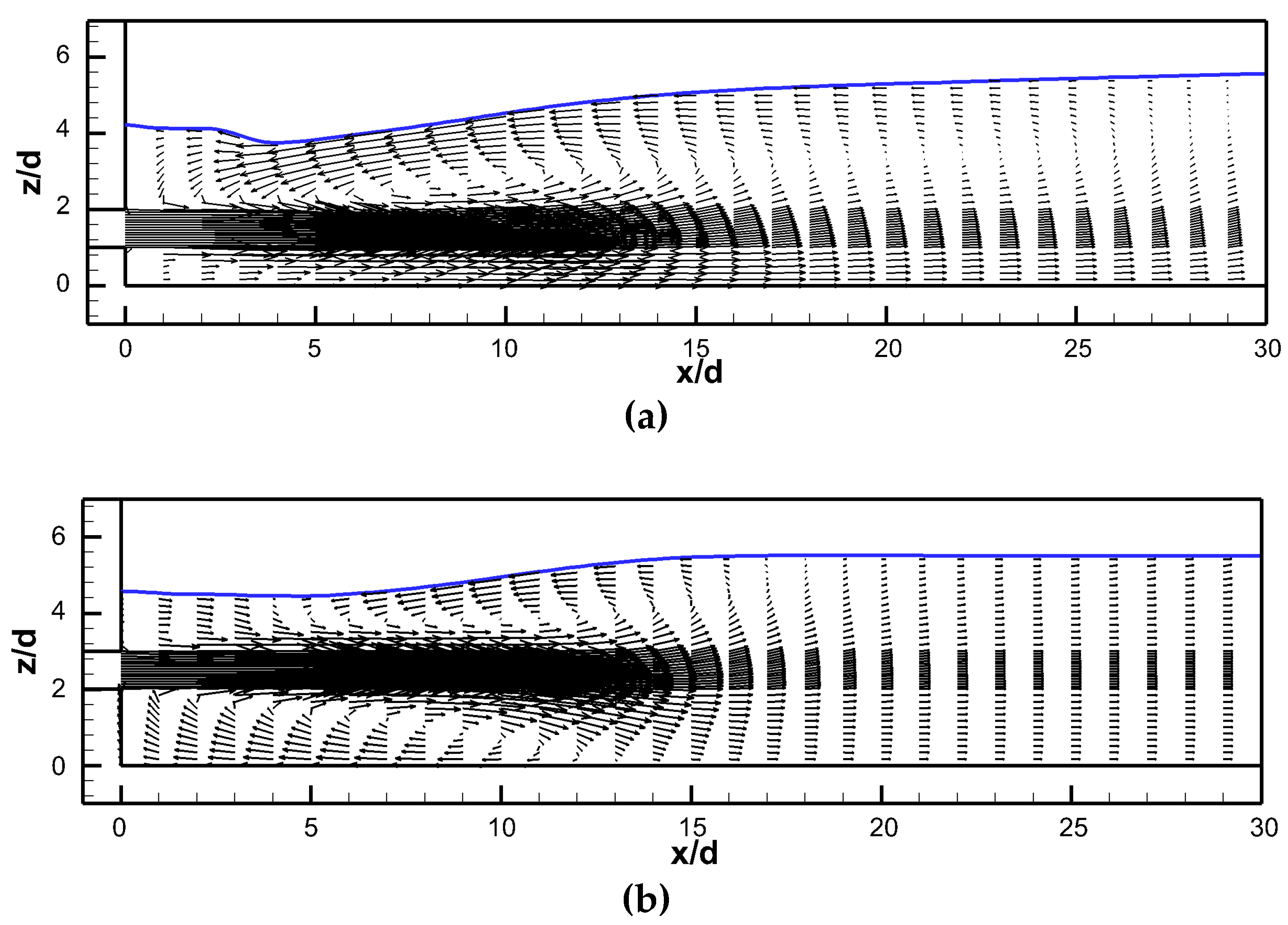
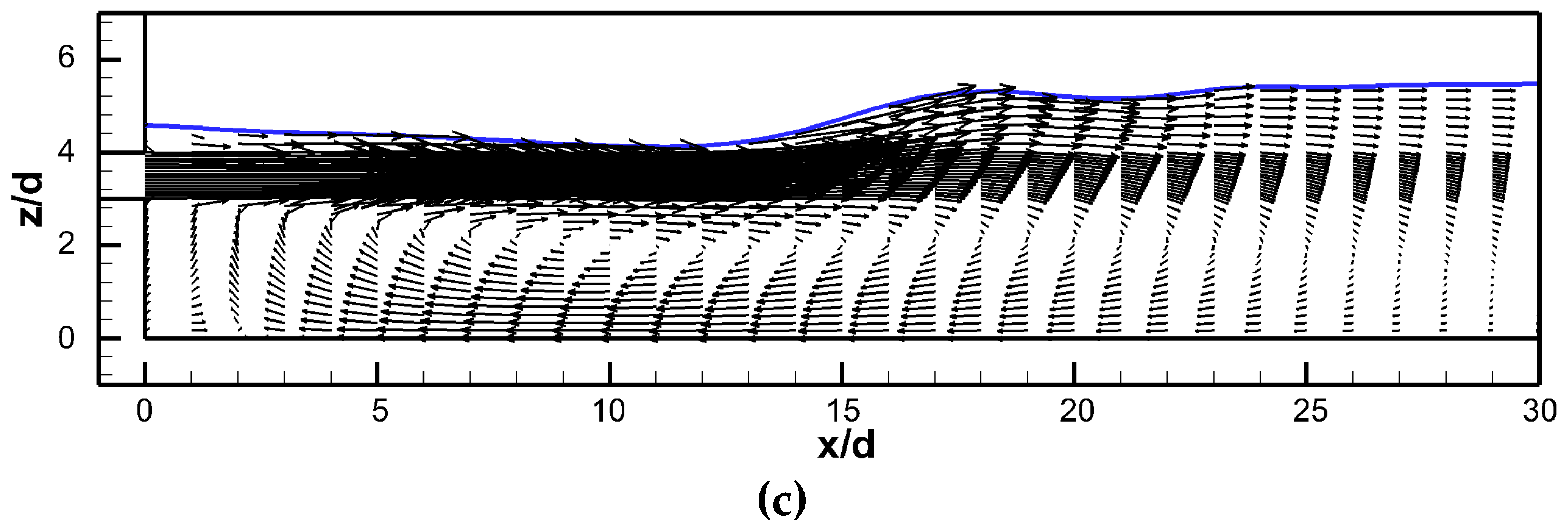
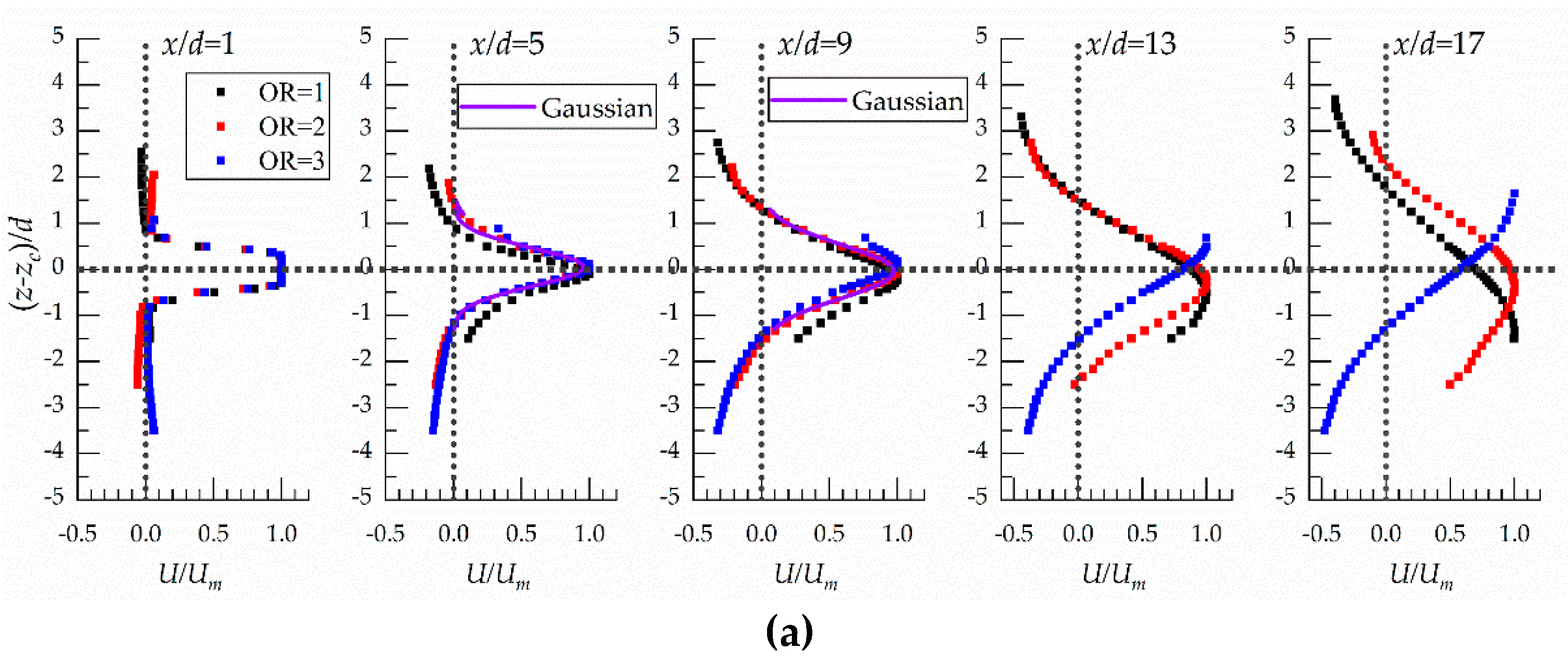
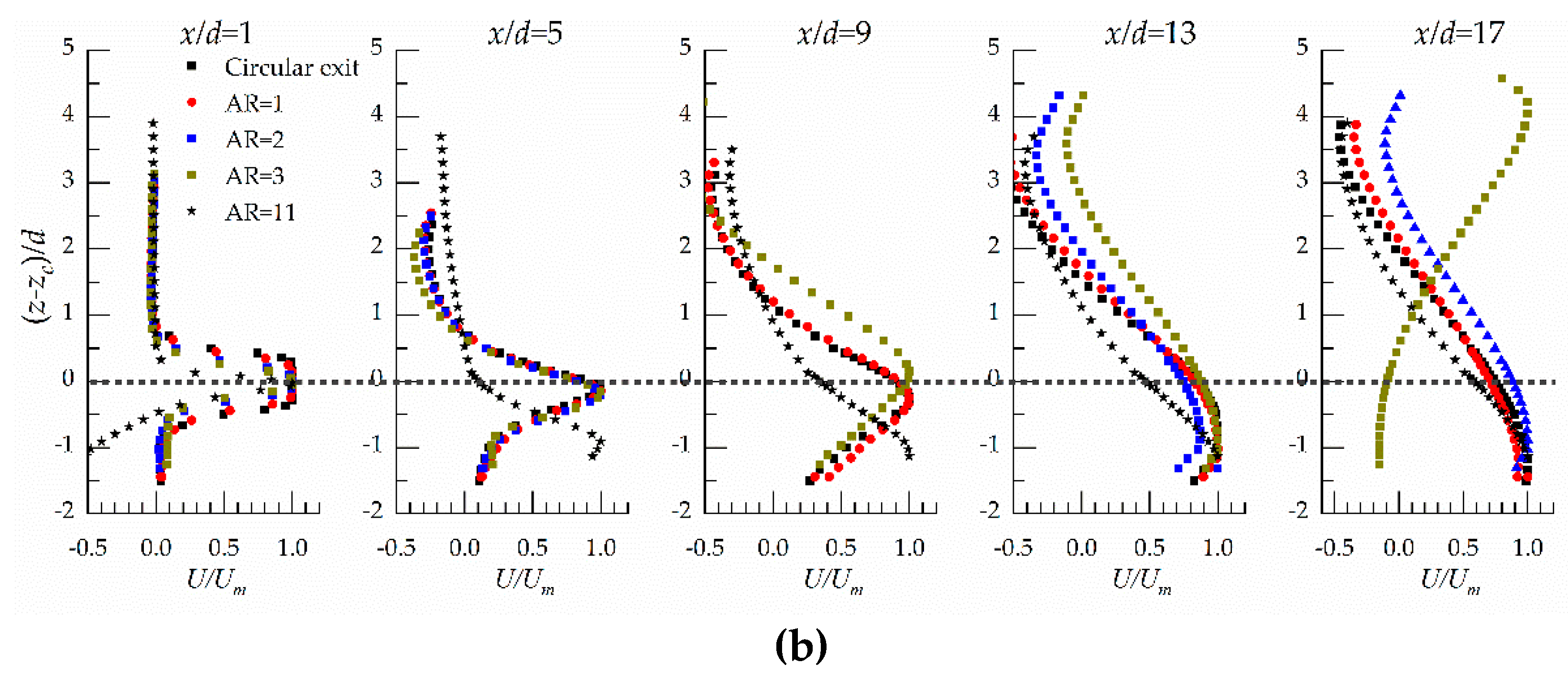
3.2. Vertical Velocity Spread
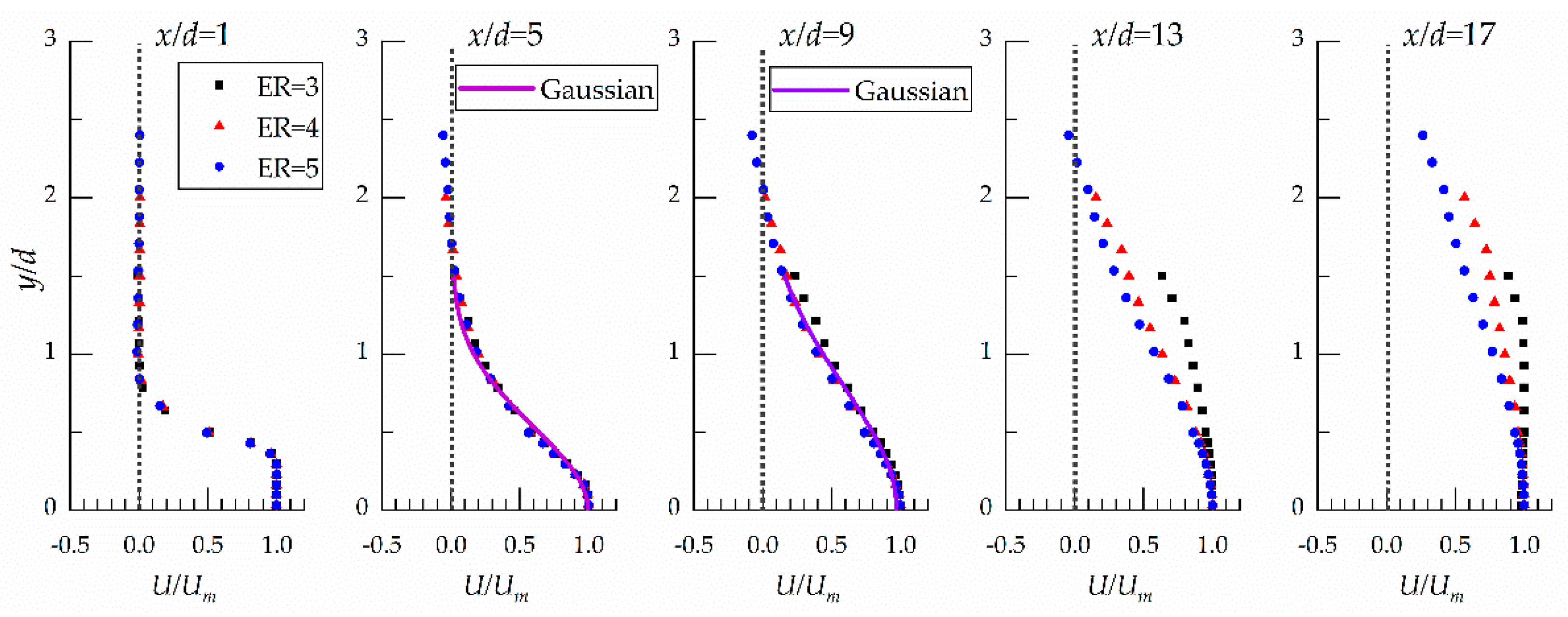
3.3. Lateral Velocity Spread
4. Conclusions
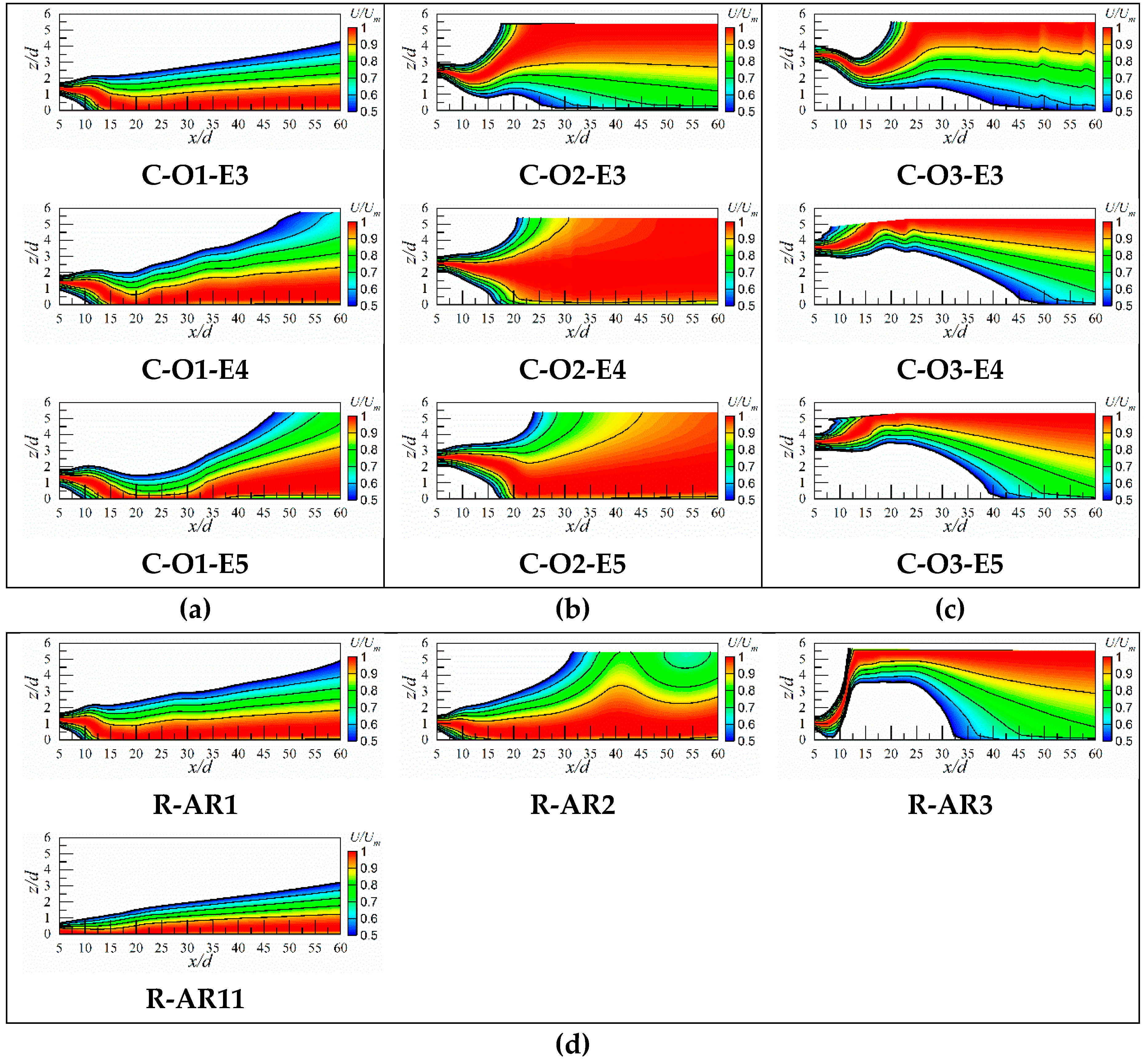
- The development of the jet within the potential core zone was observed to be dependent on the circumference of jet exits. It was noted that the length of the potential core zone decreases with the circumference of exit.
- The results showed that the development of the Um in the transition zone could be divided into two modes. That is, (a) the decay of Um could be estimated from power law fit with a decay rate n of 1.089–1.451 as the offset ratio is lower (OR = 1). (b) A linear fit was used to estimate the decay rates for higher offset ratio jet (OR = 2 or 3). It was observed that Um decay is the fastest as the offset ratio (OR) is 2. Further, the results indicate that a more confining enclosure produces a more rapid jet decay than a less confining condition.
- The spread rate of the circular jet is not affected by the expansion ratios and offset ratio in the early region of jet decay. The main flow for OR = 2 was traveled straightly, and the main flow was toward the floor and the water surface as the OR = 1 and OR = 3, respectively.
- The absence of the sudden expansion coupled with the high aspect ratio of the exit contributed to form a unique flow pattern compared with other cases.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| x | Stream wise direction |
| y | Lateral direction |
| z | Floor direction |
| Lx | Length of the jet pool in the streamwise direction (m) |
| Ly | The width of the jet pool in the lateral direction (m) |
| Lz | The height of the jet pool in the floor-normal direction (m) |
| d | The diameter of circular jet exit (m) or equivalent diameter of rectangular exit (m) |
| a0 | The height of the rectangular exit (m) |
| b0 | Width of rectangular exit (m) |
| ht | The height of tailwater (m) |
| S | Offset height of jet exit (m) |
| U | Mean velocity in streamwise (m/s) |
| Um | Cross-Sectional streamwise maximum mean velocity (m/s) |
| Uj | Velocity in jet exit (m/s) |
| LPC | Length of potential core |
| Lexit | The circumference of jet exit |
| zc | Distance from center of exit to floor, or |
| The loci of where U = 0.5 Um above the jet | |
| The loci of where U = 0.5 Um below the jet | |
| Distance from the exit to where the reaches floor | |
| Distance from the exit to where the reaches water surface | |
| n | Decay rate used in power law |
| κ | Decay rate used in the linear fit |
| R0 | Reynolds number |
| OR | Offset ratio of jet exit (S/d or S/a0) |
| ER | The expansion ratio of jet exit (Ly/d or Ly/b0) |
| AR | Aspect ratio of jet exit (b0/a0) |
References
- SoaresFrazão, S. Wastewater Hydraulics; Springer: Berlin/Heidelberg, Germany, 2010; pp. 842–843. [Google Scholar]
- Liu, M.; Rajaratnam, N.; Zhu David, Z. Mean Flow and Turbulence Structure in Vertical Slot Fishways. J. Hydraul. Eng. 2006, 132, 765–777. [Google Scholar] [CrossRef]
- Chen, J.-G.; Zhang, J.-M.; Xu, W.-L.; Li, S.; He, X.-L. Particle image velocimetry measurements of vortex structures in stilling basin of multi-horizontal submerged jets. J. Hydrodyn. 2013, 25, 556–563. [Google Scholar] [CrossRef]
- Dey, S.; Ravi Kishore, G.; Castro-Orgaz, O.; Ali, S.Z. Hydrodynamics of submerged turbulent plane offset jets. Phys. Fluids 2017, 29, 065112. [Google Scholar] [CrossRef]
- Bhuiyan, F.; Habibzadeh, A.; Rajaratnam, N.; Zhu David, Z. Reattached Turbulent Submerged Offset Jets on Rough Beds with Shallow Tailwater. J. Hydraul. Eng. 2011, 137, 1636–1648. [Google Scholar] [CrossRef]
- Durand, Z.M.J.; Clark, S.P.; Tachie, M.F.; Malenchak, J.; Muluye, G. Experimental Study of Reynolds Number Effects on Three-Dimensional Offset Jets. In Proceedings of the 12th International Conference on Nanochannels, Microchannels, and Minichannels, Chicago, IL, USA, 3–7 August 2014. [Google Scholar] [CrossRef]
- Nyantekyi-Kwakye, B.; Tachie, M.F.; Clark, S.P.; Malenchak, J.; Muluye, G.Y. Experimental study of the flow structures of 3D turbulent offset jets. J. Hydraul. Res. 2015, 53, 773–786. [Google Scholar] [CrossRef]
- Agelin-Chaab, M.; Tachie, M.F. Characteristics and structure of turbulent 3D offset jets. Int. J. Heat Fluid Flow 2011, 32, 608–620. [Google Scholar] [CrossRef]
- Li, J.-N.; Zhang, J.-M.; Peng, Y. Characterization of the mean velocity of a circular jet in a bounded basin. J. Zhejiang Univ. Sci. A 2017, 18, 807–818. [Google Scholar] [CrossRef]
- Kumar Rathore, S.; Kumar Das, M. Effect of Freestream Motion on Heat Transfer Characteristics of Turbulent Offset Jet. J. Therm. Sci. Eng. Appl. 2015, 8, 011021. [Google Scholar] [CrossRef]
- Camino, G.A.; Zhu, D.Z.; Rajaratnam, N. Jet diffusion inside a confined chamber. J. Hydraul. Res. 2012, 50, 121–128. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, Y.; Zeng, J.; Zheng, J.; Wu, X. Numerical Simulation of Vertical Buoyant Wall Jet Discharged into a Linearly Stratified Environment. J. Hydraul. Eng. 2018, 144, 06018009. [Google Scholar] [CrossRef]
- Assoudi, A.; Habli, S.; Mahjoub Saïd, N.; Bournot, H.; Le Palec, G. Three-dimensional study of turbulent flow characteristics of an offset plane jet with variable density. Heat Mass Transf. 2016, 52, 2327–2343. [Google Scholar] [CrossRef]
- Mondal, T.; Guha, A.; Das, M.K. Computational study of periodically unsteady interaction between a wall jet and an offset jet for various velocity ratios. Comput. Fluids 2015, 123, 146–161. [Google Scholar] [CrossRef]
- Vishnuvardhanarao, E.; Das, M.K. Computation of Mean Flow and Thermal Characteristics of Incompressible Turbulent Offset Jet Flows. Numer. Heat Transf. A 2007, 53, 843–869. [Google Scholar] [CrossRef]
- Gu, R. Modeling Two-Dimensional Turbulent Offset Jets. J. Hydraul. Eng. 1996, 122, 617–624. [Google Scholar] [CrossRef]
- Hnaien, N.; Marzouk, S.; Ben Aissia, H.; Jay, J. CFD investigation on the offset ratio effect on thermal characteristics of a combined wall and offset jets flow. Heat Mass Transf. 2017, 53, 2531–2549. [Google Scholar] [CrossRef]
- Abraham, J.; Magi, V. Computations of Transient Jets: RNG k-e Model Versus Standard k-e Model; SAE: Warrendale, PA, USA, 1997. [Google Scholar]
- Nasr, A.; Lai, J.C.S. A turbulent plane offset jet with small offset ratio. Exp. Fluids 1998, 24, 47–57. [Google Scholar] [CrossRef]
- Launder, B.E.; Sharma, B.I. Application of the energy-dissipation model of turbulence to the calculation of flow near a spinning disc. Lett. Heat Mass Transf. 1974, 1, 131–137. [Google Scholar] [CrossRef]
- Bai, Z.; Wang, Y.; Zhang, J. Pressure distributions of stepped spillways with different horizontal face angles. In Proceedings of the Institution of Civil Engineers-Water Management; Thomas Telford Ltd.: London, UK; pp. 1–12.
- Li, S.; Zhang, J. Numerical Investigation on the Hydraulic Properties of the Skimming Flow over Pooled Stepped Spillway. Water 2018, 10, 1478. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Peng, Y.; Mao, Y.F.; Wang, B.; Xie, B. Study on C–S and P–R EOS in pseudo-potential lattice Boltzmann model for two-phase flows. Int. J. Mod. Phys. C 2017, 28, 1750120. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, B.; Mao, Y. Study on Force Schemes in Pseudopotential Lattice Boltzmann Model for Two-Phase Flows. J. Math. Probl. Eng. 2018, 2018, 9. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, J.; Meng, J. Second-order force scheme for lattice Boltzmann model of shallow water flows. J. Hydraul. Res. 2017, 55, 592–597. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, J.M.; Zhou, J.G. Lattice Boltzmann Model Using Two Relaxation Times for Shallow-Water Equations. J. Hydraul. Eng. 2016, 142, 06015017. [Google Scholar] [CrossRef]
- Peng, Y.; Zhou, J.G.; Burrows, R. Modeling Free-Surface Flow in Rectangular Shallow Basins by Using Lattice Boltzmann Method. J. Hydraul. Eng. 2011, 137, 1680–1685. [Google Scholar] [CrossRef]
- Peng, Y.; Zhou, J.G.; Burrows, R. Modelling solute transport in shallow water with the lattice Boltzmann method. Comput. Fluids 2011, 50, 181–188. [Google Scholar] [CrossRef]
- Van Doormaal, J.P.; Raithby, G.D. Enhancements of the Simple Method for Predicting Incompressible Fluid Flows. Numer. Heat Transf. 1984, 7, 147–163. [Google Scholar] [CrossRef]
- Celik, I.; Ghia, U.; Roache, P.; Freitas, C.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef]
- Nyantekyi-Kwakye, B.; Clark, S.P.; Tachie, M.F.; Malenchak, J.; Muluye, G. Flow characteristics within the recirculation region of three-dimensional turbulent offset jet. J. Hydraul. Res. 2015, 53, 230–242. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Zhang, J. Numerical Simulation of an Offset Jet in Bounded Pool with Deflection Wall. Math. Probl. Eng. 2017, 2017, 11. [Google Scholar] [CrossRef]
- Nyantekyi-Kwakye, B.; Tachie, M.F.; Clark, S.P.; Malenchak, J.; Muluye, G.Y. Acoustic Doppler velocimeter measurements of a submerged three-dimensional offset jet flow over rough surfaces. J. Hydraul. Res. 2017, 55, 40–49. [Google Scholar] [CrossRef]
- Padmanabham, G.; Lakshmana Gowda, B.H. Mean and Turbulence Characteristics of a Class of Three-Dimensional Wall Jets—Part 1: Mean Flow Characteristics. J. Fluids Eng. 1991, 113, 620–628. [Google Scholar] [CrossRef]
- Rajaratnam, N. Turbulents Jets; Elsevier: New York, NY, USA, 1976. [Google Scholar]
- Ohtsu, I.; Yasuda, Y.; Ishikawa, M. Submerged Hydraulic Jumps below Abrupt Expansions. J. Hydraul. Eng. 1999, 125, 492–499. [Google Scholar] [CrossRef]
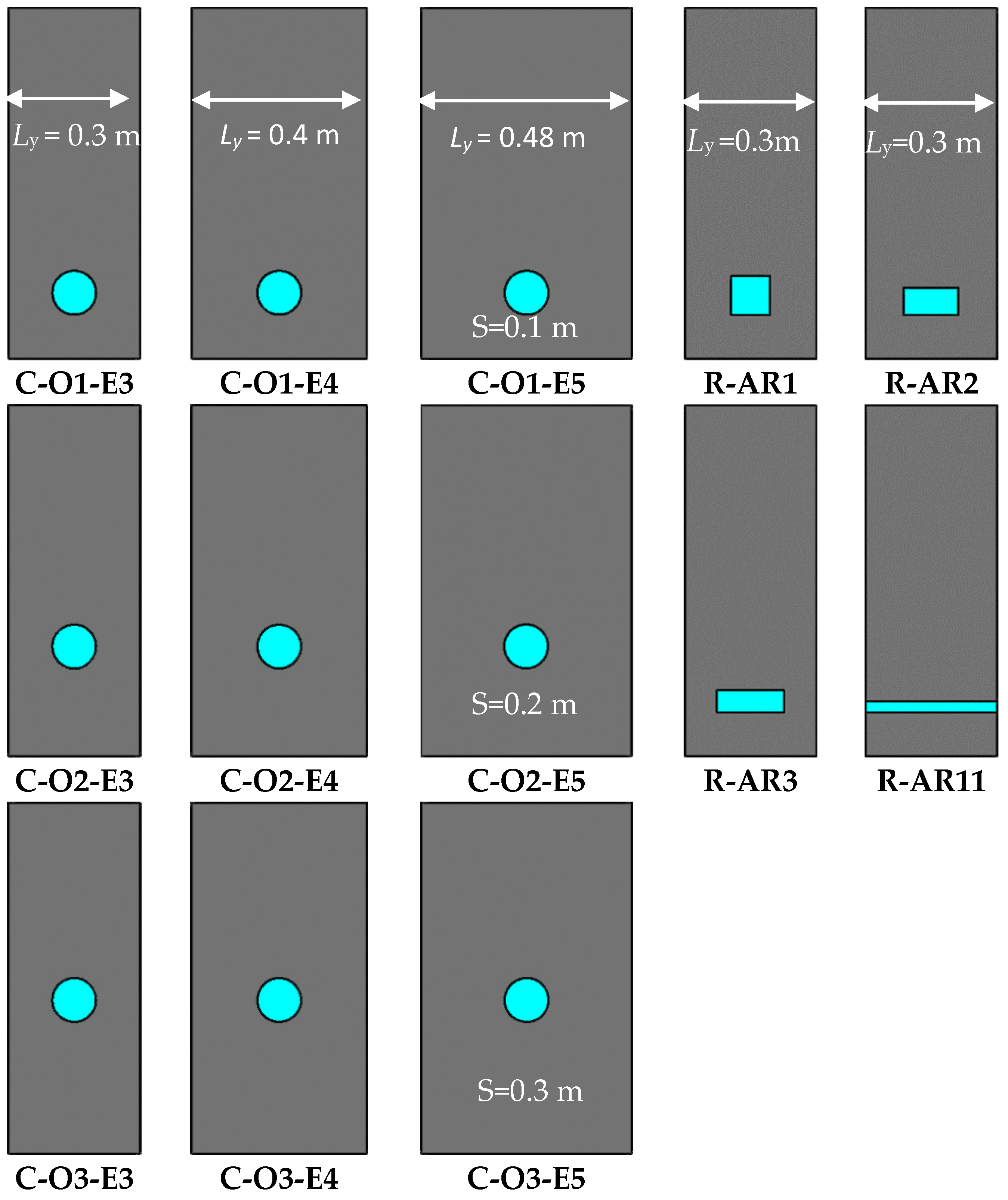
| Case Name | Jet Exit Shape | d (m) | a0 (m) | b0 (m) | S (m) | Ly (m) | Offset Ratio (OR) | Expansion Ratio (ER) | AR (b0/a0) |
|---|---|---|---|---|---|---|---|---|---|
| C-O1-E3 | circular | 0.1 | - | - | 0.1 | 0.3 | 1 | 3 | - |
| C-O1-E4 | circular | 0.1 | - | - | 0.1 | 0.4 | 1 | 4 | - |
| C-O1-E5 | circular | 0.1 | - | - | 0.1 | 0.48 | 1 | 4.8 | - |
| C-O2-E3 | circular | 0.1 | - | - | 0.2 | 0.3 | 2 | 3 | - |
| C-O2-E4 | circular | 0.1 | - | - | 0.2 | 0.4 | 2 | 4 | - |
| C-O2-E5 | circular | 0.1 | - | - | 0.2 | 0.48 | 2 | 4.8 | - |
| C-O3-E3 | circular | 0.1 | - | - | 0.3 | 0.3 | 3 | 3 | - |
| C-O3-E4 | circular | 0.1 | - | - | 0.3 | 0.4 | 3 | 4 | - |
| C-O3-E5 | circular | 0.1 | - | - | 0.3 | 0.48 | 3 | 4.8 | - |
| R-AR1 | rectangular | - | 0.089 | 0.089 | 0.1 | 0.3 | 1.13 | 3.39 | 1 |
| R-AR2 | rectangular | - | 0.125 | 0.063 | 0.1 | 0.3 | 1.60 | 2.39 | 2 |
| R-AR3 | rectangular | - | 0.153 | 0.051 | 0.1 | 0.3 | 1.95 | 1.95 | 3 |
| R-AR11 | rectangular | - | 0.1 | 0.026 | 0.1 | 0.3 | 3.82 | 1.00 | 11.46 |
| Decay Rate | n (OR = 1) | κ (OR = 2) | κ (OR = 3) |
|---|---|---|---|
| Fit Equation | Power Law | Linear Equation | |
| ER = 3 | 1.768 | 0.110 | 0.081 |
| ER = 4 | 1.448 | 0.096 | 0.049 |
| ER = 4.8 | 1.197 | 0.090 | 0.048 |
| Decay Rate | n (OR = 1) |
|---|---|
| Fit Equation | Power Law |
| AR = 1 | 1.227 |
| AR = 2 | 1.229 |
| AR = 3 | 1.068 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhou, M.; Zhang, J.; Xu, W. Numerical Study of the Velocity Decay of Offset Jet in a Narrow and Deep Pool. Water 2019, 11, 59. https://doi.org/10.3390/w11010059
Li X, Zhou M, Zhang J, Xu W. Numerical Study of the Velocity Decay of Offset Jet in a Narrow and Deep Pool. Water. 2019; 11(1):59. https://doi.org/10.3390/w11010059
Chicago/Turabian StyleLi, Xin, Maolin Zhou, Jianmin Zhang, and Weilin Xu. 2019. "Numerical Study of the Velocity Decay of Offset Jet in a Narrow and Deep Pool" Water 11, no. 1: 59. https://doi.org/10.3390/w11010059
APA StyleLi, X., Zhou, M., Zhang, J., & Xu, W. (2019). Numerical Study of the Velocity Decay of Offset Jet in a Narrow and Deep Pool. Water, 11(1), 59. https://doi.org/10.3390/w11010059





