Upscaling Mixing in Highly Heterogeneous Porous Media via a Spatial Markov Model
Abstract
1. Introduction
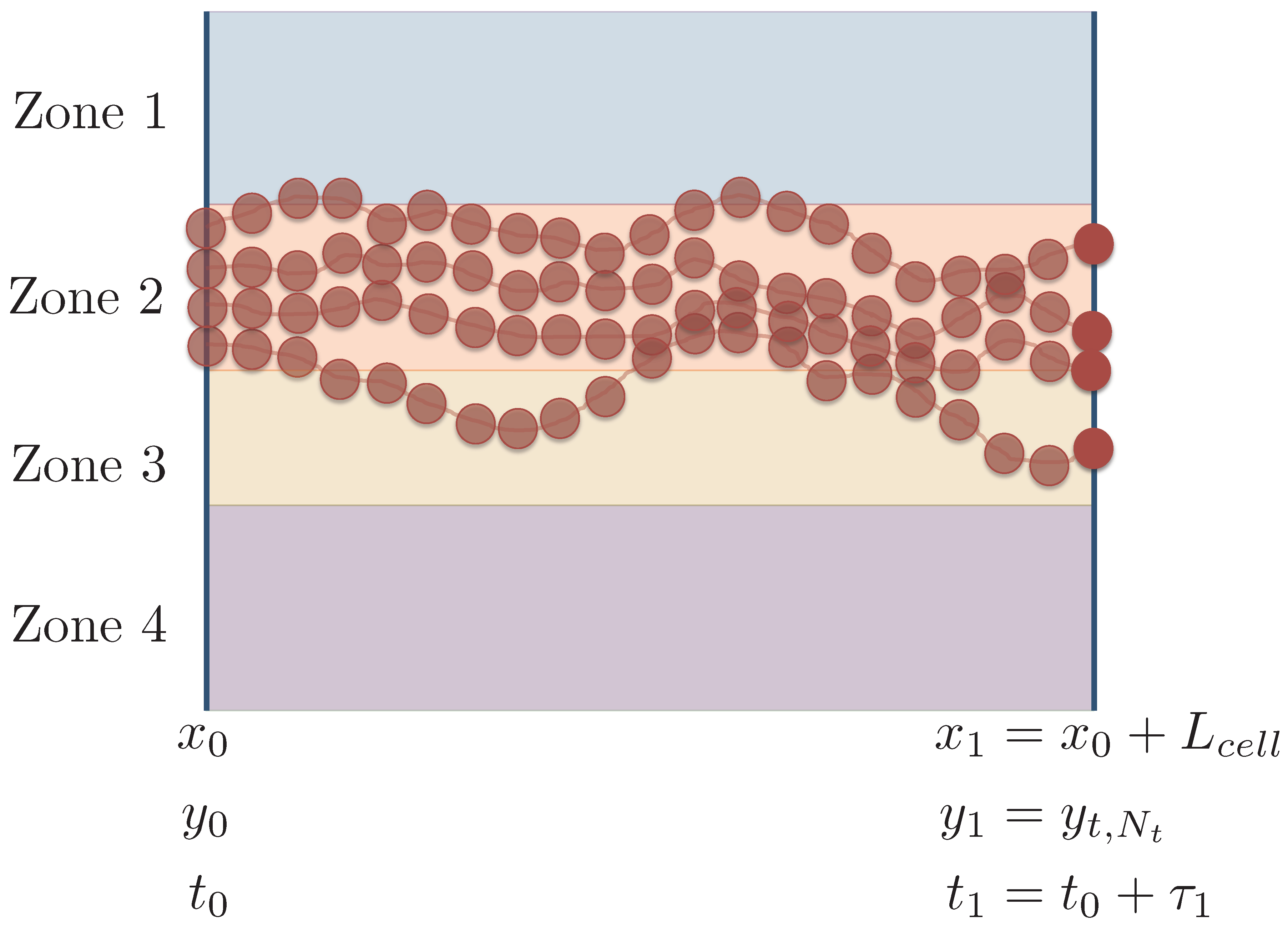
2. System Setup
3. Upscaled Model: Spatial Markov model
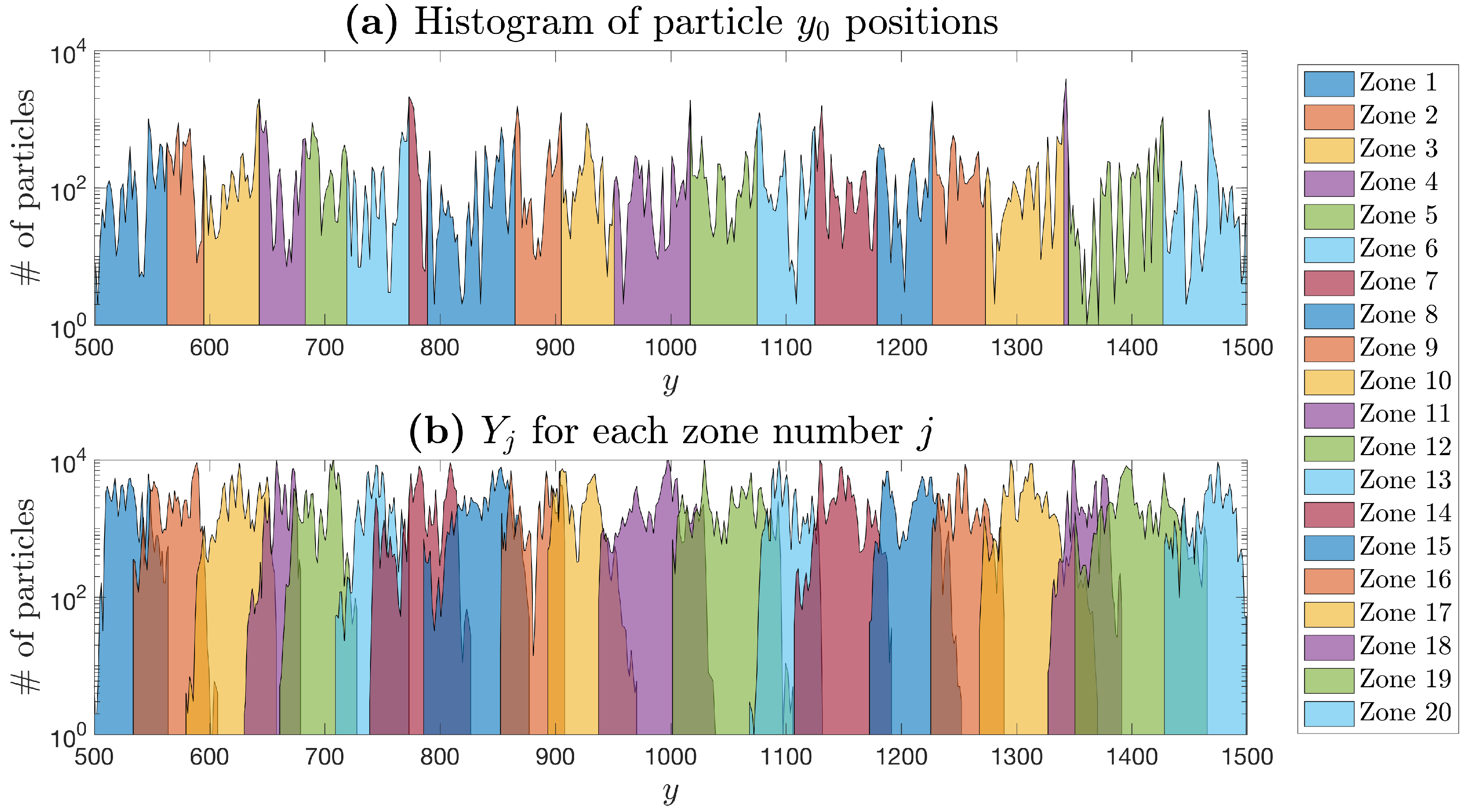
3.1. Model Parameterization
3.2. Model Mean Longitudinal Transport
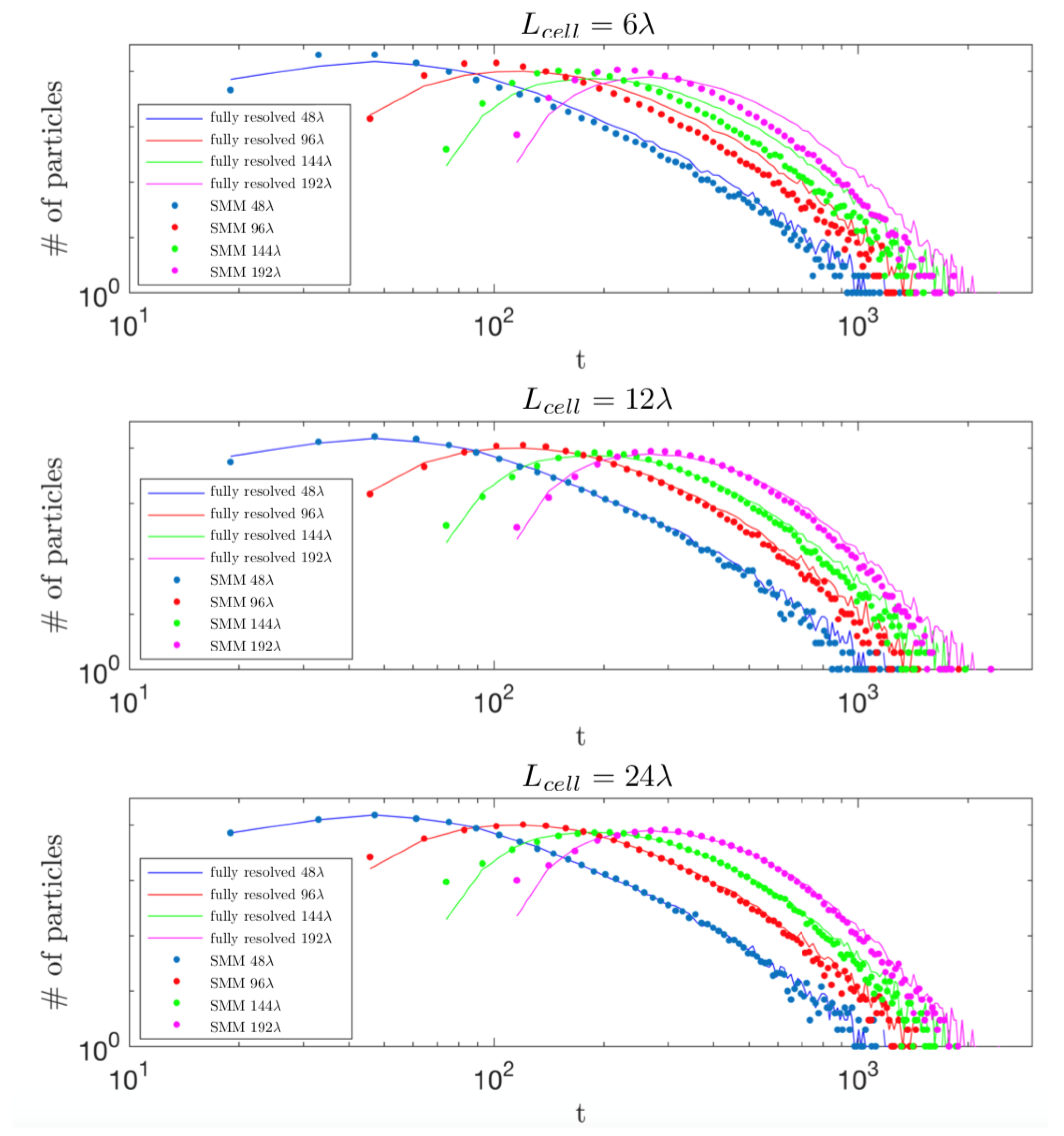
3.2.1. Choice of Cell Length
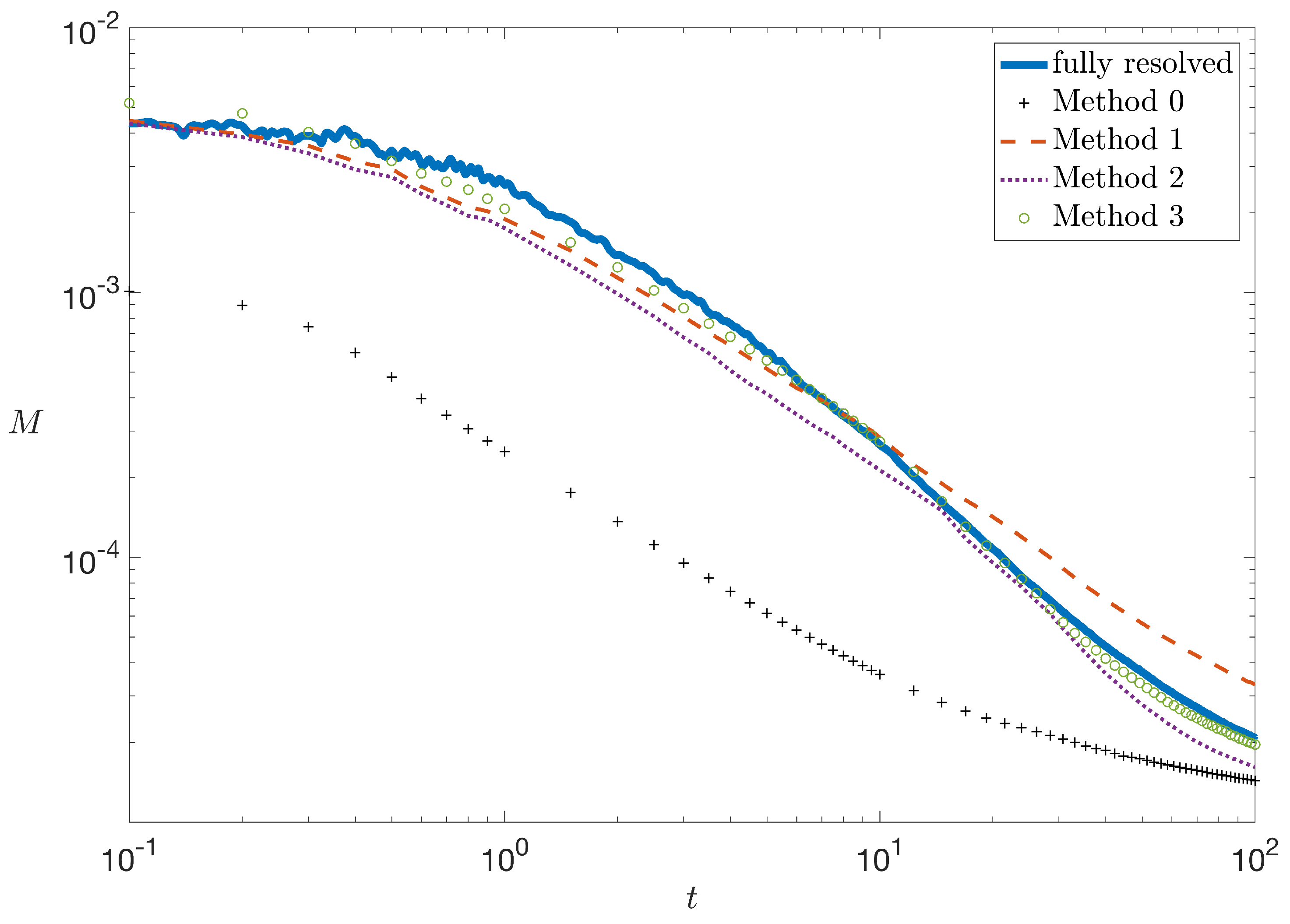
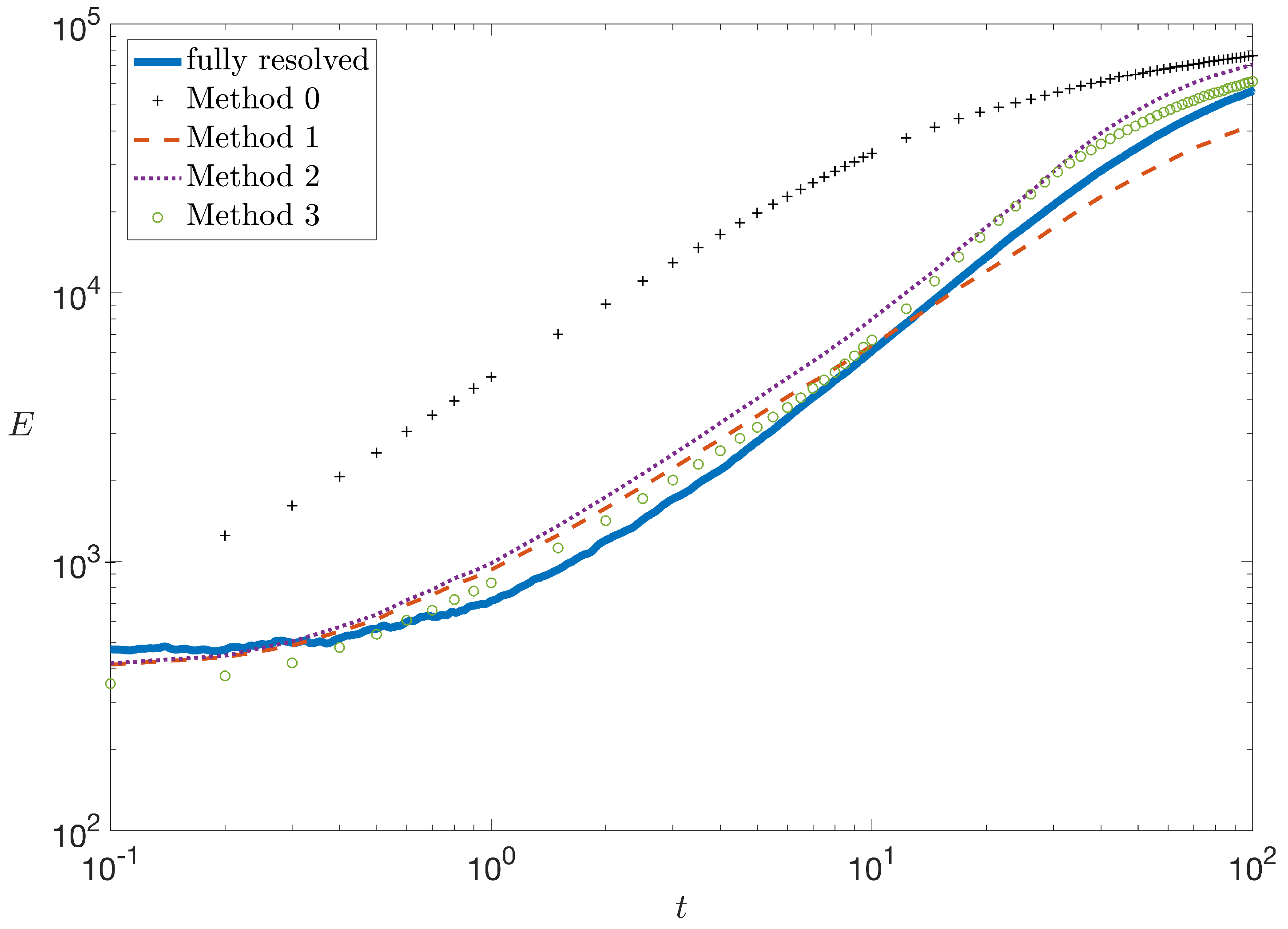
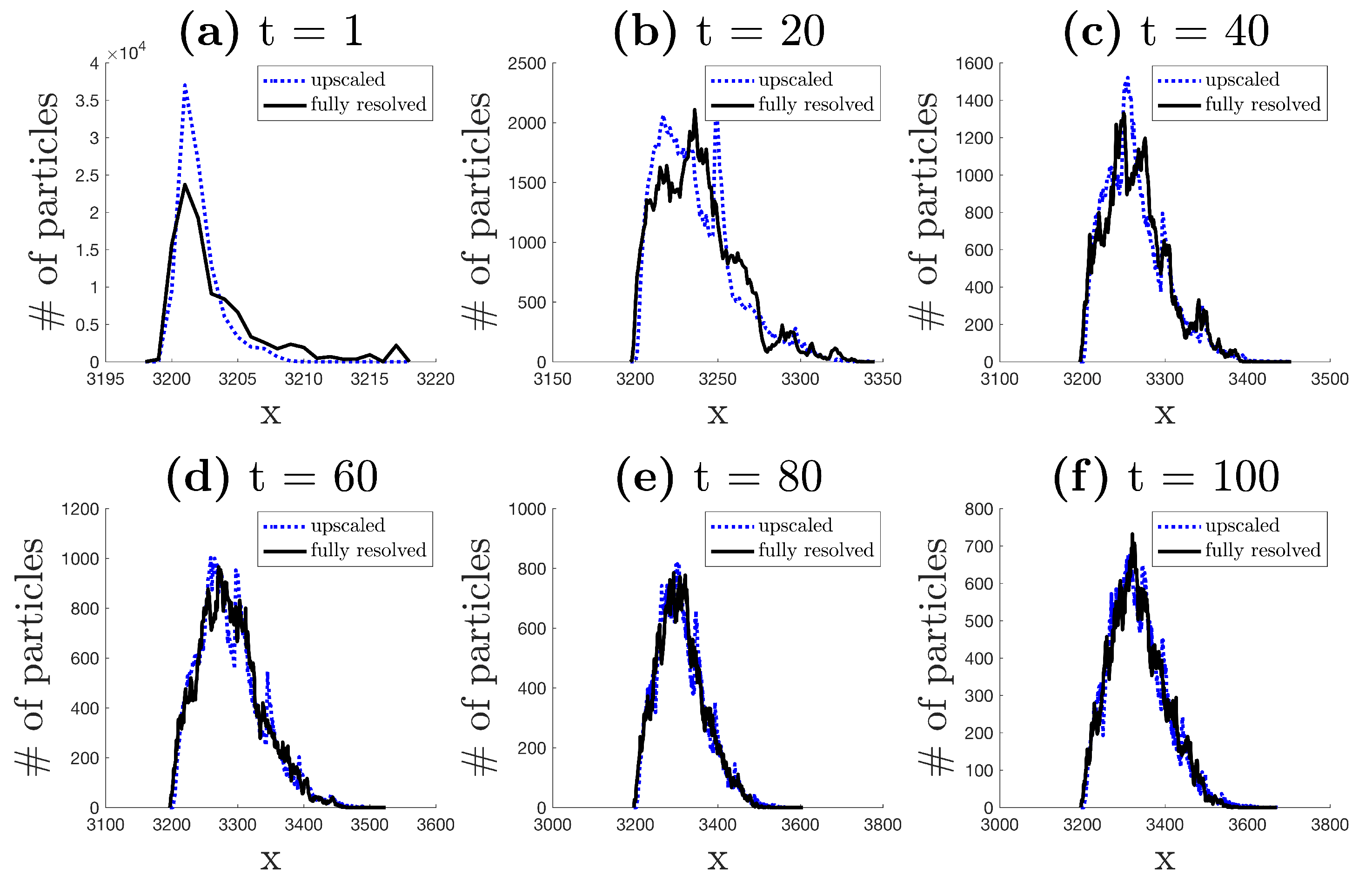
4. Downscaling Procedure to Predict Mixing
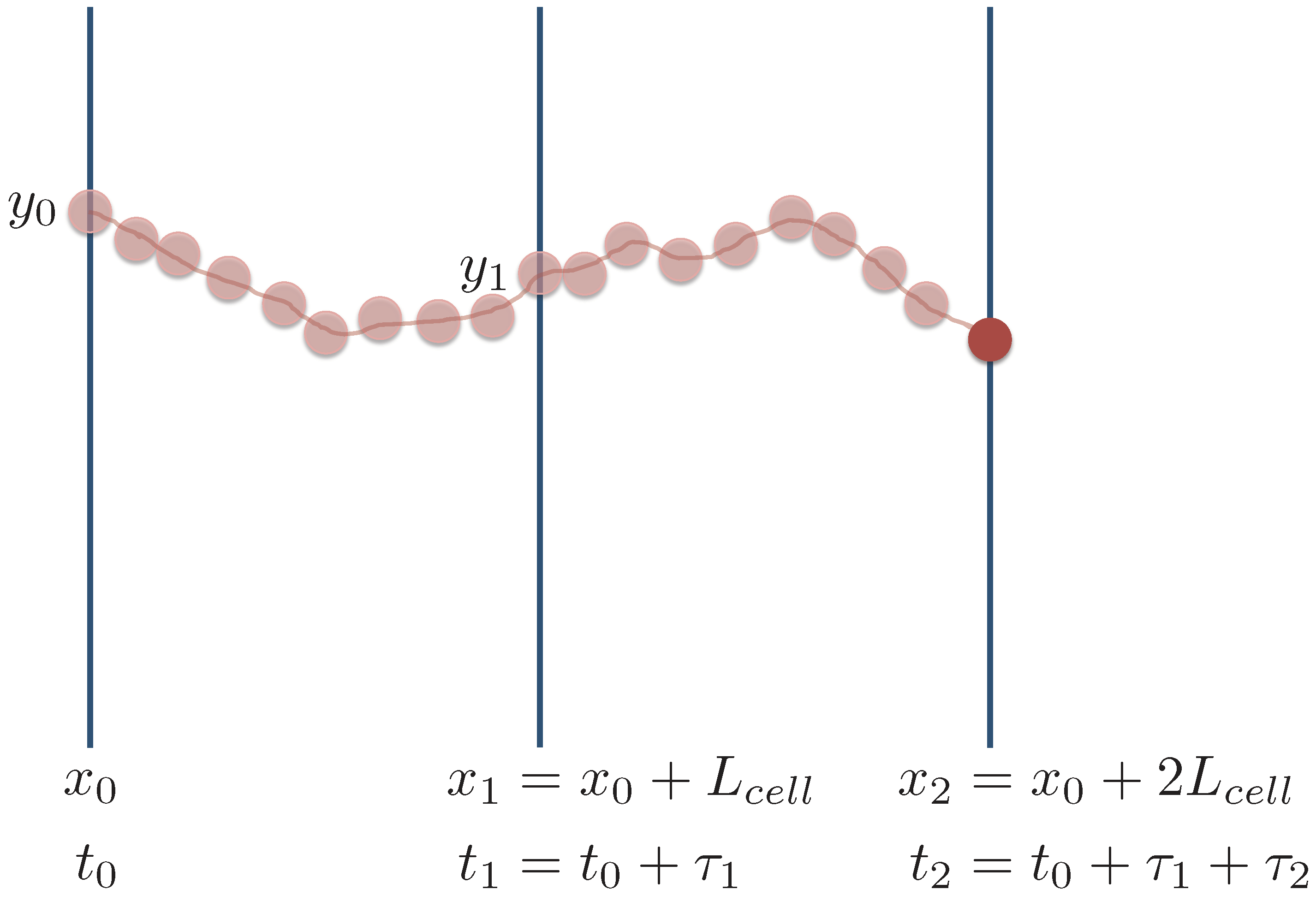
4.1. Downscaling the Streamwise Location x
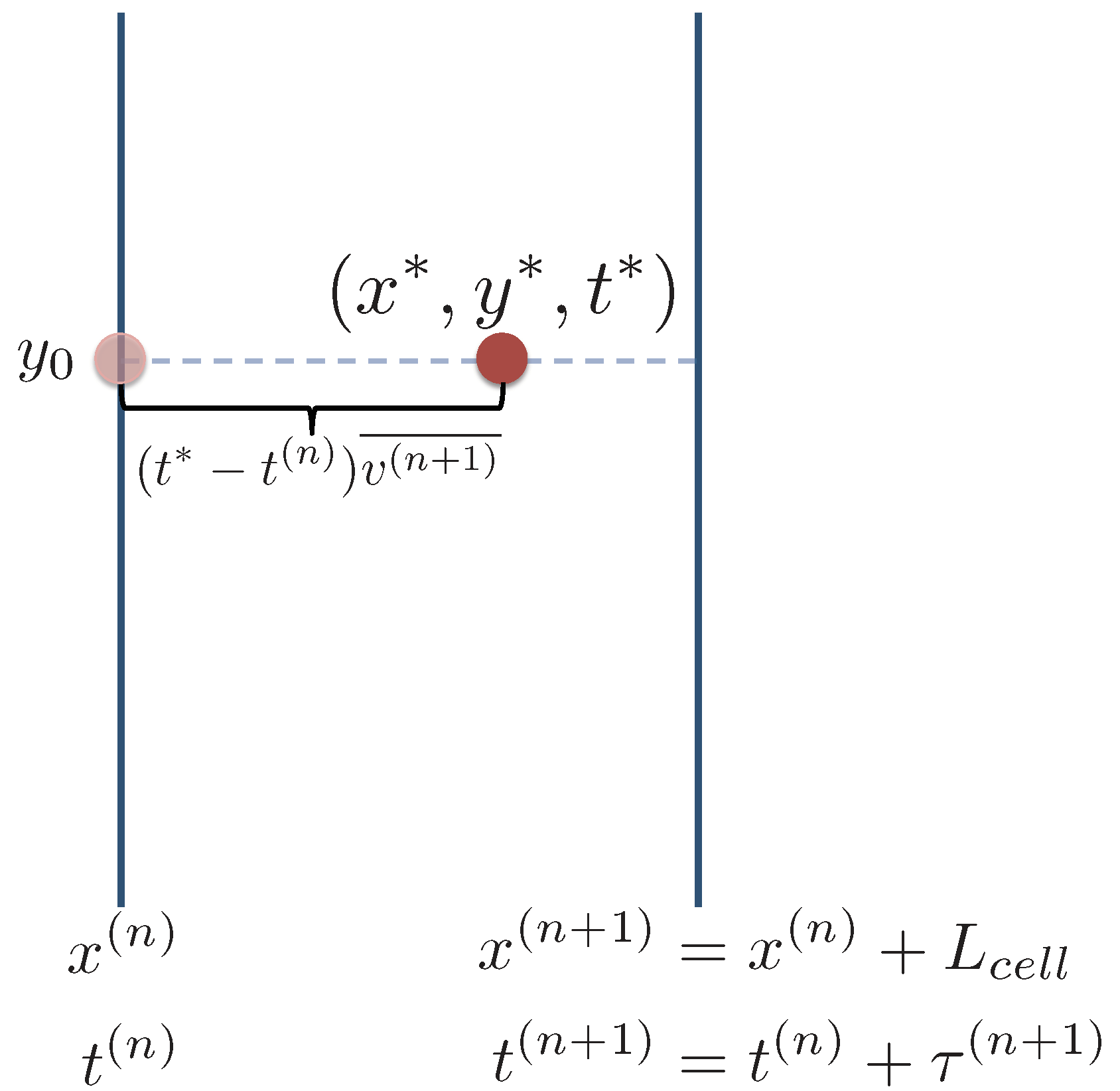
4.2. Downscaling the Spanwise Location y
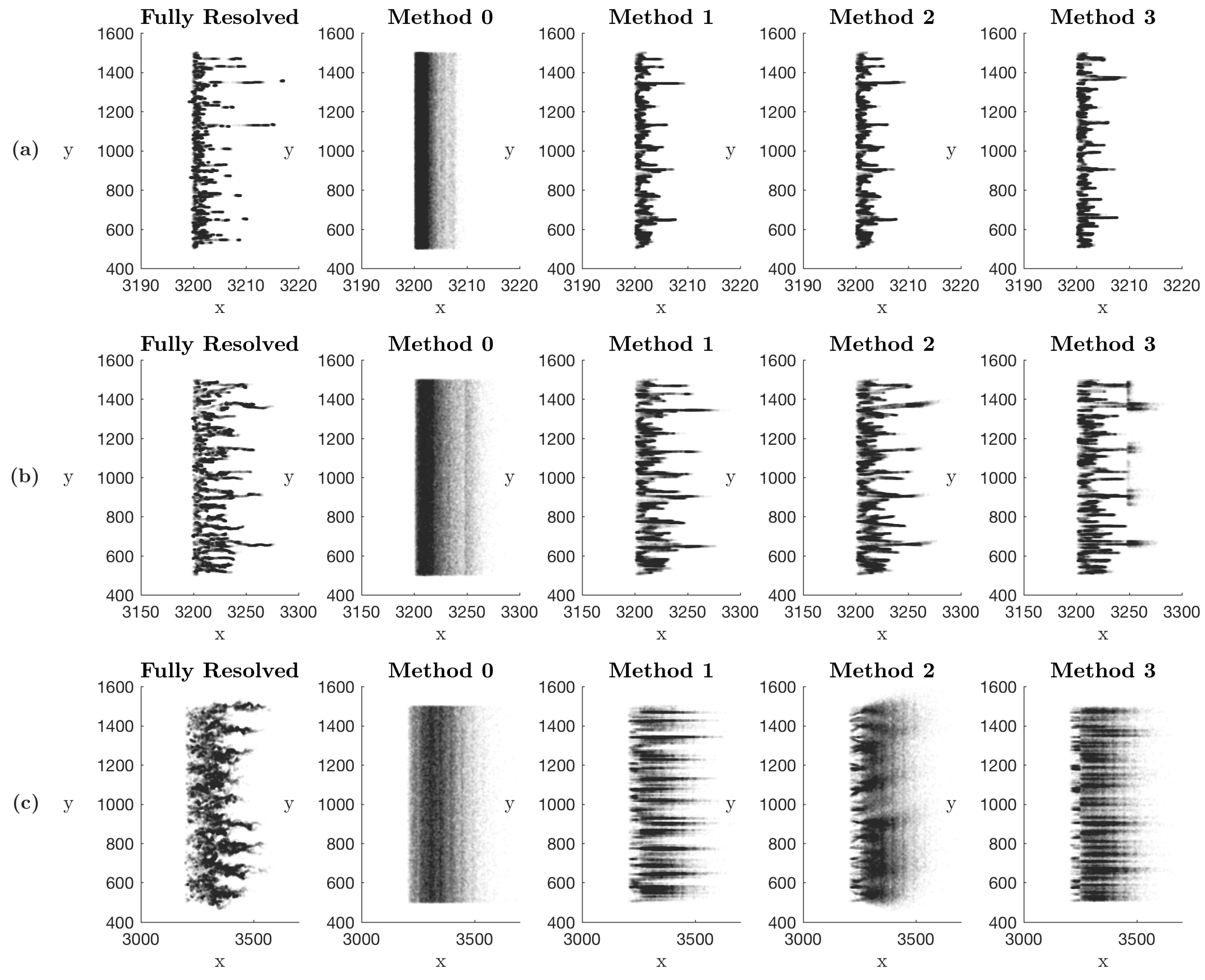
4.2.1. Method 0
4.2.2. Method 1
4.2.3. Method 2
4.2.4. Method 3
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Engdahl, N.B. Scalar dissipation rates in non-conservative transport systems. J. Contam. Hydrol. 2013, 46–60. [Google Scholar] [CrossRef]
- Dentz, M.; Le Borgne, T.; Englert, A.; Bijeljic, B. Mixing, spreading and reaction in heterogeneous media: A brief review. J. Contam. Hydrol. 2011, 120–121, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Le Borgne, T.; Ginn, T.R.; Dentz, M. Impact of fluid deformation on mixing-induced chemical reactions in heterogeneous flows. Geophys. Res. Lett. 2014, 41, 7898–7906. [Google Scholar] [CrossRef]
- Valocchi, A.J.; Bolster, D.; Werth, C.J. Mixing-Limited Reactions in Porous Media. Transp. Porous Media 2018. [Google Scholar] [CrossRef]
- Kang, K.; Redner, S. Scaling approach for the kinetics of recombination processes. Phys. Rev. Lett. 1984, 52, 955–958. [Google Scholar] [CrossRef]
- Ovchinnikov, A.A.; Zeldovich, Y.B. Role of density fluctuations in bimolecular reaction kinetics. Chem. Phys. 1978, 28, 215–218. [Google Scholar] [CrossRef]
- Toussaint, D.; Wilczec, F. Particle–antiparticle annihilation in diffusive motion. J. Chem. Phys. 1983, 78, 2642. [Google Scholar] [CrossRef]
- Bolster, D.; Benson, D.A.; Le Borgne, T.; Dentz, M. Anomalous mixing and reaction induced by superdiffusive nonlocal transport. Phys. Rev. E 2010, 82, 021119. [Google Scholar] [CrossRef]
- Ding, D.; Benson, D.A.; Paster, A.; Bolster, D. Modeling bimolecular reactions and transport in porous media via particle tracking. Adv. Water Resour. 2013, 53, 56–65. [Google Scholar] [CrossRef]
- Bolster, D.; de Anna, P.; Benson, D.A.; Tartakovsky, A.M. Incomplete mixing and reactions with fractional dispersion. Adv. Water Resour. 2012, 37, 86–93. [Google Scholar] [CrossRef]
- Gramling, C.; Harvey, C.; Meigs, L. Reactive Transport in Porous Media: A Comparison of Model Prediction with Laboratory Visualization. Environ. Sci. Technol. 2002, 36, 2508–2514. [Google Scholar] [CrossRef] [PubMed]
- Monson, E.; Kopelman, R. Observation of laser speckle effects and nonclassical kinetics in an elementary chemical reaction. Phys. Rev. Lett. 2000, 85, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Monson, E.; Kopelman, R. Nonclassical kinetics of an elementary A+B->C reaction-diffusion system showing effects of a speckled initial reactant distribution and eventual self-segregation: Experiments. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2004, 69, 1–12. [Google Scholar] [CrossRef]
- Raje, D.S.; Kapoor, V. Experimental study of bimolecular reaction kinetics in porous media. Environ. Sci. Technol. 2000, 34, 1234–1239. [Google Scholar] [CrossRef]
- Castro-Alcalá, E.; Fernàndez-Garcia, D.; Carrera, J.; Bolster, D. Visualization of mixing processes in a heterogeneous sand box aquifer. Environ. Sci. Technol. 2012, 46, 3228–3235. [Google Scholar] [CrossRef] [PubMed]
- Ding, D.; Benson, D.A.; Fernàndez-Garcia, D.; Henri, C.V.; Hyndman, D.W.; Phanikumar, M.S.; Bolster, D. Elimination of the Reaction Rate “Scale Effect”: Application of the Lagrangian Reactive Particle-Tracking Method to Simulate Mixing-Limited, Field-Scale Biodegradation at the Schoolcraft (MI, USA) Site. Water Resour. Res. 2017, 53, 10411–10432. [Google Scholar] [CrossRef]
- Guerra, P.; Gonzalez, C.; Escauriaza, C.; Pizarro, G.; Pasten, P. Incomplete Mixing in the Fate and Transport of Arsenic at a River Affected by Acid Drainage. Water Air Soil Pollut. 2016, 227. [Google Scholar] [CrossRef]
- Kang, P.K.; Bresciani, E.; An, S.; Lee, S. Impact of pore-scale incomplete mixing on biodegradation in aquifers: From batch experiment to field-scale modeling. Adv. Water Resour. 2019, 123, 1–39. [Google Scholar] [CrossRef]
- Kapoor, V.; Jafvert, C.T.; Lyn, D.A. Experimental study of a bimolecular reaction in Poiseuille flow. Water Resour. Res. 1998, 34, 1997–2004. [Google Scholar] [CrossRef]
- Chiogna, G.; Bellin, A. Analytical solution for reactive solute transport considering incomplete mixing within a reference elementary volume. Water Resour. Res. 2013, 49, 2589–2600. [Google Scholar] [CrossRef]
- Ginn, T.R. Modeling Bimolecular Reactive Transport With Mixing-Limitation: Theory and Application to Column Experiments. Water Resour. Res. 2018, 54, 256–270. [Google Scholar] [CrossRef]
- Benson, D.A.; Pankavich, S.; Bolster, D. On the separate treatment of mixing and spreading by the reactive-particle-tracking algorithm: An example of accurate upscaling of reactive Poiseuille flow. Adv. Water Resour. 2019, 123, 40–53. [Google Scholar] [CrossRef]
- Steefel, C.I.; DePaolo, D.J.; Lichtner, P.C. Reactive transport modeling: An essential tool and a new research approach for the Earth sciences. Earth Planet. Sci. Lett. 2005, 240, 539–558. [Google Scholar] [CrossRef]
- Yeh, G.T.; Tripathi, V.S. A Critical Evaluation of Recent Developments in Hydrogeochemical Transport Models of Reactive Multichemical Components. Water Resour. Res. 1989, 25, 93–108. [Google Scholar] [CrossRef]
- Mayer, K.U.; Benner, S.G.; Blowes, D.W. Process-based reactive transport modeling of a permeable reactive barrier for the treatment of mine drainage. J. Contam. Hydrol. 2006, 85, 195–211. [Google Scholar] [CrossRef]
- Knutson, C.; Valocchi, A.; Werth, C. Comparison of continuum and pore-scale models of nutrient biodegradation under transverse mixing conditions. Adv. Water Resour. 2007, 30, 1421–1431. [Google Scholar] [CrossRef]
- Le Borgne, T.; De Dreuzy, J.R.; Davy, P.; Bour, O. Characterization of the velocity field organization in heterogeneous media by conditional correlation. Water Resour. Res. 2007, 43, 1–10. [Google Scholar] [CrossRef]
- Le Borgne, T.; Dentz, M.; Carrera, J. Lagrangian statistical model for transport in highly heterogeneous velocity fields. Phys. Rev. Lett. 2008, 101, 1–4. [Google Scholar] [CrossRef]
- Weeks, S.W.; Sposito, G. Mixing and stretching efficiency in steady and unsteady groundwater flows. Water Resour. Res. 1998, 34, 3315–3322. [Google Scholar] [CrossRef]
- De Barros, F.P.J.; Dentz, M.; Koch, J.; Nowak, W. Flow topology and scalar mixing in spatially heterogeneous flow fields. Geophys. Res. Lett. 2012, 39, 1–5. [Google Scholar] [CrossRef]
- Le Borgne, T.; Dentz, M.; Villermaux, E. Stretching, coalescence, and mixing in porous media. Phys. Rev. Lett. 2013, 110, 204501. [Google Scholar] [CrossRef] [PubMed]
- Edery, Y.; Porta, G.M.; Guadagnini, A.; Scher, H.; Berkowitz, B. Characterization of Bimolecular Reactive Transport in Heterogeneous Porous Media. Transp. Porous Media 2016, 115, 291–310. [Google Scholar] [CrossRef]
- Trefry, M.; Lester, D.; Metcalfe, G.; Wu, J. Natural Groundwater Systems Can Display Chaotic Mixing at the Darcy Scale. arXiv, 2018; arXiv:1808.03641. [Google Scholar]
- Ye, Y.; Chiogna, G.; Lu, C.; Rolle, M. Effect of Anisotropy Structure on Plume Entropy and Reactive Mixing in Helical Flows. Transp. Porous Media 2018, 121, 315–332. [Google Scholar] [CrossRef]
- Bolster, D.; Dentz, M.; Le Borgne, T. Hypermixing in linear shear flow. Water Resour. Res. 2011, 47, 1–4. [Google Scholar] [CrossRef]
- Le Borgne, T.; Dentz, M.; Bolster, D.; Carrera, J.; de Dreuzy, J.R.; Davy, P. Non-Fickian mixing: Temporal evolution of the scalar dissipation rate in heterogeneous porous media. Adv. Water Resour. 2010, 33, 1468–1475. [Google Scholar] [CrossRef]
- Kitanidis, P.K. The concept of the Dilution Index. Water Resour. Res. 1994, 30, 2011–2026. [Google Scholar] [CrossRef]
- Engdahl, N.B.; Benson, D.A.; Bolster, D. Predicting the enhancement of mixing-driven reactions in nonuniform flows using measures of flow topology. Phys. Rev. E 2014, 90, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Aquino, T.; Bolster, D. Localized Point Mixing Rate Potential in Heterogeneous Velocity Fields. Transp. Porous Media 2017, 119, 391–402. [Google Scholar] [CrossRef]
- Wright, E.E.; Richter, D.H.; Bolster, D. Effects of incomplete mixing on reactive transport in flows through heterogeneous porous media. Phys. Rev. Fluids 2017, 2, 114501. [Google Scholar] [CrossRef]
- De Dreuzy, J.R.; Carrera, J. On the validity of effective formulations for transport through heterogeneous porous media. Hydrol. Earth Syst. Sci. 2016, 20, 1319–1330. [Google Scholar] [CrossRef]
- Edery, Y.; Guadagnini, A.; Scher, H.; Berkowitz, B. Origins of anomalous transport in heterogeneous media: Structural and dynamic controls. Water Resour. Res. 2014, 50, 1490–1505. [Google Scholar] [CrossRef]
- Le Borgne, T.; Dentz, M.; Carrera, J. Spatial Markov processes for modeling Lagrangian particle dynamics in heterogeneous porous media. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2008, 78, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Kang, P.K.; Dentz, M.; Le Borgne, T.; Juanes, R. Spatial Markov model of anomalous transport through random lattice networks. Phys. Rev. Lett. 2011, 107, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Kang, P.K.; Borgne, T.L.; Dentz, M.; Bour, O.; Juanes, R.; Kang, P.; Borgne, T.L.; Dentz, M.; Bour, O.; Juanes, R. Impact of velocity correlation and distribution on transport in fractured media: Field evidence and theoretical model. Water Resour. Res. 2015, 940–959. [Google Scholar] [CrossRef]
- Kang, P.K.; Dentz, M.; Le Borgne, T.; Lee, S.; Juanes, R. Anomalous transport in disordered fracture networks: Spatial Markov model for dispersion with variable injection modes. Adv. Water Resour. 2017, 106, 80–94. [Google Scholar] [CrossRef]
- Kang, P.K.; Dentz, M.; Juanes, R. Predictability of anomalous transport on lattice networks with quenched disorder. Phys. Rev. E 2011, 83, 030101. [Google Scholar] [CrossRef] [PubMed]
- Kang, P.K.; Anna, P.; Nunes, J.P.; Bijeljic, B.; Blunt, M.J.; Juanes, R. Pore-scale intermittent velocity structure underpinning anomalous transport through 3-D porous media. Geophys. Res. Lett. 2014, 41, 6184–6190. [Google Scholar] [CrossRef]
- Kang, P.K.; Dentz, M.; Le Borgne, T.; Juanes, R. Anomalous transport on regular fracture networks: Impact of conductivity heterogeneity and mixing at fracture intersections. Phys. Rev. E 2015, 92, 022148. [Google Scholar] [CrossRef] [PubMed]
- Kang, P.K.; Brown, S.; Juanes, R. Emergence of anomalous transport in stressed rough fractures. Earth Planet. Sci. Lett. 2016, 454, 46–54. [Google Scholar] [CrossRef]
- De Anna, P.; Le Borgne, T.; Dentz, M.; Tartakovsky, A.M.; Bolster, D.; Davy, P. Flow intermittency, dispersion, and correlated continuous time random walks in porous media. Phys. Rev. Lett. 2013, 110, 184502. [Google Scholar] [CrossRef]
- Sund, N.L.; Bolster, D.; Dawson, C. Upscaling transport of a reacting solute through a peridocially converging-diverging channel at pre-asymptotic times. J. Contam. Hydrol. 2015, 182, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Sund, N.; Porta, G.; Bolster, D.; Parashar, R. A Lagrangian transport Eulerian reaction spatial (LATERS) Markov model for prediction of effective bimolecular reactive transport. Water Resour. Res. 2017, 53, 9040–9058. [Google Scholar] [CrossRef]
- Bolster, D.; Méheust, Y.; Le Borgne, T.; Bouquain, J.; Davy, P. Modeling preasymptotic transport in flows with significant inertial and trapping effects—The importance of velocity correlations and a spatial Markov model. Adv. Water Resour. 2014, 70, 89–103. [Google Scholar] [CrossRef]
- Sund, N.; Bolster, D.; Mattis, S.; Dawson, C. Pre-asymptotic Transport Upscaling in Inertial and Unsteady Flows through Porous Media. Transp. Porous Media 2015, 109, 411–432. [Google Scholar] [CrossRef]
- Sund, N.L.; Porta, G.M.; Bolster, D. Upscaling of dilution and mixing using a trajectory based Spatial Markov random walk model in a periodic flow domain. Adv. Water Resour. 2017, 103, 76–85. [Google Scholar] [CrossRef]
- Aarnes, J.E.; Gimse, T.; Lie, K.A. An introduction to the numerics of flow in porous media using Matlab. In Geometric Modelling, Numerical Simulation, and Optimization; Springer: Berlin/Heidelberg, Germany, 2007; pp. 265–306. [Google Scholar]
- Wen, B.; Chang, K.W.; Laboratories, S.N.; Hesse, M.A. Rayleigh-Darcy convection with hydrodynamic dispersion. Phys. Rev. Fluids 2018, 123801, 1–18. [Google Scholar] [CrossRef]
- Wang, L.; Nakanishi, Y.; Hyodo, A.; Suekane, T. Three-dimensional structure of natural convection in a porous medium: Effect of dispersion on finger structure. Int. J. Greenh. Gas Control 2016, 53, 274–283. [Google Scholar] [CrossRef]
- Le Borgne, T.; Bolster, D.; Dentz, M.; De Anna, P.; Tartakovsky, A. Effective pore-scale dispersion upscaling with a correlated continuous time random walk approach. Water Resour. Res. 2011, 47, 1–10. [Google Scholar] [CrossRef]
- Hakoun, V.; Comolli, A.; Dentz, M. From medium heterogeneity to flow and transport: A time-domain random walk approach. In Proceedings of the AGU Fall Meeting, New Orleans, OR, USA, 11–15 December 2017. [Google Scholar]
- Porta, G.M.; Riva, M.; Guadagnini, A. Upscaling solute transport in porous media in the presence of an irreversible bimolecular reaction. Adv. Water Resour. 2012, 35, 151–162. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; de Anna, P.; Le Borgne, T.; Balter, A.; Bolster, D. Effect of spatial concentration fluctuations on effective kinetics in diffusion-reaction systems. Water Resour. Res. 2012, 48, W02526. [Google Scholar] [CrossRef]
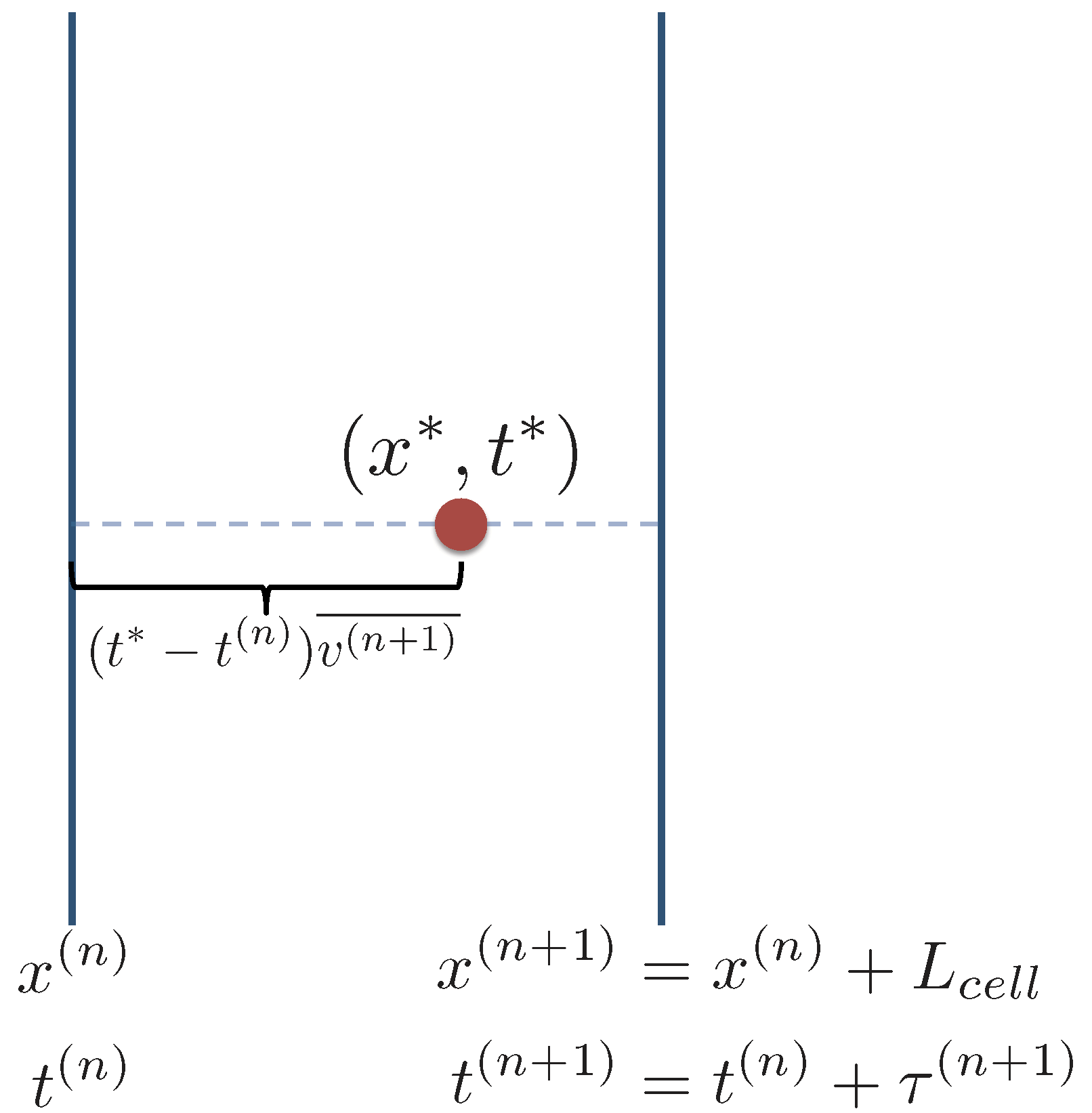
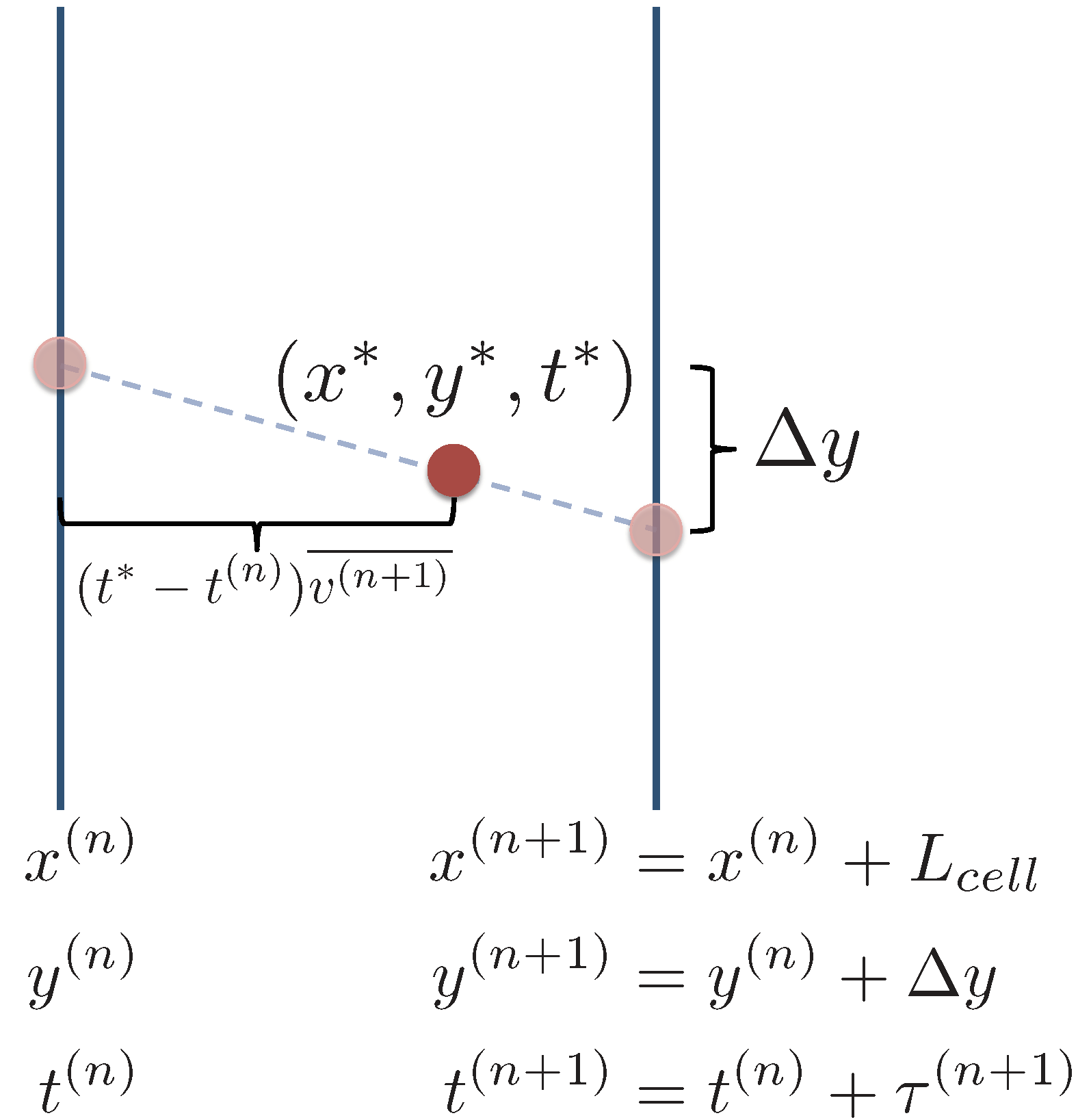
| ϵ(M) | ϵ(E) | |
|---|---|---|
| Method 0 | 0.5895 | 0.4888 |
| Method 1 | 0.1275 | 0.0893 |
| Method 2 | 0.1121 | 0.1217 |
| Method 3 | 0.0352 | 0.0646 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wright, E.E.; Sund, N.L.; Richter, D.H.; Porta, G.M.; Bolster, D. Upscaling Mixing in Highly Heterogeneous Porous Media via a Spatial Markov Model. Water 2019, 11, 53. https://doi.org/10.3390/w11010053
Wright EE, Sund NL, Richter DH, Porta GM, Bolster D. Upscaling Mixing in Highly Heterogeneous Porous Media via a Spatial Markov Model. Water. 2019; 11(1):53. https://doi.org/10.3390/w11010053
Chicago/Turabian StyleWright, Elise E., Nicole L. Sund, David H. Richter, Giovanni M. Porta, and Diogo Bolster. 2019. "Upscaling Mixing in Highly Heterogeneous Porous Media via a Spatial Markov Model" Water 11, no. 1: 53. https://doi.org/10.3390/w11010053
APA StyleWright, E. E., Sund, N. L., Richter, D. H., Porta, G. M., & Bolster, D. (2019). Upscaling Mixing in Highly Heterogeneous Porous Media via a Spatial Markov Model. Water, 11(1), 53. https://doi.org/10.3390/w11010053




