Abstract
Mathematical groundwater modelling with homogeneous permeability zones has been used for decades to manage water resources in the Almonte-Marismas aquifer (southwest Spain). This is a highly heterogeneous detrital aquifer which supports valuable ecological systems in the Doñana National Park. The present study demonstrates that it is possible to better characterize this heterogeneity by numerical discretization of the geophysical and lithological data available. We identified six hydrofacies whose spatial characteristics were quantified with indicator variogram modelling. Sequential Indicator Simulation then made it possible to construct a 3D geological model. Finally, this detailed model was included in MODFLOW through the Model Muse interface. This final process is still a challenge due to the difficulty of downscaling to a handy numerical modelling scale. New piezometric surfaces and water budgets were obtained. The classical model with zones and the model with 3D simulation were compared to confirm that, for management purposes, the effort of improving the geological heterogeneities is worthwhile. This paper also highlights the relevance of including subsurface heterogeneities within a real groundwater management model in the present global change scenario.
1. Introduction
The Almonte-Marismas sedimentary aquifer supports both Doñana National and Natural Parks. It is a site of great ecological wealth, thanks to the quantity and quality of available water. This fact makes it a vulnerable area sensitive to any climatic change [1]. In addition, it is subject to great environmental pressure due to the elevated groundwater extraction necessary for agriculture and tourism. These withdrawals are causing a decrease in the quality and quantity of groundwater that is incompatible with the health of the ecological systems that characterize this park [2].
Hydrogeological models enable the evaluation of groundwater changes under future scenarios, so they are a basic support tool for decisions concerning the management of water resources [3]. Doñana is not an exception, and groundwater resource management in the Almonte-Marismas aquifer requires the use of numerical models in order to understand how the system works, to estimate available resources, and to simulate the effects of its exploitation. Numerous mathematical models have been built by IGME (the Spanish Geological Survey) since 1975 [4,5,6,7,8,9,10,11]. Throughout the different versions, the model has improved. However, it is difficult to compare the different versions due to their diverse characteristics and results (time steps, time period, study area, initial data, boundary conditions, purpose, etc.).
All the above Almonte-Marismas numerical models represented the spatial variability of hydrogeological parameters (i.e., hydraulic permeability and storage coefficient) through homogeneous zones. The delimitation of these areas was based more on similar piezometric behavior and geological outcrops than on 3D lithological information. However, the spatial variability of subsurface geological material is responsible for flow and solute transport patterns [12,13], and, consequently, more realistic models are required [14]. This is not an easy task because of the laboriousness of getting a digitalized 3D geological model and integrating it into the numerical groundwater model. The degree of difficulty of constructing a real 3D groundwater model also depends on the spatial scale of work and the specific objective of the study [15]. An additional challenge in groundwater flow modelling is to build a congruent model linking geological properties with hydrogeological dynamics. To mitigate this difficulty, several authors, including Klingbeil et al. [16] and Anderson [17], propose to regroup lithologies into units called hydrofacies, characterized by similar hydrogeological properties [18].
Geostatistics is used extensively to estimate the value of a given attribute at a specific location by preserving the spatial distribution and quantifying the uncertainty of the estimates [19,20]. Although geostatistical facies modeling for petroleum applications is a widely used practice [21], it is not so common in groundwater applications [22]. Deterministic or smooth interpolated models of alluvial lithofacies often preclude the scale of heterogeneity, which can be much finer than characteristic inter-borehole spacing. Geostatistical tools, like variogram models and simulations, allow the quantification and modeling of the geological heterogeneity in depositional systems [23]. There are abundant geostatistical estimation and simulation methods: simple and ordinary kriging, sequential indicator simulation (SIS) [24], truncated Gaussian simulation (TGS) [25], object-based simulation (OBS) [26], multiple point statistics (MPS) [27], etc. In the SIS method, hydrofacies are transformed as indicator variables (1 if present and 0 if not present), kriged individually using variograms, and assigned to cells weighting kriging results; finally, a simulated 3D distribution is created with a specific probability distribution function [28]. SIS is preferred in situations where the geometry of geobodies is complex and when the density of data allows for accurate variogram analysis and comes from geological interpretation or geophysical measurements [29]. Also, research by Marini et al. [30] found that SIS hydrofacies prediction was better compared with TGS and OBS.
The main goal of this study is to incorporate the spatial variability of geology into the numerical flow model of the Almonte-Marismas aquifer. The objective is twofold: on the one hand we perform a 3D geological characterization of heterogeneity in the Almonte-Marismas aquifer, using all available geological and geophysical information and applying geostatistical SIS, and, on the other hand, this 3D geological structure and the hydrogeology properties are integrated into the existing numerical flow model. The improvements in the Almonte-Marismas groundwater numerical model, after adding the 3D geological simulation, are analyzed by comparing the results with those of the former model which employs zonification. The evaluation focuses on piezometry modification and water balance differences, paying special attention to groundwater contributions to ecosystems of vital importance in Doñana (e.g., La Rocina Stream, the ecotones, and the marshlands).
2. Materials and Methods
2.1. Study Site
The Almonte-Marismas groundwater system, in southwest Spain, is located in the mouth of the River Guadalquivir (Figure 1). It covers 2409 km2 of a sedimentary basin composed of basal sands, silts, Aeolian sands, and marshlands materials at the surface. The principal hydrogeological limits are the Guadalquivir to the east, the Atlantic Ocean to the south, the River Tinto to the west, and impervious geological materials to the north. The north, west, and southwest sectors of the aquifer have unconfined behavior that becomes confined from west to southeast by the Doñana marshlands (Figure 1; [31]). The principal groundwater flow runs from northwest to southeast, recharging mainly in northern and southwestern areas. Groundwater and surface water in the Almonte-Marismas aquifer flood some ponds and marshlands that represent one of the most important ecological areas in Spain today [32].
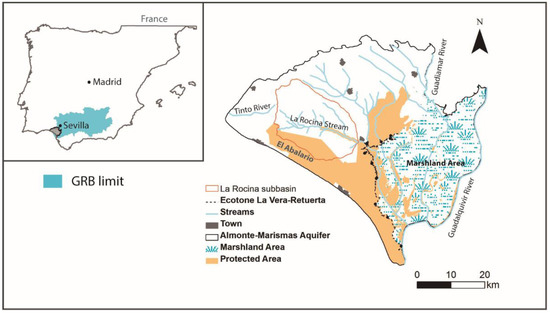
Figure 1.
Location of the Almonte-Marismas Aquifer and locations studied. The Guadalquivir River Basin (GRB) limit is also shown.
Since the end of the 19th century, the Doñana marshlands have suffered a series of anthropogenic actions that have significantly changed the natural environment [2]. The extent of the marshland decreased from 140,000 ha at the end of the 19th century to 30,000 ha that remain semi-virgin today [33].
2.2. Hydrofacies Model
The maximum total thickness of the system is 425 m with maximum top and bottom elevations of 190 masl and 235 mbsl, respectively. Based on new boreholes, Salvany et al. [34] redefined the sedimentological model of the Almonte-Marismas aquifer with nine lithologies or formations. In the present study we took Salvany’s work and the updated geological map [35] to define six hydrofacies (Figure 2). The six hydrogeological behaviors correspond to sediments of ages ranging from Neogene (Upper Miocene) to Quaternary. Between the Upper Miocene and the end of the Pliocene, the sediments are of marine origin, and from then until the Quaternary, they are of continental origin [34]. The numbering of hydrofacies did not follow a lithostratigraphic criterion. Figure 2 shows how hydrofacies from 1 to 4 emerge on the surface. The other hydrofacies, 5 and 6, do not appear in the geological map and constitute the semiconfined/confined sector of the aquifer.
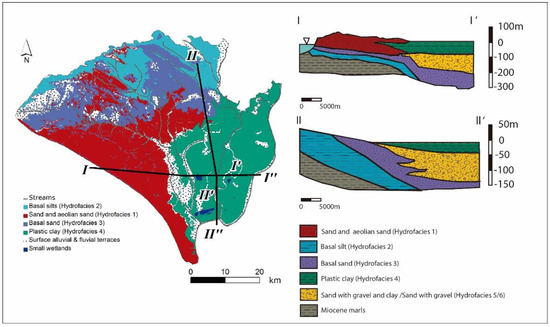
Figure 2.
Left: Modified geological map (based on [35]). Right: Schematic of geological cross sections based on [6] and [32].
Hydrofacies 6 corresponds to the Almonte sand unit described by Salvany et al. [34], the most transmissive and deepest lithology. These sands are below the marsh and have a thickness between 10 and 110 m, which increases in a southerly direction. Hydrofacies 5 corresponds to the Lebrija unit (Lower unit). With a maximum thickness of 120 m, it appears discontinuously as clay, sand, and gravel lens. Sometimes Hydrofacies 5 appears over Hydrofacies 6, and at other times it makes contact with the aquifer bottom (Figure 2). The marshlands are represented by Hydrofacies 4, formed by fine and medium plastic clays with a lot of organic matter and characterized by very low permeability. It behaves as a very slow aquitard. They are between 20 and 80 m thick, which is still increasing due to sediment transport. Hydrofacies 3 is formed by sands and corresponds to the Lebrija unit (Upper unit; [34]). Hydrofacies 2 corresponds to the outcrop of silt at the surface that can be found in the geological map (Figure 2) and has little presence in the 3D hydrogeological model. Lastly, Hydrofacies 1 corresponds to the sands of the Abalario and the Aeolian units that emerge on the surface in the geological map (Figure 2). They constitute the higher-recharge-rate area in the free aquifer sector. They also have mobile dunes and can reach a thickness of up to 150 m [34].
2.3. Geological and Geophysical Data
Geological and geophysical data were obtained from IGME [36,37]. There are a considerable number of records with raw geological and geophysical information (Figure 3): 460 well logs (more than 16,000 m) were performed between 1967 and 2009 and 895 vertical electrical soundings (VES) between 1967 and 1995, four seismic reflexion profiles of 7.8 km were made in 2007, and two different groups of reflexion seismic lines were performed in 1990 and 2002 [36].
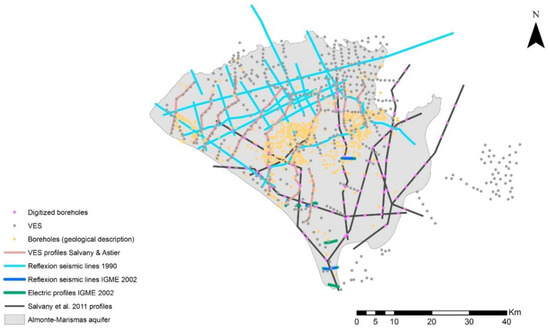
Figure 3.
Spatial distribution of geological and geophysical information in Almonte-Marismas aquifer.
The biggest challenge is to extract facies information manually from such a huge number of well logs, with subjective and heterogeneous interpretations, and meter by meter. In addition, the arduous geophysical data recompilation carried out by the IGME in 2007 was carefully reviewed, providing a large quantity of data that had never been taken into account for the construction of the previous models. All raw data were analyzed and digitized in order to transfer the facies information to the corresponding hydrofacies. The resulting 3D hydrofacies values were formatted to be compatible with the geostatistics tools described in the following subsections.
2.4. Variogram Modelling
The experimental variogram, defined within the framework of a second-order stationary hypothesis, can provide an empirical description of the spatial continuity of one variable [38]. The experimental variogram analysis gives information about the range, the sill, and the anisotropy coefficients that are necessary to determine the continuity, periodicity, and trends of the hydrofacies units [39]. Indicator (i.e., categorical) variables were used to represent the hydrofacies units for a given location within 2 m depth intervals and 500 × 500 m cells. The coding of hydrofacies units 1, 2, 3, 4, 5, and 6 to indicator variables (I) at any given point in space (uα) was assigned by defining
where k = 1, 2, 3, 4, 5, 6.
Hydrofacies proportions, which are significant parameters when an indicator-based method is used [40], were determined from digitalized hydrofacies values.
In the present study, 3D experimental variograms for each hydrofacies were computed and fitted by using Isatis software [41]. In comparison with other similar software such as SGeMS [42], Isatis has an easier and faster interface to model and interpret the 3D variograms.
2.5. Sequential Indicator Simulation (SIS)
Geostatistical simulation methods generate nonunique results and overcome the smoothing effect problem [43]. Conditional geostatistical simulation application generates a set of possible equiprobable results that are conditioned to the available data, while having global statistical behaviors very close to those of reality, such as variograms, reproducing the fine variations. The justification for the use of SIS in this case is its easy implementation, the high level of control of the statistical variables that is exercised through the variograms, and the good geological resolution that is obtained for different regional scales [44,45,46,47,48]. SIS was applied to construct one simulation using a random seed value, 20 for the maximum number of conditioning values, and 30,000 m–30,000 m–500 m for the search ellipsoid value. The computation time was 80 min using SGeMS software [42]. A categorical transformation algorithm (TRANSCAT) was then run, again with SGeMS. This transformation is necessary to clean the small-scale variations and to match the target proportions while preserving the local statistics [49]. This last step is sometimes ignored by users, but it is necessary to obtain a smooth 3D model. For interactive 3D visualizations, Isatis software [41] was used because it has a comfortable interface, it is easy to move the image, and it explores the 3D solids. However, Isatis does not allow SIS to be executed with several categorical variables at the same time.
2.6. Groundwater Modelling with MODFLOW and Model Muse GUI
The simulation of groundwater flow in the Almonte-Marismas aquifer was done with the widely known 3D finite difference model MODFLOW-2000 [50]. The graphical user interface used to run MODFLOW was Model Muse software [51], a free software package available for future applications, water management administrations, and other potential users. The model domain is oriented north–south and discretized into 500 × 500 m grid cells. These dimensions allowed the highest possible model resolution based on the computational limits, available data, and problem scale.
The basis of a good hydrogeological model begins with its robust results in steady-state. The Almonte-Marismas aquifer was modeled under steady-state conditions in order to compare (i) the new model, with heterogeneous hydrofacies read from the 3D geostatistical simulation and with appropriate permeability assigned to simulated lithofacies, and (ii) a model similar to the ones built before with homogeneous zones for both hydrogeological parameters. The new model has seven layers while the one similar to former models has two layers. Both models were calibrated independently to reproduce the piezometry observed in the 1970s, assuming that this period can correspond to a stationary state. The parameters calibrated were permeability values for each zone or hydrofacies unit (Table 1).

Table 1.
Calibrated permeability values for each hydrofacies unit (m/day).
To characterize the impervious bottom of the aquifer using the available geological and geophysical data, kriging with an external drift trend of the aquifer thickness was computed [52,53]. The total aquifer thickness was measured from the digital terrain model and the appearance of the low-permeability marls lithology at the bottom.
The boundary conditions were similar to those used in previous models [1,11] and were selected to most closely match the physical system [50]. North lateral flows were modeled with the General Head-Boundary package—water entering from the north border of the marshlands and draining in the rest of the northern limit. The River Guadalquivir contact is impervious, the Guadiamar and Tinto were modeled with the River Package, and the rest of the streams network was modeled with the Stream package. Atlantic Ocean contact was approached as cells of constant piezometric height without taking into account the effect of the tides, while also placing drain-type cells in the areas where there are springs in the coastal zone. The entire marshlands area was simulated with impermeable cells in Layer 1 for the zonification model. With the introduction of the hydrofacies model, the marshlands cells were activated. This decision could be taken as being due to the possibility that the 3D simulation can better define the interchanged gravel lens. Marshland cells became a zone of low hydraulic permeability (1.67 × 10−3 m/day). The phreatic evapotranspiration package simulates the areas of eucalyptus and pine trees. To implement the recharge, the aquifer was divided into 15 recharge subzones within which the infiltration process was assumed to be homogeneous [32].
To evaluate both models’ piezometry and water balance, differences were analyzed in the whole aquifer and in three ecosystems of special importance: La Rocina Stream, ecotones, and groundwater masses below the marshlands (Figure 1). Figure 4 shows the whole approach used in this study.
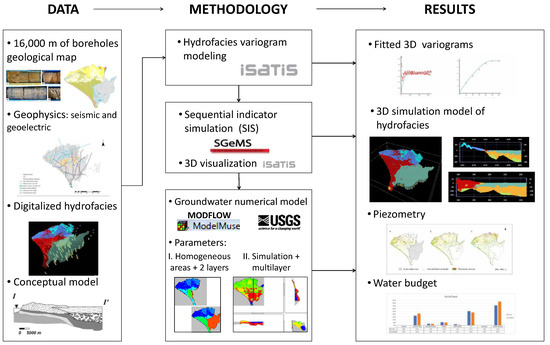
Figure 4.
Flowchart of the approach used in the current study.
3. Results
3.1. Geostatistical Model
3.1.1. Variograms
Figure 5 and Table 2 present the numerical and graphical parameters of the variogram models. Except for the variogram models for marshland clays (Hydrofacies 4), which are Gaussian and power, the models are spherical or exponential. The vertical range is from almost one or two orders of magnitude lower than the horizontals, except in Hydrofacies 6 (sand and gravels). Eleven variogram models were obtained (Figure 4) with variations depending on the origin of the sediments.
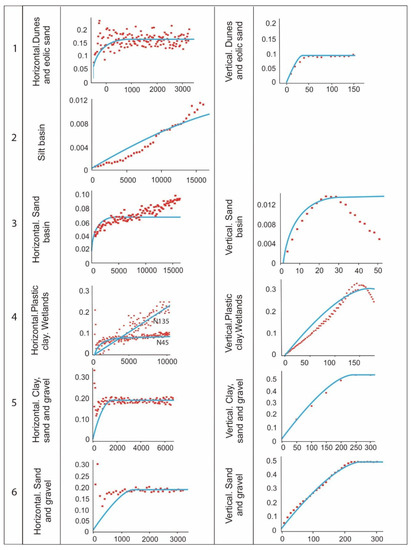
Figure 5.
Modeled variograms (horizontal and vertical) of hydrofacies.

Table 2.
Experimental variogram model parameters. Hydrofacies codes: 1. Aeolian and dune sands; 2. Silt basin: 3. Sand basin; 4. Marshlands clay; 5. Sand and gravels with clay; 6. Sand and gravels.
3.1.2. Sequential Indicator Simulation
Comparing the results with the interpretations by Salvany [34,54], the simulation was validated by both hydrofacies proportions and facies distribution (Figure 6). The proportions were 25% (Hydrofacies 1, Aeolian and dune sands), 2% (Hydrofacies 2, silt basin), 12% (Hydrofacies 3, sand basin), 15% (Hydrofacies 4, marshlands clays), 24% (Hydrofacies 5, clay, sand and gravel), and 22% (Hydrofacies 6, sand and gravel).
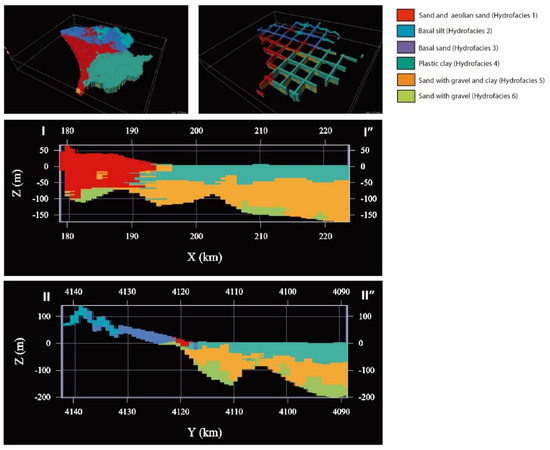
Figure 6.
3D views of SIS results with Isatis 3D Viewer and cross sections I-I’’ and II-II’’.
3.2. Groundwater Flow Model
3.2.1. Piezometry
Figure 7 shows piezometric contours for the groundwater model with the hydraulic permeability and storage coefficient approximated by zonification (Plot A for the upper layer and Plot B for the lower layer). Plot C in Figure 7 presents the piezometry for the groundwater model with the 3D geostatistical simulation, registered in Layer 6. Both models have similar flow patterns. The model with homogeneous zones for hydrogeologic parameters (Plots A and B in Figure 7) registers lower piezometric levels and a higher contour slope in the northeast zone (Plot C in Figure 7). We implemented the 3D simulation by changing the boundary conditions and activating the cells located in the marshlands (gray area in Figure 7A), this area having the deepest isopiezometric values. Plot D in Figure 7 presents the differences between the piezometry represented in Plots B and C. In Plot D it can be seen that marshlands have similar piezometric values. Except for in the northern part of the aquifer and the marshlands, positive differences seem to be more abundant (Plot D in Figure 7), the piezometry in these areas being lower for the model with 3D simulation.
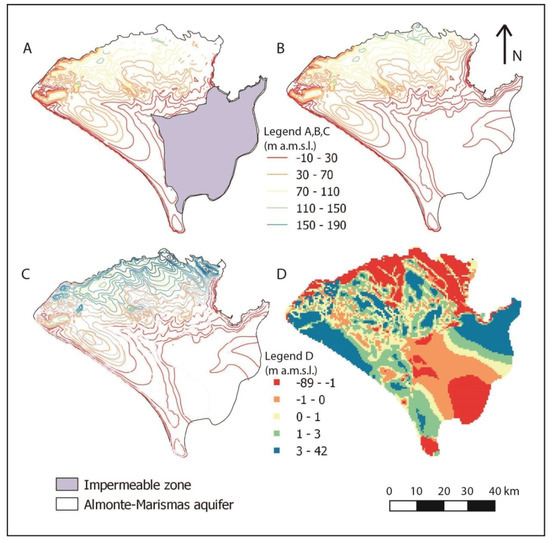
Figure 7.
Piezometric contours of groundwater models: (A) first layer of the original model; (B) second layer of the original model; (C) model with hydrofacies simulation; (D) difference between (B) and (C).
3.2.2. Water Budget
Figure 8 shows the input and output budget values obtained by running both models (i.e., the permeability and storage coefficient entered with zonification or with the 3D simulation). This budget indicates that, when integrating the hydrofacies simulation, inputs from river and stream leakage increase by 3 and 10 hm3/year, respectively; while they descend for the general head boundaries by around 1 hm3/year. On the other hand, outputs through constant head and stream leakage boundaries rise with the geostatistical simulation by 8 and 13 hm3/year, respectively. Output terms decreasing in the model with higher heterogeneities are drains (1 hm3/year less), river leakage (reduction of 2 hm3/year), evapotranspiration (decrease of 5 hm3/year), and general head boundaries (decrease of 0.5 hm3/year). The highest differences are found in stream leakage for both input and output terms, while, as expected, the recharge does not change.
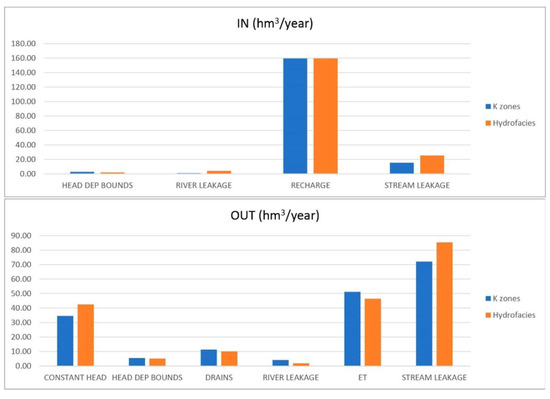
Figure 8.
In and out water budget (hm3/year) comparison between the zoned model and the model with integrated 3D simulation.
Figure 9 summarizes the interchange of fluxes between the Almonte-Marismas aquifer and some ecosystems of vital importance in Doñana (e.g., La Rocina Stream, the ecotones, and the groundwater masses under the marshlands). With respect to the former zoned model, introducing the geostatistical simulation to represent the geological heterogeneities considerably modifies the interchange of annual fluxes in these zones (Figure 9). These variations will be analyzed in Section 4.
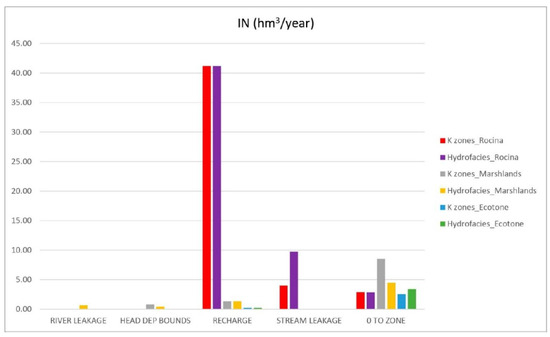
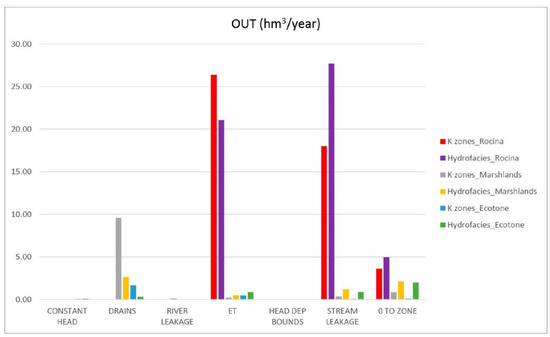
Figure 9.
In and out water budget (hm3/year) comparison between the original model (k_zones) and model with integrated simulation in different specific zones.
4. Discussion
4.1. Variogram Models
In five of the six variograms computed, the correlation range observed depends on the direction. This is explained by the lateral extent of the deposits, which is usually greater than their thickness; hence, the vertical range is much lower than the horizontal range [55]. The variogram of Hydrofacies 2, representing basal silt that emerges in a local zone at the northeast of the aquifer, is the only one that presents no anisotropy. The homogenous distribution of this kind of deposit explains this spatial behavior.
Hydrofacies 1 presents a highly continuous spatial correlation, indicated by the spherical model fitted to its experimental variogram. This fact is coherent with the soft Aeolian dune sands and ancient dunes of this hydrofacies. In the horizontal direction, the range is too small (150 m) in comparison to those of the other lithologies (greater than 500 m). The same occurs with the vertical directions, the range for Hydrofacies 1 being 47 m, while for the rest of the hydrofacies it is more than 175 m. These smaller range values can be explained by the low extent of Aeolian deposition processes.
Basal sands in the central and northern zone of the aquifer compose Hydrofacies 3. Its variogram ranges have medium values with the same order of magnitude for both the horizontal (1500 m) and vertical (900 m) directions. These values may correspond to the dynamics of these sand deposits, which are cemented and more ancient sands than Hydrofacies 1. In addition, Hydrofacies 3 has a slight horizontal trend.
This trend appears more clearly in Hydrofacies 2 (i.e., basal silt), with a sharper increase in the variogram values. The appearance of trends in sedimentary deposits indicates changes in some of the characteristics of the hydrofacies from the proximal to the distal part in depositional environments. These variations cause an increase beyond the threshold variance [55]. In these cases of nonstationary behavior, Gringarten and Deutsch [56] recommend cleaning residual data in the original variogram to remove this kind of trend. However, in the present study this removal process was not performed in order to facilitate the simulation with SGeMS software. The elimination of the trend could be included in the future, constituting a potential improvement of this work. Equally for Hydrofacies 2 and 3, there is a distinctive smooth spatial correlation structure of earth deposits revealed by the spherical and exponential models used for the variogram fitting.
The plastic clays of Hydrofacies 4 arrive through the streams that flood the marshlands. They have different variogram ranges depending on the variogram orientation: 7000 and 15,000 m, respectively, for 45° and 135°, and 175 m in the z axis. The presence of a low range in vertical behavior, it being higher in the horizontal direction, is attributable to the considerable thickness of the hydrofacies. This 3D anisotropy may indicate a variation in the depositional direction associated with different depositional steps [57]. The variety of sedimentological origins is also reflected by the diverse types of variogram model (i.e., exponential, power, and Gaussian models). The Gaussian model fit can be explained by the fact that it is a very continuous lithology on the surface.
The vertical anisotropy and intermediate correlation lengths (i.e., 2400 m for horizontal and 800 m for vertical) of the variogram for Hydrofacies 5 are explained by the elongated and discontinuous lens interleaved with Hydrofacies 6. The exponential models used to fit the corresponding experimental variograms show the continuity of these deposits.
The sixth and last hydrofacies presents quite small ranges (i.e., 500 m for horizontal directions and 300 m for vertical directions). These dimensions correspond very well to sands and gravels with a deltaic–alluvial origin. The exponential and spherical models agree on the considerable spatial continuity of the thickest hydrofacies in the area.
4.2. Geostatisical Simulation
Hydrofacies proportions quantify the hydrogeological behavior of the Almonte-Marismas aquifer. The conceptual model assumes that the largest amount of recharge occurs through sands and Aeolian sands. In total, 26% of the measured and simulated hydrofacies corresponds to these Aeolian sands, corroborating their major hydrogeological role in the aquifer. Hydrofacies 5 and 6 have a high groundwater storage power, supported by their 36% measured and simulated proportion. The prior geological model gives a conceptual model which is constructed from the surface geology (see profiles in Figure 2). The 3D simulations show improvements to this conceptual model. If we compare Profile II in Figure 2 and Figure 6, the effect of the interpolated impervious aquifer bottom can be appreciated. The aquifer thickness from north to south is much greater in the geostatistical 3D model than in the conceptual profiles. Simulated sand and Aeolian sand hydrofacies (Figure 6) seem to be deeper than in the geological profiles (Figure 2). In Profile I, from west to east, 3D estimated facies (Figure 6) with a substantial gravel component (Hydrofacies 5 and 6) reveal a thickness much lower than that in the conceptual model (Figure 2), reducing these depths to almost half (i.e., from −300 m to −150 m).
Restructuring the sediment system that makes up the Almonte-Marismas aquifer into six hydrofacies gives more geological meaning to the layers used in the numerical model, naturalizing its behavior. The 3D simulation (Figure 6) makes it possible to incorporate two improvements. Firstly, one can include low-permeability cells representing plastic clays interbedded with the sand and gravel lenses of Hydrofacies 5 and 6. Secondly, when the computing time allows it, a finer vertical discretization can be introduced, improving the two-layered modelling. In this stationary case of the Almonte-Marismas model, it was possible to increase to seven layers.
When facies are discretized with indicator variables, it is not possible to use only indicator kriging results to estimate the 3D facies distribution because indicator kriging interpolation is not a direct representation of the hydrofacies, but a probability that these hydrofacies are present in a given pixel. However, raw indicator simulations have small-scale variations and do not match the target proportions. Thanks to TRANSCAT correction [42], the simulated realization is as smooth as an interpolated 3D field from kriging and follows the measured proportions. Still, this is a simulation result representing an equiprobable 3D image. Other estimates, different from this one, can be obtained through new simulations. Ideally, a high number of hydrofacies simulations could be obtained and input into the groundwater modelling to stochastically analyze the set of numerical results. However, the computing time required for the Almonte-Marismas transient groundwater model (153 min on a system with processor an Intel(R) Core(TM) i7-4750 CPU @ 3.60 GHz, x64-based processor, and 7.98 GB usable RAM), and the required ensemble size to perform an uncertainty analysis, makes this stochastic analysis impractical. In any case, this paper aims to highlight the possibilities of developing real heterogeneous groundwater numerical models (i.e., noncontinuous lithofacies without smooth limits) from geostatistical simulations for water resource management purposes. Hence, we tested the results with just one simulated realization. This is one of the drawbacks of the results presented here, but further research could be done from this starting point: this is the first time that 3D heterogeneous values of permeability have been considered in the highly heterogeneous Almonte-Marismas groundwater numerical model. Future research could also consider the use of MPS [27], as recent studies have probed its efficiency in characterizing fluvial deposits [58].
4.3. Groundwater Flow Model
As the hydrogeologic parameters have different spatial distributions in the two models studied and the number of layers is different, they were calibrated independently from each other. Hence, the aim of the comparison discussed here is not to provide an exact analysis of the differences between the two models, but to give an idea of the implications for groundwater management decisions made with the results of these numerical models.
Upscaling flow is required to take into account the discrepancy between the scale at which we can characterize the medium with geostatistical simulations and the scale at which we can run the numerical model [59]. The methodology to couple calibration and hydraulic parameter upscaling has been already developed [58]. However, upscaling is not routinely used in real water management models because there is not an implementation in commonly used MODFLOW graphical user interfaces. Upscaling hydraulic permeability in the horizontal directions was not necessary in the present work; the discretization in the SIS is the same as that in the MODFLOW grid. However, for the vertical discretization, MODFLOW is not capable of dealing with the 2 m layers obtained with geostatistics, as dry cells cause frequent numerical instabilities. We have chosen the most abundant hydrofacies in the SIS to assign the hydrofacies to each of the seven layers that form the MODLFOW model. The impact of hydraulic permeability upscaling is greater in transport predictions than in flow and head results [59]. Consequently, 3D hydraulic permeability upscaling [60,61] should be computed if future transport modeling is performed with the model presented here.
When comparing the model with homogeneous zones and the updated model with the heterogeneities, the greatest differences in the distribution of isopiezometric contours (Figure 7) are observed in the northern and western areas. In the northeastern zone, the variation is due to the presence of basal silts that modify the hydrogeological properties of the area with respect to the original. In this area the piezometry is higher in the model with 3D simulation, since the properties of the basic sands are introduced in the modeling. This is also reflected in the higher outputs through this general head boundary (Figure 8).
Plot C in Figure 7 shows how marshlands are not impermeable in the new modelling approximation. This allows for slow flow exchange in the marshlands, shown in the extent of the isopiezometric lines, which have less gradient and elevation. When compared with the version of the model with zones, the heterogeneous model drains 7 hm3/year less from the aquifer to the marshlands. This outcome seems to be more in accordance with reality, as the Doñana marshlands are basically fed by direct rainfall on the floodplain and by several watersheds [62]. The same happens in the ecotone water budget, with the groundwater contribution decreasing from 1.66 to 0.33 hm3/year. These amounts are more difficult to corroborate as there are no studies estimating outputs from the aquifer to the ecotones.
The significant dissimilarities observed in the budget outputs from the aquifer to the streams and sea (Figure 8) imply that groundwater contributions to these water bodies could be underestimated using homogeneous zones by values of about 18% and 23%, respectively. Studies of potential future water intrusion, more likely to happen in the global climate change framework [63], can reach quite different conclusions depending on the approximation used to characterize the spatial variability of hydrogeological parameters. The water management consequences of those results are also very important. The ongoing Hydrological Plan (HP) [64] is the main water management instrument in Doñana. In the HP the actual water reserves are computed considering lateral transfers to the sea and assuming that an optimal ecological status in the present ecosystems can be maintained. Variations of about 20% in these values can lead to considerable changes in the withdrawals allowed from the aquifer. La Rocina Stream is the main permanent tributary to the marshlands and a critical area for water management, with wide areas of berry cultivation irrigated by many illegal extractions [65]. The net interchange flux between La Rocina Stream and the aquifer is 30% higher in the model, with more spatial variability. Again, this corroborates the importance of using one model or another to evaluate groundwater reserves in Doñana. Moreover, all the deviations found in the present study highlight the need for effective numerical models and uncertainty quantifications in the design of strategies for groundwater resource management in response to future climate change [1].
5. Conclusions
The main goals of this study were to incorporate the spatial variability of subsurface geology into the numerical flow model of the Almonte-Marismas aquifer and to determine whether this effort is relevant for management proposes. We were able to achieve these aims by performing a 3D geological characterization of the heterogeneities, analyzing 3D variogram models, and applying geostatistical SIS. We were also able to integrate this 3D hydrofacies structure into a steady-state MODFLOW model. Our findings confirm that water budget results can vary considerably with this new approximation. These changes are key when estimating the discharges from the aquifer to the streams, which are essential to maintaining the riparian ecosystems and the surface contribution to the marshlands. In addition, variations in the water budget estimation affect groundwater exploitation management decisions and studies of marine water intrusion in a global climate change framework. Further studies are needed to facilitate the computing operations needed to implement the 3D hydrofacies in the transient flow model (1975–2018) currently used in Almonte-Marismas aquifer management and to quantify the associated uncertainties in piezometric and water budget results.
Author Contributions
Conceptualization, C.G.-A. and N.N.-F.; Methodology, C.G.-A. and N.N.-F.; Software, C.G.-A. and N.N.-F.; Validation, C.G.-A. and N.N.-F.; Formal Analysis, C.G.-A. and N.N.-F.; Investigation, C.G.-A. and N.N.-F.; Resources, C.G.-A., E.M.-G., and N.N.-F.; Data Curation, C.G.-A. and N.N.-F.; Writing—Original Draft Preparation, C.G.-A., E.M.-G., and N.N.-F.; Writing—Review & Editing, C.G.-A., E.M.-G., and N.N.-F.; Visualization, C.G.-A., and N.N.-F.; Supervision, C.G.-A. and E.M.-G.; Project Administration, C.G.-A.; Funding Acquisition, C.G.-A.
Funding
This research was funded by the CLIGRO project (MINECO, CGL2016-77473-C3-1-R) of the Spanish National Plan for Scientific and Technical Research and Innovation and by the Ministry of Education, Youth and Sport of the Community of Madrid with ref. PEJ15/AMB/AI-0218, co-financed under the Youth Employment Operational Program, with financial resources from the Youth Employment Initiative (YEI) and the European Social Fund (ESF).
Acknowledgments
The three anonymous reviewers are thanked for their helpful comments. Spanish Geological Survey is acknowledged for providing the datasets used in this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guardiola-Albert, C.; Jackson, C.R. Potential impacts of climate change on groundwater supplies to the Doñana wetland, Spain. Wetlands 2011, 31, 907–920. [Google Scholar] [CrossRef]
- Green, A.J.; Alcorlo, P.; Peeters, E.T.; Morris, E.P.; Espinar, J.L.; Bravo-Utrera, M.A.; Bustamante, J.; Díaz-Delgado, R.; Koelmans, A.; Mateo, R.; et al. Creating a safe operating space for wetlands in a changing climate. Front. Ecol. Environ. 2017, 15, 99–107. [Google Scholar] [CrossRef]
- Sánchez-Vila, X.; Fernández-García, D. Gestión de los recursos hídricos: Los modelos hidrogeológicos como herramienta auxiliar. Enseñanza de las ciencias de la tierra 2007, 15, 250–256. [Google Scholar]
- Instituto Geológico y Minero de España (IGME). Primer Informe sobre el Modelo Matemático del Acuífero de Almonte Marismas; Instituto Geológico y Minero de España: Madrid, Spain, 1975. [Google Scholar]
- Instituto Geológico y Minero de España (IGME). Modelo Matemático Bidimensional del Sistema Acuífero n° 27: Unidad Almonte-Marismas, 1982. Available online: http://info.igme.es/SidPDF/018000/726/18726_0001.pdf (accessed on 22 September 2018).
- Instituto Geológico y Minero de España (IGME). Modelo Matemático del Acuífero de Almonte-Marismas (Parque Nacional de Doñana); Instituto Geológico y Minero de España: Madrid, Spain, 1994. [Google Scholar]
- Instituto Geológico y Minero de España (IGME). Modelo Regional de Flujo Subterráneo del Sistema Acuífero Almonte-Marismas y su Entorno; Instituto Geológico y Minero de España: Madrid, Spain, 1999. [Google Scholar]
- Universitat Politècnica de Catalunya (UPC). Regional Groundwater Flow in the Almonte-Marismas Aquifer; Groundwater Hydrology Group of the Technical University of Catalonia and Geological Institute: Madrid, Spain, 1999; 114p. [Google Scholar]
- Instituto Geológico y Minero de España (IGME). Modelo matemático del acuífero Almonte—Marismas: Actualización y realización en Visual Modflow, 2005. Available online: Https://www.researchgate.net/publication/264229860_Modelo_matematico_revisado_del_acuifero_Almonte-Marismas_aplicacion_a_distintas_hipotesis_de_gestion (accessed on 25 September 2018).
- Instituto Geológico y Minero de España (IGME). Mejora del Modelo Matemático del Acuífero Almonte-Marismas Como Apoyo a la Gestión de los Recursos Hídricos: Estimación de la Recarga, Modelo Estocástico y Actualización; Instituto Geológico y Minero de España: Madrid, Spain, 2009. [Google Scholar]
- Instituto Geológico y Minero de España (IGME). Proyecto Para la Actualización del Modelo Numérico (Visual Modflow 4.3, Igme 2007) del Sistema Acuífero Almonte-Marismas, Como Apoyo para el Desarrollo de un Modelo de Gestión y Uso Sostenible del Acuífero en el Ámbito de Doñana (Huelva-Sevilla); Instituto Geológico y Minero de España: Madrid, Spain, 2011. [Google Scholar]
- Jankowski, J.; Beck, P. Aquifer heterogeneity: Hydrogeological and hydrochemical properties of the Botany Sands aquifer and their impact on contaminant transport. Aust. J. Earth Sci. 2000, 47, 45–64. [Google Scholar] [CrossRef]
- Nœtinger, B.; Artus, V.; Zargar, G. The future of stochastic and upscaling methods in hydrogeology. Hydrogeol. J. 2005, 13, 184–201. [Google Scholar] [CrossRef]
- De Marsily, G.; Delay, F.; Gonçalvès, J.; Renard, P.; Teles, V.; Violette, S. Dealing with spatial heterogeneity. Hydrogeol. J. 2005, 13, 161–183. [Google Scholar] [CrossRef]
- Watson, C.; Richardson, J.; Wood, B.; Jackson, C.; Hughes, A. Improving geological and process model integration through TIN to 3D grid conversion. Comput. Geosci. 2015, 82, 45–54. [Google Scholar] [CrossRef]
- Klingbeil, R.; Kleineidam, S.; Asprion, U.; Aigner, T.; Teutsch, G. Relating lithofacies to hydrofacies: Outcrop-based hydrogeological characterisation of Quaternary gravel deposits. Sediment. Geol. 1991, 129, 299–310. [Google Scholar] [CrossRef]
- Anderson, M.P. Hydrogeological facies models to delineate large scale spatial trends in glacial and glacio fluvial sediments. Geol. Soc. Am. Bull. 1989, 101, 501–511. [Google Scholar] [CrossRef]
- Comunian, A.; De Micheli, L.; Lazzati, C.; Felleti, F.; Giacobbo, F.; Giudici, M.; Bersezio, R. Hierarchical simulation of aquifer heterogeneity: Implications of different simulation settings on solute-transport modeling. Hydrogeol. J. 2016, 24, 319–334. [Google Scholar] [CrossRef]
- Seifert, D.; Jensen, J.L. Using sequential indicator simulation as a tool in reservoir description: Issues and uncertainties. Math. Geol. 1991, 31, 527–550. [Google Scholar] [CrossRef]
- Renard, P. Stochastic Hydrogeology: What Professionals Really Need? Groundwater 2007, 45, 531–541. [Google Scholar] [CrossRef] [PubMed]
- Pyrcz, M.J.; Deutsch, C.V. Geostatistical Reservoir Modeling, 2nd ed.; Oxford University Press: New York, NY, USA, 2014; p. 433. [Google Scholar]
- Fiori, A.; Cvetkovic, V.; Dagan, G.; Attinger, S.; Bellin, A.; Dietrich, P.; Zech, A.; Teutsch, G. Debates—Stochastic subsurface hydrology from theory to practice: The relevance of stochastic subsurface hydrology to practical problems of contaminant transport and remediation. What is characterization and stochastic theory good for? Water Resour. Res. 2016, 52, 9228–9234. [Google Scholar] [CrossRef]
- Dell’Arciprete, D.; Bersezio, R.; Felletti, F.; Giudici, M.; Comunian, A.; Renard, P. Comparison of three geostatistical methods for hydrofacies simulation: A test on alluvial sediments. Hydrogeol. J. 2012, 20, 299–311. [Google Scholar] [CrossRef]
- Alabert, F. Stochastic Imaging of Spatial Distributions Using Hard and Soft Information. Master’s Thesis, Department of Applied Earth Sciences, Stanford University, Stanford, CA, USA, 1987. [Google Scholar]
- Beucher, H.; Renard, D. Truncated Gaussian and derived methods. C. R. Geosci. 2016, 348, 510–519. [Google Scholar] [CrossRef]
- Deutsch, C.V.; Tran, T.T. FLUVSIM: A program for object-based stochastic modelling of fluvial depositional systems. Comput. Geosci. 2002, 28, 525–535. [Google Scholar] [CrossRef]
- Hu, L.Y.; Chugunova, T. Multiple-point geostatistics for modeling subsurface heterogeneity: A comprehensive review. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Gómez-Hernández, J.J.; Srivastava, R.M. ISIM3D: An ANSI-C three-dimensional multiple indicator conditional simulation program. Comput. Geosci. 1990, 16, 395–440. [Google Scholar] [CrossRef]
- Deutsch, C.V. A sequential indicator simulation program for categorical variables with point and block data: BlockSIS. Comput. Geosci. 2006, 32, 1669–1681. [Google Scholar] [CrossRef]
- Marini, M.; Felletti, F.; Bereta, G.P.; Terrenghi, J. Three Geostatistical Methods for Hydrofacies Simulation Ranked Using a Large Borehole Lithology Dataset from Venice Hinterland (NE Italy). Water 2018, 10, 844. [Google Scholar] [CrossRef]
- Salvany, J.M.; Custodio, E. Características litoestratigráficas de los depósitos pliocuaternarios del bajo Guadalquivir en el área de Doñana: Implicaciones hidrogeológicas. Rev. Soc. Geol. España 1995, 8, 21–31. [Google Scholar]
- Custodio, E.; Manzano, M.; Montes, C. Las aguas Subterráneas en Doñana. Aspectos Ecológicos y Sociales; Junta de Andalucía: Sevilla, España, 2009; 244p, ISBN 978-84-92807-19-2. [Google Scholar]
- Rodríguez-Ramirez, A.; Yáñez-Camacho, C.; Gascó, C.; Clemente-Salas, L.; Antón, M.P. Colmatación natural y antrópica de las marismas del Parque Nacional de Doñana: Implicaciones para su manejo y conservación. Cuaternario y Geomorfología 2005, 19, 37–48. [Google Scholar]
- Salvany, J.M.; Cruz-Larrasoaña, J.; Mediavilla, C.; Rebollo, A. Chronology and tectono-sedimentary evolution of the Upper Pliocene to Quaternary deposits of the lower Guadalquivir foreland basin, SW Spain. Sediment. Geol. 2011, 241, 22–39. [Google Scholar] [CrossRef]
- Roldán, F.J.; Rodríguez-Fernández, J.; Villalobos, M.; Lastra, J.; Díaz-Pinto, G.; Pérez Rodríguez, A.B. Mapa Geológico Digital Continuo E.1:50.000, Zonas Subbético, Cuenca del Guadalquivir y Campo de Gibraltar. In GEODE Mapa Geológico Digital continuo de España. Available online: http://info.igme.es/cartografiadigital/geologica/geodezona.aspx?Id=Z2600 (accessed on 22 May 2018).
- Instituto Geológico y Minero de España (IGME). Revisión de la Información Geofísica Existente en el Acuífero Almonte-Marismas (Doñana), 2007. Available online: http://info.igme.es/SidPDF/137000/833/137833_0000001.pdf (accessed on 22 May 2018).
- Instituto Geológico y Minero de España (IGME). Informe Técnico Sobre los Sondeos Mecánicos de Reconocimiento Geológico e Hidrogeológico Realizados en el Acuífero Almonte-Marismas; Instituto Geológico y Minero de España: Madrid, Spain, 2009. [Google Scholar]
- Matheron, G. Les Variables Régionalisées et leur Estimation. Une Application de la Théorie des Fonctions Aléatoires aux Sciences de la Nature; Masson: Paris, France, 1965; 306p. [Google Scholar]
- Trevisani, S.; Fabbri, P. Geostatistical modeling of heterogeneous site bordering the Venice Lagoon, Italy. Groundwater 2010, 48, 614–623. [Google Scholar] [CrossRef] [PubMed]
- Seifert, D.; Jensen, J.L. Object and pixel-based reservoir modeling of braided fluvial reservoir. Math. Geol. 2000, 32, 581–603. [Google Scholar] [CrossRef]
- Géovariances. Isatis Technical Ref.; ver. 2012.4; Geovariances & Ecole Des Mines De Paris: Avon Cedex, France, 2009. [Google Scholar]
- Remy, N.; Boucher, A.; Wu, J. Applied Geostatistics with SGeMS: A User’s Guide; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Caers, J. Adding Local Accuracy to Direct Sequential Simulation. Mat. Geosci 2000, 32, 815–850. [Google Scholar] [CrossRef]
- Deutsch, C.V. Cleaning categorical variable (lithofacies) realizations with maximum a posteriori selection. Comput. Geosci. 1998, 24, 551–562. [Google Scholar] [CrossRef]
- Deutsch, C.V.; Journel, A.G. Geostatistical Software Library and User’s Guide; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Goovaerts, P. Stochastic simulation of cathegorical variables using a clasiffication algorithm and simulating annealing. Math. Geol. 1996, 28, 909–921. [Google Scholar] [CrossRef]
- Soares, A. Sequential indicator simulation with correction for local probabilities. Math. Geol. 1998, 30, 761–765. [Google Scholar] [CrossRef]
- Almeida, J.A. Stochastic simulation methods for characterization of lithoclasses in carbonate reservoirs. Earth Sci. Rev. 2010, 101, 250–270. [Google Scholar] [CrossRef]
- Lukjan, A.; Chalermyanont, T. Assesment of alluvial aquifer heterogeneity and development os stochastic hydrofacies models for the Hat Yai Basin in Sothern Thailand. Environ. Earth Sci. 2017, 76. [Google Scholar] [CrossRef]
- Harbaugh, A.W. MODFLOW-2005, The US Geological Survey Modular Ground-Water Model: The Ground-WaterFlow Process; Department of the Interior, Techniques and Methods 6–A16; U.S. Geological Survey: Reston, VA, USA, 2005. [Google Scholar]
- Winston, R.B. ModelMuse—A Graphical User Interface for MODFLOW–2005 and PHAST: U.S. Geological Survey Techniques and Methods 6–A29; U.S. Geological Survey: Reston, VA, USA, 1999; 52p. Available online: http://pubs.usgs.gov/tm/tm6A29 (accessed on 22 May 2018).
- Wackernagel, H. Multivariate Geostatistics: An Introduction with Applications, 2nd ed.; Springer: Berlin, Germany, 1998. [Google Scholar]
- Chiles, J.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1999; 734p, ISBN 978-0-470-18315-1. [Google Scholar]
- Salvany, J.M.; Mediavilla, C.; Rebollo, A. Las formaciones Plio-Cuaternarias de El Abalario en el litoral de la provincia de Huelva (España). Estudios Geológicos 2010, 66. [Google Scholar] [CrossRef]
- Gringarten, E.; Deutsch, C.V. Methodology for Improved Variogram Interpretation and Modeling for Petroleum Reservoir Characterization. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1999; Society of Petroleum Engineers: Houston, TX, USA, 1999. [Google Scholar]
- Gringarten, E.; Deutsch, C.V. Teacher’s Aide. Variogram Interpretation and Modeling. Math. Geol. 2001, 33, 507–534. [Google Scholar] [CrossRef]
- Johnson, N.M.; Dreiss, S.J. Hydrostratigraphic interpretation using indicator geostatistics. Water Resour. Res. 1989, 25, 2501–2510. [Google Scholar] [CrossRef]
- Li, L.; Srinivasan, S.; Zhou, H.; Gomez-Hernandez, J. Two-point or multiple-point statistics? A comparison between the ensemble Kalman filtering and the ensemble pattern matching inverse methods. Adv Water Resour 2015, 86, 297–310. [Google Scholar] [CrossRef]
- Li, L.; Zhou, H.; Gómez-Hernández, J.J. Transport upscaling using multi-rate mass transfer in three-dimensional highly heterogeneous porous media. Adv. Water Resour. 2011, 34, 478–489. [Google Scholar] [CrossRef]
- Zhou, H.; Li, L.; Gómez-Hernández, J.J. Three-dimensional hydraulic conductivity upscaling in groundwater modeling. Comput. Geosci. 2010, 36, 1224–1235. [Google Scholar] [CrossRef]
- Li, L.; Zhou, H.; Gómez-Herández, J.J. A comparative study of three-dimensional hydraulic conductivity upscaling at the macro-dispersion experiment (MADE) site, Columbus Air Force Base, Mississipi (USA). J. Hydrol. 2011, 278–293. [Google Scholar] [CrossRef]
- Serrano, L.; Reina, M.; Martín, G.; Reyes, I.; Arechedera, A.; León, D.; Toja, J. The aquatic systems of Doñana (SW Spain): Watersheds and frontiers. Limnetica 2006, 25, 11–32. [Google Scholar]
- Sherif, M.; Singh, V.P. Effect of climate change on sea water intrusion in coastal aquifers. Hydrol. Process. 1999, 13, 1277–1287. [Google Scholar] [CrossRef]
- Confederación Hidrográfica del Guadalquivir (CHG). Plan Hidrológico de la Demarcación Hidrográfica del Guadalquivir; Segundo ciclo de planificación: 2016-2021.2015; CHG: Sevilla, Spain, 2015. [Google Scholar]
- WWW. Salvemos Doñana del Peligro a la Prosperidad. 2016. Available online: http://awsassets.panda.org/downloads/wwf_dalberg_salvemos_donana_lr.pdf (accessed on 22 May 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).