Analysis and Mapping of Rainfall-Induced Landslide Susceptibility in A Luoi District, Thua Thien Hue Province, Vietnam
Abstract
1. Introduction
2. Materials and Methods
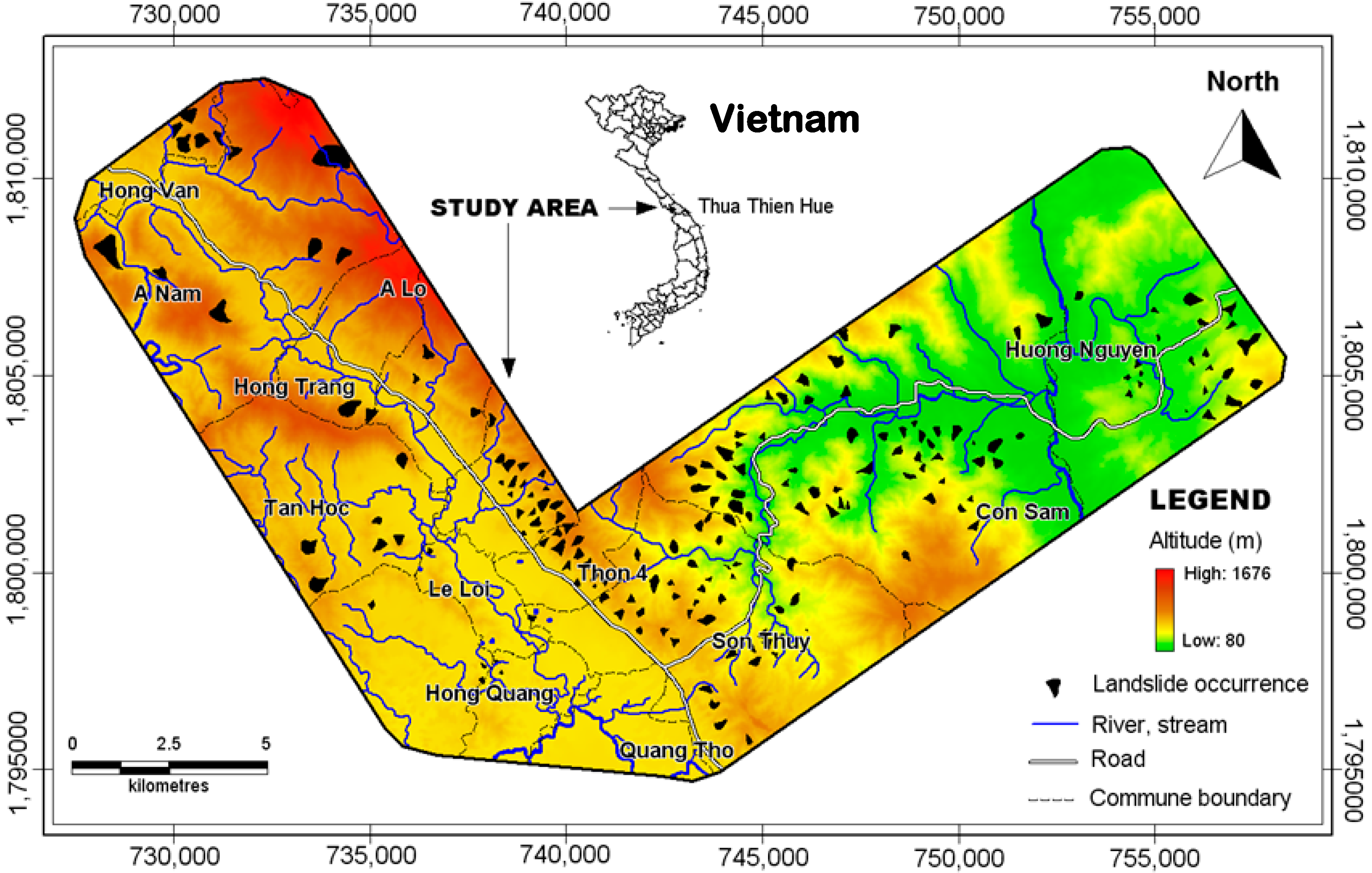
2.1. Study Area
2.2. Data Sources
- Slope: a digital slope angle map was derived from the DEM and a slope class map by separating the slope angles into six classes: (1) flat-gentle (<5°), (2) fair (5–15°), (3) moderate (15–25°), (4) fairly moderate (25–35°), (5) steep (35–45°), and (6) very steep (>45°).
- Fault density: faults were digitized from the geological map and the fault density was derived as total length of faults per 1 km2; a categorical fault density map was obtained by classifying the fault density in intervals of 500 m/km2 (Table 1).
- Weathering crust: a digital categorical map was derived from fieldwork in Thua Thien Hue Province carried out by Văn et al. [51], indicating Quaternary deposits and four types of weathering crusts: Sialite, Sialferrite, Ferrosialite, and mixtures of Silixite.
- Land use: a digital map was derived from a Landsat TM5 image of 20 February 1999 (Path/row: 125/48); four land uses were identified and verified in the field by Văn et al. [51], resulting in four land use classes: agriculture, forest, shrub and bare hills, and build-up land.
- Drainage distance: a digital map of the shortest distance to a watercourse was derived from the topographic map and a drainage distance class map was obtained by subdividing the values into classes <50 m, 50–200 m and >200 m (adapted from the literature, e.g., reference [20]).
- Precipitation: average annual precipitation was selected as rainfall causative factor for landslide analysis, because precise information about the intensity of individual storms is not available in the study area; the precipitation map was derived by spatial interpolation (inverse distance weighting) of the average annual precipitation observed from 1976 to 2003 in three climate stations in the A Luoi district [52]; the values range from about 2900 mm/year to 3500 mm/year and because this is a rather small range the precipitation class map was derived by dividing the values into just three classes: <3100 mm/year, 3100–3300 mm/year and >3300 mm/year.
2.3. Methods for Landslide Susceptibility Analysis
2.4. Model Verification
3. Results
4. Discussion
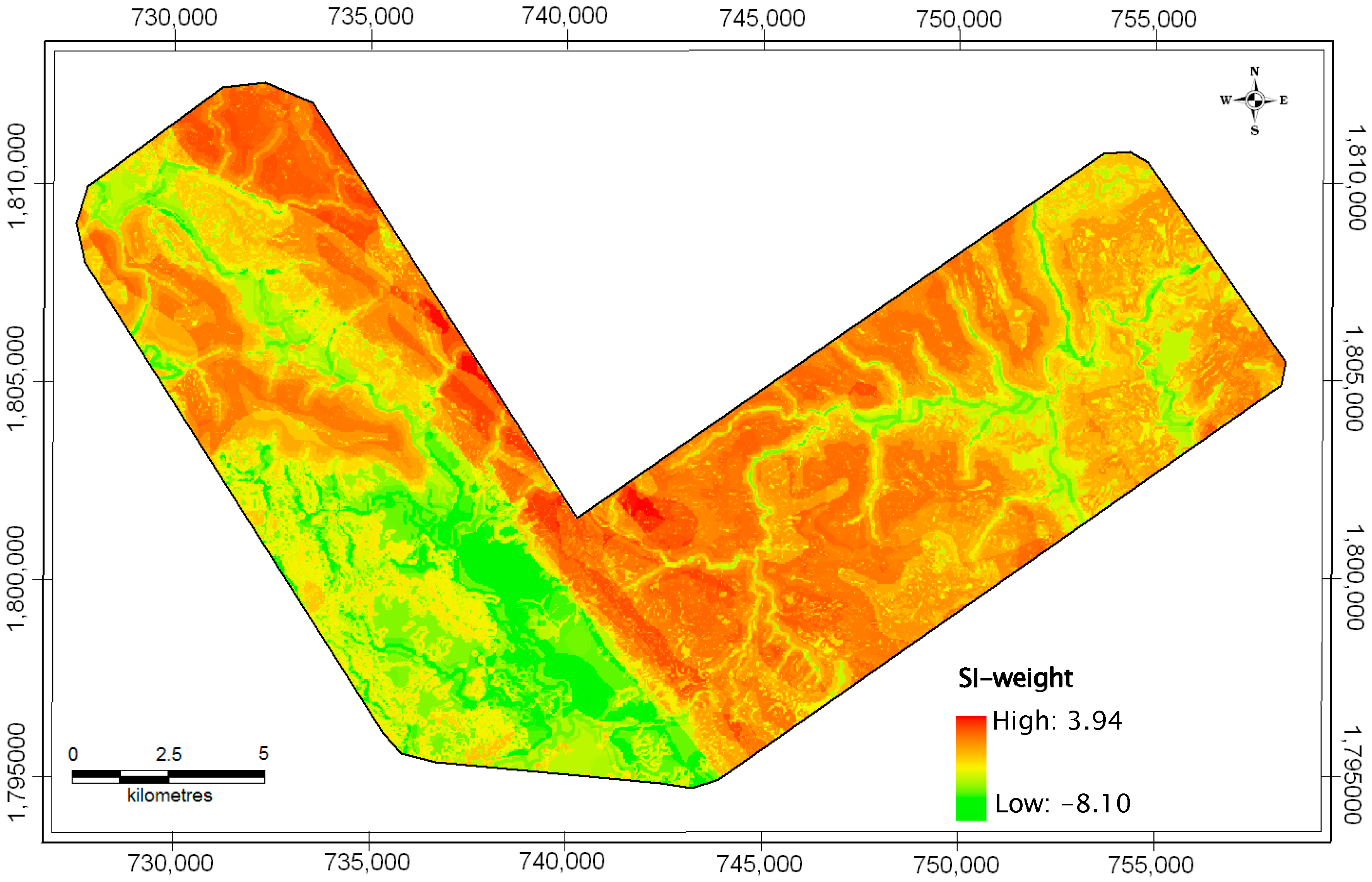
4.1. Statistical Index Model
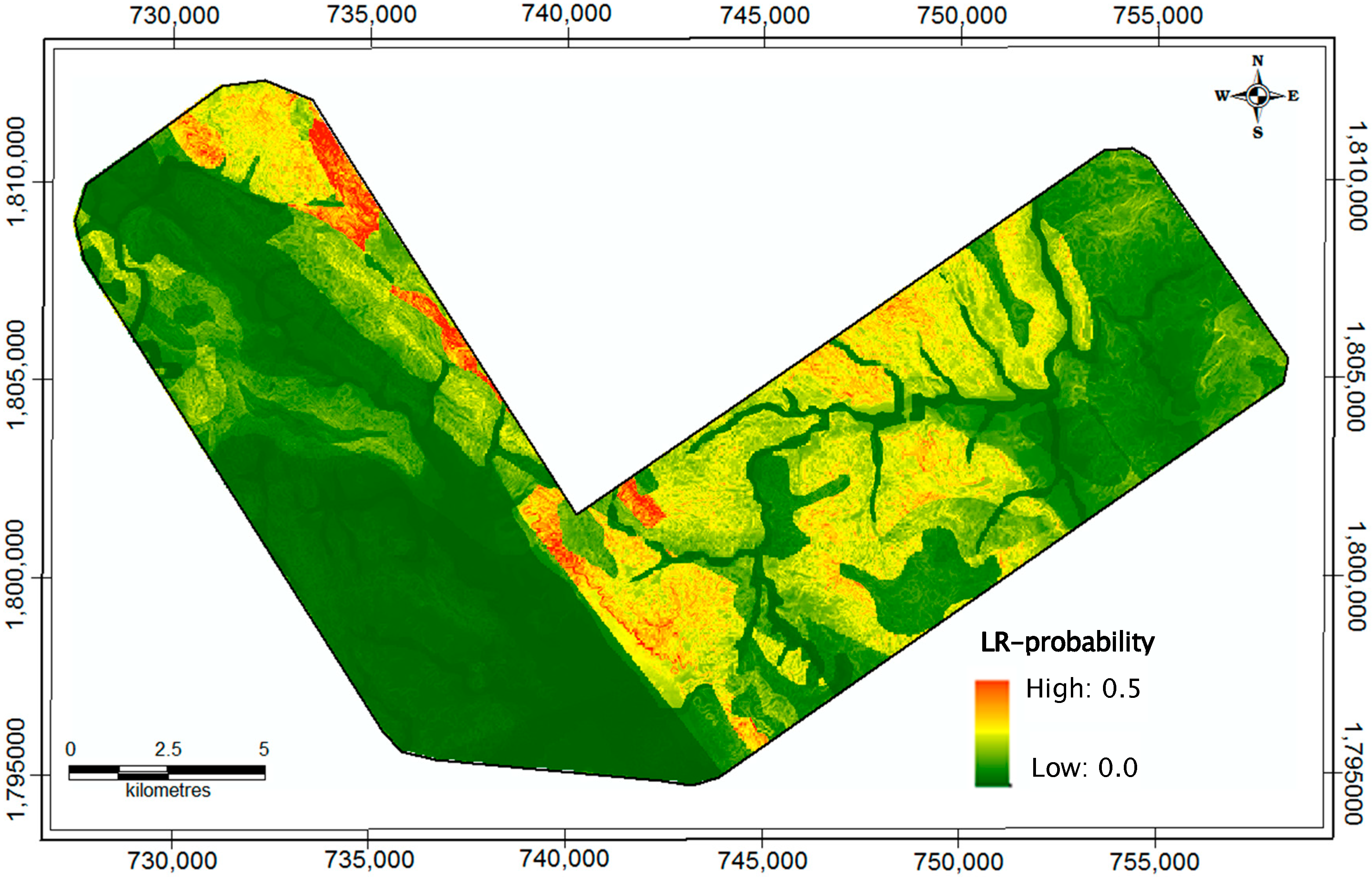
4.2. Logistic Regression Model
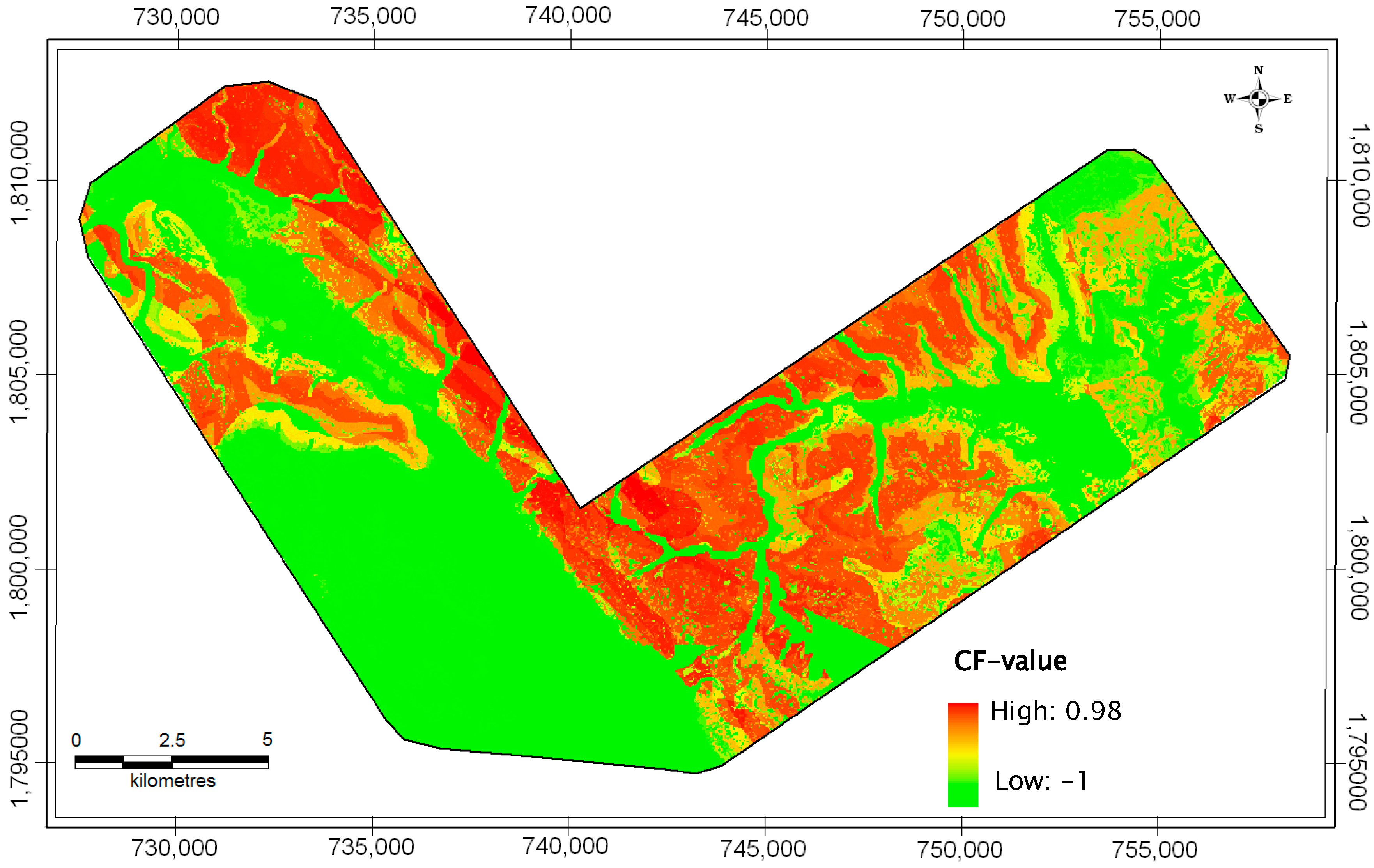
4.3. Certainty Factor Model
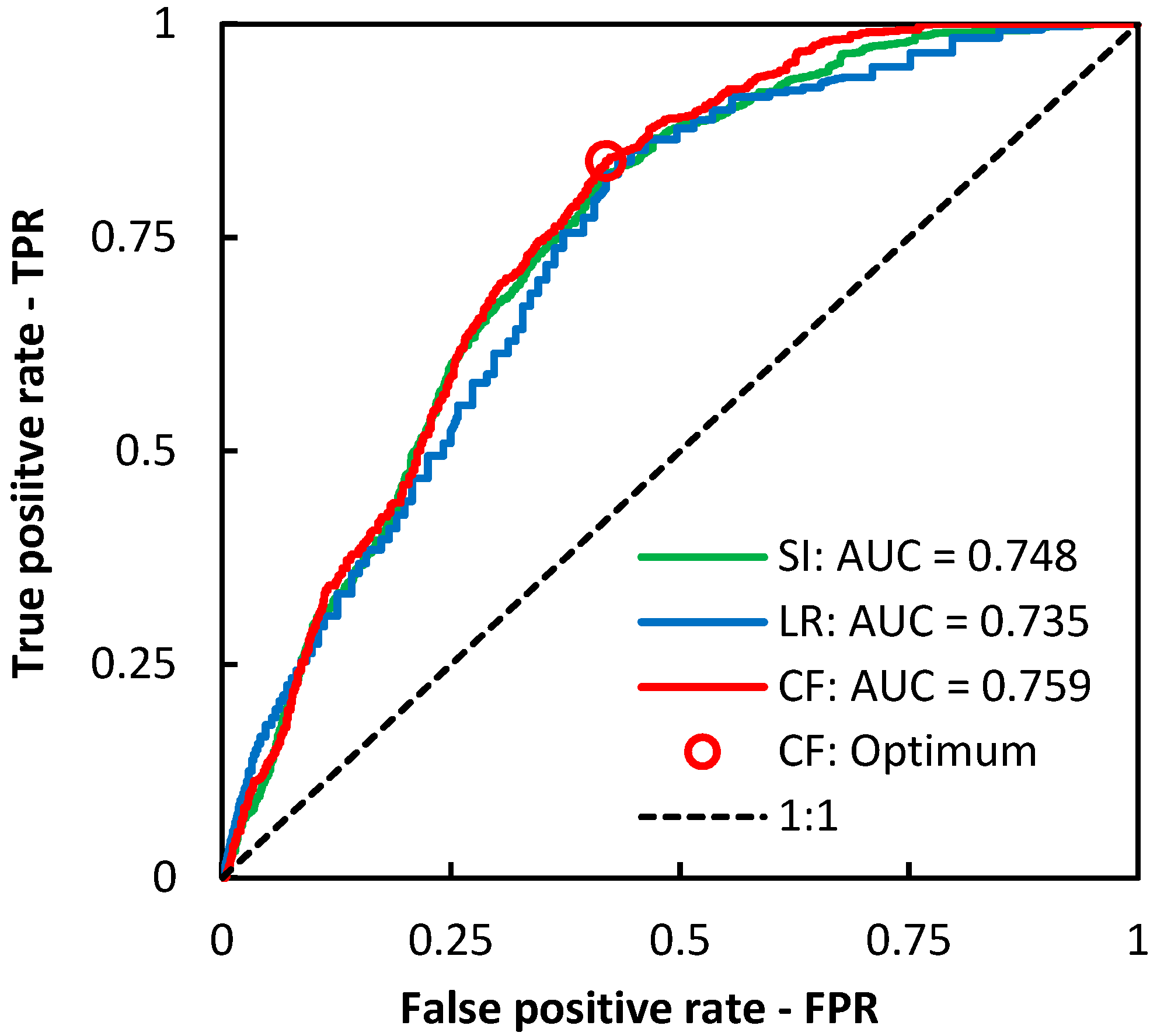
4.4. Optimal Model
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nadim, F.; Kjekstad, O.; Peduzzi, P.; Herold, C.; Jaedicke, C. Global landslide and avalanche hotspots. Landslides 2006, 3, 159–174. [Google Scholar] [CrossRef]
- Gorsevski, P.V.; Gessler, P.E.; Boll, J.; Elliot, W.J.; Foltz, R.B. Spatially and temporally distributed modeling of landslide susceptibility. Geomorphology 2006, 80, 178–198. [Google Scholar] [CrossRef]
- Corominas, J.; Moya, J.; Ledesma, A.; Lloret, A.; Gili, J.A. Prediction of ground displacements and velocities from groundwater level changes at the Vallcebre landslide (Eastern Pyrenees, Spain). Landslides 2005, 2, 83–96. [Google Scholar] [CrossRef]
- Rosso, R.; Rulli, K.M.; Vannucchi, G. A physically based model for the hydrologic control on shallow landsliding. Water Resour. Res. 2006, 42, W06410. [Google Scholar] [CrossRef]
- Ledesma, A.; Corominas, J.; Gonzàles, A.; Ferrari, A. Modelling slow moving landslides controlled by rainfall. In Proceedings of the 1st Italian Workshop on Landslides, Napoli, Italy, 8–10 June 2009; pp. 196–205. [Google Scholar]
- Conte, E.; Donato, A.; Pugliese, L.; Troncone, A. Analysis of the Maierato landslide (Calabria, Southern Italy). Landslides 2018, 15, 1935–1950. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef]
- Godt, J.W.; Baum, R.L.; Chleborad, A.F. Rainfall characteristics for shallow landsliding in Seattle, Washington, USA. Earth Surf. Proc. Land. 2006, 31, 97–110. [Google Scholar] [CrossRef]
- Salciarini, D.; Godt, J.W.; Savage, W.Z.; Baum, R.L.; Conversini, P. Modeling landslide recurrence in Seattle, Washington, USA. Eng. Geol. 2008, 102, 227–237. [Google Scholar] [CrossRef]
- Conte, E.; Troncone, A. Simplified approach for the analysis of rainfall-induced landslides. J. Geotech. Geoenviron. 2012, 138, 398–406. [Google Scholar] [CrossRef]
- Shackelford, C.D.; Chang, C.K.; Chiu, T.F. The capillary barrier effect in unsaturated flow through soil barriers. In Proceedings of the First International Congress on Environmental Geotechnics, Edomonton, AB, Canada, 10–15 July 1994; pp. 789–793. [Google Scholar]
- Lee, S.; Dan, N.T. Probabilistic landslide susceptibility mapping in the Lai Chau province of Vietnam: Focus on the relationship between tectonic fractures and landslides. Environ. Geol. 2005, 48, 778–787. [Google Scholar] [CrossRef]
- Bui, D.; Lofman, O.; Revhaug, I.; Dick, O. Landslide susceptibility analysis in the Hoa Binh province of Vietnam using statistical index and logistic regression. Nat. Hazards 2011, 59, 1413–1444. [Google Scholar] [CrossRef]
- Long, N.T.; De Smedt, F. Application of an analytical hierarchical process approach for landslide susceptibility mapping in A Luoi district, Thua Thien Hue Province, Vietnam. Environ. Earth Sci. 2012, 66, 1739–1752. [Google Scholar] [CrossRef]
- Long, N.T.; De Smedt, F. Landslide susceptibility analysis based on a physical slope stability model: A case study from Thua Thien-Hue Province, Vietnam. Landslides 2014, 11, 897–907. [Google Scholar] [CrossRef]
- Hung, L.Q.; Van, N.T.H.; Duc, D.M.; Ha, L.T.C.; Van Son, P.; Binh, L.T. Landslide susceptibility mapping by combining the analytical hierarchy process and weighted linear combination methods: A case study in the upper Lo River catchment (Vietnam). Landslides 2016, 13, 1285–1301. [Google Scholar] [CrossRef]
- van Westen, C. Statistical landslide hazard analysis. In ILWIS 2.1 for Windows Application Guide; ITC Publication: Enschede, The Netherlands, 1997; pp. 73–84. [Google Scholar]
- Cevik, E.; Topal, T. GIS–based landslide susceptibility mapping for a problematic segment of the natural gas pipeline, Hendek (Turkey). Environ. Geol. 2003, 44, 949–962. [Google Scholar] [CrossRef]
- Süzen, M.L.; Doyuran, V. A comparison of the GIS based landslide susceptibility assessment methods: Multivariate versus bivariate. Environ. Geol. 2004, 45, 665–679. [Google Scholar] [CrossRef]
- Yalcin, A. GIS-based landslide susceptibility mapping using analytical hierarchy process and bivariate statistics in Ardesen (Turkey). Catena 2007, 72, 1–12. [Google Scholar] [CrossRef]
- Regmi, A.D.; Devkota, K.C.; Yoshida, K.; Pradhan, B.; Pourghasemi, H.R.; Kumamoto, T.; Akgun, A. Application of frequency ratio, statistical index, and weights-of-evidence models and their comparison in landslide susceptibility mapping in Central Nepal Himalaya. Arab. J. Geosci. 2014, 7, 725–742. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Moradi, H.R.; Fatemi Aghda, S.M. Landslide susceptibility mapping by binary logistic regression, analytical hierarchy process, and statistical index models and assessment of their performances. Nat. Hazards 2013, 69, 749–779. [Google Scholar] [CrossRef]
- Chen, W.; Li, W.; Hou, E.; Bai, H.; Chai, H.; Wang, D.; Cui, X.; Wang, Q. Application of frequency ratio, statistical index, and index of entropy models and their comparison in landslide susceptibility mapping for the Baozhong Region of Baoji, China. Arab. J. Geosci. 2015, 8, 1829–1841. [Google Scholar] [CrossRef]
- Chen, W.; Chai, H.; Sun, X.; Wang, Q.; Ding, X.; Hong, H. A GIS–based comparative study of frequency ratio, statistical index and weights-of-evidence models in landslide susceptibility mapping. Arab. J. Geosci. 2016, 9, 204. [Google Scholar] [CrossRef]
- Chen, T.; Niu, R.; Jia, X. A comparison of information value and logistic regression models in landslide susceptibility mapping by using GIS. Environ. Earth Sci. 2016, 75, 867. [Google Scholar] [CrossRef]
- Wu, Y.; Li, W.; Wang, Q.; Liu, Q.; Yang, D.; Xing, M.; Pei, Y.; Yan, S. Landslide susceptibility assessment using frequency ratio, statistical index and certainty factor models for the Gangu County, China. Arab. J. Geosci. 2016, 9, 84. [Google Scholar] [CrossRef]
- Wang, Q.; Li, W.; Wu, Y.; Pei, Y.; Xie, P. Application of statistical index and index of entropy methods to landslide susceptibility assessment in Gongliu (Xinjiang, China). Environ. Earth Sci. 2016, 75, 599. [Google Scholar] [CrossRef]
- Razavizadeh, S.; Solaimani, K.; Massironi, M.; Kavian, A. Mapping landslide susceptibility with frequency ratio, statistical index, and weights of evidence models: A case study in northern Iran. Environ. Earth Sci. 2017, 76, 499. [Google Scholar] [CrossRef]
- van Westen, C.J. Application of Geographic Information System to Landslide Hazard Zonation; ITC-Publication No. 15; Geo-Information Science and Earth Observation (ITC): Enschede, The Netherlands, 1993. [Google Scholar]
- Brown, C.E. Applied Multiple Statistics in Geohydrology and Related Sciences; Springer-Verlag: Berlin, Germany, 1998. [Google Scholar]
- Atkinson, P.; Massari, R. Generalised linear modelling of susceptibility for landsliding in the Central Apennines, Italy. Comput. Geosci. 1998, 24, 373–385. [Google Scholar] [CrossRef]
- Lee, S.; Min, K. Statistical analysis of landslide susceptibility at Yongin, Korea. Environ. Geol. 2001, 40, 1095–1113. [Google Scholar] [CrossRef]
- Dai, F.C.; Lee, C.F. Landslide characteristics and slope instability modeling using GIS, Lantau Island, Hong Kong. Geomorphology 2002, 42, 213–228. [Google Scholar] [CrossRef]
- Ohlmacher, C.G.; Davis, C.J. Using multiple regression and GIS technology to predict landslide hazard in northeast Kansas, USA. Eng. Geol. 2003, 69, 331–343. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Lee, S.; Sambath, L. Landslide susceptibility mapping in the Damrei Romel area, Cambodia using frequency ratio and logistic regression models. Environ. Geol. 2006, 50, 847–856. [Google Scholar] [CrossRef]
- Yilmaz, I. Landslide susceptibility mapping using frequency ratio, logistic regression, artificial neural networks and their comparison: A case study from Kat landslides (Tokat–Turkey). Comput. Geosci. 2009, 35, 1125–1138. [Google Scholar] [CrossRef]
- Sujatha, E.R.; Rajamanickam, G.V.; Kumaravel, P. Landslide susceptibility analysis using probabilistic certainty factor approach: A case study on Tevankarai stream watershed, India. J. Earth Syst. Sci. 2012, 121, 1337–1350. [Google Scholar] [CrossRef]
- Devkota, K.C.; Regmi, A.D.; Pourghasemi, H.R.; Yoshida, K.; Pradhan, B.; Ryu, I.C.; Dhital, M.R.; Althuwaynee, O.F. Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in GIS and their comparison at Mugling-Narayanghat road section in Nepal Himalaya. Nat. Hazards 2013, 65, 135–165. [Google Scholar] [CrossRef]
- Nourani, V.; Pradhan, B.; Ghaffari, H.; Sharifi, S.S. Landslide susceptibility mapping at Zonouz Plain, Iran using genetic programming and comparison with frequency ratio, logistic regression, and artificial neural network models. Nat. Hazards 2014, 71, 523–547. [Google Scholar] [CrossRef]
- Sangchini, E.K.; Emami, S.N.; Tahmasebipour, N.; Pourghasemi, H.R.; Naghibi, S.A.; Arami, S.A.; Pradhan, B. Assessment and comparison of combined bivariate and AHP models with logistic regression for landslide susceptibility mapping in the Chaharmahal-e-Bakhtiari Province, Iran. Arab. J. Geosci. 2016, 9, 201. [Google Scholar] [CrossRef]
- Budimir, M.E.A.; Atkinson, I.P.M.; Lewis, I.H.G. A systematic review of landslide probability mapping using logistic regression. Landslides 2015, 12, 419–436. [Google Scholar] [CrossRef]
- Chung, C.J.F.; Fabbri, A.G. The representation of geoscience information for data integration. Nonrenew. Resour. 1993, 2, 122–139. [Google Scholar] [CrossRef]
- Youden, W.J. Index for rating diagnostic tests. Cancer 1950, 3, 32–35. [Google Scholar] [CrossRef]
- Binaghi, E.; Luzi, L.; Madella, P.; Rampini, A. Slope instability zonation: A comparison between certainty factor and fuzzy Dempster-Shafer approaches. Nat. Hazards 1998, 17, 77–97. [Google Scholar] [CrossRef]
- Lan, H.X.; Zhou, C.H.; Wang, L.J.; Zhang, H.Y.; Li, R.H. Landslide hazard spatial analysis and prediction using GIS in the Xiaojiang watershed, Yunnan, China. Eng. Geol. 2004, 76, 109–128. [Google Scholar] [CrossRef]
- Wang, Q.; Li, W.; Chen, W.; Bai, H. GIS-based assessment of landslide susceptibility using certainty factor and index of entropy models for the Qianyang County of Baoji city, China. J. Earth Syst. Sci. 2015, 124, 1399–1415. [Google Scholar] [CrossRef]
- Raja, N.B.; Çiçek, I.; Türkoğlu, N.; Aydin, O.; Kawasaki, A. Landslide susceptibility mapping of the Sera River Basin using logistic regression model. Nat. Hazards 2017, 85, 1323–1346. [Google Scholar] [CrossRef]
- Mai, D.T.; Thanh, N.T. Precipitation extremes over Vietnam. In Proceedings of the 5th International Scientific Conference on the Global Energy and Water Cycle, Orange County, CA, USA, 20–24 June 2005; p. 4. [Google Scholar]
- Long, N.T. Landslide Susceptibility Mapping of the Mountainous Area in A Luoi district, Thua Thien Hue Province, Vietnam. Ph.D. Thesis, Vrije Universiteit Brussel, Brussels, Belgium, 2008. [Google Scholar]
- Văn, T.T.; Tùy, P.K.; Giáp, N.X.; Kế, T.D.; Thái, T.N.; Giang, N.T.; Thọ, H.M.; Tuất, L.T.; San, D.N.; Hùng, L.Q.; et al. Assessment of Geological Hazards in Coastal Central Provinces from Quang Binh to Phu Yen, Present Status, Causes, Forecasts and Proposed Measures to Prevent and Mitigate Consequences (In Vietnamese); Project n° 3451; Research Institute of Geology and Mineral Resources: Hanoi, Vietnam, 2003; 215p. [Google Scholar]
- Vietnam Hydrometeorological Service. Summary Report on Hydrometeological Observation in Period 1976–2003 in Vietnam; Vietnamese Ministry of Environment and Natural Resources: Hanoi, Vietnam, 2003; 375p.
- SAS Institute Inc. SAS Software Version 9.1. 2007. Available online: http://www.sas.com/ (accessed on 11 February 2008).
| Factor | Class | Area (%) | fij/f | Wij | CFij |
|---|---|---|---|---|---|
| Elevation | <250 m | 14.6 | 0.53 | −0.63 | −0.47 |
| 250–500 m | 21.1 | 1.46 | 0.38 | 0.33 | |
| 500–750 m | 48.9 | 0.81 | −0.21 | −0.20 | |
| >750 m | 15.4 | 1.42 | 0.35 | 0.30 | |
| Slope | <5° | 21.6 | 0.10 | −2.30 | −0.90 |
| 5–15° | 19.5 | 0.57 | −0.55 | −0.43 | |
| 15–25° | 23.4 | 1.42 | 0.35 | 0.30 | |
| 25–35° | 21.1 | 1.52 | 0.42 | 0.35 | |
| 35–45° | 11.2 | 1.46 | 0.38 | 0.32 | |
| >45° | 3.3 | 1.55 | 0.44 | 0.37 | |
| Geology | Dai Loc Complex (igneous) | 8.8 | 2.16 | 0.77 | 0.55 |
| Lower A Lin (sedimentary) | 11.6 | 0.97 | −0.03 | −0.03 | |
| Lower A Vuong (metamorphic) | 5.8 | 2.19 | 0.78 | 0.56 | |
| Lower Ben Giang - Que Son (igneous) | 13.9 | 1.00 | 0.00 | 0.00 | |
| Lower Long Dai (metamorphic) | 8.4 | 1.12 | 0.11 | 0.11 | |
| Lower Nui Vu (metamorphic) | 10.5 | 0.47 | −0.76 | −0.54 | |
| Middle A Vuong (metamorphic) | 0.8 | 0 | 0 | −1.00 | |
| Middle Long Dai (metamorphic) | 17.6 | 1.26 | 0.23 | 0.21 | |
| Middle-upper Pleistocene | 2.1 | 0 | 0 | −1.00 | |
| Upper A Lin (sedimentary) | 8.0 | 0.25 | −1.37 | −0.75 | |
| Upper Ben Giang - Que Son (igneous) | 1.3 | 0 | 0 | −1.00 | |
| Upper Long Dai (metamorphic) | 9.3 | 0.52 | −0.67 | −0.49 | |
| Upper Nui Vu (metamorphic) | 1.9 | 0 | 0 | −1.00 | |
| Fault density | <500 m/km2 | 5.1 | 1.20 | 0.17 | 0.16 |
| 500–1000 m/km2 | 60.0 | 0.96 | −0.04 | −0.04 | |
| 1000–1500 m/km2 | 28.0 | 0.74 | −0.30 | −0.26 | |
| >1500 m/km2 | 6.8 | 2.28 | 0.83 | 0.58 | |
| Geomorphology | Alluvium deposits | 6.3 | 0.11 | −2.27 | −0.90 |
| Erosional channels and riverbeds | 10.7 | 0 | 0 | −1.00 | |
| Early Quaternary valley pediment | 22.5 | 0.54 | −0.62 | −0.47 | |
| Wash slope | 5.5 | 0.53 | −0.64 | −0.48 | |
| Erosional-denudational slope | 7.1 | 2.01 | 0.71 | 0.52 | |
| Quick gravity slope (debris flow) | 11.8 | 1.23 | 0.21 | 0.19 | |
| Slow gravity slope (earth flow) | 28.5 | 1.82 | 0.60 | 0.46 | |
| Planation surface | 7.6 | 0.47 | −0.73 | −0.53 | |
| Weathering crust | Quaternary deposit | 2.1 | 0 | 0 | −1.00 |
| Ferrosialite | 20.9 | 0.67 | −0.39 | −0.33 | |
| Mixtures of Silixite | 28.5 | 0.90 | −0.10 | −0.10 | |
| Sialferrite | 35.1 | 1.22 | 0.20 | 0.18 | |
| Sialite | 13.3 | 1.32 | 0.27 | 0.24 | |
| Land use | Agriculture | 4.2 | 0 | 0 | −1.00 |
| Forest | 27.2 | 1.20 | 0.18 | 0.17 | |
| Shrub and bare hill | 67.1 | 1.01 | 0.01 | 0.01 | |
| Built-up area | 1.5 | 0 | 0 | −1.00 | |
| Distance to river | ≤50 m | 8.7 | 0.21 | −1.59 | −0.80 |
| 50–200 m | 22.7 | 0.64 | −0.44 | −0.36 | |
| >200 m | 68.6 | 1.22 | 0.20 | 0.18 | |
| Precipitation | <3100 mm/y | 32.8 | 0.92 | −0.08 | −0.08 |
| 3100–3300 mm/y | 39.0 | 1.23 | 0.20 | 0.19 | |
| >3300 mm/y | 28.1 | 0.78 | −0.25 | −0.23 |
| Parameter | Coefficient | Standard Error | t-Score | p-Value |
|---|---|---|---|---|
| Intercept | −6.88 | 0.366 | −18.8 | <10−4 |
| Elevation | 4.29 × 10−4 | 0.44 × 10−4 | 9.75 | <10−4 |
| Slope | 0.018 | 0.001 | 18.0 | <10−4 |
| Geology | 0.660 | 0.021 | 31.3 | <10−4 |
| Fault density | 7.90 × 10−5 | 3.30 × 10−5 | 2.39 | 0.008 |
| Geomorphology | 0.774 | 0.021 | 37.8 | <10−4 |
| Land use | −0.134 | 0.061 | −2.21 | 0.014 |
| Weathering crust | −0.141 | 0.057 | −2.47 | 0.007 |
| Distance to river | 3.06 × 10−4 | 0.30 × 10−4 | 10.2 | <10−4 |
| Precipitation | −1.87 × 10−3 | 0.03 × 10−3 | −69.3 | <10−4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, N.T.; De Smedt, F. Analysis and Mapping of Rainfall-Induced Landslide Susceptibility in A Luoi District, Thua Thien Hue Province, Vietnam. Water 2019, 11, 51. https://doi.org/10.3390/w11010051
Long NT, De Smedt F. Analysis and Mapping of Rainfall-Induced Landslide Susceptibility in A Luoi District, Thua Thien Hue Province, Vietnam. Water. 2019; 11(1):51. https://doi.org/10.3390/w11010051
Chicago/Turabian StyleLong, Nguyen Thanh, and Florimond De Smedt. 2019. "Analysis and Mapping of Rainfall-Induced Landslide Susceptibility in A Luoi District, Thua Thien Hue Province, Vietnam" Water 11, no. 1: 51. https://doi.org/10.3390/w11010051
APA StyleLong, N. T., & De Smedt, F. (2019). Analysis and Mapping of Rainfall-Induced Landslide Susceptibility in A Luoi District, Thua Thien Hue Province, Vietnam. Water, 11(1), 51. https://doi.org/10.3390/w11010051





