Modelling the Leakage Rate and Reduction Using Minimum Night Flow Analysis in an Intermittent Supply System
Abstract
1. Introduction
2. Materials and Methods
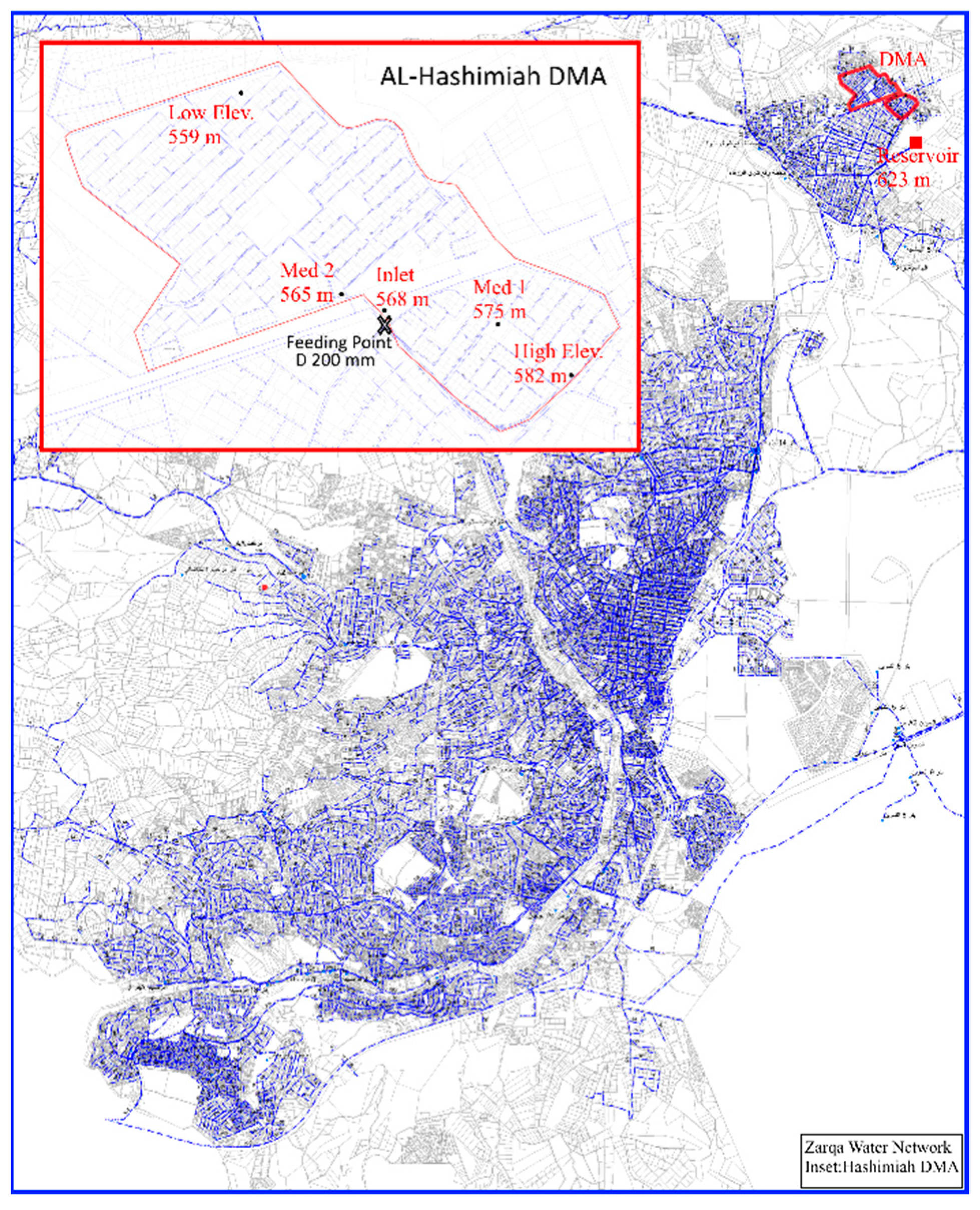
2.1. Description of the Case Study System
2.2. DMA Establishment
2.3. Instruments and Measurements
2.4. Leakage Modelling
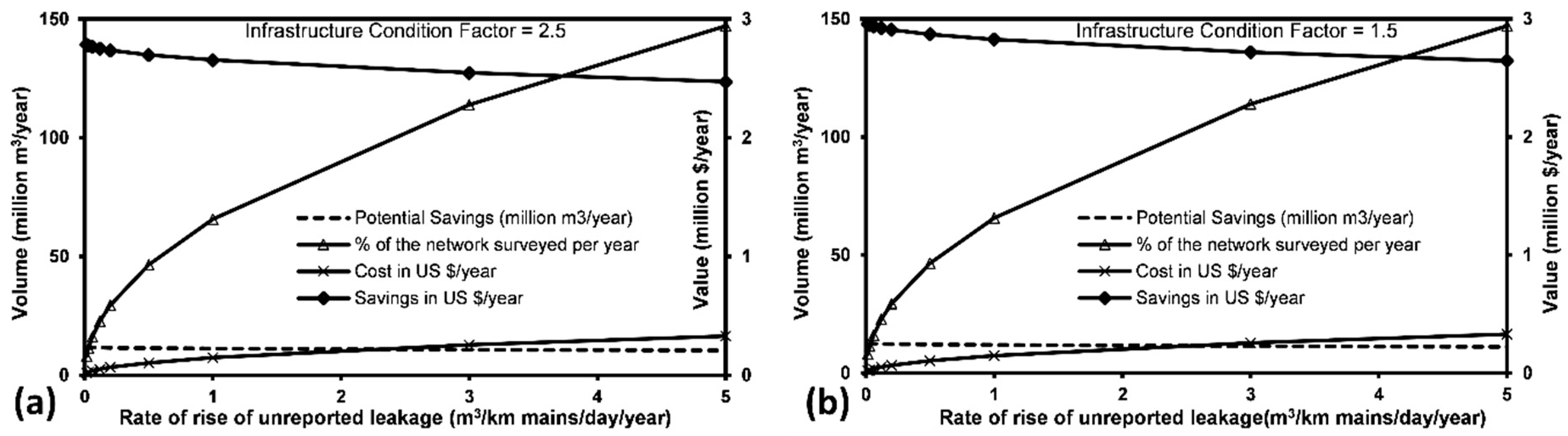
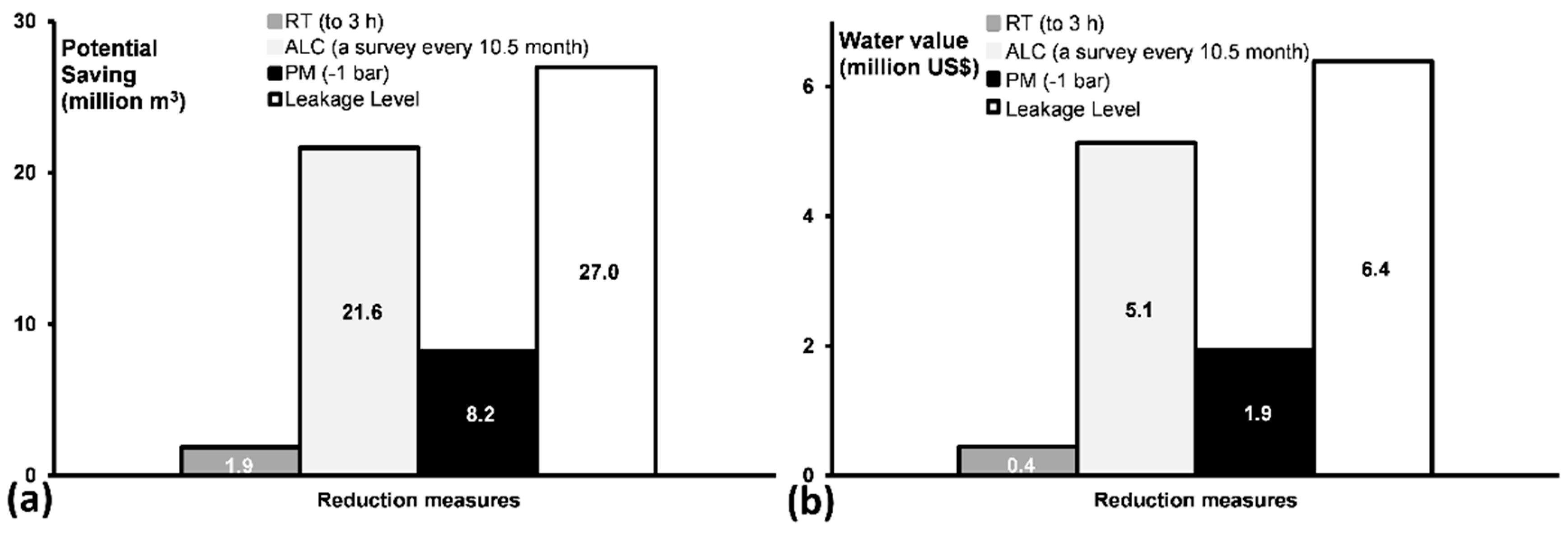
2.5. Feasibility of Leakage Reductions
3. Results and Discussion
4. Conclusions
4.1. Minimum Flow Analysis in Intermittent Supplies
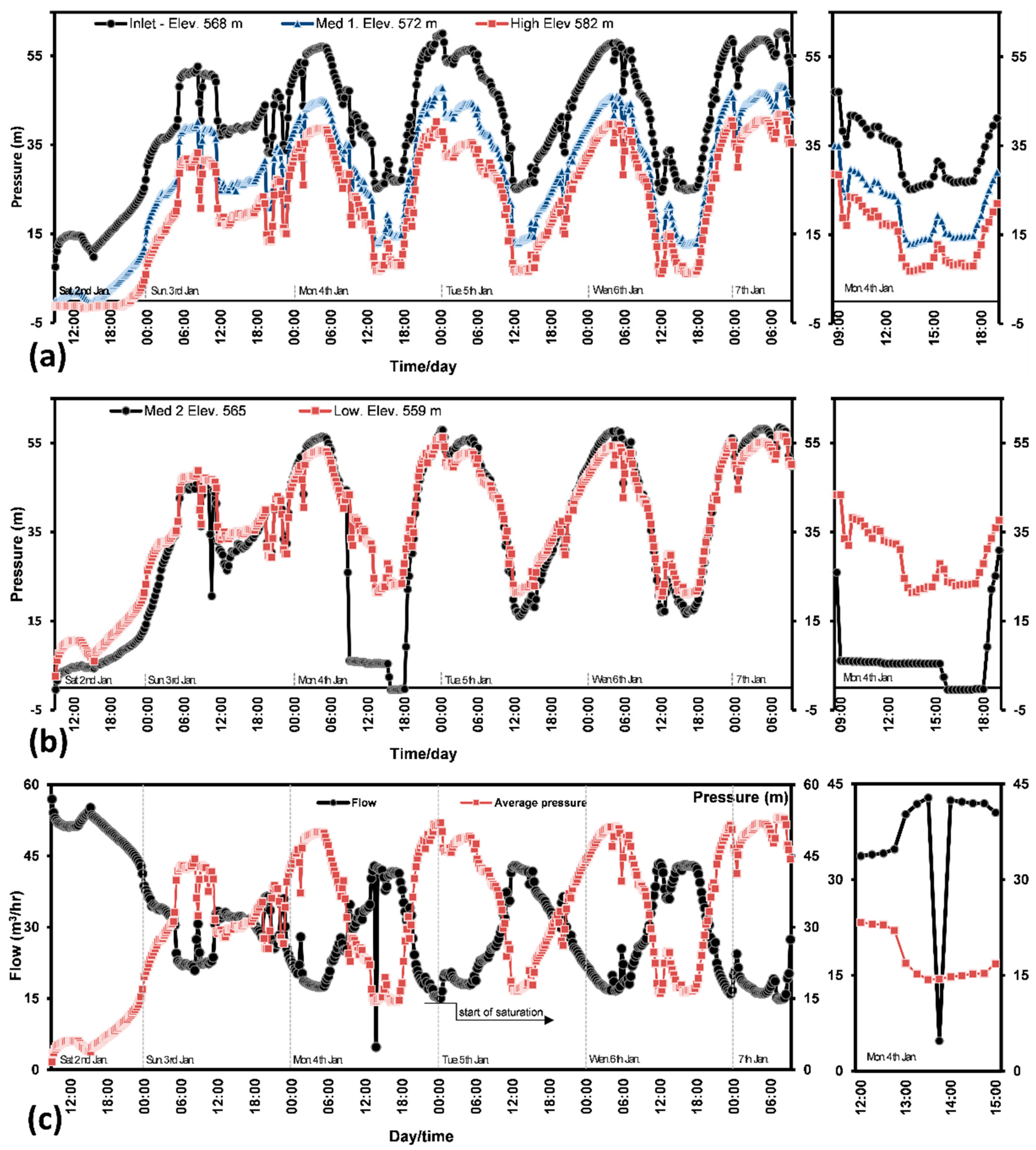
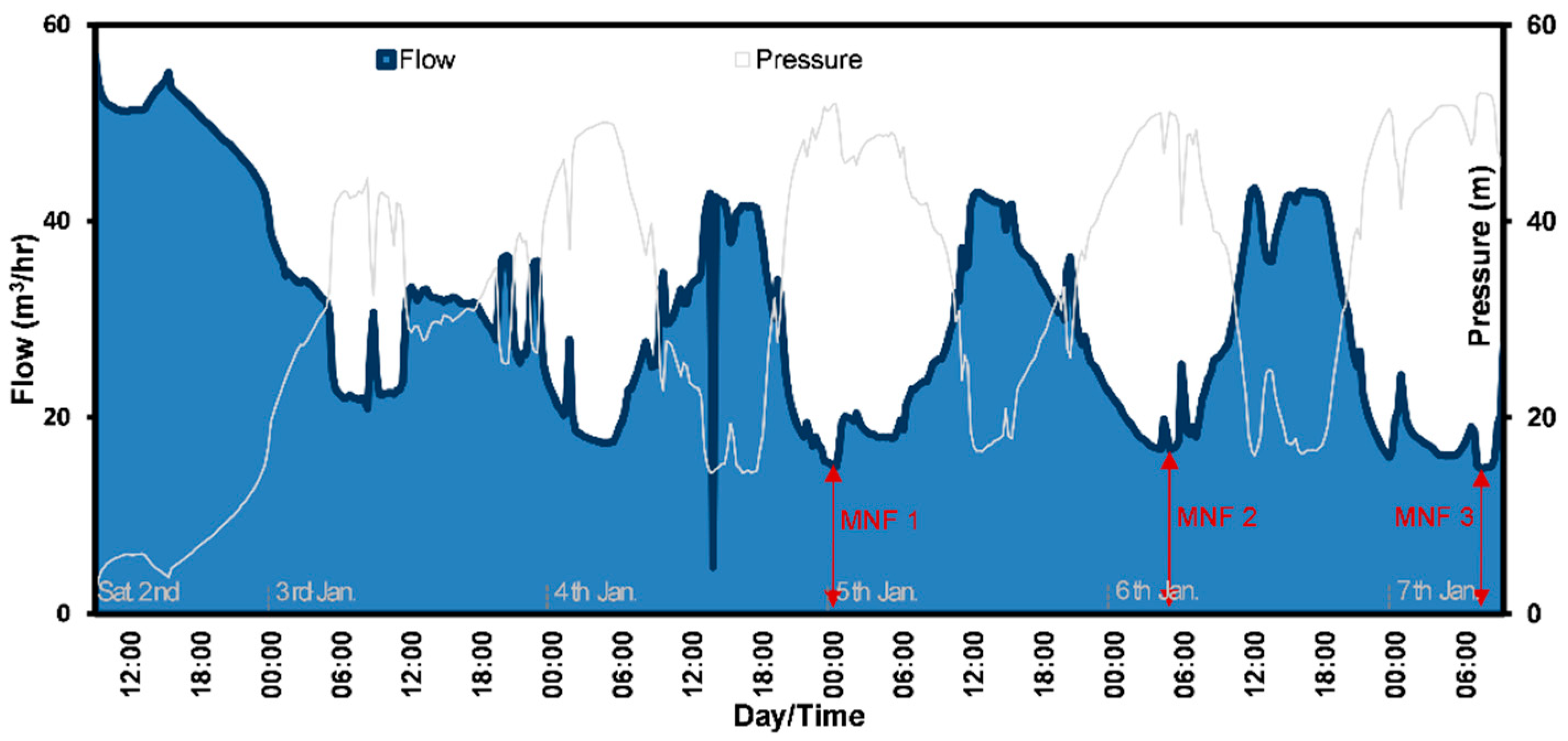
- One-day minimum night flow analysis (MNF) cannot be used to estimate the leakage rate in intermittent supplies, because water keeps flowing during night time to fill customers’ tanks in the network. Therefore, the experimented zone (DMA) should be supplied continuously for several days until the zone is saturated, or the customer ground or elevated tanks in the network are completely full, and the readings start to closely repeat themselves.
- MNF could therefore occur at night or day time, even if part the customer base are active as long as the ground tanks are full and customers do not pump water from the ground to the elevated tanks. In Zarqa, the saturation of the DMA started after 63 h of continuous supply and MNF was occurring between 12:00 a.m. and 7:00 a.m. This challenge requires more careful estimation of the legitimate nighttime consumption that is found to be a sensitive parameter in leakage estimation and modelling.
- Generalising the leakage rate at the time of the MNF for all the time of the day causes overestimating of the daily leakage, because of the usually lower pressures during the day. For this reason, the night day factor in Zarqa is a reduction factor (<24 h/day), being 14 h/day.
- While MNF analysis is reasonably accurate at a DMA scale, upscaling its result for the entire system is uncertain and sensitive. One or several DMAs cannot satisfy the diversity of the operating conditions in the network in terms of pressure, flows, pipe length and the number of connections. Therefore, estimating the leakage of the whole system has to be verified through several methods before it is used for full-system leakage reduction modelling.
4.2. Leakage Reduction Modelling in Intermittent Supplies
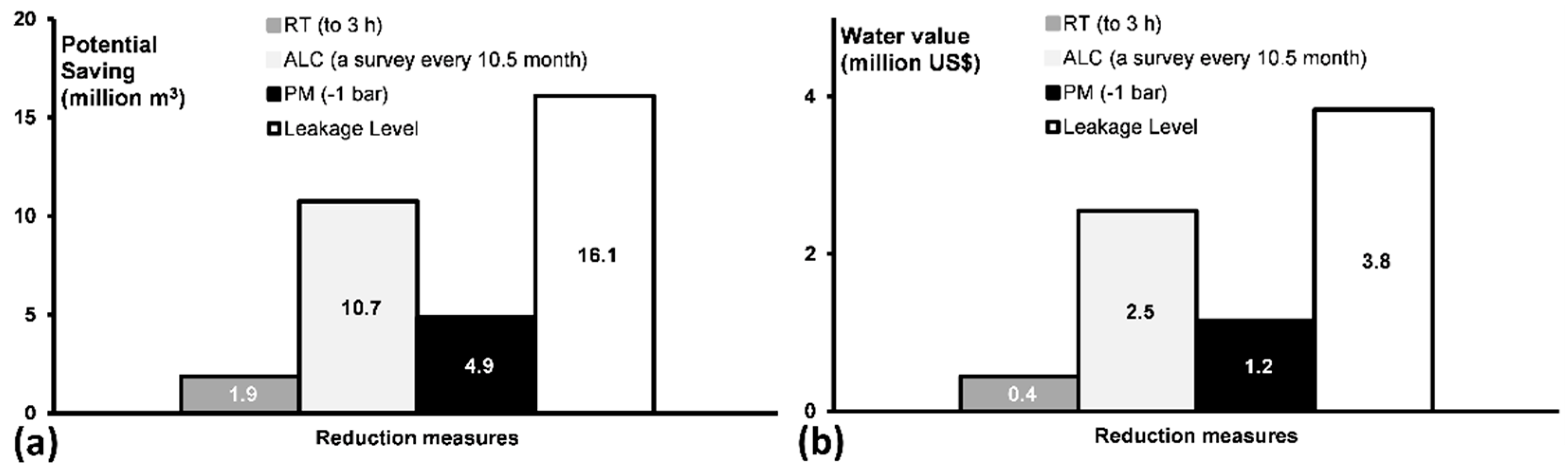
- The leakage component analysis model (BABE) analyses only a small part of the leakage (26% in the Zarqa case) and the remaining part is considered as hidden losses where the recoverable and unavoidable portions are not known. Increasing the Infrastructure Condition Factor is not sufficiently influential in the studied case, and the model may require an adaptation study for the intermittent supply context.
- Analysing the potential water savings of different leakage reduction policies independently and separately is currently possible. However, this approach is likely overestimating the potential savings significantly, due to the inter-dependency of the different policies, leading the potential savings to be more than the volume and cost of the leakage. In all cases, estimating the benefits of the frequent leakage detection survey seems to be over-estimated, and further investigation is required to clarify and confirm this issue.
- The inter-dependency relationship between the pressure management and active leakage control should be investigated too. Pressure reduction limits the failure frequencies and lowers the potential of leakage detection as leaks become harder to detect. Therefore, future leakage reduction modelling would be more reasonable when considering the influence of a specific leakage reduction policy (e.g., pressure management) on the potential of other reduction policies (e.g., ALC).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gong, W.; Suresh, M.A.; Smith, L.; Ostfeld, A.; Stoleru, R.; Rasekh, A.; Banks, M.K. Mobile sensor networks for optimal leak and backflow detection and localization in municipal water networks. Environ. Model. Softw. 2016, 80, 306–321. [Google Scholar] [CrossRef]
- AL-Washali, T.; Sharma, S.; Kennedy, M. Methods of Assessment of Water Losses in Water Supply Systems: A Review. Water Resour. Manag. 2016, 30, 4985–5001. [Google Scholar] [CrossRef]
- Dighade, R.; Kadu, M.; Pande, A. Challenges in water loss management of water distribution systems in developing countries. Int. J. Innov. Res. Sci. Eng. Technol. 2014, 3, 13838–13846. [Google Scholar]
- Meseguer, J.; Mirats-Tur, J.M.; Cembrano, G.; Puig, V.; Quevedo, J.; Pérez, R.; Sanz, G.; Ibarra, D. A decision support system for on-line leakage localization. Environ. Model. Softw. 2014, 60, 331–345. [Google Scholar] [CrossRef]
- Farley, M.; Trow, S. Losses in Water Distribution Networks; IWA Publishing: London, UK, 2003. [Google Scholar]
- AWWA. M36 Water Audits and Loss Control Programs, 4th ed.; American Water Works Association: Denver, CO, USA, 2016. [Google Scholar]
- Thornton, J.; Sturm, R.; Kunkel, G. Water Loss Control; McGraw Hill Professional: New York, NY, USA, 2008; ISBN 978-0071499187. [Google Scholar]
- Fanner, P. Assessing Real Water Losses: A Practical Approach; International Water Association, Water 21: London, UK, 2004; ISSN 15619508. [Google Scholar]
- Morrison, J.; Tooms, S.; Rogers, D. District Metered Areas, Guidance Notes; International Water Association (IWA), Specialist Group on Efficient Operation and Management of Urban Water Distribution Systems: London, UK, 2007. [Google Scholar]
- Lambert, A.; Hirner, W. Losses from Water Supply Systems: A Standard Terminology and Recommended Performance Measures; IWA Publishing: London, UK, 2000. [Google Scholar]
- Puust, R.; Kapelan, Z.; Savic, D.; Koppel, T. A review of methods for leakage management in pipe networks. Urban Water J. 2010, 7, 25–45. [Google Scholar] [CrossRef]
- Liemberger, R.; Farley, M. Developing a nonrevenue water reduction strategy Part 1: Investigating and assessing water losses. In Proceedings of the IWA Specialized Conference: The 4th IWA World Water Congress Marrakech, Marrakech, Morocco, 19–24 September 2004. [Google Scholar]
- Farah, E.; Shahrour, I. Leakage Detection Using Smart Water System: Combination of Water Balance and Automated Minimum Night Flow. Water Resour. Manag. 2017, 31, 4821–4833. [Google Scholar] [CrossRef]
- Latchoomun, L.; King, R.A.; Busawon, K. A new approach to model development of water distribution networks with high leakage and burst rates. Procedia Eng. 2015, 119, 690–699. [Google Scholar] [CrossRef]
- Eugine, M. Predictive Leakage Estimation using the Cumulative Minimum Night Flow Approach. Am. J. Water Resour. 2017, 5, 1–4. [Google Scholar]
- Werner, M.; Maggs, I.; Petkovic, M. Accurate measurements of minimum night flows for water loss analysis. In Proceedings of the 5th Annual WIOA NSW Water Industry Engineers & Operators Conference, Water Loss Management Program NSW, Exhileracing Events Centre, Newcastle, UK, 29–31 March 2011; pp. 31–37. [Google Scholar]
- Alkasseh, J.M.; Adlan, M.N.; Abustan, I.; Aziz, H.A.; Hanif, A.B.M. Applying minimum night flow to estimate water loss using statistical modeling: A case study in Kinta Valley, Malaysia. Water Resour. Manag. 2013, 27, 1439–1455. [Google Scholar] [CrossRef]
- Fantozzi, M.; Lambert, A. Legitimate night use component of minimum night flows initiative. In Proceedings of the IWA Water Loss Conference, São Paulo, Brazil, 6–9 June 2010. [Google Scholar]
- Hamilton, S.; McKenzie, R. Water Management and Water Loss; IWA Publishing: London, UK, 2014. [Google Scholar]
- Lambert, A. What do we know about pressure-leakage relationships in distribution systems. In Proceedings of the IWA Conference in Systems Approach to Leakage Control and Water Distribution System Management, Brno, Czech Republic, 16–18 May 2001. [Google Scholar]
- Thornton, J.; Lambert, A. Progress in practical prediction of pressure: Leakage, pressure: Burst frequency and pressure: Consumption relationships. In Proceedings of the IWA Specialised Conference ‘Leakage 2005’, Halifax, NS, Canada, 12–14 September 2005; pp. 12–14. [Google Scholar]
- Van Zyl, J.; Lambert, A.; Collins, R. Realistic Modeling of Leakage and Intrusion Flows through Leak Openings in Pipes. J. Hydraul. Eng. 2017, 143, 04017030. [Google Scholar] [CrossRef]
- Alonso, J.M.; Alvarruiz, F.; Guerrero, D.; Hernández, V.; Ruiz, P.A.; Vidal, A.M.; Martínez, F.; Vercher, J.; Ulanicki, B. Parallel computing in water network analysis and leakage minimization. J. Water Resour. Plan. Manag. 2000, 126, 251–260. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Sage, P.; Turtle, D. Pressure-dependent leak detection model and its application to a district water system. J. Water Resour. Plan. Manag. 2009, 136, 116–128. [Google Scholar] [CrossRef]
- Jowitt, P.W.; Xu, C. Optimal valve control in water-distribution networks. J. Water Resour. Plan. Manag. 1990, 116, 455–472. [Google Scholar] [CrossRef]
- Mazzolani, G.; Berardi, L.; Laucelli, D.; Martino, R.; Simone, A.; Giustolisi, O. A methodology to estimate leakages in water distribution networks based on inlet flow data analysis. Procedia Eng. 2016, 162, 411–418. [Google Scholar] [CrossRef]
- Mazzolani, G.; Berardi, L.; Laucelli, D.; Simone, A.; Martino, R.; Giustolisi, O. Estimating Leakages in Water Distribution Networks Based Only on Inlet Flow Data. J. Water Resour. Plan. Manag. 2017, 143, 04017014. [Google Scholar] [CrossRef]
- Lambert, A.; Lalonde, A. Using practical predictions of economic intervention frequency to calculate short-run economic leakage level, with or without pressure management. In Proceedings of the IWA Specialised Conference ‘Leakage 2005’, Halifax, NS, Canada, 12–14 September 2005; pp. 310–321. [Google Scholar]
- Lambert, A.; Fantozzi, M. Recent advances in calculating economic intervention frequency for active leakage control, and implications for calculation of economic leakage levels. Water Sci. Technol. Water Supply 2005, 5, 263–271. [Google Scholar] [CrossRef]
- Lambert, A.; Charalambous, B.; Fantozzi, M.; Kovac, J.; Rizzo, A.; St John, S.G. 14 years’ experience of using IWA best practice water balance and water loss performance indicators in Europe. In Proceedings of the IWA Specialized Conference: Water Loss 2014, Vienna, Austria, 31 March–2 April 2014. [Google Scholar]
- Lambert, A.; Brown, T.G.; Takizawa, M.; Weimer, D. A review of performance indicators for real losses from water supply systems. J. Water Supply Res. Technol. AQUA 1999, 48, 227–237. [Google Scholar] [CrossRef]
- Amoatey, P.; Minke, R.; Steinmetz, H. Leakage estimation in developing country water networks based on water balance, minimum night flow and component analysis methods. Water Pract. Technol. 2018, 13, 96–105. [Google Scholar] [CrossRef]
- AL-Washali, T.; Sharma, S.; Kennedy, M.; AL-Nozaily, F.; Haidera, M. Monitoring the Non-Revenue Water Performance in Intermittent Supplies. Water Resour. Manag 2019. in preparation. [Google Scholar]
- Di Nardo, A.; Di Natale, M.; Santonastaso, G.F.; Venticinque, S. An automated tool for smart water network partitioning. Water Resour. Manag. 2013, 27, 4493–4508. [Google Scholar] [CrossRef]
- Galdiero, E.; De Paola, F.; Fontana, N.; Giugni, M.; Savic, D. Decision support system for the optimal design of district metered areas. J. Hydroinform. 2015, 18, 49–61. [Google Scholar] [CrossRef]
- Kesavan, H.; Chandrashekar, M. Graph-theoretical models for pipe network analysis. J. Hydraul. Div. 1972, 98, 345–364. [Google Scholar]
- Deuerlein, J.W. Decomposition model of a general water supply network graph. J. Hydraul. Eng. 2008, 134, 822–832. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Di Mauro, A. Water Supply Network District Metering: Theory and Case Study; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Herrera, M.; Izquierdo, J.; Pérez-García, R.; Ayala-Cabrera, D. Water supply clusters by multi-agent based approach. In Water Distribution Systems Analysis 2010, Proceedings of 12th Annual Conference on Water Distribution Systems Analysis, Tucson, AZ, USA, 12–15 September 2010; pp. 861–869.
- Perelman, L.; Ostfeld, A. Topological clustering for water distribution systems analysis. Environ. Model. Softw. 2011, 26, 969–972. [Google Scholar] [CrossRef]
- Creaco, E.; Pezzinga, G. Multiobjective optimization of pipe replacements and control valve installations for leakage attenuation in water distribution networks. J. Water Resour. Plan. Manag. 2014, 141, 04014059. [Google Scholar] [CrossRef]
- De Paola, F.; Fontana, N.; Galdiero, E.; Giugni, M.; Savic, D.; Sorgenti degli Uberti, G. Automatic multi-objective sectorization of a water distribution network. Procedia Eng. 2014, 89, 1200–1207. [Google Scholar] [CrossRef]
- Fantozzi, M.; Lambert, A. Residential night consumption–assessment, choice of scaling units and calculation of variability. In Proceedings of the IWA Water Loss Conference, Manila, Philippines, 26–29 February 2012; pp. 26–29. [Google Scholar]
- May, J. Pressure Dependent Leakage; World Water and Environmental Engineering, Water Environment Federation: Washington, DC, USA, 1994. [Google Scholar]
- Lambert, A. Pressure management/leakage relationships: Theory, concepts and practical applications. In Proceedings of the IQPC Seminar, London, UK, April 1997. [Google Scholar]
- McKenzie, R.S. Water Demand Management Cookbook; Rand Water: Johannesburg, South Africa, 2003. [Google Scholar]
- Lambert, A.; Fantozzi, M.; Shepherd, M. FAVAD Pressure & Leakage:How Does Pressure Influence N1? In Proceedings of the IWA Water Efficient 2017 Conference, Bath, UK, 18–20 July 2017. [Google Scholar]
- Van Zyl, J.; Cassa, A. Modeling elastically deforming leaks in water distribution pipes. J. Hydraul. Eng. 2014, 140, 182–189. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Gisonni, C.; Iervolino, M. A genetic algorithm for demand pattern and leakage estimation in a water distribution network. J. Water Supply Res. Technol. Aqua. 2015, 64, 35–46. [Google Scholar] [CrossRef]
- Lambert, A. Fast Track NDF Calculations Using the Correction Factor Method. Available online: http://www.leakssuite.com/night-day-factor-update/ (accessed on 9 December 2018).
- Kanakoudis, V.; Tsitsifli, S.; Papadopoulou, A. Integrating the carbon and water footprints’ costs in the water framework directive 2000/60/EC full water cost recovery concept: Basic principles towards their reliable calculation and socially just allocation. Water 2012, 4, 45–62. [Google Scholar] [CrossRef]
- Ashton, C.; Hope, V. Environmental valuation and the economic level of leakage. Urban Water 2001, 3, 261–270. [Google Scholar] [CrossRef]
- Pearson, D.; Trow, S. Calculating economic levels of leakage. In Proceedings of the IWA Water Loss 2005 Conference, Halifax, NS, Canada, 12–14 September 2005. [Google Scholar]
- Lambert, A. Accounting for losses: The bursts and background concept. Water Environ. J. 1994, 8, 205–214. [Google Scholar] [CrossRef]
- Sturm, R.; Gasner, K.; Wilson, T.; Preston, S.; Dickinson, M.A. Real Loss Component Analysis: A Tool for Economic Water Loss Control; Water Research Foundation: Denver, CO, USA, 2014. [Google Scholar]
- Aboelnga, H.; Saidan, M.; Al-Weshah, R.; Sturm, M.; Ribbe, L.; Frechen, F.-B. Component analysis for optimal leakage management in Madaba, Jordan. J. Water Supply Res. Technol.-Aqua 2018, 67, 384–396. [Google Scholar] [CrossRef]
- Fanner, P.; Thornton, J. The importance of real loss component analysis for determining the correct intervention strategy. In Proceedings of the IWA Water Loss 2005 Conference, Halifax, NS, Canada, 12–14 September 2005. [Google Scholar]
- Fanner, P.; Lambert, A. Calculating SRELL with pressure management, active leakage control and leak run-time options, with confidence limits. In Proceedings of the 5th IWA Water Loss Reduction Specialist Conference, Cape Town, South Africa, 26–30 April 2009; pp. 373–380. [Google Scholar]


| Date | MNF | MNF Time | LNC | LNC Duration | NNL | NDF | Daily Leakage | Leakage Volume | Leakage Level |
|---|---|---|---|---|---|---|---|---|---|
| m3/h | a.m. | m3/h | h | m3/h | h/day | m3/day | m3 | % SIV | |
| 5 January | 15.0 | 12:15 | 1.88 | 2.0 | 13.1 | 14.2 | 185.8 | 932.7 | 25.5% |
| 2.51 | 1.5 | 12.5 | 14.2 | 176.9 | 888.1 | 24.3% | |||
| 6 January. | 16.4 | 4:45 | 1.88 | 2.0 | 14.5 | 14.2 | 205.0 | 1029.4 | 28.2% |
| 2.51 | 1.5 | 13.9 | 14.2 | 196.2 | 984.8 | 26.9% | |||
| 7 January. | 14.8 | 7:15 | 1.88 | 2.0 | 13.0 | 14.2 | 183.5 | 921.3 | 25.2% |
| 2.51 | 1.5 | 12.3 | 14.2 | 174.6 | 876.7 | 24.0% | |||
| Average | 15.4 | - | 1.88 | 2.0 | 13.5 | 14.2 | 191.4 | 961.2 | 26.3% |
| 2.51 | 1.5 | 12.9 | 14.2 | 182.6 | 916.6 | 25.1% | |||
| Average 5 & 7 January | 14.9 | - | 1.88 | 2.0 | 13.0 | 14.2 | 184.6 | 927.0 | 25.4% |
| 2.51 | 1.5 | 12.4 | 14.2 | 175.8 | 882.4 | 24.1% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
AL-Washali, T.; Sharma, S.; AL-Nozaily, F.; Haidera, M.; Kennedy, M. Modelling the Leakage Rate and Reduction Using Minimum Night Flow Analysis in an Intermittent Supply System. Water 2019, 11, 48. https://doi.org/10.3390/w11010048
AL-Washali T, Sharma S, AL-Nozaily F, Haidera M, Kennedy M. Modelling the Leakage Rate and Reduction Using Minimum Night Flow Analysis in an Intermittent Supply System. Water. 2019; 11(1):48. https://doi.org/10.3390/w11010048
Chicago/Turabian StyleAL-Washali, Taha, Saroj Sharma, Fadhl AL-Nozaily, Mansour Haidera, and Maria Kennedy. 2019. "Modelling the Leakage Rate and Reduction Using Minimum Night Flow Analysis in an Intermittent Supply System" Water 11, no. 1: 48. https://doi.org/10.3390/w11010048
APA StyleAL-Washali, T., Sharma, S., AL-Nozaily, F., Haidera, M., & Kennedy, M. (2019). Modelling the Leakage Rate and Reduction Using Minimum Night Flow Analysis in an Intermittent Supply System. Water, 11(1), 48. https://doi.org/10.3390/w11010048




