Numerical Simulation of Hydraulic Jumps. Part 1: Experimental Data for Modelling Performance Assessment
Abstract
1. Introduction
2. The Hydraulic Jump Case Study
2.1. General Remarks
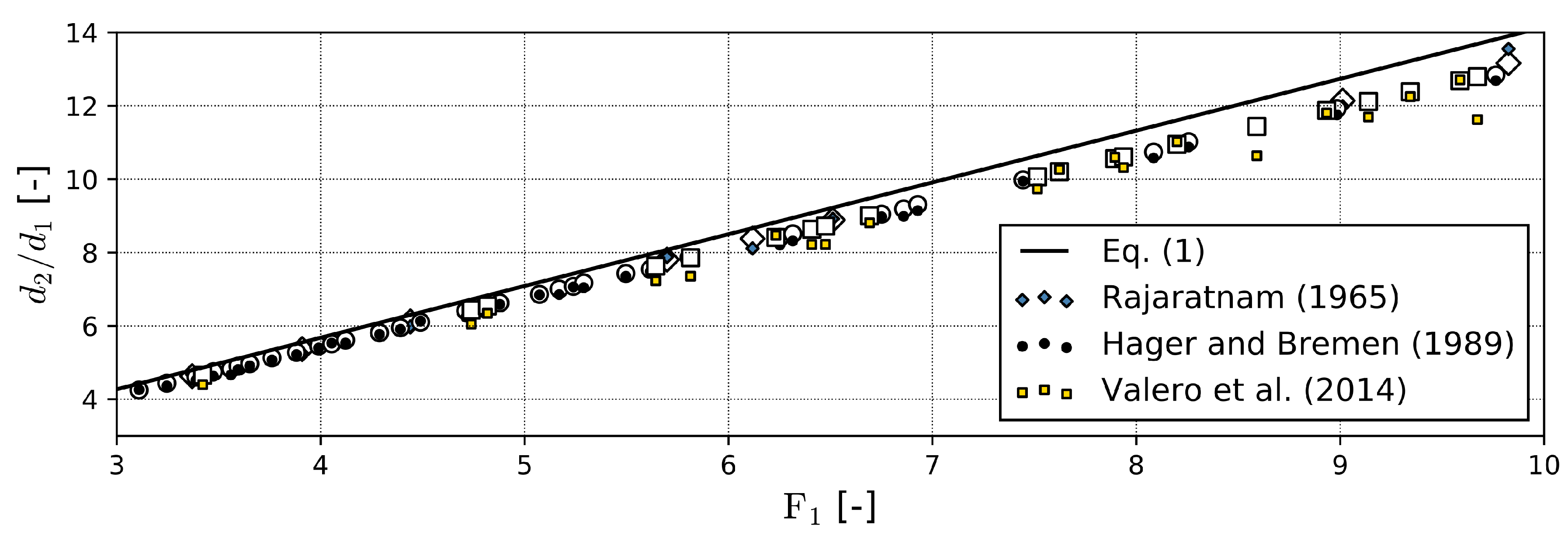
2.2. Inflow Froude Number and Hydraulic Jump Typology
2.3. Hydraulic Jump Flow Structure and Related Experimental Studies
- Wall jet velocity decay: the high-speed inlet flow impacts the slower moving water body and the shearing reduces the maximum velocity through the hydraulic jump length, likewise a turbulent wall jet decay. The shear layer also expands into the roller region. The analogy between hydraulic jumps and turbulent wall jets was first conducted by Rajaratnam [14]. This parameter is highly relevant as it holds the biggest part of the kinetic energy which, during the decay, is transformed into pressure and potential energy (depth). Experimental data can be found in Wang and Chanson [51], Chanson [56], Liu et al. [57], Chanson and Brattberg [16], Wu and Rajaratnam [58], Hager [2] and Ohtsu et al. [59].
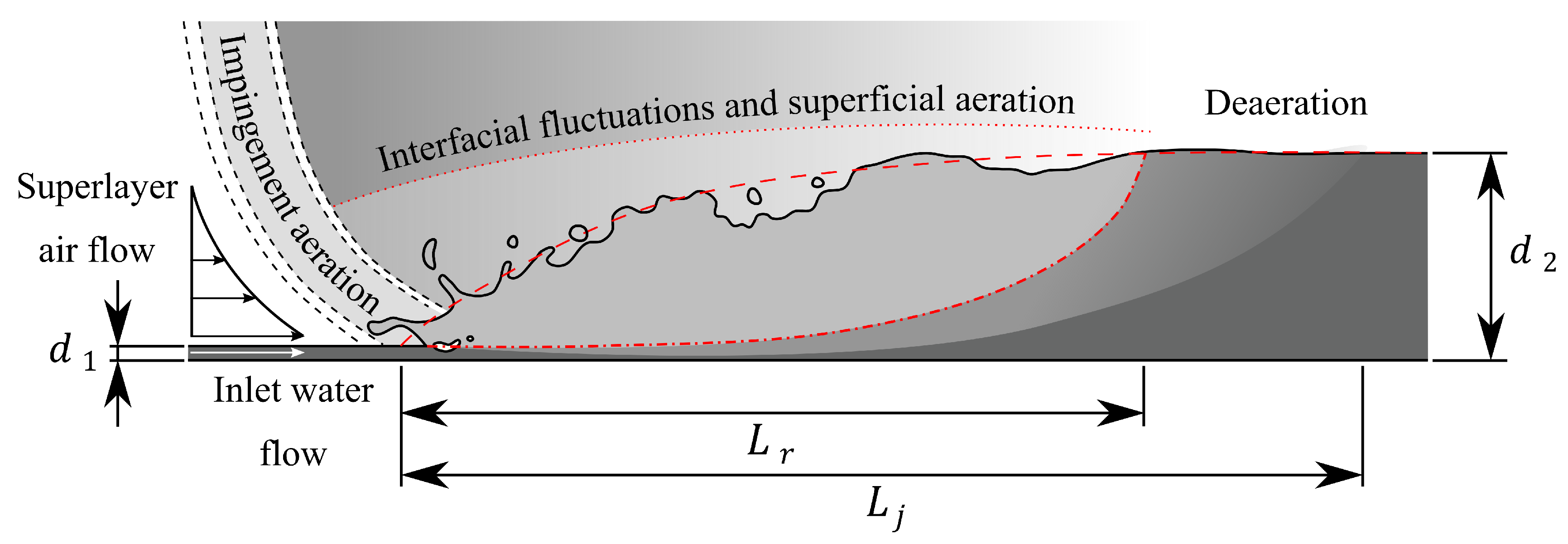
- Roller length: marked in Figure 4 as , it is one of the most distinctive features of a hydraulic jump. Some of the inflow uplifts to the free surface, reaching a stagnation point and reversing, hence falling back again to the toe, where it impacts with the inflow jet. As the stagnation point moves continuously, its visual estimation is affected from a certain uncertainty in a physical model. Experimental data can be found in Murzyn et al. [60]. Wang and Chanson [52], Carollo et al. [36] and Hager [2] presented a nearly parabolic experimental relationship.
- Hydraulic jump length: marked in Figure 4 as . Different methods have been discussed concerning its identification as, for instance: a horizontal free surface can be observed, a hydrostatic pressure distribution is established or where the hydraulic jump is fully deaerated. However, it is also difficult to estimate as the free surface is wavy downstream and tends smoothly to horizontal, which implies a large degree of uncertainty. Pressure distribution is not commonly measured and deaeration may strongly depend on the modelling scale. Bayon et al. [61] argued that the turbulence produced in the toe of the hydraulic jump tended at the end of the hydraulic jump to the values commonly observed in open channel flows, but, for an experimental study, this is even more rare to measure. Given the difficulty of all these methods, visual determination is oftentimes the experimentalist preferred choice.
- Mean free surface profile: it necessarily matches the supercritical flow depth at the toe while it asymptotically tends to the downstream water depth at the end of the hydraulic jump. With an abrupt increase at the toe, it presents a concave curve during the hydraulic jump extension for Froude numbers over the undular jump limit (Table 1). In addition to the aforementioned studies, relations for this parameter were also suggested by Wang [50], Bakhmeteff and Matzke [12] and, analytically, by Valiani [55]. For undular jumps, experimental data can be found in Lennon and Hill [62] and analytical considerations were proposed by Bose et al. [63].
- Mean velocities: the high-speed jet entering the hydraulic jump splits, partly reversing and partly reducing its velocity, thus matching the downstream open channel flow velocity profile. This yields a complex velocity distribution zero-value-crossing at the roller region with an important negative velocity reaching a magnitude of up to 0.4 to 0.6 of the inlet velocity [3,56,64]. Recently, Wang and Chanson [51] suggested that this magnitude has an inverse relation with the Froude number. Empirical velocity distributions were proposed by Chanson and Carvalho [3] and Hager [2]. Literature is rich in experimental data too; see Wang and Chanson [51], Wang et al. [65], among others. Lin et al. [66] studied, separately, the velocity of the water and air phases by using Particle Image Velocimetry (PIV) and Bubble Image Velocimetry (BIV), alternatively. For undular jumps, experimental data can be found in Lennon and Hill [62].
- Aeration (impingement and interfacial): large quantities of air are entrained inside the hydraulic jump via the toe impingement. These large air volumes are subject to break-up and coalescence depending on the surrounding turbulence quantities. A second air entrainment mechanism is related to the interfacial fluctuations occurring in the upper region of the roller at higher Froude numbers. Large quantities of spray and splashing can be visually observed and have a clear footprint in the air concentration profiles. For both mechanisms, different air concentration profiles can be fitted, hence revealing different air entrainment mechanisms [67,68]. Far downstream, the flow deaerates as the velocity decreases and the transport capacity is reduced. The air concentration is, probably, one of the most case sensitive mean flow variables as it is a result of the combination of Froude, Reynolds and Weber—or equivalently, Morton—numbers [69]. Another reason for the case-sensitivity of the air entrained quantities should be related to the level of development of the inflow boundary layer, as reported by Takahashi and Ohtsu [70]. Takahashi and Ohtsu [70] noted that the advective diffusion region showed larger aeration, with greater development of the inlet boundary layer, while the (upper) breaking region was nearly insensitive to this variable. Ervine [71] also discussed on the relevance of the inlet flow free surface perturbations on the total air entrained. Moreover, the interaction between air bubbles diffusion and momentum transfer is not completely understood [68]. Air transport in the streamwise direction is mainly due to advection, whereas transport in the spanwise and normalwise direction is necessarily driven by turbulent diffusion. In the vertical direction, buoyant forces can also play an important role, especially at the end of the hydraulic jump where lower velocities occur. Experimental data on air concentrations and different semi-empirical relations can be found in Wang and Chanson [51], Takahashi and Ohtsu [70], Gualtieri and Chanson [68], Murzyn et al. [67], Chanson and Brattberg [16], among others.
- Inlet boundary layers (water and air): the supercritical flow impacting the hydraulic jump develops from farther upstream as long as its extension allows. Two boundary layers take place, the water boundary layer that can affect the hydraulic jump characteristics [44,70]—and thus it is common to distinguish between partially developed and fully developed inlet flows—and the interfacial air layer flow [72], which could affect the hydraulic jump air entrained quantities according to Ervine [71]. For the supercritical water boundary layer development, several methods exist, such as Castro-Orgaz and Hager [73] and Castro-Orgaz [74] based on spillway prototype scale velocity profiles. For the interfacial air flow, the only data-set was collected by Valero and Bung [72], which also discussed on the occurring free surface instabilities in supercritical flows that were suggested by Ervine [71] to affect the entrained quantities. A general framework for the computation of the free surface perturbations can be found in Valero and Bung [75]. Recently, Bertola et al. [76] showed that inlet disturbances considerably affect the air entrainment rates for planar plunging jets.
- Velocity fluctuations: given the turbulent nature of hydraulic jumps, instantaneous velocities oscillate around the mean value. Velocity fluctuations were first reported by Rouse et al. [13] using an air flow channel. Long et al. [77] studied velocity fluctuations in submerged hydraulic jumps for Froude numbers up to 8.0, highlighting the three-dimensional nature of the hydraulic jump; and Liu et al. [57] presented turbulence measurements for low Froude numbers, including turbulence spectra. Turbulence intensity has also been approximated using the width of the cross-correlation function between the signals of the two tips of phase detection probes; see Chanson and Toombes [78] for further description and limitations and study of Murzyn and Chanson [49] for an application to hydraulic jumps. For undular jumps, experimental data were collected by Lennon and Hill [62]. Velocity fluctuations are of utmost interest to ensure the stability of downstream environment.
- Interfacial oscillations: the hydraulic jump free surface shows a wide range of turbulent motions. These oscillations play an important role in the study of the total air entrained in the hydraulic jump, as discussed above. Recently, some experimental studies have found that the maximum oscillation occurs close to the toe location and that the intensity of these oscillations increases with the Froude number. Experimental data can be found in Wang and Chanson [51], Chachereau and Chanson [79], Murzyn and Chanson [80].
- Toe oscillations: the roller flow backwards periodically as a consequence of all the hydrodynamic processes that occur inside the hydraulic jump. The Strouhal number (dimensionless frequency based on the toe frequency, inflow depth and mean velocity) is oftentimes used to describe this phenomenon. Toe oscillations have been reported by Zhang et al. [64], Chachereau and Chanson [79], Chanson and Gualtieri [69], Gualtieri and Chanson [68], Mossa and Tolve [81], and Long et al. [82].
- Large vortices advection: large vortices are created in the shear region between the inlet high-speed jet and the roller (vortex shedding). These are advected downstream with a velocity around 0.4 times the inlet velocity. It has not been noticed a clear effect of the Reynolds number. Experimental data can be found in Chanson [56] and Wang [50].
- Pressure fluctuations: the high-speed inlet jet has an impact against the slower water body abruptly slowing down while transforming some of the kinetic energy into pressure, which is later converted into potential energy (in the form of increasing depth). Considerable turbulent pressure fluctuations occur inside the hydraulic jump, thereby compromising the structural stability. Fiorotto and Rinaldo [83] discussed on the spatial structure and magnitude of these pressure oscillations at the channel bed level. Abdul Khader and Elango [84], additionally, also provided insight on the pressures spectra. Hydraulic jump related high pressure fluctuations also have a complex impact on the hyporheic flows occurring in river flows [4,5]. Special care must be taken to properly understand some recent experimental data reporting results on total pressure, which accounts both for the pressure and the velocity head and needs to be corrected with simultaneous velocity estimations and air concentrations to extract the real pressure head. Further description on this technique applied to hydraulic jumps can be found in Wang et al. [65,85] and Wang [50].
- Hydraulic jump vorticity: it is produced at the toe of the hydraulic jump. The inlet flow is abruptly subject to large shearing quantities after impinging the roller flow. The shearing reduces as the flow advances streamwise and the turbulence produced in the toe is slowly dissipated. Hornung et al. [86] analytically studied the mean vorticity downstream of a hydraulic jump and its relation with the Froude number.
- Inner turbulent structures: turbulent length and timescales have been measured using arrays of conductivity probes. Several synchronized sensors can be placed inside the flow and correlation of two signals allow a certain physical insight. Integration of the correlation functions (across time or spatial lag) leads to the estimation of the integral turbulent scales (temporary and spatial scales, respectively). These turbulent scales can be understood as an average measure of the turbulent structures taking place inside the hydraulic jump. A complete data bench of experimental data can be found in Wang and Murzyn [17].
- Bubble characteristics: bubble frequencies, chord lengths and times and bubble clustering are the result of an interaction among turbulent processes. Its determination may be one of the most challenging—if not the most—for a numerical model. These variables have been, however, reported in some experimental studies (e.g., [67,68,87,88]).
3. Adequacy of the Hydraulic Jump as a Benchmark for Numerical Modelling
- Deep understanding of the phenomenon, as presented in Section 2.3.
- Large hydraulic tradition, which makes most of the community familiar with this type of flow.
- It represents an extreme case for turbulence, aeration and flow recirculation, which ensures that numerical models representing properly a CHJ are likely to be useful for other environmental applications.
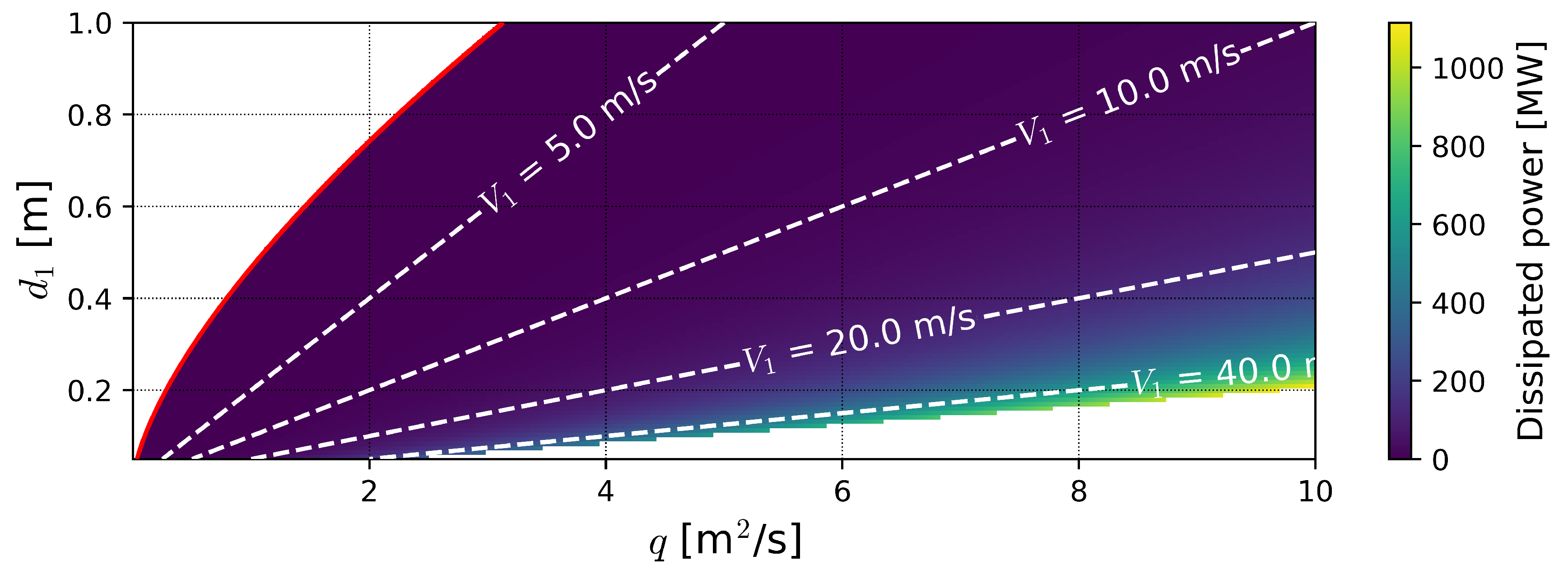
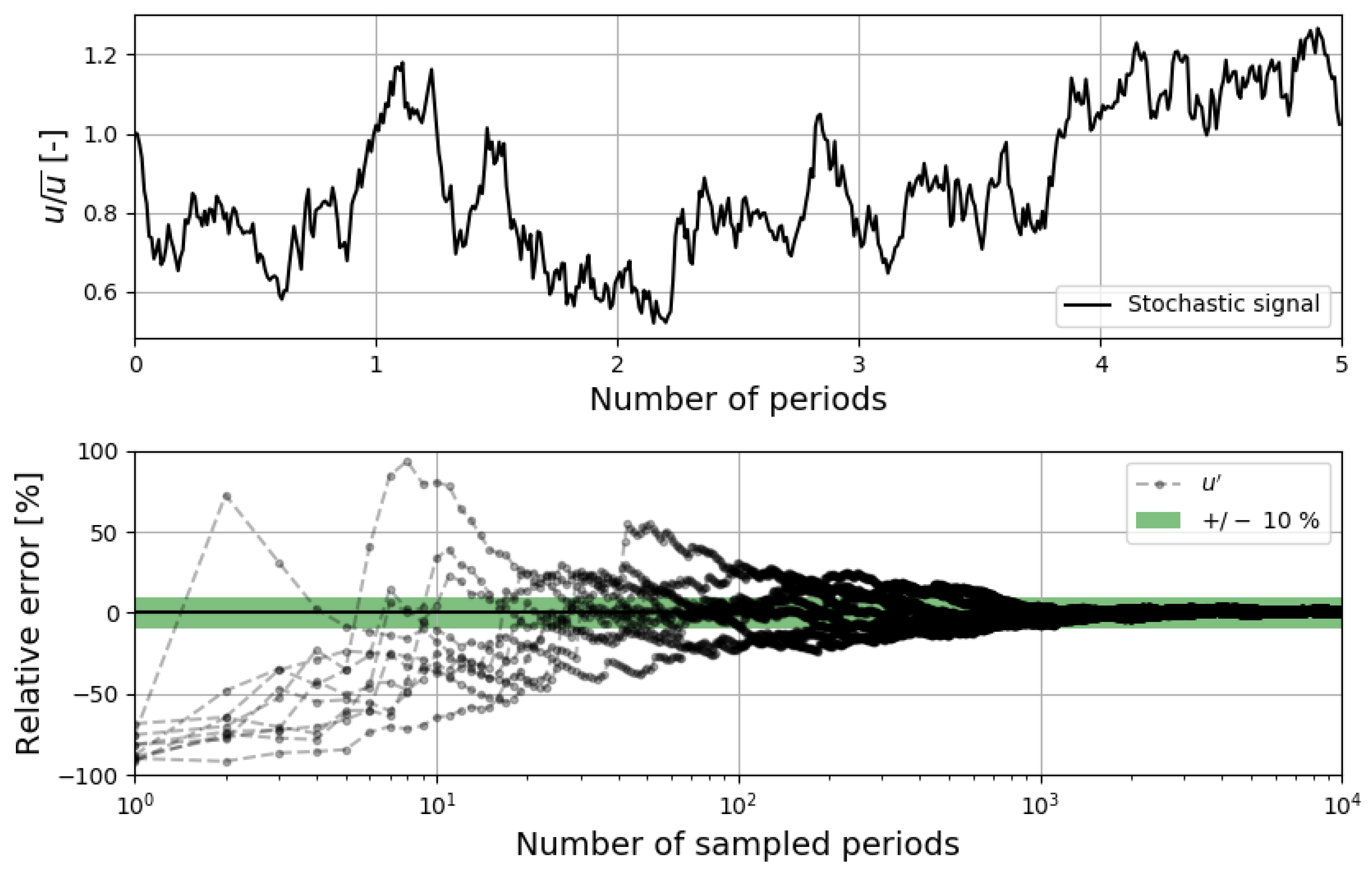
4. Discussion on Experimental Uncertainties
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rajaratnam, N. Hydraulic Jumps. Adv. Hydrosci. 1967, 4, 197–280. [Google Scholar] [CrossRef]
- Hager, W.H. Energy Dissipators and Hydraulic Jump; Water Science and Technology Library; Springer Science & Business Media: Dordrecht, The Netherlands, 1992; Volume 8, ISBN 978-90-481-4106-7. [Google Scholar]
- Chanson, H.; Carvalho, R. Hydraulic jumps and stilling basins. In Energy Dissipation in Hydraulic Structures; Chanson, H., Ed.; CRC Press: Leiden, The Netherlands, 2015; pp. 65–104. ISBN 978-1-138-02755-8. [Google Scholar]
- Endreny, T.; Lautz, L.; Siegel, D.I. Hyporheic flow path response to hydraulic jumps at river steps: Flume and hydrodynamic models. Water Resour. Res. 2011, 47, 2517. [Google Scholar] [CrossRef]
- Endreny, T.; Lautz, L.; Siegel, D.I. Hyporheic flow path response to hydraulic jumps at river steps: Hydrostatic model simulations. Water Resour. Res. 2011, 47, 2518. [Google Scholar] [CrossRef]
- Chanson, H. Energy Dissipation in Hydraulic Structures; CRC Press: Leiden, The Netherlands, 2015; ISBN 978-1-138-02755-8. [Google Scholar]
- Bidone, G. Expériences sur la propagation des remous. Memorie della Reale Accademia de/le Scienze di Torino 1820, 30, 195–292. [Google Scholar]
- Mossa, M.; Petrillo, A. A brief history of the jump of Bidone. In XXX IAHR Congress: August 2003, Thessaloniki, Greece; Ganoulis, J., Prinos, P., Armamimi, A., Latinopoulos, P., Eds.; International Association for Hydraulic Engineering and Research (IAHR): Thessaloniki, Greece, 2003. [Google Scholar]
- Bélanger, J.B. Essai sur la Solution NuméRique de Quelques ProblèMes Relatifs au Mouvement Permanent des Eaux Courantes; Carilian-Goeury: Paris, France, 1828. [Google Scholar]
- Chanson, H. Development of the Bélanger equation and backwater equation by Jean-Baptiste Bélanger (1828). J. Hydraul. Eng. 2009, 135, 159–163. [Google Scholar] [CrossRef]
- Bidone, G. Notes sur l’hydraulique; École Royale des Ponts et Chaussées: Champs-sur-Marne, France, 1841. [Google Scholar]
- Bakhmeteff, B.A.; Matzke, A.E. The hydraulic jump in terms of dynamic similarity. ASCE Trans. 1936, 101, 630–647. [Google Scholar]
- Rouse, H.; Siao, T.T.; Nagaratnam, S. Turbulence characteristics of the hydraulic jump. J. Hydraul. Div. ASCE 1958, 84, 1–30. [Google Scholar]
- Rajaratnam, N. The hydraulic jump as a wall jet. J. Hydraul. Div. ASCE 1965, 91, 107–132. [Google Scholar]
- Resch, F.J.; Leutheusser, H.J. Reynolds stress measurements in hydraulic jumps. J. Hydraul. Res. 1972, 10, 409–429. [Google Scholar] [CrossRef]
- Chanson, H.; Brattberg, T. Experimental study of the air–water shear flow in a hydraulic jump. Int. J. Multiph. Flow 2000, 26, 583–607. [Google Scholar] [CrossRef]
- Wang, H.; Murzyn, F. Experimental assessment of characteristic turbulent scales in two-phase flow of hydraulic jump: From bottom to free surface. Environ. Fluid Mech. 2017, 17, 7–25. [Google Scholar] [CrossRef]
- Warnock, J.E. Spillways and Energy Dissipators. In Proceedings of the Hydraulic Conference, Iowa City, IA, USA, 12–15 June 1939. [Google Scholar]
- Ead, S.A.; Rajaratnam, N. Hydraulic jumps on corrugated beds. J. Hydraul. Eng. 2002, 128, 656–663. [Google Scholar] [CrossRef]
- Pagliara, S.; Lotti, I.; Palermo, M. Hydraulic jump on rough bed of stream rehabilitation structures. J. Hydro-Environ. Res. 2008, 2, 29–38. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Air-Water Flow Patterns of Hydraulic Jumps on Uniform Beds Macroroughness. J. Hydraul. Eng. 2018, 144, 04017068. [Google Scholar] [CrossRef]
- Peterka, A.J. Hydraulic Design of Stilling Basins and Energy Dissipators; Department of the Interior, Bureau of Reclamation: Washington, DC, USA, 1978.
- Blaisdell, F.W. The SAF Stilling Basin: A Structure to Dissipate the Destructive Energy in High-Velocity Flow from Spillways; Agriculture Handbook No. 156; United States Department of Agriculture: Washington, DC, USA, 1959.
- Chanson, H.; Lubin, P. Discussion of Verification and validation of a computational fluid dynamics (CFD) model for air entrainment at spillway aerators. Can. J. Civ. Eng. 2010, 37, 135–138. [Google Scholar] [CrossRef]
- Chanson, H. Hydraulics of aerated flows: Qui pro quo? J. Hydraul. Res. 2013, 51, 223–243. [Google Scholar] [CrossRef]
- Viti, N.; Valero, D.; Gualtieri, C. Numerical Simulation of Hydraulic Jumps. Part 2: Recent Results and Future Outlook. Water 2019, 11, 28. [Google Scholar] [CrossRef]
- Kabiri-Samani, A.; Rabiei, M.H.; Safavi, H.; Borghei, S.M. Experimental-analytical investigation of super-to subcritical flow transition without a hydraulic jump. J. Hydraul. Res. 2014, 52, 129–136. [Google Scholar] [CrossRef]
- Kabiri-Samani, A.; Naderi, S. Turbulent structure in the transition from super-to subcritical flow without a hydraulic jump. J. Hydraul. Res. 2017, 55, 50–62. [Google Scholar] [CrossRef]
- Koch, C.; Chanson, H. Turbulence measurements in positive surges and bores. J. Hydraul. Res. 2009, 47, 29–40. [Google Scholar] [CrossRef]
- Gualtieri, C.; Chanson, H. Experimental study of a positive surge. Part 2: Comparison with literature theories and unsteady flow field analysis. Environ. Fluid Mech. 2011, 11, 641–651. [Google Scholar] [CrossRef]
- Gualtieri, C.; Chanson, H. Experimental study of a positive surge. Part 1: Basic flow patterns and wave attenuation. Environ. Fluid Mech. 2012, 12, 145–159. [Google Scholar] [CrossRef]
- Leng, X.; Chanson, H. Breaking bore: Physical observations of roller characteristics. Mech. Res. Commun. 2015, 65, 24–29. [Google Scholar] [CrossRef]
- Leng, X.; Chanson, H. Unsteady velocity profiling in bores and positive surges. Flow Meas. Instrum. 2017, 54, 136–145. [Google Scholar] [CrossRef]
- Chanson, H. Momentum considerations in hydraulic jumps and bores. J. Irrig. Drain. Eng. 2012, 138, 382–385. [Google Scholar] [CrossRef]
- Hager, W.H.; Bremen, R. Classical hydraulic jump: Sequent depths. J. Hydraul. Res. 1989, 27, 565–585. [Google Scholar] [CrossRef]
- Carollo, F.G.; Ferro, V.; Pampalone, V. New solution of classical hydraulic jump. J. Hydraul. Eng. 2009, 135, 565–585. [Google Scholar] [CrossRef]
- Pagliara, S.; Palermo, M. Hydraulic jumps on rough and smooth beds: Aggregate approach for horizontal and adverse-sloped beds. J. Hydraul. Res. 2015, 53, 243–252. [Google Scholar] [CrossRef]
- Palermo, M.; Pagliara, S. Semi-theoretical approach for energy dissipation estimation at hydraulic jumps in rough sloped channels. J. Hydraul. Res. 2018, 56, 786–795. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. An Experimental Study of Air-Water Flows in Hydraulic Jumps with Channel Bed Roughness; UNSW Report No. WRL 259; Water Research Laboratory: Allambie Heights, Australia, 2016. [Google Scholar]
- Frizell, K.W.; Svoboda, C.D. Performance of Type III Stilling Basins-Stepped Spillway Studies: Do Stepped Spillways Affect Traditional Design Parameters? US Department of the Interior, Bureau of Reclamation: Washington, DC, USA, 2012.
- Valero, D.; Bung, D.B.; Crookston, B.M. Energy dissipation of a Type III basin under design and adverse conditions for stepped and smooth spillways. J. Hydraul. Eng. 2018, 144, 04018036. [Google Scholar] [CrossRef]
- Chanson, H. The Hydraulics of Open Channel Flow: An Introduction, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2004; ISBN 978-0750659789. [Google Scholar]
- Valero, D.; Fullana, O.; Gacía-Bartual, R.; Andrés-Domenech, I.; Valles, F. Analytical formulation for the aerated hydraulic jump and physical modelling comparison. In Proceedings of the 3rd IAHR Europe Congress, Porto, Portugal, 14–16 April 2014. [Google Scholar]
- Chanson, H. Air-Water Gas Transfer at Hydraulic Jump with Partially Developed Inflow. Water Res. 1995, 29, 2247–2254. [Google Scholar] [CrossRef]
- Chanson, H. Flow Characteristics of Undular Hydraulic Jumps. Comparison With Near-Critical Flows; CH45/95; Department of Civil Engineering, The University of Queensland: Brisbane, QLD, Australia, 1995. [Google Scholar]
- Bradley, J.N.; Peterka, A.J. Hydraulic Design of Stilling Basins. J. Hydraul. Div. ASCE 1957, 83, 1401–1406. [Google Scholar]
- Chow, V.T. Hydraulics of Open Channel Flow; American Society of Civil Engineers (ASCE) Press: Reston, VA, USA, 1998. [Google Scholar]
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1973. [Google Scholar]
- Murzyn, F.; Chanson, H. Free Surface, Bubbly Flow and Turbulence Measurements in Hydraulic Jumps; CH63/07; Department of Civil Engineering, The University of Queensland: Brisbane, QLD, Australia, 2007. [Google Scholar]
- Wang, H. Turbulence and Air Entrainment in Hydraulic Jumps. Ph.D. Thesis, Department of Civil Engineering, The University of Queensland, Brisbane, QLD, Australia, 2014. [Google Scholar]
- Wang, H.; Chanson, H. Energy Self-similarity and scale effects in physical modelling of hydraulic jump roller dynamics, air entrainment and turbulent scales. Environ. Fluid Mech. 2016, 16, 1087–1110. [Google Scholar] [CrossRef]
- Wang, H.; Chanson, H. Experimental study of turbulent fluctuations in hydraulic jumps. J. Hydraul. Eng. 2015, 141, 04015010. [Google Scholar] [CrossRef]
- Carollo, F.G.; Ferro, V.; Pampalone, V. New expression of the hydraulic jump roller length. J. Hydraul. Eng. 2012, 138, 995–999. [Google Scholar] [CrossRef]
- Schulz, H.E.; Simões, A.L.A.; Nóbrega, J.D. Roller lengths, sequent depths, surface profiles for pre-design of dissipation basins. In Proceedings of the 2nd International Workshop on Hydraulic Structures: Data Validation, Coimbra, Portugal, 7–9 May 2015. [Google Scholar]
- Valiani, A. Linear and angular momentum conservation in hydraulic jump. J. Hydraul. Res. 1997, 35, 323–354. [Google Scholar] [CrossRef]
- Chanson, H. Convective transport of air bubbles in strong hydraulic jumps. Int. J. Multiph. Flow 2010, 36, 798–814. [Google Scholar] [CrossRef]
- Liu, M.; Rajaratnam, N.; Zhu, D.Z. Turbulence structure of hydraulic jumps of low Froude numbers. J. Hydraul. Eng. 2004, 130, 511–520. [Google Scholar] [CrossRef]
- Wu, S.; Rajaratnam, N. Free jumps, submerged jumps and wall jets. J. Hydraul. Res. 1995, 33, 197–212. [Google Scholar] [CrossRef]
- Ohtsu, I.; Koike, M.; Yasuda, Y.; Awazu, S.; Yamanaka, T. Free and Submerged Hydraulic Jumps in Rectangular Channels; Report of Research Institute of Science and Technology, No. 35; Nihon University: Tokyo, Japan, 1990. [Google Scholar]
- Murzyn, F.; Mouaze, D.; Chaplin, J.R. Air-water interface dynamic and free surface features in hydraulic jumps. J. Hydraul. Res. 2007, 45, 679–685. [Google Scholar] [CrossRef]
- Bayon, A.; Valero, D.; García-Bartual, R.; Vallés-Morán, F.J.; López-Jiménez, P.A. Performance assessment of OpenFOAM and FLOW-3D in the numerical modeling of a low Reynolds number hydraulic jump. Environ. Soft. 2016, 80, 322–335. [Google Scholar] [CrossRef]
- Lennon, J.M.; Hill, D. Particle image velocity measurements of undular and hydraulic jumps. J. Hydraul. Eng. 2006, 132, 1283-0-1294. [Google Scholar] [CrossRef]
- Bose, S.K.; Castro-Orgaz, O.; Dey, S. Free surface profiles of undular hydraulic jumps. J. Hydraul. Eng. 2011, 138, 362–366. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, H.; Chanson, H. Turbulence and aeration in hydraulic jumps: Free-surface fluctuation and integral turbulent scale measurements. Environ. Fluid Mech. 2013, 13, 189–204. [Google Scholar] [CrossRef]
- Wang, H.; Murzyn, F.; Chanson, H. Total pressure fluctuations and two-phase flow turbulence in hydraulic jumps. Exp. Fluids 2014, 55, 1847. [Google Scholar] [CrossRef]
- Lin, C.; Hsieh, S.C.; Lin, I.J.; Chang, K.A.; Raikar, R.V. Flow property and self-similarity in steady hydraulic jumps. Exp. Fluids 2012, 53, 1591–1616. [Google Scholar] [CrossRef]
- Murzyn, F.; Mouaze, D.; Chaplin, J.R. Optical fibre probe measurements of bubbly flow in hydraulic jumps. Int. J. Multiph. Flow 2005, 31, 141–154. [Google Scholar] [CrossRef]
- Gualtieri, C.; Chanson, H. Experimental analysis of Froude number effect on air entrainment in the hydraulic jump. Environ. Fluid Mech. 2007, 7, 217–238. [Google Scholar] [CrossRef]
- Chanson, H.; Gualtieri, C. Similitude and scale effects of air entrainment in hydraulic jumps. J. Hydraul. Res. 2013, 46, 35–44. [Google Scholar] [CrossRef]
- Takahashi, M.; Ohtsu, I. Effects of inflows on air entrainment in hydraulic jumps below a gate. J. Hydraul. Res. 2017, 55, 259–268. [Google Scholar] [CrossRef]
- Ervine, D.A. Air entrainment in hydraulic structures: A review. Proc. Inst. Civ. Engrs Water Marit. Energy 1998, 130, 142–153. [Google Scholar] [CrossRef]
- Valero, D.; Bung, D.B. Development of the interfacial air layer in the non-aerated region of high-velocity spillway flows. Instabilities growth, entrapped air and influence on the self-aeration onset. Int. J. Multiph. Flow 2016, 84, 66–74. [Google Scholar] [CrossRef]
- Castro-Orgaz, O.; Hager, W.H. Drawdown curve and turbulent boundary layer development for chute flow. J. Hydraul. Res. 2010, 48, 591–602. [Google Scholar] [CrossRef]
- Castro-Orgaz, O. Velocity profile and flow resistance models for developing chute flow. J. Hydraul. Eng. 2009, 136, 447–452. [Google Scholar] [CrossRef]
- Valero, D.; Bung, D.B. Reformulating self-aeration in hydraulic structures: Turbulent growth of free surface perturbations leading to air entrainment. Int. J. Multiph. Flow 2018, 100, 127–142. [Google Scholar] [CrossRef]
- Bertola, N.; Wang, H.; Chanson, H. A physical study of air–water flow in planar plunging water jet with large inflow distance. Int. J. Multiph. Flow 2018, 100, 155–171. [Google Scholar] [CrossRef]
- Long, D.; Steffler, P.M.; Rajaratnam, N. LDA study of flow structure in submerged hydraulic jump. J. Hydraul. Res. 1990, 28, 437–460. [Google Scholar] [CrossRef]
- Chanson, H.; Toombes, L. Air-water flows down stepped chutes: turbulence and flow structure observations. Int. J. Multiph. Flow 2018, 28, 1737–1761. [Google Scholar] [CrossRef]
- Chachereau, Y.; Chanson, H. Free-surface fluctuations and turbulence in hydraulic jumps. Exp. Therm. Fluid Sci. 2018, 35, 896–909. [Google Scholar] [CrossRef]
- Murzyn, F.; Chanson, H. Free-surface fluctuations in hydraulic jumps: Experimental observations. Exp. Therm. Fluid Sci. 2018, 33, 1055–1064. [Google Scholar] [CrossRef]
- Mossa, M.; Tolve, U. Flow visualization in bubbly two-phase hydraulic jump. J. Fluids Eng. 1998, 120, 160–165. [Google Scholar] [CrossRef]
- Long, D.; Rajaratnam, N.; Steffler, P.M.; Smy, P.R. Structure of flow in hydraulic jumps. J. Hydraul. Res. 1991, 29, 207–218. [Google Scholar] [CrossRef]
- Fiorotto, V.; Rinaldo, A. Turbulent pressure fluctuations under hydraulic jumps. J. Hydraul. Res. 1992, 30, 499–520. [Google Scholar] [CrossRef]
- Abdul Khader, M.H.; Elango, K. Turbulent pressure field beneath a hydraulic jump. J. Hydraul. Res. 1992, 12, 469–489. [Google Scholar] [CrossRef]
- Wang, H.; Murzyn, F.; Chanson, H. Interaction between free-surface, two-phase flow and total pressure in hydraulic jump. Exp. Therm. Fluid Sci. 2015, 64, 30–41. [Google Scholar] [CrossRef]
- Hornung, H.G.; Willert, C.; Turner, S. The flow field downstream of a hydraulic jump. J. Fluid Mech. 1995, 287, 299–316. [Google Scholar] [CrossRef]
- Gualtieri, C.; Chanson, H. Effect of Froude number on bubble clustering in a hydraulic jump. J. Hydraul. Res. 2010, 48, 504–508. [Google Scholar] [CrossRef]
- Gualtieri, C.; Chanson, H. Interparticle arrival time analysis of bubble distributions in a dropshaft and hydraulic jump. J. Hydraul. Res. 2013, 51, 253–264. [Google Scholar] [CrossRef]
- Blocken, B.; Gualtieri, C. Ten iterative steps for model development and evaluation applied to Computational Fluid Dynamics for Environmental Fluid Mechanics. Environ. Soft. 2012, 33, 1–22. [Google Scholar] [CrossRef]
- Bradshaw, P.; Launder, B.E.; Lumley, J.L. Collaborative testing of turbulence models. J. Fluids Eng. 1996, 118, 243–247. [Google Scholar] [CrossRef]
- Chanson, H. Turbulent air–water flows in hydraulic structures: dynamic similarity and scale effects. Environ. Fluid Mech. 2009, 9, 125–142. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Turbulence, dynamic similarity and scale effects in high-velocity free-surface flows above a stepped chute. Exp. Fluids 2009, 47, 1–18. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Scale effects in microscopic air–water flow properties in high-velocity free-surface flows. Exp. Therm. Fluid Sci. 2017, 83, 19–36. [Google Scholar] [CrossRef]
- Zhang, G.; Valero, D.; Bung, D.B.; Chanson, H. On the estimation of free-surface turbulence using ultrasonic sensors. Flow Meas. Inst. 2018, 60, 171–184. [Google Scholar] [CrossRef]
- Montano, L.; Li, R.; Felder, S. Continuous measurements of time-varying free-surface profiles in aerated hydraulic jumps with a LIDAR. Exp. Therm. Fluid Sci. 2018, 93, 379–397. [Google Scholar] [CrossRef]
- Chanson, H. Phase-detection measurements in free-surface turbulent shear flows. J. Geophys. Eng. 2016, 13, S74. [Google Scholar] [CrossRef]
- Felder, S.; Pfister, M. Comparative analyses of phase-detective intrusive probes in high-velocity air–water flows. Int. J. Multiph. Flow 2017, 90, 88–101. [Google Scholar] [CrossRef]
- Kramer, M.; Valero, D.; Chanson, H.; Bung, D.B. Towards reliable turbulence estimations with phase‑detection probes: An adaptive window cross‑correlation technique. Exp. Fluids 2018. [Google Scholar] [CrossRef]
- Bung, D.B. Non-intrusive measuring of air–water flow properties in self-aerated stepped spillway flow. In Proceedings of the 34th IAHR World Congress, Brisbane, Australia, 26 June–1 July 2011. [Google Scholar]
- Leandro, J.; Bung, D.B.; Carvalho, R. Measuring void fraction and velocity fields of a stepped spillway for skimming flow using non-intrusive methods. Exp. Fluids 2014, 55, 1732. [Google Scholar] [CrossRef]
- Bung, D.B.; Valero, D. Image processing for bubble image velocimetry in self-aerated flows. In Proceedings of the 36th IAHR World Congress, The Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- Bung, D.B.; Valero, D. Optical flow estimation in aerated flows. J. Hydraul. Res. 2016, 54, 575–580. [Google Scholar] [CrossRef]
- Bung, D.B.; Valero, D. Application of the optical flow method to velocity determination in hydraulic structure models. In Proceedings of the 6th International Symposium on Hydraulic Structures, Portland, OR, USA, 27–30 June 2016. [Google Scholar]
- Bung, D.B.; Valero, D. Image processing techniques for velocity estimation in highly aerated flows: Bubble Image Velocimetry vs. Optical Flow. In Proceedings of the 4th IAHR Europe Congress, Liège, Belgium, 27–29 July 2016. [Google Scholar]
- Zhang, G.; Chanson, H. Application of local optical flow methods to high-velocity free-surface flows: Validation and application to stepped chutes. Exp. Therm. Fluid Sci. 2018, 90, 186–199. [Google Scholar] [CrossRef]
- Goring, D.G.; Nikora, V.I. Despiking acoustic Doppler velocimeter data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef]
- Thomas, R.E.; Schindfessel, L.; McLelland, S.J.; Creëlle, S.; De Mulder, T. Bias in mean velocities and noise in variances and covariances measured using a multistatic acoustic profiler: The Nortek Vectrino Profiler. Meas. Sci. Technol. 2017, 28, 075302. [Google Scholar] [CrossRef]
- Bung, D.B.; Valero, D. FlowCV—An open source toolbox for computer vision applications in turbulent flows. In Proceedings of the 37th IAHR World Congress, Kuala Lumpur, Malaysia, 13–18 August 2017. [Google Scholar]

| Bradley and Peterka [46], Hager [2] | Montes [47] | Chow [48], Chanson [42] | |||
|---|---|---|---|---|---|
| range | Classification | range | Classification | range | Classification |
| 1–1.7 | Without roller | 1.2–2 | Undular | 1–1.7 | Undular |
| 1.7–2.5 | Pre-jump | 2–4 | Oscillating | 1.7–2.5 | Weak |
| 2.5–4.5 | Transition | 4–9 | Stable | 2.5–4.5 | Oscillating |
| 4.5–9 | Stabilized | 4.5–9 | Steady | ||
| >9 | Choppy | >9 | High dissipation | >9 | Strong |
| Flow Variables | Hager [2] | Murzyn and Chanson [49] | Wang [50] | Other Relevant Studies |
|---|---|---|---|---|
| Sequent depths | ER | ED (*) | ED | ER: Palermo and Pagliara [38], |
| Chanson [34], | ||||
| Pagliara et al. [20] | ||||
| Maximum velocity decay | ER | ED | ER, ED | ER: Wang and Chanson [51], |
| Chanson and Brattberg [16], | ||||
| Rajaratnam [14] | ||||
| Roller length | ER, ED | ED | ER, ED | ER: Wang and Chanson [52], |
| Carollo et al. [53] | ||||
| Jump length | ER | ED | ER: Schultz et al. [54], | |
| Peterka [22] | ||||
| Mean free surface profile | ER, ED | ED | ER, ED | ER: Wang and Chanson [51], |
| Valiani [55], | ||||
| Bakhmeteff and Matzke [12] | ||||
| Mean velocity profiles | ER | ER, ED | ER, ED | ER: Wang and Chanson [51] |
| Air concentrations | ED (**) | ER, ED | ER, ED | ER: Wang and Chanson [51], |
| Chanson and Brattberg [16] |
| Techniques | Basic Variables Measured | Description | Relevant References |
|---|---|---|---|
| Point gauge | Static flow depth | Static measurements, low accuracy for turbulent free surfaces | – |
| Acoustic Displacement Meters (ADM) or Ultrasonic Sensors (USS) | Instantaneous flow depth | Low-band frequency capped, preference for foreground obstacles | Zhang et al. [94] |
| Light Detection and Ranging (LiDAR) | Instantaneous free surface profiles | Both spatial and temporal free surface detection, large surface detection, amounts of outliers | Montano et al. [95] |
| Phase detection probes: conductivity or optical fibre probes | Air concentration, Mean velocity | Problems in regions with recirculation, only measures in the probe direction, intrusive | Wang [50] Chanson [96] Felder and Pfister [97] Kramer et al. [98] |
| Acoustic Doppler Velocimeters (ADV) | Instantaneous flow velocities | Can only be applied in regions with low presence of bubbles | Liu et al. [57] |
| Particle Image Velocimetry (PIV) | Instantaneous flow velocities | Can only be applied in regions with low presence of bubbles | Lin et al. [66] |
| Bubble Image Velocimetry (BIV) | Instantaneous flow velocities | Underprediction of flow velocities, when compared against other intrusive techniques | Bung [99] Leandro et al. [100] Bung and Valero [101] |
| Optical Flow (OF) | Instantaneous flow velocities | Better match with intrusive techniques, more robust to strong noises present in the bubbly images | Bung and Valero [102,103,104] Zhang and Chanson [105] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valero, D.; Viti, N.; Gualtieri, C. Numerical Simulation of Hydraulic Jumps. Part 1: Experimental Data for Modelling Performance Assessment. Water 2019, 11, 36. https://doi.org/10.3390/w11010036
Valero D, Viti N, Gualtieri C. Numerical Simulation of Hydraulic Jumps. Part 1: Experimental Data for Modelling Performance Assessment. Water. 2019; 11(1):36. https://doi.org/10.3390/w11010036
Chicago/Turabian StyleValero, Daniel, Nicolò Viti, and Carlo Gualtieri. 2019. "Numerical Simulation of Hydraulic Jumps. Part 1: Experimental Data for Modelling Performance Assessment" Water 11, no. 1: 36. https://doi.org/10.3390/w11010036
APA StyleValero, D., Viti, N., & Gualtieri, C. (2019). Numerical Simulation of Hydraulic Jumps. Part 1: Experimental Data for Modelling Performance Assessment. Water, 11(1), 36. https://doi.org/10.3390/w11010036






