Recent Advances in Experimental Studies of Steady-State Dilution and Reactive Mixing in Saturated Porous Media
Abstract
1. Introduction
2. Theory
3. Laboratory Experiments
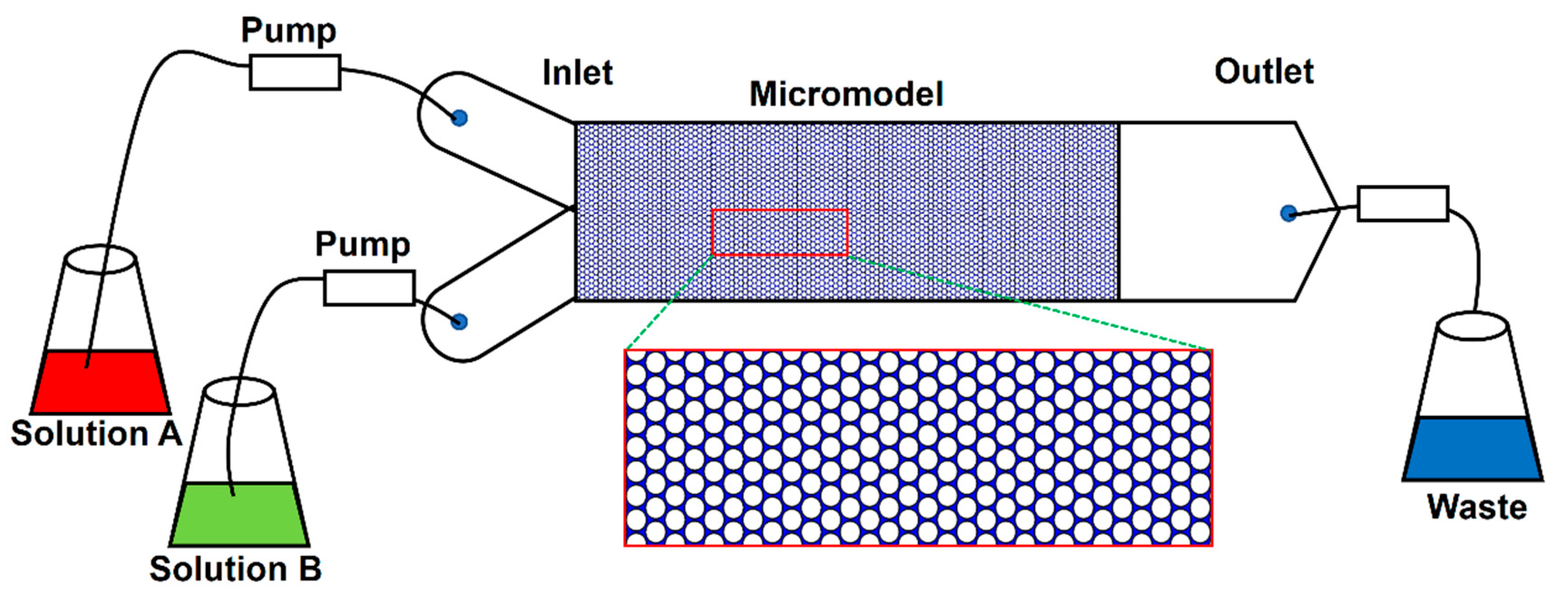
3.1. Pore Scale
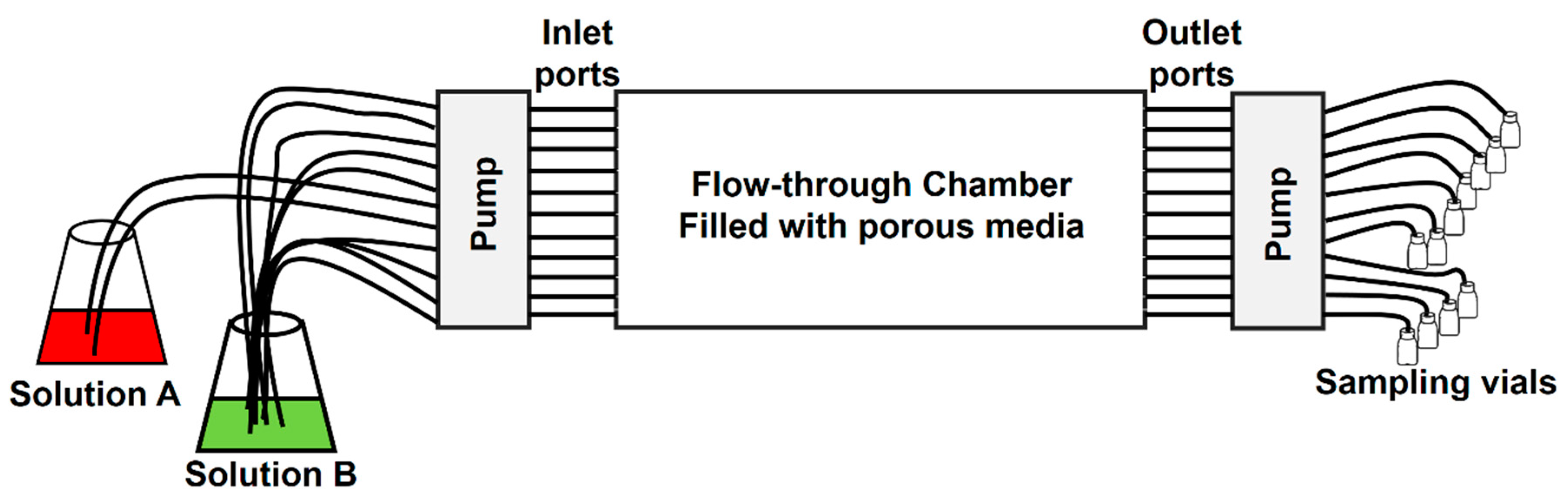
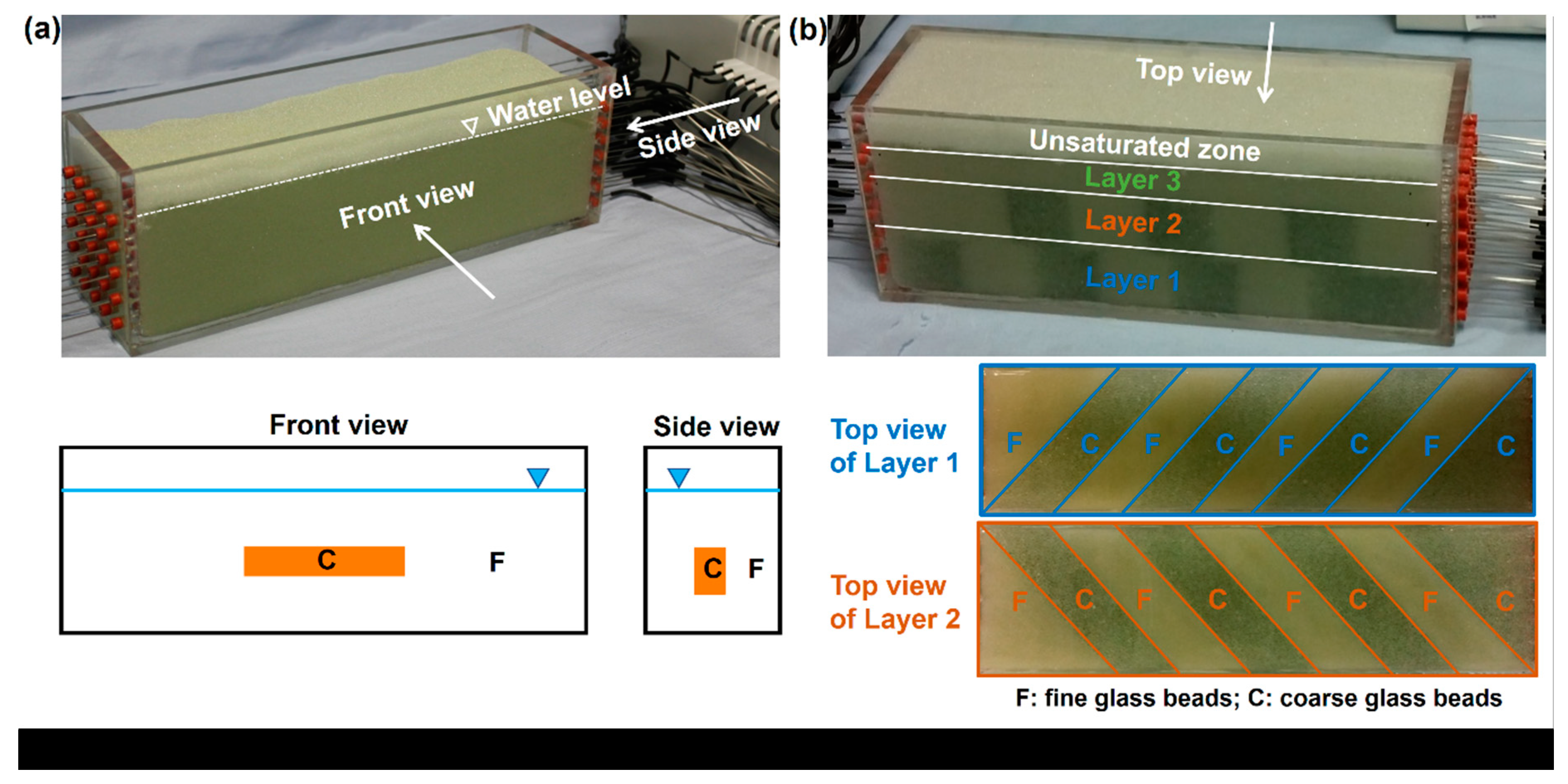
3.2. Darcy Scale
4. Quantification of Dilution and Reactive Mixing
4.1. Conservative Transport
4.1.1. Moment Analysis
4.1.2. Flux-Related Dilution Index
4.2. Reactive Transport
4.2.1. Plume Length
4.2.2. Mass Flux
5. Summary and Outlook
- In most performed experiments, glass beads and clean sands were used as the porous medium to exclude the external effects such as the irregular shapes of the grains and the sorption of the compounds on the grain surfaces. However, natural porous media indeed has irregular shapes and physical and chemical sorption potentials. Such characteristics of the natural porous media have additional effects on solute dilution and mixing. In future laboratory experiments, we suggest more applications of the porous medium taken from the natural field. To simplify the experimental conditions, we could pre-treat the porous medium. For instance, we could sieve and classify the grains if the target of our research interest is the influence of the grain sizes and shapes on dilution and reactive mixing.
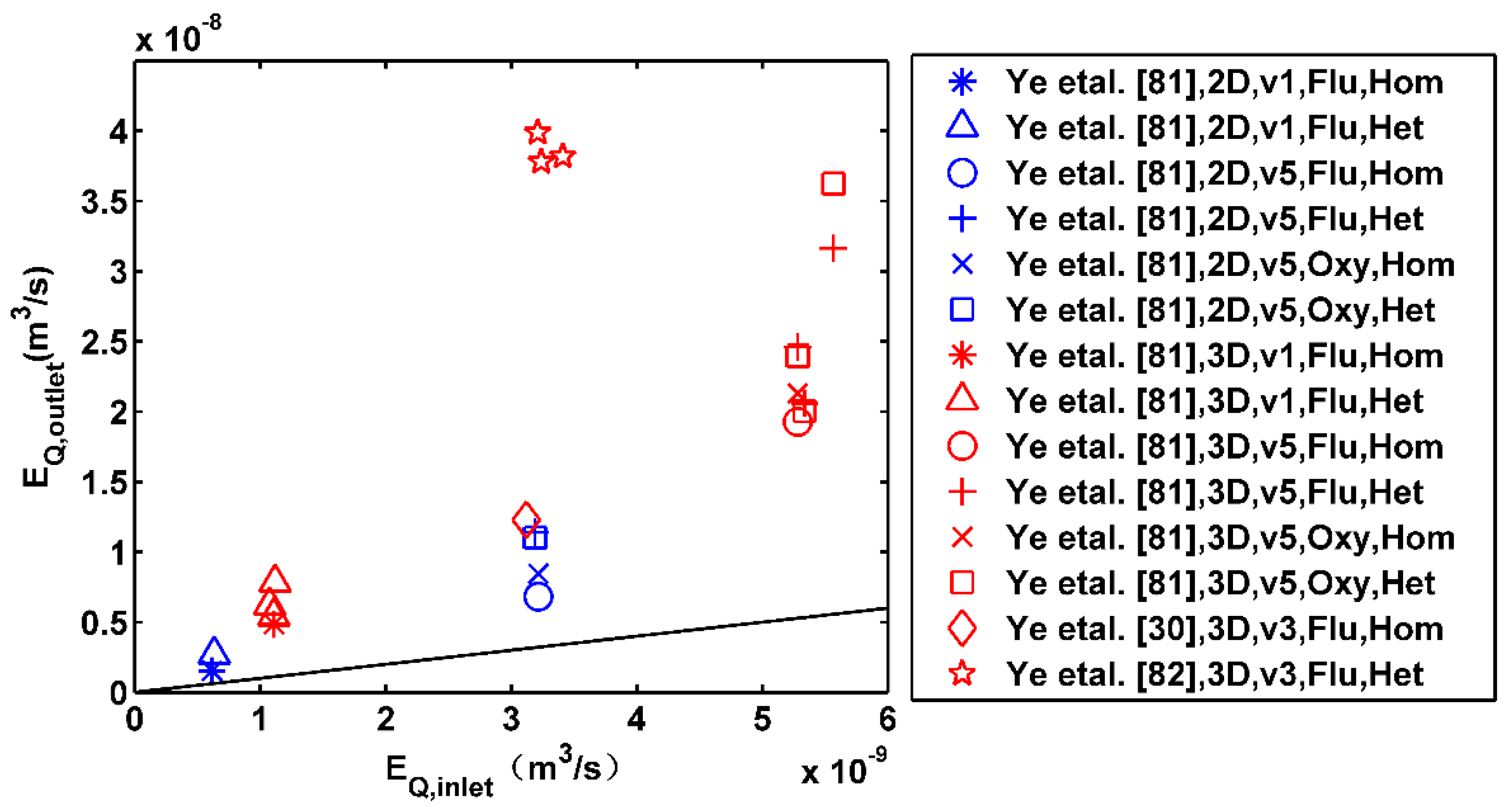
- The experimental studies have shown the importance of single or several high-permeability inclusions and macroscopic anisotropic lenses to dilution and reactive mixing. As to the larger scale, Di Dato et al. [106] performed numerical simulations to calculate the influence of multiple heterogeneous microstructures on macrodispersion and showed a high relevance between macrodispersion and heterogeneous microstructures. However, no experiments have ever been performed to test the different spatial distributions of multiple inclusions and lenses on large-scale dilution and mixing. In future laboratory experiments, we suggest properly enlarging the scale of the flow-through domain and including more heterogeneous lenses to resemble spatial features observed in the natural aquifers.
- So far, most experiments were performed involving conservative transport or very simple reactions. However biogeochemical reactive transport is the common phenomenon in natural aquifer systems. Even though complex reactive transport is rather difficult to operate in laboratory experiments, it should be tested to help better understand reactive mixing.
- Hydrodynamic dispersion, particularly mechanical dispersion, has an impact on the structure of fingers in density-driven nature convection. Recent experimental studies found that hydrodynamic dispersion enhances the merging of fingers and thus reduces the finger numbers [107,108,109]. Such a process indicates an effect of hydrodynamic dispersion on dilution and reactive mixing of solute fingers in density-driven natural convection. Therefore, density effects may also be considered and included in the future investigation of dilution and reactive mixing laboratory experiments.
- By complicating the experimental conditions, more advanced experimental operation and measurement techniques are required. Particularly in the three-dimensional systems, development of an easy and cheap method for observation and quantification of plume distributions in the inner porous media would help dramatically advance our understanding of dilution and reactive mixing from an experimental perspective. Therefore, during future experimental studies, development of better experimental methods and techniques could also be a key point to break through experimental studies of dilution and reactive mixing.
Author Contributions
Funding
Conflicts of Interest
References
- Chiogna, G.; Cirpka, O.A.; Grathwohl, P.; Rolle, M. Transverse mixing of conservative and reactive tracers in porous media: Quantification through the concepts of flux-related and critical dilution indices. Water Resour. Res. 2011, 47, W02505. [Google Scholar] [CrossRef]
- Chiogna, G.; Hochstetler, D.L.; Bellin, A.; Kitanidis, P.K.; Rolle, M. Mixing, entropy and reactive solute transport. Geophy. Res. Lett. 2012, 39, L20405. [Google Scholar] [CrossRef]
- Rolle, M.; Eberhardt, C.; Chiogna, G.; Cirpka, O.A.; Grathwohl, P. Enhancement of dilution and transverse reactive mixing in porous media: Experiments and model-based interpretation. J. Contam. Hydrol. 2009, 110, 130–142. [Google Scholar] [CrossRef]
- Mace, R.E.; Fisher, R.S.; Welch, D.M.; Parra, S.P. Extent, Mass, and Duration of Hydrocarbon Plumes from Leaking Petroleum Storage Tank Sites in Texas; Geologic Circular 97-1; Bureau of Economic Geology, University of Texas at Austin: Austin, TX, USA, 1997. [Google Scholar]
- Wiedemeier, T.H.; Rifai, H.S.; Newell, C.J.; Wilson, J.T. Natural Attenuation and Fuels and Chlorinated Solvents in the Subsurface; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1999. [Google Scholar]
- Anneser, B.; Einsiedl, F.; Meckenstock, R.U.; Richters, L.; Wisotzky, F.; Griebler, C. High-resolution monitoring of biogeochemical gradients in a tar oil-contaminated aquifer. Appl. Geochem. 2008, 23, 1715–1730. [Google Scholar] [CrossRef]
- Cirpka, O.A.; Frind, E.O.; Helmig, R. Numerical simulation of biodegradation controlled by transverse mixing. J. Contam. Hydrol. 1999, 40, 159–182. [Google Scholar] [CrossRef]
- Ham, P.A.S.; Schotting, R.J.; Prommer, H.; Davis, G.B. Effects of hydrodynamic dispersion on plume lengths for instantaneous bimolecular reactions. Adv. Water Resour. 2004, 27, 803–813. [Google Scholar] [CrossRef]
- Knutson, C.; Valocchi, A.; Werth, C. Comparison of continuum and pore-scale models of nutrient biodegradation under transverse mixing conditions. Adv. Water Resour. 2007, 30, 1421–1431. [Google Scholar] [CrossRef]
- Mayer, K.U.; Benner, S.G.; Frind, E.O.; Thornton, S.F.; Lerner, D.N. Reactive transport modeling of processes controlling the distribution and natural attenuation of phenolic compounds in a deep sandstone aquifer. J. Contam. Hydrol. 2001, 53, 341–368. [Google Scholar] [CrossRef]
- Prommer, H.; Anneser, B.; Rolle, M.; Einsiedl, F.; Griebler, C. Biogeochemical and isotopic gradients in a BTEX/PAH contaminant plume: Model-based interpretation of a high-resolution field data set. Environ. Sci. Technol. 2009, 43, 8206–8212. [Google Scholar] [CrossRef]
- Amos, R.T.; Berkins, B.A.; Delin, G.N.; Cozzarelli, I.M.; Blowes, D.W.; Kirshtein, J.D. Methane oxidation in a crude oil contaminated aquifer: Delineation of aerobic reactions at the plume fringes. J. Contam. Hydrol. 2011, 125, 13–25. [Google Scholar] [CrossRef]
- Davis, G.B.; Barber, C.; Power, T.R.; Thierrin, J.; Patterson, B.M.; Rayner, J.L.; Wu, Q. The variability and intrinsic remediation of a BETX plume in anaerobic sulphate-rich groundwater. J. Contam. Hydrol. 1999, 36, 265–290. [Google Scholar] [CrossRef]
- Thornton, S.F.; Quigley, S.; Spence, M.J.; Banwart, S.A.; Bottrell, S.; Lerner, D.N. Processes controlling the distribution and natural attenuation of dissolved phenolic compounds in a deep sandstone aquifer. J. Contam. Hydrol. 2001, 53, 233–267. [Google Scholar] [CrossRef]
- Tuxen, N.; Albrechtsen, H.-J.; Bjerg, P.L. Identification of a reactive degradation zone at a landfill leachate plume fringe using high resolution sampling and incubation techniques. J. Contam. Hydrol. 2006, 85, 179–194. [Google Scholar] [CrossRef]
- Dentz, M.; Le Borgne, T.; Englert, A.; Bijeljic, B. Mixing, spreading and reaction in heterogeneous media: A brief review. J. Contam. Hydrol. 2011, 120, 1–17. [Google Scholar] [CrossRef]
- Chiogna, G. Transverse Mixing of Conservative and Reactive Tracers in Porous Media. Ph.D. Thesis, University of Tübingen, Tübingen, Germany, 2010. [Google Scholar]
- Cirpka, O.A.; de Barros, F.P.J.; Chiogna, G.; Rolle, M.; Nowak, W. Stochastic flux-related analysis of transverse mixing in two-dimensional heterogeneous porous media. Water Resour. Res. 2011, 47, WR010279. [Google Scholar] [CrossRef]
- Chiogna, G.; Cirpka, O.A.; Grathwohl, P.; Rolle, M. Relevance of local compound-specific transverse dispersion for conservative and reactive mixing in heterogeneous porous media. Water Resour. Res. 2011, 47, W07540. [Google Scholar] [CrossRef]
- Boving, T.B.; Grathwohl, P. Tracer diffusion coefficients in sedimentary rocks correlation to porosity and hydraulic conductivity. J. Contam. Hydrol. 2001, 53, 85–100. [Google Scholar] [CrossRef]
- Grathwohl, P. Diffusion in Natural Porous Media: Contaminant Transport, Sorption/Desorption, and Dissolution Kinetics; Kluwer Academic Publishers: Boston, MA, USA, 1998. [Google Scholar]
- De Josselin de Jong, G. Longitudinal and transverse diffusion in granular deposits. EOS Trans. AGU 1958, 39, 67–74. [Google Scholar] [CrossRef]
- Saffman, P.G. A theory of dispersion in a porous medium. J. Fluid Mech. 1959, 6, 321–349. [Google Scholar] [CrossRef]
- Scheidegger, A.E. General theory of dispersion in porous media. J. Geophys. Res. 1961, 66, 3273–3278. [Google Scholar] [CrossRef]
- Scheidegger, A.E. Statistical hydrodynamics in porous media. J. Appl. Phys. 1954, 25, 994–1001. [Google Scholar] [CrossRef]
- Bear, J.; Bachmat, Y. A Generalized Theory on Hydrodynamic Dispersion in Porous Media. In Proceedings of the IASH Symposium on Artificial Recharge and Management of Aquifers, Haifa, Israel, 1967; Available online: http://hydrologie.org/redbooks/a072/07201.pdf (accessed on 20 October 2018).
- Chiogna, G.; Eberhardt, C.; Grathwohl, P.; Cirpka, O.A.; Rolle, M. Evidence of compound-dependent hydrodynamic and mechanical transverse dispersion by multitracer laboratory experiments. Environ. Sci. Technol. 2010, 44, 688–693. [Google Scholar] [CrossRef]
- Hochstetler, D.L.; Rolle, M.; Chiogna, G.; Haberer, C.M.; Grathwohl, P.; Kitanidis, P.K. Effects of compound-specific transverse mixing on steady-state reactive plumes: Insights from pore-scale simulations and Darcy-scale experiments. Adv. Water Resour. 2013, 54, 1–10. [Google Scholar] [CrossRef]
- Rolle, M.; Hochstetler, D.; Chiogna, G.; Kitanidis, P.K.; Grathwohl, P. Experimental investigation and pore-scale modeling interpretation of compound-specific transverse dispersion in porous media. Transp. Porous Media 2012, 93, 347–362. [Google Scholar] [CrossRef]
- Ye, Y.; Chiogna, G.; Cirpka, O.A.; Grathwohl, P.; Rolle, M. Experimental investigation of compound-specific dilution of solute plumes in saturated porous media: 2-D vs. 3-D flow-through systems. J. Contam. Hydrol. 2015, 172, 33–47. [Google Scholar] [CrossRef]
- Chiogna, G.; Bellin, A. Analytical solution for reactive solute transport considering incomplete mixing within a reference elementary volume. Water Resour. Res. 2013, 49, 2589–2600. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Tartakovsky, G.D.; Scheibe, T.D. Effects of incomplete mixing on multicomponent reactive transport. Adv. Water Resour. 2009, 32, 1674–1679. [Google Scholar] [CrossRef]
- Blackwell, R.J. Laboratory studies of microscopic dispersion phenomena. Soc. Petrol. Engrs. J. 1962, 225, 1–8. [Google Scholar] [CrossRef]
- Carvalho, J.F.; Delgado, J.M.P.Q. Lateral dispersion in liquid flow through packed beds at Pe < 1400. Am. Inst. Chem. Eng. 2000, 46, 1089–1095. [Google Scholar] [CrossRef]
- Delgado, J.M.P.Q.; Carvalho, J.F.R. Measurement of the coefficient of transverse dispersion in flow through packed beds for a wide range of values of the Schmidt number. Transp. Porous Media 2001, 44, 165–180. [Google Scholar] [CrossRef]
- Harleman, D.R.F.; Rumer, R.R. Longitudinal and lateral dispersion in an isotropic porous medium. J. Fluid Mech. 1964, 16, 385–394. [Google Scholar] [CrossRef]
- Huang, W.E.; Oswald, S.E.; Lerner, D.N.; Smith, C.C.; Zheng, C.M. Dissolved oxygen imaging in a porous medium to investigate biodegradation in a plume with limited electron acceptor supply. Environ. Sci. Technol. 2003, 37, 1905–1911. [Google Scholar] [CrossRef] [PubMed]
- Klenk, I.D.; Grathwohl, P. Transverse vertical dispersion in groundwater and the capillary fringe. J. Contam. Hydrol. 2002, 58, 111–128. [Google Scholar] [CrossRef]
- Olsson, Å.; Grathwohl, P. Transverse dispersion of non-reactive tracers in porous media: A new nonlinear relationship to predict dispersion coefficients. J. Contam. Hydrol. 2007, 92, 149–161. [Google Scholar] [CrossRef] [PubMed]
- de Anna, P.; Jimenez-Martinez, J.; Tabuteau, H.; Turuban, R.; Le Borgne, T.; Derrien, M.; Meheust, Y. Mixing and reaction kinetics in porous media: An experimental pore scale quantification. Environ. Sci. Technol. 2014, 48, 508–516. [Google Scholar] [CrossRef] [PubMed]
- Fanizza, M.F.; Yoon, H.; Zhang, C.; Oostrom, M.; Wietsma, T.W.; Hess, N.J.; Bowden, M.E.; Strathmann, T.J.; Finneran, K.T.; Werth, C.J. Pore-scale evaluation of uranyl phosphate precipitation in a model groundwater system. Water Resour. Res. 2013, 49, 874–890. [Google Scholar] [CrossRef]
- Ghaderi, S.M.; Kharrat, R.; Tahmasebi, H.A. Experimental and theoretical study of calcium sulphate precipitation in porous media using glass micromodel. Oil Gas Sci. Technol. 2009, 64, 489–501. [Google Scholar] [CrossRef]
- Nambi, I.M.; Werth, C.J.; Sanford, R.A.; Valocchi, A.J. Pore-scale analysis of anaerobic halorespiring bacterial growth along the transverse mixing zone of an etched silicon pore network. Environ. Sci. Technol. 2003, 37, 5617–5624. [Google Scholar] [CrossRef] [PubMed]
- Yoon, H.; Valocchi, A.J.; Werth, C.J.; Dewers, T. Pore-scale simulation of mixing-induced calcium carbonate precipitation and dissolution in a microfluidic pore network. Water Resour. Res. 2012, 48, W02524. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Dehoff, K.; Hess, N.; Oostrom, M.; Wietsma, T.W.; Valocchi, A.J.; Fouke, B.W.; Werth, C.J. Pore-scale study of transverse mixing induced CaCO3 precipitation and permeability reduction in a model subsurface sedimentary system. Environ. Sci. Technol. 2010, 44, 7833–7838. [Google Scholar] [CrossRef]
- Oostrom, M.; Mehmani, Y.; Romero-Gomez, P.; Tang, Y.; Liu, H.; Yoon, H.; Kang, Q.; Joekar-Niasar, V.; Balhoff, M.T.; Dewers, T.; et al. Pore-scale and continuum simulations of solute transport micromodel benchmark experiments. Computat. Geosci. 2016, 20, 857–879. [Google Scholar] [CrossRef]
- Willingham, T.W.; Werth, C.J.; Valocchi, A.J. Evaluation of the effects of porous media structure on mixing-controlled reactions using pore-scale modeling and micromodel experiments. Environ. Sci. Technol. 2008, 42, 3185–3193. [Google Scholar] [CrossRef] [PubMed]
- Willingham, T.W.; Zhang, C.; Werth, C.J.; Valocchi, A.J.; Oostrom, M.; Wietsma, T.W. Using dispersivity values to quantify the effects of pore-scale flow focusing on enhanced reaction along a transverse mixing zone. Adv. Water Resour. 2010, 33, 525–535. [Google Scholar] [CrossRef]
- Karadimitriou, N.K.; Hassanizadeh, S.M. A review of micromodels and their use in two-phase flow studies. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef]
- Chomsurin, C.; Werth, C.J. Analysis of pore-scale nonaqueous phase liquid dissolution in etched silicon pore networks. Water Resour. Res. 2003, 39, WR001643. [Google Scholar] [CrossRef]
- Acharya, R.C.; Valocchi, A.J.; Werth, C.J.; Willingham, T.W. Pore-scale simulation of dispersion and reaction along a transverse mixing zone in two-dimensional porous media. Water Resour. Res. 2007, 43, W10435. [Google Scholar] [CrossRef]
- Alhashmi, Z.; Blunt, M.J.; Bijeljic, B. Predictions of dynamic changes in reaction rates as a consequence of incomplete mixing using pore scale reactive transport modeling on images of porous media. J. Contam. Hydrol. 2015, 179, 171–181. [Google Scholar] [CrossRef]
- Rolle, M.; Chiogna, G.; Hochstetler, D.L.; Kitanidis, P.K. On the importance of diffusion and compound-specific mixing for groundwater transport: An investigation from pore to field scale. J. Contam. Hydrol. 2013, 153, 51–68. [Google Scholar] [CrossRef]
- Rolle, M.; Kitanidis, P.K. Effects of compound-specific dilution on transient transport and solute breakthrough: A pore-scale analysis. Adv. Water Resour. 2014, 71, 186–199. [Google Scholar] [CrossRef]
- Porta, G.M.; Chaynikov, S.; Thovert, J.F.; Riva, M.; Guadagnini, A.; Adler, P.M. Numerical investigation of pore and continuum scale formulations of bimolecular reactive transport in porous media. Adv. Water Resour. 2013, 62, 243–253. [Google Scholar] [CrossRef]
- Bauer, R.D.; Maloszewski, P.; Zhang, Y.C.; Meckenstock, R.U.; Griebler, C. Mixing-controlled biodegradation in a toluene plume—Results from two-dimensional laboratory experiments. J. Contam. Hydrol. 2008, 96, 150–168. [Google Scholar] [CrossRef] [PubMed]
- Castro-Alcalá, E.; Fernandez-Garcia, D.; Carrera, J.; Bolster, D. Visualization of mixing processes in a heterogeneous sand box aquifer. Environ. Sci. Technol. 2012, 46, 3228–3235. [Google Scholar] [CrossRef] [PubMed]
- McNeil, J.D.; Oldenborger, G.A.; Schincariol, R.A. Quantitative imaging of contaminant distributions in heterogeneous porous media laboratory experiments. J. Contam. Hydrol. 2006, 84, 36–54. [Google Scholar] [CrossRef] [PubMed]
- Muniruzzaman, M.; Rolle, M. Experimental investigation of the impact of compound-specific dispersion and electrostatic interactions on transient transport and solute breakthrough. Water Resour. Res. 2017, 53, 1189–1209. [Google Scholar] [CrossRef]
- Haberer, C.M.; Rolle, M.; Cirpka, O.A.; Grathwohl, P. Impact of heterogeneity on oxygen transfer in a fluctuating capillary fringe. Groundwater 2013, 53, 57–70. [Google Scholar] [CrossRef] [PubMed]
- Katz, G.E.; Berkowitz, B.; Guadagnini, A.; Saaltink, M.W. Experimental and modeling investigation of multicomponent reactive transport in porous media. J. Contam. Hydrol. 2011, 120, 27–44. [Google Scholar] [CrossRef] [PubMed]
- Levy, M.; Berkowitz, B. Measurement and analysis of non-Fickian dispersion in heterogeneous porous media. J. Contam. Hydrol. 2003, 64, 203–226. [Google Scholar] [CrossRef]
- Rolle, M.; Muniruzzaman, M.; Haberer, C.M.; Grathwohl, P. Coulombic effects in advection-dominated transport of electrolytes in porous media: Multicomponent ionic dispersion. Geochim. Cosmochim. Acta 2013, 120, 195–205. [Google Scholar] [CrossRef]
- Amini, N.; Hassan, Y.A. An investigation of matched index of refraction technique and its application in optical measurements of fluid flow. Exp. Fluids 2012, 53, 2011–2020. [Google Scholar] [CrossRef]
- Rashidi, M.; Peurrung, L.; Tompson, A.F.B.; Kulp, T.J. Experimental analysis of pore-scale flow and transport in porous media. Adv. Water Resour. 1996, 19, 163–180. [Google Scholar] [CrossRef]
- Stöhr, M.; Roth, K.; Jähne, B. Measurement of 3D pore-scale flow in index-matched porous media. Exp. Fluids 2003, 35, 159–166. [Google Scholar] [CrossRef]
- Rubol, S.; Tonina, D.; Vincent, L.; Sohm, J.A.; Basham, W.; Budwig, R.; Savalia, P.; Kanso, E.; Capone, D.G.; Nealson, K.H. Seeing through porous media: An experimental study for unveiling interstitial flows. Hydrol. Proc. 2018, 32, 402–407. [Google Scholar] [CrossRef]
- Huang, W.E.; Smith, C.C.; Lerner, D.N.; Thornton, S.F.; Oram, A. Physical modelling of solute transport in porous media, evaluation of an imaging technique using UV excited fluorescent dye. Water Res. 2002, 36, 1843–1853. [Google Scholar] [CrossRef]
- Zinn, B.; Meigs, L.C.; Harvey, C.F.; Haggerty, R.; Peplinski, W.J.; Schwerin, C.F. Experimental visualization of solute transport and mass transfer processes in two-dimensional conductivity fields with connected regions of high conductivity. Environ. Sci. Technol. 2004, 38, 3916–3926. [Google Scholar] [CrossRef] [PubMed]
- Hofstee, C.; Oostrom, M.; Dane, J.H.; Walker, R.W. Infiltration and redistribution of perchloroethylene in partially saturated, stratified porous media. J. Contam. Hydrol. 1998, 34, 293–313. [Google Scholar] [CrossRef]
- Oostrom, M.; Dane, J.H.; Guven, O.; Hayworth, J.S. Experimental investigation of dense solute plumes in an unconfined aquifer model. Water Resour. Res. 1992, 28, 2315–2326. [Google Scholar] [CrossRef]
- Betson, M.; Barker, J.; Barnes, P.; Atkinson, T. Use of synchrotron tomographic techniques in the assessment of diffusion parameters for solute transport in groundwater flow. Transp. Porous Media 2005, 60, 217–223. [Google Scholar] [CrossRef]
- Perret, J.; Prasher, S.O.; Kantzas, A.; Langford, C. A two-domain approach using CAT scanning model solute transport in soil. J. Environ. Qual. 2000, 29, 995–1010. [Google Scholar] [CrossRef]
- Amin, M.H.G.; Chorely, R.J.; Richards, K.S.; Hall, L.D.; Carpenter, T.A.; Cislerova, M.; Vogel, T. Study of infiltration into a heterogeneous soil using magnetic resonance imaging. Hydrol. Proc. 1997, 11, 471–483. [Google Scholar] [CrossRef]
- Deurer, M.; Vogeler, I.; Clothier, B.E.; Scotter, D.R. Magnetic resonance imaging of hydrodynamic dispersion in a saturated porous medium. Transp. Porous Media 2004, 54, 145–166. [Google Scholar] [CrossRef]
- Werth, C.J.; Zhang, C.; Brusseau, M.L.; Oostrom, M.; Baumann, T. A review of non-invasive imaging methods and applications in contaminant hydrogeology research. J. Contam. Hydrol. 2010, 113, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Oates, P.M.; Harvey, C.F. A colorimetric reaction to quantify fluid mixing. Exp. Fluids 2006, 41, 673–683. [Google Scholar] [CrossRef]
- Rahman, M.A.; Jose, S.C.; Nowak, W.; Cirpka, O.A. Experiments on vertical transverse mixing in a large-scale heterogeneous model aquifer. J. Contam. Hydrol. 2005, 80, 130–148. [Google Scholar] [CrossRef] [PubMed]
- Haberer, C.M.; Rolle, M.; Liu, S.; Cirpka, O.A.; Grathwohl, P. A high-resolution non-invasive approach to quantify oxygen transport across the capillary fringe and within the underlying groundwater. J. Contam. Hydrol. 2011, 122, 26–39. [Google Scholar] [CrossRef] [PubMed]
- Ye, Y.; Chiogna, G.; Cirpka, O.A.; Grathwohl, P.; Rolle, M. Experimental investigation of transverse mixing in porous media under helical flow conditions. Phys. Rev. E 2016, 94, 013113. [Google Scholar] [CrossRef] [PubMed]
- Ye, Y.; Chiogna, G.; Cirpka, O.A.; Grathwohl, P.; Rolle, M. Enhancement of plume dilution in two-dimensional and three-dimensional porous media by flow focusing in high-permeability inclusions. Water Resour. Res. 2015, 51, 5582–5602. [Google Scholar] [CrossRef]
- Ye, Y.; Chiogna, G.; Cirpka, O.A.; Grathwohl, P.; Rolle, M. Experimental evidence of helical flow in porous media. Phys. Rev. Lett. 2015, 115, 194502. [Google Scholar] [CrossRef] [PubMed]
- Prommer, H.; Barry, D.A.; Davis, G.B. Modelling of physical and reactive processes during biodegradation of a hydrocarbon plume under transient groundwater flow conditions. J. Contam. Hydrol. 2002, 59, 113–131. [Google Scholar] [CrossRef]
- Prommer, H.; Tuxen, N.; Bjerg, P. Fringe-controlled natural attenuation of phenoxy acids in a landfill plume: Integration of field-scale processes by reactive transport modeling. Environ. Sci. Technol. 2006, 40, 4732–4738. [Google Scholar] [CrossRef]
- Bauer, R.D.; Rolle, M.; Bauer, S.; Eberhardt, C.; Grathwohl, P.; Kolditz, O.; Meckenstock, R.U.; Griebler, C. Enhanced biodegradation by hydraulic heterogeneities in petroleum hydrocarbon plumes. J. Contam. Hydrol. 2009, 105, 56–68. [Google Scholar] [CrossRef]
- Bauer, R.D.; Rolle, M.; Kürzinger, P.; Grathwohl, P.; Meckenstock, R.U.; Griebler, C. Two-dimensional flow-through microcosms—Versatile test systems to study biodegradation processes in porous aquifers. J. Hydrol. 2009, 369, 284–295. [Google Scholar] [CrossRef]
- Fox, D.T.; Guo, L.J.; Fujita, Y.; Huang, H.; Redden, G. Experimental and numerical analysis of parallel reactant flow and transverse mixing with mineral precipitation in homogeneous and heterogeneous porous media. Transp. Porous Media 2016, 111, 605–626. [Google Scholar] [CrossRef]
- Kitanidis, P.K. The concept of the dilution index. Water Resour. Res. 1994, 30, 2011–2026. [Google Scholar] [CrossRef]
- Werth, C.J.; Cirpka, O.A.; Grathwohl, P. Enhanced mixing and reaction through flow focusing in heterogeneous porous media. Water Resour. Res. 2006, 42, W12414. [Google Scholar] [CrossRef]
- Chiogna, G.; Rolle, M.; Alberto, B.; Cirpka, O.A. Helicity and flow topology in three-dimensional anisotropic porous media. Adv. Water Resour. 2014, 73, 134–143. [Google Scholar] [CrossRef]
- Chiogna, G.; Cirpka, O.A.; Rolle, M.; Alberto, B. Helical flow in three-dimensional nonstationary anisotropic heterogeneous porous media. Water Resour. Res. 2015, 51, 261–280. [Google Scholar] [CrossRef]
- Cirpka, O.A.; Chiogna, G.; Rolle, M.; Bellin, A. Transverse mixing in three-dimensional nonstationary anisotropic heterogeneous porous media. Water Resour. Res. 2015, 51, 241–260. [Google Scholar] [CrossRef]
- Hemker, K.; Baker, M. Analytical solutions for whirling groundwater flow in two-dimensional heterogeneous anisotropic aquifers. Water Resour. Res. 2006, 42, W12419. [Google Scholar] [CrossRef]
- Stauffer, F. Impact of highly permeable sediment units with inclined bedding on solute transport in aquifers. Adv. Water Resour. 2007, 30, 2194–2201. [Google Scholar] [CrossRef]
- Ye, Y.; Chiogna, G.; Lu, C.; Rolle, M. Effect of anisotropy structures on plume entropy and reactive mixing in helical flows. Transp. Porous Media 2018, 121, 315–332. [Google Scholar] [CrossRef]
- Boon, M.; Bijeljic, B.; Niu, B.; Krevor, S. Observations of 3-D transverse dispersion and dilution in natural consolidated rock by X-ray tomography. Adv. Water Resour. 2016, 96, 266–281. [Google Scholar] [CrossRef]
- Bolster, D.; Benson, D.A.; Le Borgne, T.; Dentz, M. Anomalous mixing and reaction induced by superdiffusive nonlocal transport. Phys. Rev. E 2010, 82, 021119. [Google Scholar] [CrossRef] [PubMed]
- Adams, E.E.; Gelhar, L.W. Field study of dispersion in a heterogeneous aquifer: 2. Spatial moments analysis. Water Resour. Res. 1992, 28, 3293–3307. [Google Scholar] [CrossRef]
- Dagan, G. Transport in heterogeneous porous formations: Spatial moments, ergodicity, and effective dispersion. Water Resour. Res. 1990, 26, 1281–1290. [Google Scholar] [CrossRef]
- Harvey, C.F.; Gorelick, S.M. Temporal moment-generating equations: Modeling transport and mass transfer in heterogeneous aquifers. Water Resour. Res. 1995, 31, 1895–1911. [Google Scholar] [CrossRef]
- Valocchi, A.J. Spatial moment analysis of the transport of kinetically adsorbing solutes through stratified aquifers. Water Resour. Res. 1989, 25, 273–279. [Google Scholar] [CrossRef]
- Ballarini, E.; Sauer, S.; Eberhardt, C.; Beyer, C. Evaluation of the role of heterogeneities on transverse mixing in bench-scale tank experiments by numerical modeling. Groundwater 2014, 52, 368–377. [Google Scholar] [CrossRef]
- Dentz, M.; Carrera, J. Mixing and spreading in stratified flow. Phys. Fluids 2007, 19, 017107. [Google Scholar] [CrossRef]
- Ursino, N.; Gimmi, T.; Flühler, H. Dilution of non-reactive tracers in variably saturated sandy structures. Adv. Water Resour. 2001, 24, 877–885. [Google Scholar] [CrossRef]
- Cirpka, O.A.; Olsson, Å.; Ju, Q.; Rahman, M.A.; Grathwohl, P. Determination of transverse dispersion coefficients from reactive plume lengths. Groundwater 2006, 44, 212–221. [Google Scholar] [CrossRef]
- Di Dato, M.; de Barros, F.P.J.; Fiori, A.; Bellin, A. Effects of the hydraulic conductivity microstructure on macrodispersivity. Water Resour. Res. 2016, 52, 6818–6832. [Google Scholar] [CrossRef]
- Wang, L.; Nakanishi, Y.; Hyodo, A.; Suekane, T. Three-dimensional structure of natural convection in a porous media: Effect of dispersion on finger structure. Int. J. Greenh. Gas Control 2016, 53, 274–283. [Google Scholar] [CrossRef]
- Nakanishi, Y.; Hyodo, A.; Wang, L.; Suekane, T. Experimental study of 3D Rayleigh-Taylor convection between miscible fluids in a porous medium. Adv. Water Resour. 2016, 97, 224–232. [Google Scholar] [CrossRef]
- Liang, Y.; Wen, B.; Hesse, M.A.; DiCarlo, D. Effect of dispersion on solutal convection in porous media. Geophy. Res. Lett. 2018, 45, 9690–9698. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, T.; Ye, Y.; Zhang, Y.; Xie, Y. Recent Advances in Experimental Studies of Steady-State Dilution and Reactive Mixing in Saturated Porous Media. Water 2019, 11, 3. https://doi.org/10.3390/w11010003
Xu T, Ye Y, Zhang Y, Xie Y. Recent Advances in Experimental Studies of Steady-State Dilution and Reactive Mixing in Saturated Porous Media. Water. 2019; 11(1):3. https://doi.org/10.3390/w11010003
Chicago/Turabian StyleXu, Tiantian, Yu Ye, Yu Zhang, and Yifan Xie. 2019. "Recent Advances in Experimental Studies of Steady-State Dilution and Reactive Mixing in Saturated Porous Media" Water 11, no. 1: 3. https://doi.org/10.3390/w11010003
APA StyleXu, T., Ye, Y., Zhang, Y., & Xie, Y. (2019). Recent Advances in Experimental Studies of Steady-State Dilution and Reactive Mixing in Saturated Porous Media. Water, 11(1), 3. https://doi.org/10.3390/w11010003



