Sensitivity Analysis of a Wall Boundary Condition for the Turbulent Pipe Flow of Herschel–Bulkley Fluids
Abstract
:1. Introduction
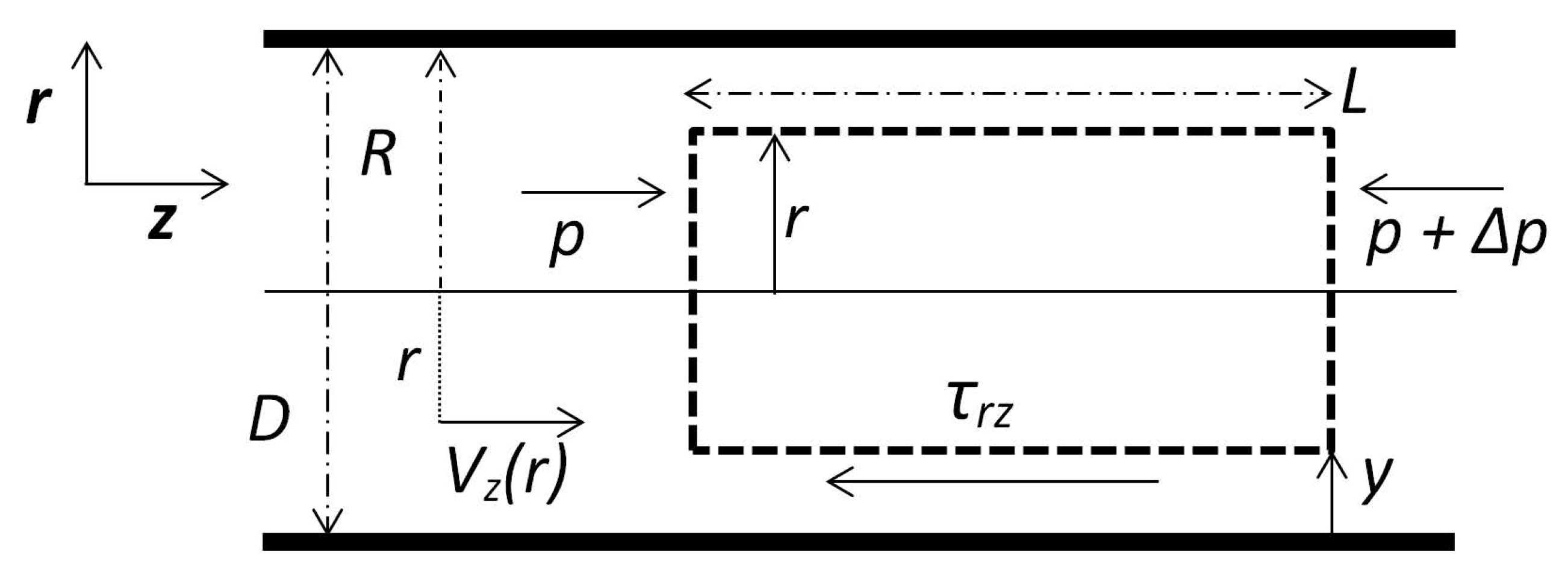
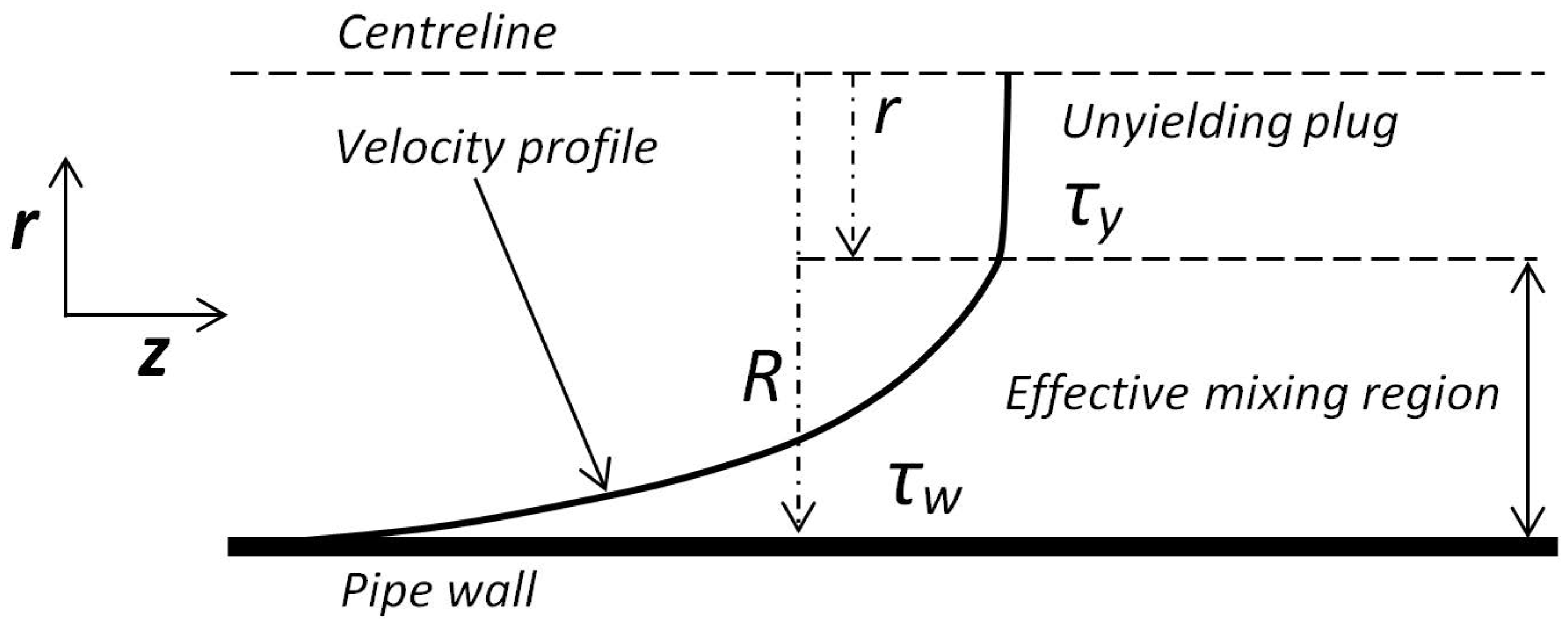
1.1. Herschel–Bulkley Fluids
1.2. A Wall Function for a Non-Newtonian Fluid
1.3. Approach
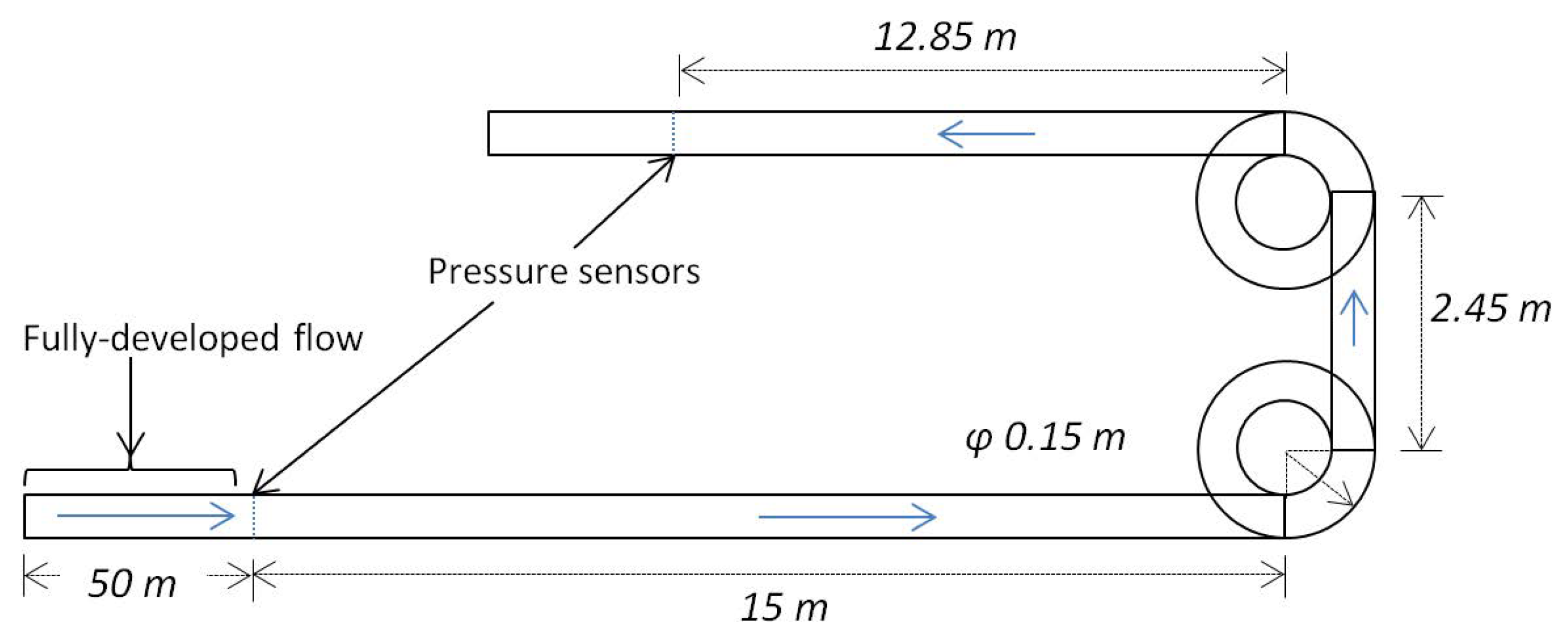
2. Experiments
3. Methodology
3.1. Solver and Numerics
3.1.1. An Appropriate Reynolds Number
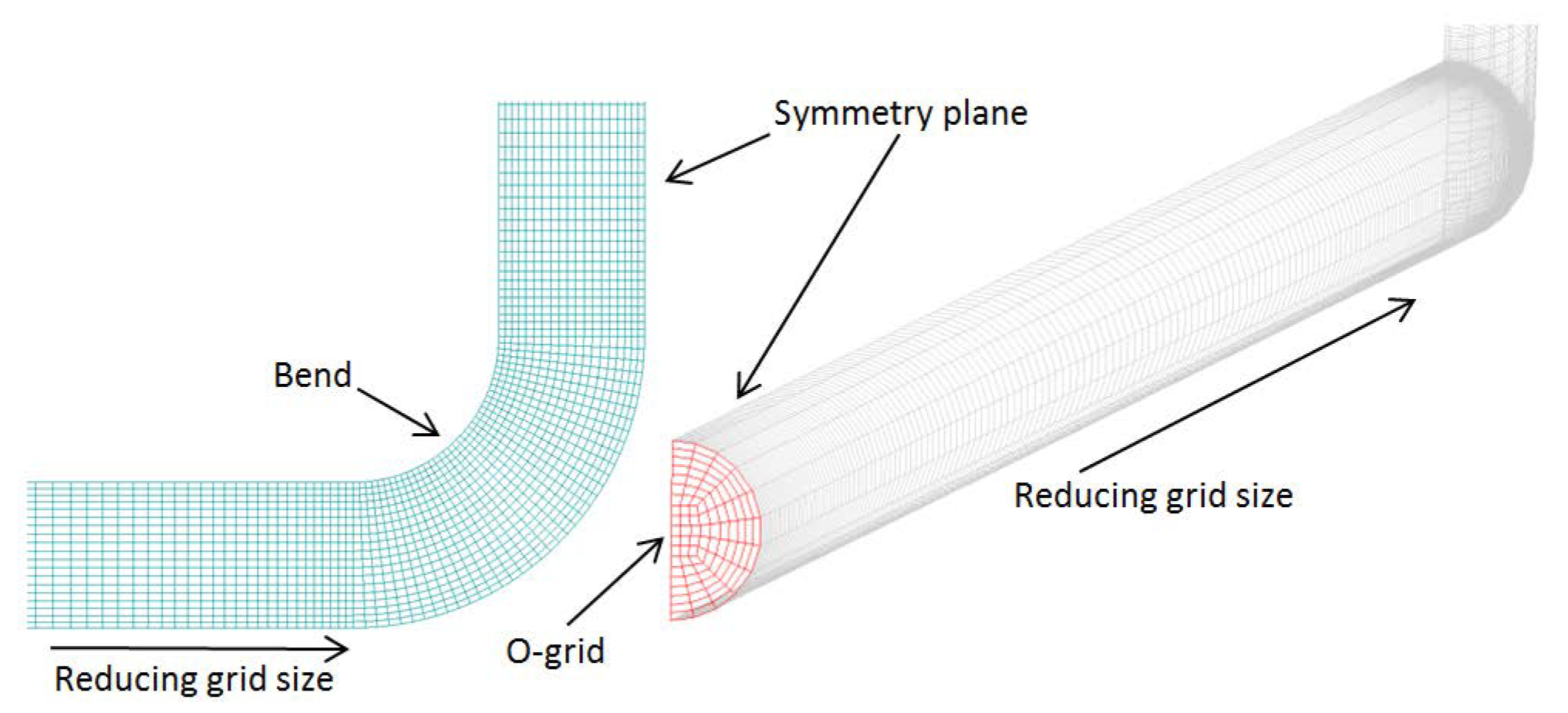
3.2. Mesh
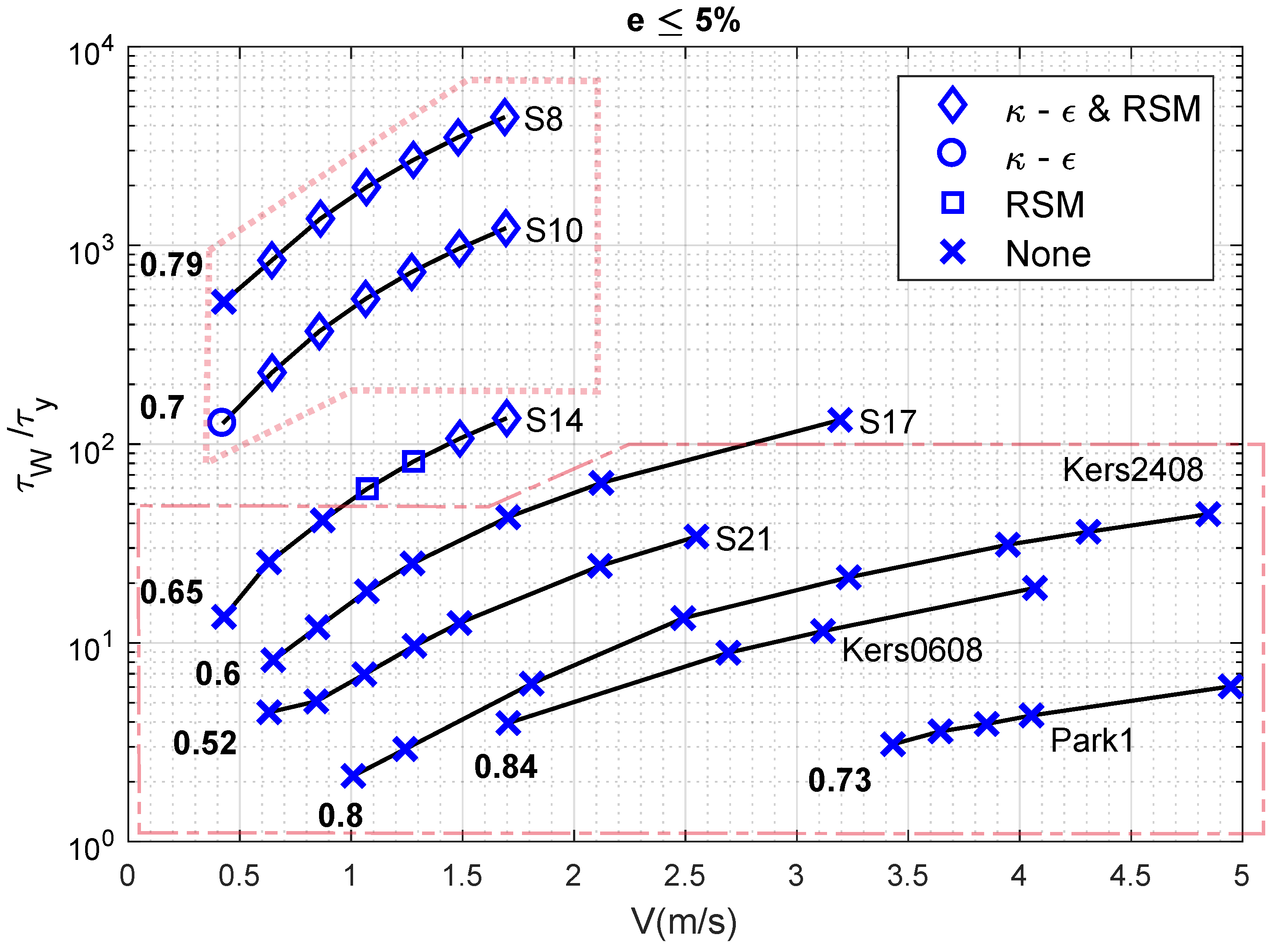
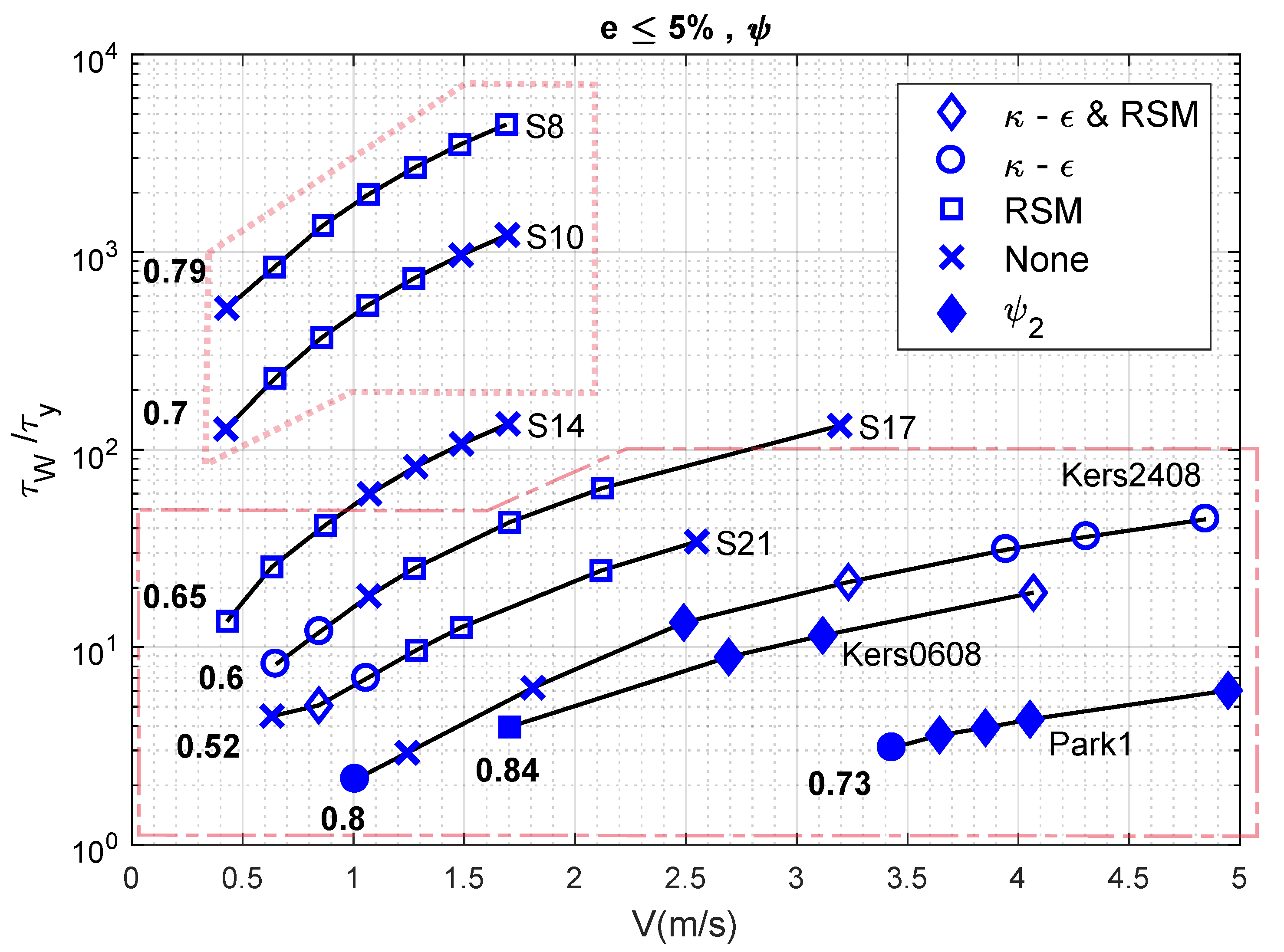
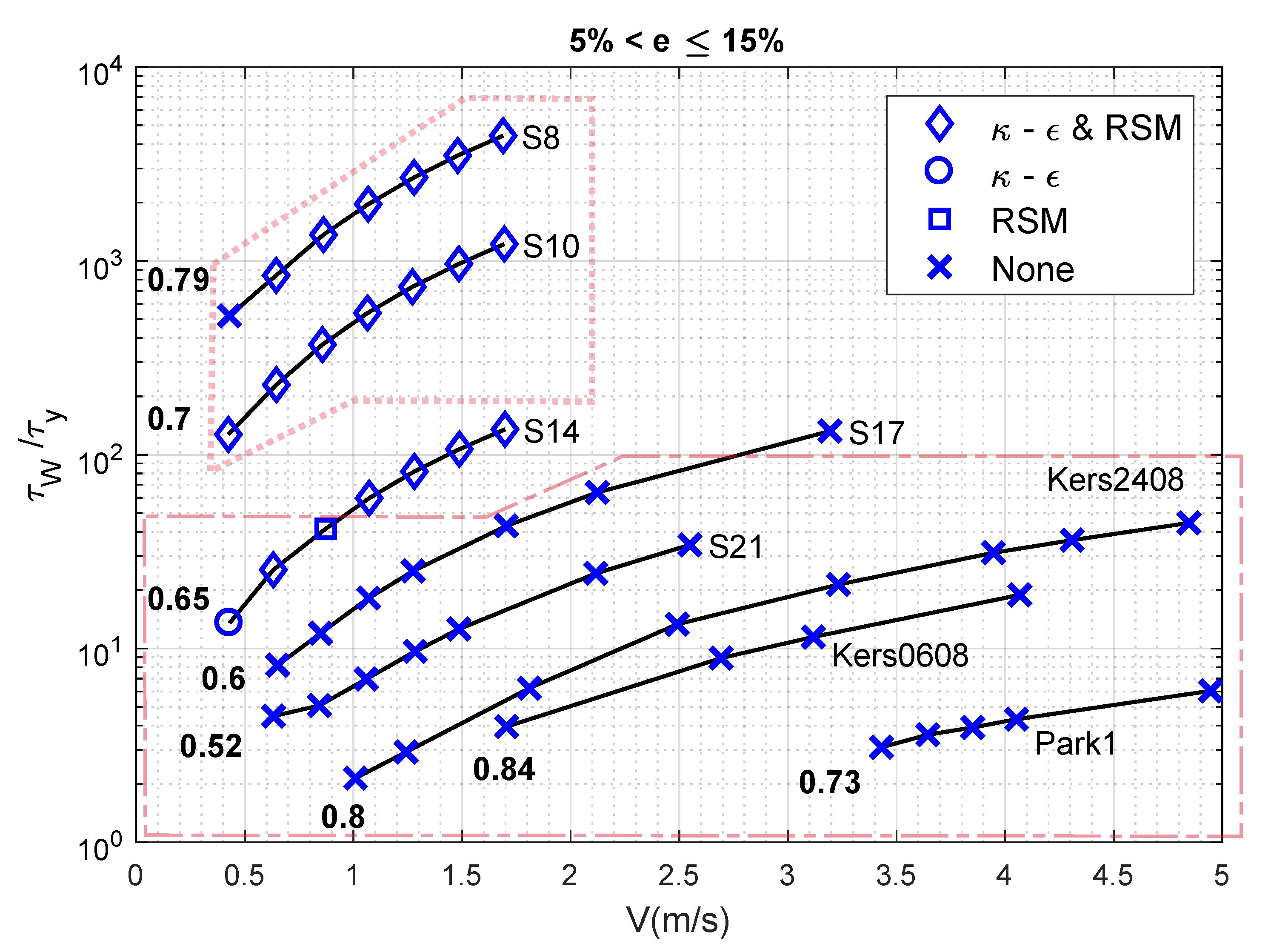
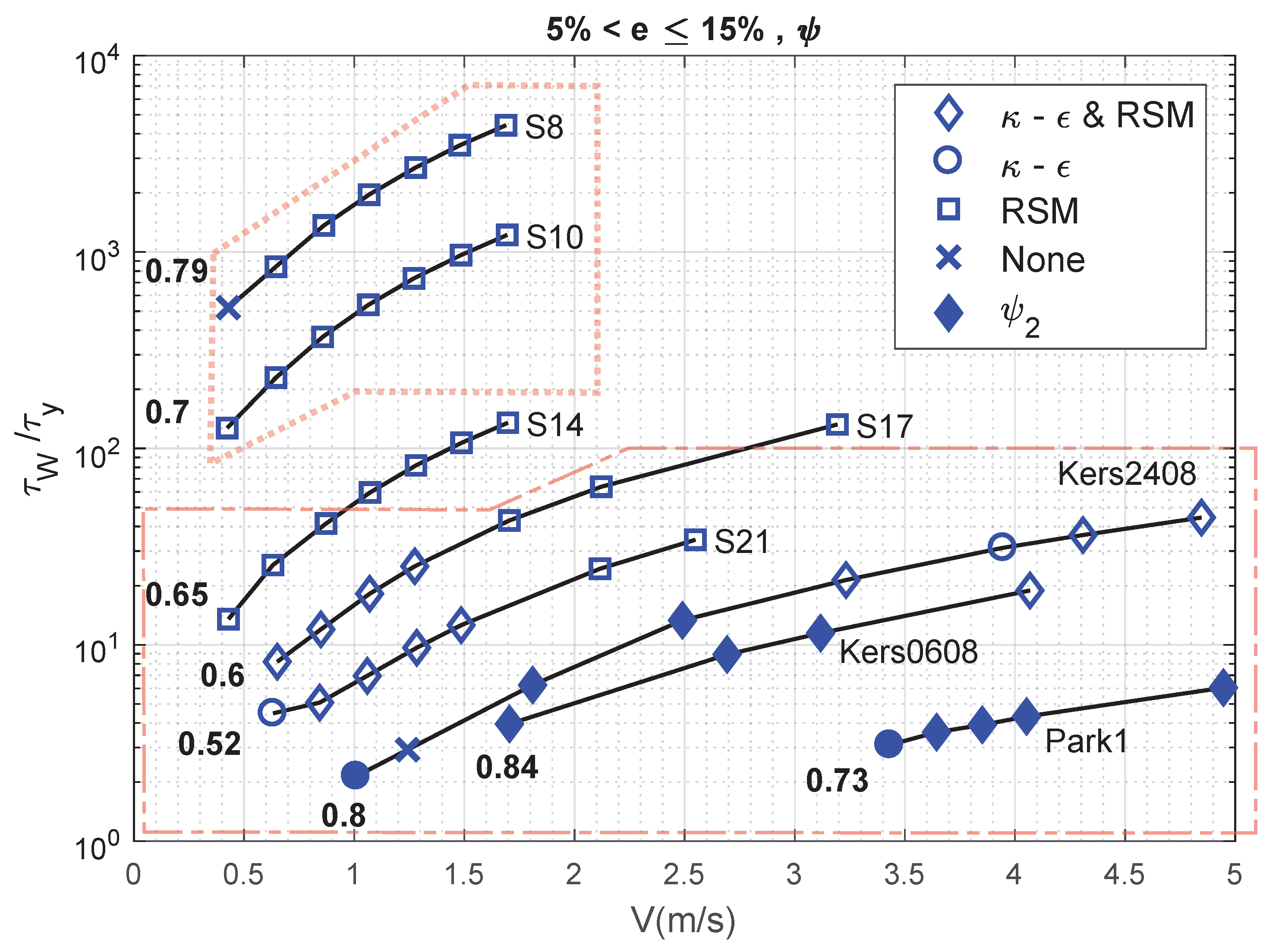
4. Sensitivity Analysis
4.1. Flow Velocity, Behaviour Index and Accuracy
4.2. Flow Velocity, Yield Stress and RANS Model
4.3. Reynolds Number, Yield Stress and RANS Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| NS | Navier-Stokes |
| CFD | Computational fluid dynamics |
| RANS | Reynolds-averaged Navier-Stokes |
| RSM | Reynolds stress model |
| SIMPLE | Semi-implicit method for pressure-linked equations |
| NWO | Nederlandse Organisatie voor Wetenschappelijk Onderzoek |
| TTW | Toegepaste en Technische Wetenschappen |
References
- Thota Radhakrishnan, A.; van Lier, J.; Clemens, F. Rheological characterisation of concentrated domestic slurry. Water Res. 2018, 141, 235–250. [Google Scholar] [CrossRef]
- Thota Radhakrishnan, A.K.; van Lier, J.; Clemens, F. Rheology of Un-Sieved Concentrated Domestic Slurry: A Wide Gap Approach. Water 2018, 10, 1287. [Google Scholar] [CrossRef]
- Chabbra, R.P.; Richardson, J.F. Non-Newtonian Flow in the Process Industries, 1st ed.; Butterworth-Heinemann: Oxford, UK, 1999. [Google Scholar]
- Mehta, D.; Thota-Radhakrishnan, A.K.; van Lier, J.; Clemens, F. A wall boundary condition for the simulation of a turbulent non-Newtonian domestic slurry in pipes. Water 2018, 10, 124. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Herschel, W.H.; Bulkley, R. Konsistenzmessungen von Gummi-Benzollösungen. Kolloid-Zeitschrift 1926, 39, 291–300. [Google Scholar] [CrossRef]
- Oldroyd, J.G. A rational formulation of the equations of plastic flow for a Bingham solid. Math. Proc. Camb. Philos. Soc. 1947, 43, 100–105. [Google Scholar] [CrossRef]
- Skelland, A.H.P. Non-Newtonian Flow and Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 1967. [Google Scholar]
- Govier, G.W.; Aziz, K. The Flow of Complex Mixtures in Pipes; R.E. Krieger Pub. Co.: New York, NY, USA, 1972. [Google Scholar]
- Bird, R.B.; Dai, G.C.; Yarusso, B.J. The rheology and flow of viscoplastic materials. Rev. Chem. Eng. 1983, 1, 1–70. [Google Scholar] [CrossRef]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids, Vol. 1: Fluid Mechanics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1987. [Google Scholar]
- Heywood, N.I.; Cheng, D.C.H. Comparison of methods for predicting head loss in turbulent pipe flow of non-Newtonian fluids. Trans. Inst. Meas. Control 1984, 6, 33–45. [Google Scholar] [CrossRef]
- Torrance, B.M. Friction factors for turbulent non-Newtonian fluid flow in circular pipes. S. Afr. Mech. Eng. 1963, 13, 89–91. [Google Scholar]
- Hanks, R.W. Low Reynolds number turbulent pipeline flow of pseudohomogeneous slurries. In Proceedings of the Hydrotransport 5 Conference, Hanover, Germany, 8–11 May 1978; pp. 8–11. [Google Scholar]
- Ferziger, J.; Perić, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer Science and Business Media: New York, NY, USA, 2012. [Google Scholar]
- Davidson, P.A. Turbulence—An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Schlichting, H. Boundary-Layer Theory, 8th ed.; Springer: New York, NY, USA, 2017. [Google Scholar]
- Prandtl, L. Zur turbulenten Strömung in glatten Röhren. Z. Angew. Math. Mech. 1925, 5, 136–139. [Google Scholar]
- Prandtl, L. Neure Ergebnisse der Turbulenzforschung. Z. Ver. Deutsch. Ingenieure 1933, 77, 105–114. [Google Scholar]
- von Kármán, T. Mechanische Ähnlichkeit und Turbulenz; Sonderdrucke aus den Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen: Mathematisch-physische Klasse; Weidmannsche Buchh: Berlin, Germany, 1930. [Google Scholar]
- Rudman, M.; Blackburn, H.M. Direct numerical simulation of turbulent non-Newtonian flow using a spectral element method. App. Math. Model. 2006, 30, 1229–1248. [Google Scholar] [CrossRef]
- Slatter, P.T. Transitional and Turbulent Flow of Non-Newtonian Slurries in Pipes. Ph.D. Thesis, University of Cape Town, Cape Town, South Africa, 1995. [Google Scholar]
- Park, J.T.; Mannheimer, R.J.; Grimley, T.A.; Morrow, T.B. Pipe flow measurements of a transparent non-Newtonian slurry. J. Fluids Eng. 1989, 111, 331–336. [Google Scholar] [CrossRef]
- ANSYS. ANSYS FLUENT User’s Guide; Ansys Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- Rudman, M.; Blackburn, H.M.; Graham, L.J.W.; Pullum, L. Turbulent pipe flow of shear-thinning fluids. J. Non-Newton. Fluid Mech. 2004, 118, 33–48. [Google Scholar] [CrossRef]
- Malin, M.R. The turbulent flow of Bingham plastic fluids in smooth circular tubes. Int. Commun. Heat Mass Transf. 1997, 24, 793–804. [Google Scholar] [CrossRef]
- Malin, M.R. Turbulent pipe flow of Herschel-Bulkley fluids. Int. Commun. Heat Mass Transf. 1998, 25, 321–330. [Google Scholar] [CrossRef]
- Bartosik, A.S. Modification of κ-ϵ model for slurry flow with yield stress. In Proceedings of the 10th International Conference on Numerical Methods in Laminar and Turbulent Flows, Swansea, UK, 21–25 July 1997; Volume 10, pp. 265–274. [Google Scholar]
- Bartosik, A.S. Modelling of a turbulent flow using the Herschel-Bulkley rheological model. Chem. Process Eng. Inzynieria Chem. Proces. 2006, 27, 623–632. [Google Scholar]
- Tanner, R.I.; Milthorpe, J.H. Numerical simulation of the flow of fluids with yield stress. In Numerical Methods in Laminar and Turbulent Flow, Proceedings of the Third International Conference, Seattle, WA, 8–11 August 1983; Pineridge Press: Swansea, UK, 1983. [Google Scholar]
- Mitsoulis, E. Flows of Viscoplastic Materials: Models and Computations; Rheology Reviews, British Society of Rheology: London, UK, 2007; pp. 135–178. [Google Scholar]
- Metzner, A.B.; Reed, J.C. Flow of non-Newtonian fluids—Correlation of the laminar, transition and turbulent-flow regions. AIChE J. 1955, 1, 434–440. [Google Scholar] [CrossRef]
- Dean, W. XVI. Note on the motion of fluid in a curved pipe. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1927, 4, 208–223. [Google Scholar] [CrossRef]
- Tunstall, M.J.; Harvey, J.K. On the effect of a sharp bend in a fully developed turbulent pipe-flow. J. Fluid Mech. 1968, 34, 595–608. [Google Scholar] [CrossRef]
- Rütten, F.; Schröder, W.; Meinke, M. Large-eddy simulation of low frequency oscillations of the Dean vortices in turbulent pipe bend flows. Phys. Fluids 2005, 17, 035107. [Google Scholar] [CrossRef]
- Kalpakli, A.; Örlü, R. Turbulent pipe flow downstream a 90° pipe bend with and without superimposed swirl. Int. J. Heat Fluid Flow 2013, 41, 103–111. [Google Scholar] [CrossRef]
- Wilson, K.C.; Thomas, A.D. A new analysis of the turbulent flow of non-Newtonian fluids. Can. J. Chem. Eng. 1985, 63, 539–546. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling in CFD, 3rd ed.; DCW Industries: La Canada Flintridge, CA, USA, 2006. [Google Scholar]
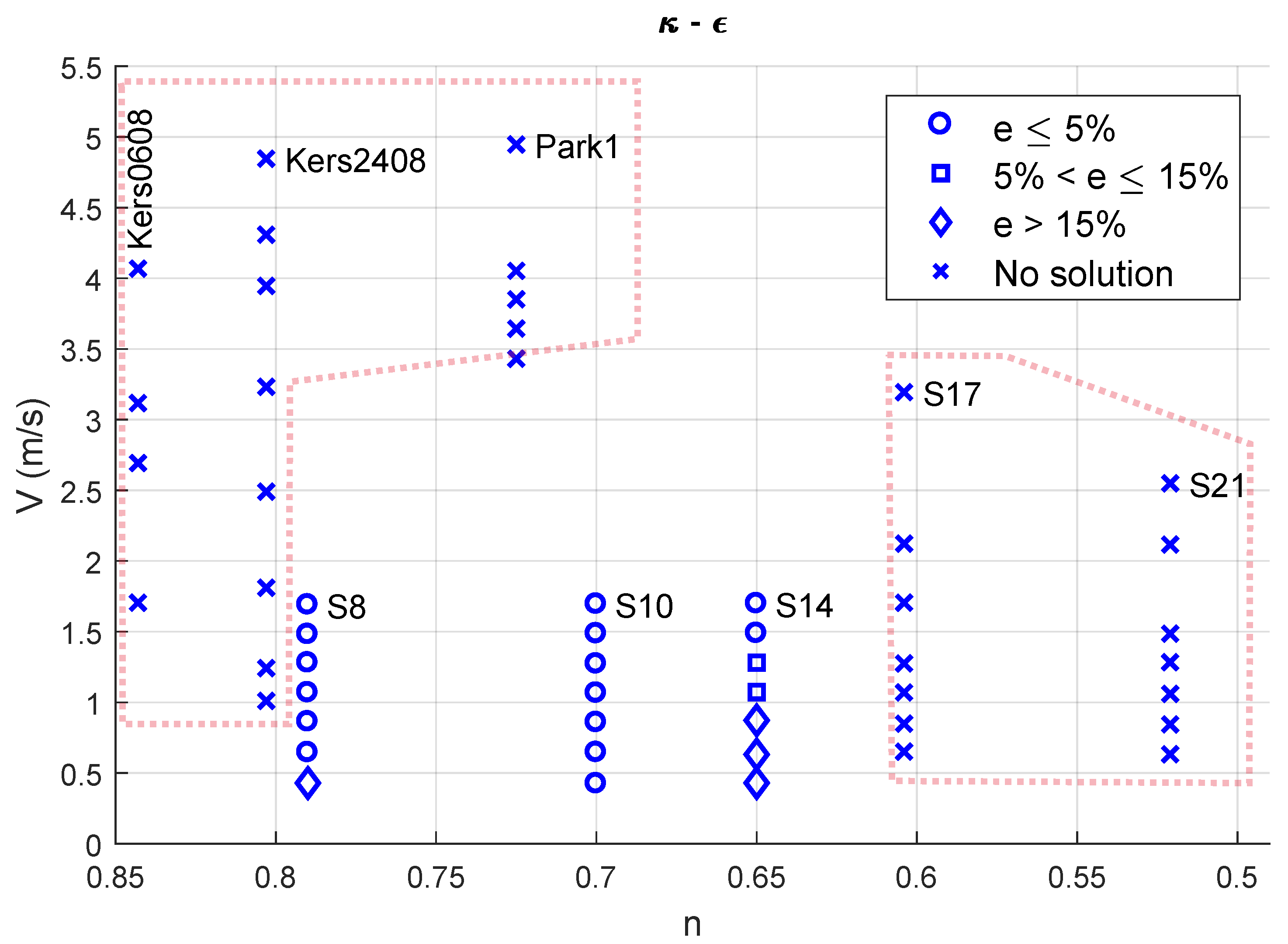
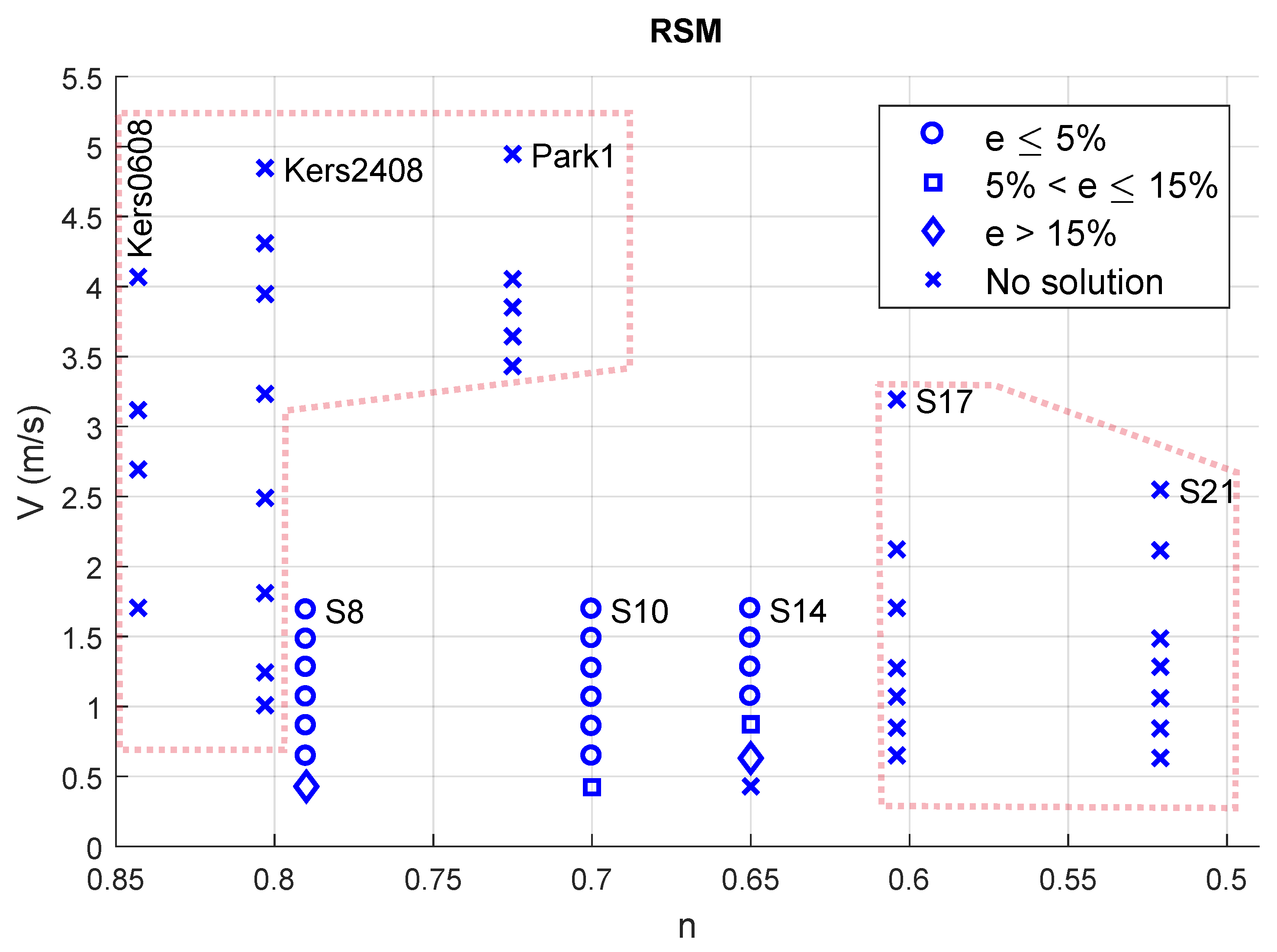
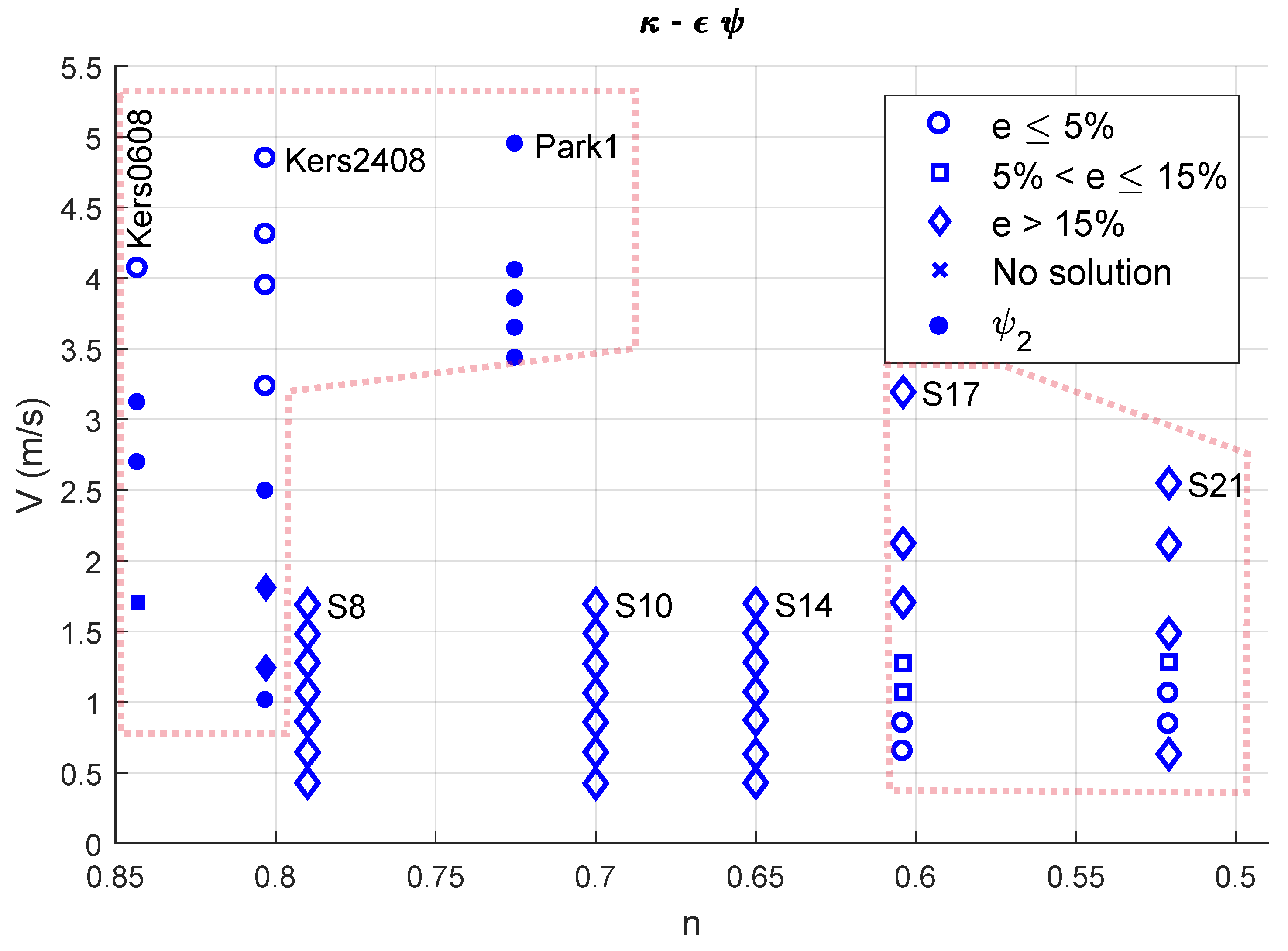
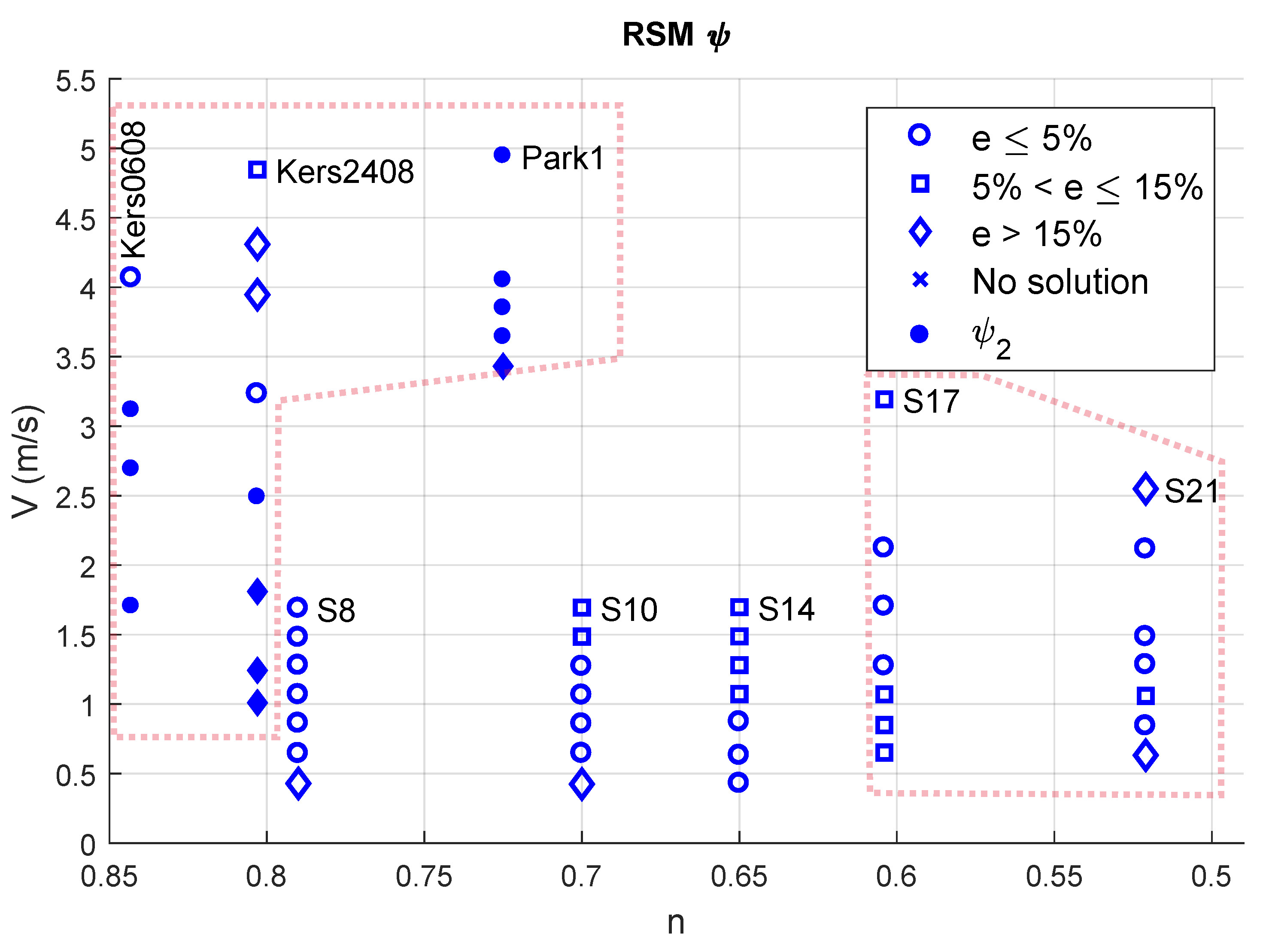
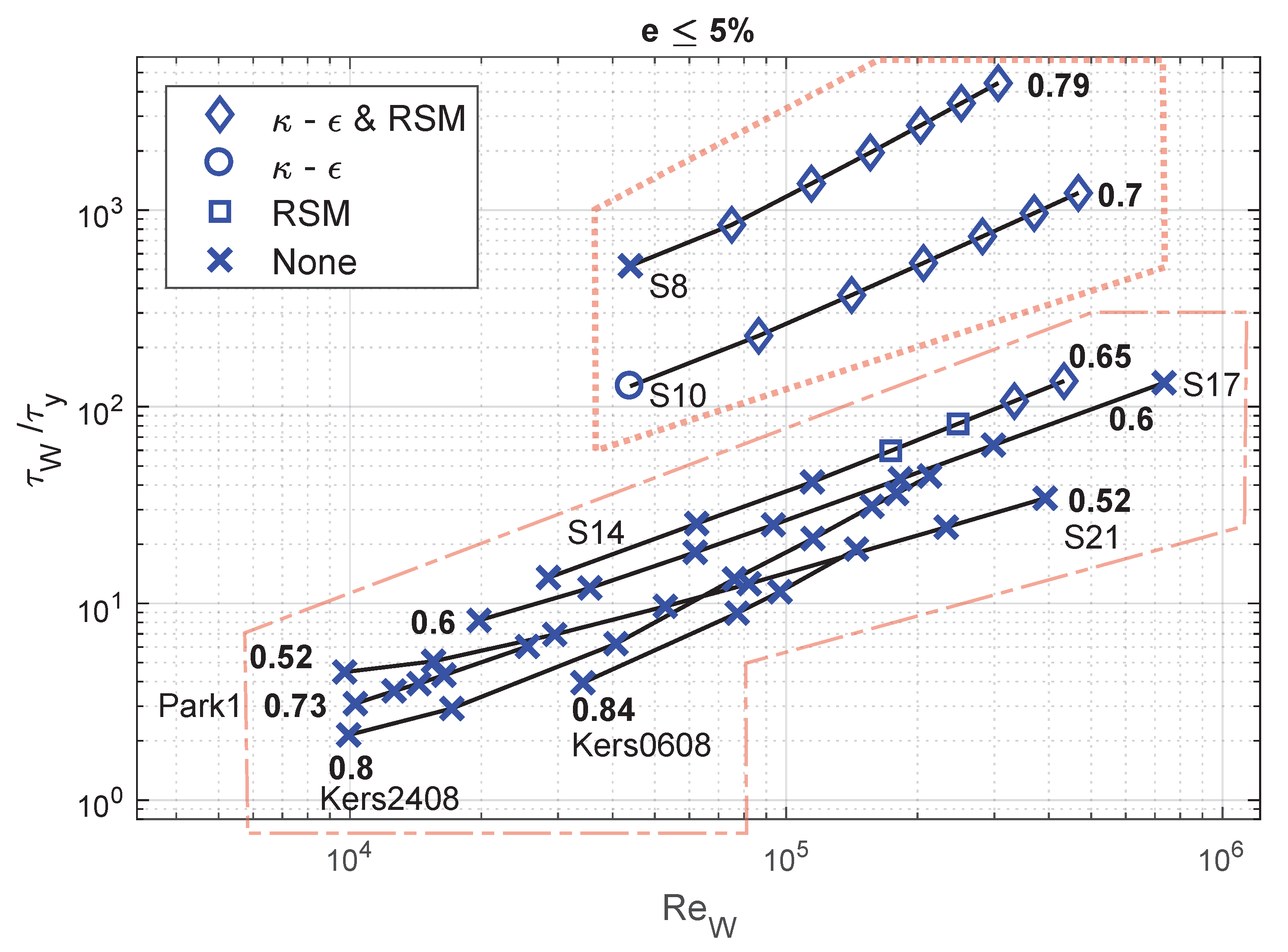
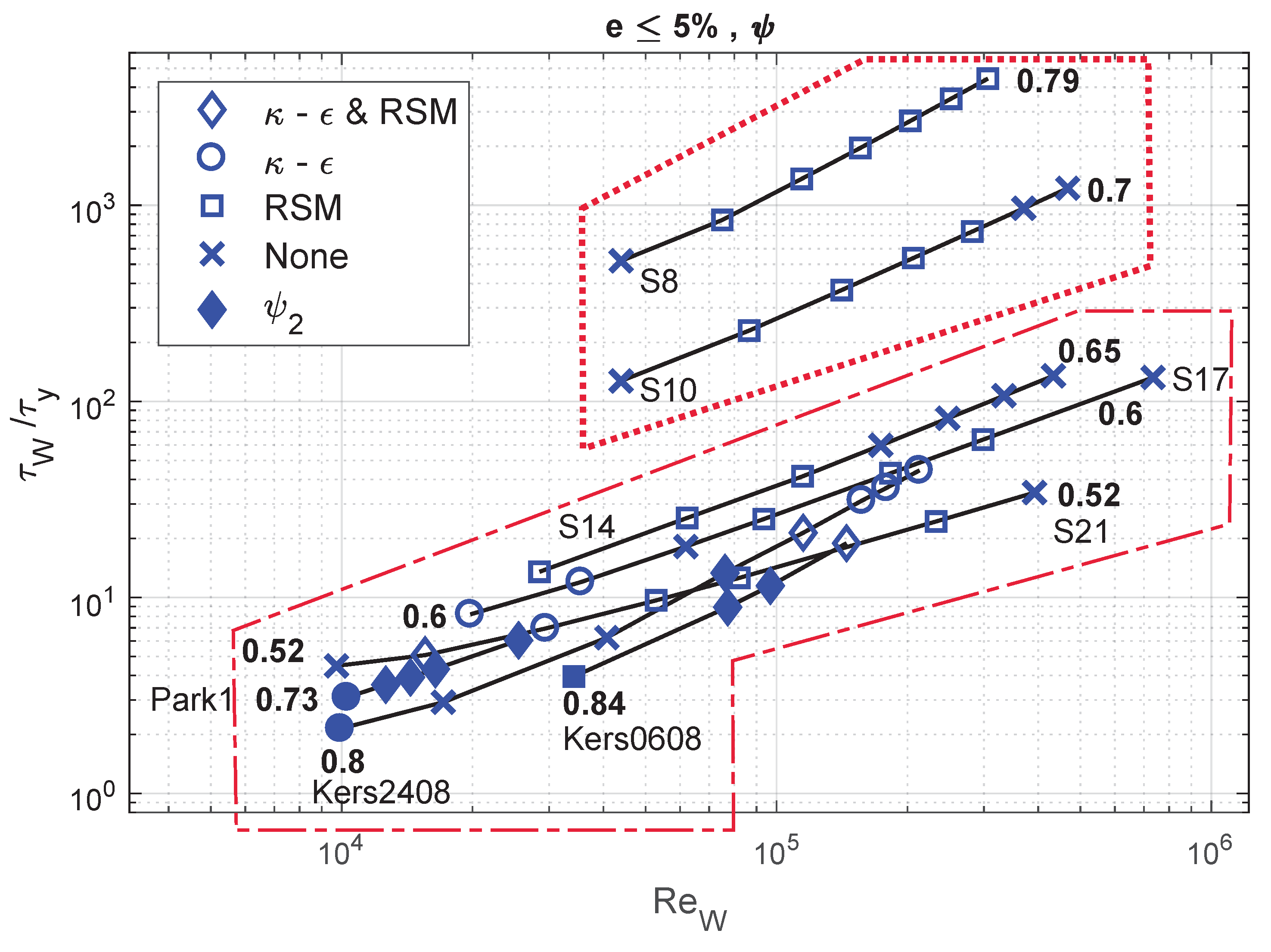
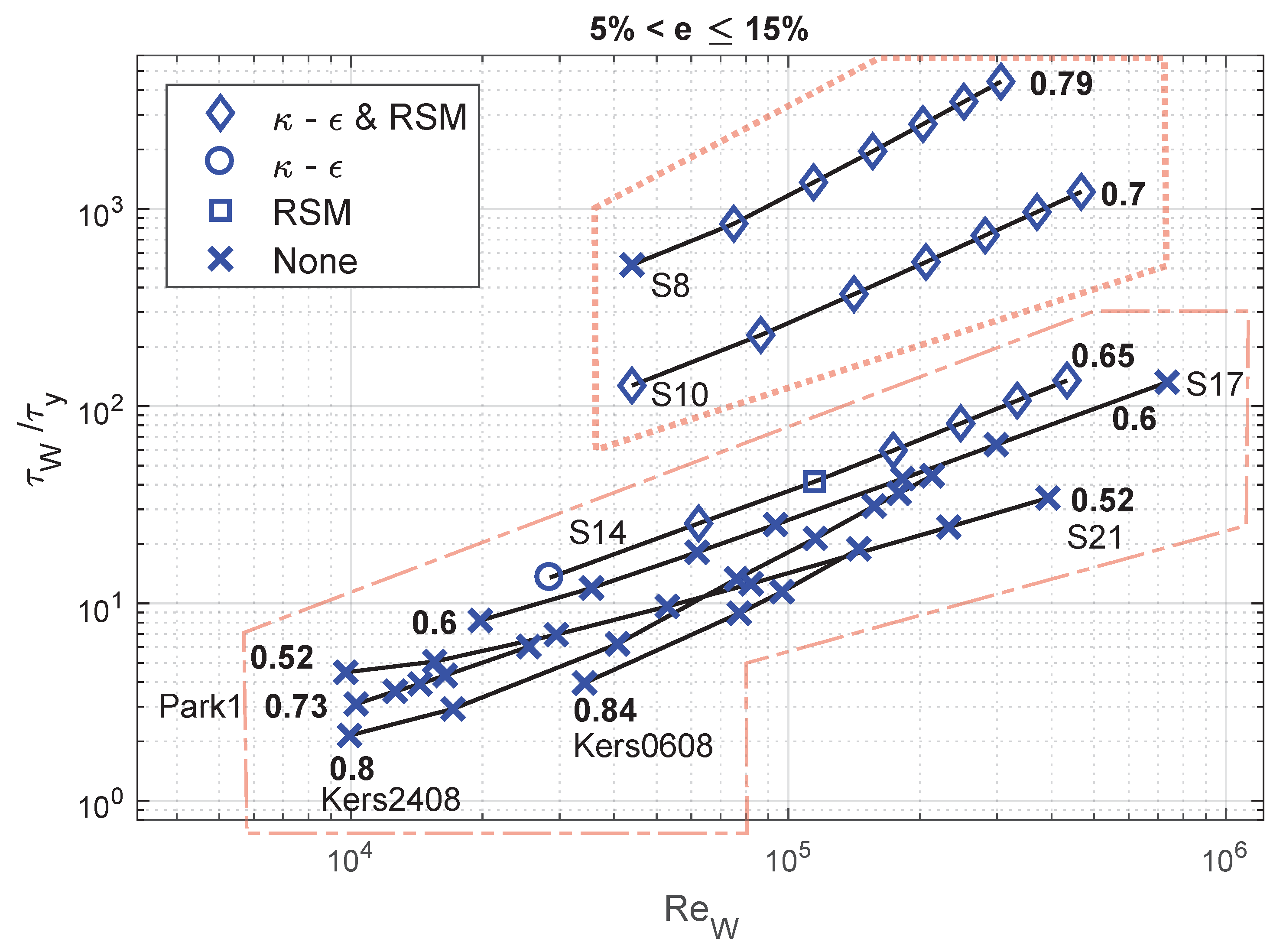
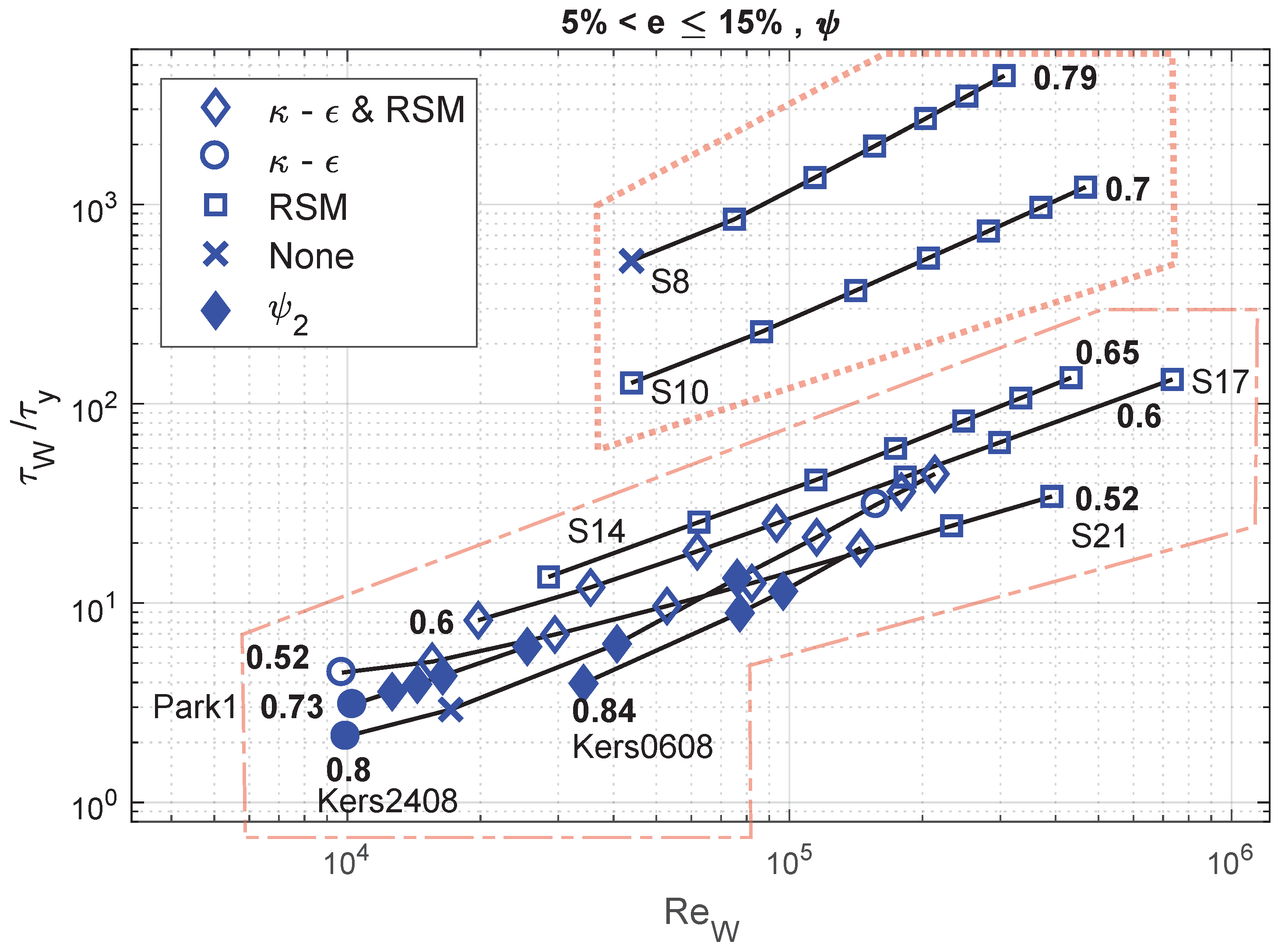
| Case | (kg/m) | (Pa) | m (Pas) | n | D (m) | Reference | |
|---|---|---|---|---|---|---|---|
| KERS2408 | 1061 | 1.04 | 0.0136 | 0.8031 | 0.079 | 380 | Slatter [22] |
| KERS0608 | 1071 | 1.88 | 0.0102 | 0.8428 | 0.079 | 380 | Slatter [22] |
| PARK1 | 1012 | 9.30 | 0.0894 | 0.7254 | 0.051 | 590 | Park et al. [23] |
| S8 | 1052 | 0.0014 | 0.0041 | 0.7900 | 0.100 | 450 | Thota Radhakrishnan et al. [1] |
| S10 | 1068 | 0.0052 | 0.0071 | 0.7000 | 0.100 | 450 | Thota Radhakrishnan et al. [1] |
| S14 | 1091 | 0.0490 | 0.0124 | 0.6500 | 0.100 | 450 | Thota Radhakrishnan et al. [1] |
| S17 | 1113 | 0.1585 | 0.0328 | 0.6043 | 0.100 | 450 | Thota Radhakrishnan et al. [1] |
| S21 | 1146 | 0.4316 | 0.0831 | 0.5207 | 0.100 | 450 | Thota Radhakrishnan et al. [1] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehta, D.; Thota Radhakrishnan, A.K.; Van Lier, J.; Clemens, F. Sensitivity Analysis of a Wall Boundary Condition for the Turbulent Pipe Flow of Herschel–Bulkley Fluids. Water 2019, 11, 19. https://doi.org/10.3390/w11010019
Mehta D, Thota Radhakrishnan AK, Van Lier J, Clemens F. Sensitivity Analysis of a Wall Boundary Condition for the Turbulent Pipe Flow of Herschel–Bulkley Fluids. Water. 2019; 11(1):19. https://doi.org/10.3390/w11010019
Chicago/Turabian StyleMehta, Dhruv, Adithya Krishnan Thota Radhakrishnan, Jules Van Lier, and Francois Clemens. 2019. "Sensitivity Analysis of a Wall Boundary Condition for the Turbulent Pipe Flow of Herschel–Bulkley Fluids" Water 11, no. 1: 19. https://doi.org/10.3390/w11010019
APA StyleMehta, D., Thota Radhakrishnan, A. K., Van Lier, J., & Clemens, F. (2019). Sensitivity Analysis of a Wall Boundary Condition for the Turbulent Pipe Flow of Herschel–Bulkley Fluids. Water, 11(1), 19. https://doi.org/10.3390/w11010019






