A Case Study of a Small Diameter Gravity Sewerage System in Zolkiewka Commune, Poland

Abstract

This article presents a small diameter gravity sewerage system in a rural area. In this system, domestic wastewater was preliminarily treated in septic tanks equipped with outlet filters, so the effluent features were similar to those of clear water. Additionally, some outlets were equipped with floating-ball check valves to avoid backflow. One of the pressure mains was used as a gravity collector conveying septic tank effluent in the direction of the pumping station during pump idle time. The operation of the system was simulated using SWMM computer code. The simulation results were validated for data obtained from part of a sewerage system in Kolonia Zolkiew and Rozki village consisting of two pumping stations and 86 serviced households using polyethylene pipes of outer diameter 50–63 mm. The results of the measurement of the outflows from one pumping station are presented. The simulation results showed good agreement with the empirical data, especially after several simulation days. The greatest discrepancy during the start-up period was the consequence of the initial conditions describing the empty pipework. Thanks to storage in the pump sumps, septic tank and pipes, as well as their smart operation, a relatively uniform inflow to the pumping stations was achieved. Simulations in SWMM showed that there is still potential to optimize the sewerage system through more adequate pump selection and pipe diameters.

1. Introduction

In rural areas of Poland, in the decade 2007–2016, 39,000 km of sanitary sewers were built, and the percentage of the rural population using sewerage systems increased from 12% to 41% [1]. Although the progress has been enormous, the choice of sewerage systems was not always rational. The designers’ experience, gained from urban sewerage systems, resulted in their being copied in rural areas. Mostly, classic gravity sewerage systems with numerous pumping stations were built, while alternative sewerage systems, including pressure and vacuum systems, were constructed only as exceptions. Rural areas are characterized by low population density in villages. Furthermore, the distances between the villages and towns are often 5–6 or more kilometers. In the case of sewerage systems with a central wastewater treatment plant for the whole commune, the length of force mains may exceed the length of the gravity sewerage system. This standard of sewerage system based on gravity sewers, numerous pumping stations, and long pressurized force mains to a central wastewater treatment plant has become almost obligatory in Poland since 2007. As a consequence, the unit capital costs of numerous sewerage systems related to one resident have been excessively high. Within the European Funding in the years 2007–2013 (structural funds), the mean unit capital costs of sanitary systems build in Poland were about 1000 EUR cap⁻¹, but in some cases they reached even 4000 EUR cap⁻¹ [2]. To avoid excessively high capital costs, a minimum population density factor equal to 120 inhab. km⁻¹ of sewer length is required in Poland. This was a prerequisite for granting subsidies for the sanitary sewerage systems. At the average unit capital cost 120 EUR m⁻¹ it gives 1000 EUR cap⁻¹, which corresponds to about three times the average monthly income in Poland [3].

In the light of the experience from the years 2007–2013 it is important to revise the selection criteria for sewerage systems. There is a need caused by limited funds to apply solutions better suited to rural areas. Without financial support from the EU, it will not be possible to sustain the same pace of development of sewerage systems in rural areas. Similar problems exist in many developing countries all over the world [4]. There is a need for cheap sewerage systems, with low capital and operational costs. In fact, simplified sewerage systems may be cheaper compared to conventional sewerage systems by up to 50% while providing similar effects [5,6,7,8]. Unfortunately, the majority of designers have no tools and experience in the hydraulic calculation of such systems. For this reason, the presentation of an exemplary system of this type and a tool to simulate its operation may increase its popularity among investors and designers.

The operation of new and existing sewerage systems is also hindered by reduced wastewater flows caused by a decrease in water consumption mainly due to the increase in water prices and the improvement of public environmental awareness, as well as the increasing efficiency of household appliances (e.g., washing machines, dishwashers, toilets). In Poland and other EU countries, a steady decline in household water consumption has been observed [1,9]. In some villages, the daily consumption of drinking water is as low as 30 dm³ per capita [10,11,12,13,14]. Classical gravity sewerage systems are very sensitive to sediments in wastewater. The sediments, settled in the channels, require flushing—even several times a year. This is an important problem in gravity sewers with small slopes and without self-cleaning velocities [15]. In addition, many pumping stations cannot cope with coarse solids [16]. Among other reasons, in non-urban areas it may be rational to use alternative systems that are insensitive to reduced wastewater flows. Such alternatives are pressure, vacuum and small diameter gravity sewerage systems [17]. If the population density is very low and the capital costs of such systems are very high, then the on-site method of wastewater treatment can be applied (e.g., a small wastewater treatment plant) [18].

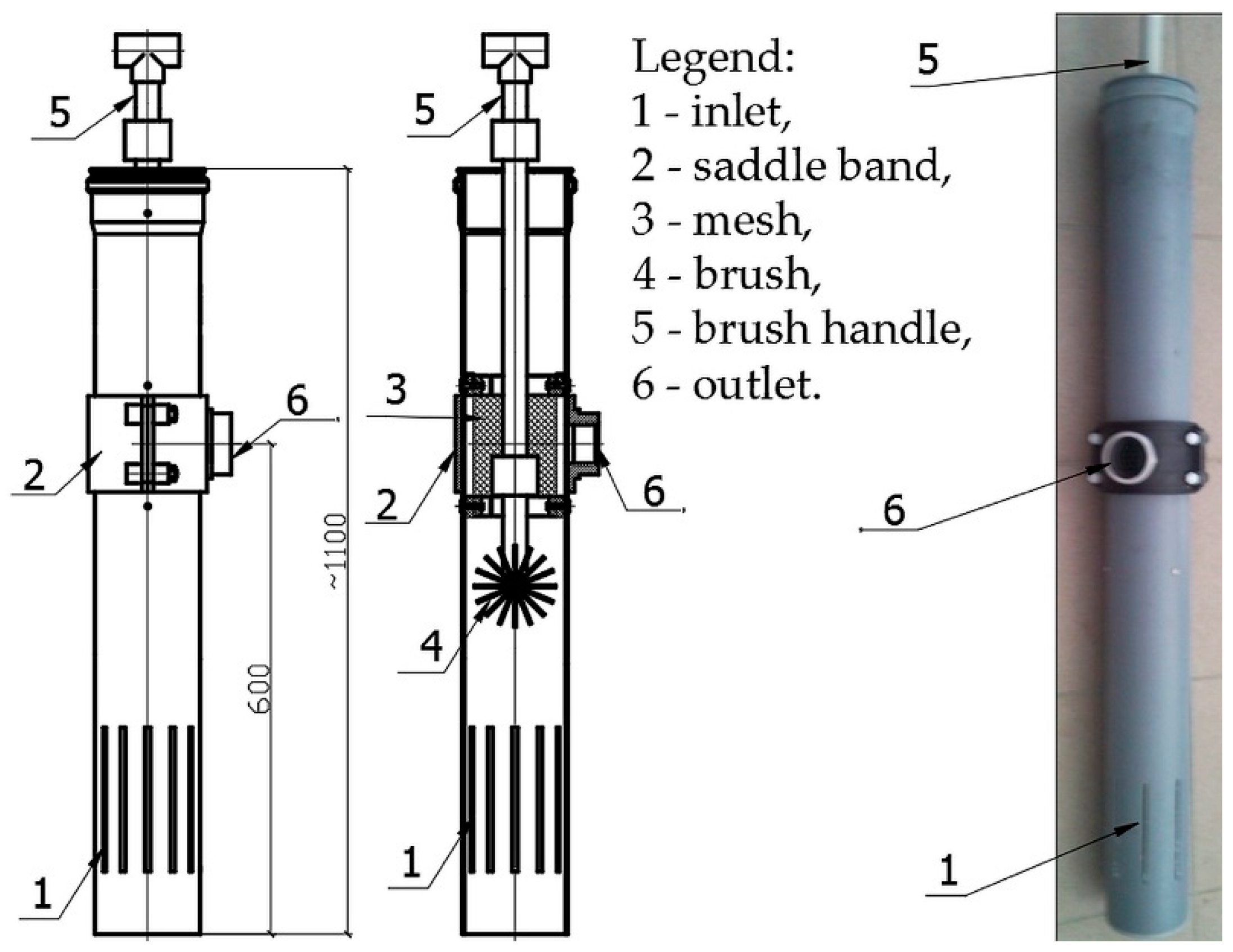
Important components of the small diameter gravity sewerage (SDGS) system are septic tanks (STs) to which wastewater flows from households. In STs, preliminary treatment takes place to reduce the concentration of suspended solids and organic matter [19,20,21]. Additionally, STs remove problematic solids from wastewater such as fibers, hairs, flushable wipes, rags, cotton sticks, bags, etc. In terms of hydraulic properties, they have properties similar to water [22]. From the ST, the wastewater flows into the wastewater treatment plant through a network of small diameter (from 25 to 100 mm), made of plastic (polyethylene—PE or polyvinyl chloride—PVC). Small diameter gravity sewerage pipes can be laid in parallel to the terrain with a possible negative slope (only the difference in levels between the inlet and outlet from the mains must be greater than the pressure loss) [23]. The ST effluent is typically carried out by gravity. Some households located lower in relation to the sewer main are equipped with small wastewater pumping stations to make the profile of the conduit more shallow [17]. In this system, in contrast to the traditional gravity sewerage system, instead of manholes, system access points at critical intersections and at least every 500 m are installed [19]. The SDGS system is used in unfavorable field conditions, such as flat or hilly terrain, a high level of groundwater, or a low population density [17].

This system has the following advantages:

• reduced water volume needed for the transport of suspended solids, compared with pressure and gravity [17],
• lower excavation costs than in a conventional gravity sewerage system [17,24],
• possibility of using trenchless methods of laying conduits, thanks to the use of small pipe diameters [17,19],
• lower capital costs and operating costs than those generated by a traditional sewerage system at the same level of service [20,25,26],
• ease of expanding the system or building a new network as opposed to traditional gravity sewerage, which is often oversized by design for 30 years (due to very high capital costs and land reconstruction costs) [20,26],
• minimizing the risk of failure, which generally affects only one household at a given time; during the failure periods, septic tanks provide reserve volume [27].

The disadvantages of such a system are as follows:

• necessity of periodic inspection, cleaning of outlet filter, emptying STs and sludge management [17,24],
• odor problems and corrosive aggressiveness of sewage and gases [17,24],
• poor knowledge of the system specificity and the lack of extensive experience in its operation [17,24],
• no possibility of cooperating with other alternative systems as a wastewater receiver [17].

The SDGS system, as part of a conventional gravitational system, was created in 1960 in Zambia [20]. In 1962, in Australia, an independent SDGS system was erected. It replaced a malfunctioning soil absorption system. In 2001, over 110,000 residents were serviced by such systems [28]. In Poland, this system is not widespread. It is mainly implemented by the company Biotop from Zamosc and the Department of Hydraulic and Sanitary Engineering of the Poznan University of Life Sciences. The oldest system in the village of Nieledew was built over 22 years ago [5] and has been working so far with a small number of failures, resulting mainly from improper operation and management. The low popularity of this system in Poland is probably due to the designers’ convictions regarding the superiority of traditional gravity sewerage and the lack of professional knowledge about the operation of such a system.

Because STs lengthen the hydraulic retention time of wastewater to several days and sludge and scum are deposited over several months, the effluent is putrefied. It releases, among other gases, hydrogen sulfide, which is corrosive, toxic and generates odors. These problems can be resolved by increasing the oxygen supply [29] into the transported wastewater and/or by installing odor control biofilters [29,30,31]. Robust treatment technologies in wastewater treatment plants should be applied (e.g., trickling filters, rotating biological contactors or constructed wetlands) rather than those vulnerable to toxic hydrogen sulfide (e.g., activated sludge) [31].

Designing an SDGS system raises many problems, which are connected with the lack of understanding of hydraulic conditions in the networks. The main problem is the determination of the design flow. Most often, this is calculated using empirical equations. Unfortunately, these equations are suitable for specific conditions characterizing the studied area. For example, Crites and Tchobanoglous [32] recommend the design flow calculated by the following equation (valid for N > 50):

$$Q_{max}=76+1.9N$$

(1)

where Q_max is maximum instantaneous design peak flow occurring once or twice per day (dm³ min⁻¹), and N is the number of contributing equivalent dwelling units (EDU).

Recently, Vincent [4] recommended the following equation:

$$Q_{max}=\frac{k_1\times k_2\times n\times q}{\mathrm{86,400}}$$

(2)

where Q_max is the maximum instantaneous design peak flow (dm³ s⁻¹); k₁ is the daily peak factor (for SDGS 1.2 ≤ k₁ ≥ 1.5); k₂ is the hourly peak factor (for SDGS 1.5 ≤ k₂ ≥ 2.2); n is the number of contributing inhabitants; and q is the unit water use (dm³·cap⁻¹·d⁻¹).

A design peak flow, taking into account the probability of its occurrence, based on different averaging time intervals and the number of serviced EDUs can be calculated as in [33]:

$$Q_{max}=Q_{dav}\times (1+t_{Pr}{C}_{vm})\sqrt{\frac{1440}{{\tau }_{av}+N-1}}$$

(3)

where Q_max is the maximum design peak flow (dm³ min⁻¹); Q_dav is the average daily flow (dm³ min⁻¹); N is the number of contributing equivalent dwelling units (EDU); t_Pr is the radius of confidence (e.g., t_Pr = 1.17 for exceedance Pr = 10%); C_vm is the variation coefficient of maximum flows for a single EDU (C_vm = 0.3–0.5); and τ_av is the number of minutes in the averaging interval (e.g., 1, 15 or 60).

There are many other formulas for calculating the design peak flow [17,20,21,23,34,35,36,37,38]. Unfortunately, they differ from each other, reflecting local conditions, e.g., unit water consumption per capita. In Poland, the average unit water consumption per capita (90 dm³·cap⁻¹·d⁻¹ [39]) is lower than in the USA (170–190 dm³·cap⁻¹·d⁻¹ [36]) and the EU (128 dm³·cap⁻¹·d⁻¹ [39]), and in rural areas these values are even twice as low as the average equal to 73 dm³·cap⁻¹·d⁻¹ [14,40]).

The aim of the study was to analyze in detail and present an unconventional sewerage system applied in a sparsely populated rural area with undulating terrain with a high groundwater level and low water use by inhabitants. The second objective was to examine the feasibility of applying the Storm Water Management Model (SWMM) to simulate operation of the SDGS system. In our previous works [22,41], the feasibility of applying the SWMM to simulate the emptying of a simple SDGS (four tanks without an effluent filter) system was checked in semi-technical and laboratory studies. As far we know, the SWMM has not been applied before for the simulation of such a system, and therefore its validation in a real case study seemed to be attractive. The working hypothesis was that the use of septic tanks positively influences the selection of pumps and their energy consumption.

2. Materials and Methods

2.1. Research Facility—Small Diameter Sewerage System in Zolkiewka Commune

The research was carried out on an active reference object of an SDGS system along with a wastewater treatment plant, built under the project Demonstrator + in the Zolkiewka commune (Lublin province). The system was built in 2015 in the villages of Kolonia Zolkiew and Rozki. A scheme is shown in Figure 1.

The studied SDGS system was made of PE pipes of diameter DN 63 mm (D_in = 55 mm) and lateral connections made of PE pipes of diameter 50 mm (D_in = 44 mm). The network worked generally as gravitational, but in some parts it could work alternately as gravitational or pressure. Two pumping stations on the network were installed. This network serves 86 households. The main profiles of this system are shown in Figure 2 and Figure 3. Invert depths, i.e., the vertical distances between the ground elevation and the pipe invert at a given node, ranged from 1.2 m to 3.4 m.

The pumping station PS_2 received wastewater from three branch lines (Z111.2-PS_2; Z63.2-PS_2; Z78.2-PS_2) to which 59 households were connected. At the beginning of the network four small individual pumping stations were connected to the section between the Z111.2 and PS_2 nodes. The wastewater from PS_2 was pumped periodically to PS_1. There were 20 additional households connected to the reach PS_2-PS_1. In this section, each ST was equipped with an effluent filter and a check valve to prevent the backflow of wastewater during the operation of the pump in PS_2.

Wastewater flowing to PS_1 was further pumped up to the manhole Sr1, from where it gravitationally flowed into the existing traditional gravity sewerage network. In the section between PS_1 and Sr1, there were seven households with STs connected to the bi-functional conduit which worked as a force main and alternatively as a gravity collector. During idle time of the pump in PS_1 the wastewater from the force-main has been run back to PS_1 through the emitter. The technical parameters of the studied system are summarized in

Table 1. Technical parameters of the reference system in Zolkiewka commune.

Reach	Number of Connected Households	Length of Lateral Connections (m)	Length of Network Conduits (m)
Z78.2-PS_2	12	429	428
Z63.2-PS_2	14	274	405
Z111.2-PS_2	33	840	1385
PS_2-PS_1	20	166	1206
PS_1-Sr1	7	122	636

and

Table A1. Technical parameters of the conduits.

Conduit Name	from Node	to Node	Length (m)	Inlet Offset (m)	Outlet Offset (m)
K44	K111	K110	32	0	0
Bypass1	P1.2	PS_1	1.5	0	1.42
Bypass2	P2.2	PS_2	1.5	0	0.7
K1	K78.1	K78.2	42	0	0
K10	K72	K71	32	0	0
K11	K71	K70	22	0	0
K12	K70	K69	25	0	0
K13	K69	K67	24	0	0
K14	K68	K67.1	2	0	0
K15	K67	K66	69	0	0
K16	K72.1	K72	36.5	0	0
K17	K71.1	K71	3.5	0	0
K18	K70.1	K70	4.5	0	0
K19	K69.1	K69	2.5	0	0
K2	K78.2	K78	12.5	0	0
K20	K67.1	K67	11	0	0
K21	K66	K65	71	0	0
K22	K65	K65.1	10	0	0
K23	K65.1	PS_2	23.5	0	0.17
K24	K63.1	K63.2	20	0	0
K25	K63.2	K63	35	0	0
K26	K63	K61	32	0	0
K27	K62.1	K62	41	0	0
K28	K62	K61	29	0	0
K29	K61	K60	14	0	0
K3	K78	K75	36	0	0
K30	K60	K58	46	0	0
K31	K58	K57	41	0	0
K32	K59	K58	43	0	0
K33	K57.1	K57	21.5	0	0
K34	K57	K56	70	0	0
K35	K56.1	K56	27	0	0
K36	K56	K55	57	0	0
K37	K55	K55.1	71.5	0	0
K38	K55.1	K64	20	0	0
K39	K64	K64.1	42.5	0	0
K4	K77	K76	7	0	0
K40	K64.1	PS_2	5	0	1.4
K41	Pp4.1	K111.2	13.5	0	0
K42	K111.2	K111	44	0	0
K43	K111.1	K111	15.5	0	0
K44.1	Pp3.1	K110	125.5	0	0
K45	K110	K109	44	0	0
K46	K109	K108	44	0	0
K47	K108	K107	14	0	0
K48	K107	K106	22	0	0
K49	K106	K105	24	0	0
K5	K76	K75	7.5	0	0
K50	K105.1	K105	25	0	0
K51	K105	K104	115	0	0
K52	K104.1	K104	6	0	0
K53	Pp2.1	K103.1	37	0	0
K54	K103.1	K103	33	0	0
K55	Pp1.1	K103	8.5	0	0
K56	K103	K102	63	0	0
K57	K102	K101	13.5	0	0
K58	K104	K101	25.5	0	0
K59	K101	K101.1	52.5	0	0
K6	K75	K74	26.5	0	0
K60	K101.1	K100	51	0	0
K61	K100	K100.1	53	0	0
K62	K100.1	K99	26	0	0
K63	K99	K91	24	0	0
K64	K98	K97	22	0	0
K65	K97	K96	38.5	0	0
K66	K96.1	K96	25	0	0
K67	K96	K95	15.5	0	0
K69	K94	K92	26	0	0
K7	K74.1	K74	4	0	0
K70	K93	K92	22.5	0	0
K71	K92	K91	19.5	0	0
K71.1	Z71.1	K71.1	5.2	0.9	0
K72	K91	K90	72	0	0
K73	K90	K89	20	0	0
K74	K89	K88	26.5	0	0
K75	K88	K85	60	0	0
K76	K87	K86	21	0	0
K77	K86	K85	23.5	0	0
K78	K85	K84	135	0	0
K79	K84	K83	43	0	0
K8	K74	K72	23	0	0
K80	K83	K82.1	40	0	0
K81	K82.1	K82	20	0	0
K82	K82	K81	35	0	0
K83	K81	K79	59	0	0
K84	K80.1	K80	25	0	0
K85	K80	K79	39	0	0
K86	K79	PS_2	77	0	1.4
K9	K73	K72	13	0	0
L68	K95	K94	33.5	0	0
P102.1	Z102.1	K102	5	0.9	0
P103.1	Z103.1	Pp1	1.5	0.9	0.6
P103.2	Z103.2	Pp2	1.5	0.9	0.6
P104.1	Z104.1	K104.1	15	0.9	0
P105.1	Z105.1	K105.1	6	0.9	0
P105.2	Z105.2	K105	1.5	0.9	0
P106.1	Z106.1	K106	5	0.9	0
P107.1	Z107.1	K107	4	0.92	0
P108.1	Z108.1	K108	16	0.9	0
P109.1	Z109.1	K109	6	0.9	0
P110.1	Z110.1	Pp3	1.5	0.9	0.6
P111.1	Z111.1	K111.1	7.5	0.9	0
P111.2	Z111.2	Pp4	1.5	0.85	0.55
P29.1	W29.1	K29.1	13.5	0	0
P30.1	W30.1	K30	8.5	0	0
P31.1	W31.1	K31	1	0	0
P31.2	W31.2	K31	42.5	0	0
P33.1	W33.1	K33	6.5	0	0
P34.1	W34.1	K34	1.5	0	0
P34.2	W34.2	K34	17.5	0	0
P36.1	W36.1	K36.1	9.5	0	0
P37.1	W37.1	K37	1.5	0	0.51
P38.1	W38.1	K38	1.5	0	0
P39.1	W39.1	K39	3.5	0	0.2
P39.2	W39.2	K39.1	19.5	0	0
P40.1	W40.1	K40	9.5	0	0.51
P41.1	W41.1	K41	1.5	0	0.51
P42.1	W42.1	K42	1.5	0	0
P44.1	W44.1	K44	27.5	0	0
P44.2	W44.2	K44	5.5	0	0
P45.1	W45.1	K45	0.2875	0	0
P46.1	W46.1	K46	7.5	0	0
P47.1	W47.1	K47	5.5	0	0
P48.1	W48.1	K48	4.5	0	0
P49.1	W49.1	K49	6.5	0	0
P50.1	W50.1	K50	6.5	0	0
P51.1	W51.1	K51	5	0	0
P52.1	W52.1	K52	15.5	0	0
P53.1	W53.1	K53	7.5	0	0
P54.1	W54.1	K54	5	0	0
P55.1	Z55.1	K55	8	0.4	0
P56.1	Z56.1	K56.1	33	0.3	0
P57.1	Z57.1	K57.1	90	0.4	0
P59.1	Z59.1	K59	10	1.1	0
P59.2	Z59.2	K59	5	1.1	0
P60.1	Z60.1	K60	23	0.8	0
P61.1	Z61.1	K61	26	0.8	0
P62.1	Z62.1	K62	3	0.4	0
P62.2	Z62.2	K62.1	9	0.4	0
P63.1	Z63.1	K63	26	0.9	0
P63.2	Z63.2	K63.1	5.5	0.9	0
P64.1	Z64.1	K64	2.5	0.9	0
P68.1	Z68.1	K68	2	0.9	0
P68.2	Z68.2	K68	16	0.9	0
P69.1	Z69.1	K69.1	7.5	0.85	0
P70.1	Z70.1	K70.1	12	0.8	0
P72.1	Z72.1	K72.1	10	0.8	0
P73.1	Z73.1	K73	4.5	0.9	0
P73.2	Z73.2	K73	6.5	0.8	0
P74.1	Z74.1	K74.1	3	0.9	0
P76.1	Z76.1	K76	2.5	1.2	0
P77.1	Z77.1	K77	23	1.3	0
P77.2	Z77.2	K77	2.5	1.2	0
P78.1	Z78.1	K78	13	0.9	0
P78.2	Z78.2	K78.1	12	1.1	0
P80.2	Z80.2	K80	21	0.9	0
P80.3	Z80.3	K80	66.5	0.8	0
P80.4	Z80.1	K80.1	9	0.7	0
P81.1	Z81.1	K81	11	0.9	0
P82.1	Z82.1	K82	13	0.9	0
P83.1	Z83.1	K83	66	0.9	0
P83.2	Z83.2	K83	1.5	0.9	0
P84.1	Z84.1	K84	18	0.9	0
P86.1	Z86.1	K86	2	0.9	0
P87.1	Z87.1	K87	2.5	0.9	0
P87.2	Z87.2	K87	37	0.9	0
P93.1	Z93.1	K93	11	0.9	0
P93.2	Z93.2	K93	6	0.9	0
P94.1	Z94.1	K94	24	0.9	0
P95.1	Z95.1	K95	2	0.9	0
P96.1	Z96.1	K96	8	0.9	0
P96.2	Z96.2	K96.1	8	0.9	0
P98.1	Z98.1	K98	20	1.3	0
P98.2	Z98.2	K98	6	1.3	0
P99.1	Z99.1	K99	10	0.9	0
PK1	K35	PS_1	75.5	0	1.69
PK10	K53	K52	38.5	0	0
PK11	K54	K53	48	0	0
PK12	K54a	K54	19.5	0	0
PK13	K54b	K54a	42	0	0
PK14	K36	K35	72.5	0	0
PK15	K37	K36	68	0	0
PK16	K40	K37	52.5	0	0
PK17	K41	K40	43	0	0
PK18	K42	K41	28.5	0	0
PK19	K43	K42	121.5	0	0
PK2	K45	K35	21	0	0
PK20	K44	K43	30.5	0	0
PK27	K39.1	K39	26	0	0
PK28	K39	K38.1	22	0	0
PK29	K38.1	K38	7	0	0
PK3	K46	K45	30	0	0
PK30	K38	K37	31.5	0	0
PK35	K36.1	K36	6	0	0
PK4	K47	K46	63	0	0
PK5	K48	K47	85.5	0	0
PK6	K49	K48	37	0	0
PK7	K50	K49	20	0	0
PK8	K51	K50	95	0	0
PK9	K52	K51	123.5	0	0
W29.1	Z29.1	W29.1	0.2875	0.9	0
W30.1	Z30.1	W30.1	0.2875	0.9	0
W31.1	Z31.1	W31.1	0.2875	0.9	0
W31.2	Z31.2	W31.2	0.2875	0.7	0
W33.1	Z33.1	W33.1	0.2875	0.9	0
W34.1	Z34.1	W34.1	0.2875	0.9	0
W34.2	Z34.2	W34.2	0.2875	0.7	0
W36.1	Z36.1	W36.1	0.2875	0.9	0
W37.1	Z37.1	W37.1	0.2875	0.9	0
W38.1	Z38.1	W38.1	0.2875	0.9	0
W39.1	Z39.1	W39.1	0.2875	0.9	0
W39.2	Z39.2	W39.2	0.2875	0.9	0
W40.1	Z40.1	W40.1	0.2875	0.9	0
W41.1	Z41.1	W41.1	0.2875	0.9	0
W42.1	Z42.1	W42.1	0.2875	0.9	0
W44.1	Z44.1	W44.1	0.2875	1.3	0
W44.2	Z44.2	W44.2	0.2875	1.3	0
W45.1	Z45.1	W45.1	0.2875	0.9	0
W46.1	Z46.1	W46.1	0.2875	0.9	0
W47.1	Z47.1	W47.1	0.2875	0.9	0
W48.1	Z48.1	W48.1	0.2875	0.9	0
W49.1	Z49.1	W49.1	0.2875	0.9	0
W50.1	Z50.1	W50.1	0.2875	0.9	0
W51.1	Z51.1	W51.1	0.2875	0.9	0
W52.1	Z52.1	W52.1	0.2875	0.9	0
W53.1	Z53.1	W53.1	0.2875	0.9	0
W54.1	Z54.1	W54.1	0.2875	0.7	0

,

Table A2. Technical parameters of the junctions.

Junction Name	Invert Elevation (m)	Maximum Depth (m)
K100	231.24	1.79
K100.1	231.24	2.56
K101	231.45	1.85
K101.1	231.34	1.69
K102	231.03	1.8
K103	228.1	1.8
K103.1	228.1	1.8
K104	231.45	2.45
K104.1	231.38	2.8
K105	231.45	1.65
K105.1	231.45	1.85
K106	231.6	2.1
K107	231.6	1.7
K108	231.7	1.8
K109	232.75	1.65
K110	233.29	1.71
K111	233.35	1.75
K111.1	233.35	3.39
K111.2	233.6	1.4
K27	234.7	1.4
K27.1	232.29	1.4
K27.2	232.35	1.4
K28	228.83	1.87
K28.1	228.11	1.69
K28.2	228.1	1.8
K29	230	1.8
K29.1	230.07	2.06
K30	232.7	1.8
K31	234.4	1.8
K32	227.12	2.18
K32.1	225.35	2.35
K33	227.15	1.8
K34	227.57	1.85
K35	225.64	1.4
K36	227.54	1.6
K36.1	228.03	2.67
K37	227.9	3.05
K38	230.89	2.35
K38.1	231.21	2.05
K39	231.25	1.8
K39.1	231.95	1.59
K40	227.95	2.9
K41	227.99	2.31
K42	228.02	1.8
K43	229.34	1.8
K44	232.55	1.4
K45	225.8	1.4
K46	225.89	1.61
K47	225.89	2.17
K48	225.89	2.33
K49	225.89	2.17
K50	225.89	1.61
K51	226.36	1.56
K52	226.36	1.8
K53	226.83	1.8
K54	227.25	1.8
K54a	227.4	1.8
K54b	225.8	1.4
K55	230.73	1.63
K55.1	227.25	1.8
K56	231.1	2.7
K56.1	232.83	2.2
K57	231.24	1.46
K57.1	232.46	2.07
K58	231.32	2.28
K59	231.56	1.51
K60	231.41	1.79
K61	231.44	1.8
K62	233.38	1.8
K62.1	233.4	1.6
K63	231.81	1.73
K63.1	232.36	2.61
K63.2	232.16	1.26
K64	227.23	1.97
K64.1	226.55	1.6
K65	224.3	2.6
K65.1	224.29	2.31
K66	229.79	1.4
K67	231.78	1.42
K67.1	231.78	2.42
K68	232.21	2.01
K69	232.3	1.8
K69.1	232.3	1.9
K70	233.4	1.9
K70.1	233.4	1.8
K71	233.85	1.82
K71.1	233.85	1.82
K72	234.23	1.77
K72.1	235.1	1.9
K73	234.49	2
K74	234.28	1.82
K74.1	234.9	1.5
K75	234.33	1.87
K76	234.64	1.36
K77	234.75	1.35
K78	234.4	1.8
K78.1	234.9	1.4
K78.2	234.4	1.8
K79	225.5	1.6
K80	227.8	1.8
K80.1	228.1	1.8
K81	225.7	1.6
K82	227.42	1.68
K82.1	227.46	2.34
K83	227.54	2.36
K84	227.63	1.77
K85	227.81	1.89
K86	227.86	1.84
K87	227.9	1.7
K88	230.41	1.79
K89	230.46	1.54
K90	230.5	1.2
K91	231.24	2.56
K92	231.64	2.26
K93	233.1	1.8
K94	231.67	2.03
K95	231.7	1.95
K96	231.72	1.98
K96.1	231.95	1.25
K97	231.76	2.24
K98	231.78	1.45
K99	231.24	2.55
P1.1	225.35	1.95
P1.2	225.35	1.95
P2.1	225.7	1.4
P2.2	225.7	1.4
Pp1.1	229.7	1.6
Pp2.1	227	1.6
Pp3.1	229.97	1.6
Pp4.1	232.15	1.65

,

Table A3. Technical parameters of the tanks.

Tank Name	Invert Elevation (m)	Maximum Depth (m)	Initial Depth (m)
Pp1	229	2.2	0.25
Pp2	226.4	2.2	0.25
Pp3	229.37	2.2	0.25
Pp4	231.5	2.2	0.25
PS_1	223.95	3.5	1
PS_2	225.1	4.1	0.55
W29.1	230.1	1.6	0
W30.1	233.1	1.6	0
W31.1	234.68	1.6	0
W31.2	236.34	1.8	0
W33.1	227.9	1.6	0
W34.1	227.82	1.6	0
W34.2	228.44	1.8	0
W36.1	229.2	1.6	0
W37.1	229.35	1.6	0
W38.1	231.82	1.6	0
W39.1	231.81	1.6	0
W39.2	232.04	1.6	0
W40.1	228.7	1.6	0
W41.1	228.7	1.6	0
W42.1	228.32	1.6	0
W44.1	232.76	1.2	0
W44.2	232.76	1.2	0
W45.1	226.35	1.6	0
W46.1	226.93	1.6	0
W47.1	226.43	1.6	0
W48.1	227.03	1.6	0
W49.1	226.4	1.6	0
W50.1	226.5	1.6	0
W51.1	226.66	1.6	0
W52.1	227.4	1.6	0
W53.1	227.64	1.6	0
W54.1	226.5	1.8	0
Z102.1	230.4	2.5	0.9
Z103.1	228.7	2.5	0.9
Z103.2	226.1	2.5	0.9
Z104.1	231.9	2.5	0.9
Z105.1	230.8	2.5	0.9
Z105.2	230.63	2.5	0.9
Z106.1	231.05	2.5	0.9
Z107.1	230.75	2.52	0.92
Z108.1	230.89	2.5	0.9
Z109.1	231.9	2.5	0.9
Z110.1	229.07	2.5	0.9
Z111.1	235.5	2.5	0.9
Z111.2	231.3	2.5	0.85
Z29.1	229.2	2.5	0.9
Z30.1	232.2	2.5	0.9
Z31.1	233.78	2.5	0.9
Z31.2	235.64	2.5	0.7
Z33.1	227	2.5	0.9
Z34.1	226.92	2.5	0.9
Z34.2	227.74	2.5	0.7
Z36.1	228.3	2.5	0.9
Z37.1	228.45	2.5	0.9
Z38.1	230.92	2.5	0.9
Z39.1	230.91	2.5	0.9
Z39.2	231.14	2.5	0.9
Z40.1	227.8	2.5	0.9
Z41.1	227.8	2.5	0.9
Z42.1	227.42	2.5	0.9
Z44.1	231.46	2.5	1.3
Z44.2	231.46	2.5	1.3
Z45.1	225.45	2.5	0.9
Z46.1	226.03	2.5	0.9
Z47.1	225.53	2.5	0.9
Z48.1	226.13	2.5	0.9
Z49.1	225.5	2.5	0.9
Z50.1	225.6	2.5	0.9
Z51.1	225.76	2.5	0.9
Z52.1	226.5	2.5	0.9
Z53.1	226.74	2.5	0.9
Z54.1	226.5	2.5	0.7
Z55.1	230.36	2.5	0.4
Z56.1	233.05	2.5	0.3
Z57.1	233	2.5	0.4
Z59.1	230.5	2.5	1.1
Z59.2	230.61	2.5	1.1
Z60.1	230.7	2	0.8
Z61.1	230.78	2	0.8
Z62.1	233.21	2	0.4
Z62.2	233.58	2	0.4
Z63.1	230.98	2	0.9
Z63.2	232.74	2.5	0.9
Z64.1	226.7	2.5	0.9
Z68.1	232.62	2.5	0.9
Z68.2	231.34	2.5	0.9
Z69.1	232.18	2.5	0.85
Z70.1	233.6	2.5	0.8
Z71.1	233.92	2.5	0.9
Z72.1	234.45	2.5	0.8
Z73.1	234.45	2.5	0.9
Z73.2	233.95	2.5	0.8
Z74.1	234	2.5	0.9
Z76.1	233.5	2.5	1.2
Z77.1	234.8	2.5	1.3
Z77.2	233.62	2.5	1.2
Z78.1	233.9	2.5	0.9
Z78.2	234	2.5	1.1
Z80.1	227.8	2.5	0.7
Z80.2	228.3	2.5	0.9
Z80.3	229.24	2.5	0.8
Z81.1	227.4	2.5	0.9
Z82.1	229.2	2.5	0.9
Z83.1	229.5	2.5	0.9
Z83.2	227.4	2.5	0.9
Z84.1	229	2.5	0.9
Z86.1	227.5	2.5	0.9
Z87.1	227.1	2.5	0.9
Z87.2	227.2	2.5	0.9
Z93.1	232.5	2.5	0.9
Z93.2	232.45	2.5	0.9
Z94.1	231.29	2.5	0.9
Z95.1	231.11	2.5	0.9
Z96.1	231.15	2.5	0.9
Z96.2	231.05	2.5	0.9
Z98.1	230.91	2.5	1.3
Z98.2	230.5	2.5	1.3
Z99.1	230.97	2.5	0.9
Sr1	234.1	1.4	0

and

Table A4. Technical parameters of the pumps.

Pump Name	from Node	to Node	Level of Pump Start-Up (m)	Level of Pump Shut-Off (m)
P1	PS_1	P1.1	1.68	1
P2	PS_2	P2.1	1.05	0.55
Pp4	Pp4	Pp4.1	0.6	0.25
Pp3	Pp3	Pp3.1	0.6	0.25
Pp2	Pp2	Pp2.1	0.6	0.25
Pp1	Pp1	Pp1.1	0.6	0.25

(in Appendix A). The parameters and names of individual components of the SDGS system were adopted in accordance with the design project provided by the company Biotop.

The vertical section through the pumping station PS_1 is shown in Figure 4. The main element of the station was a 3.5 m high tank of mean diameter of 1.5 m made of polyester resin reinforced with fiberglass. The total volume was about 5.0 m³, and the active capacity was about 1.1 m³. The wastewater flows via a pipeline with a diameter DN = 63 mm, equipped with a shut-off valve (2), a tee and a check valve (3) at the inlet to the pumping station. Thanks to the suction made by a vacuum pump and hermetic tank with a capacity of about 100 dm³ (4), additional suction of wastewater is created by generating a negative pressure equal to −3.0 m H₂O, which is later released from the tank as a result of a pressure increase in the network. It was provided as an emergency option. Initially, a single centrifugal pump (8) type SEG40.09.1-50B—Maximum flow of 4.1 dm³·s⁻¹ at head 2 m H₂O and maximum head of 14 m H₂O at 0.1 dm³·s⁻¹—was used for pressurized wastewater transport [42]. The pumps installed in pumping station PS_1 and PS_2 were equal. After 18 months of operation, the pumps (in both PS) were replaced by more efficient (doubled) centrifugal pumps with closed impellers SP 5A-4-3P with a maximum flow of 1.8 dm³·s⁻¹ at head 9 m H₂O and a maximum head of 25.5 m H₂O at 0.1 dm³·s⁻¹ [43]. To control the pump operation and to measure wastewater levels a hydrostatic probe was used, equipped with a measuring bell (15) at the bottom.

All 86 homesteads had their own septic tank (ST). Every septic tank in the reference system was constructed of concrete rings of diameter 1.2 m. The depth of these STs associated with the outlet of wastewater to the network was in most cases 0.9 m. The initial storage volume of the ST was therefore about 1 m³. Septic tanks were equipped with innovative fittings in the form of effluent filters (Figure 5) and floating-ball valves (check valves) (Figure 6). The floating-ball valves acted as check valves and prevented air from entering the system. These valves were installed mainly at the outflow from unfavorably low-laid ST or connected to the force main (PS_2-PS_1; PS_1-Sr1), which could be flooded with wastewater from the network during the period of emptying an ST located more favorably or during the work of the pump in the pumping stations (PS).

Another innovative solution used in this system was the work of the force main connecting PS_1 with Sr1 as a force main at the time of operation of the pump in PS_1 and gravity during its idle time. Seven septic tanks, equipped with floating-ball valves (check valves), were connected to this force main. During the operation of the pump, the check valves prevented the backflow of wastewater from the force main to septic tanks. During this time, wastewater from the connected households was retained in the septic tanks. When the pump was shut down, the force main was slowly drained via an emitter back to the pumping station and the wastewater was aerated, decreasing its putridity. At the end of the emitter, a nearly closed ball valve was installed, which significantly limited the emptying of the pipeline. The pipeline was never drained out. However, its partial emptying enabled the opening of the check valves installed behind seven septic tanks connected to the force main.

2.2. Supervisory Control and Data Acquisition

In the presented system, the pressure and wastewater levels in both pumping stations were measured. Pressure was monitored in gravity-pressure collectors downstream from wastewater pumps (9) (Figure 7). The wastewater levels in the pumping station tank were monitored by means of hydrostatic probes and additionally by means of a pressure sensor. The Fluxus ADM 5107 ultrasonic flow meter was installed to assess the operation of the pumping station at the force main downstream from the PS_1 pumping station. Although the flow measurements allowed assessment of the system’s operation, they are not indispensable for normal operation of the pumping stations.

The used programmable logic controller was equipped with a function detecting pressure lasting for a long period of time (more than 24 h) inside the pipeline (14) (Figure 7). This enabled detection of abnormal network operating states, in particular, the emptying of drainage pipes taking tool long (together with the STs) or lack of wastewater inflow. This latter problem may be caused by blocked ST outflows or clogged drainage pipelines. However, most often pipeline clogging is caused by trapped air.

2.3. Usage of SWMM for the Simulation of Small Diameter Sewerage Systems

The following components can be distinguished in a model of a small diameter gravity sewerage system:

• junctions,
• connections,
• septic tank with effluent filter,
• floating-ball valves acting as check valves,
• home and network wastewater pumping stations,
• manholes,
• outlet from SDGS system to traditional gravity system.

The junctions are placed at characteristic points of the sewerage network, i.e., at changes in sewer slope, direction and/or diameter, and also at connections of other sewers. In the SWMM 5.1 program junctions are represented by manholes (the terms in bold are described in the SWMM manual [44]). In the SDGS system, the traditional manholes are replaced by tee or elbow fittings. For this reason, in the program options in the field minimum surface area (cross-sectional area of manhole representing junction—a kind of Preissmann’s slot), a very small value of 10⁻⁵ m² was introduced. In addition, the surcharge depth (manhole depth at which terrain flooding occurs) value was set as high as 1000 m—the limit value of pressure that the fitting can withstand—and the value 0 in the ponded area (lack of flooding).

The septic tanks in the SDGS system were simulated in the program using the storage unit. The max. depth value (tank maximum depth) was assumed to be 2.5 m (according to the design project), and the type of storage curve function was functional. The values of this function were the products of wastewater depth and the cross-sectional area of the septic tank (C = (π × D²)/4 = (π × 1.2²)/4 = 1.131 m²). The initial level of wastewater in the tank was assumed to be equal to the inverted level of the outlet from the ST (0.9 m above the tank bottom). The minor loss at the effluent filter from the ST was simulated using the value of the coefficient ξ = 2.5 (obtained from previous research [22]).

The floating-ball check valves in the project were placed in manholes of diameter 425 mm. In the SWMM, check valves and manholes were simulated using the storage unit. Head losses during wastewater flow through the check valve were simulated by providing the minor loss coefficient equal to ξ = 10 (obtained from previous research [22]). The presence of the check valve was simulated by setting the value of YES in the field flap gate for the connection between the manhole and the network.

The pipelines of the SDGS system were simulated by conduits. At gravitational flow the circular shape was chosen. The Manning roughness coefficient was assumed to be n = 0.01 s·m^−1/3 [45] for a partially filled conduit. When the flow was only pressure-driven, a cylindrical shape of fully-filled force_main shape was selected (a pipeline roughness equal to 0.01 mm was assumed [46]) and the Darcy–Weisbach equation for the calculation of frictional head losses was applied.

In the case of the pumping stations, the pump sump was simulated separately as a storage unit and the pump as a pump installed inline in a short conduit. In the pump curve editor in the field pump type, TYPE3 was selected and values of the pump heads and the corresponding flows in tabular form were introduced. Additionally, the emitter installed in the pumping station was simulated by conduit links PT1.1, PT1.2 and Bypass 1 (Figure 8). The pump sumps of pumping stations PS_1 and PS_2 were described by providing the elevation of the tank bottom and the initial wastewater level, equal to the shut-off level (Figure 8). In addition, due to the irregular shape of the tank in the storage curve field, the tabular values were given, and in the curve name field the name of the curve describing the change in the cross-sectional area of the tank in relation to the corresponding wastewater depth was given.

In the actual pumping station PS_1 during the pump’s work, a part of the wastewater was returned via the emitter back to the pumping station tank. During the pump’s idle time via the emitter (almost closed valve) the force main was slowly drained out. The emptying of the force main allowed for the emptying of all seven STs, located downhill, into the force main. When the pump started working again, the wastewater was pumped uphill to the manhole Sr1. The properties of this conduit—diameter (26 mm) and length (1.5 m)—were set in accordance with the design project and field measurements. The presence of the check valve was simulated by setting the value YES in the field flap gate and the minor loss coefficient for the emitter in the pumping station equal to 4000 was taken [22], typical for an almost closed ball valve. This head loss was also influenced by the emitter connection to the force main via a check valve. Unfortunately, such a set made the local minor coefficient variable in time.

An important issue was the simulation of the wastewater inflow to the SDGS system in the SWMM 5.1 program. The total number of served inhabitants was 172. In 86 buildings, there lived an average of two people per household. For this purpose, eight different patterns of wastewater inflow to the ST were created [11], which were replicated without any changes for nine days of simulation. When creating inflow patterns, the use of sanitary appliances in the time, quantity and volume of outflowing wastewater from the household was assumed according to

Table 2. Assumed values of parameters describing appliances used in a typical household [47].

Sanitary Appliance	Time of Wastewater Outflow (s)	Volume of Wastewater Outflow (dm3/use)	Volumetric Flow Rate of Wastewater (dm3·s−1)	Frequency of Uses per Person Per Day (d−1)
Shower	180	25.0	0.14	0.5
Water closet	3	6.0	2.00	1.0
Water closet—Urine flushing only	3	2.5	0.83	1.0
Wash-basin—Hands washing	30	1.5	0.05	2.0
Wash-basin—Teeth brushing using a cup	2	0.2	0.10	1.0
Automatic washing machine	150	30.0	0.20	0.5
Dish washing by hand in the sink	120	15.0	0.125	0.5

. In the time series editor, the name (No. 1–8) of the inflow pattern was input and the values from relevant inflow histograms were pasted (Figure 9). The eight different patterns, shown in Figure 9, were assigned to STs at random. Each ST got one inflow pattern of the eight different patterns (No. 1–8).

After implementing eight different patterns of wastewater inflow to the SWMM 5.1 program, they were treated as inflows to different STs. As a result, inflows to the network nodes were defined. The created patterns of wastewater inflow corresponding to the mean daily outflow of wastewater from a household equal to 93 dm³ EDU⁻¹ were assumed to be the same for each ST. Due to this fact, a multiplier equal to 1.0 was set in the scale factor field in window inflows for each ST.

2.4. Cost Analysis Methodology

To compare the investigated SDGS system with a conventional gravity system, the capital costs and operation and maintenance (O&M) cost were estimated. As a part of feasibility study made by Biotop Company [48], both the conventional gravity and SDGS systems were considered with pumping stations. Further comparison of both alternatives was based on the cost–effectiveness analysis (CEA) method, in which the financial costs are compared with the non-pecuniary benefits obtained [7,49,50]. There are several methods used for estimating cost effectiveness. Equivalent annual cost (EAC) was estimated using the following equation [51]:

$$EAC=I_0 \frac{d{(1+d)}^T}{{(1+d)}^T-1}+C_{av}$$

(4)

where I₀ is capital costs (EUR); C_av is average O&M cost (EUR·y-r⁻¹); d is discount rate; and T is lifetime of the investment (y-r).

Equivalent unit cost (EUC) has been also used in the form [51]:

$$EUC=\frac{EAC}{{{\displaystyle \sum }}_{n=1}^{365}{\mathrm{Q}}_{dn}}$$

(5)

where Q_d is the daily wastewater flow (m³·d⁻¹).

3. Results

3.1. Wastewater Levels and Outflows from Pumping Stations

The measured values of the pump operation times along with the number of pump starts and daily wastewater flows for PS_2 and PS_1 are given in

Table 3. Measured pumping station’s operational characteristics.

Date	Pump Operation Time		Number of Pump Starts		Daily Flow Qdout
	PS_1	PS_2	PS_1	PS_2	PS_1	PS_2
Year-Month-Day	s·d−1	s·d−1	d−1	d−1	m3·d−1	m3·d−1
2016-08-11	7243	3299	9	5	7.35	4.0
2016-08-12	7542	3299	11	5	8.15	4.0
2016-08-13	9301	3136	10	8	9.34	6.4
2016-08-14	9469	3287	11	5	8.56	4.0
2016-08-15	7505	2643	9	4	8.56	3.2
2016-08-16	6869	3386	9	5	6.33	4.0
2016-08-17	6590	2604	9	4	7.48	3.2
2016-10-12	7932	3302	7	8	8.15	6.4
2016-10-13	9301	3136	10	8	8.41	6.4
2016-10-14	9713	3453	9	8	7.66	6.4
2016-10-15	10,144	3916	9	9	7.88	7.2
2016-10-16	10,071	3916	9	9	8.46	7.2
2016-10-17	7560	2985	7	7	5.35	5.6
2016-10-18	7640	2138	6	5	5.09	4.0
2016-10-19	7686	3015	7	7	8.18	5.6
2016-10-20	8369	3461	7	8	7.65	6.4
2016-10-21	8794	3318	7	8	6.97	6.4
2016-10-22	13,153	5097	7	11	12.56	8.8
2016-10-23	9793	3911	6	9	10.88	7.2
2016-10-24	6898	3424	4	8	5.19	6.4
2016-10-25	13,460	3465	7	8	10.14	6.4
Average	8811	3342	8.1	7.1	8.02	5.68
Std. deviation of the average value	398	125	0.4	0.4	0.38	0.33
Coefficient of variation (CV)	0.21	0.17	0.22	0.26	0.22	0.26
Number of EDU	86	59	86	59	86	59

. The results of the measurement of wastewater flow, using an ultrasonic flow meter in PS_1, for three consecutive days are shown in Figure 10. When the pump starts, a significant increase in flow rate can be observed, which then decreases. This phenomenon results from an earlier partial emptying of the force main by the emitter in the pumping station. For this reason, the static and friction heads at the pump start-up were much lower than at the moment of pump shut-off. Moreover, the force-main PS_1-Sr1 with lateral connections were rarely fully filled due to their storage capacity (1.7 m³) being much higher than the active storage in PS_1 (1.05 m³). When the pump was shut off, a reverse flow occurred through the emitter back to the pumping station. In the initial phase, after the pump was shut off, it was the highest (around 0.26 dm³·s⁻¹), and then it quickly decreased to about 0.01 dm³·s⁻¹. It remained at this rate until the next pump start in the pumping station.

There was no flowmeter in PS_2. Daily outflows from PS_2 were estimated by the volumetric method multiplying the number of pump starts by active storage volume (0.80 m³). The pump operation time and number of pump starts were highly variable. This was probably caused by the high variability of use of sanitary appliances in individual households. An additional factor affecting the volume of flow could be a different number of current residents using sanitary appliances. In these areas, very often, part of the population emigrates in search of work and returns from time to time. Many young people are studying and only periodically return to the family home. The number of pump starts in PS_1 and PS_2 ranged from 4 to 11 per day. The average number of pump starts in PS_1 was 8.1 ± 0.4 d⁻¹, and for the pump in PS_2 it was 7.1 ± 0.4 d⁻¹. The pump operation time in PS_1 was twice as long as the pump operation time in PS_2. It was caused by the higher static head (PS_1 −9 m vs. PS_2 −2 m), as well as by the higher wastewater volume. Analyzing the data in Table 3, one may conclude that the higher the number of dwelling units, the smaller the variation in pump operation and outflows rates. In Figure 10 one can observe relatively uniform inflow and outflow thanks to the large retention volume of the system.

3.2. Results of the Simulation of the SDGS System in SWMM 5.1

The results of the pump operation time and the number of pump starts per day in PS_1 and PS_2 obtained from the simulation are presented in

Table 4. Simulated pumping station’s operational characteristics.

Day	Pump Operation Time (s·d−1)		Number of Pump Starts (d−1)		Daily Flow (m3·d−1)		Qd/Qdav out
	PS_1	PS_2	PS_1	PS_2	PS_1	PS_2	PS_1	PS_2
1	4088	1578	4	4	3.11	2.39	0.39	0.42
2	9930	3951	9	8	8.45	6.22	1.05	1.10
3	9455	3378	8	6	7.73	5.33	0.96	0.94
4	9287	4068	8	6	7.76	6.38	0.97	1.12
5	8835	3322	8	6	7.25	5.23	0.90	0.92
6	8924	3352	8	7	7.30	5.25	0.91	0.92
7	8820	3251	8	6	6.97	5.10	0.87	0.90
8	9426	3264	9	7	7.80	5.17	0.97	0.91
9	7848	3134	8	8	6.23	4.93	0.78	0.87
Average without the first day	9066	3465	8.3	6.8	7.44	5.45	0.93	0.96
Std. deviation of the average value without the first day	193	108	0.1	0.3	0.21	0.17	0.03	0.03
Coefficient of variation (CV) without the first day	0.06	0.09	0.05	0.12	0.08	0.09	0.08	0.09
RoM without the first day	1.03	1.04	1.02	0.95	0.93	0.96	-	-

. In addition, wastewater outflow from pumping stations PS_1 and PS_2 is given. Based on the results of the simulation for the first day, it can be concluded that there are very large discrepancies between the results obtained from the simulation and the results obtained from the measurements. However, it should be taken into account that the measurements were performed more than half a year after the network start-up period. The results from the simulations for the first day show in the early hours of the day no pump starts, which is related to the filling of pipelines in the initial phase of the simulation (Figure 11). After this period the work of the pumping station begins. Due to the lack of balancing of the inflow and outflow in the first days of simulation, there are still large discrepancies between the obtained results. On the next days of simulation the results are more convergent (Figure 12 and Figure 13). The simulation results obtained for the second and subsequent days turned out to be closer to the results obtained from the measurements. On the basis of the performed simulation it can be stated that there is a need for initiation of the simulation (equal to one day in this case) and only the results of subsequent days should be compared with measurements. In some places the pump start time converges with the results obtained from the measurements. Full convergence of the simulation results with the results from the measurements was not obtained, but it is hardly possible due to the lack of water use measurements. Flows in the SDGS system depends on the amount of wastewater flowing into the system as well as the time and place of its inflow. Such flows are characterized by high randomness. The results of field measurements indicate large variability on individual days of measurements in the amount of pumped wastewater (Q_dav = 8.02 ± 0.38 m³·d⁻¹), pump operation time (8811 ± 398 s), numbers (8.1 ± 0.4 d⁻¹) and moments of pump starts. For this reason, it is possible only to a certain extent to imitate the flow in the SDGS system using the SWMM. In the case of semi-technical and laboratorial studies, good concordance of the simulation tools with measurements was obtained [22,41]. Omitting the first day of simulation, the values for the average pump operation time in PS_1 and in PS_2 were close to the mean value obtained from the field measurements. A similar convergence occurs in the number of pump starts and outflow from PS_1 (Table 4).

The results obtained from measurements and from the simulation were subjected to statistical analysis. To check the fit of the model, the ratio of mean values was used in the following form:

$$RoM=\frac{\overline{z_s}}{\overline{z_m}}$$

(6)

where $\overline{z_m}$ is the mean measured value, and $\overline{z_s}$ is the mean simulated value. The best results are achieved when RoM → 1.0.

Analyzing the values of RoM in Table 4, it can be concluded that the simulation results from the SWMM 5.1 program show practically good convergence with the measured values. In the case of numerous connections to a sewer main, it is possible to determine the required retention volume in individual STs and the sequence of their emptying. The values of the coefficient of variation for the results obtained from the simulation are smaller than for the measurements, because they do not reflect the variability of wastewater inflow from households, but only the variability resulting from the retention of wastewater in conduits, STs and PSs. This variability should be considered in future work.

The wastewater pumping simulation was performed in a quasi-steady state flow. The water hammer in the force main was not considered. This phenomenon can be partly responsible for the high initial pressure peaks. It should be addressed especially in cases of higher pressure heads and flows to avoid structural failures. The negative flows were relatively low and their measurement was biased by systematic errors up to 250%.

3.3. Operation and Maintenance of the SDGS System.

Besides the function of eliminating coarse solids and fibrous matter, septic tanks provide periodic retention of wastewater. It was confirmed (by the use of SWMM) that the retention capacity (active volume) between the inlet and outlet invert levels equal that a mean daily wastewater volume would be sufficient. The retentive capacity in the investigated STs performed the following functions:

• storage during long-term (up to several hours) power outages (a common problem in Zolkiewka commune),
• equalization of wastewater flows in collective pipes and reduction of maximum flow rates, thus reduction of peak inflows to the pumping station.

In the presented wastewater system, a significant design problem was the liquid levels in the STs. At the stage of developing the system concept in Zolkiewka, a monitoring system was planned for wastewater levels in each ST. During our hydraulic analysis of the sewer system using the SWMM program, the possibility of assessing the degree of emptying of STs by measuring pressure at the outlet pipe (force-main) to the pumping station (Figure 7) was noticed. Because STs are connected at different levels to the common sewer, the hydraulic pressure may be associated with the emptying of specific STs. Only one ST was connected to the ascending force-main downstream of PS_2. When the retention capacity of the ST was exhausted, its component of the hydrostatic pressure disappeared. It is visible in the form of a “stepped” pressure profile (Figure 14). The described regularity allowed the simplification of the ST control system to one place, i.e., the PS. In the study, such monitoring was carried out on both bidirectional pipelines. The monitoring of ST drainage should include, in particular, those tanks with long emptying times. If the sewerage system is overloaded, STs located unfavorably can be flooded by domestic wastewater. The selection of the ST is carried out as a result of simulation in the SWMM. In extremely severe conditions, the outflow from the ST should be alleviated by a pump.

The studied wastewater pumping stations were modified by equipping them with vacuum support of wastewater drainage. Gravity conduits were connected via an internal vacuum reservoir (IVR) (4) (Figure 7). During hydraulic overloading of the network (e.g., at weekends and in the evenings) the retention capacity of septic tanks may be exhausted. Then an additional vacuum in the IVR increases the pressure gradient in the gravity sewer, and hence it accelerates the emptying of the septic tanks. This also removes air trapped in the pipelines. For energy saving reasons, this function is switched on upon request. It also supports the removal of biofilm from sewers.

The transport of sanitary wastewater requires energy consumption from 0.14 kWh·m⁻³ to 0.56 kWh·m⁻³ for black wastewater in a low-pressure system [52]. In the case of some unconventional systems, the energy demand is even higher and may be (for vacuum systems) up to 1 kWh·m⁻³ [53,54]. Energy expenditure for wastewater treatment shows a wide range depending on the capacity of the wastewater treatment plant, as well as the treatment technology. Biological trickling filters provide the smallest energy consumption, and bioreactors with activated sludge technology provide the largest, on average 0.9 kWh·m⁻³ [55]. The use of septic tanks in the system makes it possible to stop problematic solids at the beginning of the wastewater system, such as paper, sand, rags, etc. This eliminates most of the operational problems (silting of the pumping station, blockage of pumps, clogging of pipes) occurring in gravity sewers with pumping stations or pressure wastewater systems. The lack of coarse particles or fibrous matter in the ST effluent makes it possible to use pumps for dirty water with closed impellers instead of those with open ones (e.g., the Vortex type). Such pumps have higher efficiency; hence their installed power and electricity consumption are lower by approx. 40–50% [32,56]. Similarly, in our case the average energy consumption for the transport of domestic wastewater in pumping station PS_1 was initially 0.31 kWh·m⁻³, whereas after the pump replacement it decreased to 0.17 kWh·m⁻³. Since pump replacement in the year 2016, the two new pumps have been working without any failures, which confirms the high screening efficiency of the ST effluent filters.

The SDGS system has been operated in Zolkiewka commune since 2015. During this period, sludge accumulation in STs was monitored, the first time one year after operation commencement and then every six months. By the end of August 2018, 27 STs had been emptied, and the next 60 STs will probably be emptied by the end of March 2019. This is 18% and 60%, respectively. Due to the smaller than typical volume of the STs (~1 m³ vs. 2–3 m³), their effectiveness for the removal of solids is also lower. Therefore, the sludge accumulation rate is lower and the STs can be emptied with frequencies similar to typical STs, i.e., every 2–3 years [57].

3.4. Cost Analysis

The capital costs for the two options of the sewerage system in the whole Zolkiewka commune were compared. As a part of the feasibility study made by Biotop Company [48], both the conventional gravity and SDGS systems were considered with pumping stations. The gross capital cost of the gravity sewerage system for 248 households was estimated to be as high as EUR 1.94 million gross, and that of the SDGS system only EUR 0.95 million (

Table 5. Cost–effectiveness analysis for two alternatives of the sewerage system—gravity and SDGS—system for the Zolkiewka commune.

Index	Unit	Sewerage System
		Gravity	SDGS
Number of households		248	248
Length of sewers	m	19,008	18,069
Investment lifetime	y-rs	50	50
Capital costs	EUR	1,940,224	951,949
O&M costs	EUR	19,409	6679
Discount rate	%	3	3
Discounted O&M	EUR	429,562	147,817
EAC	EUR·y-r−1	92,647	42,599
EUC	EUR·m−3	5.65	2.60

). The difference in capital costs is 49% in favor of the SDGS system. Such a significant saving of capital costs was obtained due to the much cheaper pipelines and the use of horizontal directional drilling technology instead of traditional excavation. The calculation of the EAC and EUC was made with reference to the data shown in Table 5.

Figure 15 shows the O&M costs in the year 2017, which reached about EUR 2460 gross, i.e., EUR 14.3 cap⁻¹ y-r⁻¹. The current wastewater price is EUR 0.93 m⁻³, which means that the users pay for O&M only. The real price, including the depreciation cost, would be about two and half time as high. The subsidy is covered by the grant beneficiary of the project.

Comparing the real wastewater and tap water costs with the average disposable income in Lubelskie voivodship, which is 302 EUR per person per month [58], one may find that due to low water use the payments make up only 0.8%. This is still much lower than the maximum acceptable value of 3–5% [59]; therefore the system is now financially unsustainable. After five years of operation within the innovative project, the wastewater prices should be 3–4 times higher.

Pump replacement in the pumping stations has reduced the O&M costs by 9% and the total costs (EAC) by 1.5%. The costs related to energy consumption are significantly lower than the costs related to pump inspections and service as well as to network inspection. However, reducing energy consumption may make it possible to shift from external energy sources to renewable ones. However, a further feasibility study is needed.

The operating costs are also lower thanks to the diminishing of pump failures due to the elimination of fibers and sand from sewage. This is particularly important in the case of the improper use of sewerage systems by residents who are accustomed to using holding tanks. In Poland, there are no consequences for residents who discharge solid waste such as rags, sponges and packaging to holdings tank or gravity sewers, which creates numerous operational problems in the sewerage system. In the gravity sewerage systems, the residents responsible for problems are anonymous, but in the SDGS system they can be easily identified from the contents of septic tanks. In the case study, when inappropriate waste was found in sludge during emptying, then the inhabitants were charged with additional costs for sludge removal. This action and additional instructions quickly corrected their improper behavior.

4. Discussion

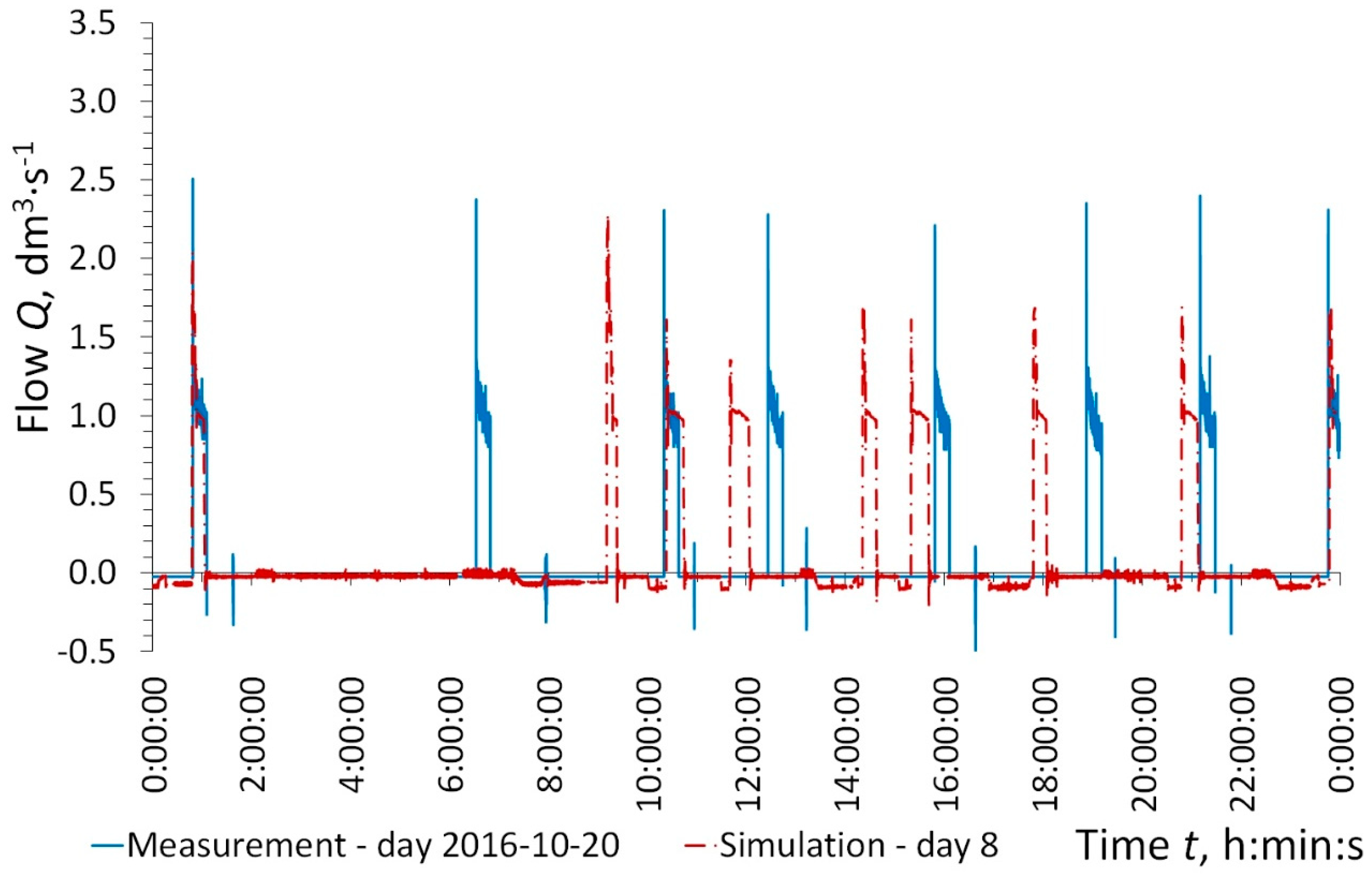
The most important parameters for design purposes are different peak flows: instantaneous, 1-min average and 1-h average maxima. The 1-min and hourly average maximum wastewater inflows to pumping station PS_2 from 59 buildings are given in

Table 6. Comparison of 1-min and hourly maximum wastewater inflows to pumping station PS_2.

Inflow	Measured Flow Rate	Equation (1)		Equation (2)		Equation (3)		SWMM
		Min	Max	Min	Max	Min	Max
Qm, dm3·s−1	-	0.81	3.14	-	-	0.42	0.50	0.50
Qh, dm3·s−1	0.19	-	-	0.11	0.21	0.30	0.35	0.33
Error, %	±2	-	-	−42	+11	+58	+84	+74

. The design flow treated as 1-min average maximum flow obtained from Equation (1) was estimated as 3.14 dm³·s⁻¹. The value obtained by Equation (1) turns out to be much larger than the value obtained from the simulation. This discrepancy may result from the fact that it was an empirical equation and in the case of Equation (1) significantly higher average daily wastewater flows per capita were assumed. In the simulation the average daily flow value of 46.5 dm³·cap⁻¹·d⁻¹ was assumed. The American conditions often adopt a value of average daily flow in the range of 170 to 190 dm³·cap⁻¹·d⁻¹ [36], which is a value almost four times higher. When this factor was taken into account, the value obtained from Equation (1) could be equal to 0.81 dm³·s⁻¹. It is a value still larger than the value obtained from the simulation, and therefore it probably should be treated as instantaneous, but not the 1-min average peak flow. The 1-min average peak flows calculated using Equation (3) were slightly lower than or equal to that obtained from the computer simulation. Similarly good agreement was achieved for maximum hourly flows, but unfortunately they were 58–84% higher than the measured one. To validate this discrepancy a longer analysis seems to be necessary. The best results were obtained from Equation (2).

Various authors recommend various self-cleaning velocities of pipelines in the SDGS system: 0.5 m∙s⁻¹ [20]; 0.3–0.45 m∙s⁻¹ [36]; 0.2 m∙s⁻¹ [17]; 0.15 m∙s⁻¹ [15]; 0 m∙s⁻¹—no need for a self-cleaning velocity at a low concentration of suspended solids (wastewater pretreatment in ST) [24]. Most of the above-mentioned velocities were determined based on the operational experience of an existing SDGS system. A few researchers have determined these velocities based on the size of the suspended solid particles that constitute the effluent from STs [15]. The maximum velocities in all conduits under investigation were compared with the values of self-cleaning velocity given by various authors (

Table 7. Number and percent of conduits that did not reach self-cleaning velocity on the basis of simulation in the SWMM 5.1 program.

Assumed Self-Cleaning Velocity (m·s−1)	Number of Connections with Unreached Self-Cleaning Velocity	% of Connections with Unreached Self-Cleaning Velocity (%)
0.15	16	6
0.20	33	11
0.30	68	23
0.45	115	40
0.50	133	46

).

A self-cleaning velocity of 0.15 m·s⁻¹, which should occur at least once per day, was not reached in only 16 conduits out of 290, which is only 6% of all connections, but if it is taken to be 0.5 m·s⁻¹, the percentage rises to 46%. The reaches that did not meet this requirement were lateral connections and a conduit (sewer) network just below the septic tank lateral connection, where the maximum instantaneous velocity reached 0.14 m·s⁻¹.

An even more important factor than self-cleaning velocity is the critical bed shear stress. According to [15], the critical value of shear bed stress is 0.15 N·m⁻². In

Table 8. Number and percent of conduits that did not reach assumed bed shear stress on the basis of simulation in the SWMM 5.1 program.

Assumed Critical Bed Shear Stress (N·m−2)	Number of Connections with Unreached Critical Bed Shear Stress	% of Connections with Unreached Critical Bed Shear Stress (%)
0.10	21	7
0.15	28	10
0.20	35	12
0.25	47	16
0.30	51	18

, a comparison of the calculated bed shear stress values with different critical values is presented. The critical shear bed stress of 0.15 N·m⁻², which should occur at least once per day, was not reached in only 28 conduits out of 290, which is only 10% of all connections. This value is larger in the case of the self-cleaning velocity, but in this case many more lateral connections did not reach the critical bed shear stress. The reaches that did not meet this requirement were mainly lateral connections and a conduit (sewer) network just below the septic tank lateral connection.

Thanks to SWMM 5.1, one can check the correctness of the design assumptions and solutions, such as the magnitude of the retention volume in pumping stations and STs, conduit diameters, and the occurrence of self-cleaning velocity or hydraulic overloads. The SDGS system simulation in the SWMM 5.1 program allows for the simulation of various network operation variants—under unsteady state conditions as opposed to traditional design, in which steady state conditions are assumed. It is also easy to simulate STs as wastewater reservoirs.

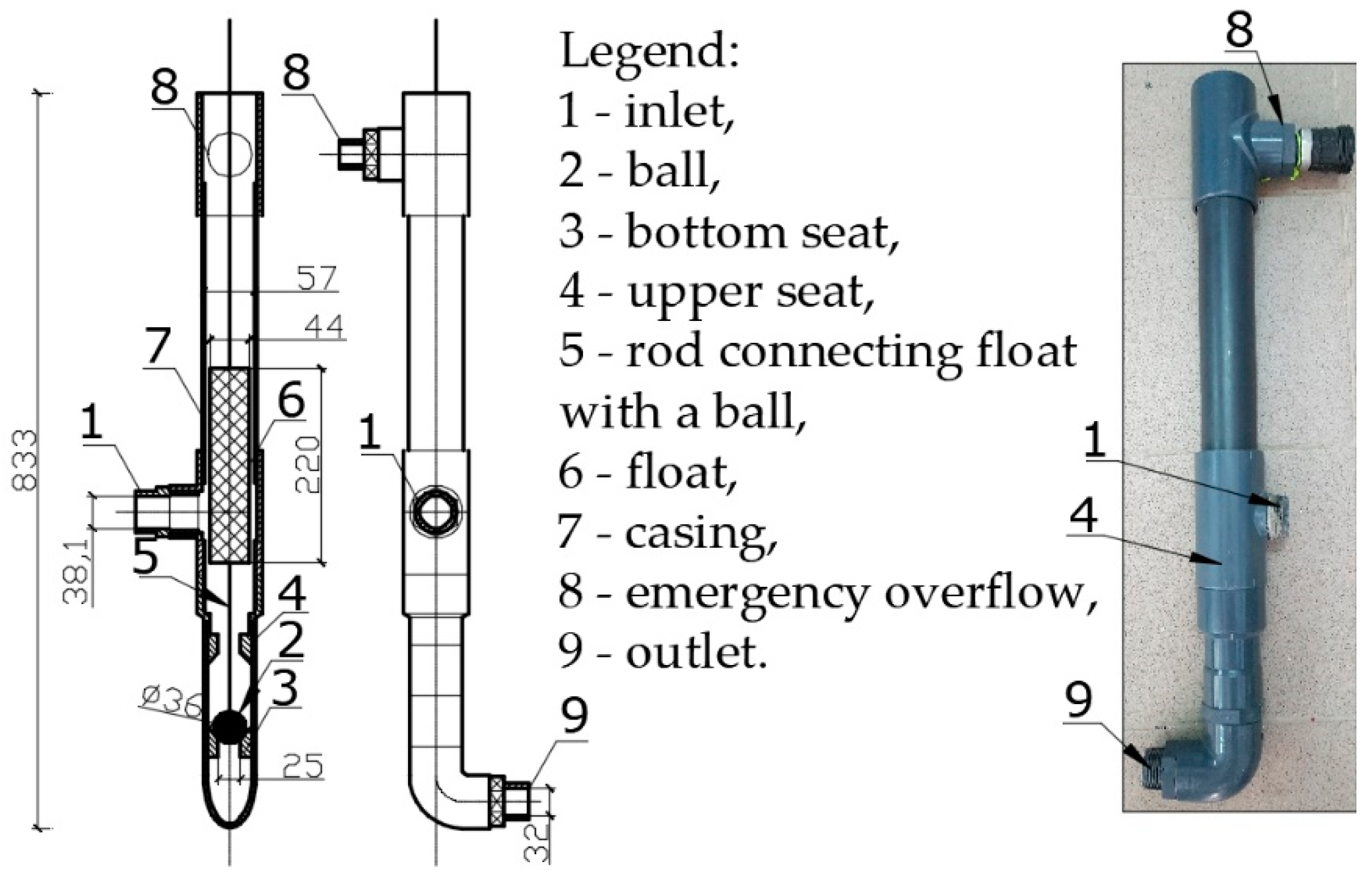
Using traditional methods of system design, it is also not possible to determine a suitable emitter flow rate. The emitter allows for the possibility of emptying septic tanks connected to the force main (between PS_1 and Sr1), by emptying the force main during pump idle time. The suitable emitter flow rate should be the smallest that allows the emptying of the connected STs.

Comparing the capital costs of different SDGS systems with conventional gravity sewers, the former have been up to 65% cheaper than the latter [15,17,20,24,36], and the 49% lower capital costs are not an exception.

The O&M of the gravity sewerage system depends on many factors including population density, the number of the residents served and the number of used pumping stations. In rural areas in Poland, the O&M costs often lie in the range of 2–3% of capital costs (without depreciation) [47,60]. The O&M costs of SDGS systems, estimated by the US EPA for a hypothetical rural commune, were from 4 to 5.5 times lower than those generated by traditional gravity sewerage systems [61]. In our case study, the forecast O&M costs of the gravity sewerage system would reach approximately 65 EUR cap⁻¹ y-r⁻¹, i.e., four to five times those of the constructed SDGS system.

Further investigations concerning the flow variability and reliability of the system are ongoing. More realistic patterns of wastewater outflow distribution can be provided using short-interval (10, 30 or 60 s) measurements of water usage [13,62] in individual dwellings. There is also a need for the further monitoring of sludge and scum in STs. To date, one-third of all STs have been emptied after approximately two years of operation. Although no complaints about odors were recorded during the operation of the investigated system, further work is needed to estimate the risk connected with hydrogen sulphide generation and exposure. Measurement of the H2S concentrations in critical parts the SDGS system (STs, pumping stations and release manholes) is also planned. Additional research is needed to assess the energy consumption and feasibility of use of renewable energy sources.

5. Conclusions

• The simulation of the operation of an SDGS system with force mains is possible and effective using the SWMM code. It is also recommended for design purposes.
• Simplified supervisory control and data acquisition are needed for model tuning to simulate the operation of the SDGS system and its possible extension.
• To achieve better simulation results, more realistic patterns of water use must be applied based on user surveys and/or measurements, and the simulation period should cover at minimum several days. Furthermore, the water hammer phenomenon should be addressed, especially in cases of higher pressure heads and flows to avoid structural failures.
• Although the septic tanks used in SDGS require emptying, they simultaneously improve operating conditions by eliminating problematic waste from wastewater. In the Zolkiewka commune, it allowed the use of pumps with higher efficiency and lower energy consumption.
• Further work is required to optimize the design and maintenance of septic tanks, especially concerning their optimal volumes and the purposefulness of the application of bio-additives.
• The capital costs of the SDGS system in Zolkiewka commune are significantly lower than the gravity sewerage variant with pumping stations. In addition, due to the low operating costs, it was possible to calculate a low price for domestic wastewater, acceptable to residents.