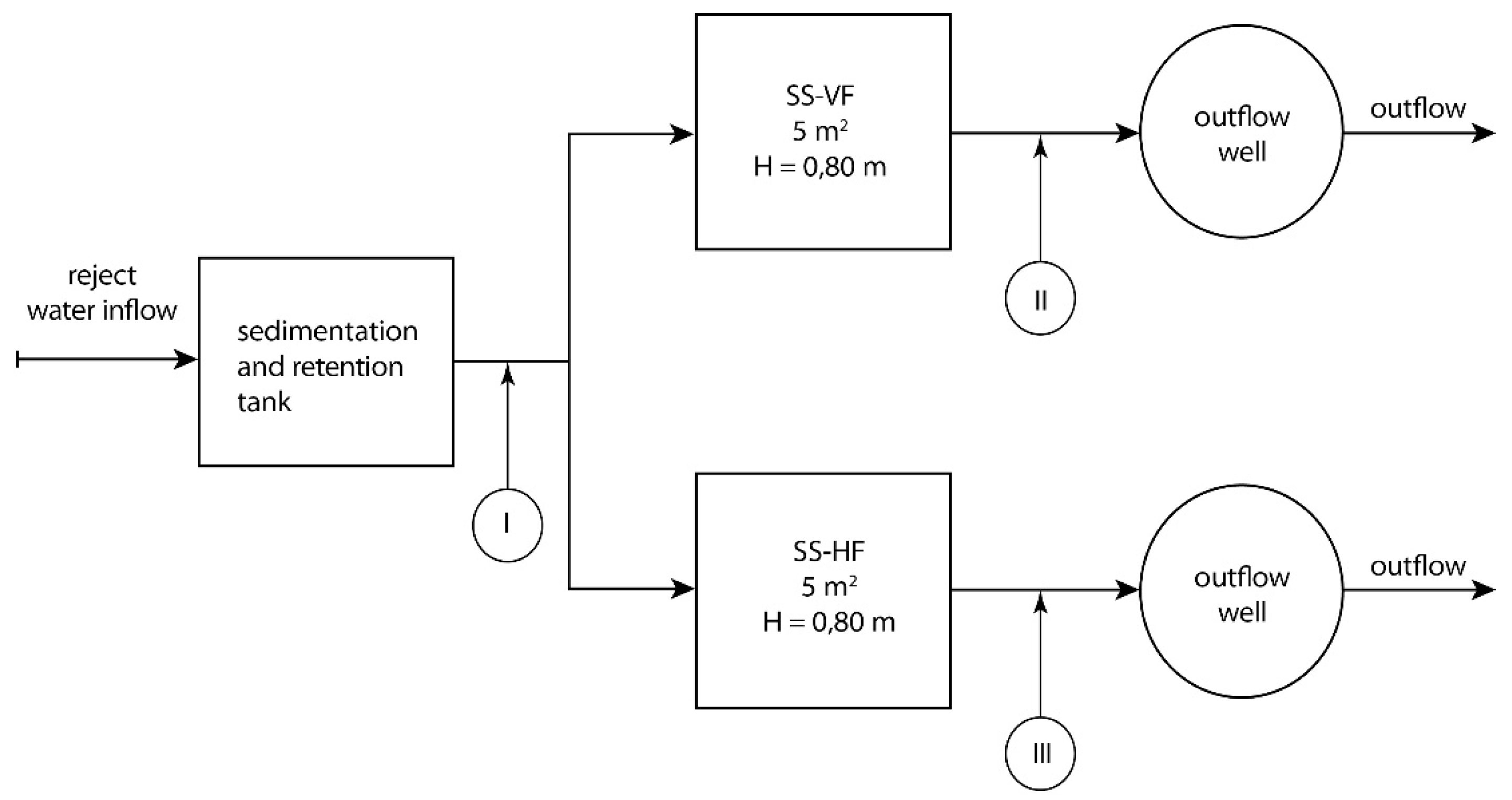
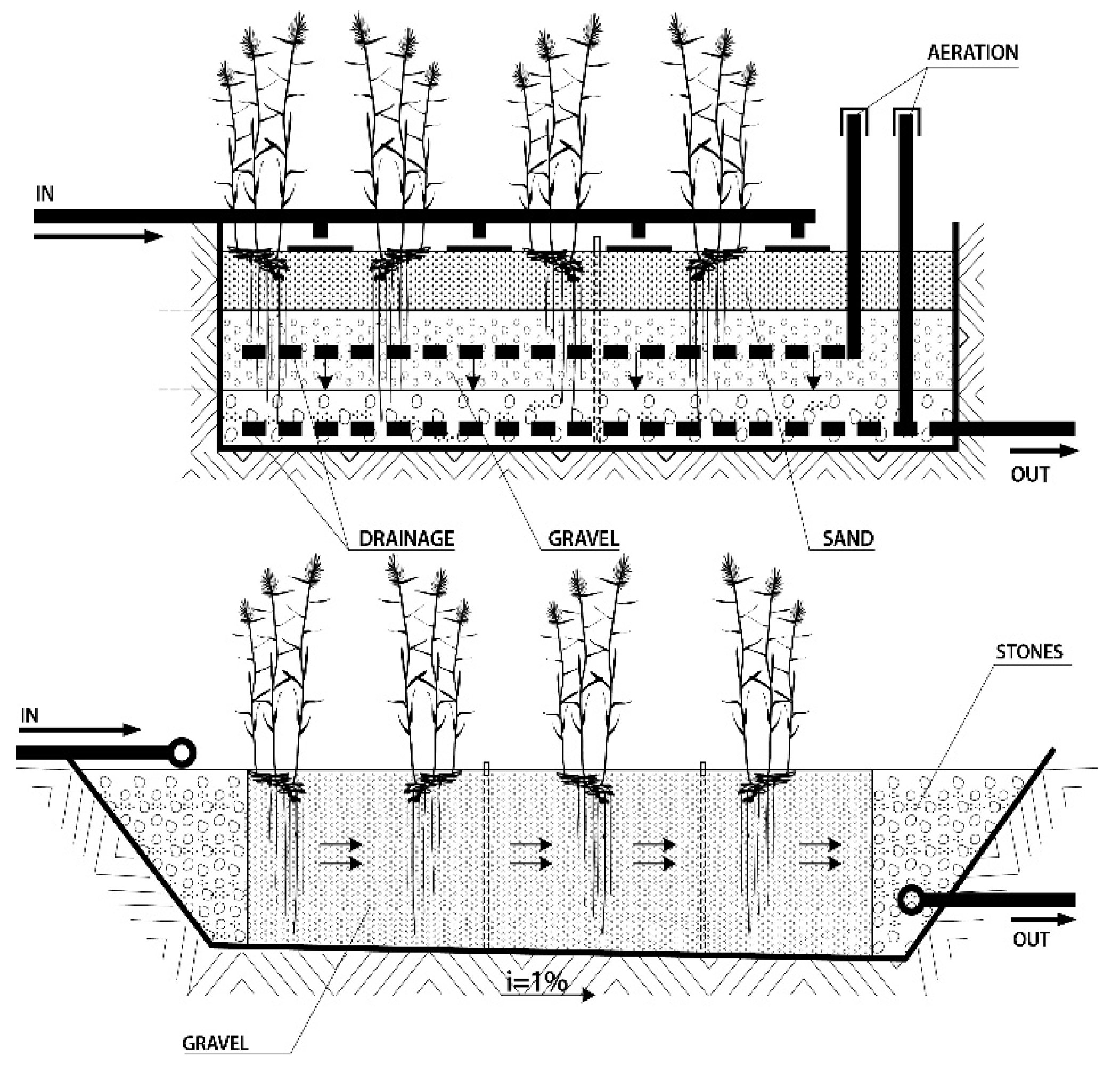
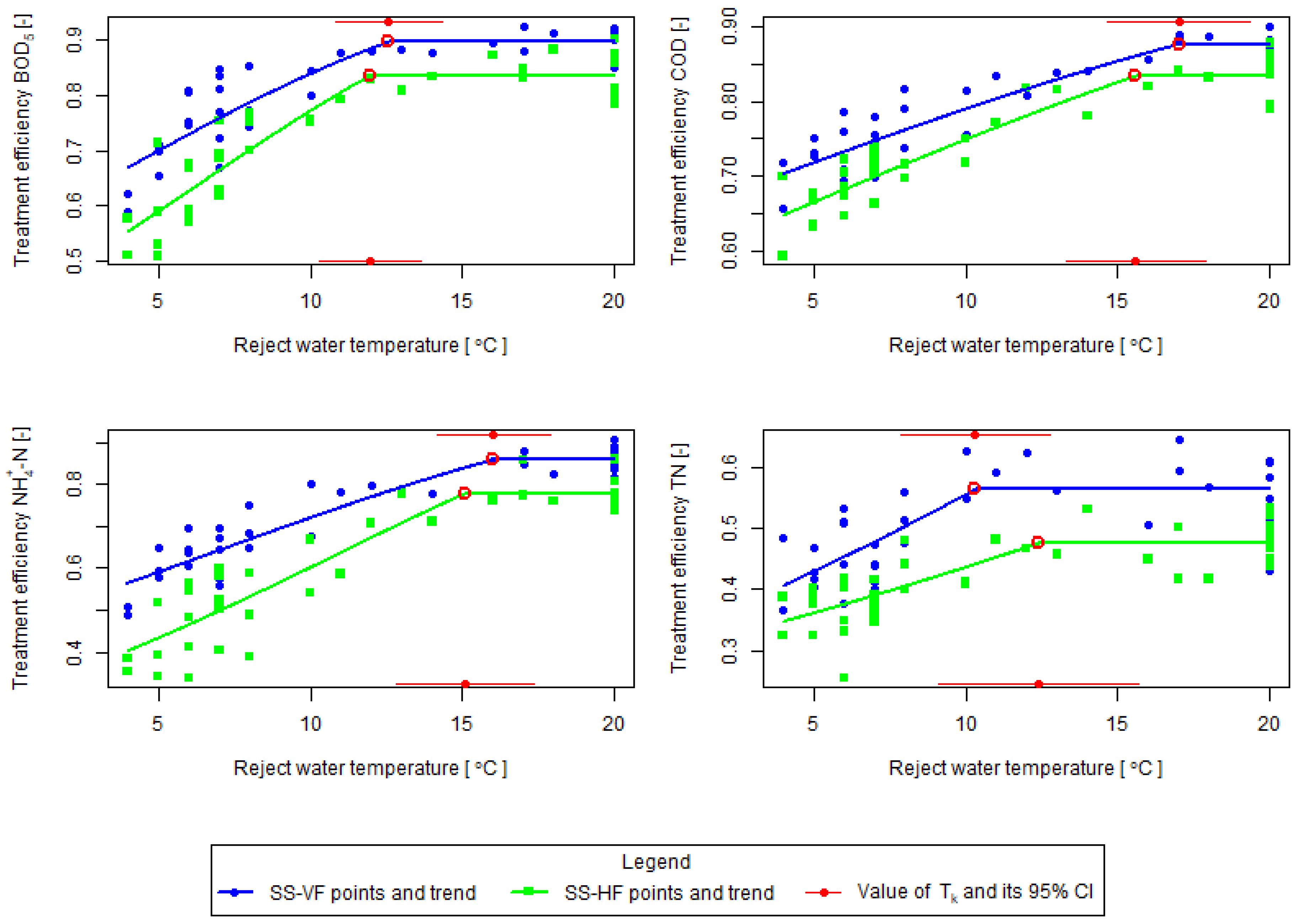
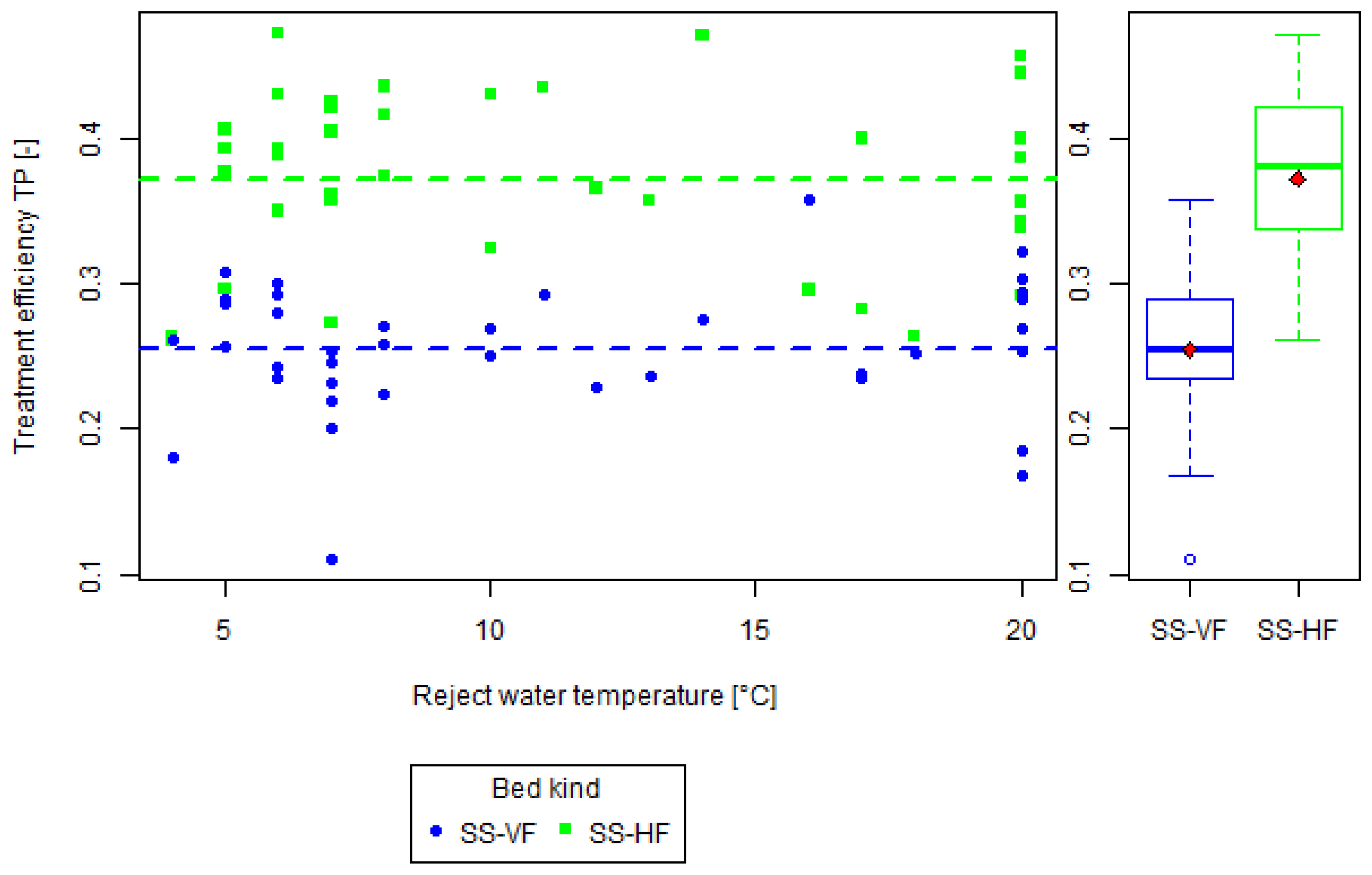
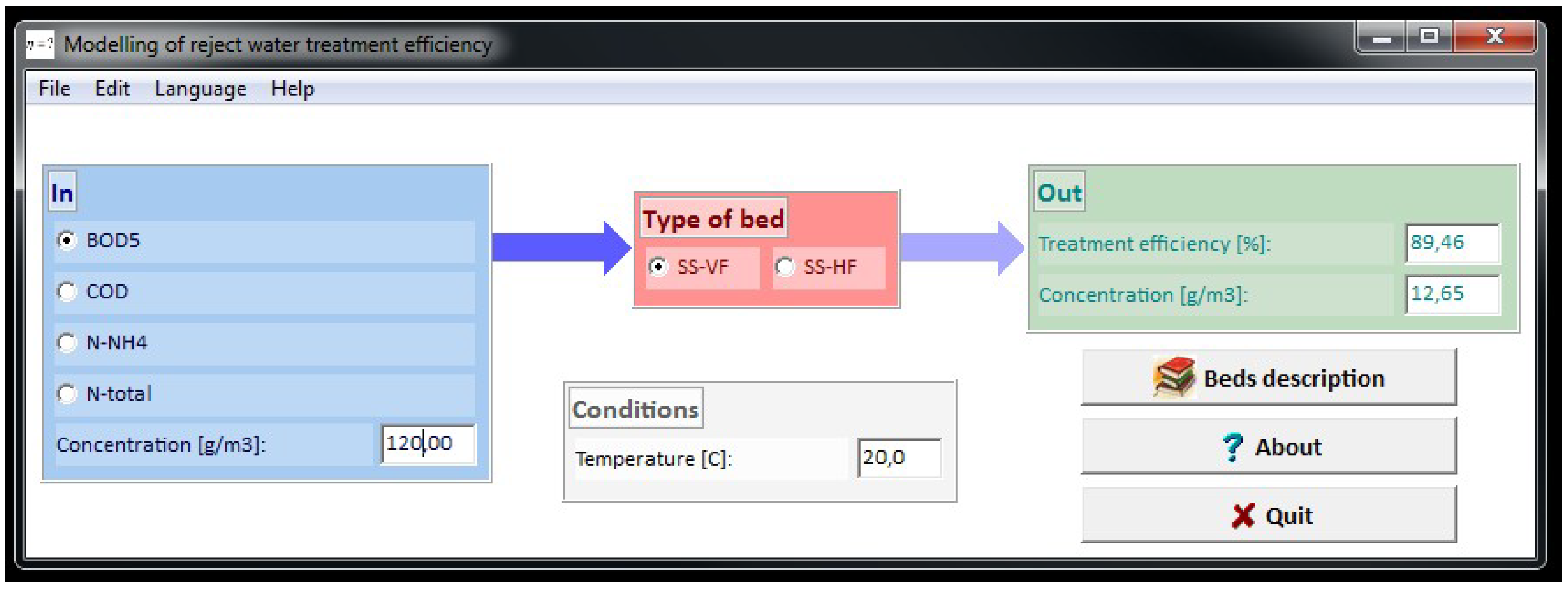
Appendix A. Statistical Modeling
The 16 models obtained from (1) were constructed by taking limit of certain variables simplifying the expression:
(allowed to vary or set to 0)
(allowed to vary or taken limit resulting in (3) dependency)
(allowed to vary or set to )
and related (if is present, then (5) form was used, otherwise (4)).
All models were estimated using non-linear least squares procedure with a variant of Levenberg-Marquardt’s algorithm for optimization [
30]. It is worth noting that both sides of (1) are always constrained to a (0–1) interval. Residuals from modeling this dependency will be therefore non-homoscedastic. Final model estimation procedure reweighted them by term proportional to [
31]:
where
—estimated and right-hand side of (1),
—residual correction for
i-th observation.
Model parameter selection was performed using methodology from [
23]. After all 16 models were built, they were weighted using Akaike weight
s, which is a measure of a model fit to the data, normalized to (0–1) interval, relative to the best model from the set of analyzed ones. The Akaike weight was calculated from differences
of second order [
32] AIC [
33]. Models with very similar logarithmic likelihood and residual distribution, containing only additional parameters, were removed from weighting procedure [
23]. Top weighted models, forming 0.90–0.95 of summary Akaike weights, were retained for further analysis. Residuals structure of the remaining parameter sets was also checked, to further reject oversimplified ones using an approach based on [
34]. Remaining parameter subsets were presented along with their basic statistics. Parameter
, if present, was presented graphically in a similar way to [
35].
Model calculation was performed using R version 3.5.1 [
36]. The nlfb procedure from nlsr package [
37] was used for optimization of models. Second order AIC was calculated using AICc procedure from AICcmodavg package [
38].
Appendix B. Result of Statistical Modeling
Table A1,
Table A2,
Table A3 and
Table A4 present fitted models grouped by almost identical values of logarithmic likelihood and residuals structure. Analysis revealed three preferred groups of models, each with stable core parameters, which dominate the variability of logarithmic likelihood and residuals distribution. For the simplest models from each group, containing the core parameters, Akaike weight was calculated. Any other model, with addition of one or more parameters, does not change its fit significantly.
Analysis results consistently supported choice of model with parameter subset , , —a model with no temperature dependency after . In almost all cases, Akaike weight for this preferred model is greater than 0.95, with suggests strong support. The second one is , —a model with non-changing temperature dependency. Model , for total nitrogen for horizontal flow bed had approximately equal to 0.16, suggesting some support for further analysis. The third model contains only variable, and obviously does not depend on temperature. It has almost no support, and was not chosen for residual analysis.
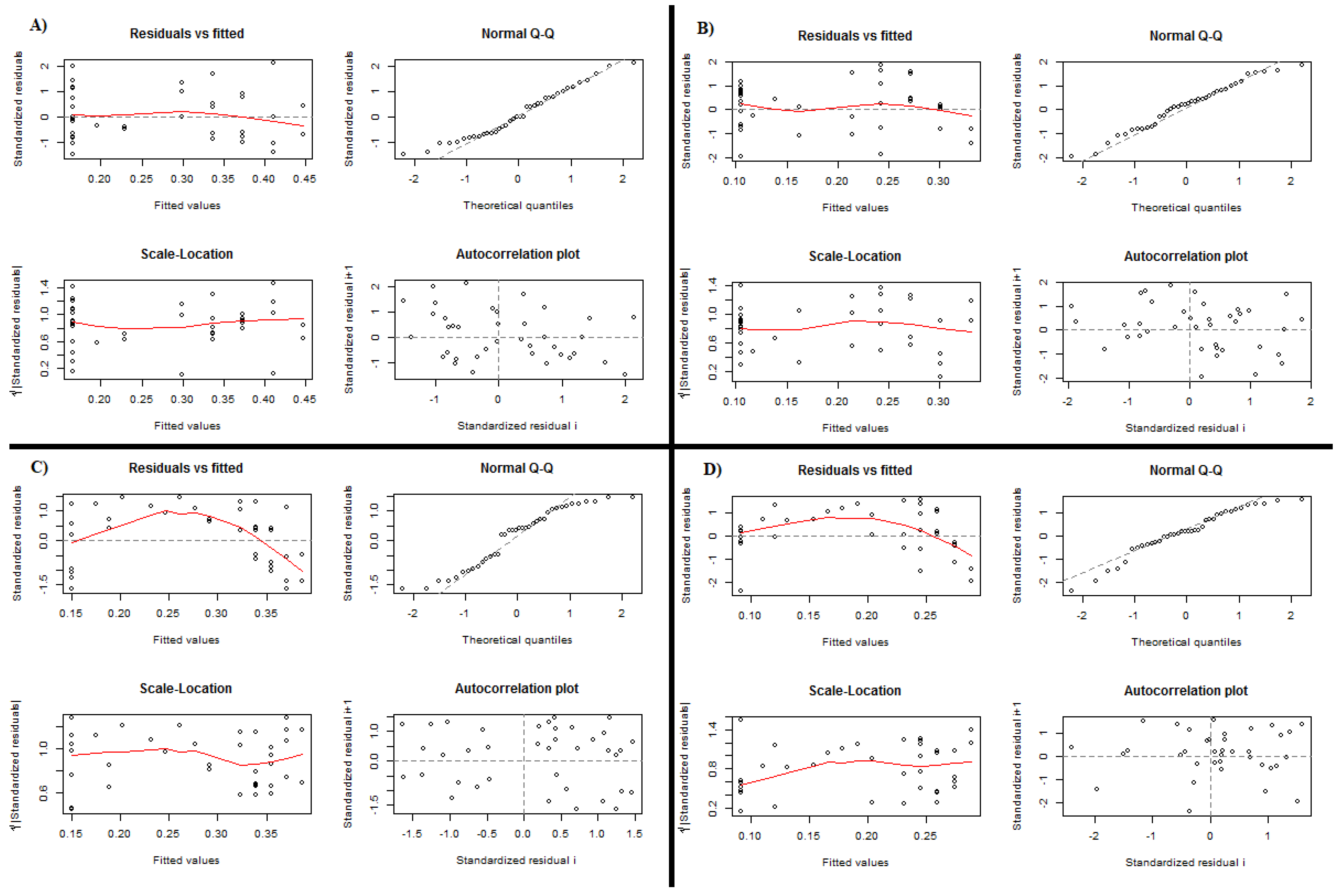
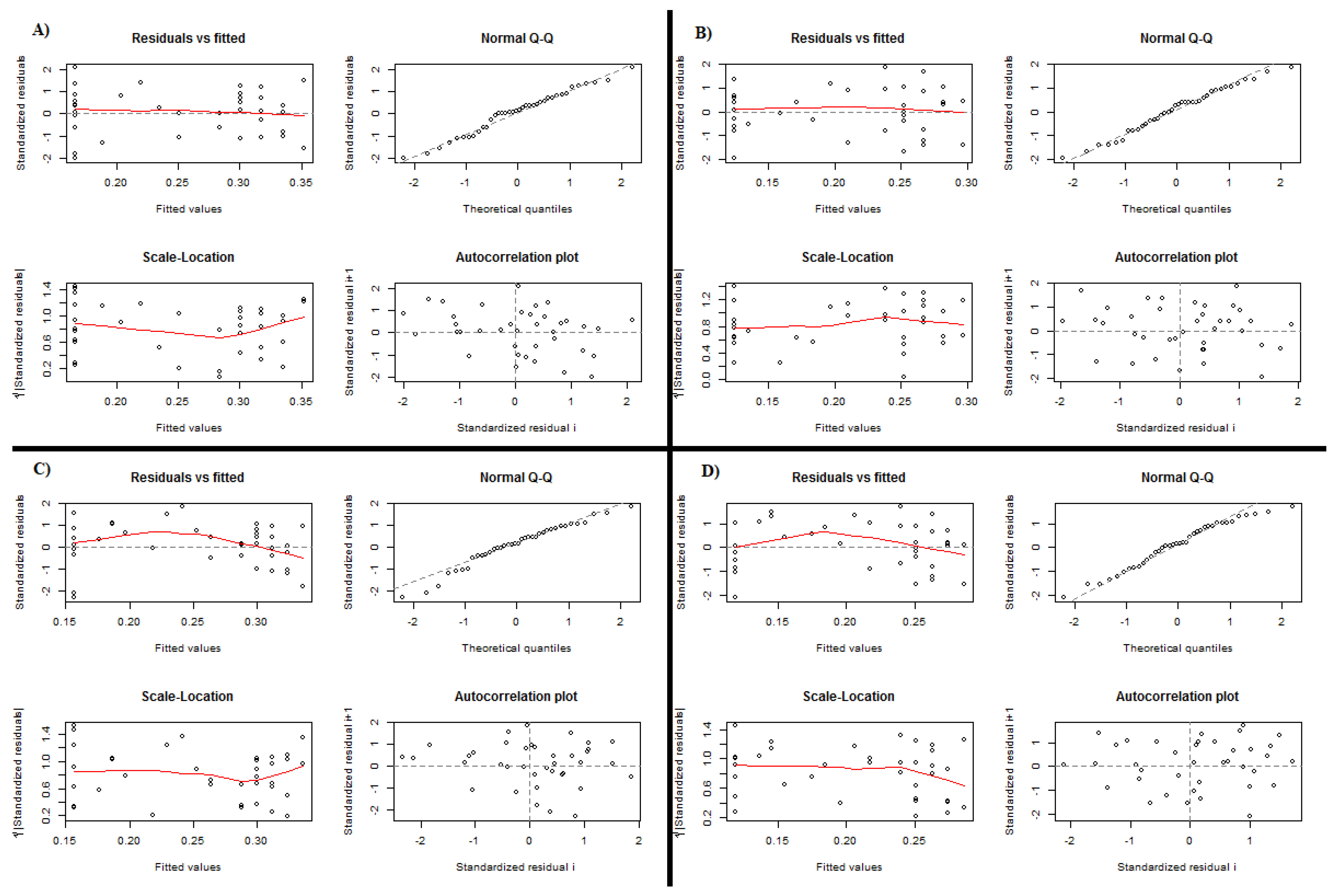
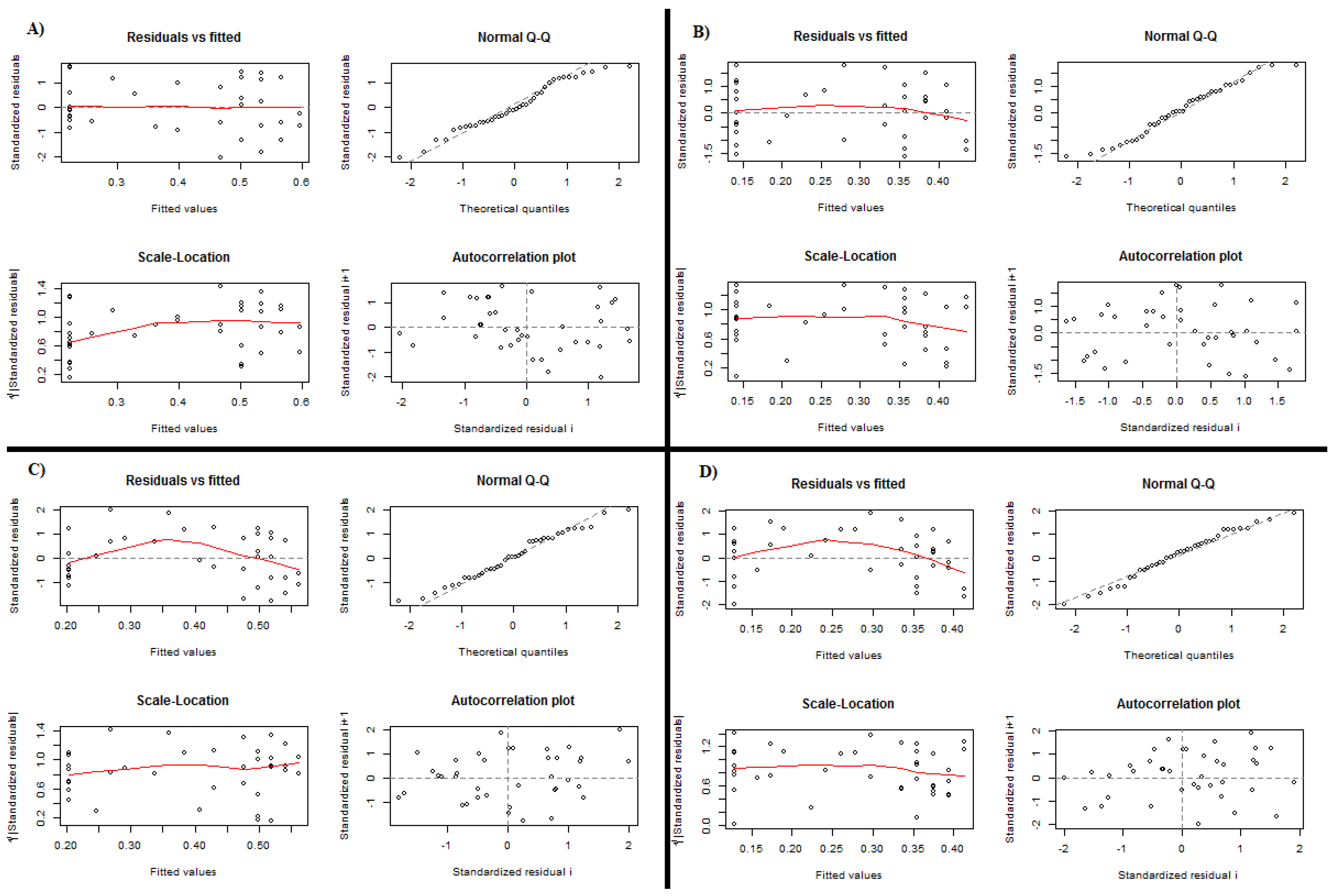
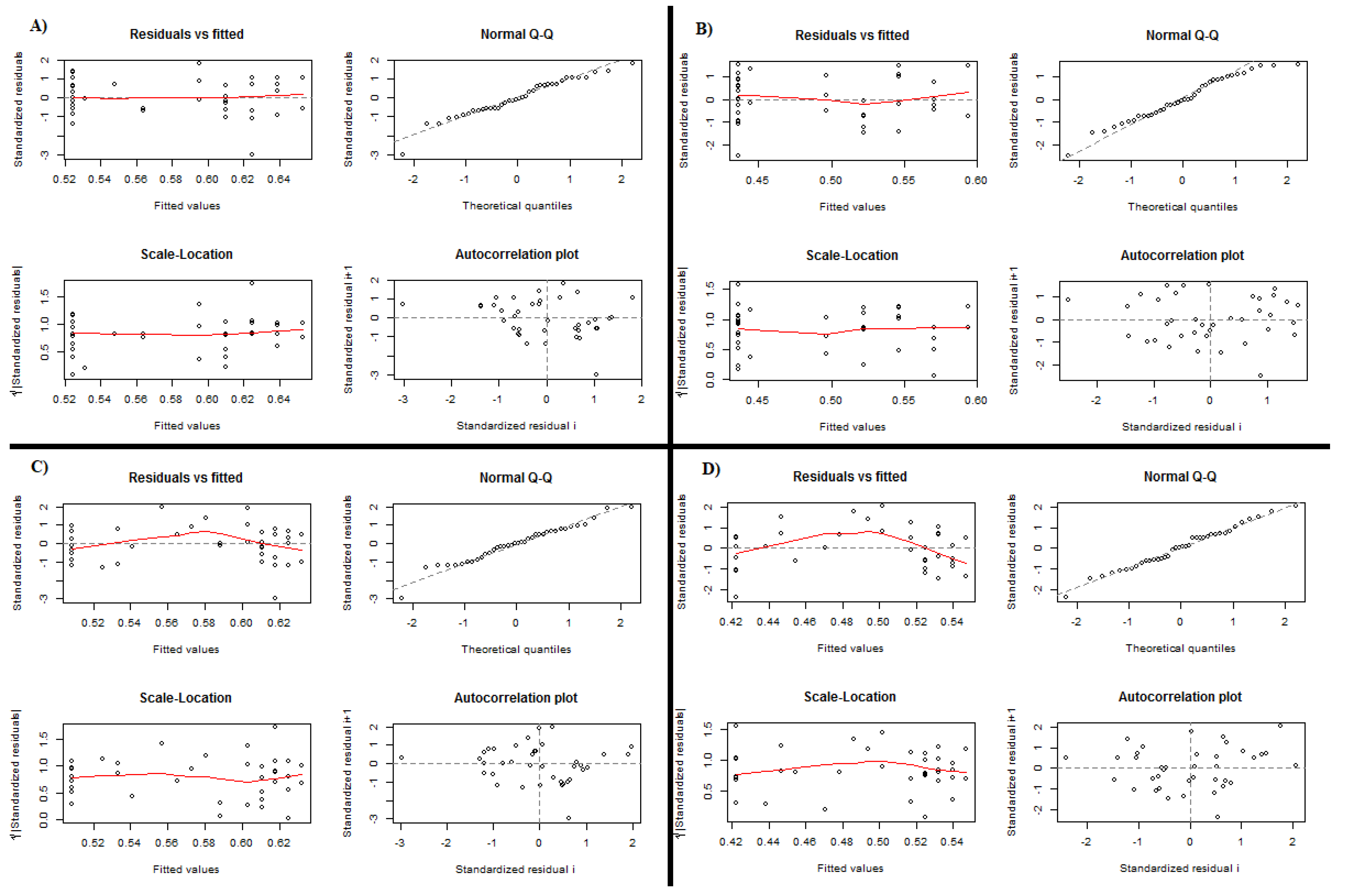
Residual analysis, presented in
Figure A1,
Figure A2,
Figure A3 and
Figure A4, support selection for first preferred model in all cases; there is signal of non-linearity in models
,
, even a slight one for total nitrogen in horizontal flow bed. Residuals analysis suggests that models with
,
,
parameters also have properties allowing for further analysis of those models parameters—normal distribution, homoscedasticity and no visible autocorrelation—which were also performed.
Table A1.
Fitted models for BOD5 with their statistics.
Table A1.
Fitted models for BOD5 with their statistics.
| Horizontal Flow Bed SS-HF | Vertical Flow Bed SS-VF |
|---|
| Model | Variables | k | logLik | AICc | | | Model | Variables | k | logLik | AICc | | |
|---|
| 1 | , , | 4 | 2.272 | 4.668 | 0.000 | >0.999 | 1 | , , | 4 | −0.855 | 10.923 | 0.000 | >0.996 |
| 2 | , , , | 5 | 2.485 | 6.905 | 2.237 | | 2 | , , , | 5 | −0.260 | 12.394 | 1.471 | |
| 3 | , , , | 5 | 2.280 | 7.315 | 2.648 | 3 | , , , | 5 | −0.606 | 13.088 | 2.164 |
| 4 | , , , | 5 | 2.272 | 7.330 | 2.663 | 4 | , , , | 5 | −0.855 | 13.586 | 2.663 |
| 5 | , , , , | 6 | 2.485 | 9.739 | 5.072 | 5 | , , , , | 6 | −0.031 | 14.772 | 3.849 |
| 6 | , , , , | 6 | 2.485 | 9.740 | 5.072 | 6 | , , , , | 6 | −0.260 | 15.229 | 4.306 |
| 7 | , , , , | 6 | 2.280 | 10.150 | 5.483 | 7 | , , , , | 6 | −0.606 | 15.922 | 4.999 |
| 8 | , , , , , | 7 | 2.485 | 12.763 | 8.096 | 8 | , , , , , | 7 | −0.031 | 17.796 | 6.873 |
| 9 | , | 3 | −8.793 | 24.293 | 19.625 | 5.476 × 10−5 | 9 | , | 3 | −7.783 | 11.349 | 11.349 | 3.421 × 10−3 |
| 10 | , , | 4 | −7.897 | 25.007 | 20.339 | | 10 | , , | 4 | −6.763 | 22.738 | 11.815 | |
| 11 | , , | 4 | −8.793 | 26.799 | 22.131 | 11 | , , | 4 | −7.783 | 24.778 | 13.855 |
| 12 | , , , | 5 | −7.897 | 27.670 | 23.002 | 12 | , , , | 5 | −6.763 | 25.401 | 14.478 |
| 13 | | 2 | −31.510 | 67.364 | 62.696 | 5.430 × 10−14 | 13 | | 2 | −32.052 | 68.446 | 57.523 | 3.218 × 10−13 |
| 14 | , | 3 | −31.510 | 69.727 | 65.059 | | 14 | , | 3 | −32.052 | 59.886 | 70.809 | |
| 15 | , | 3 | −31.510 | 69.727 | 65.059 | 15 | , | 3 | −32.052 | 59.886 | 70.809 |
| 16 | , , | 4 | −31.510 | 72.233 | 67.565 | 16 | , , | 4 | −32.052 | 62.392 | 73.316 |
Table A2.
Fitted models for COD with their statistics.
Table A2.
Fitted models for COD with their statistics.
| Horizontal Flow Bed SS-HF | Vertical Flow Bed SS-VF |
|---|
| Model | Variables | k | logLik | AICc | | | Model | Variables | k | logLik | AICc | | |
|---|
| 1 | , , | 4 | 18.702 | −28.193 | 0.000 | >0.965 | 1 | , , | 4 | 17.528 | −25.844 | 0.000 | >0.970 |
| 2 | , , , | 5 | 18.823 | −25.772 | 2.421 | | 2 | , , , | 5 | 18.001 | −24.127 | 1.716 | |
| 3 | , , , | 5 | 18.711 | −25.547 | 2.645 | 3 | , , , | 5 | 17.591 | −23.307 | 2.537 |
| 4 | , , , | 5 | 18.702 | −25.530 | 2.663 | 4 | , , , | 5 | 17.528 | −23.181 | 2.663 |
| 5 | , , , , | 6 | 18.832 | −22.955 | 5.238 | 5 | , , , , | 6 | 18.002 | −21.295 | 4.549 |
| 6 | , , , , | 6 | 18.823 | −22.937 | 5.256 | 6 | , , , , | 6 | 18.001 | −21.293 | 4.551 |
| 7 | , , , , | 6 | 18.711 | −22.713 | 5.480 | 7 | , , , , | 6 | 17.591 | −20.472 | 5.372 |
| 8 | , , , , , | 7 | 18.832 | −19.931 | 8.261 | 8 | , , , , , | 7 | 18.002 | −18.271 | 7.573 |
| 9 | , | 3 | 14.117 | −21.528 | 6.664 | 3.449 × 10−2 | 9 | , | 3 | 12.794 | −18.883 | 6.961 | 2.986 × 10−2 |
| 10 | , , | 4 | 14.821 | −20.430 | 7.762 | | 10 | , , | 4 | 13.497 | −17.782 | 8.062 | |
| 11 | , , | 4 | 14.117 | −19.022 | 9.170 | 11 | , , | 4 | 12.794 | −16.376 | 9.468 |
| 12 | , , , | 5 | 14.821 | −17.768 | 10.425 | 12 | , , , | 5 | 13.497 | −15.119 | 10.725 |
| 13 | | 2 | −18.244 | 40.831 | 69.023 | 9.922 × 10−16 | 13 | | 2 | −20.165 | 44.672 | 70.516 | 4.726 × 10−16 |
| 14 | , | 3 | −18.244 | 43.194 | 71.386 | | 14 | , | 3 | −20.165 | 47.035 | 72.879 | |
| 15 | , | 3 | −18.244 | 43.194 | 71.386 | 15 | , | 3 | −20.165 | 47.035 | 72.879 |
| 16 | , , | 4 | −18.244 | 45.700 | 73.892 | 16 | , , | 4 | −20.165 | 49.542 | 75.385 |
Table A3.
Fitted models for NH4+-N with their statistics.
Table A3.
Fitted models for NH4+-N with their statistics.
| Horizontal Flow Bed SS-HF | Vertical Flow Bed SS-VF |
|---|
| Model | Variables | k | logLik | AICc | | | Model | Variables | k | logLik | AICc | | |
|---|
| 1 | , , | 4 | −4.371 | 17.954 | 0.000 | >0.980 | 1 | , , | 4 | 4.583 | 0.046 | 0.000 | >0.940 |
| 2 | , , , | 5 | −4.342 | 20.559 | 2.605 | | 2 | , , , | 5 | 5.060 | 1.754 | 1.708 | |
| 3 | , , , | 5 | −4.370 | 20.615 | 2.662 | 3 | , , , | 5 | 4.883 | 2.109 | 2.063 |
| 4 | , , , | 5 | −4.371 | 20.617 | 2.663 | 4 | , , , | 5 | 4.583 | 2.709 | 2.663 |
| 5 | , , , , | 6 | −4.342 | 23.394 | 5.440 | 5 | , , , , | 6 | 5.117 | 4.476 | 4.429 |
| 6 | , , , , | 6 | −4.370 | 23.450 | 5.497 | 6 | , , , , | 6 | 5.060 | 4.589 | 4.542 |
| 7 | , , , , | 6 | −4.638 | 23.986 | 6.032 | 7 | , , , , | 6 | 4.883 | 4.944 | 4.897 |
| 8 | , , , , , | 7 | −4.638 | 27.010 | 9.056 | 8 | , , , , , | 7 | 5.117 | 7.499 | 7.453 |
| 9 | , | 3 | −9.506 | 25.719 | 7.765 | 2.018 × 10−2 | 9 | , | 3 | 0.566 | 5.574 | 5.527 | 5.932 × 10−2 |
| 10 | , , | 4 | −8.692 | 26.597 | 8.643 | | 10 | , , | 4 | 1.709 | 5.793 | 5.747 | |
| 11 | , , | 4 | −9.506 | 28.225 | 10.271 | 11 | , , | 4 | 0.566 | 8.080 | 8.034 |
| 12 | , , , | 5 | −8.692 | 29.260 | 11.306 | 12 | , , , | 5 | 1.709 | 8.456 | 8.410 |
| 13 | | 2 | −37.860 | 80.062 | 62.108 | 3.195 × 10−14 | 13 | | 2 | −33.102 | 70.547 | 70.500 | 4.618 × 10−16 |
| 14 | , | 3 | −37.860 | 82.425 | 64.471 | | 14 | , | 3 | −33.102 | 72.910 | 72.863 | |
| 15 | , | 3 | −37.860 | 82.425 | 64.471 | 15 | , | 3 | −33.102 | 72.910 | 72.863 |
| 16 | , , | 4 | −37.860 | 84.931 | 66.978 | 16 | , , | 4 | −33.102 | 75.416 | 75.370 |
Table A4.
Fitted models for TN with their statistics.
Table A4.
Fitted models for TN with their statistics.
| Horizontal Flow Bed SS-HF | Vertical Flow Bed SS-VF |
|---|
| Model | Variables | k | logLik | AICc | | | Model | Variables | k | logLik | AICc | | |
|---|
| 1 | , , | 4 | 14.709 | −20.206 | 0.000 | >0.838 | 1 | , , | 4 | 5.926 | −2.640 | 0.000 | >0.992 |
| 2 | , , , | 5 | 14.744 | −17.613 | 2.593 | | 2 | , , , | 5 | 6.384 | −0.893 | 1.747 | |
| 3 | , , , | 5 | 14.709 | −17.543 | 2.663 | 3 | , , , | 5 | 5.926 | 0.023 | 2.663 |
| 4 | , , , | 5 | 14.709 | −17.543 | 2.663 | 4 | , , , | 5 | 5.926 | 0.023 | 2.663 |
| 5 | , , , , | 6 | 14.744 | −14.779 | 5.428 | 5 | , , , , | 6 | 6.384 | 1.942 | 4.582 |
| 6 | , , , | 6 | 14.732 | −14.755 | 5.451 | 6 | , , , , | 6 | 6.384 | 1.942 | 4.582 |
| 7 | , , , , | 6 | 14.709 | −14.709 | 5.498 | 7 | , , , , | 6 | 5.926 | 2.858 | 5.498 |
| 8 | , , , , , | 7 | 14.732 | −11.731 | 8.475 | 8 | , , , , , | 7 | 6.384 | 4.966 | 7.605 |
| 9 | , | 3 | 11.810 | −16.915 | 3.291 | >0.161 | 9 | , | 3 | −0.182 | 7.071 | 9.710 | 7.729 × 10−3 |
| 10 | , , | 4 | 11.887 | −14.562 | 5.644 | | 10 | , , | 4 | −0.084 | 9.381 | 12.020 | |
| 11 | , , | 4 | 11.810 | −14.409 | 5.798 | 11 | , , | 4 | −0.182 | 9.577 | 12.216 |
| 12 | , , , | 5 | 11.887 | −11.899 | 8.307 | 12 | , , , | 5 | −0.084 | 12.044 | 14.683 |
| 13 | | 2 | −2.405 | 9.154 | 29.360 | 3.532 × 10−7 | 13 | | 2 | −9.124 | 22.590 | 25.229 | 3.297 × 10−6 |
| 14 | , | 3 | −2.405 | 11.517 | 31.723 | | 14 | , | 3 | −9.124 | 24.953 | 27.592 | |
| 15 | , | 3 | −2.405 | 11.517 | 31.723 | 15 | , | 3 | −9.124 | 24.953 | 27.592 |
| 16 | , , | 4 | −2.405 | 14.023 | 34.229 | 16 | , , | 4 | −9.124 | 27.459 | 30.099 |
Figure A1.
Diagnostic for BOD5 models. (A) Horizontal bed, model , , ; (B) vertical bed, model , , ; (C) horizontal bed, model , ; (D) vertical bed, model , .
Figure A1.
Diagnostic for BOD5 models. (A) Horizontal bed, model , , ; (B) vertical bed, model , , ; (C) horizontal bed, model , ; (D) vertical bed, model , .
Figure A2.
Diagnostic for COD models. (A) Horizontal bed, model , , ; (B) vertical bed, model , , ; (C) horizontal bed, model , ; (D) vertical bed, model , .
Figure A2.
Diagnostic for COD models. (A) Horizontal bed, model , , ; (B) vertical bed, model , , ; (C) horizontal bed, model , ; (D) vertical bed, model , .
Figure A3.
Diagnostic for NH4+-N models. (A) Horizontal bed, model , , ; (B) vertical bed, model , , ; (C) horizontal bed, model , ; (D) vertical bed, model , .
Figure A3.
Diagnostic for NH4+-N models. (A) Horizontal bed, model , , ; (B) vertical bed, model , , ; (C) horizontal bed, model , ; (D) vertical bed, model , .
Figure A4.
Diagnostic for TN models. (A) Horizontal bed, model , , ; (B) vertical bed, model , , ; (C) horizontal bed, model , ; (D) vertical bed, model , .
Figure A4.
Diagnostic for TN models. (A) Horizontal bed, model , , ; (B) vertical bed, model , , ; (C) horizontal bed, model , ; (D) vertical bed, model , .