Effect of Particle Size and Shape on Separation in a Hydrocyclone
Abstract
1. Introduction
2. Experimental Modes and Methods
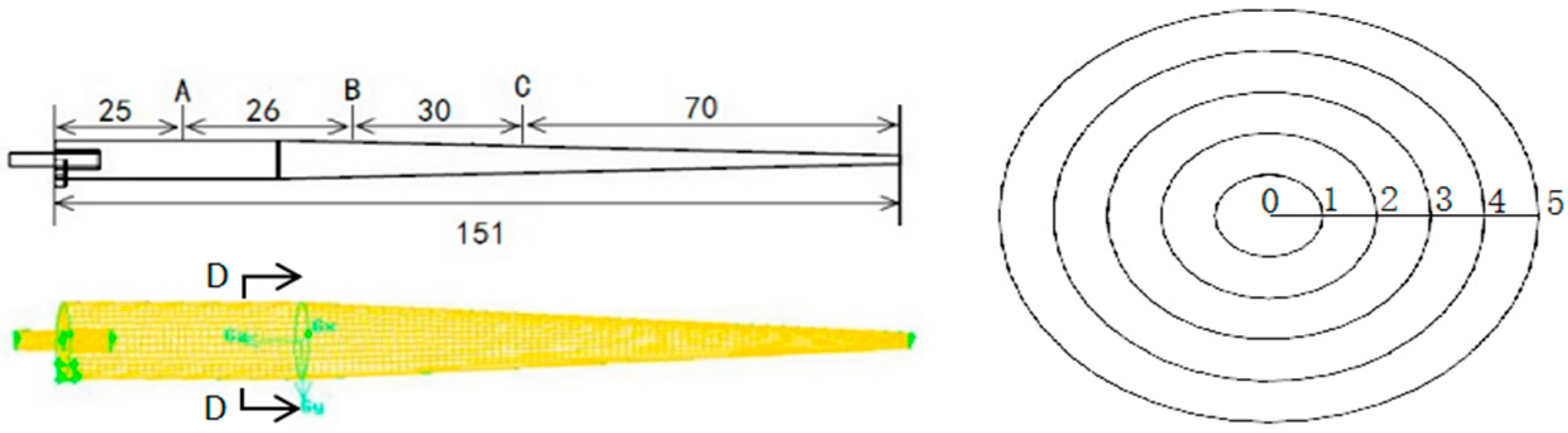
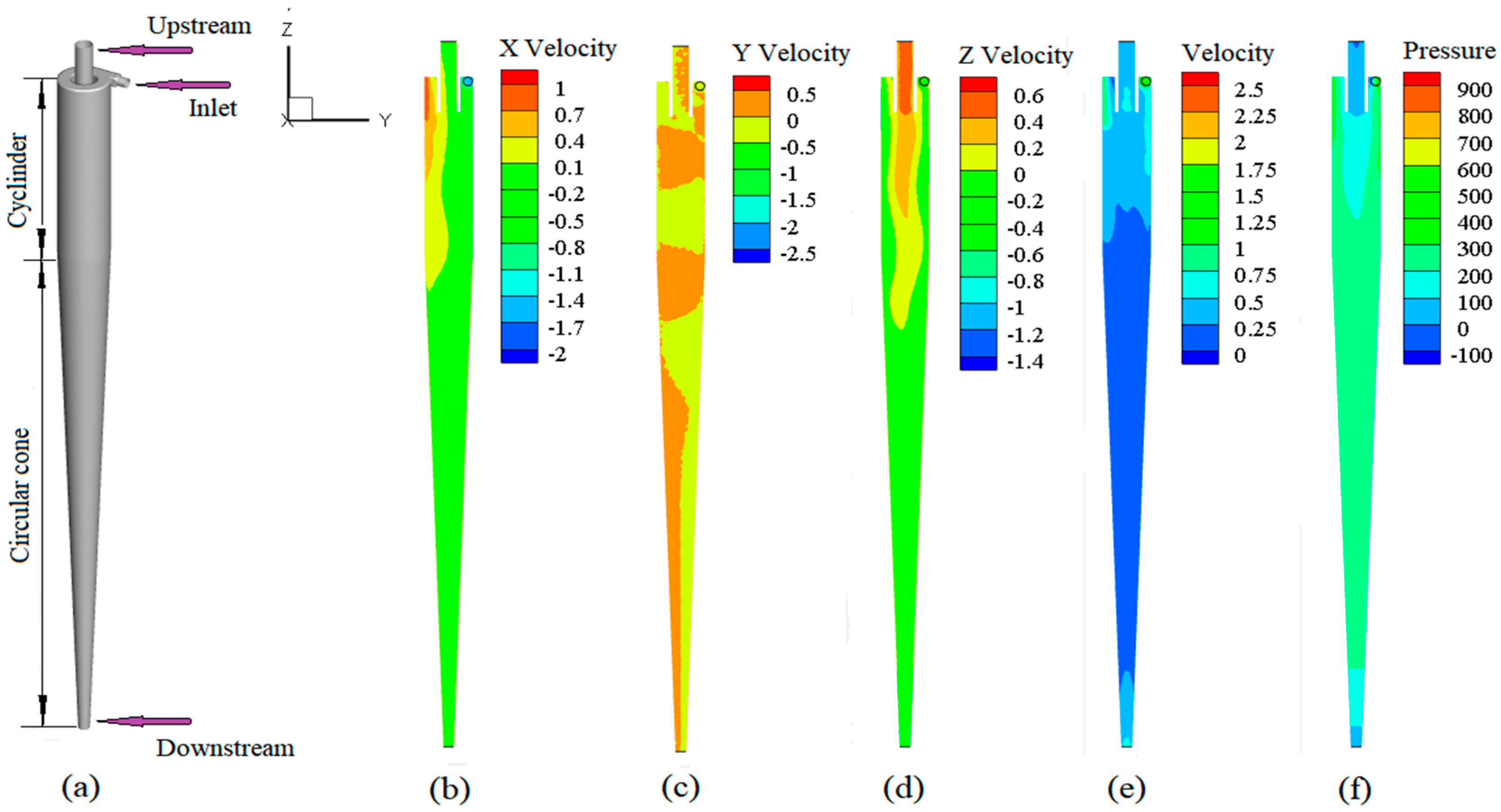
2.1. Hydrocyclone Model
2.2. Numerical Simulation
2.2.1. Particle Characteristics
2.2.2. Mathematical Model and Simulation Method
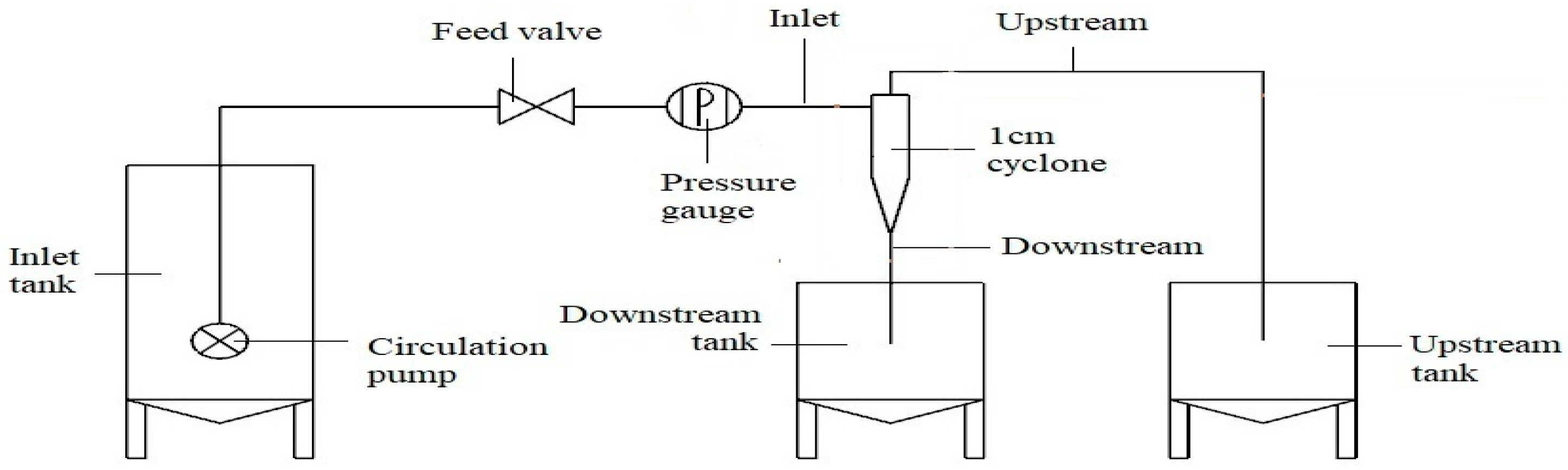
2.3. Separation Experiments
3. Analysis of Experimental Results
3.1. Flow Field, Flow Rate and Particle Distribution
3.2. Relationship between Maximum Projected Area and Separation Results
3.2.1. Radial Concentration Distribution of Particles
3.2.2. Separation Results in Numerical Simulation
3.3. Separation Mechanism of Single and Mixed Particles
3.3.1. Distribution of Axial Velocity and Radial Concentration
3.3.2. Particle Separation Results
4. Experimental Tests
4.1. Test on the Effect of Cross-Section Change on Separation
4.2. Separation Test of Sand Particles 60 and 120 μm
5. Discussion
5.1. Influence of Maximum Projected Area and Volume Changes on Separation Results
5.2. Analysis of the Following Phenomenon of Fine Particles
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | measure of area |
| Ap | maximum projected area of sand particles in the direction of fluid flow, m2 |
| CLS | Saffman lit coefficient |
| CLM | magnus lift coefficient |
| D1 | drag |
| D2 | particle diameter |
| dp | particle diameter, m |
| d | damping |
| di | diameter of sand particles, m |
| f | fluid phase |
| FA | added mass force per unit mass, m·s−2 |
| FB | basset force per unit mass, m·s−2 |
| FD | total drag force; |
| FM | Magus force per unit mass, m·s−2 |
| FP | pressure gradient force per unit mass, m·s−2 |
| Fp-f | interaction forces between fluid and solids phases |
| FS | Saffman lift force per unit mass, m·s−2 |
| g | gravity acceleration vector, 9.81 m·s−2 |
| i(j) | corresponding to i(j)th particle |
| kc | number of particles in a computational cell, dimensionless |
| Ndownstream | number of sand particles separated from the downstream |
| Nupstream | number of sand particles separated from the upstream |
| Pdownstream | fractional flow of the downstream |
| Pupstream | fractional flow of the upstream |
| P | pressure, Pa |
| pg | pressure gradient |
| p | particle phase |
| Re | Reynolds number, dimensionless |
| T | particle shape factor (thickness) |
| t | time, s |
| u | fluid velocity vector, m·s−1 |
| ut | settling velocity, m·s−1 |
| ur | relative velocity, m·s−1 |
| V | volume, m3 |
| v | fluid kinematic viscosity, kg·m−1 s−1 |
| ΔVc | volume of a computational cell, m3 |
| ΔP | pressure drop, Pa |
| ∇p | pressure gradient, kg·m−2s−2 |
| Greek letters | |
| ε | porosity, dimensionless |
| μ | fluid viscosity, kg·m−1·s−1 |
| τ | viscous stress tensor, N·m−3 |
| ρ | density, kg·m−3 |
| β | Empirical coefficient defined in Equation (3), dimensionless |
| ρp | particle density, kg·m−3 |
| γ | fluid strain rate, s−1 |
| ωr | relative angular velocity, rad·s−1 |
| ω | particle rotation angular velocity, rad·s−1 |
| ξ | drag force coefficient |
| Ω | fluid rotation angular velocity, rad·s−1 |
| f | force |
References
- Fu, S.; Yong, F.; Yuan, H.; Tan, W.; Dong, Y. Effect of the medium’s density on the hydrocyclonic separation of waste plastics with different densities. Waste Manag. 2017, 67, 27–31. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Cai, P.; Jiang, F.; Dong, K.; Jiang, Y.; Wang, B. Understanding the separation of particles in a hydrocyclone by force analysis. Powder Technol. 2017, 322, 471–489. [Google Scholar] [CrossRef]
- Neesse, T.; Dueck, J.; Schwemmer, H.; Farghaly, M. Using a high pressure hydrocyclone for solids classification in the submicron range. Miner. Eng. 2015, 71, 85–88. [Google Scholar] [CrossRef]
- Yu, L.; Zou, X.; Hong, T.; Yan, W.; Chen, L.; Xiong, Z. 3D numerical simulation of water and sediment flow in hydrocyclone based on coupled cfd-dem. Trans. Chin. Soc. Agric. Mach. 2016, 01, 126–132. [Google Scholar]
- Zhu, G.; Liow, J. Experimental study of particle separation and the fishhook effect in a mini-hydrocyclone. Chem. Eng. Sci. 2014, 111, 94–105. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y.; Han, T. Influence of vortex finder configurations on separation of fine particles. CIESC J. 2017, 05, 1921–1931. [Google Scholar]
- Tang, B.; Xu, Y.; Song, X.; Xu, J. Effect of inlet configuration on hydrocyclone performance. Trans. Nonferrous Met. Soc. China 2017, 27, 1645–1655. [Google Scholar] [CrossRef]
- Hwang, K.-J.; Chou, S.-P. Designing vortex finder structure for improving the particle separation efficiency of a hydrocyclone. Sep. Purif. Technol. 2017, 172, 76–84. [Google Scholar] [CrossRef]
- Vakamalla, T.R.; Koruprolu, V.B.R.; Arugonda, R.; Mangadoddy, N. Development of novel hydrocyclone designs for improved fines classification using multiphase cfd model. Sep. Purif. Technol. 2017, 175, 481–497. [Google Scholar] [CrossRef]
- Zhang, C.; Wei, D.Z.; Cui, B.Y.; Li, T.S.; Luo, N. Effects of curvature radius on separation behaviors of the hydrocyclone with a tangent-circle inlet. Powder Technol. 2017, 305, 156–165. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, C.; Wang, H.; Wang, J. Eulerian–lagrangian study of dense liquid–solid flow in an industrial-scale cylindrical hydrocyclone. Int. J. Miner. Process. 2016, 151, 40–50. [Google Scholar] [CrossRef]
- Zhao, Q.; Li, W.; He, W. Experimental study of pressure drop characteristics of a novel solid/liquid hydrocyclone. J. Eng. Thermophys. 2010, 01, 61–63. [Google Scholar]
- Wang, B.; Chu, K.W.; Yu, A.B. Numerical study of particle–fluid flow in a hydrocyclone. Ind. Eng. Chem. Res. 2007, 46, 4695–4705. [Google Scholar] [CrossRef]
- Wang, B.; Chu, K.W.; Yu, A.B.; Vince, A. Modelling the multiphase flow in a dense medium cyclone. Ind. Eng. Chem. Res. 2009, 48, 3628–3639. [Google Scholar] [CrossRef]
- Asakura, K.; Asari, T.; Nakajima, I. Simulation of solid–liquid flows in a vertical pipe by a collision model. Powder Technol. 1997, 94, 201–206. [Google Scholar] [CrossRef]
- Chu, K.W.; Wang, B.; Yu, A.B.; Vince, A. Cfd-dem modelling of multiphase flow in dense medium cyclones. Powder Technol. 2009, 193, 235–247. [Google Scholar] [CrossRef]
- Niu, W.; Liu, L.; Chen, X. Influence of fine particle size and concentration on the clogging of labyrinth emitters. Irrig. Sci. 2013, 31, 545–555. [Google Scholar] [CrossRef]
- Kashiwaya, K.; Noumachi, T.; Hiroyoshi, N.; Ito, M.; Tsunekawa, M. Effect of particle shape on hydrocyclone classification. Powder Technol. 2012, 226, 147–156. [Google Scholar] [CrossRef]
- Zhang, J.; Fan, L.S. A semianalytical expression for the drag force of an interactive particle due to wake effect. Ind. Eng. Chem. Res. 2002, 41, 5094–5097. [Google Scholar] [CrossRef]
- Niazi, S.; Habibian, M.; Rahimi, M. A comparative study on the separation of different-shape particles using a mini-hydrocyclone. Chem. Eng. Technol. 2017, 40, 699–708. [Google Scholar] [CrossRef]
- Abdollahzadeh, L.; Habibian, M.; Etezazian, R.; Naseri, S. Study of particle’s shape factor, inlet velocity and feed concentration on mini-hydrocyclone classification and fishhook effect. Powder Technol. 2015, 283, 294–301. [Google Scholar] [CrossRef]
- Endoh, S. Study of the shape separation of fine particles using fluid fields-dynamic properties of irregular shaped particles in wet cyclones. J. Soc. Powder Technol. Jpn. 1992, 29, 125–132. [Google Scholar] [CrossRef]
- Wills, B.A.; Napier-Munn, T. Wills’ Mineral Processing Technology, 7th ed.; Elsevier Science & Technology Books: Amsterdam, The Netherlands, 2006; pp. 145–206. [Google Scholar]
- Wang, B.; Yu, A.B. Computational investigation of the mechanisms of particle separation and “fish-hook” phenomenon in hydrocyclones. AIChE J. 2010, 56, 1703–1715. [Google Scholar] [CrossRef]
- Xu, P.; Wu, Z.; Mujumdar, A.S.; Yu, B. Innovative hydrocyclone inlet designs to reduce erosion-induced wear in mineral dewatering processes. Dry. Technol. 2009, 27, 201–211. [Google Scholar] [CrossRef]
- Zhu, C.; Liang, S.C.; Fan, L.S. Particle wake effects on the drag force of an interactive particle. Int. J. Multiph. Flow 1994, 20, 117–129. [Google Scholar] [CrossRef]
- Peng, Y.; Zhou, J.G.; Burrows, R. Modelling the free surface flow in rectangular shallow basins by lattice Boltzmann method. J. Hydraul. Eng. ASCE 2011, 137, 1680–1685. [Google Scholar] [CrossRef]
- Peng, Y.; Zhou, J.G.; Burrows, R. Modelling solute transport in shallow water with the lattice Boltzmann method. Comput. Fluids 2011, 50, 181–188. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, J.M.; Zhou, J.G. Lattice Boltzmann Model Using Two-Relaxation-Time for Shallow Water Equations. J. Hydraul. Eng. ASCE 2016, 142, 06015017. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, J.M.; Meng, J.P. Second order force scheme for lattice Boltzmann model of shallow water flows. J. Hydraul. Res. 2017, 55, 592–597. [Google Scholar] [CrossRef]
- Peng, Y.; Zhou, J.G.; Zhang, J.M.; Burrows, R. Modeling moving boundary in shallow water by LBM. Int. J. Mod. Phys. C 2013, 24, 1–17. [Google Scholar] [CrossRef]
- Peng, Y.; Zhou, J.G.; Zhang, J.M.; Liu, H.F. Lattice Boltzmann Modelling of Shallow Water Flows over Discontinuous Beds. Int. J. Numer. Method Fluids 2014, 75, 608–619. [Google Scholar] [CrossRef]
- Peng, Y.; Zhou, J.G.; Zhang, J.M. Mixed numerical method for bed evolution. Proc. Inst. Civ. Eng. Water Manag. 2015, 168, 3–15. [Google Scholar] [CrossRef]
- Peng, Y.; Meng, J.P.; Zhang, J.M. Multispeed lattice Boltzmann model with stream-collision scheme for transcritical shallow water flows. Math. Probl. Eng. 2017, 2017, 8917360. [Google Scholar] [CrossRef]
- Peng, Y.; Mao, Y.F.; Wang, B.; Xie, B. Study on C-S and P-R EOS in pseudo-potential lattice Boltzmann model for two-phase flows. Int. J. Mod. Phys. C 2017, 28, 1750120. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, B.; Mao, Y.F. Study on force schemes in pseudopotential lattice Boltzmann model for two-phase flows. Math. Probl. Eng. 2018, 2018, 6496379. [Google Scholar] [CrossRef]
- Tsuji, Y.; Morikawa, Y.; Terashima, K. Fluid-dynamic interaction between two spheres. Int. J. Multiph. Flow 1982, 8, 71–82. [Google Scholar] [CrossRef]
- Zhu, G.; Liow, J.L.; Neely, A. Computational study of the flow characteristics and separation efficiency in a mini-hydrocyclone. Chem. Eng. Res. Des. 2012, 90, 2135–2147. [Google Scholar] [CrossRef]
- Schubert, H. On the origin of “Anomalous” shapes of the separation curve in hydrocyclone separation of fine particles. Part. Sci. Technol. 2004, 22, 219–234. [Google Scholar] [CrossRef]
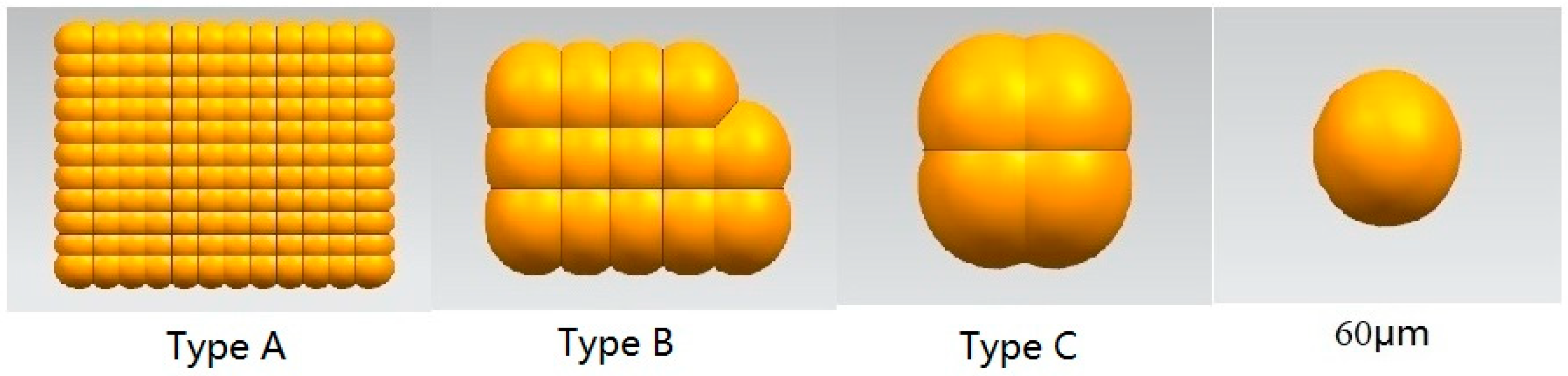
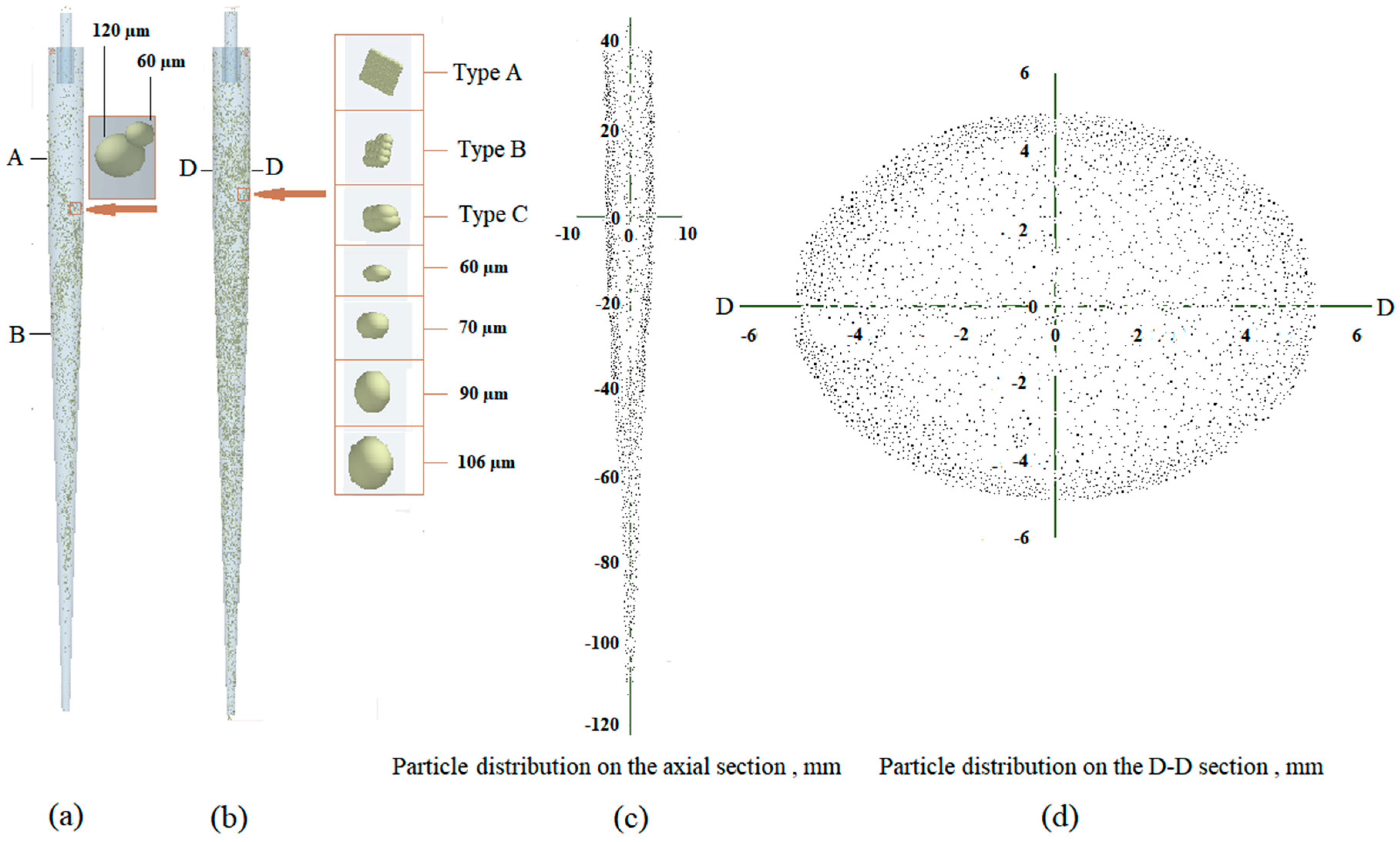

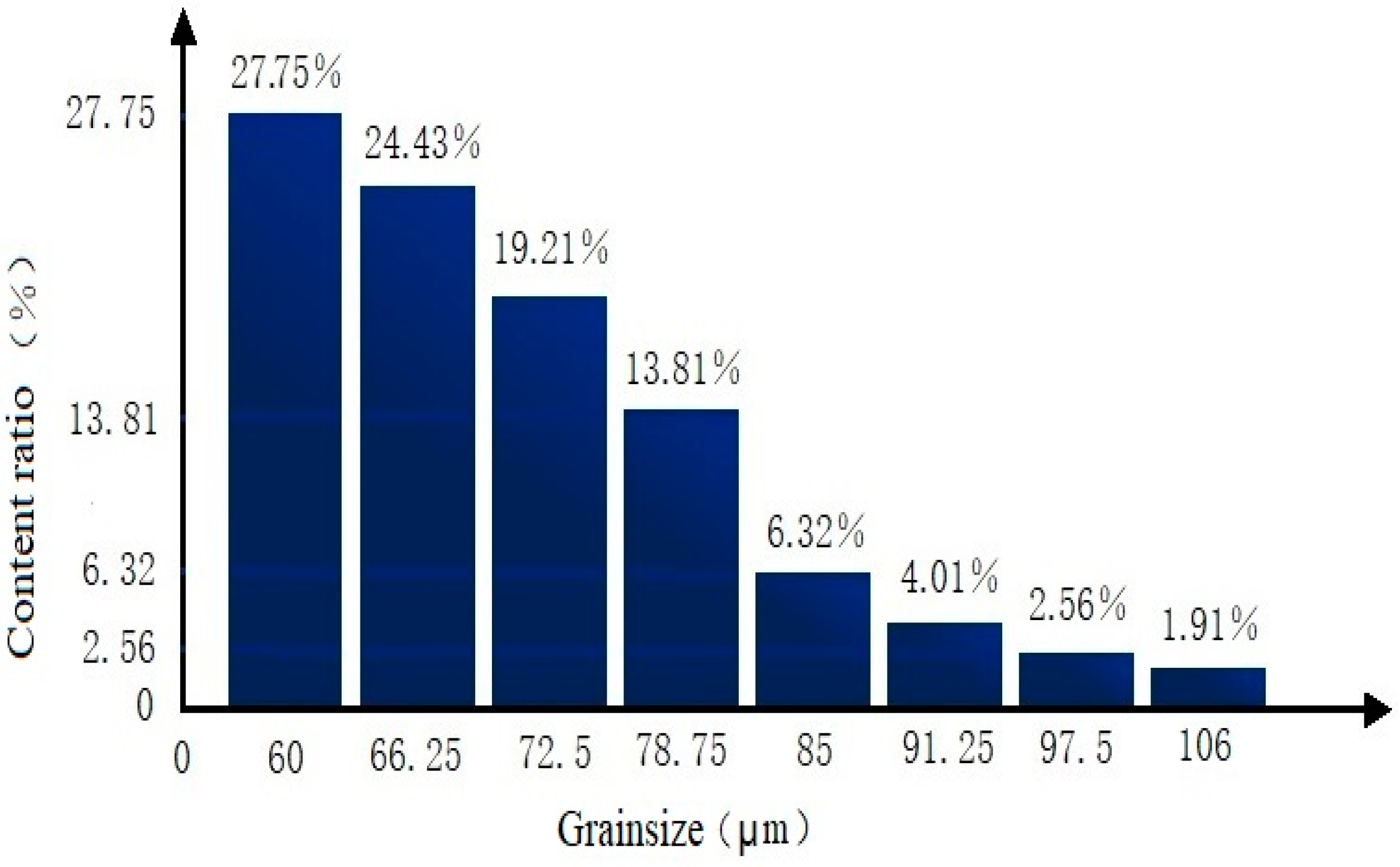

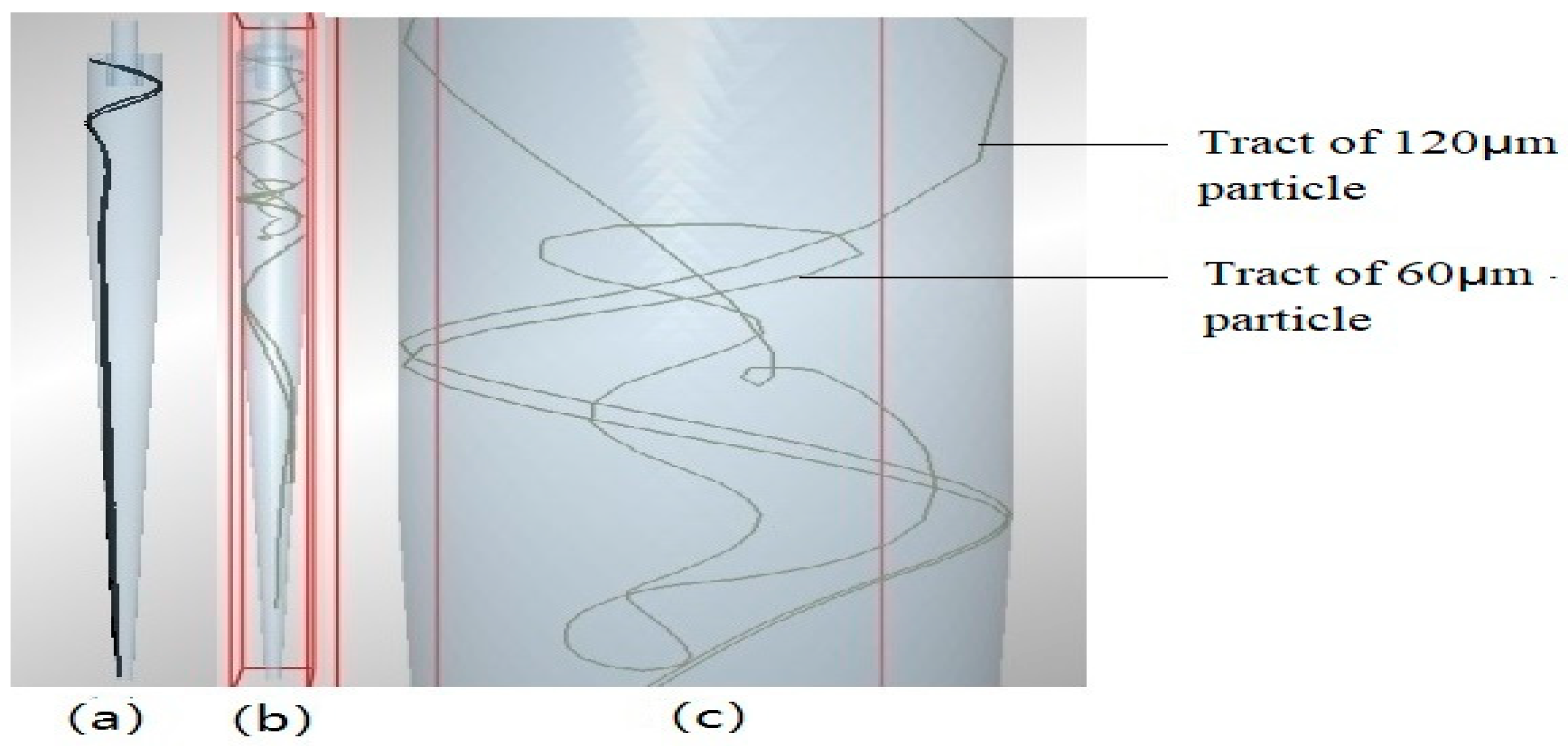
| Title 1 | Type A | Type B | Type C | 60 µm | 70 µm | 90 µm | 106 µm | 120 µm |
|---|---|---|---|---|---|---|---|---|
| Mass (μg) | 0.28 | 0.28 | 0.28 | 0.28 | 0.44 | 0.95 | 1.54 | 2.23 |
| Thickness (mm) | 0.015 | 0.030 | 0.045 | 0.060 | 0.070 | 0.090 | 0.106 | 0.120 |
| Maximum projected area (S) | 3.11 | 2.24 | 1.36 | 1.00 | 1.36 | 2.24 | 3.11 | 4.00 |
| Phase | Parameter | Symbol | Units | Value |
|---|---|---|---|---|
| Solid | Density distribution | ρ | kg·m−3 | 2500 |
| Rolling friction coefficient | μr | - | 0.01 | |
| Sliding friction coefficient | μs | - | 0.30 | |
| Poisson’s ratio | V | - | 0.40 | |
| Young’s modulus | E | N·m−2 | 2 × 10−7 | |
| Coefficient of Restitution | cr | - | 0.55 | |
| fluid | Density | ρ | kg·m−3 | 998.20 |
| Viscosity | μ | kg·m−1·s−1 | 0.001 |
| Symbol | Units | Value | |
|---|---|---|---|
| Particle velocity at inlet | v | m·s−1 | 2.00 |
| Viscosity of Water Phase | v | m·s−1 | 2.00 |
| Turbulent intensity | I | - | 5% |
| Hydraulic radius | D | mm | 2.00 |
| Pressure at upstream | - | Pa | 0.00 |
| Pressure at downstream | - | Pa | 0.00 |
| Back-flow turbulence intensity | Ih | - | 5% |
| Number of particle | - | N·s−1 | 1000 |
| Particle diameter | di | μm | - |
| S/N | Name | Formula | Description |
|---|---|---|---|
| 1 | The normal force (Fn) | R* is the equivalent radius α is the normal overlap | |
| 2 | The equivalent elastic modulus (E*) | E1, v1 and E1, v1 are elastic modulus and Poisson’s ratio of sand 1 and sand 2 | |
| 3 | The damping force (Fnd) | is the normal relative velocity; Sn is the normal stiffness β is coefficient | |
| 4 | The equivalent mass (m*) | m1 and m2 are the mass of sand 1 and sand 2 | |
| 5 | The tangential force among the sands (Ft) | δ is the tangential overlap | |
| 6 | The tangential stiffness (St) | ||
| 7 | The equivalent shear modulus (G*) | G1 and G2 are shear modulus of sand 1 and sand 2 | |
| - | V1 and V2 are velocity of sand 1 and sand 2 | ||
| 8 | The tangential damping force among sand particles (Ft) | is the tangential relative velocity | |
| 9 | The rolling friction (Ti) | μr is coefficient of rolling friction Ri is the distance between the center of mass to the point of contact; ωi is unit angular velocity vector of object at the contact point |
| Particles | Particle Size (µm) | Concentration (kg·m−3) | Separation Time (s) |
|---|---|---|---|
| Singe | 60 | 5 | 16 |
| 120 | 40 | 16 | |
| Mixed | 60 + 120 | 5 + 40 | 16 |
| Radial Distance | Type A | Type B | Type C | 60 µm | 70 µm | 90 µm | 106 µm |
|---|---|---|---|---|---|---|---|
| Percentage of Content (%) | |||||||
| 0–1 | 8.10 | 6.82 | 3.96 | 2.65 | 2.11 | 1.81 | 1.01 |
| 1–2 | 9.01 | 7.12 | 5.39 | 5.14 | 3.23 | 2.34 | 1.96 |
| 2–3 | 12.87 | 11.12 | 9.01 | 8.63 | 7.05 | 5.91 | 3.21 |
| 3–4 | 18.59 | 17.36 | 16.20 | 13.85 | 11.61 | 7.32 | 6.89 |
| 4–5 | 51.43 | 57.58 | 65.44 | 69.73 | 76.00 | 82.62 | 86.93 |
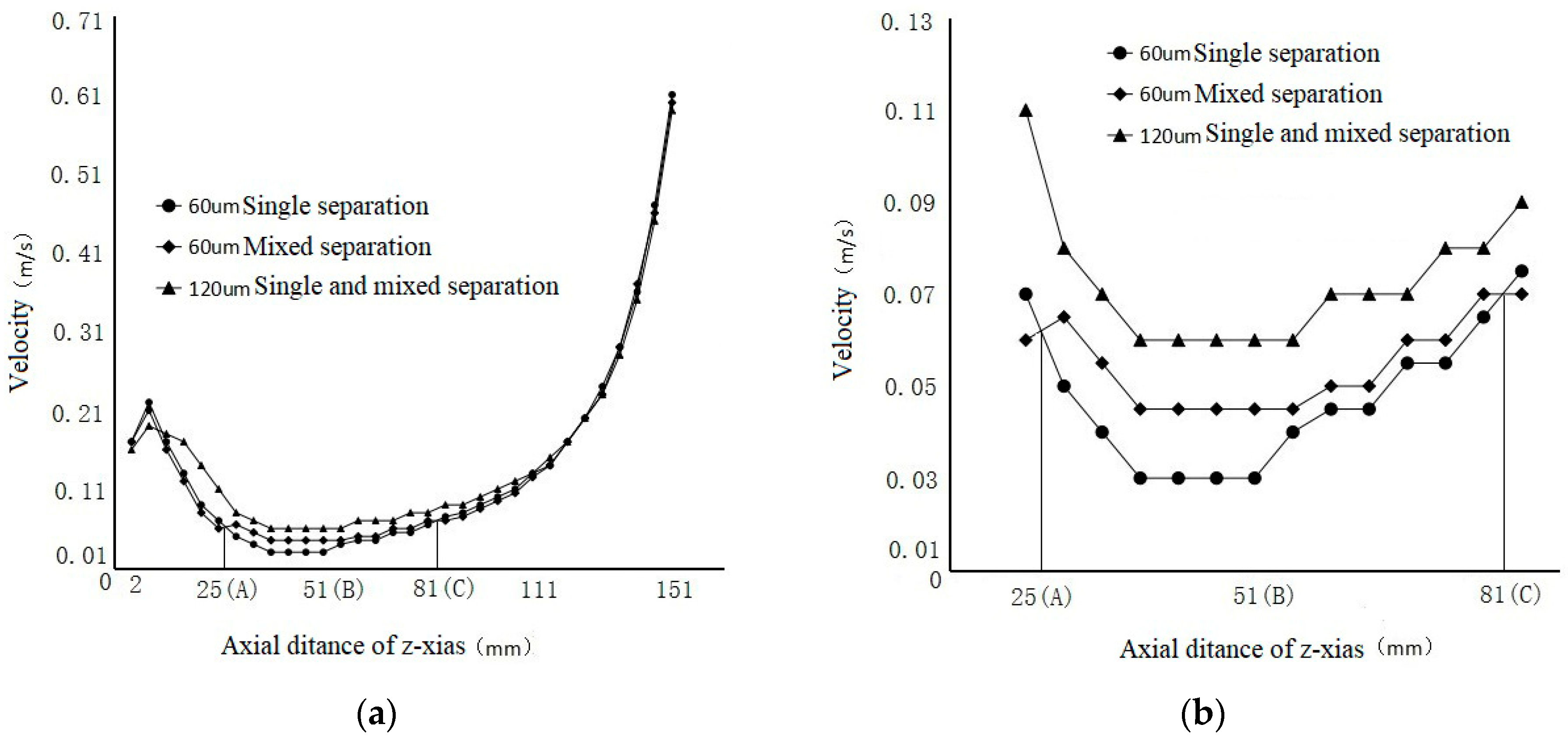
| Radial Distance | Maximum Projected Area (S) | tupstream (s) | tdownstream (s) | Vupstream (m s−1) | Vdownstream (m s−1) | Lupstream (m) | Ldownstream (m) | p (%) |
|---|---|---|---|---|---|---|---|---|
| Type A | 3.11 | 0.63 | 2.21 | 0.41 | 0.59 | 0.26 | 1.30 | 24.0 |
| Type B | 2.24 | 0.66 | 2.15 | 0.41 | 0.59 | 0.27 | 1.27 | 17.8 |
| Type C | 1.36 | 0.69 | 2.11 | 0.41 | 0.59 | 0.28 | 1.25 | 14.9 |
| 60 µm | 1.00 | 0.72 | 2.08 | 0.40 | 0.58 | 0.29 | 1.21 | 9.4 |
| 70 µm | 1.36 | 0.75 | 2.02 | 0.39 | 0.59 | 0.29 | 1.19 | 7.4 |
| 90 µm | 2.24 | 0.79 | 1.98 | 0.39 | 0.60 | 0.31 | 1.19 | 3.2 |
| 106 µm | 3.11 | 0.81 | 1.92 | 0.39 | 0.60 | 0.32 | 1.15 | 0.9 |
| 0–1 mm | 1–2 mm | 2–3 mm | 3–4 mm | 4–5 mm | ||
|---|---|---|---|---|---|---|
| 60 µm particles | Single | 2.65 | 5.14 | 8.63 | 13.85 | 69.73 |
| Mixed | 1.41 | 1.16 | 1.19 | 5.78 | 90.46 | |
| Difference | −1.24 | −3.98 | −7.44 | −8.07 | 20.73 | |
| 120 µm particles | Single | 1.33 | 1.50 | 1.64 | 2.30 | 93.23 |
| Mixed | 1.21 | 1.32 | 1.79 | 2.95 | 92.73 | |
| Difference | −0.12 | −0.18 | 0.15 | 0.65 | −0.5 |
| tavearge | Ndownstream | Nupstream | p (%) | ||
|---|---|---|---|---|---|
| Single | X | 2.00 | 906 | 94 | 90.6 |
| D | 1.70 | 1000 | 0 | 100 | |
| Mixed | X | 1.80 | 947 | 53 | 94.7 |
| D | 1.70 | 1000 | 0 | 100 |
| Single | Mixed | |||
|---|---|---|---|---|
| 60 µm | 120 µm | 60 µm | 120 µm | |
| Upstream | 0.312 | 0 | 0.255 | 0 |
| Downstream | 28.85 | 29.25 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Z.; Yu, L.; Wang, F.; Li, N.; Chang, L.; Cui, N. Effect of Particle Size and Shape on Separation in a Hydrocyclone. Water 2019, 11, 16. https://doi.org/10.3390/w11010016
Tang Z, Yu L, Wang F, Li N, Chang L, Cui N. Effect of Particle Size and Shape on Separation in a Hydrocyclone. Water. 2019; 11(1):16. https://doi.org/10.3390/w11010016
Chicago/Turabian StyleTang, Zhaojia, Liming Yu, Fenghua Wang, Na Li, Liuhong Chang, and Ningbo Cui. 2019. "Effect of Particle Size and Shape on Separation in a Hydrocyclone" Water 11, no. 1: 16. https://doi.org/10.3390/w11010016
APA StyleTang, Z., Yu, L., Wang, F., Li, N., Chang, L., & Cui, N. (2019). Effect of Particle Size and Shape on Separation in a Hydrocyclone. Water, 11(1), 16. https://doi.org/10.3390/w11010016





