Numerical Analysis of the Impact Factors on the Flow Fields in a Large Shallow Lake
Abstract
1. Introduction
2. Methodology
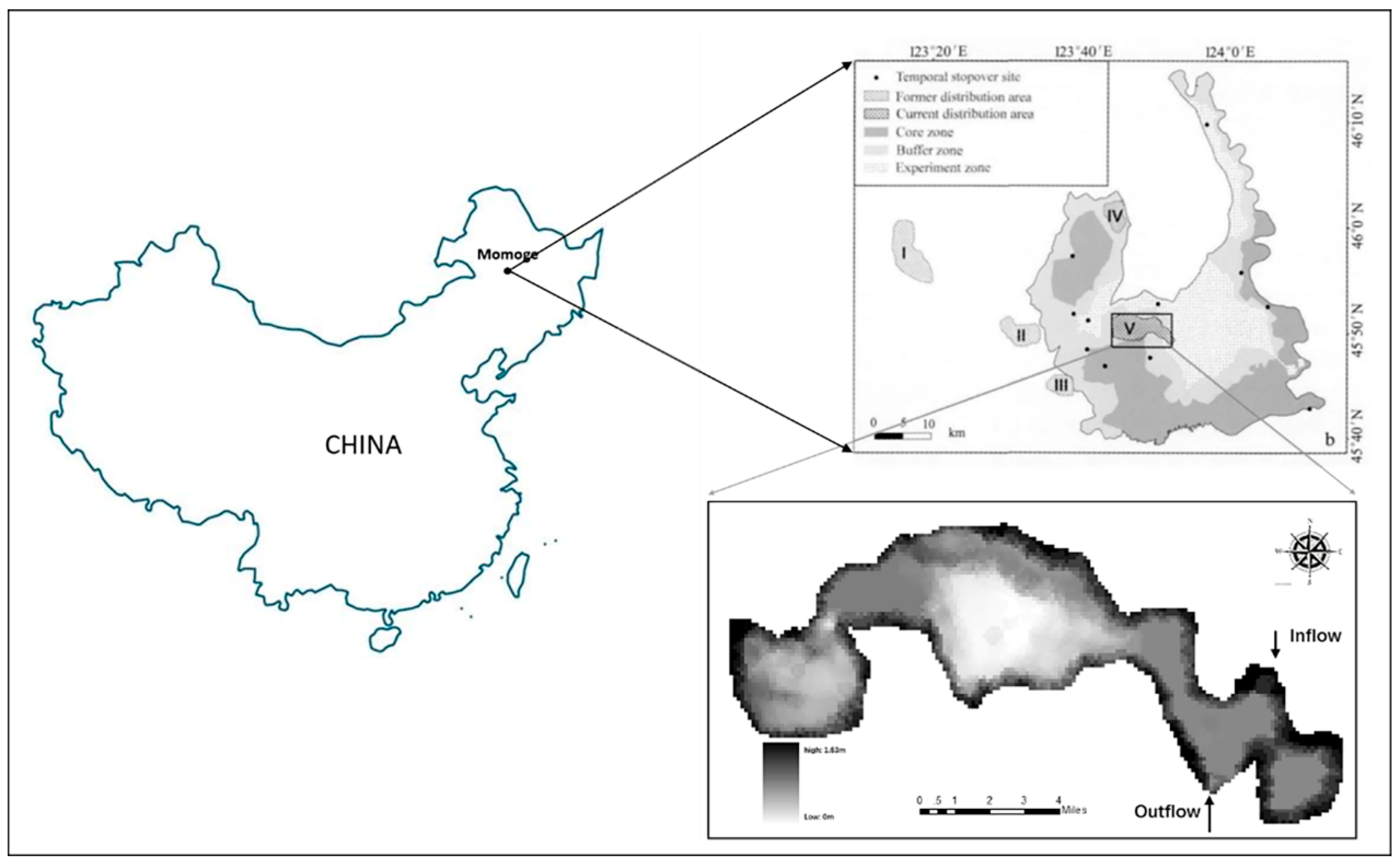
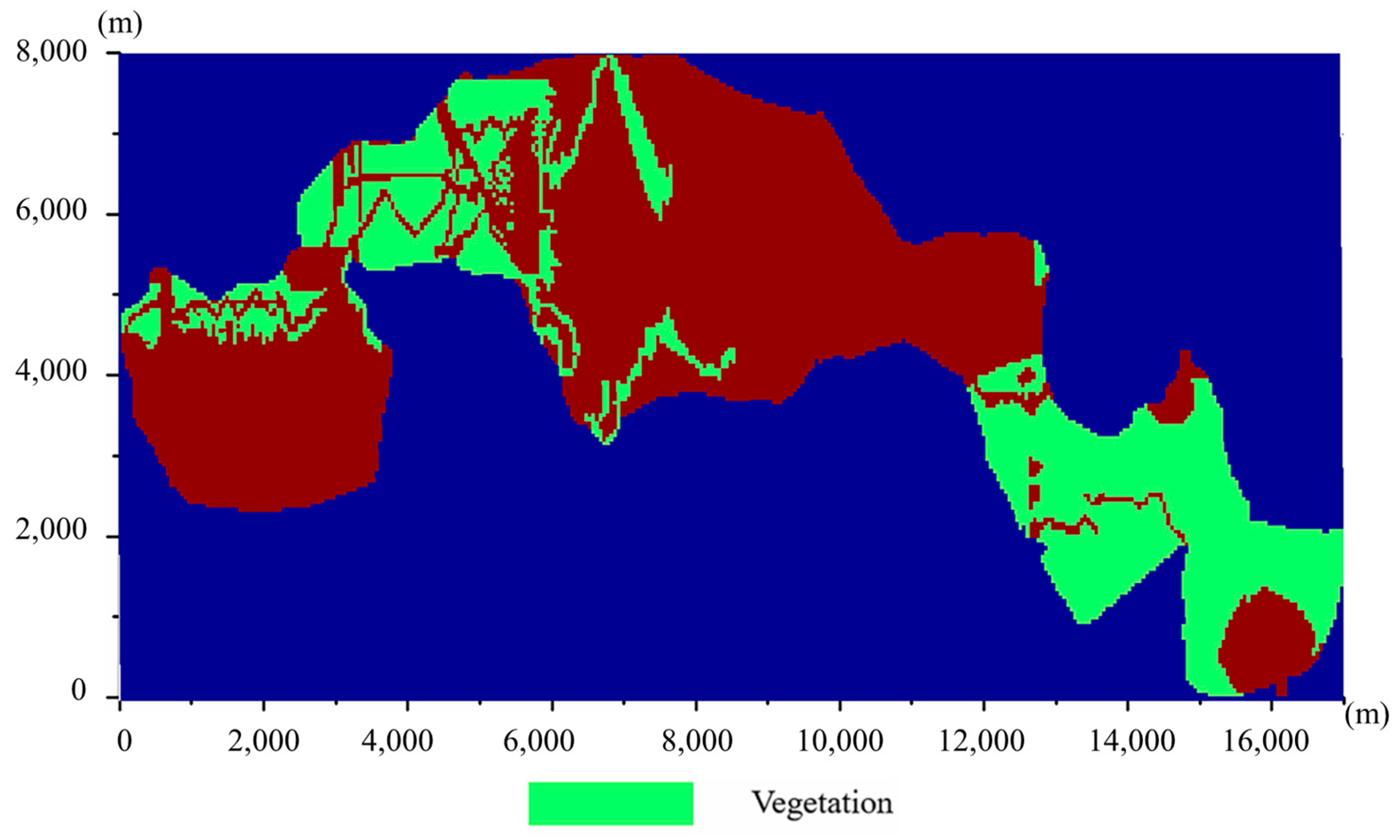
2.1. Study Area
2.2. Governing Equations
2.3. External Force Term
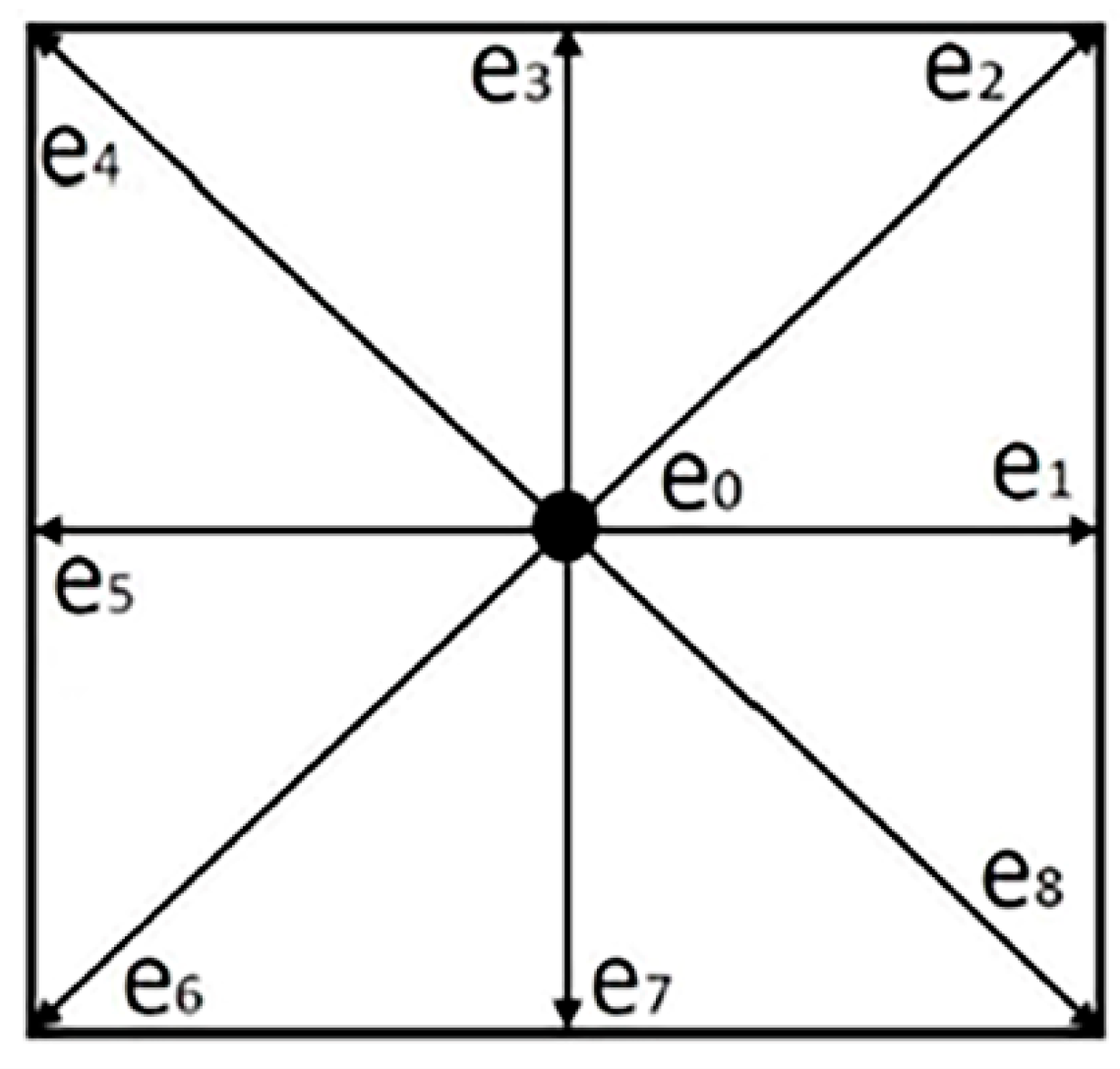
2.4. Lattice Boltzmann Method (LBM)
2.5. Rainfall
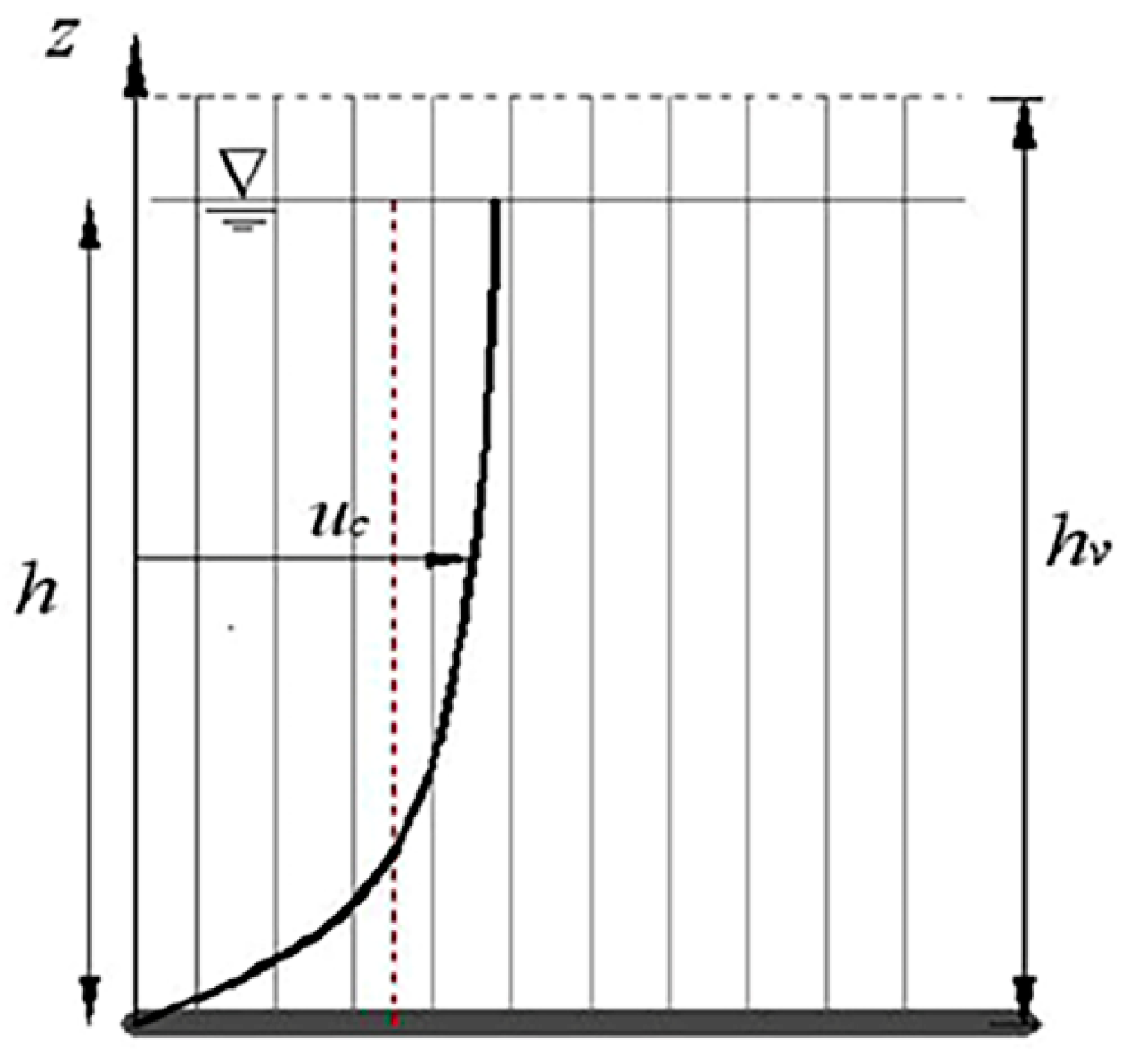
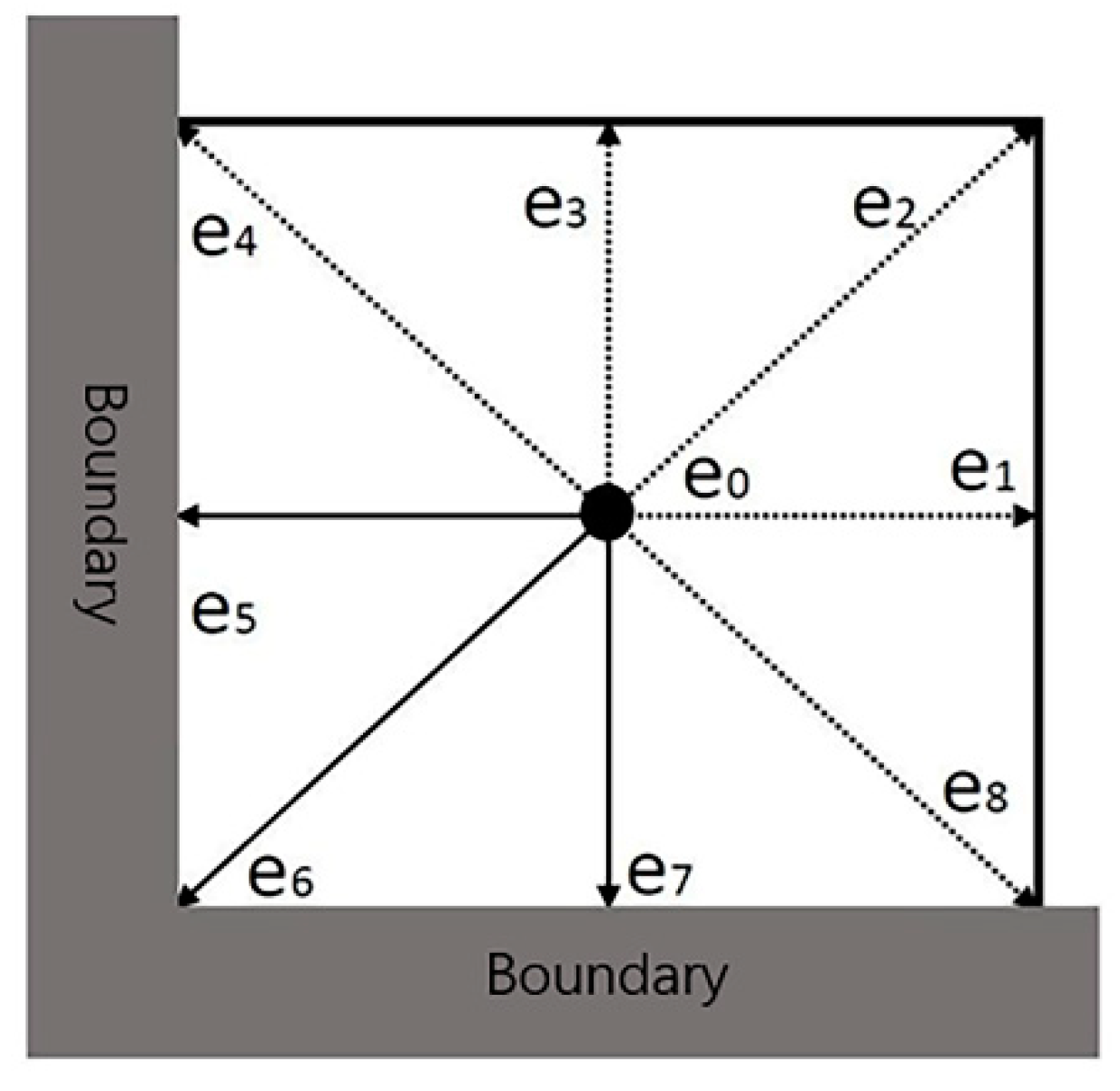
2.6. Boundary Conditions
3. Results
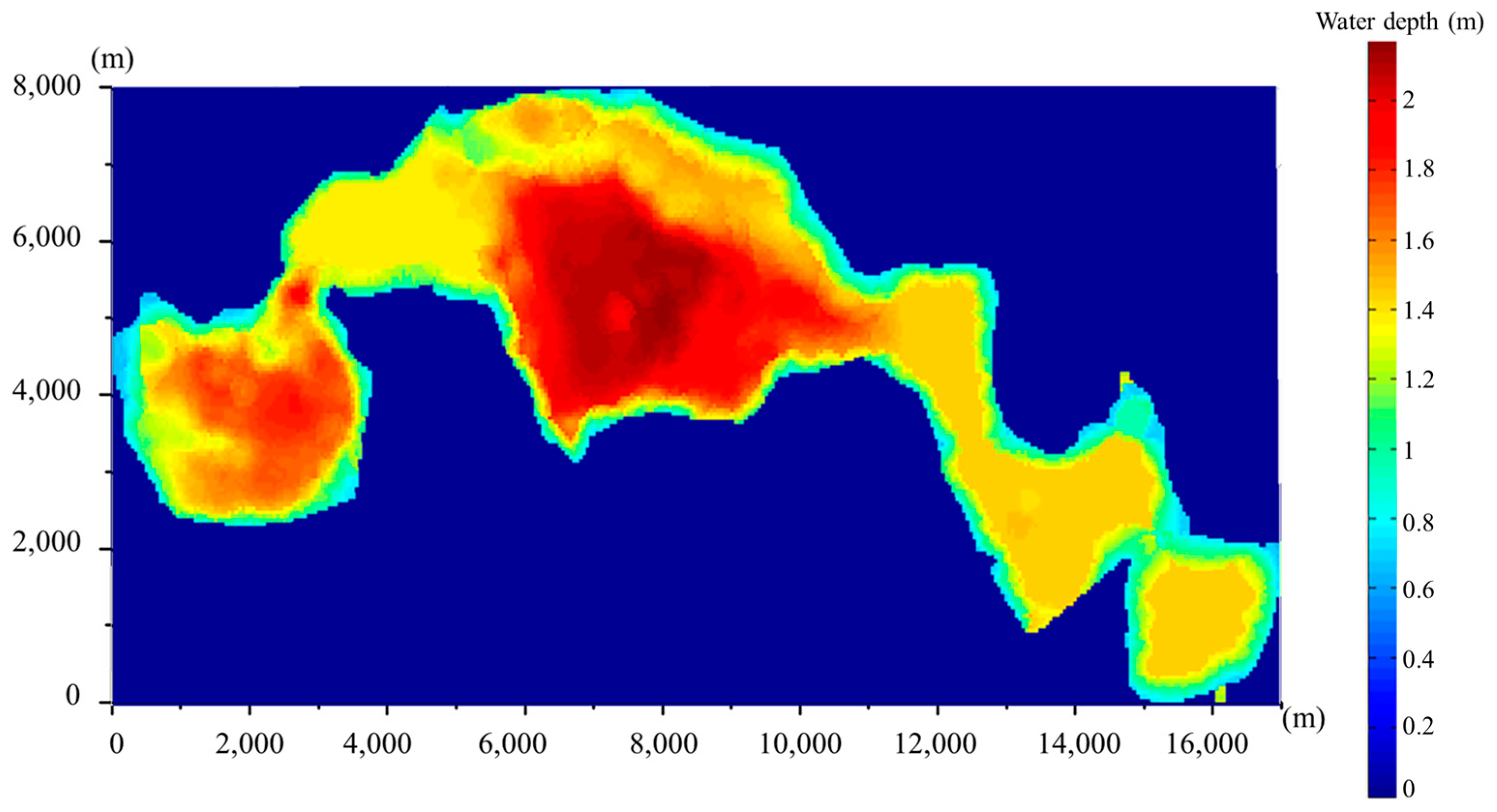
3.1. Initial Conditions
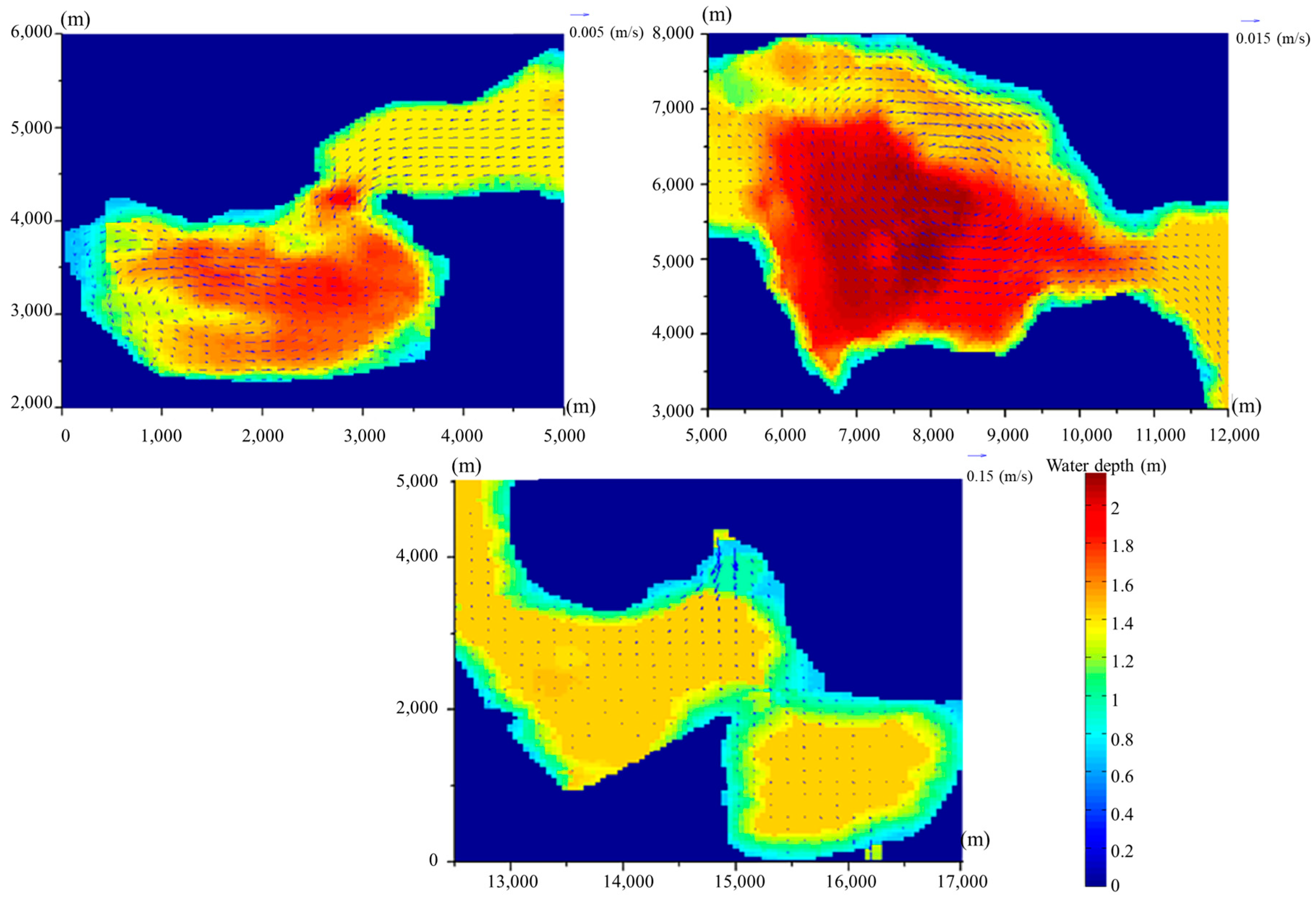
3.2. Numerical Tests
3.3. Sensitivity Analysis
3.3.1. Wind Speed
3.3.2. Inflow Discharge
3.3.3. Vegetation Density
3.3.4. Rain Density
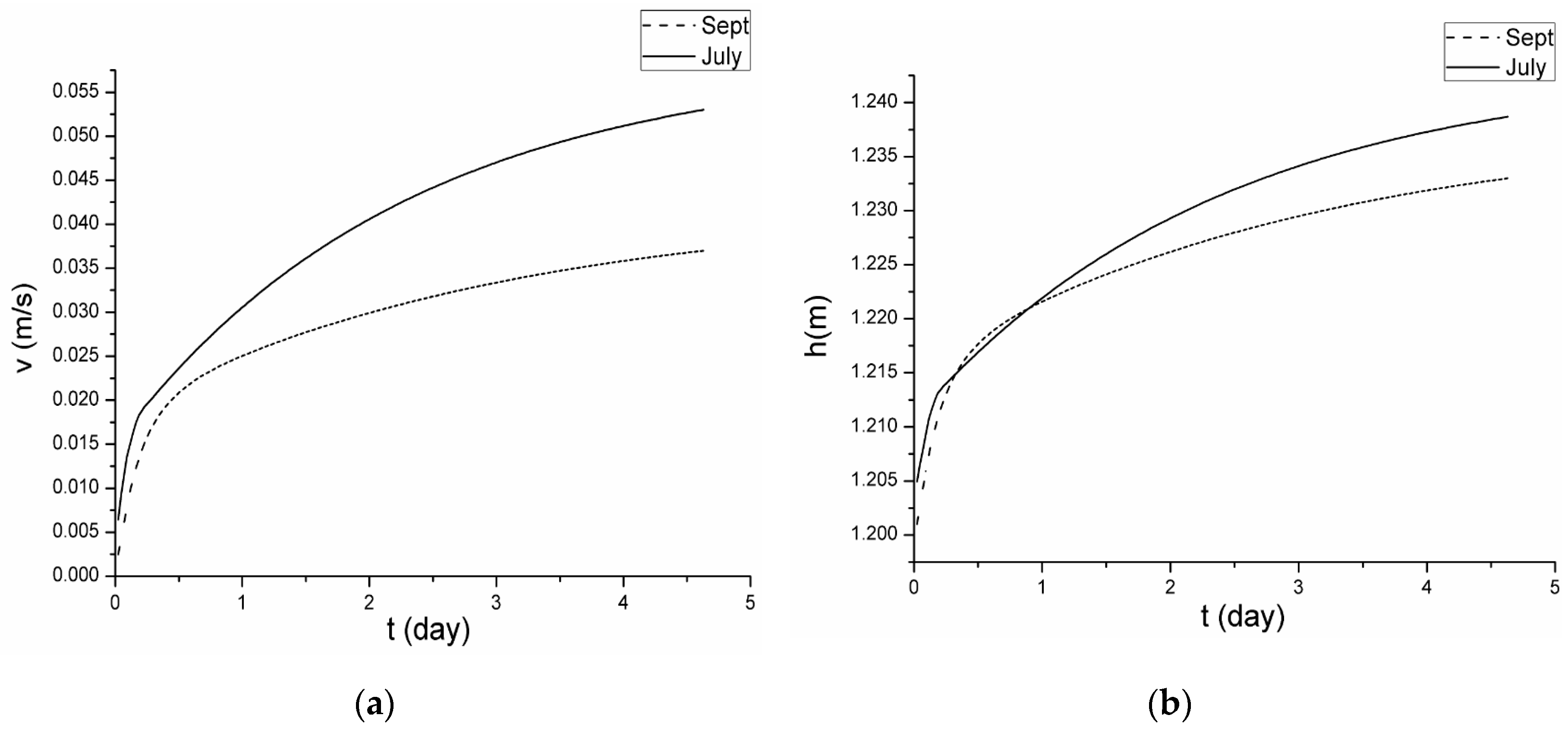
3.4. Scenario Simulation
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zeng, L.; Chen, G.Q. Flow distribution and environmental dispersivity in a tidal wetland channel of rectangular cross-section. Commun. Nonlinear Sci. 2009, 17, 4192–4209. [Google Scholar] [CrossRef]
- Calhoun, A.J.; Mushet, D.M.; Bell, K.P.; Boix, D.; Fitzsimons, J.A.; Isselin-Nondedeu, F. Temporary wetlands: Challenges and solutions to conserving a ‘disappearing’ ecosystem. Biol. Conserv. 2017, 211, 3–11. [Google Scholar] [CrossRef]
- Hui, F.; Xu, B.; Huang, H.; Yu, Q.; Gong, P. Modelling spatial-temporal change of Poyang Lake using multitemporal Landsat imagery. Int. J. Remote. Sens. 2008, 29, 5767–5784. [Google Scholar] [CrossRef]
- Yang, R.; Cui, B. A wetland network design for water allocation based on environmental flow requirements. Clean Soil Air Water 2012, 40, 1047–1056. [Google Scholar] [CrossRef]
- Stephan, U.; Gutknecht, D. Hydraulic resistance of submerged flexible vegetation. J. Hydrol. 2002, 269, 27–43. [Google Scholar] [CrossRef]
- Kouwen, N. Friction factors for coniferous tress along rivers. J. Hydraul. Eng. 2000, 126, 732–740. [Google Scholar] [CrossRef]
- Huai, W.X.; Zeng, Y.H.; Xu, Z.G. Three-layer model for vertical velocity distribution in open channel flow with submerged rigid vegetation. Adv. Water. Resour. 2009, 32, 487–492. [Google Scholar] [CrossRef]
- Yang, Z.; Bai, F.; Huai, W.; An, R.; Wang, H. Modelling open-channel flow with rigid vegetation based on two-dimensional shallow water equations using the lattice Boltzmann method. Ecol. Eng. 2017, 106, 75–81. [Google Scholar] [CrossRef]
- Yang, S.; Bai, Y.; Xu, H. Experimental analysis of river evolution with riparian vegetation. Water 2018, 10, 1500. [Google Scholar] [CrossRef]
- Zhou, J.G. A lattice Boltzmann model for the shallow water equations. Int. J. Mod. Phys. C 2002, 13, 1135–1150. [Google Scholar] [CrossRef]
- Liu, Q.; Qin, Y.; Zhang, Y.; Li, Z. A coupled 1D–2D hydrodynamic model for flood simulation in flood detention basin. Nat. Hazards 2015, 75, 1303–1325. [Google Scholar] [CrossRef]
- Patro, S.; Chatterjee, C.; Mohanty, S.; Singh, R.; Raghuwanshi, N.S. Flood inundation modeling using MIKE FLOOD and remote sensing data. J. Indian Soc. Remote Sens. 2009, 37, 107–118. [Google Scholar] [CrossRef]
- Arifin, R.R.; James, S.C.; de Alwis Pitts, D.A.; Hamlet, A.F.; Sharma, A.; Fernando, H.J. Simulating the thermal behavior in Lake Ontario using EFDC. J. Great Lakes Res. 2016, 42, 511–523. [Google Scholar] [CrossRef]
- Bai, H.; Chen, Y.; Wang, D.; Zou, R.; Zhang, H.; Ye, R.; Ma, W.; Sun, Y. Developing an EFDC and numerical source-apportionment model for nitrogen and phosphorus contribution analysis in a Lake Basin. Water 2018, 10, 1315. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Ann. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Succi, S.; Santangelo, P.; Benzi, R. High-resolution lattice-gas simulation of two-dimensional turbulence. Phys. Rev. Lett. 1988, 60, 2738–2740. [Google Scholar] [CrossRef] [PubMed]
- Salmon, R. The lattice Boltzmann method as a basis for ocean circulation modeling. J. Mar. Res. 1999, 57, 503–535. [Google Scholar] [CrossRef]
- Dellar, P.J. Non-hydrodynamic modes and a priori construction of shallow water lattice Boltzmann equations. Phys. Rev. E 2002, 65, 036309. [Google Scholar] [CrossRef]
- Liu, H.; Ding, Y.; Wang, H.; Zhang, J. Lattice Boltzmann method for the age concentration equation in shallow water. J. Comput. Phys. 2015, 299, 613–629. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, J.G. Inlet and outlet boundary conditions for the Lattice-Boltzmann modelling of shallow water flows. Prog. Comput. Fluid. Dyn. 2012, 12, 11–18. [Google Scholar] [CrossRef]
- Ottolenghi, L.; Prestininzi, P.; Montessori, A.; Adduce, C.; La Rocca, M. Lattice Boltzmann simulations of gravity currents. Eur. J. Mech. B-Fluid 2018, 67, 125–136. [Google Scholar] [CrossRef]
- O’Brien, G.S.; Bean, C.J.; Mcdermott, F. A comparison of published experimental data with a coupled lattice Boltzmann-analytic advection–diffusion method for reactive transport in porous media. J. Hydrol. 2002, 268, 143–157. [Google Scholar] [CrossRef]
- Zhou, J.G. A rectangular lattice Boltzmann method for groundwater flows. Mod. Phys. Lett. B 2007, 21, 531–542. [Google Scholar] [CrossRef]
- Tubbs, K.R.; Tsai, T.C. Multilayer shallow water flow using lattice Boltzmann method with high performance computing. Adv. Water. Resour. 2009, 32, 1767–1776. [Google Scholar] [CrossRef]
- Liu, H.; Li, M.; Shu, A. Large eddy simulation of turbulent shallow water flows using multi-relaxation-time lattice Boltzmann model. Int. J. Numer. Meth. Fluids 2012, 70, 1573–1589. [Google Scholar] [CrossRef]
- Prestininzi, P.; Montessori, A.; Rocca, M.; Sciortino, G. Simulation of arrested salt wedges with a multi-layer Shallow Water Lattice Boltzmann model. Adv. Water Resour. 2016, 96, 282–289. [Google Scholar] [CrossRef]
- Chávarri, E.; Crave, A.; Bonnet, M.P.; Mejía, A.; Da Silva, J.S.; Guyot, J.L. Hydrodynamic modelling of the Amazon River: Factors of uncertainty. J. S. Am. Earth. Sci. 2013, 44, 94–103. [Google Scholar] [CrossRef]
- Stone, B.M.; Shen, H.T. Hydraulic resistance of flow in channels with cylindrical roughness. J. Hydraul. Eng. 2002, 128, 500–506. [Google Scholar] [CrossRef]
- Konings, A.G.; Katul, G.G.; Thompson, S.E. A phenomenological model for the flow resistance over submerged vegetation. Water. Resour. Res. 2012, 48, 2478. [Google Scholar] [CrossRef]
- Poggi, D.; Krug, C.; Katul, G.G. Hydraulic resistance of submerged rigid vegetation derived from first-order closure models. Water. Resour. Res. 2009, 45, 2381–2386. [Google Scholar] [CrossRef]
- Guan, M.; Liang, Q. A two-dimensional hydro-morphological model for river hydraulics and morphology with vegetation. Environ. Modell. Softw. 2017, 88, 10–21. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, H.; Peng, Y.; Xing, L. Lattice Boltzmann method for rain-induced overland flow. J. Hydrol. 2018, 562, 789–795. [Google Scholar] [CrossRef]
| Variation Range | Wind Speed (m/s) | Outflow Velocity (m/s) | Outflow Velocity Variation | Average Velocity (m/s) | Average Velocity Variation |
|---|---|---|---|---|---|
| −30% | 1.25 | 0.0381 | −5.93% | 0.00149 | −7.18% |
| −20% | 1.42 | 0.0386 | −4.69% | 0.00152 | −5.01% |
| −10% | 1.60 | 0.0395 | −2.47% | 0.00155 | −2.98% |
| 0% | 1.78 | 0.0405 | 0.00% | 0.00160 | 0.00% |
| 10% | 1.96 | 0.0411 | 1.48% | 0.00164 | 2.55% |
| 20% | 2.14 | 0.0433 | 6.91% | 0.00172 | 7.81% |
| 30% | 2.31 | 0.0457 | 12.84% | 0.00184 | 14.98% |
| Variation Range | Inflow Discharge (m3/s) | Outflow Velocity (m/s) | Outflow Velocity Variation | Average Velocity (m/s) | Average Velocity Variation |
|---|---|---|---|---|---|
| −30% | 18.55 | 0.0338 | −16.56% | 0.00125 | −21.99% |
| −20% | 21.20 | 0.0358 | −11.53% | 0.00137 | −14.58% |
| −10% | 23.85 | 0.0370 | −8.71% | 0.00144 | −10.24% |
| 0% | 26.50 | 0.0405 | 0.00% | 0.00160 | 0.00% |
| 10% | 29.15 | 0.0436 | 7.66% | 0.00178 | 11.42% |
| 20% | 31.80 | 0.0467 | 15.23% | 0.00188 | 17.63% |
| 30% | 34.45 | 0.0503 | 24.11% | 0.00204 | 27.65% |
| Variation Range | Vegetation Density | Outflow Velocity (m/s) | Outflow Velocity Variation | Average Velocity (m/s) | Average Velocity Variation |
|---|---|---|---|---|---|
| −30% | 0.14 | 0.0424 | 4.71% | 0.00165 | 2.97% |
| −20% | 0.16 | 0.0417 | 3.03% | 0.00164 | 2.57% |
| −10% | 0.18 | 0.0411 | 1.49% | 0.00162 | 1.09% |
| 0% | 0.20 | 0.0405 | 0.00% | 0.00160 | 0.00% |
| 10% | 0.22 | 0.0399 | −1.57% | 0.00158 | −1.23% |
| 20% | 0.24 | 0.0392 | −3.11% | 0.00155 | −2.98% |
| 30% | 0.26 | 0.0385 | −4.88% | 0.00154 | −3.72% |
| Variation Range | Rainfall (mm) | Outflow Velocity (m/s) | Outflow Velocity Variation | Average Velocity (m/s) | Average Velocity Variation |
|---|---|---|---|---|---|
| −30% | 50.82 | 0.0347 | −14.23% | 0.00137 | −14.17% |
| −20% | 58.08 | 0.0370 | −8.56% | 0.00147 | −8.34% |
| −10% | 65.34 | 0.0385 | −4.78% | 0.00153 | −4.66% |
| 0% | 72.60 | 0.0405 | 0.00% | 0.00160 | 0.00% |
| 10% | 79.86 | 0.0433 | 6.97% | 0.00171 | 6.85% |
| 20% | 87.12 | 0.0446 | 10.23% | 0.00176 | 9.98% |
| 30% | 94.38 | 0.0490 | 21.11% | 0.00193 | 20.44% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Zhu, Z.; Liu, J.; Liu, Q. Numerical Analysis of the Impact Factors on the Flow Fields in a Large Shallow Lake. Water 2019, 11, 155. https://doi.org/10.3390/w11010155
Liu H, Zhu Z, Liu J, Liu Q. Numerical Analysis of the Impact Factors on the Flow Fields in a Large Shallow Lake. Water. 2019; 11(1):155. https://doi.org/10.3390/w11010155
Chicago/Turabian StyleLiu, Haifei, Zhexian Zhu, Jingling Liu, and Qiang Liu. 2019. "Numerical Analysis of the Impact Factors on the Flow Fields in a Large Shallow Lake" Water 11, no. 1: 155. https://doi.org/10.3390/w11010155
APA StyleLiu, H., Zhu, Z., Liu, J., & Liu, Q. (2019). Numerical Analysis of the Impact Factors on the Flow Fields in a Large Shallow Lake. Water, 11(1), 155. https://doi.org/10.3390/w11010155






