Feed Spacer Geometries and Permeability Coefficients. Effect on the Performance in BWRO Spriral-Wound Membrane Modules
Abstract
1. Introduction
2. Methodology
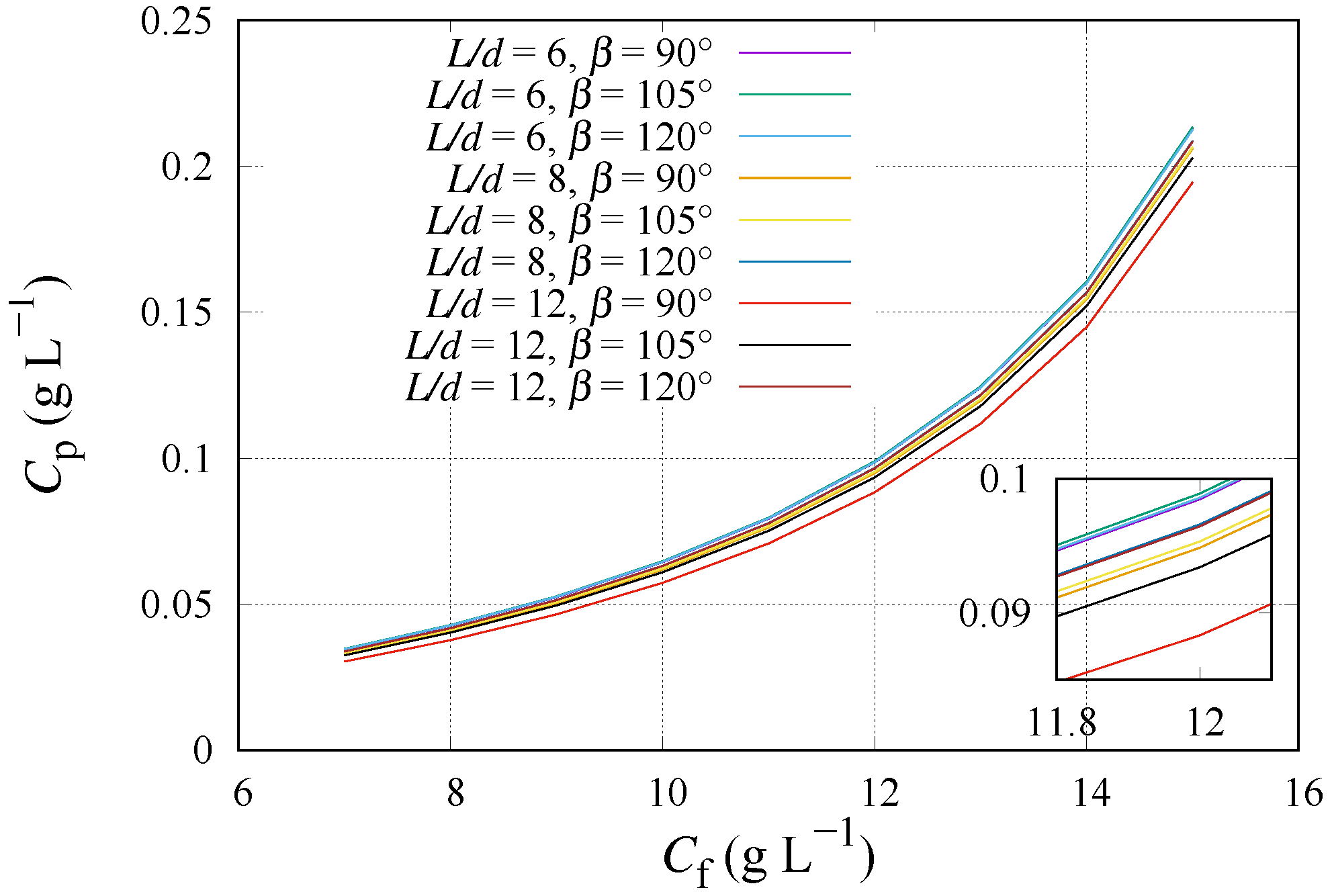
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Acronyms | |
| PV | Pressure vessel |
| RO | Reverse osmosis |
| A | Water permeability coefficient (m day kg cm) |
| B | Ion permeability coefficient ( day) |
| C | Concentration () |
| D | Solute diffusivity () |
| d | Filament diameter () |
| Hydraulic diameter () | |
| Flow factor | |
| J | Flow per unit area ( day) |
| Additional pressure losses factor | |
| k | Mass transfer coefficient |
| L | Cylinder spacing () |
| m | Molal concentration (mol ) |
| Net driven pressure () | |
| P | Solute pass (%) |
| Polarization factor | |
| PV | Pressure vessel |
| p | Pressure () |
| Q | Flow ( day) |
| R | Flow recovery (%) |
| Reynolds number | |
| RO | Reverse osmosis |
| Membrane surface () | |
| Schmidt number | |
| Specific energy consumption (KW ) | |
| Sherwood number | |
| Temperature correction factor | |
| Y | Fraction recovery |
| Greek letters | |
| Angle between crossing filaments | |
| Dynamic viscosity () | |
| Friction factor | |
| Velocity () | |
| Osmotic pressure () | |
| Density () | |
| Pressure gradient () | |
| Osmotic pressure gradient () | |
| Concentration gradient () | |
| Subscripts | |
| av | Average |
| f | Feed |
| m | Membrane |
| p | Permeate |
| b | Brine |
| s | Solute |
References
- Miller, S.; Shemer, H.; Semiat, R. Energy and environmental issues in desalination. Desalination 2015, 366, 2–8. [Google Scholar] [CrossRef]
- Gao, L.; Yoshikawa, S.; Iseri, Y.; Fujimori, S.; Kanae, S. An Economic Assessment of the Global Potential for Seawater Desalination to 2050. Water 2017, 9, 763. [Google Scholar] [CrossRef]
- Shemer, H.; Semiat, R. Sustainable RO desalination—Energy demand and environmental impact. Desalination 2017, 424, 10–16. [Google Scholar] [CrossRef]
- Stillwell, A.S.; Webber, M.E. Predicting the Specific Energy Consumption of Reverse Osmosis Desalination. Water 2016, 8, 601. [Google Scholar] [CrossRef]
- Kurihara, M.; Takeuchi, H. SWRO-PRO System in “Mega-ton Water System” for Energy Reduction and Low Environmental Impact. Water 2018, 10, 48. [Google Scholar] [CrossRef]
- Park, H.G.; Kwon, Y.N. Long-Term Stability of Low-Pressure Reverse Osmosis (RO) Membrane Operation—A Pilot Scale Study. Water 2018, 10, 93. [Google Scholar] [CrossRef]
- Goh, P.; Matsuura, T.; Ismail, A.; Hilal, N. Recent trends in membranes and membrane processes for desalination. Desalination 2016, 391, 43–60. [Google Scholar] [CrossRef]
- Ismail, A.; Padaki, M.; Hilal, N.; Matsuura, T.; Lau, W. Thin film composite membrane—Recent development and future potential. Desalination 2015, 356, 140–148. [Google Scholar] [CrossRef]
- Aani, S.A.; Haroutounian, A.; Wright, C.J.; Hilal, N. Thin Film Nanocomposite (TFN) membranes modified with polydopamine coated metals/carbon-nanostructures for desalination applications. Desalination 2018, 427, 60–74. [Google Scholar] [CrossRef]
- Haidari, A.; Heijman, S.; van der Meer, W. Optimal design of spacers in reverse osmosis. Separ. Purif. Technol. 2018, 192, 441–456. [Google Scholar] [CrossRef]
- Kavianipour, O.; Ingram, G.D.; Vuthaluru, H.B. Investigation into the effectiveness of feed spacer configurations for reverse osmosis membrane modules using Computational Fluid Dynamics. J. Membr. Sci. 2017, 526, 156–171. [Google Scholar] [CrossRef]
- Dong, C.; Wang, Z.; Wu, J.; Wang, Y.; Wang, J.; Wang, S. A green strategy to immobilize silver nanoparticles onto reverse osmosis membrane for enhanced anti-biofouling property. Desalination 2017, 401, 32–41. [Google Scholar] [CrossRef]
- Saeki, D.; Tanimoto, T.; Matsuyama, H. Anti-biofouling of polyamide reverse osmosis membranes using phosphorylcholine polymer grafted by surface-initiated atom transfer radical polymerization. Desalination 2014, 350, 21–27. [Google Scholar] [CrossRef]
- Werber, J.R.; Deshmukh, A.; Elimelech, M. The Critical Need for Increased Selectivity, Not Increased Water Permeability, for Desalination Membranes. Environ. Sci. Technol. Lett. 2016, 3, 112–120. [Google Scholar] [CrossRef]
- Abid, H.S.; Johnson, D.J.; Hashaikeh, R.; Hilal, N. A review of efforts to reduce membrane fouling by control of feed spacer characteristics. Desalination 2017, 420, 384–402. [Google Scholar] [CrossRef]
- Xie, P.; Murdoch, L.C.; Ladner, D.A. Hydrodynamics of sinusoidal spacers for improved reverse osmosis performance. J. Membr. Sci. 2014, 453, 92–99. [Google Scholar] [CrossRef]
- Schock, G.; Miquel, A. Mass transfer and pressure loss in spiral wound modules. Desalination 1987, 64, 339–352. [Google Scholar] [CrossRef]
- Geraldes, V.; Pereira, N.E.; de Pinho, M.N. Simulation and Optimization of Medium-Sized Seawater Reverse Osmosis Processes with Spiral-Wound Modules. Ind. Eng. Chem. Res. 2005, 44, 1897–1905. [Google Scholar] [CrossRef]
- Abbas, A. Simulation and analysis of an industrial water desalination plant. Chem. Eng. Process. 2005, 44, 999–1004. [Google Scholar] [CrossRef]
- Costa, A.D.; Fane, A.; Wiley, D. Spacer characterization and pressure drop modelling in spacer-filled channels for ultrafiltration. J. Membr. Sci. 1994, 87, 79–98. [Google Scholar] [CrossRef]
- Schwinge, J.; Neal, P.; Wiley, D.; Fletcher, D.; Fane, A. Spiral wound modules and spacers: Review and analysis. J. Membr. Sci. 2004, 242, 129–153. [Google Scholar] [CrossRef]
- Koutsou, C.; Yiantsios, S.; Karabelas, A. Direct numerical simulation of flow in spacer-filled channels: Effect of spacer geometrical characteristics. J. Membr. Sci. 2007, 291, 53–69. [Google Scholar] [CrossRef]
- Koutsou, C.; Yiantsios, S.; Karabelas, A. A numerical and experimental study of mass transfer in spacer-filled channels: Effects of spacer geometrical characteristics and Schmidt number. J. Membr. Sci. 2009, 326, 234–251. [Google Scholar] [CrossRef]
- Guillen, G.; Hoek, E.M. Modeling the impacts of feed spacer geometry on reverse osmosis and nanofiltration processes. Chem. Eng. J. 2009, 149, 221–231. [Google Scholar] [CrossRef]
- Haidari, A.; Heijman, S.; van der Meer, W. Effect of spacer configuration on hydraulic conditions using PIV. Separ. Purif. Technol. 2018, 199, 9–19. [Google Scholar] [CrossRef]
- Wijmans, J.; Baker, R. The solution-diffusion model: A review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Al-Obaidi, M.; Kara-Zaitri, C.; Mujtaba, I. Scope and limitations of the irreversible thermodynamics and the solution diffusion models for the separation of binary and multi-component systems in reverse osmosis process. Comput. Chem. Eng. 2017, 100, 48–79. [Google Scholar] [CrossRef]
- Water, D.; Solutions, P. Filmtec Reverse Osmosis Membranes Technical Manual; Dow Water and Process Solutions: Midland, MI, USA, 2005. [Google Scholar]
- Ruiz-García, A.; Nuez, I. Long-term performance decline in a brackish water reverse osmosis desalination plant. Predictive model for the water permeability coefficient. Desalination 2016, 397, 101–107. [Google Scholar] [CrossRef]
- Ruiz-García, A.; Melián-Martel, N.; Nuez, I. Short Review on Predicting Fouling in RO Desalination. Membranes 2017, 7, 62. [Google Scholar] [CrossRef]
- Du, Y.; Xie, L.; Liu, J.; Wang, Y.; Xu, Y.; Wang, S. Multi-objective optimization of reverse osmosis networks by lexicographic optimization and augmented epsilon constraint method. Desalination 2014, 333, 66–81. [Google Scholar] [CrossRef]
- Boudinar, M.; Hanbury, W.; Avlonitis, S. Numerical simulation and optimisation of spiral-wound modules. Desalination 1992, 86, 273–290. [Google Scholar] [CrossRef]
- Ruiz-García, A.; de la Nuez-Pestana, I. A computational tool for designing BWRO systems with spiral wound modules. Desalination 2018, 426, 69–77. [Google Scholar] [CrossRef]
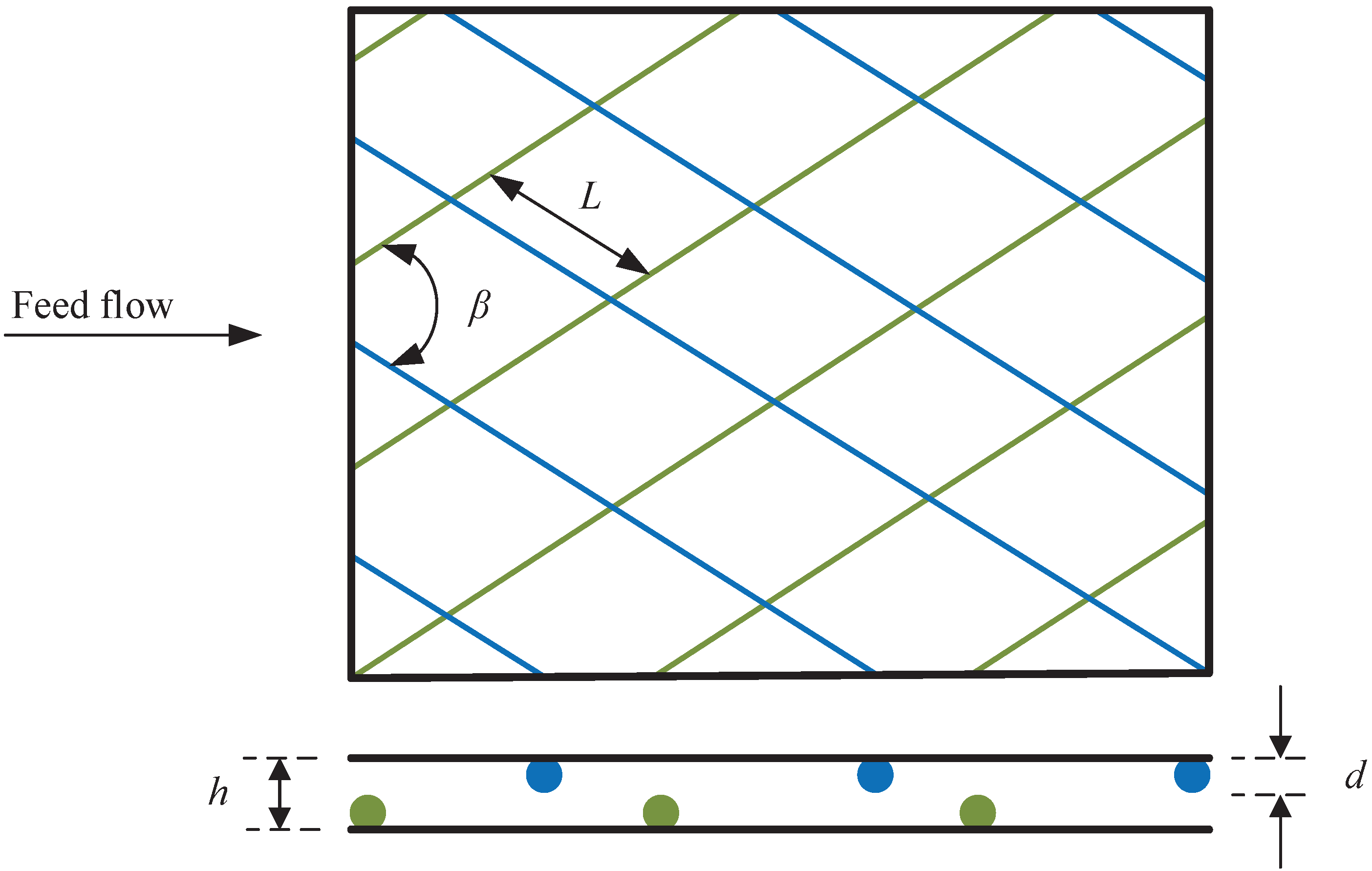
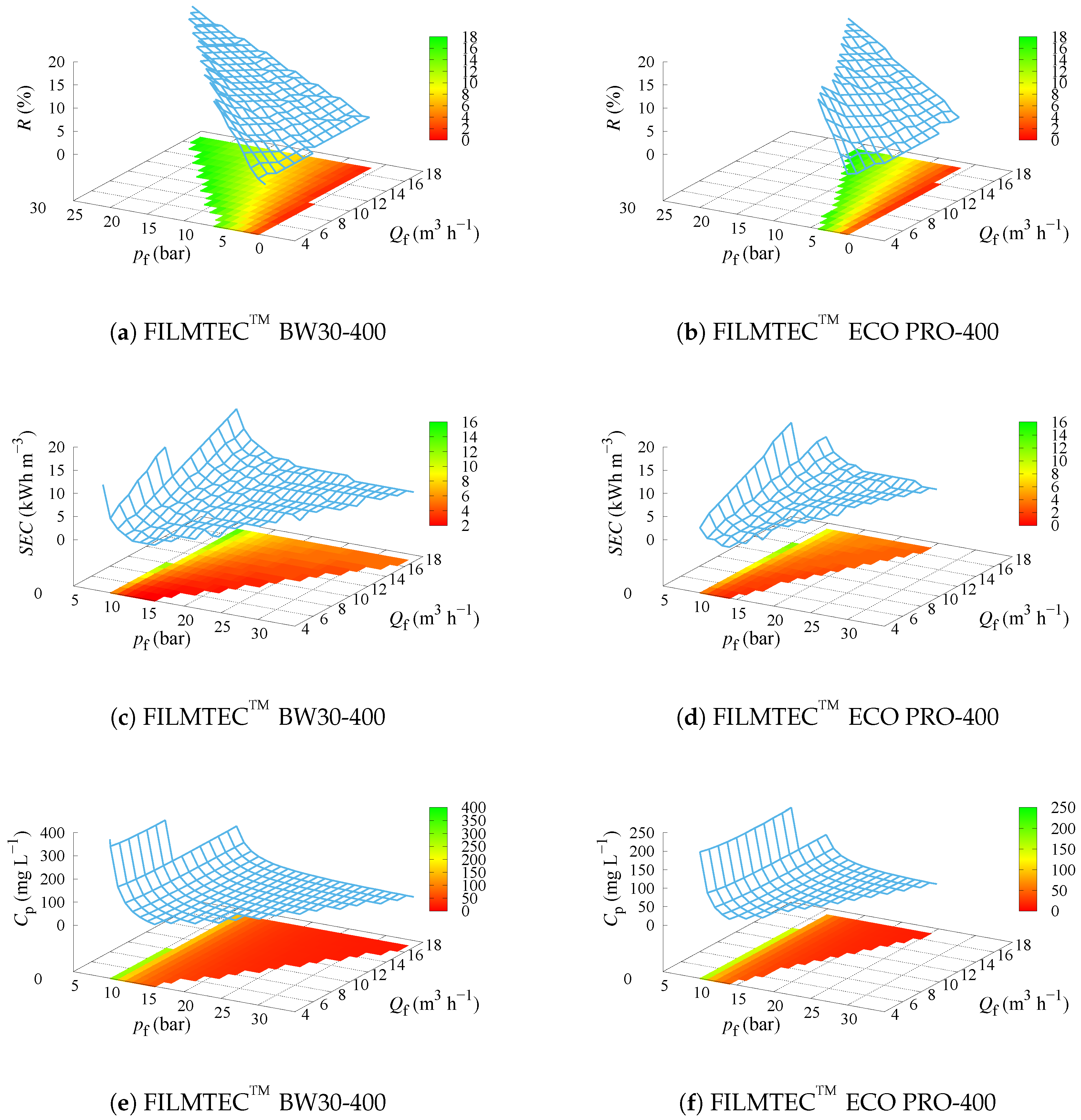

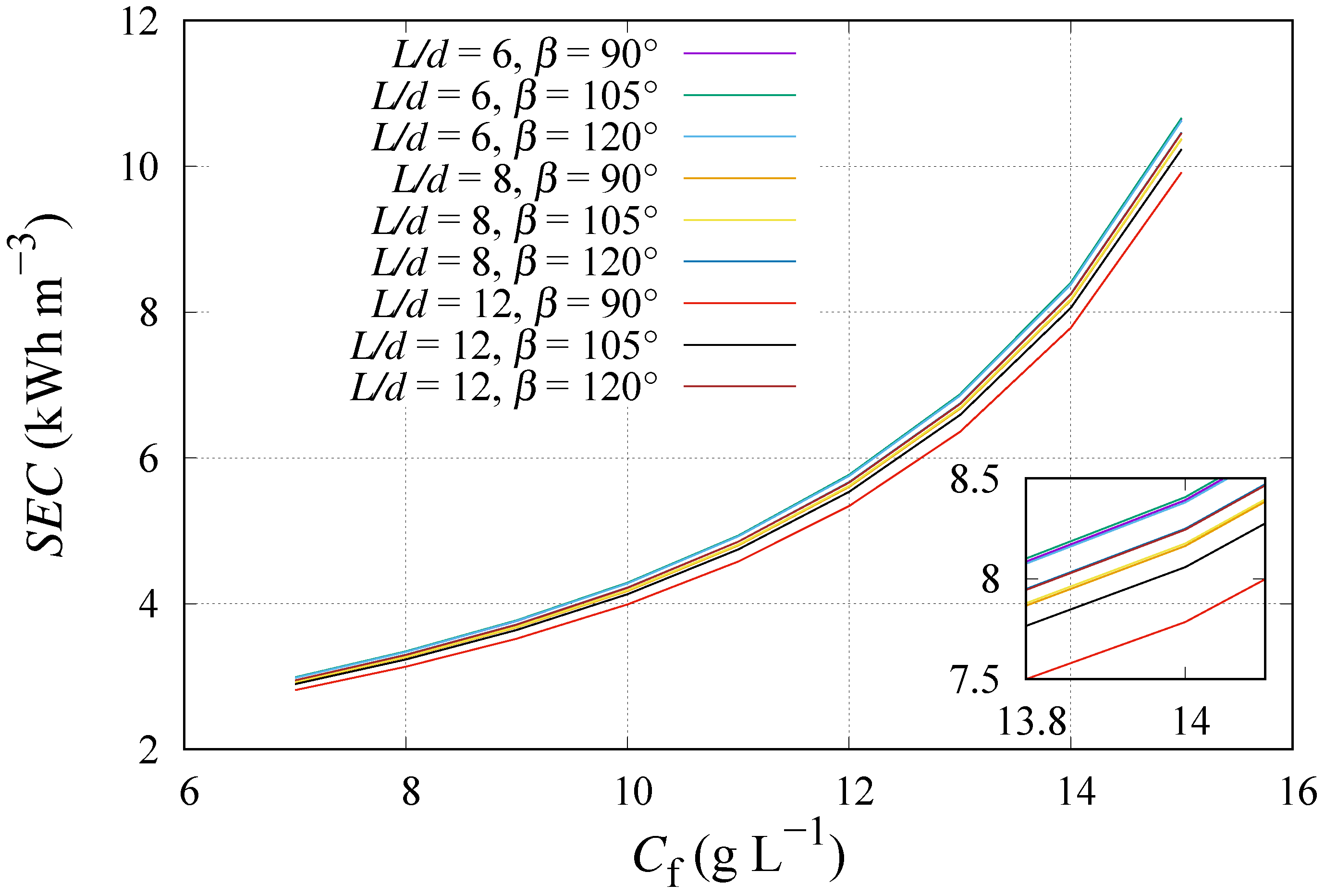
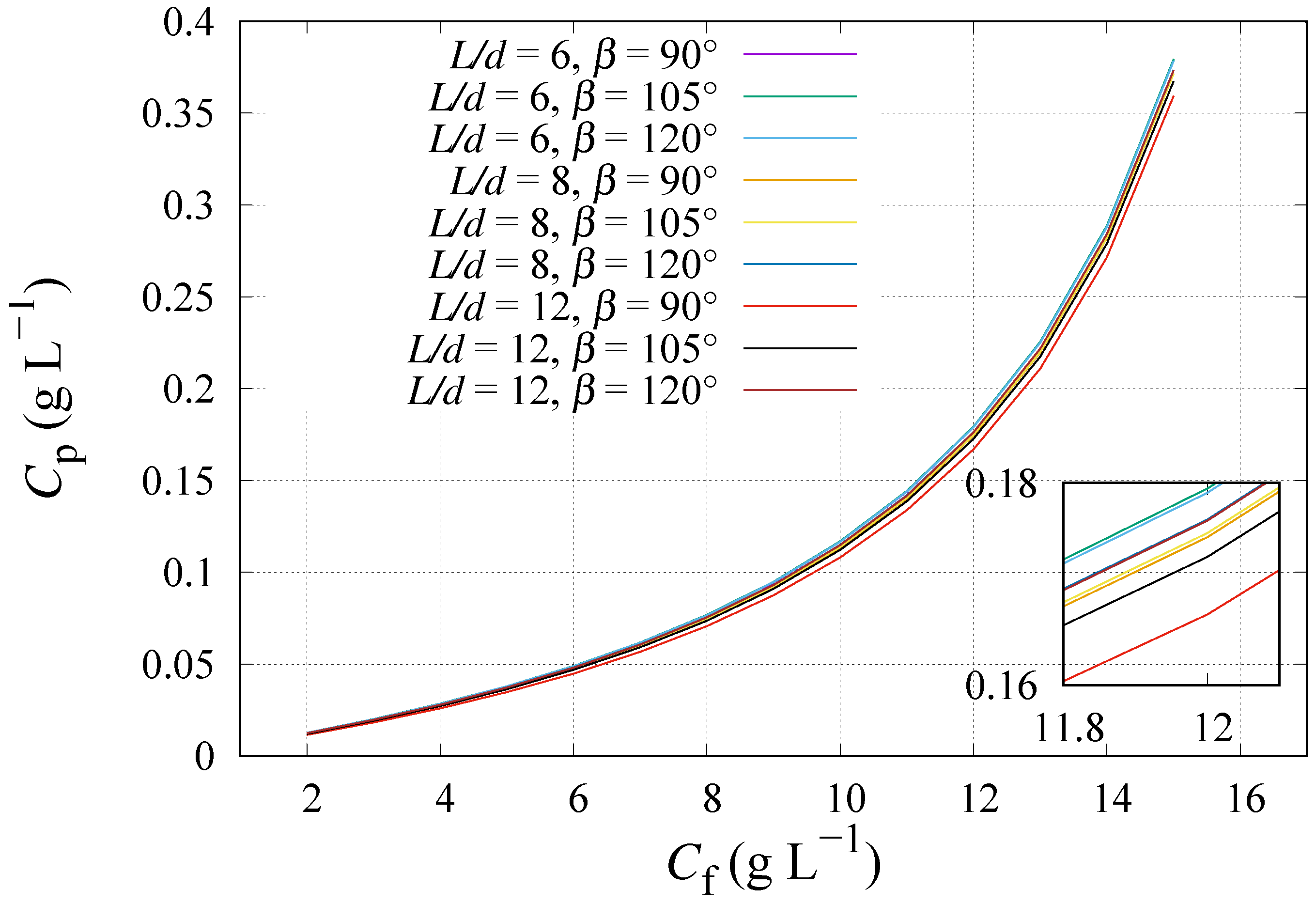
| Membrane | A (m Pa s−1) | B (m s−1) |
|---|---|---|
| FILMTEC™ BW30-400 | ||
| FILMTEC™ ECO PRO-400 | ||
| FILMTEC™ FORTLIFE™ CR100 PRO-400 |
| = 90° | = 105° | = 120° | |
|---|---|---|---|
| = 6 | |||
| = 8 | |||
| = 12 |
| = 90° | = 105° | = 120° | |
|---|---|---|---|
| = 6 | |||
| = 8 | |||
| = 12 |
| Inputs | BW30-400 | ECO PRO-400 | FORTLIFE | ||
|---|---|---|---|---|---|
| (case 1) | 6 | 90° | 5.1617 | 3.2923 | 4.7354 |
| 105° | 5.1288 | 3.2501 | 4.6984 | ||
| 120° | 5.0984 | 3.1908 | 4.6622 | ||
| 8 | 90° | 5.1606 | 3.2954 | 4.7329 | |
| 105° | 5.1257 | 3.2542 | 4.6969 | ||
| 120° | 5.1065 | 3.2304 | 4.6787 | ||
| 12 | 90° | 5.1555 | 3.2927 | 4.7290 | |
| 105° | 5.1283 | 3.2633 | 4.7024 | ||
| 120° | 5.1284 | 3.2625 | 4.7023 | ||
| (case 2) | 6 | 90° | 3.5373 | - | 3.2560 |
| 105° | 3.5051 | - | 3.2230 | ||
| 120° | 3.4523 | - | 3.1675 | ||
| 8 | 90° | 3.5379 | - | 3.2569 | |
| 105° | 3.5041 | - | 3.2225 | ||
| 120° | 3.4891 | - | 3.2068 | ||
| 12 | 90° | 3.5329 | - | 3.2524 | |
| 105° | 3.5153 | - | 3.2346 | ||
| 120° | 3.5145 | - | 3.2338 | ||
| (case 3) | 6 | 90° | 6.8082 | 4.5469 | 6.2941 |
| 105° | 6.7110 | 4.4351 | 6.1922 | ||
| 120° | 6.5656 | 4.2523 | 6.0408 | ||
| 8 | 90° | 6.8175 | 4.5638 | 6.3049 | |
| 105° | 6.7236 | 4.4583 | 6.2101 | ||
| 120° | 6.6688 | 4.3935 | 6.1523 | ||
| 12 | 90° | 6.8118 | 4.5601 | 6.2996 | |
| 105° | 6.7475 | 4.4887 | 6.2328 | ||
| 120° | 6.7452 | 4.4851 | 6.2304 | ||
| (case 4) | 6 | 90° | 4.7850 | 3.3178 | 4.4495 |
| 105° | 4.7044 | 3.2282 | 4.3669 | ||
| 120° | 4.5547 | - | 4.2134 | ||
| 8 | 90° | 4.7916 | 3.3263 | 4.4570 | |
| 105° | 4.7081 | 3.2350 | 4.3717 | ||
| 120° | 4.6676 | - | 4.3311 | ||
| 12 | 90° | 4.7811 | 3.3157 | 4.4465 | |
| 105° | 4.7391 | 3.2706 | 4.4040 | ||
| 120° | 4.7367 | 3.2679 | 4.4018 |
| Inputs | BW30-400 | ECO PRO-400 | FORTLIFE | ||
|---|---|---|---|---|---|
| (case 1) | 6 | 90° | 0.0421 | 0.0224 | 0.0292 |
| 105° | 0.0412 | 0.0215 | 0.0285 | ||
| 120° | 0.0397 | 0.0202 | 0.0273 | ||
| 8 | 90° | 0.0423 | 0.0225 | 0.0293 | |
| 105° | 0.0414 | 0.0217 | 0.0286 | ||
| 120° | 0.0408 | 0.0213 | 0.0282 | ||
| 12 | 90° | 0.0422 | 0.0225 | 0.0293 | |
| 105° | 0.0416 | 0.0220 | 0.0288 | ||
| 120° | 0.0416 | 0.0220 | 0.0288 | ||
| (case 2) | 6 | 90° | 0.0456 | - | 0.0319 |
| 105° | 0.0445 | - | 0.0310 | ||
| 120° | 0.0423 | - | 0.0294 | ||
| 8 | 90° | 0.0458 | - | 0.0320 | |
| 105° | 0.0446 | - | 0.0311 | ||
| 120° | 0.0440 | - | 0.0307 | ||
| 12 | 90° | 0.0456 | - | 0.0319 | |
| 105° | 0.0450 | - | 0.0315 | ||
| 120° | 0.0450 | - | 0.0314 | ||
| (case 3) | 6 | 90° | 0.0809 | 0.0446 | 0.0565 |
| 105° | 0.0785 | 0.0426 | 0.0547 | ||
| 120° | 0.0744 | 0.0391 | 0.0515 | ||
| 8 | 90° | 0.0813 | 0.0450 | 0.0568 | |
| 105° | 0.0790 | 0.0431 | 0.0551 | ||
| 120° | 0.0776 | 0.0419 | 0.0540 | ||
| 12 | 90° | 0.0813 | 0.0450 | 0.0568 | |
| 105° | 0.0797 | 0.0437 | 0.0556 | ||
| 120° | 0.0796 | 0.0437 | 0.0556 | ||
| (case 4) | 6 | 90° | 0.0896 | 0.0522 | 0.0632 |
| 105° | 0.0867 | 0.0499 | 0.0610 | ||
| 120° | 0.0812 | - | 0.0568 | ||
| 8 | 90° | 0.0899 | 0.0525 | 0.0634 | |
| 105° | 0.0870 | 0.0501 | 0.0612 | ||
| 120° | 0.0856 | - | 0.0601 | ||
| 12 | 90° | 0.0896 | 0.0522 | 0.0632 | |
| 105° | 0.0882 | 0.0511 | 0.0621 | ||
| 120° | 0.0881 | 0.0510 | 0.0620 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruiz-García, A.; de la Nuez Pestana, I. Feed Spacer Geometries and Permeability Coefficients. Effect on the Performance in BWRO Spriral-Wound Membrane Modules. Water 2019, 11, 152. https://doi.org/10.3390/w11010152
Ruiz-García A, de la Nuez Pestana I. Feed Spacer Geometries and Permeability Coefficients. Effect on the Performance in BWRO Spriral-Wound Membrane Modules. Water. 2019; 11(1):152. https://doi.org/10.3390/w11010152
Chicago/Turabian StyleRuiz-García, Alejandro, and Ignacio de la Nuez Pestana. 2019. "Feed Spacer Geometries and Permeability Coefficients. Effect on the Performance in BWRO Spriral-Wound Membrane Modules" Water 11, no. 1: 152. https://doi.org/10.3390/w11010152
APA StyleRuiz-García, A., & de la Nuez Pestana, I. (2019). Feed Spacer Geometries and Permeability Coefficients. Effect on the Performance in BWRO Spriral-Wound Membrane Modules. Water, 11(1), 152. https://doi.org/10.3390/w11010152






