Calibration of SWAT and Two Data-Driven Models for a Data-Scarce Mountainous Headwater in Semi-Arid Konya Closed Basin
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Soil and Water Assessment Tool (SWAT)
- SWt: Final soil water content (mm);
- SW0: Initial soil water content (mm);
- Rday: Amount of precipitation on day i (mm);
- Qsurf: Amount of surface runoff on day i (mm);
- Ea: Amount of evapotranspiration on day i (mm);
- Wseep: Amount of percolation and bypass flow exiting the soil profile bottom on day i (mm);
- Qgw: Groundwater return flow on day i (mm).
2.2.1. SWAT Model Setup and Data Set
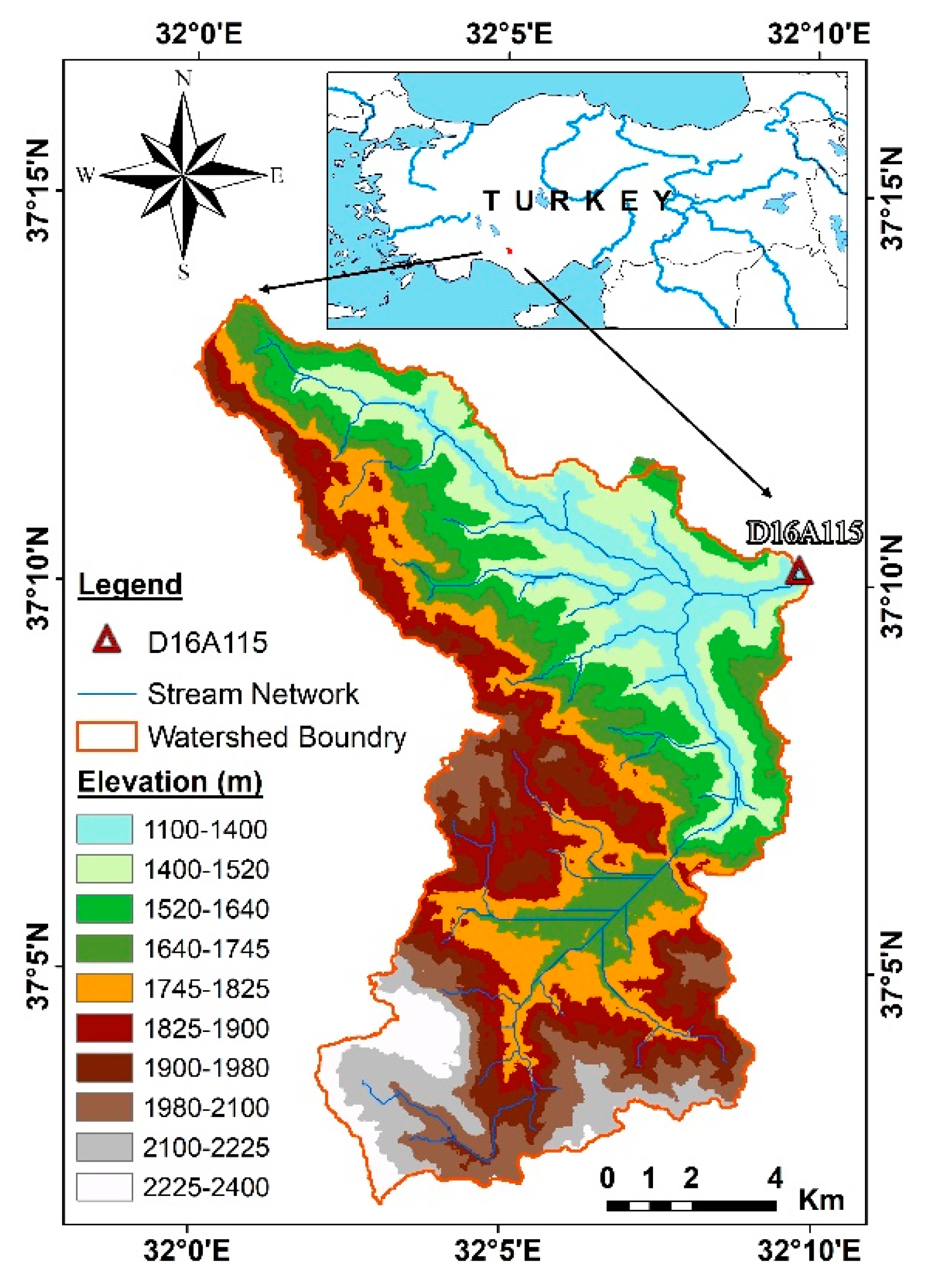
- Digital Elevation Model (DEM): SWAT determines the direction of water flow by utilizing DEM maps representing the topographical of the basin. The DEM map used in this study is given in Figure 1. In this study, DEM maps created from Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) data were used. The DEM map created represents raster data and therefore has a resolution of 30 × 30 m. The quality (altitude errors) of the DEM used in this study has not been checked. However, altitude errors of ASTER-GDEM data are given as root mean square error (RMSE) = ±7.97 m in the literature [33]. DEM map was also transformed into UTM (Zone-36, WGS84 spheroid) projection system.
- Land Use/Land Cover (LULC): the LULC map is a significant physical data for the modelling of runoff and infiltration within the SWAT model. The LULC map used in this study is seen in Figure 2. The LULC map used for the SWAT model was denoted from the Coordination of Information on the Environment (CORINE) data. CORINE which was established in 1985 is a program that aims to gather environmental data in Europe, to ensure the coordination of data collection institutions, and to test the reliability of the data obtained. The LULC map is one of the data types produced within CORINE [34].
- Soil Types: the soil data was retrieved from the Harmonized World Soil Database v1.2 (HWSD v1.2) data, prepared in collaboration with several organizations, including the Food and Agriculture Organization (FAO) of the United Nations. Since there is no detailed map of soil properties for the study area, HWSD v1.2 data with 30 arc seconds (approximately 1 km) resolution is used. The reference soil depth is 100 cm. The study area was divided into five slope classes (Table 2). According to Table 2, approximately 80% of the study area has a slope class of more than 15%, indicating that the region is quite mountainous.
- Hydro-Meteorological Dataset: precipitation and temperature (max and min) are among the basic climate variables required by the SWAT model. Depending on the PET calculation method used in the model, relative humidity, wind speed and solar radiation may also be necessary. There is no meteorology station with an adequate observation period within the boundaries of the study area. Therefore, the data of the Hadim and Seydişehir meteorological stations operated by the General Directorate of State Meteorology and located near the basin were used. The meteorological data representing the study area were determined by the Thiessen method using the data of these two stations.
2.2.2. Calibration and Validation Process
2.3. Radial Based Neural Network (RBNN)
2.4. Support Vector Machines (SVM)
2.5. Artificial Intelligence (AI) Models Setup
2.6. Model Evaluation Criteria
3. Results and Discussion
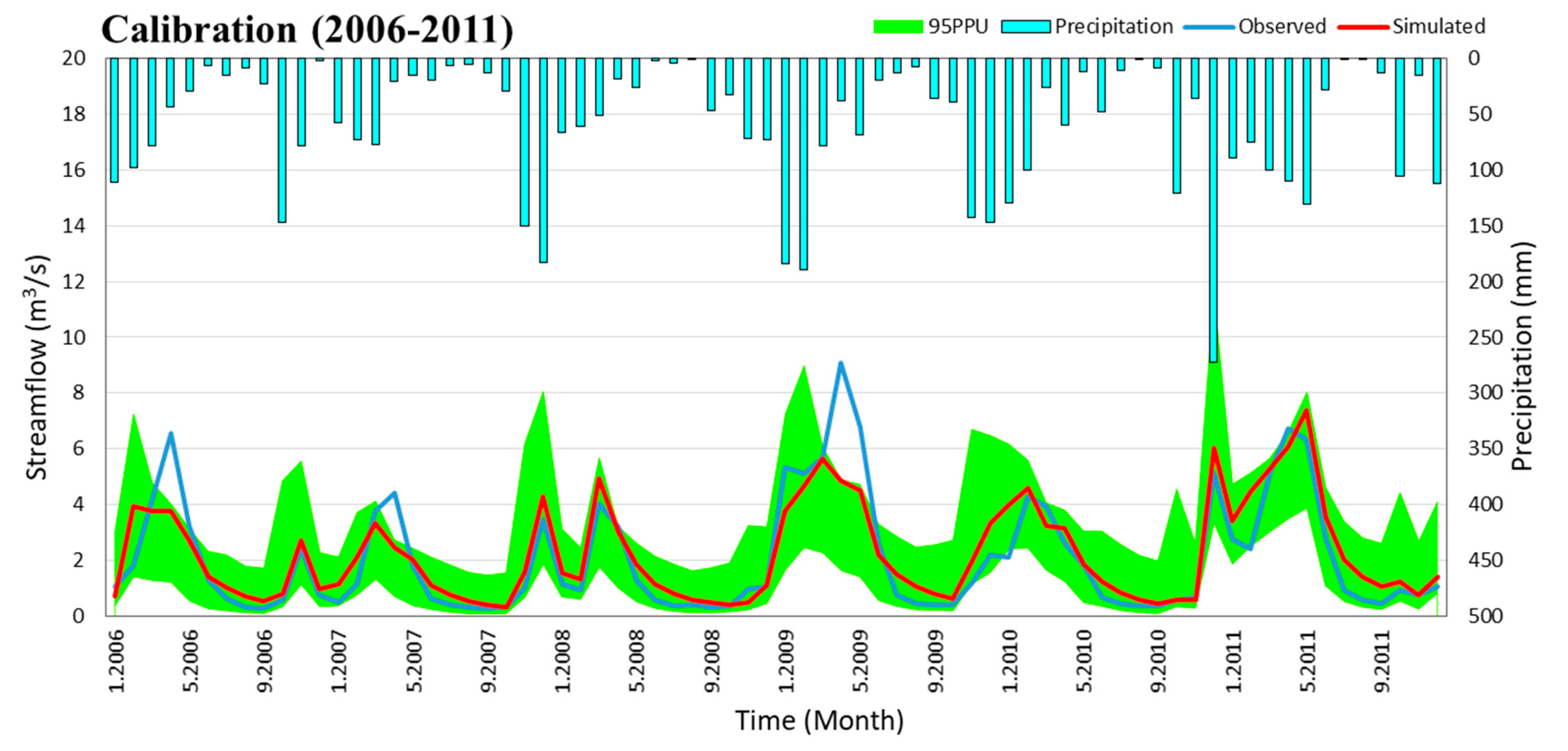
3.1. Results of SWAT
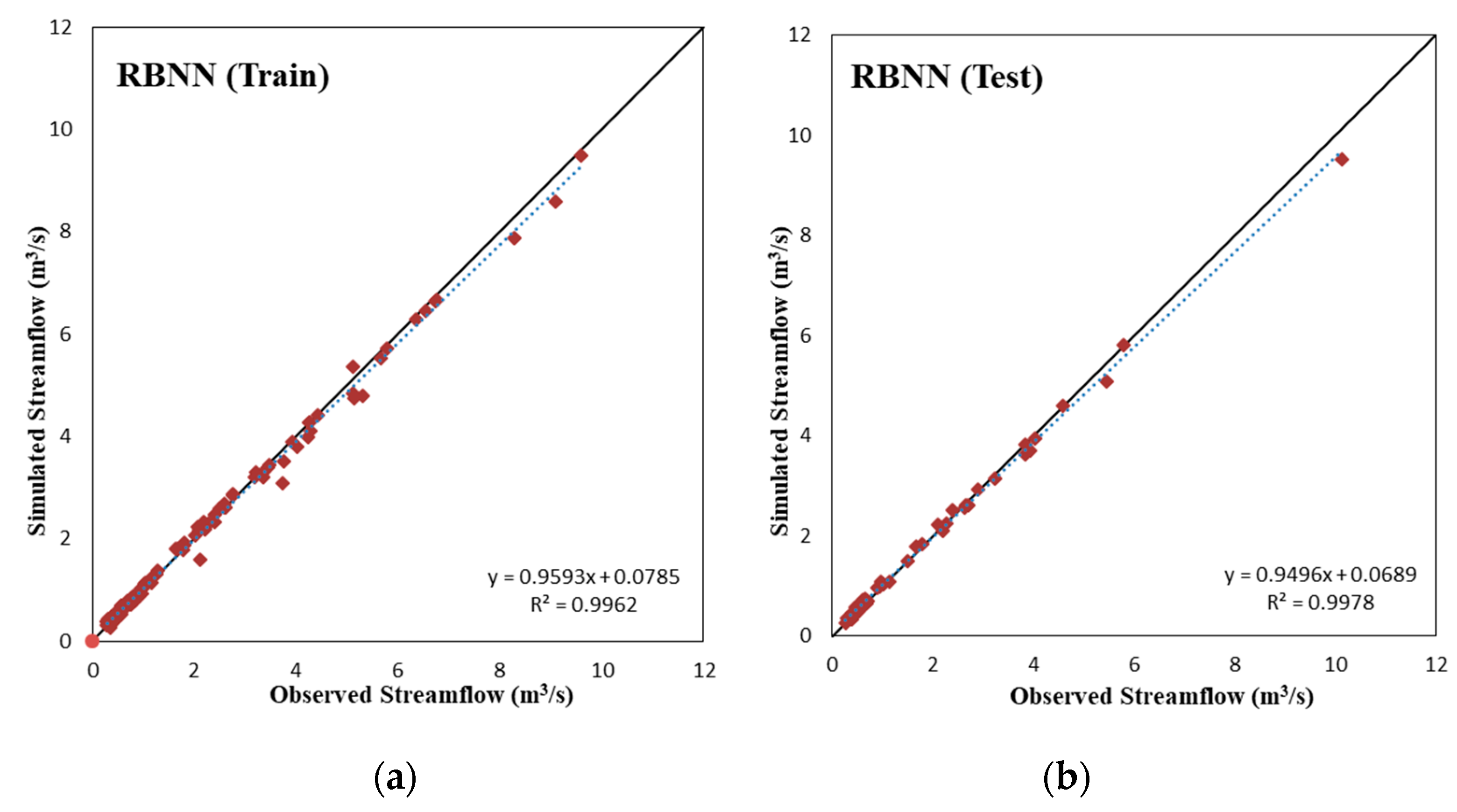
3.2. Comparison of SWAT and AI Methods
4. Conclusions
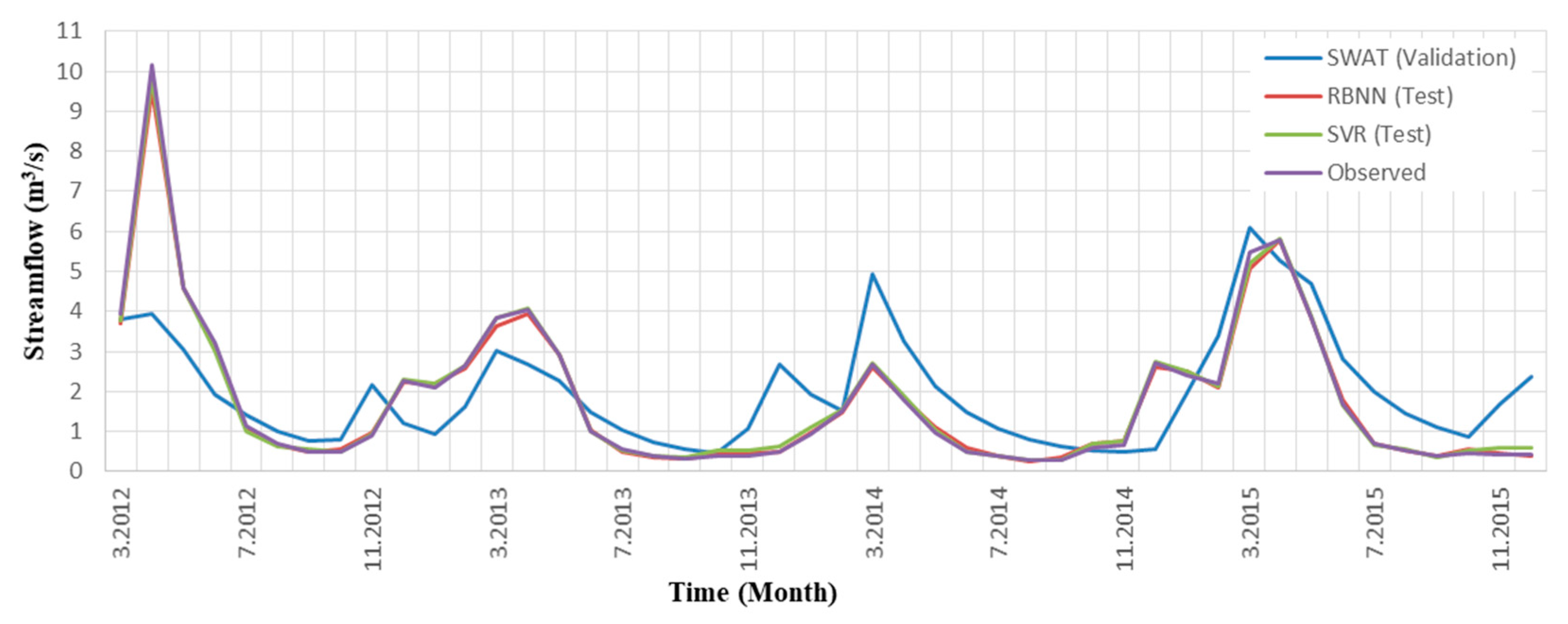
- In the SWAT model, the use of the SUFI-2 algorithm for calibration further increased the success of the model compared to manual calibration. According to the results obtained in the validation stage, it is observed that the model produces satisfactory results for changing conditions.
- The SWAT simulations revealed that fast runoff occurs in this mountainous region which can cause a flood risk. The SWAT model performs better during the low flow period as compared to capturing peak flows.
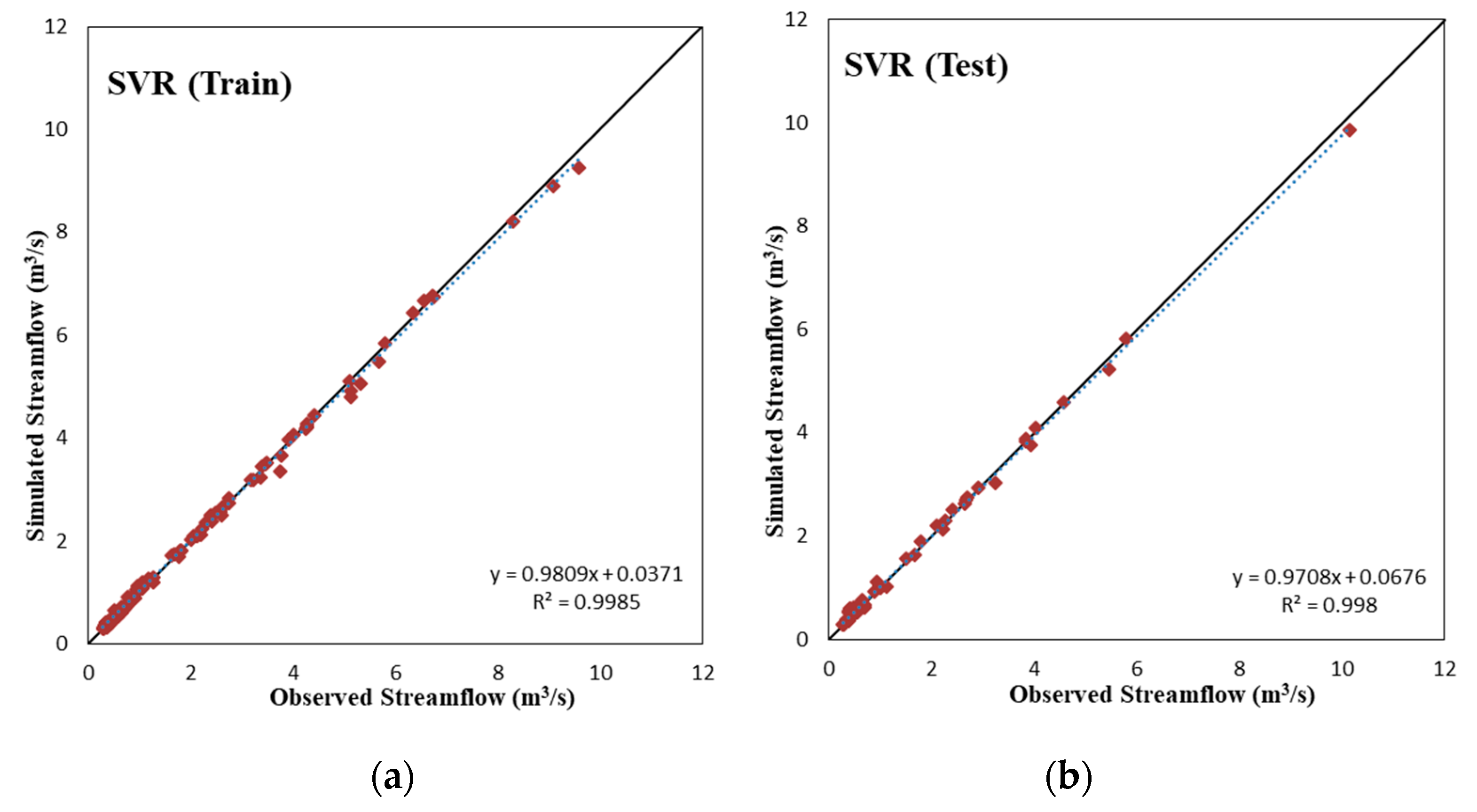
- The comparison of all three models showed that two data-driven models performed better than SWAT. Moreover, the results of SVR model were slightly more successful than those from RBNN.
- The scatter plots show that there was no overfitting problem in the two AI models.
- Although high-accuracy results are obtained with AI models, they only provide discharge outputs. However, the SWAT model is appropriate for solving physical problems related to hydrological processes including snow melt, soil moisture and groundwater. The effect of land cover and land use change on hydrologic fluxes can be assessed by this model too.
- Obviously the quality of the data directly affects the success of the model. The results could improve if there were at least one meteorological station within the catchment.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sharma, S.K.; Kansal, M.L.; Tyagi, A. Integrated water management plan for Shimla City in India using geospatial techniques. Water Sci. Technol. Water Supply 2016, 16, 641–652. [Google Scholar]
- Anandhi, A.; Kannan, N. Vulnerability assessment of water resources—Translating a theoretical concept to an operational framework using systems thinking approach in a changing climate: Case study in Ogallala Aquifer. J. Hydrol. 2018, 557, 460–474. [Google Scholar] [CrossRef]
- Ayivi, F.; Jha, M.K. Estimation of water balance and water yield in the Reedy Fork-Buffalo Creek Watershed in North Carolina using SWAT. Int. Soil Water Conserv. Res. 2018, 6, 203–213. [Google Scholar] [CrossRef]
- Naschen, K.; Diekkruger, B.; Leemhuis, C.; Steinbach, S.; Seregina, L.S.; Thonfeld, F.; van der Linden, R. Hydrological modeling in data-scarce catchments: The kilombero floodplain in Tanzania. Water 2018, 10, 599. [Google Scholar] [CrossRef]
- Vilaysane, B.; Takara, K.; Luo, P.P.; Akkharath, I.; Duan, W.L. Hydrological stream flow modelling for calibration and uncertainty analysis using SWAT model in the Xedone river basin, Lao PDR. Proc.Environ. Sci. 2015, 28, 380–390. [Google Scholar] [CrossRef]
- Dias, V.D.; da Luz, M.P.; Medero, G.M.; Nascimento, D.T.F.; de Oliveira, W.N.; Merelles, L.R.D. Historical streamflow series analysis applied to furnas HPP reservoir watershed using the SWAT model. Water 2018, 10, 458. [Google Scholar] [CrossRef]
- Swain, S.; Verma, M.K.; Verma, M.K. Streamflow estimation using SWAT model over Seonath River basin, Chhattisgarh, India. Hydrol. Model. 2018, 81, 659–665. [Google Scholar]
- Solomatine, D.; See, L.M.; Abrahart, R.J. Data-Driven Modelling: Concepts, Approaches and Experiences, Practical Hydroinformatics. In Water Science and Technology Library; Springer: Berlin, Germany, 2008; Volume 68. [Google Scholar]
- Kemanian, A.R.; Julich, S.; Manoranjan, V.S.; Arnold, J.R. Integrating soil carbon cycling with that of nitrogen and phosphorus in the watershed model SWAT: Theory and model testing. Ecol. Model. 2011, 222, 1913–1921. [Google Scholar] [CrossRef]
- Iizumi, T.; Sakurai, G.; Yokozawa, M. An ensemble approach to the representation of subgrid-scale heterogeneity of crop phenology and yield in coarse-resolution large-area crop models. J. Agric. Meteorol. 2013, 69, 243–254. [Google Scholar] [CrossRef]
- Abouali, M.; Nejadhashemi, A.P.; Daneshvar, F.; Adhikari, U.; Herman, M.R.; Calappi, T.J.; Rohn, B.G. Evaluation of wetland implementation strategies on phosphorus reduction at a watershed scale. J. Hydrol. 2017, 552, 105–120. [Google Scholar] [CrossRef]
- Vaghefi, S.A.; Abbaspour, K.C.; Faramarzi, M.; Srinivasan, R.; Arnold, J.G. Modeling crop water productivity using a coupled SWAT-MODSIM model. Water 2017, 9, 157. [Google Scholar] [CrossRef]
- Panagopoulos, Y.; Gassman, P.W.; Jha, M.K.; Kling, C.L.; Campbell, T.D.; Srinivasan, R.; White, M.; Arnold, J.G. A refined regional modeling approach for the Corn Belt—Experiences and recommendations for large-scale integrated modeling. J. Hydrol. 2015, 524, 348–366. [Google Scholar] [CrossRef]
- Panagopoulos, Y.; Gassman, P.W.; Kling, C.L.; Cibin, R.; Chaubey, I. Water quality assessment of large-scale bioenergy cropping scenarios for the Upper Mississippi and Ohio-Tennesee River Basins. J. Am. Water Resour. Assoc. 2017, 53, 1355–1367. [Google Scholar] [CrossRef]
- Hallouz, F.; Meddi, M.; Mahé, G.; Alirahmani, S.; Keddar, A. Modeling of discharge and sediment transport through the SWAT model in the basin of Harraza (Northwest of Algeria). Water Sci. 2018, 32, 79–88. [Google Scholar]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment—Part 1: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Faramarzi, M.; Ghasemi, S.S.; Yang, H. Assessing the impact of climate change on water resources in Iran. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Bekele, E.G.; Knapp, H.V. Watershed modeling to assessing impacts of potential climate change on water supply availability. Water Resour. Manag. 2010, 24, 3299–3320. [Google Scholar] [CrossRef]
- Setegn, S.G.; Melesse, A.M.; Haiduk, A.; Webber, D.; Wang, X.; McClain, M.E. Modeling hydrological variability of fresh water resources in the Rio Cobre watershed, Jamaica. Catena 2014, 120, 81–90. [Google Scholar] [CrossRef]
- Sisay, E.; Halefom, A.; Khare, D.; Singh, L.; Worku, T. Hydrological modelling of ungauged urban watershed using SWAT model. Model. Earth Syst. Environ. 2017, 3, 693–702. [Google Scholar] [CrossRef]
- Neto, A.A.M.; Oliveira, P.T.S.; Rodrigues, D.B.B.; Wendland, E. Improving streamflow prediction using uncertainty analysis and bayesian model averaging. J. Hydrol. Eng. 2018, 23. [Google Scholar] [CrossRef]
- Tongal, H. Nonlinear forecasting of stream flows using a chaotic approach and artificial neural networks. Earth Sci. Res. J. 2013, 17, 119–126. [Google Scholar]
- Buyukyildiz, M.; Tezel, G.; Yilmaz, V. Estimation of the change in lake water level by artificial intelligence methods. Water Res. Manag. 2014, 28, 4747–4763. [Google Scholar] [CrossRef]
- Temizyurek, M.; Dadaser-Celik, F. Modelling the effects of meteorological parameters on water temperature using artificial neural networks. Water Sci. Technol. 2018, 77, 1724–1733. [Google Scholar] [CrossRef] [PubMed]
- Radzi, M.R.B.; Shamshirband, S.; Aghabozorgi, S.; Misra, S.; Akib, S.; Kiah, L.M. Potential of support-vector regression for forecasting stream flow. Teh. Vjesn. Tech. Gaz. 2014, 21, 1017–1024. [Google Scholar]
- Zhu, S.; Zhou, J.Z.; Ye, L.; Meng, C.Q. Streamflow estimation by support vector machine coupled with different methods of time series decomposition in the upper reaches of Yangtze River, China. Environ. Earth Sci. 2016, 75, 531. [Google Scholar] [CrossRef]
- Hamaamin, Y.A.; Nejadhashemi, A.P.; Zhang, Z.; Subhasis, G.; Woznicki, S.A. Bayesian regression and neuro-fuzzy methods reliability assessment for estimating streamflow. Water 2016, 8, 287. [Google Scholar] [CrossRef]
- Demirel, M.C.; Venancio, A.; Kahya, E. Flow forecast by SWAT model and ANN in Pracana basin, Portugal. Adv. Eng. Softw. 2009, 40, 467–473. [Google Scholar] [CrossRef]
- Jajarmizadeh, M.; Lafdani, E.K.; Harun, S.; Ahmadi, A. Application of SVM and SWAT models for monthly streamflow prediction, a case study in South of Iran. KSCE J. Civ. Eng. 2015, 19, 345–357. [Google Scholar] [CrossRef]
- Noori, N.; Kalin, L. Coupling SWAT and ANN models for enhanced daily streamflow prediction. J. Hydrol. 2016, 533, 141–151. [Google Scholar] [CrossRef]
- Neitsch, S.J.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; College of Agriculture and Life Sciences, Texas A&M University System: College Station, TX, USA, 2009. [Google Scholar]
- Tessema, S.M.; Lyon, S.W.; Setegn, S.G.; Mortberg, U. Effects of different retention parameter estimation methods on the prediction of surface runoff using the SCS curve number method. Water Res. Manag. 2014, 28, 3241–3254. [Google Scholar] [CrossRef]
- Elkhrachy, I. Vertical accuracy assessment for SRTM and ASTER Digital Elevation Models: A case study of Najran city, Saudi Arabia. Ain Shams Eng. J. 2017. [Google Scholar] [CrossRef]
- European Environment Agency. Available online: https://www.eea.europa.eu/publications/COR0-landcover (accessed on 2 December 2018).
- Monteith, J.L. Evaporation and Environment. In The State and Movement of Water in Living Organisms; Fogg, G.F., Ed.; Cambridge University Press: Cambridge, UK, 1965; pp. 205–234. [Google Scholar]
- Abbaspour, K.C. SWAT-CUP: SWAT Calibration and Uncertainty Programs—A User Manual; Swiss Federal Institute of Aquatic Science and Technology (Eawag): Dübendorf, Switzerland, 2015. [Google Scholar]
- Abbaspour, K.C.; Johnson, C.A.; van Genuchten, M.T. Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volumes 1–6, pp. 1942–1948. [Google Scholar]
- Beven, K.; Binley, A. The future of distributed models—Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Van Griensven, A.; Meixner, T. A global and efficient multi-objective auto-calibration and uncertainty estimation method for water quality catchment models. J. Hydroinform. 2007, 9, 277–291. [Google Scholar] [CrossRef]
- Kuczera, G.; Parent, E. Monte Carlo assessment of parameter uncertainty in conceptual catchment models: The Metropolis algorithm. J. Hydrol. 1998, 211, 69–85. [Google Scholar] [CrossRef]
- Khoi, D.N.; Thom, V.T. Parameter uncertainty analysis for simulating streamflow in a river catchment of Vietnam. Global Ecol. Conserv. 2015, 4, 538–548. [Google Scholar] [CrossRef]
- Notter, B.; Hurni, H.; Wiesmann, U.; Abbaspour, K.C. Modelling water provision as an ecosystem service in a large East African river basin. Hydrol. Earth Syst. Sci. 2012, 16, 69–86. [Google Scholar] [CrossRef]
- Setegn, S.G.; Srinivasan, R.; Melesse, A.M.; Dargahi, B. SWAT model application and prediction uncertainty analysis in the Lake Tana Basin, Ethiopia. Hydrol. Process. 2010, 24, 357–367. [Google Scholar] [CrossRef]
- Hosseini, M.; Ghafouri, M.; Tabatabaei, M.; Goodarzi, M.; Mokarian, Z. Estimating hydrologic budgets for six Persian Gulf watersheds, Iran. Appl. Water Sci. 2017, 7, 3323–3332. [Google Scholar] [CrossRef]
- Moody, J.; Darken, C.J. Fast learning in networks of locally-tuned processing units. Neural Comput. 1989, 1, 281–294. [Google Scholar] [CrossRef]
- Sudheer, K.P.; Jain, S.K. Radial basis function neural network for modeling rating curves. J. Hydrol. Eng. 2003, 8, 161–164. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Van Liew, M.W.; Arnold, J.G.; Garbrecht, J.D. Hydrologic simulation on agricultural watersheds: Choosing between two models. Trans. ASABE 2003, 46, 1539–1551. [Google Scholar] [CrossRef]
- Fernandez, G.P.; Chescheir, G.M.; Skaggs, R.W.; Amatya, D.M. Development and testing of watershed-scale models for poorly drained soils. Trans. ASABE 2005, 48, 639–652. [Google Scholar] [CrossRef]
- Jimeno-Sáez, P.; Senent-Aparicio, J.; Pérez-Sánchez, J.; Pulido-Velazquez, D. A Comparison of SWAT and ANN models for daily runoff simulation in different climatic zones of Peninsular Spain. Water 2018, 10, 192. [Google Scholar] [CrossRef]
- Kim, M.; Baek, S.; Ligaray, M.; Pyo, J.; Park, M.; Cho, K.H. Comparative studies of different imputation methods for recovering streamflow observation. Water 2015, 7, 6847–6860. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Hansen, N.; Ostermeier, A. Adapting arbitrary normal normal mutation distributions in evolution strategies: The covariance matrix adaptation. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996; pp. 312–317. [Google Scholar]
- Koycegiz, C. Flow Forecast by SWAT and Artificial Intelligence Methods. Master’s Thesis, Selcuk University, Konya, Turkey, 2018. (In Turkish). [Google Scholar]
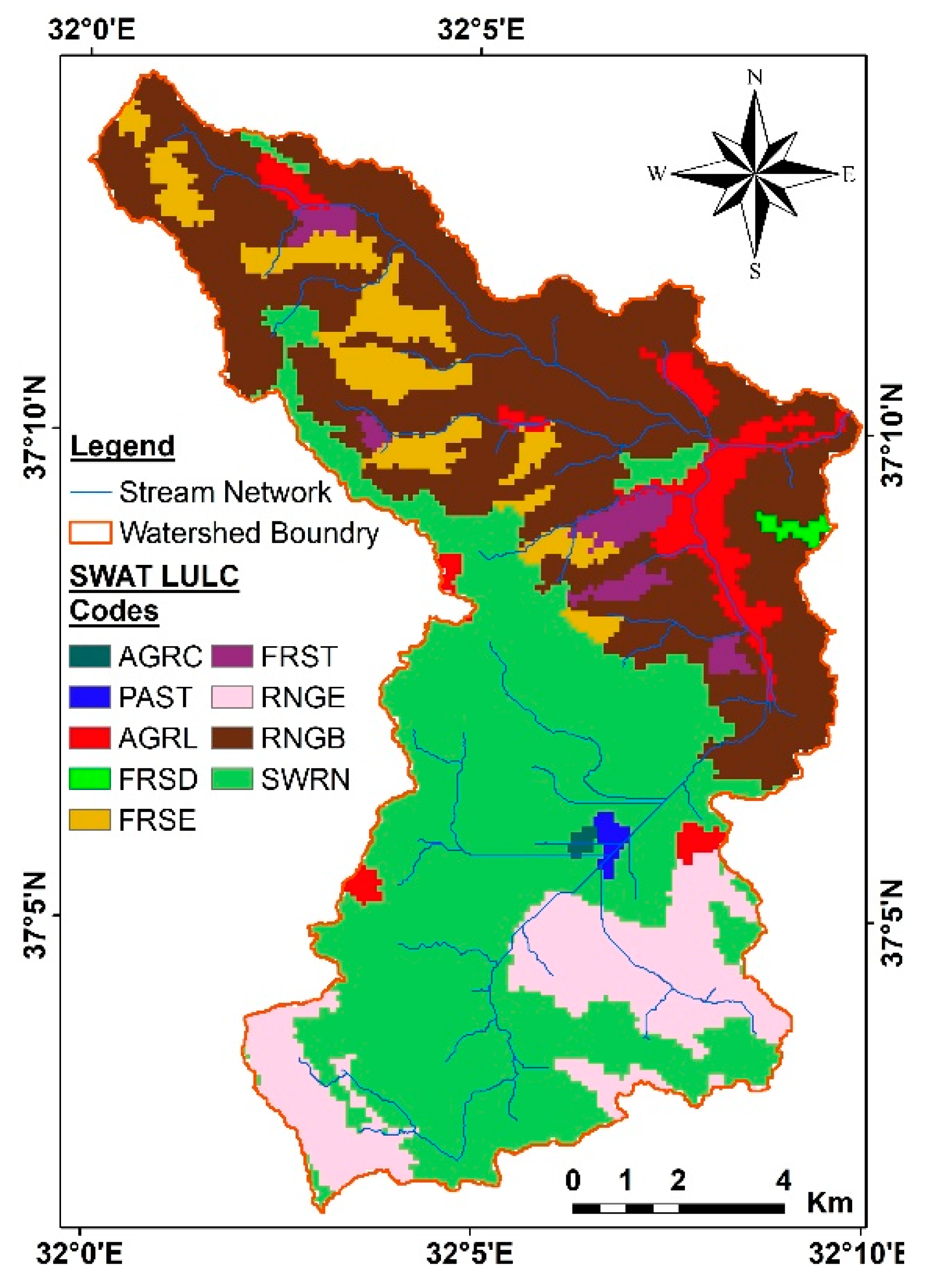


| SWAT LULC Codes | Definition of SWAT LULC Codes | Area (km2) | Area (%) |
|---|---|---|---|
| AGRC | Agricultural Land-Close Grown | 0.24 | 0.16 |
| PAST | Pasture | 0.50 | 0.32 |
| AGRL | Agricultural Land-Generic | 7.61 | 4.94 |
| FRSD | Forest-Deciduous | 0.42 | 0.27 |
| FRSE | Forest-Evergreen | 9.46 | 6.14 |
| FRST | Forest-Mixed | 3.22 | 2.09 |
| RNGE | Range-Grasses | 16.32 | 10.60 |
| RNGB | Range-Brush | 52.97 | 34.42 |
| SWRN | South Western Range-Bare Rock | 63.1 | 41.00 |
| Soil Codes | Area (km2) | Area (%) | |
| Soil features | I-Lc-E-2b-3114 | 98.1 | 63.75 |
| I-Be-E-c-3504 | 43.5 | 28.26 | |
| I-Be-c-3093 | 12.3 | 7.99 | |
| Slope Class | Area (km2) | Area (%) | |
| Slope class of the study area | 0-15 | 29.95 | 19.46 |
| 15-24 | 32.99 | 21.44 | |
| 24-35 | 38.00 | 24.7 | |
| 35-49 | 32.33 | 21.01 | |
| >49 | 20.58 | 13.37 |
| Station Number | Station Name | Altitude (m) | Latitude | Longitude |
|---|---|---|---|---|
| 17898 | Seydişehir | 1129 | 37°25′36′′ N | 31°50′56′′ E |
| 17928 | Hadim | 1552 | 36°59′21′′ N | 32°27′20′′ E |
| D16A115 | Çarşamba River (Sorkun) | 1150 | 37°10′12′′ N | 32°09′44′′ E |
| Model Name | Parameters | Parameters Range | Inputs | Output |
|---|---|---|---|---|
| Radial-based neural network (RBNN) | The number of neurons Spread parameter (σ) | (1–10) (0.01–5) | Qt−1, Qt−2, Qt−3, Pt, Pt−1, Tmax, Tmin, RH, WS, SR | Qt |
| Support vector machine (SVM) | Regulatory factor (C) Insensitive error term (ε) Kernel parameter (γ) | (1–100) (0.01–0.5) (0.1–8) |
| NSE | R2 | PBias (%) | Performance Rating |
|---|---|---|---|
| 0.75 < NSE ≤ 1.00 | 0.75 < R2 ≤ 1.00 | PBIAS ≤ ±10 | Very Good (VG) |
| 0.60 < NSE ≤ 0.75 | 0.60 < R2 ≤ 0.75 | ±10 < PBIAS ≤ ±15 | Good (G) |
| 0.36 < NSE ≤ 0.60 | 0.50 < R2 ≤ 0.60 | ±15 < PBIAS ≤ ±25 | Satisfactory (S) |
| 0.00 < NSE ≤ 0.36 | 0.25 < R2 ≤ 0.50 | ±25 < PBIAS ≤ ±50 | Unsatisfactory (U) |
| NSE ≤ 0.00 | R2 ≤ 0.25 | ±50 ≤ PBIAS | Inappropriate (I) |
| Parameters | Parameter Definitions | Range | Fitted Value | Min | Max |
|---|---|---|---|---|---|
| R_CN2.mgt | Soil conservation services (SCS) runoff curve number | −0.1–0.1 | 0.02 | −0.07 | 0.04 |
| V_SFTMP.bsn | Snowmelt base temperature (°C) | −5–5 | −0.31 | −5.88 | 1.38 |
| V_ESCO.hru | Soil evaporation compensation factor | 0–1 | 0.10 | −0.23 | 0.58 |
| V_SURLAG.bsn | Surface runoff lag coefficient | 1–24 | 23.78 | 9.42 | 26.38 |
| V_GWQMN.gw | Threshold depth of water in shallow aquifer for return flow (mm) | 0–5000 | −1544.75 | −1943.54 | 2693.54 |
| V_ALPHA_BF.gw | Base flow alpha factor | 0–1 | 0.97 | 0.34 | 1.04 |
| R_SOL_AWC.sol | Soil available water storage capacity | −0.1–0.1 | −0.01 | −0.12 | 0.02 |
| V_CH_N1.sub | Manning’s value for tributary channels | 0.01–1 | 0.30 | −0.46 | 0.51 |
| V_SMFMX.bsn | Melt factor for snow on June 21 (mm/day-°C) | 0–9 | 7.32 | 3.70 | 11.14 |
| V_SMFMN.bsn | Melt factor for snow on December 21 (mm/day-°C) | 0–9 | 7.05 | 2.57 | 7.77 |
| V_GW_REVAP.gw | Groundwater revap coefficient | 0.02–0.2 | 0.00 | −0.04 | 0.11 |
| V_REVAPMN.gw | Threshold depth of water in the shallow aquifer for revap (mm) | 0–500 | 83.28 | −246.83 | 251.83 |
| V_EPCO.hru | Plant uptake compensation factor | 0.01–1 | 0.67 | 0.48 | 1.44 |
| V_CH_N2.rte | Manning’s value for the main channel length | 0–0.3 | 0.07 | −0.12 | 0.15 |
| V_TIMP.bsn | Snow peak temperature lag factor | 0–0.9 | 0.45 | 0.06 | 0.62 |
| V_SNOCOVMX.bsn | Threshold depth of snow, above which there is 100% cover | 0–500 | 232.40 | 148.19 | 446.80 |
| V_SMTMP.bsn | Threshold temperature for snow melt (°C) | −5–5 | 0.78 | −7.53 | 0.83 |
| V_RCHRG_DP.gw | Deep aquifer percolation fraction | 0–1 | 0.73 | 0.19 | 0.73 |
| V_GW_DELAY.gw | Groundwater delay time (days) | 0–500 | 162.14 | −186.92 | 271.92 |
| V_SNO50COV.bsn | Fraction of SNOCOVMX that provides 50% cover | 0–0.9 | 0.51 | 0.28 | 0.87 |
| Calibration (SUFI-2) | Validation | |
|---|---|---|
| P-factor | 0.92 | 0.63 |
| R-factor | 0.94 | 1.14 |
| R2 | 0.787 (VG) | 0.508 (S) |
| NSE | 0.779 (VG) | 0.502 (S) |
| RMSE (m3/s) | 0.962 | 1.334 |
| MAE (m3/s) | 0.645 | 0.917 |
| PBIAS (%) | −7.562 (VG) | −8.163 (VG) |
| Period | R2 | NSE | RMSE (m3/s) | MAE (m3/s) | PBIAS (%) | |
|---|---|---|---|---|---|---|
| SWAT (SUFI-2) | 2006–2011 | 0.787 (VG) | 0.779 (VG) | 0.962 | 0.645 | −7.562 (VG) |
| SWAT (Validation) | 2012–2015 | 0.508 (S) | 0.502 (S) | 1.334 | 0.917 | −8.163 (VG) |
| RBNN (Train) | 2003–2011 | 0.996 (VG) | 0.995 (VG) | 0.149 | 0.098 | 0.254 (VG) |
| RBNN (Test) | 2012–2015 | 0.998 (VG) | 0.995 (VG) | 0.132 | 0.079 | 1.297 (VG) |
| SVR (Train) | 2003–2011 | 0.998 (VG) | 0.988 (VG) | 0.089 | 0.059 | 0.102 (VG) |
| SVR (Test) | 2012–2015 | 0.998 (VG) | 0.997 (VG) | 0.099 | 0.070 | −0.758 (VG) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koycegiz, C.; Buyukyildiz, M. Calibration of SWAT and Two Data-Driven Models for a Data-Scarce Mountainous Headwater in Semi-Arid Konya Closed Basin. Water 2019, 11, 147. https://doi.org/10.3390/w11010147
Koycegiz C, Buyukyildiz M. Calibration of SWAT and Two Data-Driven Models for a Data-Scarce Mountainous Headwater in Semi-Arid Konya Closed Basin. Water. 2019; 11(1):147. https://doi.org/10.3390/w11010147
Chicago/Turabian StyleKoycegiz, Cihangir, and Meral Buyukyildiz. 2019. "Calibration of SWAT and Two Data-Driven Models for a Data-Scarce Mountainous Headwater in Semi-Arid Konya Closed Basin" Water 11, no. 1: 147. https://doi.org/10.3390/w11010147
APA StyleKoycegiz, C., & Buyukyildiz, M. (2019). Calibration of SWAT and Two Data-Driven Models for a Data-Scarce Mountainous Headwater in Semi-Arid Konya Closed Basin. Water, 11(1), 147. https://doi.org/10.3390/w11010147





