Effect of Mimic Vegetation with Different Stiffness on Regular Wave Propagation and Turbulence
Abstract
1. Introduction
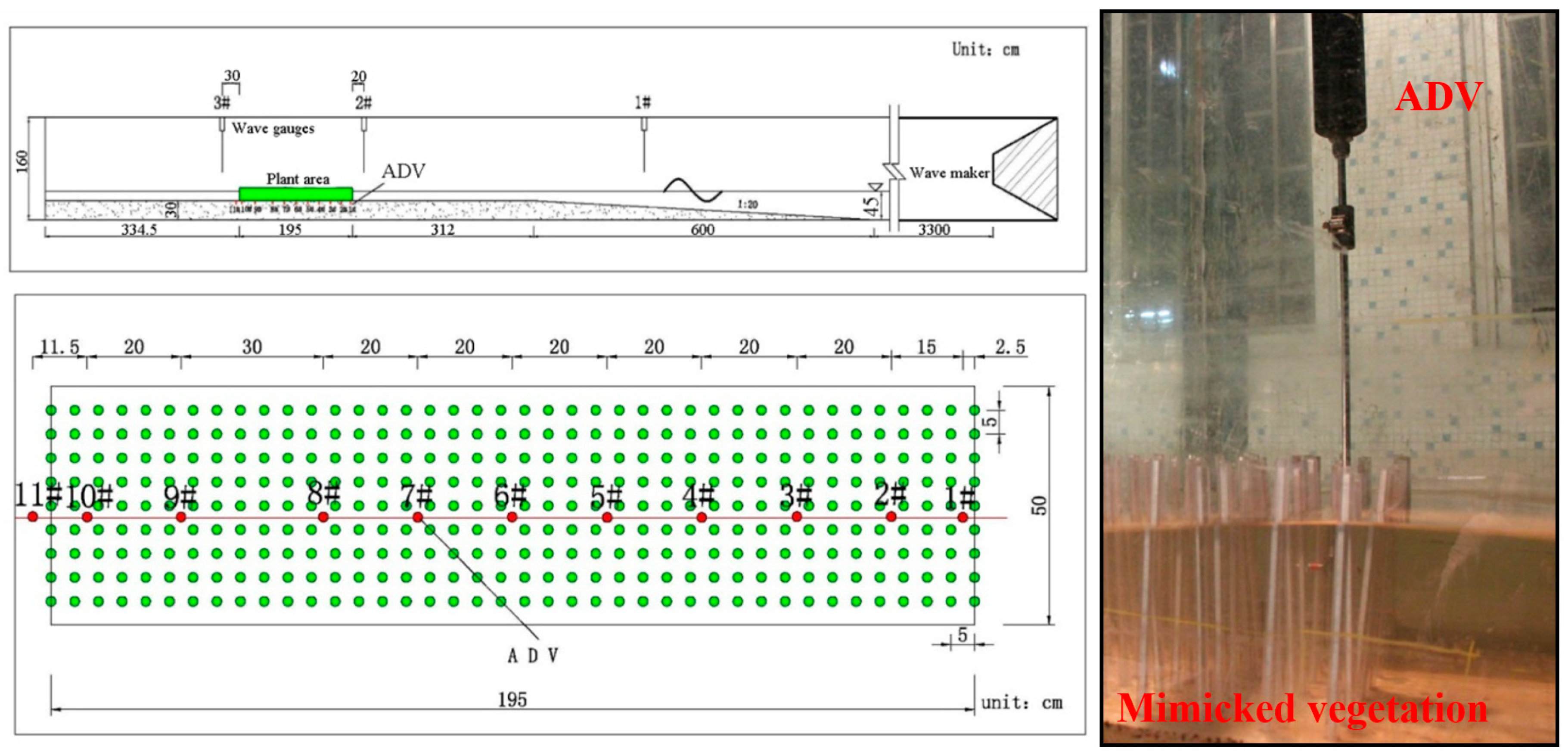
2. Experimental Setup
2.1. Experimental Design
2.2. Experiment Materials
2.3. Data Processing
3. Results and Discussion
3.1. Velocity Variations in the Mimicked Vegetation Canopy with Different Stiffnesses
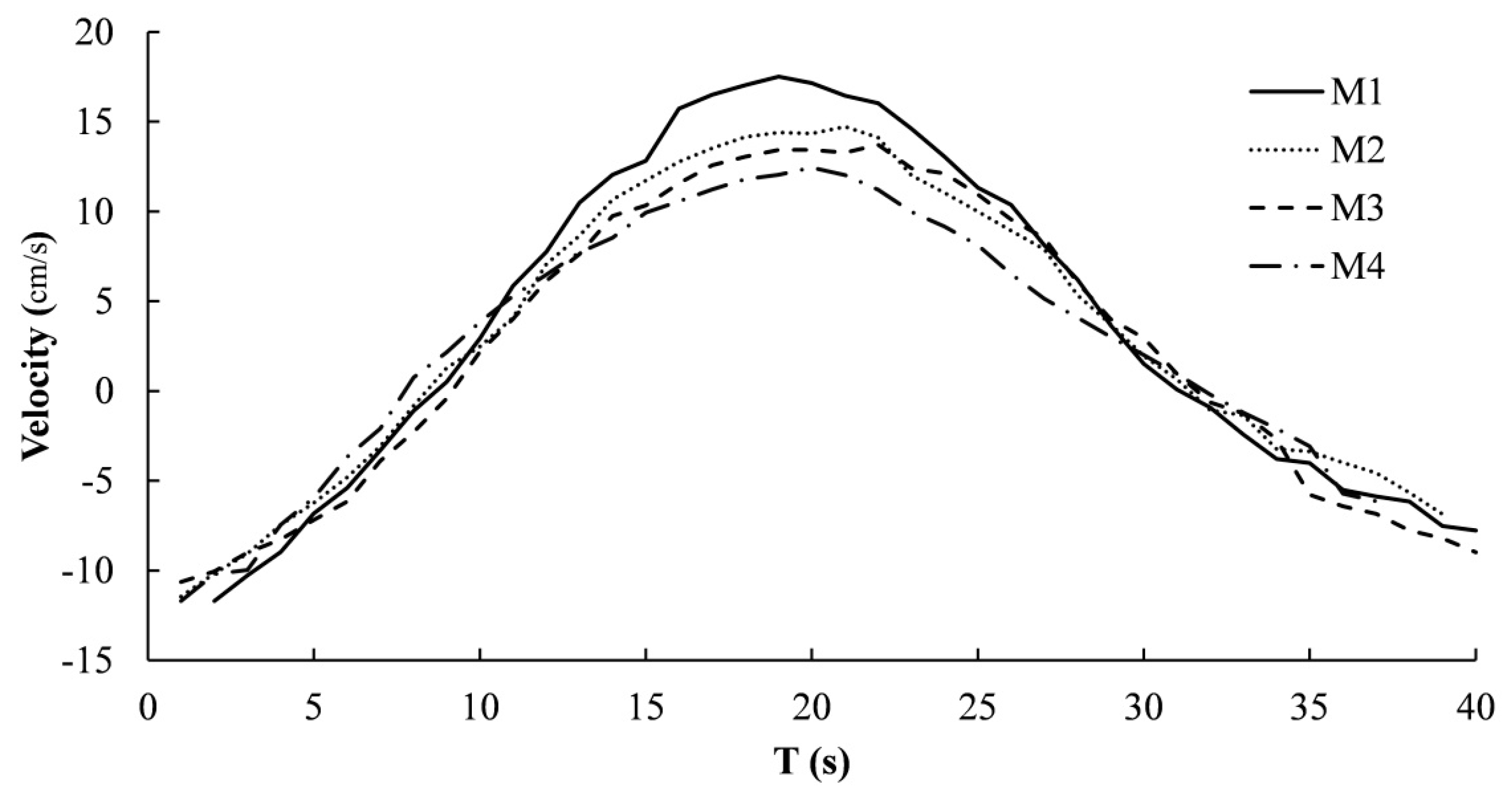
3.1.1. Peak Velocities
3.1.2. Phase Averaged Velocity
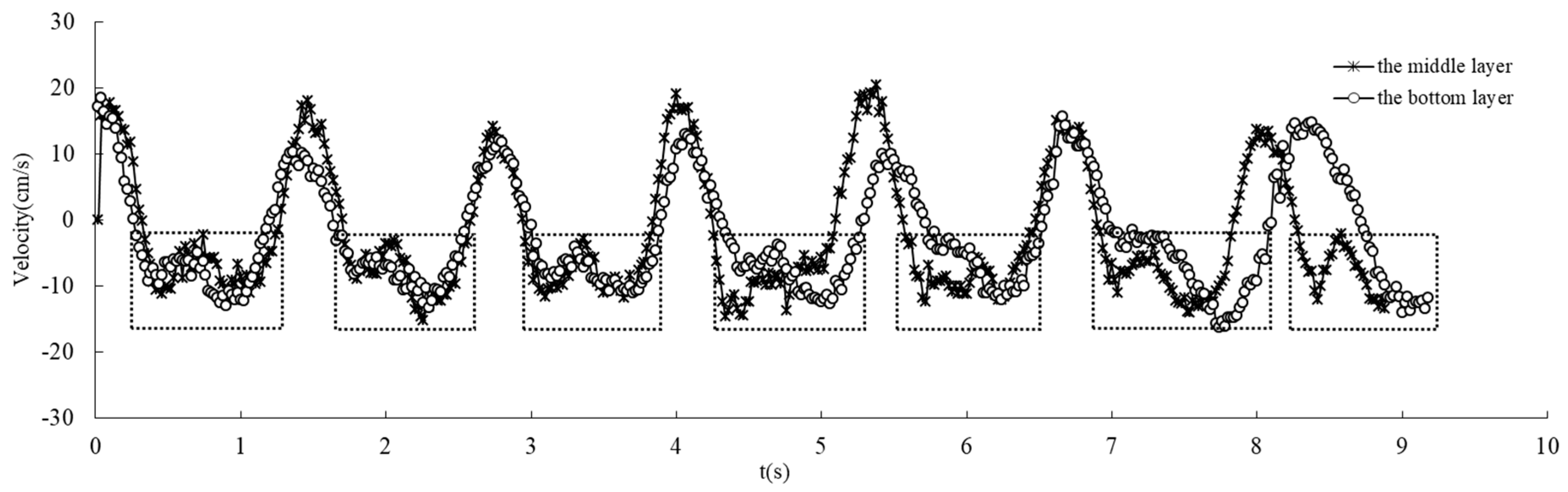
3.1.3. The Secondary Wave Peak in the Flexible Rod Groups
3.2. Turbulence Characteristics of the Different Rod Groups
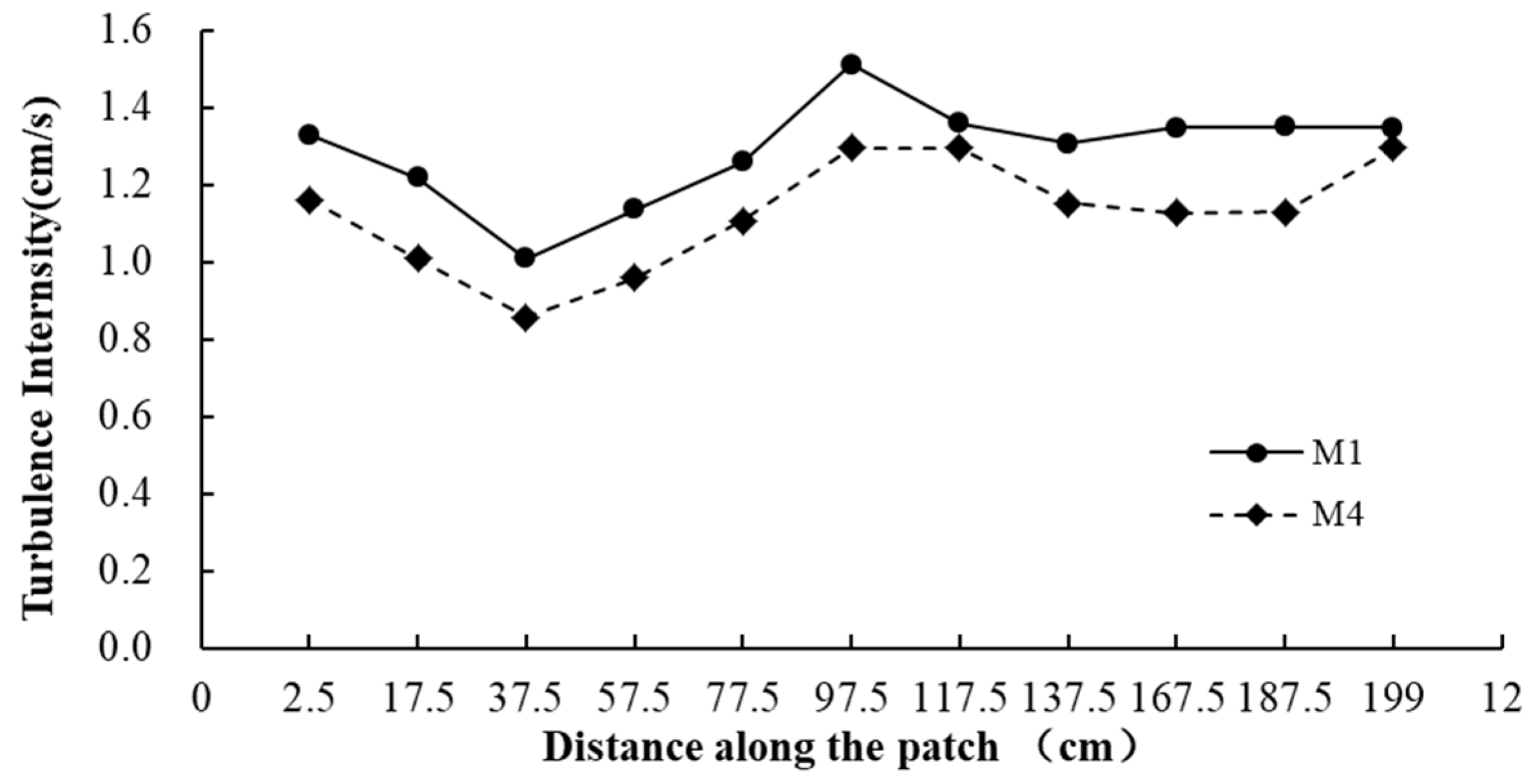
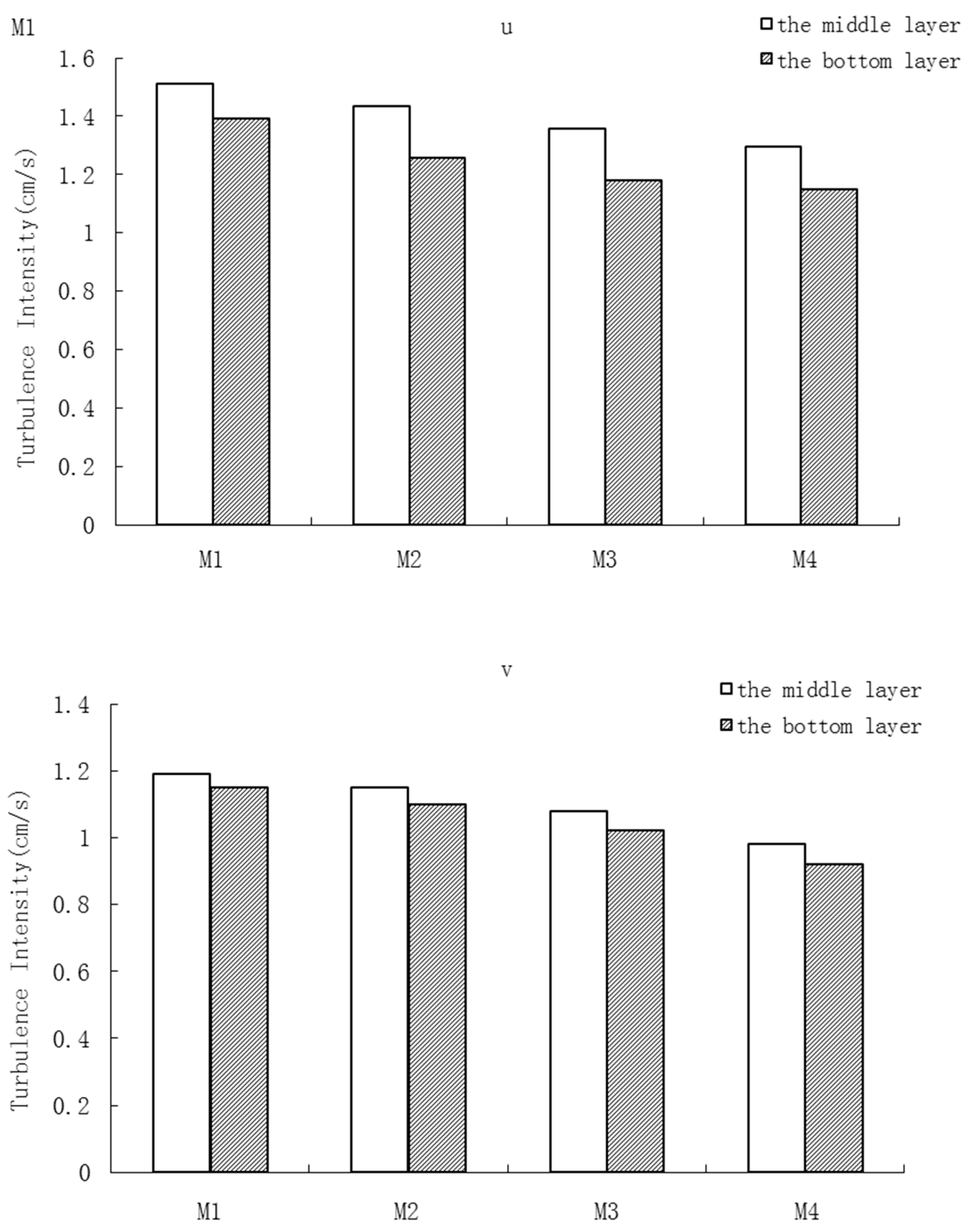
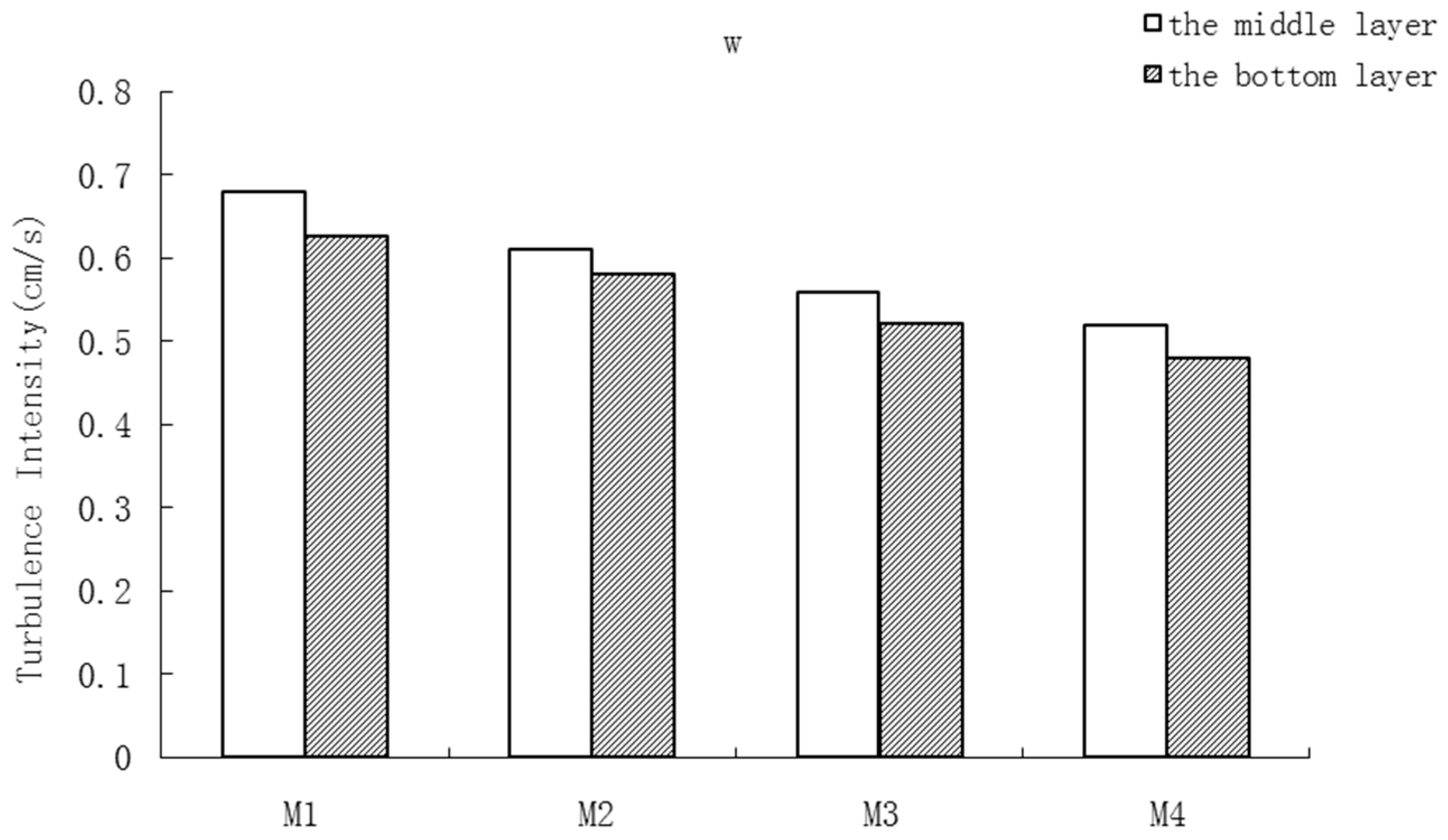
3.2.1. Turbulence Intensity
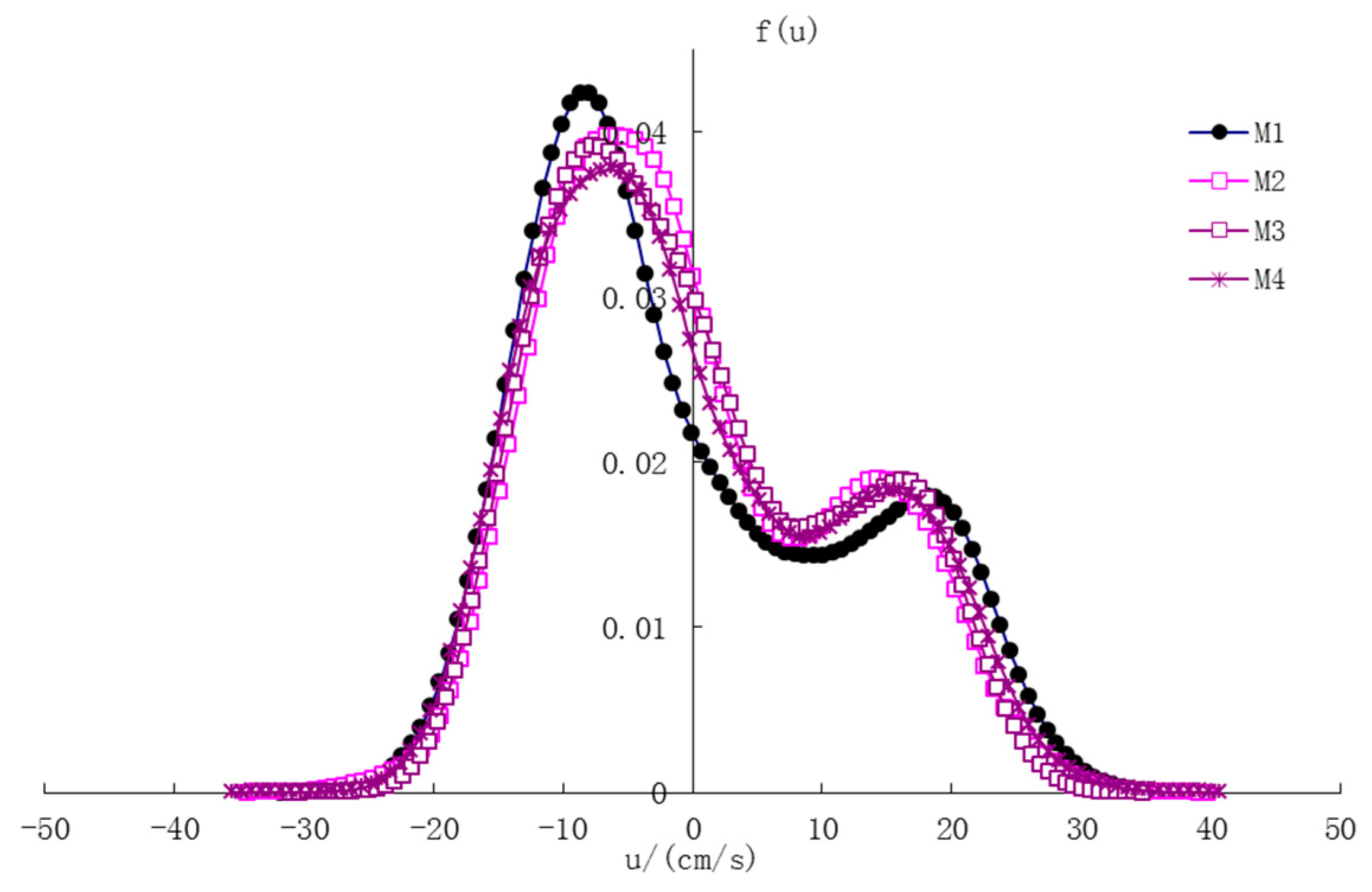
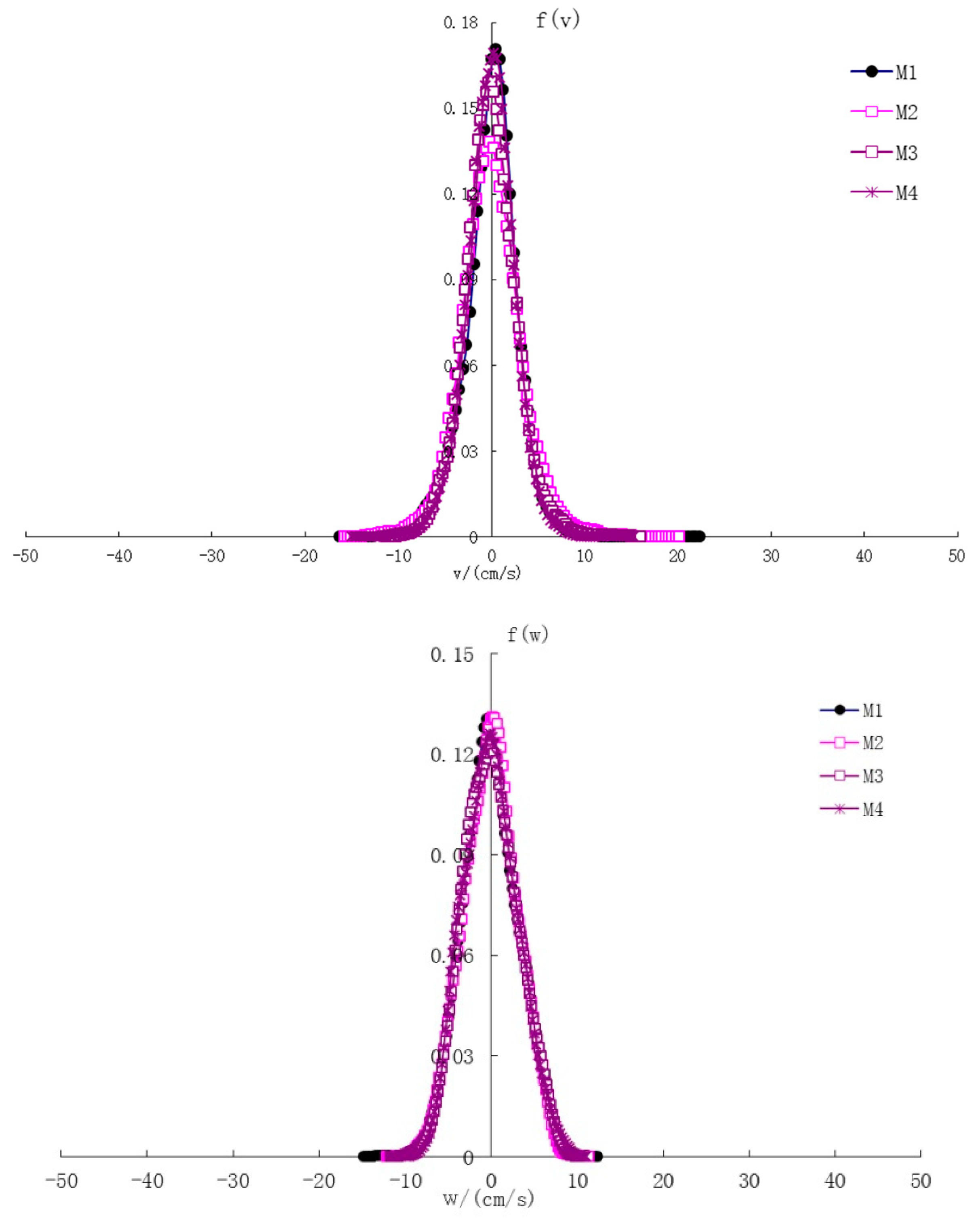
3.2.2. Probability Density of the Fluctuating Velocity
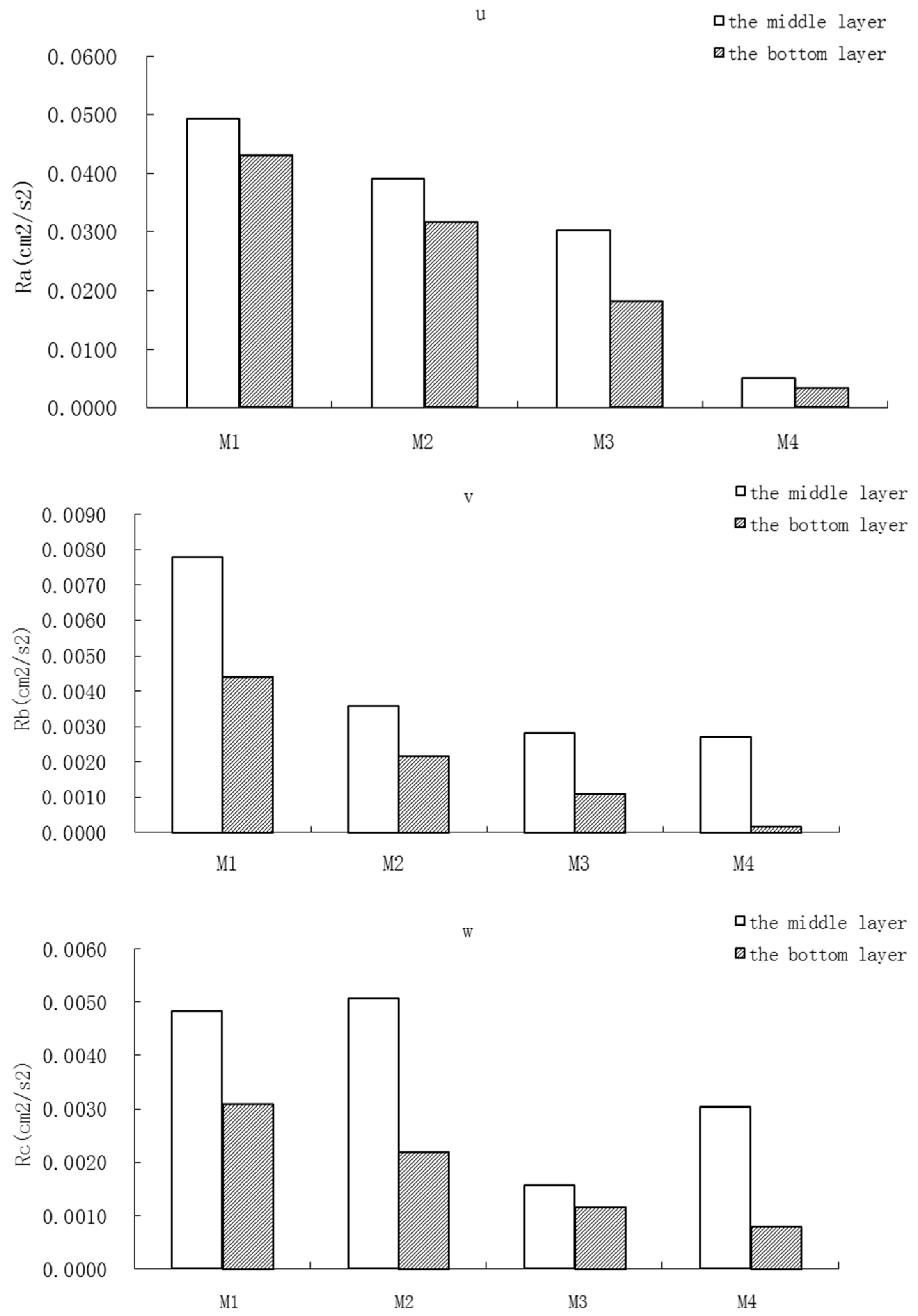
3.2.3. Reynolds Stress
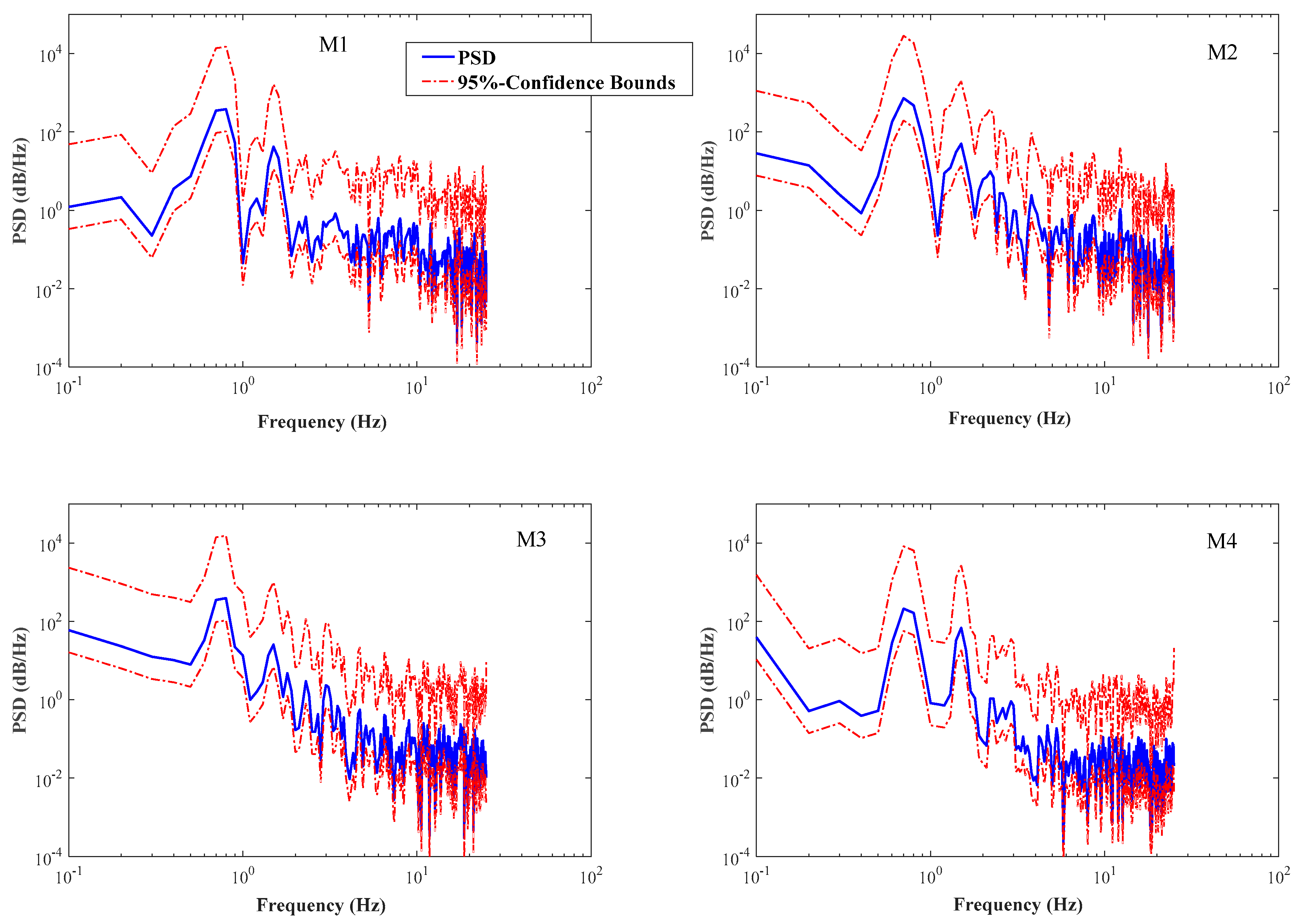
3.2.4. Energy Spectrum Density
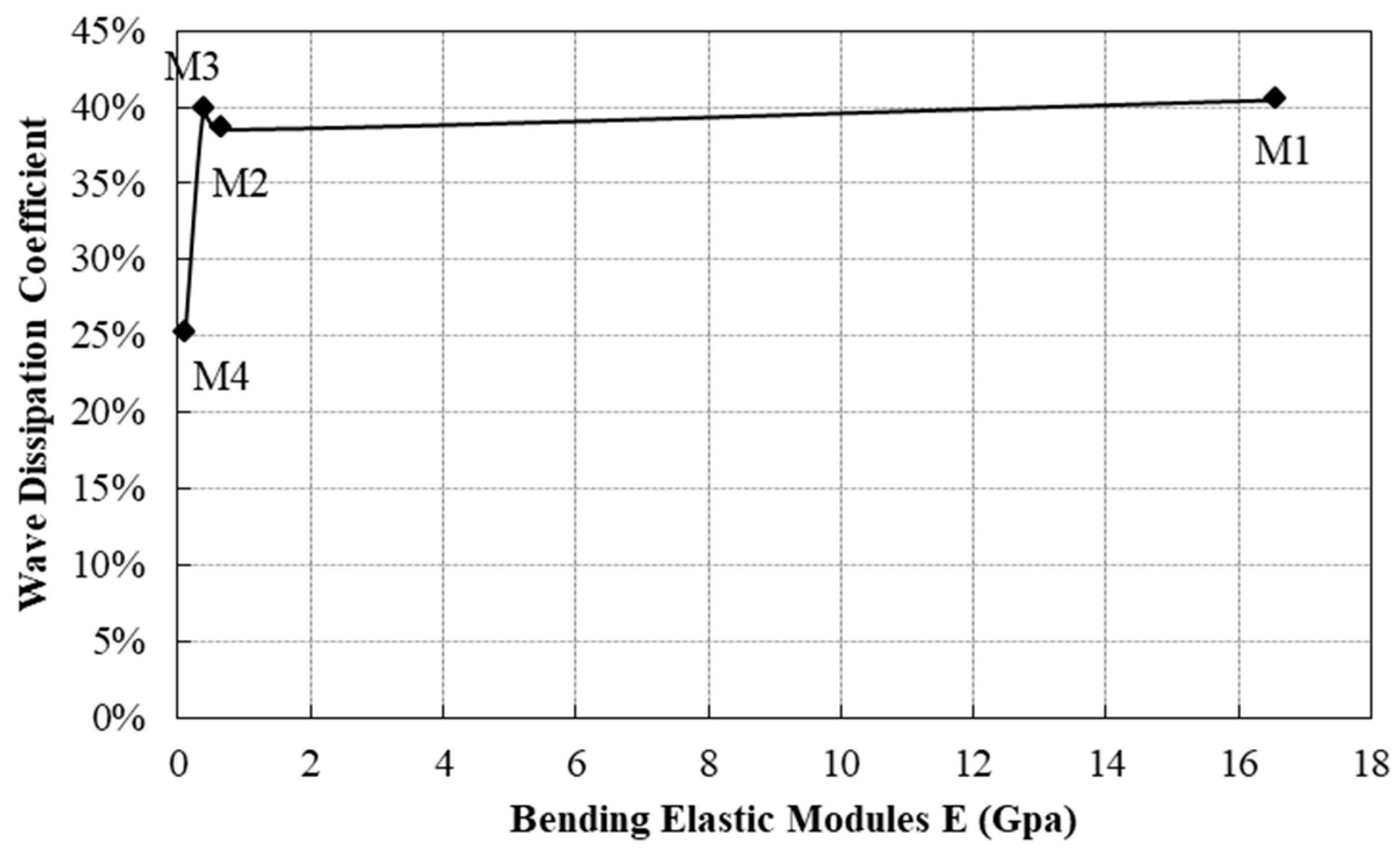
3.3. Wave Dissipation Effect in the Different Rod Groups
4. Conclusions
- (1)
- When waves went through different material rod groups, the peak velocity of the wave was in decay. The more flexible the rod group, the smaller the peak flow velocity. With a low flow velocity, the differences among the flow velocities of the different materials was not apparent.
- (2)
- When waves go through the flexible rod group, the velocity period gradually changed from unimodal to bimodal. Owing to rod group swing, the more flexible the rod group was, the more obvious the secondary wave peak was. With a reduction in material rigidity, the second peak value of the wave energy decreased, which was related to flow shocks that were caused by the swing of the flexible rod group. It is expected that, with different wave periods, the swing behavior and the wave energy transmission will be different, which should be further studied.
- (3)
- High turbulence intensity existed in the areas at the front and in the middle of the rod group. This was because when the wave entered the rod group, the wave propagated from one interface to another, resulting in intensified turbulence.
- (4)
- The greater the material stiffness was, the stronger the turbulence velocity and intensity were. The Reynolds stress decreased with increased flexibility. Additionally, the middle layer Reynolds stress was generally larger than that at the bottom layer.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Green, M.O. Very small waves and associated sediment resuspension on an estuarine intertidal flat. Estuar. Coast. Shelf Sci. 2011, 93, 449–459. [Google Scholar] [CrossRef]
- Green, M.O.; Coco, G. Review of wave-driven sediment resuspension and transport in estuaries. Rev. Geophys. 2014, 52, 77–117. [Google Scholar] [CrossRef]
- Callaghan, D.P.; Leon, J.X.; Saunders, M.I. Wave modelling as a proxy for seagrass ecological modelling: Comparing fetch and process-based predictions for a bay and reef lagoon. Estuar. Coast. Shelf Sci. 2015, 153, 108–120. [Google Scholar] [CrossRef]
- Le Hir, P.; Roberts, W.; Cazaillet, O.; Christie, M.; Bassoullet, P.; Bacher, C. Characterization of intertidal flat hydrodynamics. Cont. Shelf Res. 2000, 20, 1433–1459. [Google Scholar] [CrossRef]
- Stive, M.J.F.; De, S.; Luijendijk, A.P.; Aarninkhof, S.G.J.; Van, G.-M.; Van, T.D.V.; De, V.; Henriquez, M.; Marx, S.; Ranasinghe, R. A new alternative to saving our beaches from sea-level rise: The sand engine. J. Coast. Res. 2013, 29, 1001–1008. [Google Scholar] [CrossRef]
- Temmerman, S.; Meire, P.; Bouma, T.J.; Herman, P.M.; Ysebaert, T.; De Vriend, H.J. Ecosystem-based coastal defence in the face of global change. Nature 2013, 504, 79–83. [Google Scholar] [CrossRef]
- Nepf, H.M. Flow and Transport in Regions with Aquatic Vegetation. Annu. Rev. Fluid Mech. 2011, 44, 123–142. [Google Scholar] [CrossRef]
- Luhar, M.; Nepf, H.M. Wave-induced dynamics of flexible blades. J. Fluids Struct. 2016, 61, 20–41. [Google Scholar] [CrossRef]
- Suzuki, T.; Zijlema, M.; Burger, B.; Meijer, M.C.; Narayan, S. Wave dissipation by vegetation with layer schematization in SWAN. Coast. Eng. 2012, 59, 64–71. [Google Scholar] [CrossRef]
- Cao, H.; Feng, W.; Hu, Z.; Suzuki, T.; Stive, M.J.F. Numerical modeling of vegetation-induced dissipation using an extended mild-slope equation. Ocean Eng. 2015, 110, 258–269. [Google Scholar] [CrossRef]
- Augustin, L.N.; Irish, J.L.; Lynett, P. Laboratory and numerical studies of wave damping by emergent and near-emergent wetland vegetation. Coast. Eng. 2009, 56, 332–340. [Google Scholar] [CrossRef]
- Dalrymple, R.; Kirby, J.; Hwang, P. Wave Diffraction Due to Areas of Energy Dissipation. J. Waterw. Port Coast. Ocean Eng. 1984, 110, 67–79. [Google Scholar] [CrossRef]
- Bos, A.R.; Bouma, T.J.; de Kort, G.L.J.; van Katwijk, M.M. Ecosystem engineering by annual intertidal seagrass beds: Sediment accretion and modification. Estuar. Coast. Shelf Sci. 2007, 74, 344–348. [Google Scholar] [CrossRef]
- Christianen, M.J.A.; van Belzen, J.; Herman, P.M.J.; van Katwijk, M.M.; Lamers, L.P.M.; van Leent, P.J.M.; Bouma, T.J. Low-Canopy Seagrass Beds Still Provide Important Coastal Protection Services. PLoS ONE 2013, 8, e62413. [Google Scholar] [CrossRef] [PubMed]
- Ondiviela, B.; Losada, I.J.; Lara, J.L.; Maza, M.; Galvan, C.; Bouma, T.J.; van Belzen, J. The role of seagrasses in coastal protection in a changing climate. Coast. Eng. 2014, 87, 158–168. [Google Scholar] [CrossRef]
- De Boer, W.F. Seagrass-sediment interactions, positive feedbacks and critical thresholds for occurrence: A review. Hydrobiologia 2007, 591, 5–24. [Google Scholar] [CrossRef]
- Huang, B.S.; Lai, G.W.; Qiu, J.; Lin, S.Z. Hydraulice of compound channel with vegetated flood plains. J. Hydrodyn. Ser. B 2002, 14, 23–28. [Google Scholar]
- Jiang, C.B.; Wang, R.X.; Chen, J.; Chen, J.K.; Zhi-Yuan, W.U. Laboratory investigation on solitary wave transformation through the emergent rigid vegetation. J. Changsha Univ. Sci. Technol. 2012, 9, 50–55. [Google Scholar]
- Möller, I.; Spencer, T. Wave dissipation over macro-tidal saltmarshes: Effects of marsh edge typology and vegetation change. J. Coast. Res. 2002, 36, 506–521. [Google Scholar] [CrossRef]
- Quartel, S.; Kroon, A.; Augustinus, P.G.E.F.; Santen, P.V.; Tri, N.H. Wave attenuation in coastal mangroves in the Red River Delta, Vietnam. J. Asian Earth Sci. 2007, 29, 576–584. [Google Scholar] [CrossRef]
- Bradley, K.; Houser, C. Relative velocity of seagrass blades: Implications for wave attenuation in low-energy environments. J. Geophys. Res. Earth Surf. 2009, 114, F01004. [Google Scholar] [CrossRef]
- Fonseca, M.S.; Cahalan, J.A. A preliminary evaluation of wave attenuation by four species of seagrass. Estuar. Coast. Shelf Sci. 1992, 35, 565–576. [Google Scholar] [CrossRef]
- Tschirky, P.; Hall, K.; Turcke, D. Wave attenuation by emergent wetland vegetation. In Proceedings of the 27th International Conference on Coastal Engineering, Sydney, Australia, 16–21 July 2000. ASCE.865-877. [Google Scholar]
- Lima, S.F.; Neves, C.F.; Rosauro, N.M.L. Damping of gravity waves by fields of flexible vegetation. In Proceedings of the 30th International Coastal Engineering Conference, San Diego, CA, USA, 3–8 September 2006; pp. 491–503. [Google Scholar]
- Mazda, Y.; Magi, M.; Ikeda, Y.; Kurokawa, T.; Asano, T. Wave reduction in a mangrove forest dominated by Sonneratia sp. Wetl. Ecol. Manag. 2006, 14, 365–378. [Google Scholar] [CrossRef]
- Horstman, E.; Dohmen-Janssen, M.; Narra, P.; van den Berg, N.-J.; Siemerink, M.; Balke, T.; Bouma, T.; Hulscher, S. Wave attenuation in mangrove forests; field data obtained in Trang, Thailand. Coast. Eng. Proc. 2012, 1, 40. [Google Scholar] [CrossRef]
- Cruise, J.F.; Musleh, F.A. Functional Relationships of Resistance in Wide Flood Plains with Rigid Unsubmerged Vegetation. J. Hydraul. Eng. 2006, 132, 163–171. [Google Scholar] [CrossRef]
- White, B.; Nepf, H. A vortex-based model of velocity and shear stress in a partially vegetated shallow channel. Water Resour. Res. 2008, 44, W01412. [Google Scholar] [CrossRef]
- Pujol, D.; Serra, T.; Colomer, J.; Casamitjana, X. Flow structure in canopy models dominated by progressive waves. J. Hydrol. 2013, 486, 281–292. [Google Scholar] [CrossRef]
- Lowe, R.J.; Koseff, J.R.; Monismith, S.G. Oscillatory flow through submerged canopies: 1. Velocity structure. J. Geophys. Res. C Oceans 2005, 110, C10016. [Google Scholar] [CrossRef]
- Luhar, M.; Nepf, H.M. Flow-induced reconfiguration of buoyant and flexible aquatic vegetation. Limnol. Oceanogr. 2011, 56, 2003–2017. [Google Scholar] [CrossRef]
- Ghisalberti, M.; Nepf, H. The structure of the shear layer in flows over rigid and flexible canopies. Environ. Fluid Mech. 2006, 6, 277–301. [Google Scholar] [CrossRef]
- Riffe, K.C.; Henderson, S.M.; Mullarney, J.C. Wave dissipation by flexible vegetatio. Geophys. Res. Lett. 2011, 38, L18607. [Google Scholar] [CrossRef]
- Stevens, A.W.; Lacy, J.R. The Influence of Wave Energy and Sediment Transport on Seagrass Distribution. Estuaries Coasts 2012, 35, 92–108. [Google Scholar] [CrossRef]
- Luhar, M.; Infantes, E.; Orfila, A.; Terrados, J.; Nepf, H.M. Field observations of wave-induced streaming through a submerged seagrass (Posidonia oceanica) meadow. J. Geophys. Res. Oceans 2013, 118, 1955–1968. [Google Scholar] [CrossRef]
- Bouma, T.J.; De Vries, M.B.; Low, E.; Peralta, G.; Tánczos, I.C.; Van De Koppel, J.; Herman, P.M.J. Trade-offs related to ecosystem engineering: A case study on stiffness of emerging macrophytes. Ecology 2005, 86, 2187–2199. [Google Scholar] [CrossRef]
- Horstman, E.M.; Bryan, K.R.; Mullarney, J.C.; Pilditch, C.A.; Eager, C.A. Are flow-vegetation interactions well represented by mimics? A case study of mangrove pneumatophores. Adv. Water Resour. 2018, 111, 360–371. [Google Scholar] [CrossRef]
- Paul, M.; Henry, P.-Y.T.; Thomas, R.E. Geometrical and mechanical properties of four species of northern European brown macroalgae. Coast. Eng. 2014, 84, 73–80. [Google Scholar] [CrossRef]
- Bouma, T.J.; De Vries, M.B.; Herman, P.M.J. Comparing ecosystem engineering efficiency of two plant species with contrasting growth strategies. Ecology 2010, 91, 2696–2704. [Google Scholar] [CrossRef]
- Cox, D.T.; Kobayashi, N.; Okayasu, A. Experimental and Numerical Modeling of Surf Zone Hydrodynamics; University of Delaware, Center for Applied Coastal Research, Ocean Engineering Laboratory: Newark, DE, USA, 1995; pp. 32–50. [Google Scholar]
- Nepf, H.M. Flow Over and Through Biota. In Treatise on Estuarine and Coastal Science; Wolanski, E., McLusky, D., Eds.; Academic Press: Waltham, MA, USA, 2011; pp. 267–288. ISBN 978-0-08-087885-0. [Google Scholar]
- Ma, D. Wave turbulence and calculation. J. Tianjin Univ. 1964, 14, 16–19. [Google Scholar]
- Cui, C.; Zhang, N.C.; Guo, C.S.; Fang, Z. Impact of water depth variation on simulated freak waves and their time-frequency energy spectrum. Acta Oceanol. Sin. 2011, 33, 174–179. [Google Scholar]

| Material | Application | Elasticity Modulus E (Gpa) | Measuring Point of 5# | |
|---|---|---|---|---|
| Force (N) | Middle Layer Velocity (cm/s) | Bottom Layer Velocity (cm/s) | ||
| M1 | 30 | 16.56 | 22.17 | 19.95 |
| M2 | 1.2 | 0.66 | 18.10 | 17.33 |
| M3 | 0.7 | 0.39 | 17.23 | 16.08 |
| M4 | 0.2 | 0.11 | 15.28 | 13.54 |
| Material | Bending Elastic Modulus E (Gpa) | Wave Height before the Rod Groups (cm) | Wave Height after the Rod Groups (cm) | Wave Dissipation Coefficient |
|---|---|---|---|---|
| M 1 | 16.56 | 5.81 | 3.46 | 40.45% |
| M 2 | 0.66 | 5.79 | 3.56 | 38.51% |
| M 3 | 0.39 | 5.83 | 3.51 | 39.79% |
| M 4 | 0.11 | 5.84 | 4.37 | 25.17% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, C.; Huang, B.; Liu, D.; Qiu, J.; Chen, H.; Li, Y.; Hu, Z. Effect of Mimic Vegetation with Different Stiffness on Regular Wave Propagation and Turbulence. Water 2019, 11, 109. https://doi.org/10.3390/w11010109
Tan C, Huang B, Liu D, Qiu J, Chen H, Li Y, Hu Z. Effect of Mimic Vegetation with Different Stiffness on Regular Wave Propagation and Turbulence. Water. 2019; 11(1):109. https://doi.org/10.3390/w11010109
Chicago/Turabian StyleTan, Chao, Bensheng Huang, Da Liu, Jing Qiu, Hui Chen, Yulong Li, and Zhan Hu. 2019. "Effect of Mimic Vegetation with Different Stiffness on Regular Wave Propagation and Turbulence" Water 11, no. 1: 109. https://doi.org/10.3390/w11010109
APA StyleTan, C., Huang, B., Liu, D., Qiu, J., Chen, H., Li, Y., & Hu, Z. (2019). Effect of Mimic Vegetation with Different Stiffness on Regular Wave Propagation and Turbulence. Water, 11(1), 109. https://doi.org/10.3390/w11010109




