Evaluation and Hydrological Application of CMADS against TRMM 3B42V7, PERSIANN-CDR, NCEP-CFSR, and Gauge-Based Datasets in Xiang River Basin of China
Abstract
1. Introduction
2. Materials and Methods
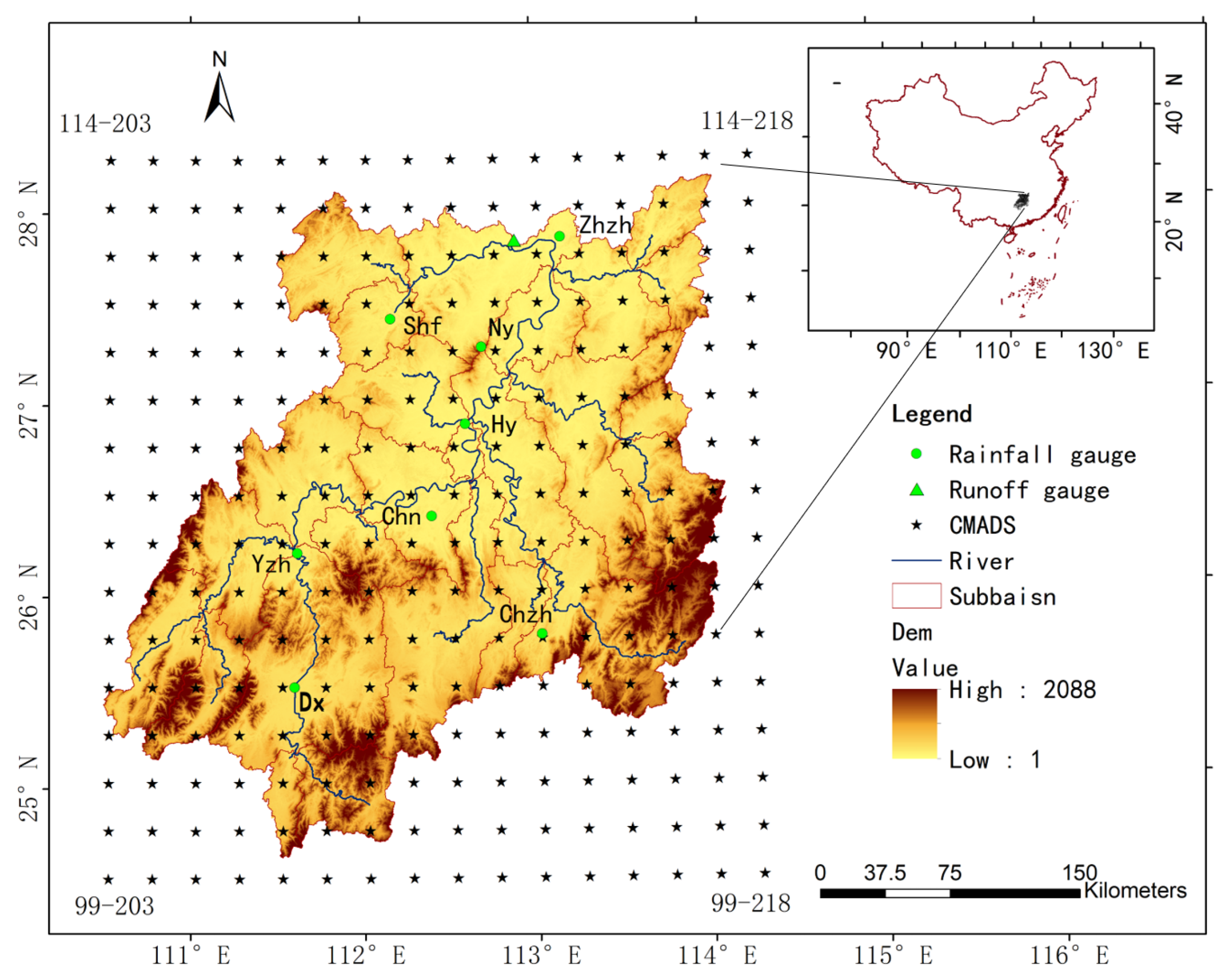
2.1. Study Area
2.2. Meteorological Data
2.2.1. Satellite-Based and Reanalysis Precipitation Estimates
2.2.2. Ground Gauge Observations
2.3. Straightforward Comparison
Diagnostic Statistics
2.4. Ensemble Bayesian Model Averaging
2.5. Model Creation
2.6. Model Calibration and Validation
3. Results
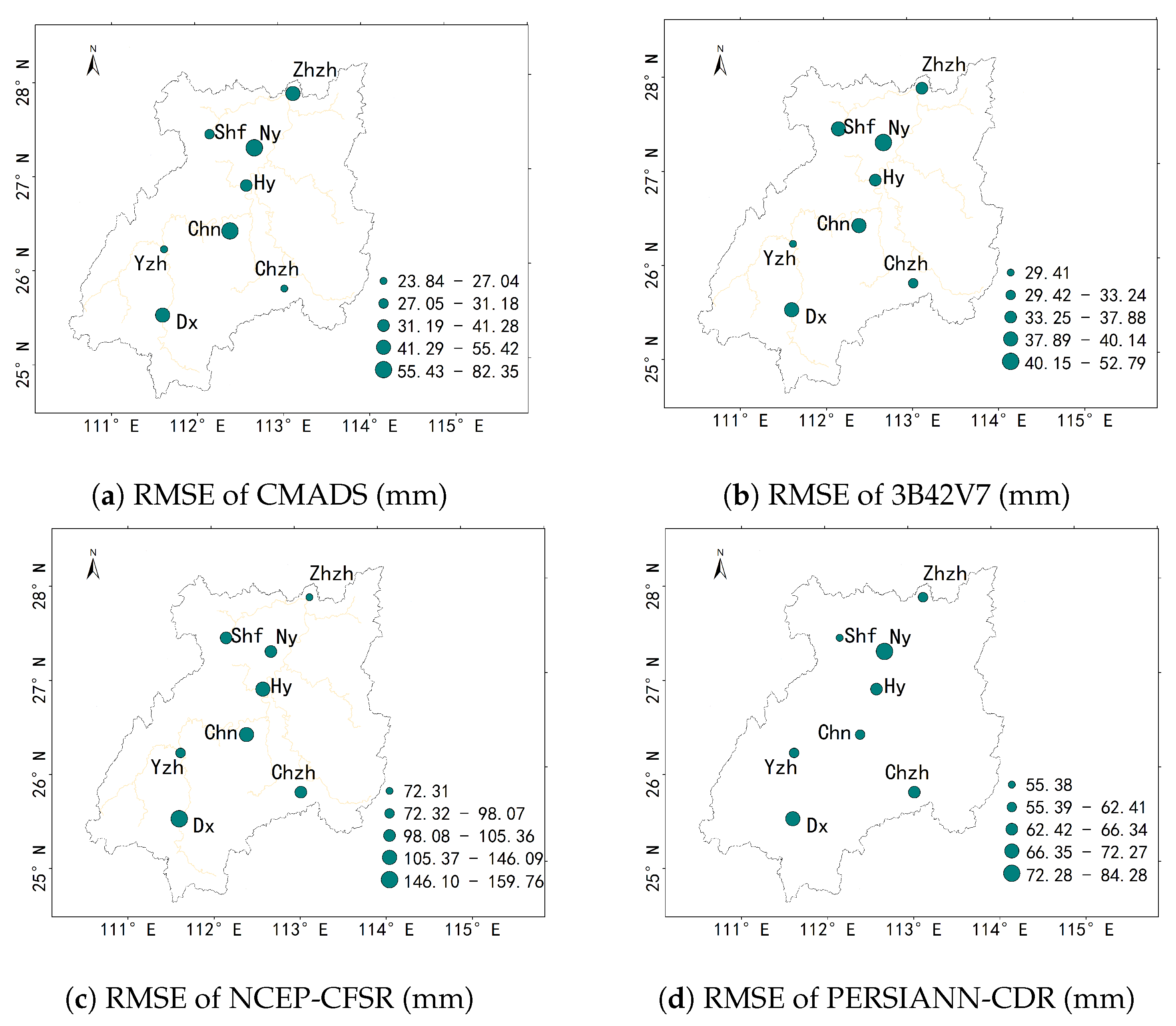
3.1. Comparison of Precipitation Estimates
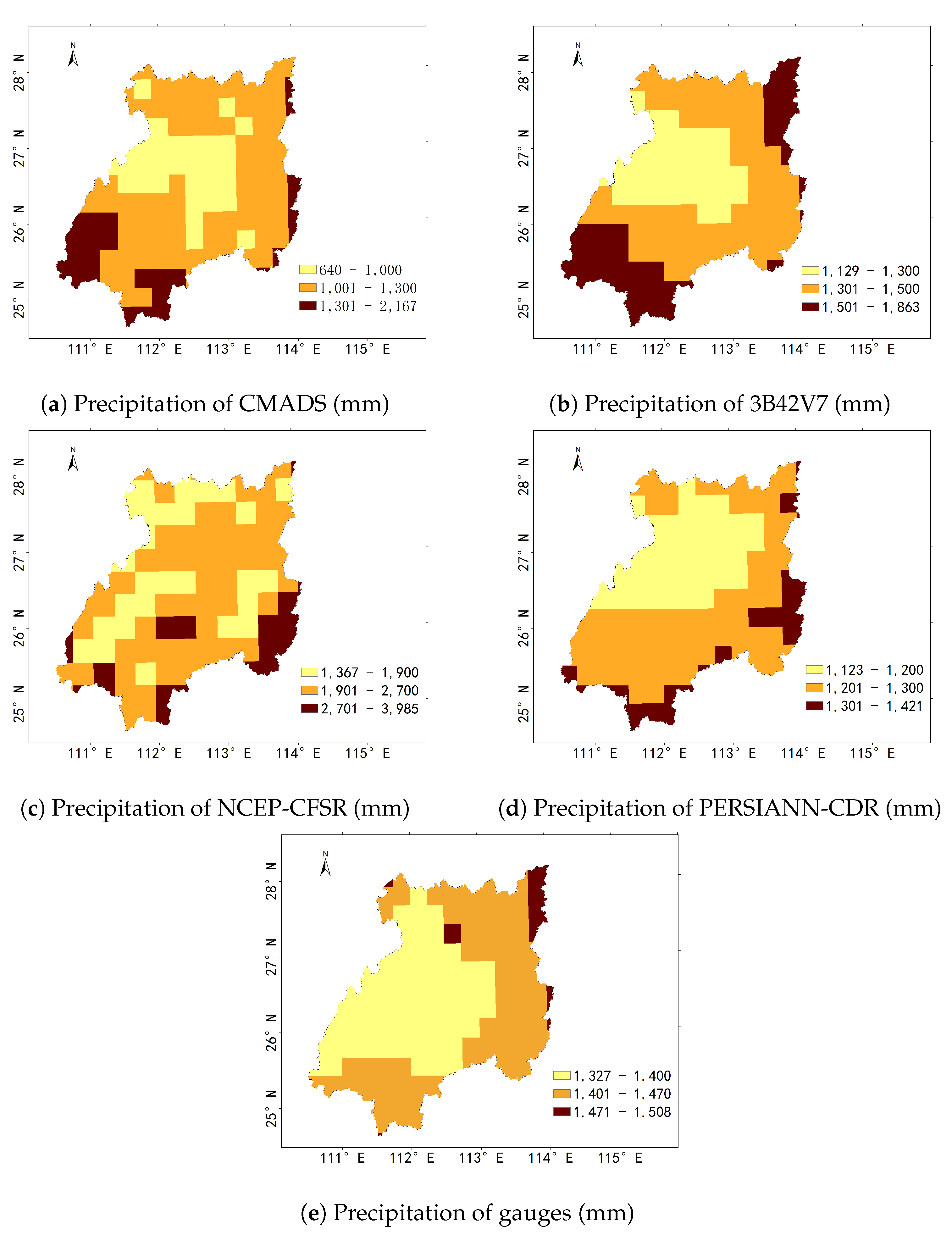
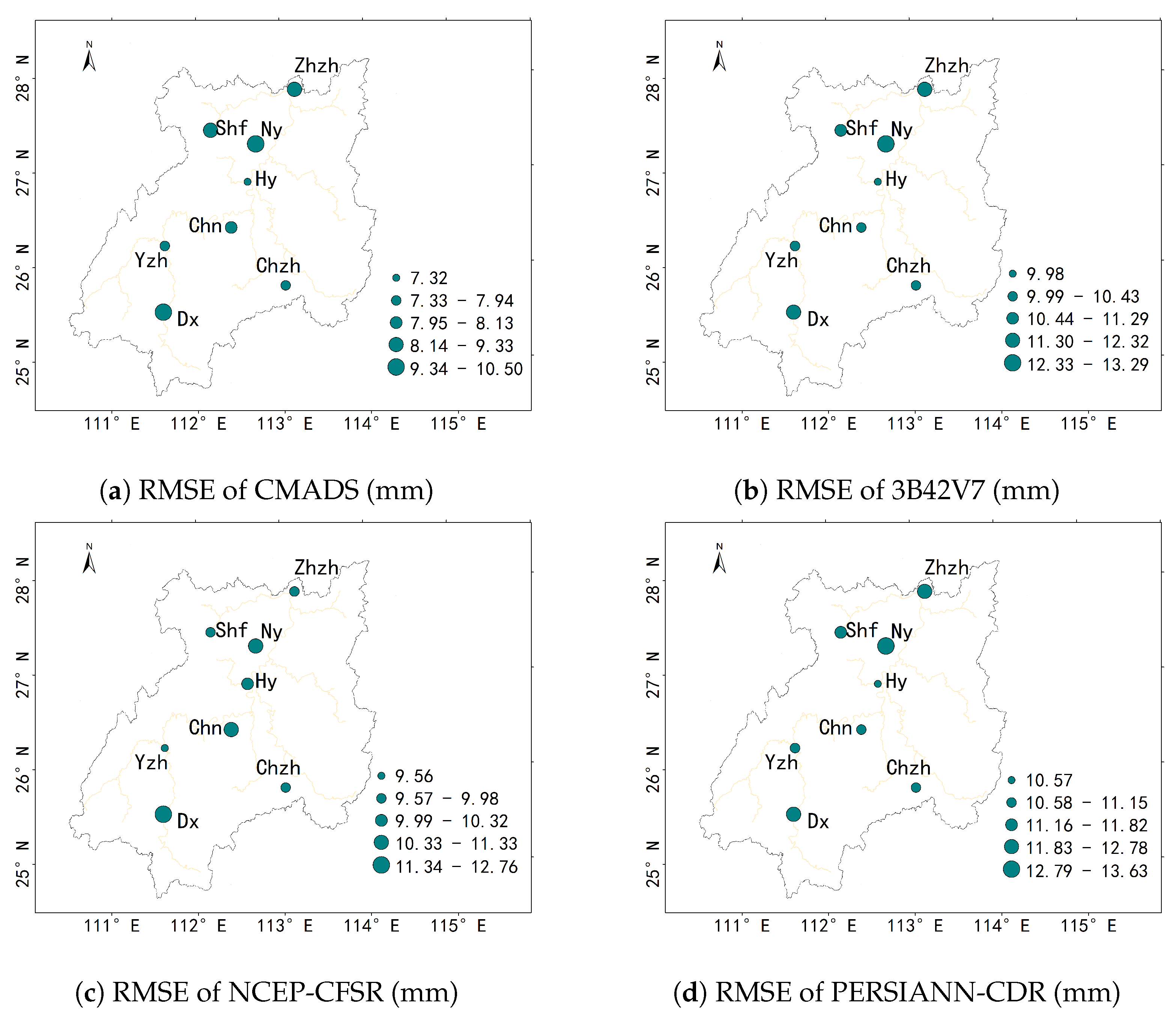
3.1.1. Spatial Distribution of Annual Precipitation Estimates
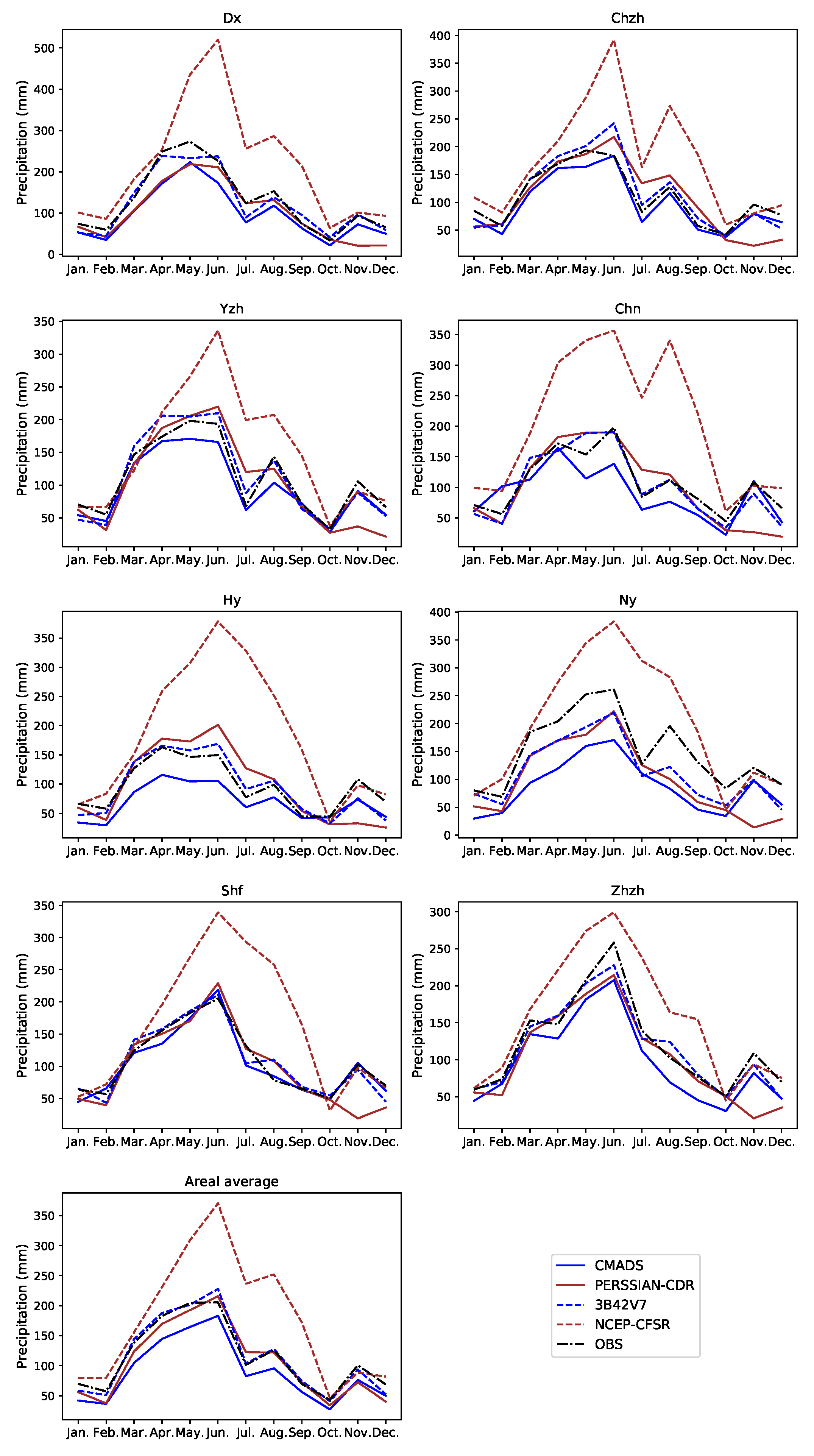
3.1.2. Comparison at Monthly Scale
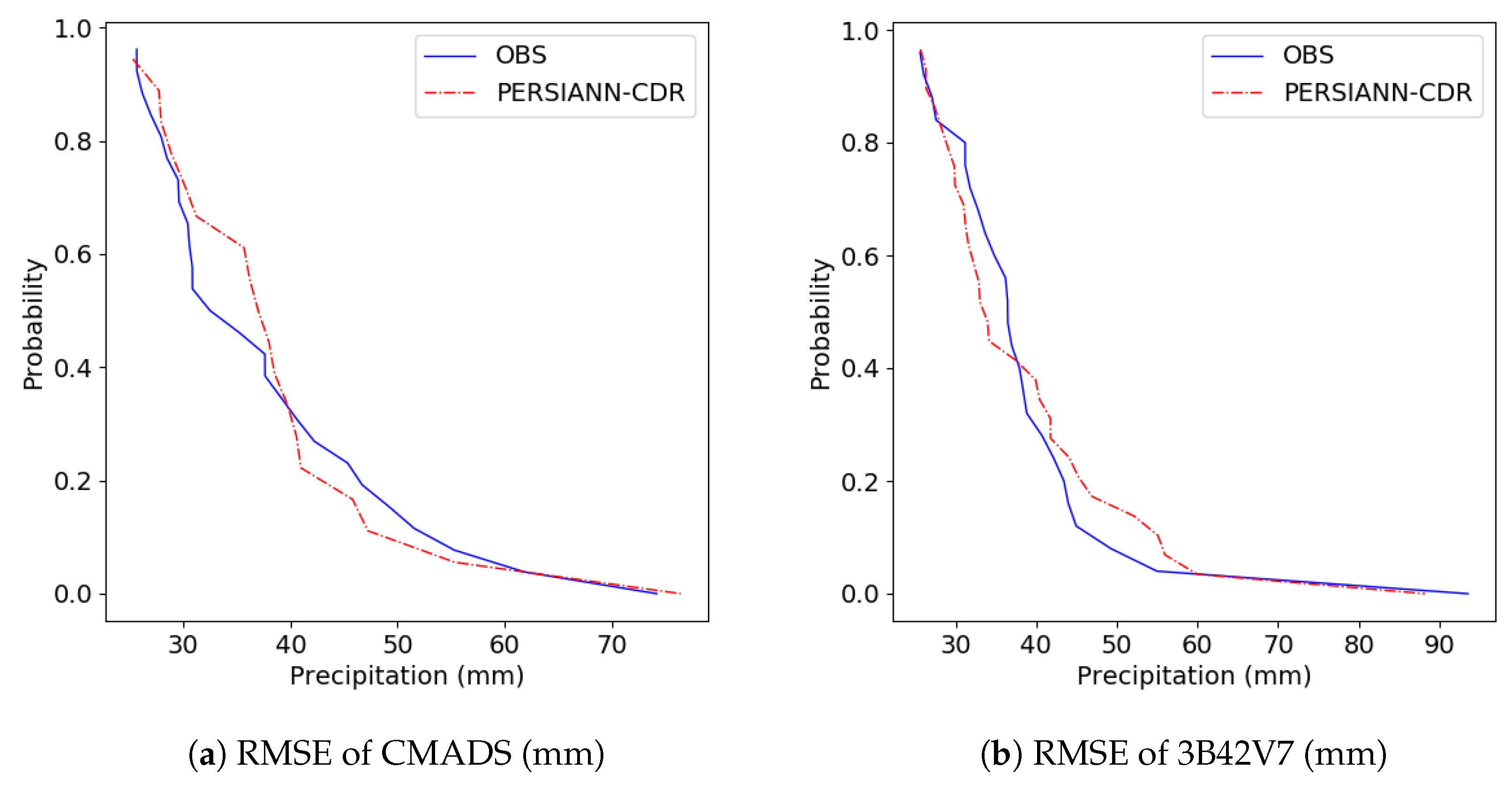
3.1.3. Comparison at Daily Scale
3.2. Comparison of Streamflow Simulations
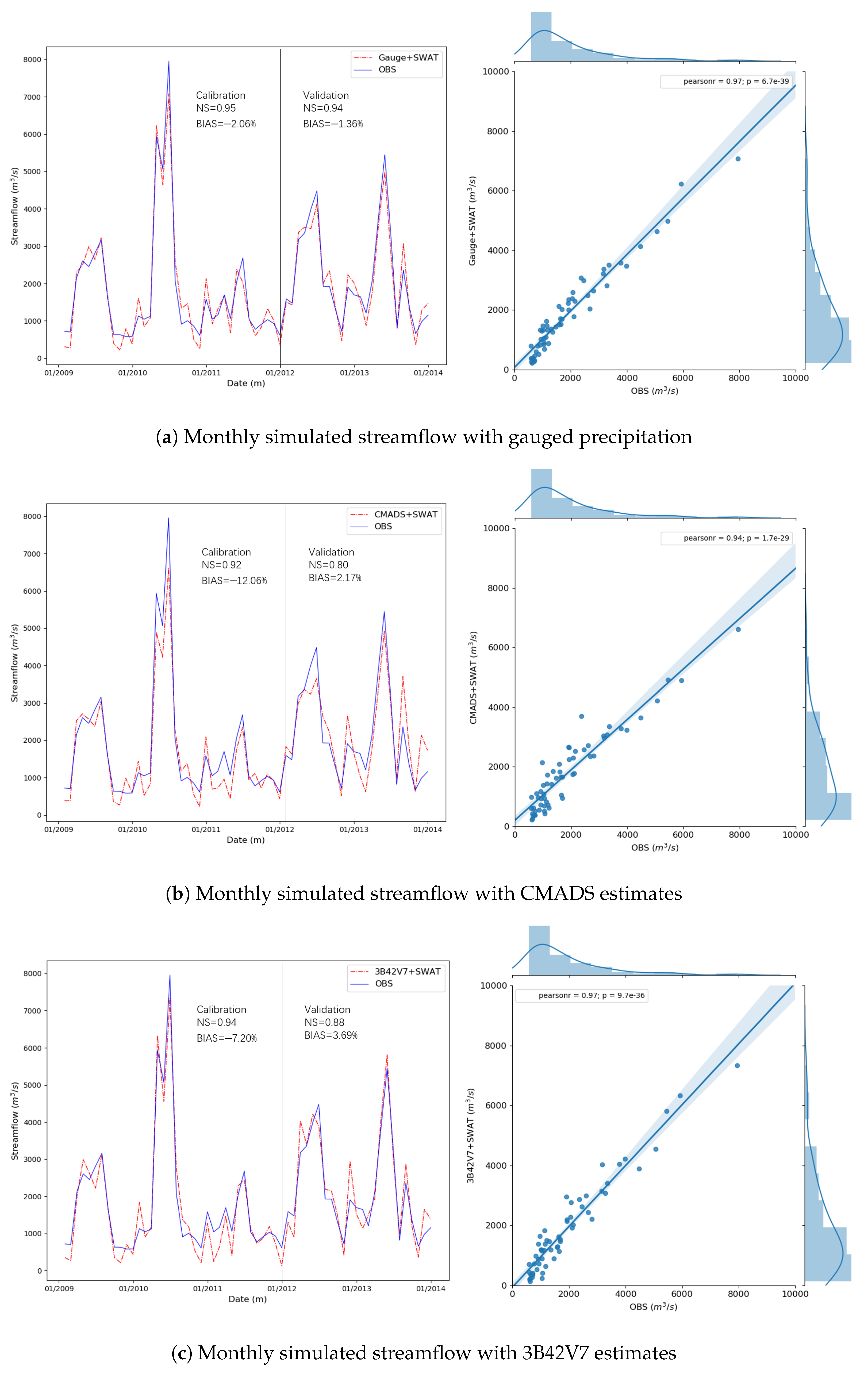
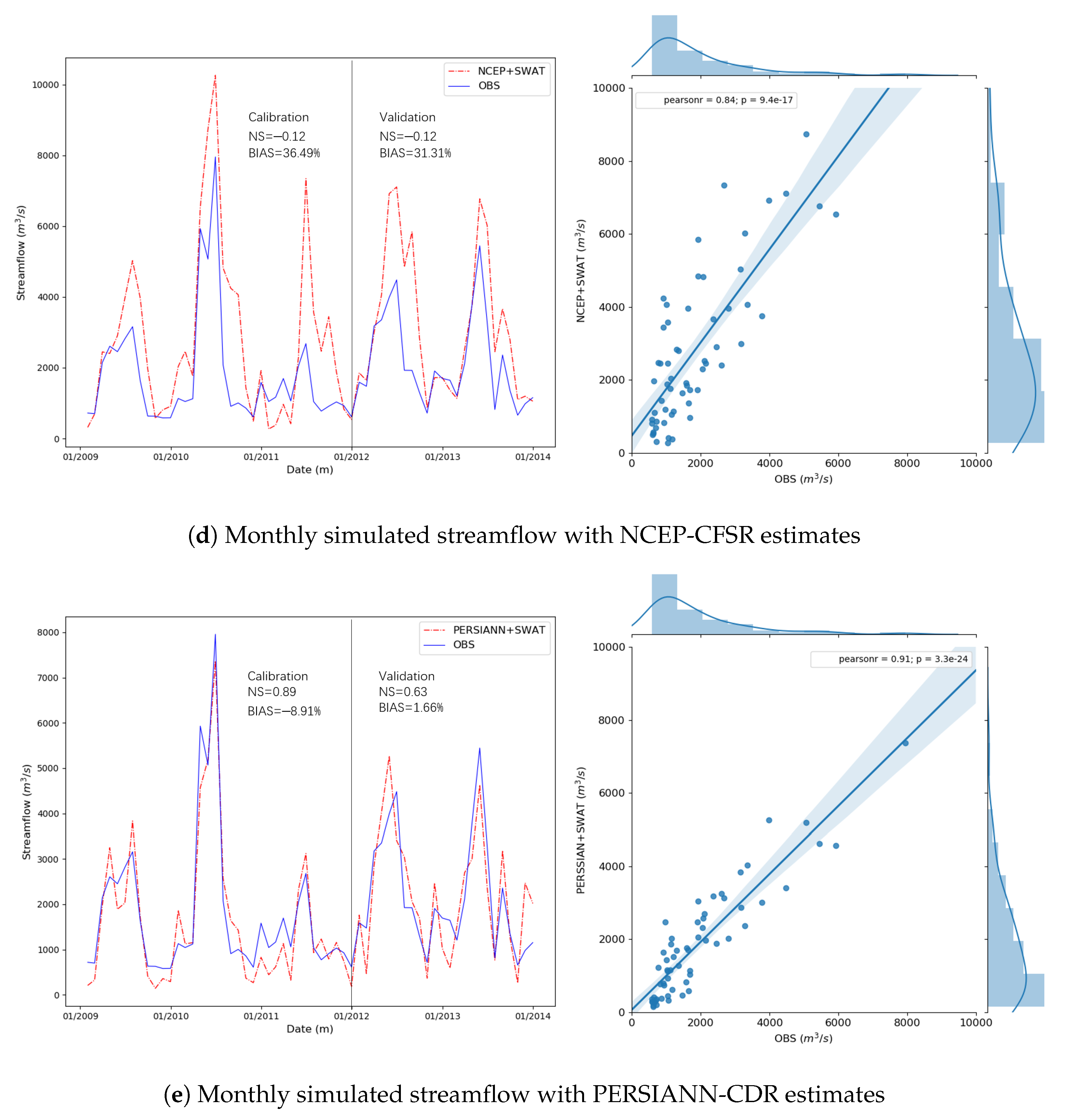
3.2.1. Comparison at Monthly Scale
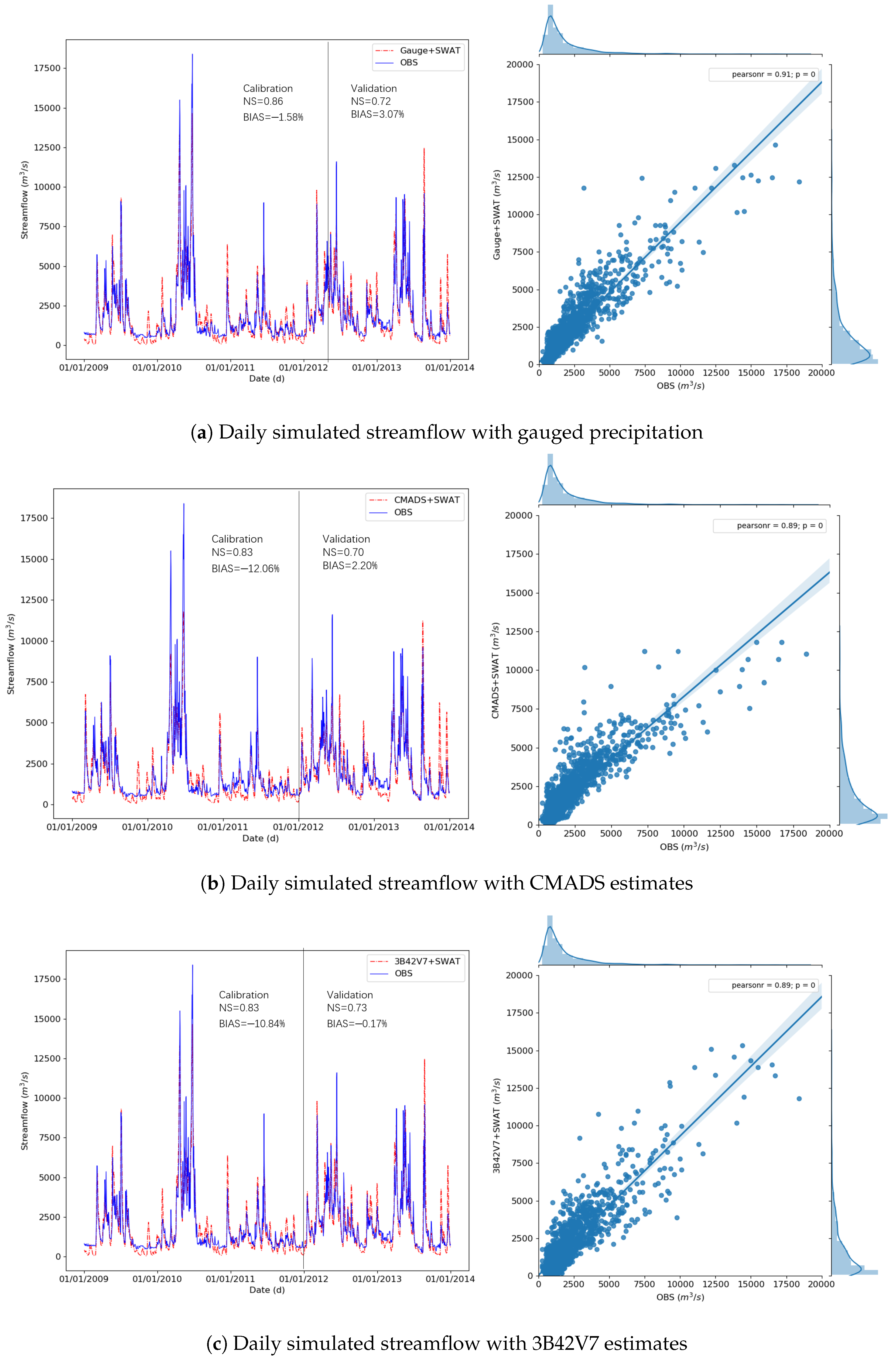
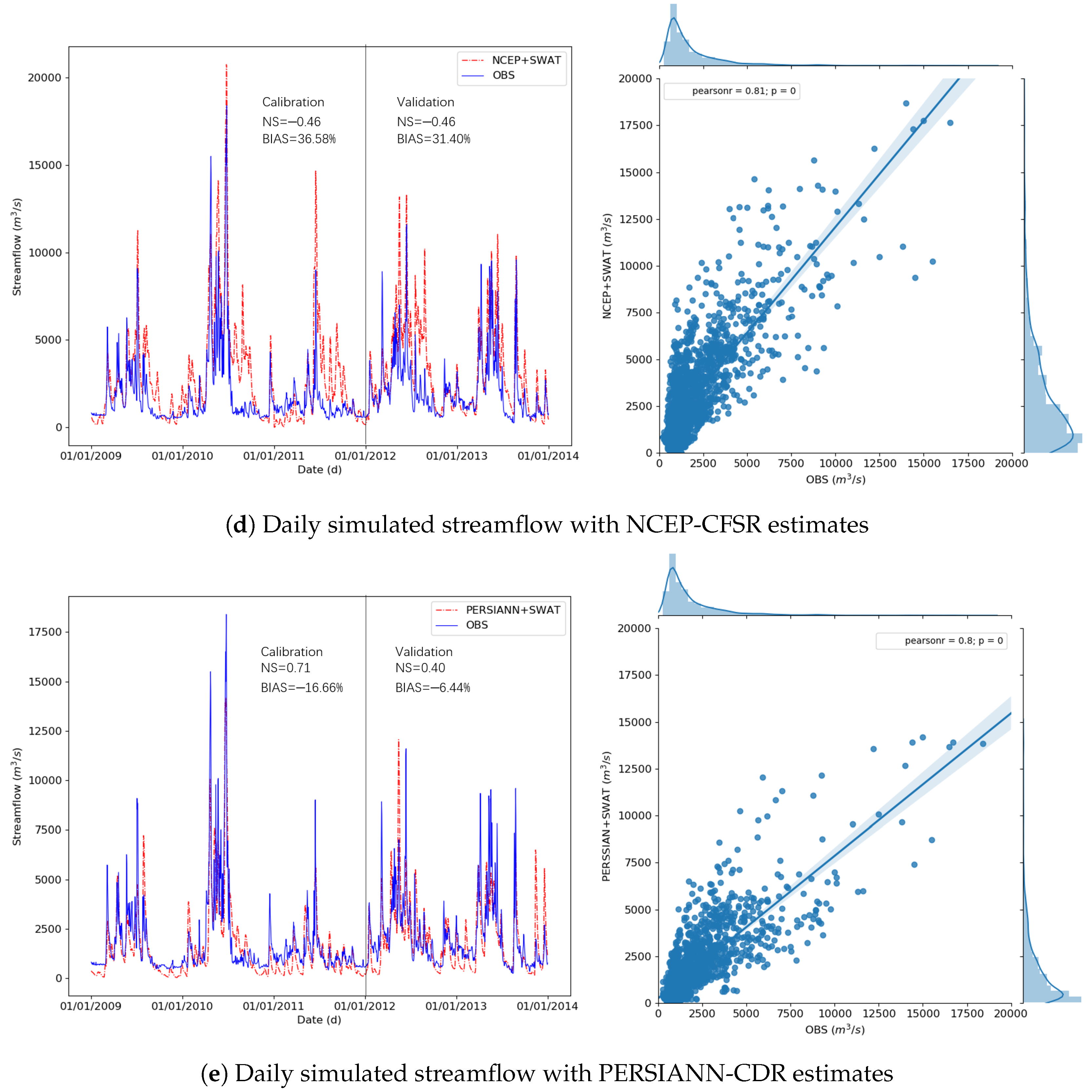
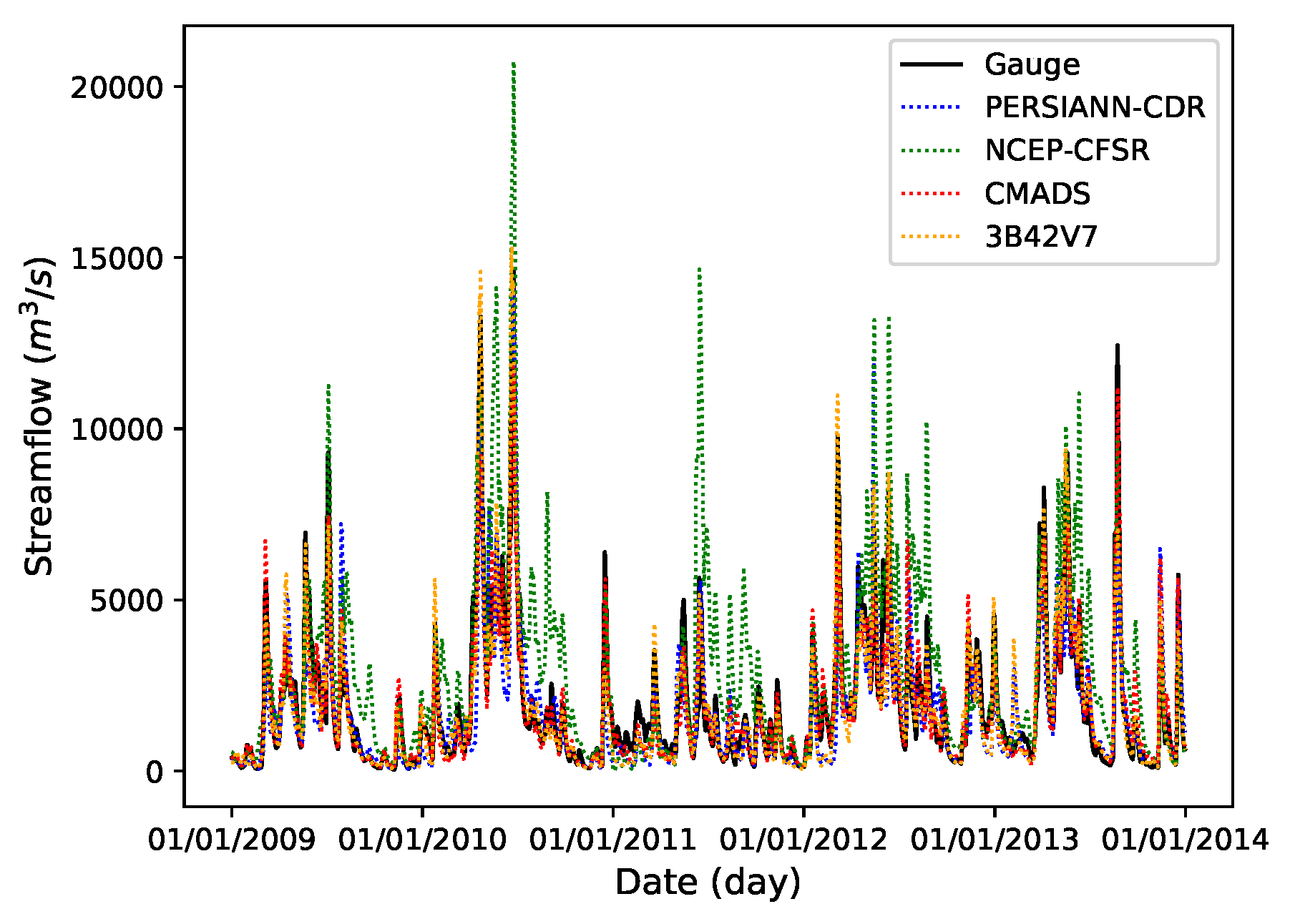
3.2.2. Comparison at Daily Scale
3.3. Analysis of Anomalies in Hydrological Simulation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Faurès, J.M.; Goodrich, D.C.; Woolhiser, D.A.; Sorooshian, S. Impact of small-scale spatial rainfall variability on runoff modeling. J. Hydrol. 1995, 173, 309–326. [Google Scholar] [CrossRef]
- Etchevers, P.; Durand, Y.; Habets, F.; Martin, E.; Noilhan, J. Impact of spatial resolution on the hydrological simulation of the Durance high-Alpine catchment, France. Ann. Glaciol. 2001, 32, 87–92. [Google Scholar] [CrossRef]
- Himanshu, S.K.; Pandey, A.; Yadav, B. Assessing the applicability of TMPA-3B42V7 precipitation dataset in wavelet-support vector machine approach for suspended sediment load prediction. J. Hydrol. 2017, 550, 103–117. [Google Scholar] [CrossRef]
- Michelson, D.B. Systematic correction of precipitation gauge observations using analysed metrological variables. J. Hydrol. 2004, 290, 161–177. [Google Scholar] [CrossRef]
- Meng, J.; Li, L.; Hao, Z.; Wang, J.; Shao, Q. Suitability of TRMM satellite rainfall in driving a distributed hydrological model in the source region of Yellow River. J. Hydrol. 2014, 509, 320–332. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.L.; Gao, X.; Gupta, H.V.; Imam, B.; Dan, B. Evaluation of PERSIANN System Satellite-Based Estimates of Tropical Rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method That Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2003, 5, 287–296. [Google Scholar] [CrossRef]
- Kidd, C.; Huffman, G. Global precipitation measurement. Meteorol. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of near-real-time precipitation estimates from satellite observations and numerical models. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales; Springer: Dordrecht, The Netherlands, 2010; pp. 3–22. [Google Scholar]
- Villarini, G.; Krajewski, W.F.; Smith, J.A. New paradigm for statistical validation of satellite precipitation estimates: Application to a large sample of the TMPA 0.25 3-hourly estimates over Oklahoma. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Nijssen, B.; Lettenmaier, D.P. Effect of precipitation sampling error on simulated hydrological fluxes and states: Anticipating the Global Precipitation Measurement satellites. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Conti, F.L.; Hsu, K.L.; Noto, L.V.; Sorooshian, S. Evaluation and comparison of satellite precipitation estimates with reference to a local area in the Mediterranean Sea. Atmos. Res. 2014, 138, 189–204. [Google Scholar] [CrossRef]
- Seyyedi, H.; Anagnostou, E.N.; Beighley, E.; Mccollum, J. Hydrologic evaluation of satellite and reanalysis precipitation datasets over a mid-latitude basin. Atmos. Res. 2015, 164–165, 37–48. [Google Scholar] [CrossRef]
- Li, C.; Tang, G.; Hong, Y. Cross-evaluation of ground-based, multi-satellite and reanalysis precipitation products: Applicability of the Triple Collocation method across Mainland China. J. Hydrol. 2018, 562, 71–83. [Google Scholar] [CrossRef]
- Inoue, T.; Matsumoto, J. A Comparison of Summer Sea Level Pressure over East Eurasia between NCEP-NCAR Reanalysis and ERA-40 for the Period 1960-99. J. Meteorol. Soc. Jpn. Ser. II 2004, 82, 951–958. [Google Scholar] [CrossRef]
- Marshall, G.J. Trends in Antarctic Geopotential Height and Temperature: A Comparison between Radiosonde and NCEP-NCAR Reanalysis Data. J. Clim. 2002, 15, 659–674. [Google Scholar] [CrossRef]
- Hodges, K.I.; Lee, R.W.; Bengtsson, L. A Comparison of Extratropical Cyclones in Recent Reanalyses ERA-Interim, NASA MERRA, NCEP CFSR, and JRA-25. J. Clim. 2011, 24, 4888–4906. [Google Scholar] [CrossRef]
- Ebisuzaki, W.; Zhang, L. Assessing the performance of the CFSR by an ensemble of analyses. Clim. Dyn. 2011, 37, 2541–2550. [Google Scholar] [CrossRef]
- Dee, D.; Uppala, S.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Smith, C.A.; Compo, G.P.; Hooper, D.K. Web-Based Reanalysis Intercomparison Tools (WRIT) for analysis and comparison of reanalyses and other datasets. Bull. Am. Meteorol. Soc. 2015, 95, 1671–1678. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H.; Meng, X.; Wang, H. Significance of the China Meteorological Assimilation Driving Datasets for the SWAT Model (CMADS) of East Asia. Water 2017, 9, 765. [Google Scholar] [CrossRef]
- Zhao, F.; Wu, Y.; Qiu, L.; Sun, Y.; Sun, L.; Li, Q.; Niu, J.; Wang, G. Parameter Uncertainty Analysis of the SWAT Model in a Mountain-Loess Transitional Watershed on the Chinese Loess Plateau. Water 2018, 10, 690. [Google Scholar] [CrossRef]
- Thom, V.; Li, L.; Jun, K.S. Evaluation of Multi-Satellite Precipitation Products for Streamflow Simulations: A Case Study for the Han River Basin in the Korean Peninsula, East Asia. Water 2018, 10, 642. [Google Scholar]
- Meng, X.; Long, A.; Wu, Y.; Yin, G.; Wang, H.; Ji, X. Simulation and spatiotemporal pattern of air temperature and precipitation in Eastern Central Asia using RegCM. Sci. Rep. 2018, 8, 3639. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.Y.; Yu, D.L.; Liu, Z.H. Energy balance-based SWAT model to simulate the mountain snowmelt and runoff—Taking the application in Juntanghu watershed (China) as an example. J. Mt. Sci. 2015, 12, 368–381. [Google Scholar] [CrossRef]
- Meng, X.; Sun, Z.; Zhao, H.; Ji, X.; Wang, H.; Xue, L.; Wu, H.; Zhu, Y. Spring Flood Forecasting Based on the WRF-TSRM Mode. Tehnički Vjesnik 2018, 25, 27–37. [Google Scholar]
- Meng, X.; Wang, H.; Lei, X.; Cai, S.; Wu, H.; Ji, X.; Wang, J. Hydrological modeling in the Manas River Basin using soil and water assessment tool driven by CMADS. Tehnicki Vjesnik 2017, 24, 525–534. [Google Scholar]
- Meng, X.; Wang, H.; Wu, Y.; Long, A.; Wang, J.; Shi, C.; Ji, X. Investigating spatiotemporal changes of the land-surface processes in Xinjiang using high-resolution CLM3.5 and CLDAS: Soil temperature. Sci. Rep. 2017, 7, 13286. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Shanguan, D.; Liu, S.; Ding, Y. Evaluation and Hydrological Simulation of CMADS and CFSR Reanalysis Datasets in the Qinghai-Tibet Plateau. Water 2018, 10, 513. [Google Scholar] [CrossRef]
- Pombo, S.; de Oliveira, R.P. Evaluation of extreme precipitation estimates from TRMM in Angola. J. Hydrol. 2015, 523, 663–679. [Google Scholar] [CrossRef]
- Li, D.; Christakos, G.; Ding, X.; Wu, J. Adequacy of TRMM satellite rainfall data in driving the SWAT modeling of Tiaoxi catchment (Taihu lake basin, China). J. Hydrol. 2018, 556, 1139–1152. [Google Scholar] [CrossRef]
- Katiraie-Boroujerdy, P.S.; Asanjan, A.A.; Hsu, K.; Sorooshian, S. Intercomparison of PERSIANN-CDR and TRMM-3B42V7 precipitation estimates at monthly and daily time scales. Atmos. Res. 2017, 193, 36–49. [Google Scholar] [CrossRef]
- Cabrera, J.; Yupanqui, R.T.; Rau, P. Validation of TRMM Daily Precipitation Data for Extreme Events Analysis. The Case of Piura Watershed in Peru. Procedia Eng. 2016, 154, 154–157. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2014, 96, 197–210. [Google Scholar] [CrossRef]
- Hsu, K.L.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks. J. Appl. Meteorol. 2003, 36, 1176–1190. [Google Scholar] [CrossRef]
- Tan, M.L.; Santo, H. Comparison of GPM IMERG, TMPA 3B42 and PERSIANN-CDR satellite precipitation products over Malaysia. Atmos. Res. 2018, 202, 63–76. [Google Scholar] [CrossRef]
- Yang, X.; Yong, B.; Hong, Y.; Chen, S.; Zhang, X. Error analysis of multi-satellite precipitation estimates with an independent raingauge observation network over a medium-sized humid basin. Int. Assoc. Sci. Hydrol. Bull. 2015, 61, 1813–1830. [Google Scholar] [CrossRef]
- Tan, M.L.; Ibrahim, A.L.; Duan, Z.; Cracknell, A.P.; Chaplot, V. Evaluation of Six High-Resolution Satellite and Ground-Based Precipitation Products over Malaysia. Remote Sens. 2015, 7, 1504–1528. [Google Scholar] [CrossRef]
- Zhu, Q.; Xuan, W.; Liu, L.; Xu, Y. Evaluation and hydrological application of precipitation estimates derived from PERSIANN-CDR, TRMM 3B42V7, and NCEP-CFSR over humid regions in China. Hydrol. Process. 2016, 30, 3061–3083. [Google Scholar] [CrossRef]
- Li, X.; Wan, W.; Yu, Y.; Ren, Z. Yearly variations of the stratospheric tides seen in the CFSR reanalysis data. Adv. Space Res. 2015, 56, 1822–1832. [Google Scholar] [CrossRef]
- Tomy, T.; Sumam, K. Determining the Adequacy of CFSR Data for Rainfall-Runoff Modeling Using SWAT. Procedia Technol. 2016, 24, 309–316. [Google Scholar] [CrossRef]
- Blacutt, L.A.; Herdies, D.L.; de Gonçalves, L.G.G.; Vila, D.A.; Andrade, M. Precipitation comparison for the CFSR, MERRA, TRMM3B42 and Combined Scheme datasets in Bolivia. Atmos. Res. 2015, 163, 117–131. [Google Scholar] [CrossRef]
- Wang, Y.J.; Meng, X.Y.; Liu, Z.H.; Ji, X.N. Snowmelt Runoff Analysis under Generated Climate Change Scenarios for the Juntanghu River Basin, in Xinjiang, China. Water Sci. Technol. 2016, 7, 41–54. [Google Scholar]
- Sorooshian, S.; Aghakouchak, A.; Arkin, P.; Eylander, J.; Foufoulageorgiou, E.; Harmon, R.; Hendrickx, J.M.H.; Imam, B.; Kuligowski, R.; Skahill, B. Advanced Concepts on Remote Sensing of Precipitation at Multiple Scales. Bull. Am. Meteorol. Soc. 2011, 92, 1353–1357. [Google Scholar] [CrossRef]
- Kenawy, A.M.E.; Lopez-Moreno, J.I.; McCabe, M.F.; Vicente-Serrano, S.M. Evaluation of the TMPA-3B42 precipitation product using a high-density rain gauge network over complex terrain in northeastern Iberia. Glob. Planet. Chang. 2015, 133, 188–200. [Google Scholar] [CrossRef]
- Omranian, E.; Sharif, H.O. Evaluation of the Global Precipitation Measurement (GPM) Satellite Rainfall Products over the Lower Colorado River Basin, Texas. J. Am. Water Resour. Assoc. 2018, 54, 882–898. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.L.; Wu, X.R.; Wang, J.D.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D. The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1057. [Google Scholar] [CrossRef]
- Nkiaka, E.; Nawaz, N.R.; Lovett, J.C. Evaluating global reanalysis precipitation datasets with rain gauge measurements in the Sudano-Sahel region: Case study of the Logone catchment, Lake Chad Basin. Meteorol. Appl. 2017, 24, 9–18. [Google Scholar] [CrossRef]
- Caracciolo, D.; Francipane, A.; Viola, F.; Noto, L.V.; Deidda, R. Performances of GPM satellite precipitation over the two major Mediterranean islands. Atmos. Res. 2018, 213, 309–322. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Diks, C.G.H.; Clark, M.P. Ensemble Bayesian model averaging using Markov Chain Monte Carlo sampling. Environ. Fluid Mech. 2008, 8, 579–595. [Google Scholar] [CrossRef]
- Diks, C.G.H.; Vrugt, J.A. Comparison of point forecast accuracy of model averaging methods in hydrologic applications. Stoch. Environ. Res. Risk Assess. 2010, 24, 809–820. [Google Scholar] [CrossRef]
- Artan, G.; Gadain, H.; Smith, J.L.; Asante, K.; Bandaragoda, C.J.; Verdin, J.P. Adequacy of satellite derived rainfall data for stream flow modeling. Nat. Hazards 2007, 43, 167–185. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M.; Ghebremichael, L.T.; Bayissa, Y.A. Evaluation of High-Resolution Satellite Rainfall Products through Streamflow Simulation in a Hydrological Modeling of a Small Mountainous Watershed in Ethiopia. J. Hydrometeorol. 2012, 13, 338–350. [Google Scholar] [CrossRef]
- Terink, W.; Leijnse, H.; van den Eertwegh, G.; Uijlenhoet, R. Spatial resolutions in areal rainfall estimation and their impact on hydrological simulations of a lowland catchment. J. Hydrol. 2018, 563, 319–335. [Google Scholar] [CrossRef]
- Afshari, S.; Tavakoly, A.A.; Rajib, A.; Zheng, X.; Follum, M.L.; Omranian, E.; Fekete, B.M. Comparison of new generation low-complexity flood inundation mapping tools with a hydrodynamic model. J. Hydrol. 2018, 556, 539–556. [Google Scholar] [CrossRef]
| Datasets | Spatial Resolution | Temporal Resolution | Available Period | Coverage | Source of Data |
|---|---|---|---|---|---|
| Gauge | Point | Daily | 1987–2013 | Xiang River Basin | China Meteorological Administration |
| CMADS | Daily | 2008–2016 | East Asia | www.cmads.org | |
| 3B42V7 | Daily | 1998–present | S– N | Goddard Space Flight Centre | |
| NCEP-CFSR | 38 km | Daily | 1979–present | Global | National Centers for Environment precipitation |
| PERSIANN-CDR | Daily | 1983–present | S– N | University of California, Irvine, CA, USA |
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS |
| CMADS | 0.96 | 49.57 | −33.29 | −34.24 |
| PERSIANN-CDR | 0.79 | 72.27 | −27.75 | −27.01 |
| 3B42V7 | 0.93 | 40.14 | −7.27 | −5.90 |
| NCEP-CFSR | 0.61 | 159.76 | 85.86 | 39.68 |
| (a) Station Dx | ||||
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS |
| CMADS | 0.97 | 23.84 | −13.21 | −13.69 |
| PERSIANN-CDR | 0.67 | 66.34 | −2.74 | −2.56 |
| 3B42V7 | 0.92 | 33.24 | 3.46 | 3.05 |
| NCEP-CFSR | 0.73 | 101.79 | 64.97 | 37.21 |
| (b) Station Chzh | ||||
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS |
| CMADS | 0.97 | 27.04 | −14.85 | −15.54 |
| PERSIANN-CDR | 0.76 | 62.41 | −7.48 | −7.26 |
| 3B42V7 | 0.94 | 29.41 | 0.44 | 0.40 |
| NCEP-CFSR | 0.66 | 98.07 | 41.59 | 27.35 |
| (c) Station Yzh | ||||
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS |
| CMADS | 0.55 | 81.06 | −17.80 | −20.09 |
| PERSIANN-CDR | 0.72 | 62.25 | −7.20 | −7.26 |
| 3B42V7 | 0.87 | 38.98 | −5.59 | −5.55 |
| NCEP-CFSR | 0.67 | 142.98 | 98.02 | 47.95 |
| (d) Station Chn | ||||
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS |
| CMADS | 0.89 | 41.28 | −28.12 | −41.37 |
| PERSIANN-CDR | 0.65 | 63.98 | 1.16 | 1.19 |
| 3B42V7 | 0.86 | 36.86 | −2.01 | −2.14 |
| NCEP-CFSR | 0.62 | 146.09 | 87.04 | 47.53 |
| (e) Station Hy | ||||
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS |
| CMADS | 0.84 | 82.35 | −63.46 | −73.29 |
| PERSIANN-CDR | 0.73 | 84.28 | −51.63 | −52.46 |
| 3B42V7 | 0.92 | 52.79 | −37.18 | −32.94 |
| NCEP-CFSR | 0.77 | 105.36 | 49.44 | 24.78 |
| (f) Station Ny | ||||
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS |
| CMADS | 0.93 | 31.18 | −5.11 | −5.00 |
| PERSIANN-CDR | 0.79 | 55.38 | −9.27 | −9.47 |
| 3B42V7 | 0.88 | 40.13 | −0.33 | −0.31 |
| NCEP-CFSR | 0.74 | 102.18 | 57.05 | 34.74 |
| (g) Station Shf | ||||
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS |
| CMADS | 0.83 | 55.42 | −24.80 | −25.83 |
| PERSIANN-CDR | 0.76 | 60.80 | −18.90 | −18.55 |
| 3B42V7 | 0.90 | 37.88 | −5.08 | −4.39 |
| NCEP-CFSR | 0.84 | 72.31 | 36.28 | 23.10 |
| (h) Station Zhzh | ||||
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS |
| CMADS | 0.98 | 31.86 | −25.41 | −28.67 |
| PERSIANN-CDR | 0.93 | 30.07 | −9.14 | −8.71 |
| 3B42V7 | 0.98 | 16.78 | −0.37 | −0.33 |
| NCEP-CFSR | 0.81 | 93.90 | 61.17 | 34.91 |
| (i) Areal average |
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS (%) | POD | FAR | CSI |
| CMADS | 0.59 | 10.13 | −1.09 | −34.24 | 0.72 | 0.26 | 0.58 |
| PERSIANN-CDR | 0.36 | 12.78 | −0.91 | −27.01 | 0.47 | 0.48 | 0.33 |
| 3B42V7 | 0.51 | 11.77 | −0.24 | −5.90 | 0.62 | 0.49 | 0.39 |
| NCEP-CFSR | 0.55 | 12.76 | 2.82 | 39.68 | 0.47 | 0.07 | 0.45 |
| (a) Station Dx | |||||||
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS (%) | POD | FAR | CSI |
| CMADS | 0.60 | 7.83 | −0.43 | −13.69 | 0.74 | 0.25 | 0.59 |
| PERSIANN-CDR | 0.32 | 11.15 | −0.09 | −2.56 | 0.51 | 0.45 | 0.36 |
| 3B42V7 | 0.50 | 10.25 | 0.11 | 3.05 | 0.65 | 0.51 | 0.39 |
| NCEP-CFSR | 0.58 | 9.98 | 2.13 | 37.21 | 0.52 | 0.09 | 0.50 |
| (b) Station Chzh | |||||||
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS (%) | POD | FAR | CSI |
| CMADS | 0.62 | 7.94 | −0.49 | −15.54 | 0.69 | 0.27 | 0.55 |
| PERSIANN-CDR | 0.39 | 10.97 | −0.25 | −7.26 | 0.49 | 0.45 | 0.35 |
| 3B42V7 | 0.50 | 10.33 | 0.01 | 0.40 | 0.62 | 0.52 | 0.37 |
| NCEP-CFSR | 0.55 | 9.56 | 1.37 | 27.35 | 0.52 | 0.10 | 0.49 |
| (c) Station Yzh | |||||||
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS (%) | POD | FAR | CSI |
| CMADS | 0.55 | 8.13 | −1.20 | −53.50 | 0.69 | 0.34 | 0.51 |
| PERSIANN-CDR | 0.34 | 10.97 | −0.24 | −7.26 | 0.49 | 0.46 | 0.35 |
| 3B42V7 | 0.44 | 10.43 | −0.18 | −5.55 | 0.66 | 0.55 | 0.37 |
| NCEP-CFSR | 0.56 | 11.24 | 3.22 | 47.95 | 0.51 | 0.09 | 0.48 |
| (d) Station Chn | |||||||
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS (%) | POD | FAR | CSI |
| CMADS | 0.55 | 7.32 | −0.92 | −41.37 | 0.69 | 0.33 | 0.51 |
| PERSIANN-CDR | 0.31 | 10.54 | 0.04 | 1.19 | 0.46 | 0.48 | 0.32 |
| 3B42V7 | 0.42 | 9.98 | −0.07 | −2.14 | 0.65 | 0.54 | 0.37 |
| NCEP-CFSR | 0.55 | 10.32 | 2.86 | 47.53 | 0.49 | 0.11 | 0.46 |
| (e) Station Hy | |||||||
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS (%) | POD | FAR | CSI |
| CMADS | 0.58 | 10.50 | −2.08 | −73.29 | 0.71 | 0.36 | 0.51 |
| PERSIANN-CDR | 0.28 | 13.63 | −1.70 | −52.46 | 0.54 | 0.47 | 0.36 |
| 3B42V7 | 0.39 | 13.29 | −1.22 | −32.94 | 0.70 | 0.55 | 0.38 |
| NCEP-CFSR | 0.60 | 11.33 | 1.62 | 24.78 | 0.58 | 0.12 | 0.54 |
| (f) Station Ny | |||||||
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS (%) | POD | FAR | CSI |
| CMADS | 0.59 | 9.12 | −0.17 | −5.00 | 0.67 | 0.30 | 0.53 |
| PERSIANN-CDR | 0.31 | 11.82 | −0.30 | −9.47 | 0.48 | 0.44 | 0.35 |
| 3B42V7 | 0.43 | 11.29 | −0.01 | −0.31 | 0.65 | 0.50 | 0.39 |
| NCEP-CFSR | 0.62 | 9.86 | 1.87 | 34.74 | 0.51 | 0.11 | 0.48 |
| (g) Station Shf | |||||||
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS (%) | POD | FAR | CSI |
| CMADS | 0.65 | 9.33 | −0.81 | −25.83 | 0.69 | 0.26 | 0.56 |
| PERSIANN-CDR | 0.33 | 12.73 | −0.62 | −18.55 | 0.46 | 0.42 | 0.34 |
| 3B42V7 | 0.48 | 12.32 | −0.17 | −4.39 | 0.63 | 0.51 | 0.38 |
| NCEP-CFSR | 0.66 | 9.95 | 1.19 | 23.10 | 0.56 | 0.09 | 0.53 |
| (h) Station Zhzh | |||||||
| Datasets | CC | RMSE (mm) | ME (mm) | BIAS (%) | POD | FAR | CSI |
| CMADS | 0.70 | 5.77 | −0.83 | −28.67 | 0.77 | 0.21 | 0.64 |
| PERSIANN-CDR | 0.49 | 7.85 | −0.30 | −8.71 | 0.62 | 0.36 | 0.46 |
| 3B42V7 | 0.60 | 7.35 | −0.01 | −0.33 | 0.71 | 0.31 | 0.54 |
| NCEP-CFSR | 0.78 | 6.08 | 2.01 | 34.91 | 0.62 | 0.04 | 0.60 |
| (textbfi) Areal average | |||||||
| Datasets | NS in Calibration | NS in Validation | BIAS in Calibration (%) | BIAS in Validation (%) |
|---|---|---|---|---|
| Gauge | 0.95 | 0.94 | −2.06 | −1.36 |
| CMADS | 0.92 | 0.80 | −12.06 | 2.17 |
| 3B42V7 | 0.94 | 0.88 | −7.20 | 3.69 |
| NCEP-CFSR | −0.12 | −0.12 | 36.49 | 31.31 |
| PERSIANN-CDR | 0.89 | 0.63 | −8.91 | 1.66 |
| Datasets | NS in Calibration | NS in Validation | BIAS in Calibration (%) | BIAS in Validation (%) |
|---|---|---|---|---|
| Gauge | 0.86 | 0.72 | −1.58 | 3.07 |
| CMADS | 0.83 | 0.70 | −12.06 | 2.20 |
| 3B42V7 | 0.83 | 0.73 | −10.84 | −0.17 |
| NCEP-CFSR | −0.46 | −0.46 | 36.58 | 31.40 |
| PERSIANN-CDR | 0.71 | 0.40 | −16.66 | −6.44 |
| 3B42V7 | CMADS | |
|---|---|---|
| Weights | 0.47 | 0.53 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Zhu, Q.; Yang, Z.; Wang, H. Evaluation and Hydrological Application of CMADS against TRMM 3B42V7, PERSIANN-CDR, NCEP-CFSR, and Gauge-Based Datasets in Xiang River Basin of China. Water 2018, 10, 1225. https://doi.org/10.3390/w10091225
Gao X, Zhu Q, Yang Z, Wang H. Evaluation and Hydrological Application of CMADS against TRMM 3B42V7, PERSIANN-CDR, NCEP-CFSR, and Gauge-Based Datasets in Xiang River Basin of China. Water. 2018; 10(9):1225. https://doi.org/10.3390/w10091225
Chicago/Turabian StyleGao, Xichao, Qian Zhu, Zhiyong Yang, and Hao Wang. 2018. "Evaluation and Hydrological Application of CMADS against TRMM 3B42V7, PERSIANN-CDR, NCEP-CFSR, and Gauge-Based Datasets in Xiang River Basin of China" Water 10, no. 9: 1225. https://doi.org/10.3390/w10091225
APA StyleGao, X., Zhu, Q., Yang, Z., & Wang, H. (2018). Evaluation and Hydrological Application of CMADS against TRMM 3B42V7, PERSIANN-CDR, NCEP-CFSR, and Gauge-Based Datasets in Xiang River Basin of China. Water, 10(9), 1225. https://doi.org/10.3390/w10091225





