The Effect of Ca and Mg Ions on the Filtration Profile of Sodium Alginate Solution in a Polyethersulfone-2-(methacryloyloxy) Ethyl Phosphorylchloline Membrane
Abstract
1. Introduction
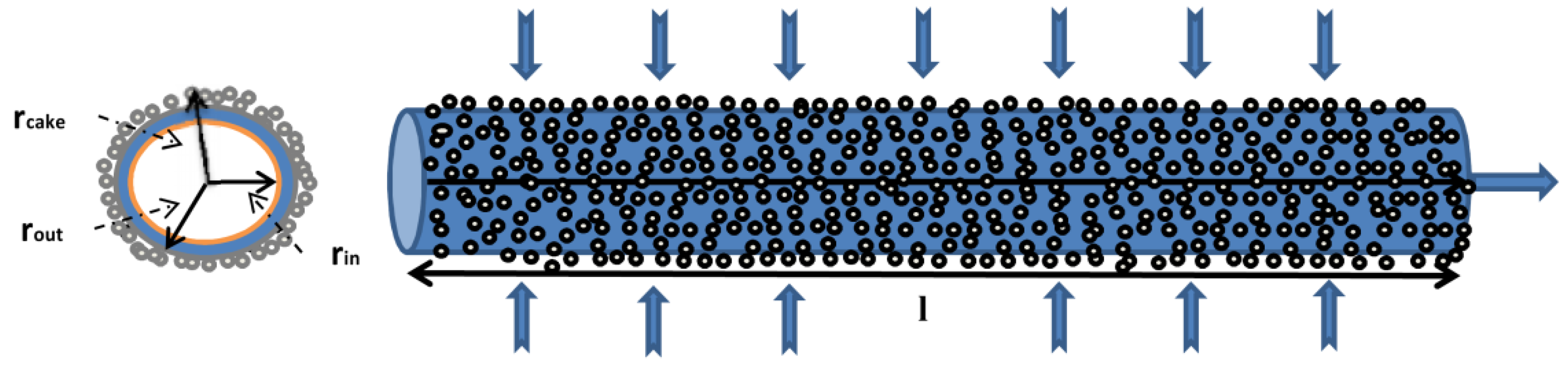
2. Theory
3. Method
3.1. Material
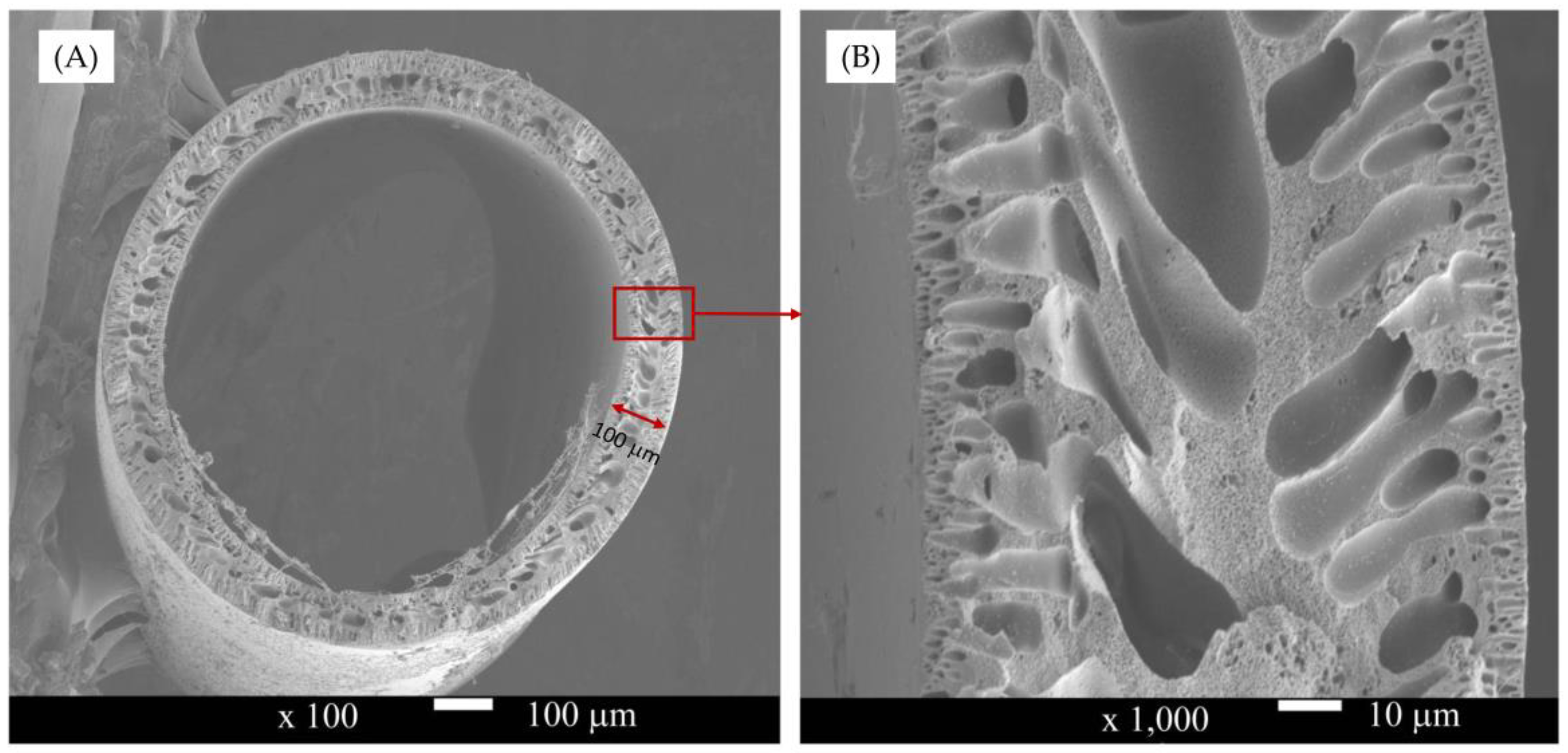
3.2. Membrane Preparation and Characterization
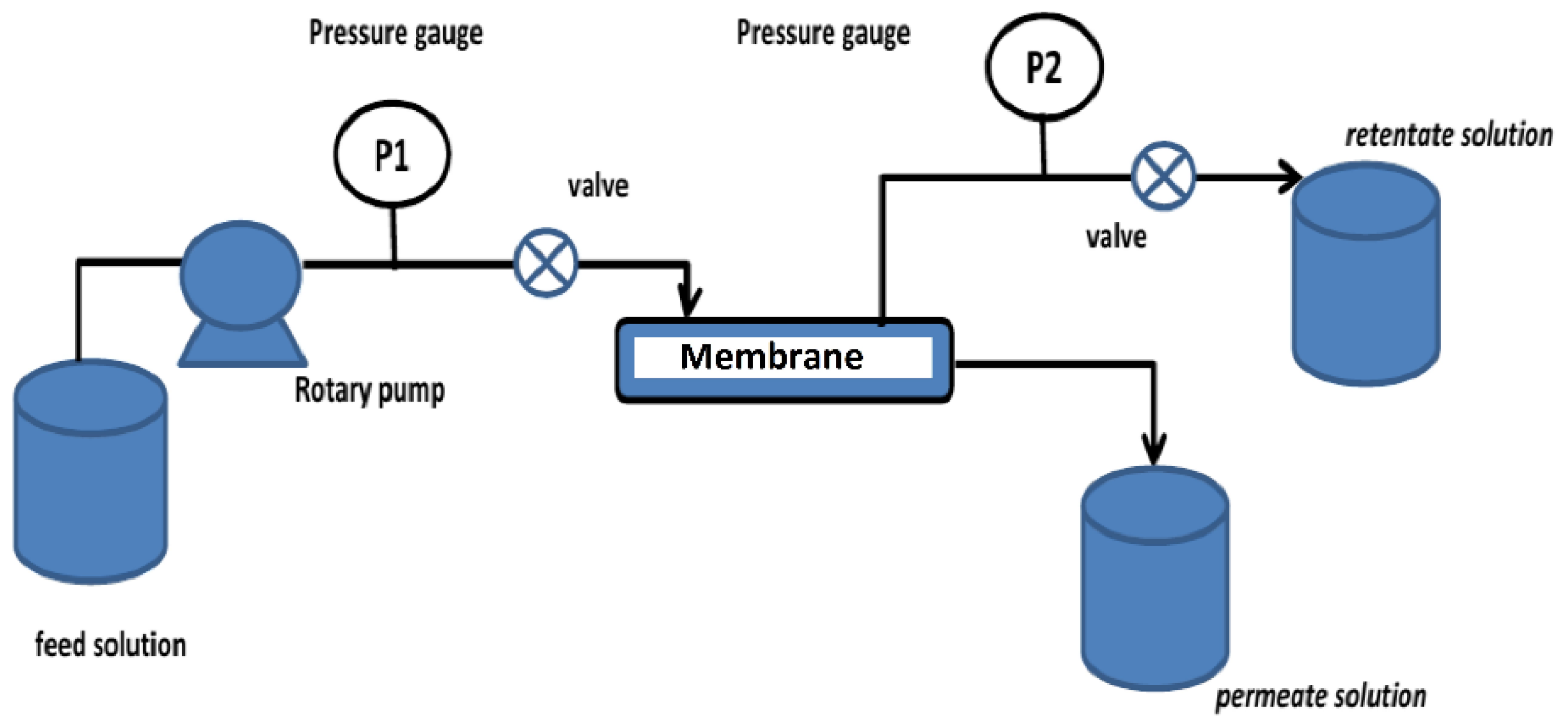
3.3. Ultrafiltration Process
3.4. Cake Layer Model
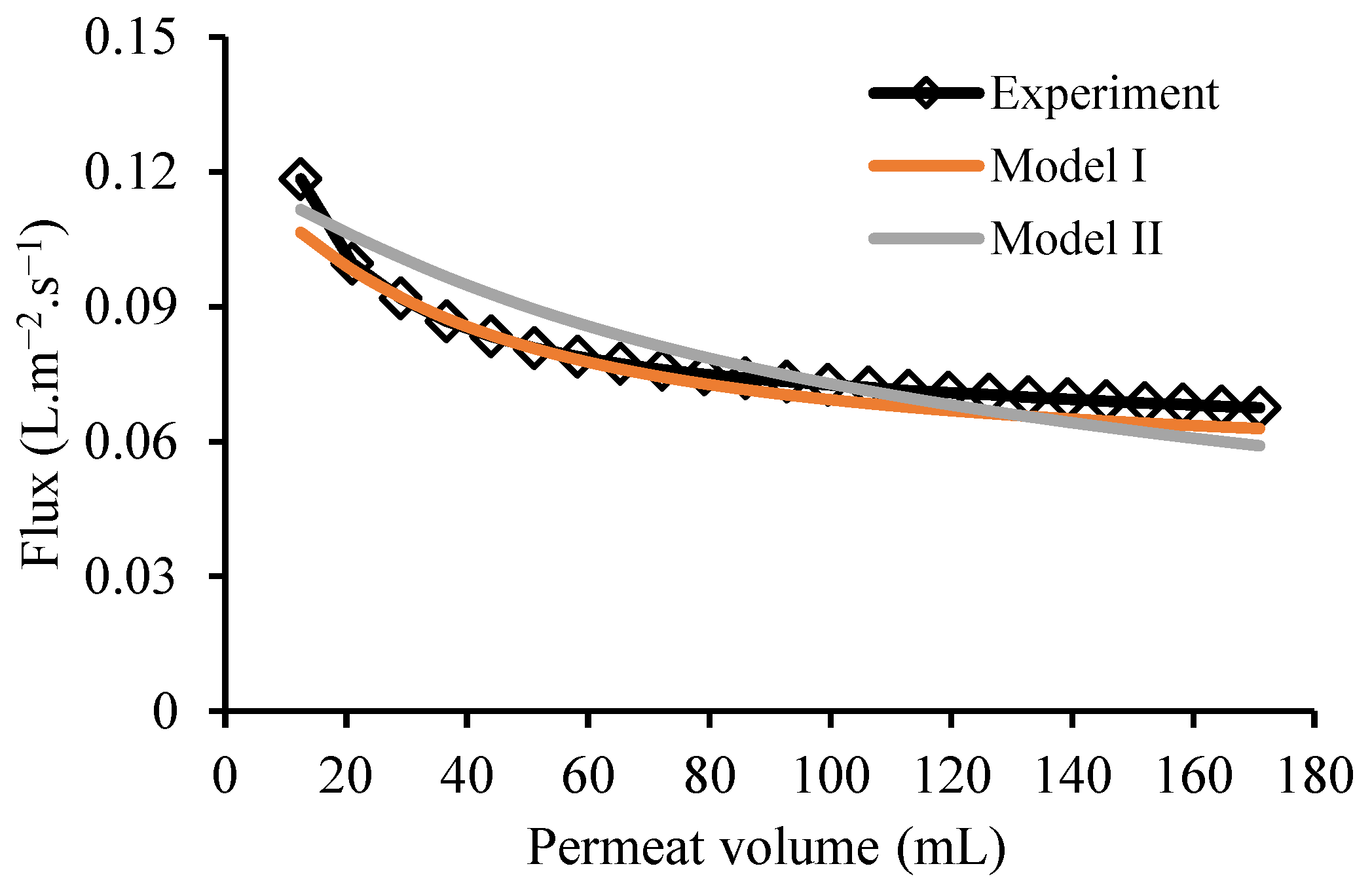
3.5. Model Validation
4. Results and Discussion
4.1. Membrane Characteristic
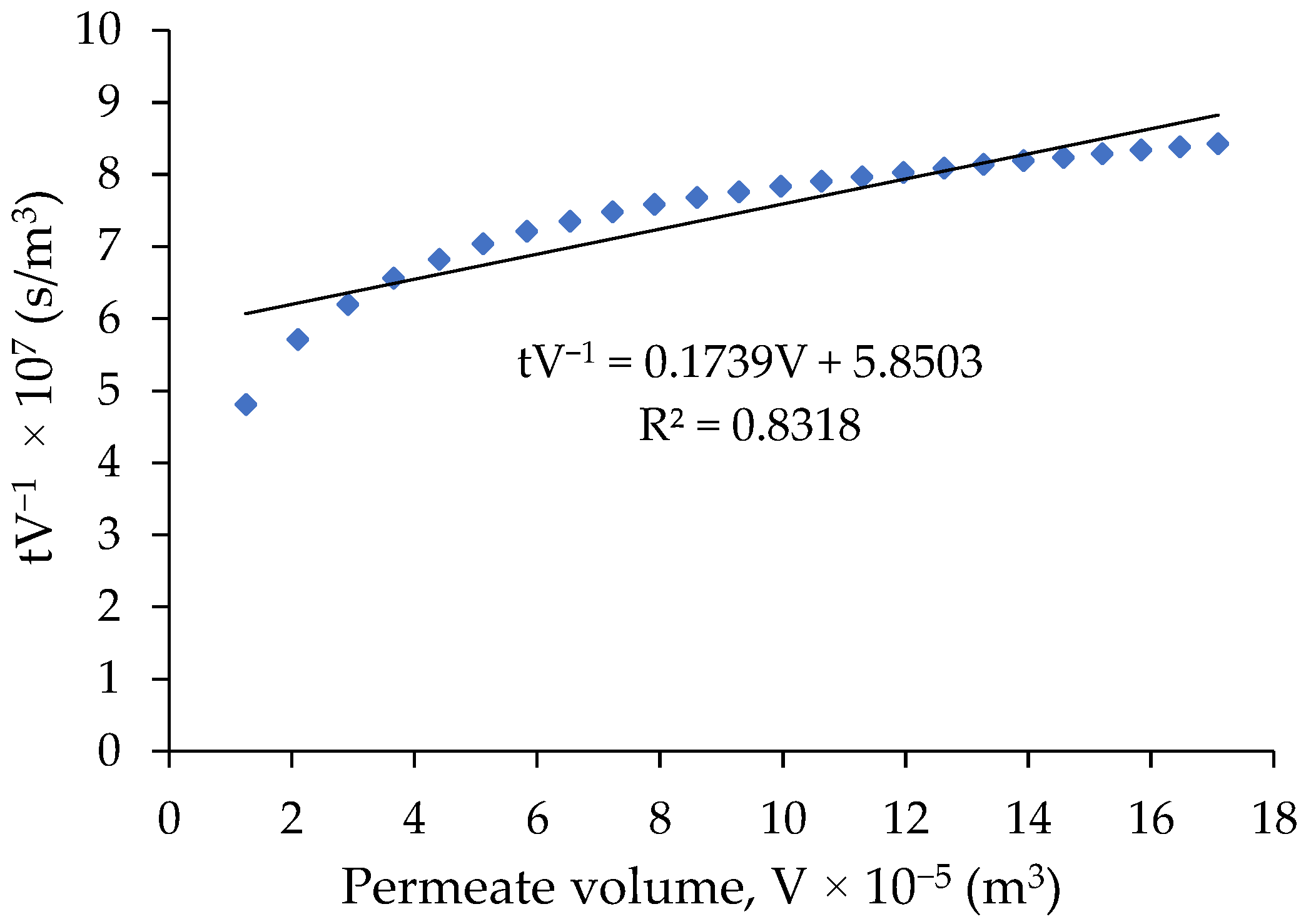
4.2. Pure Water Filtration
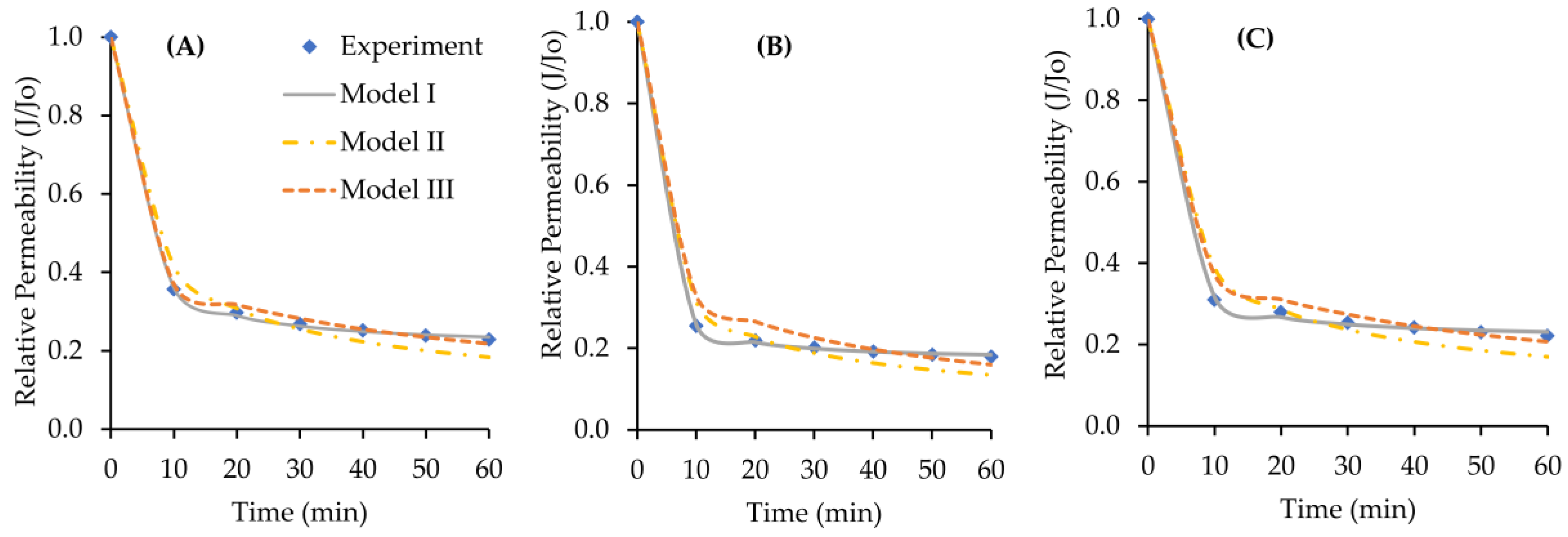
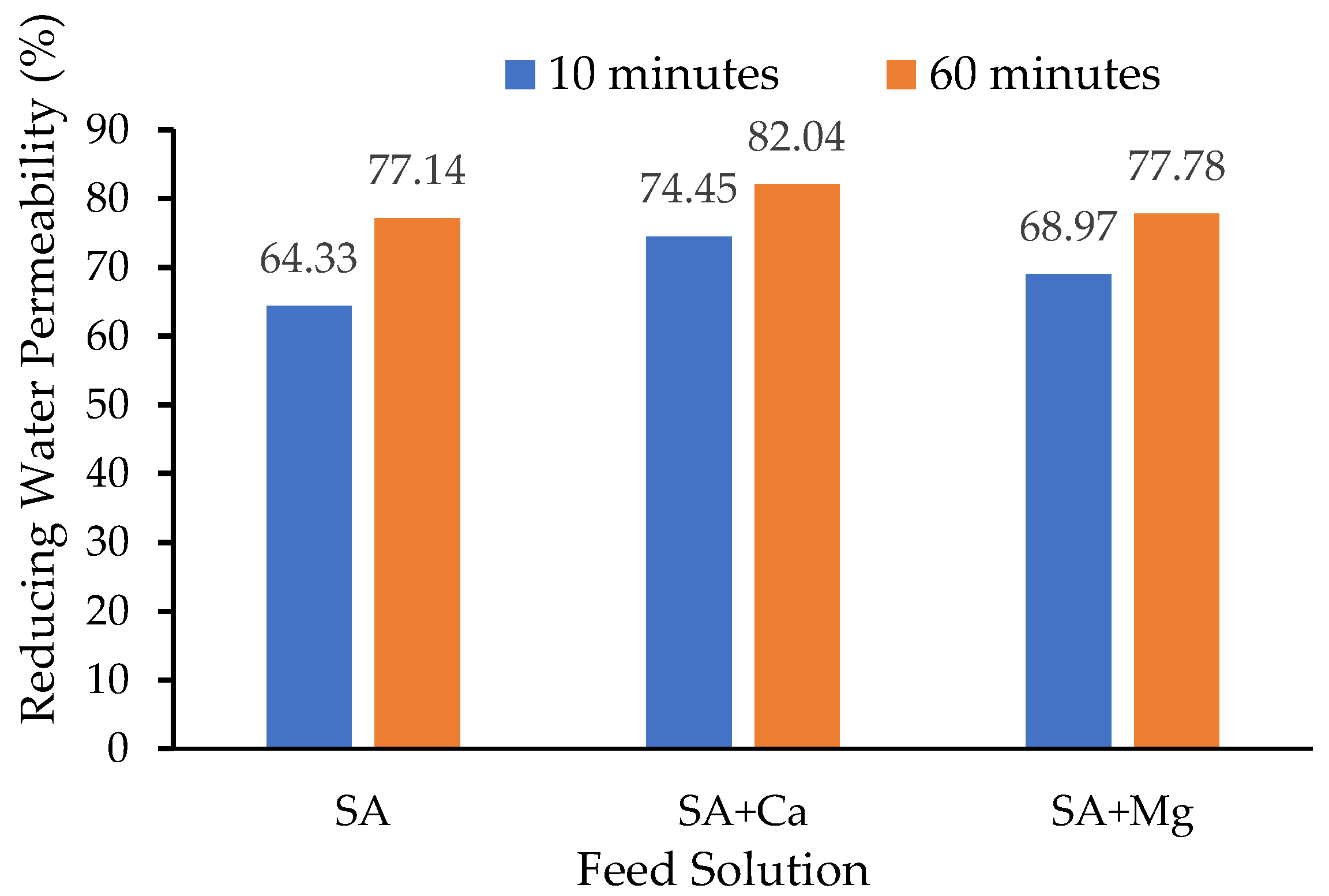
4.3. Filtration of Sodium Alginate Solution
4.4. Membrane Resistance (Rm)
4.5. Cake Resistance Model
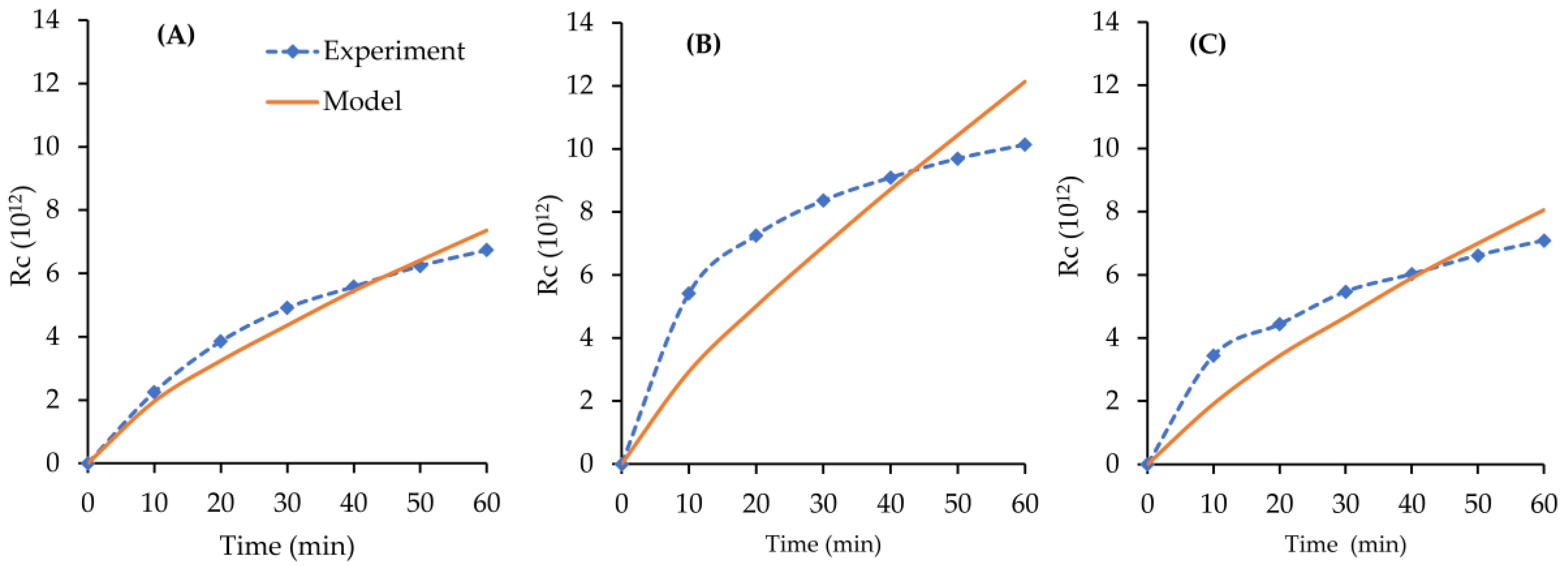
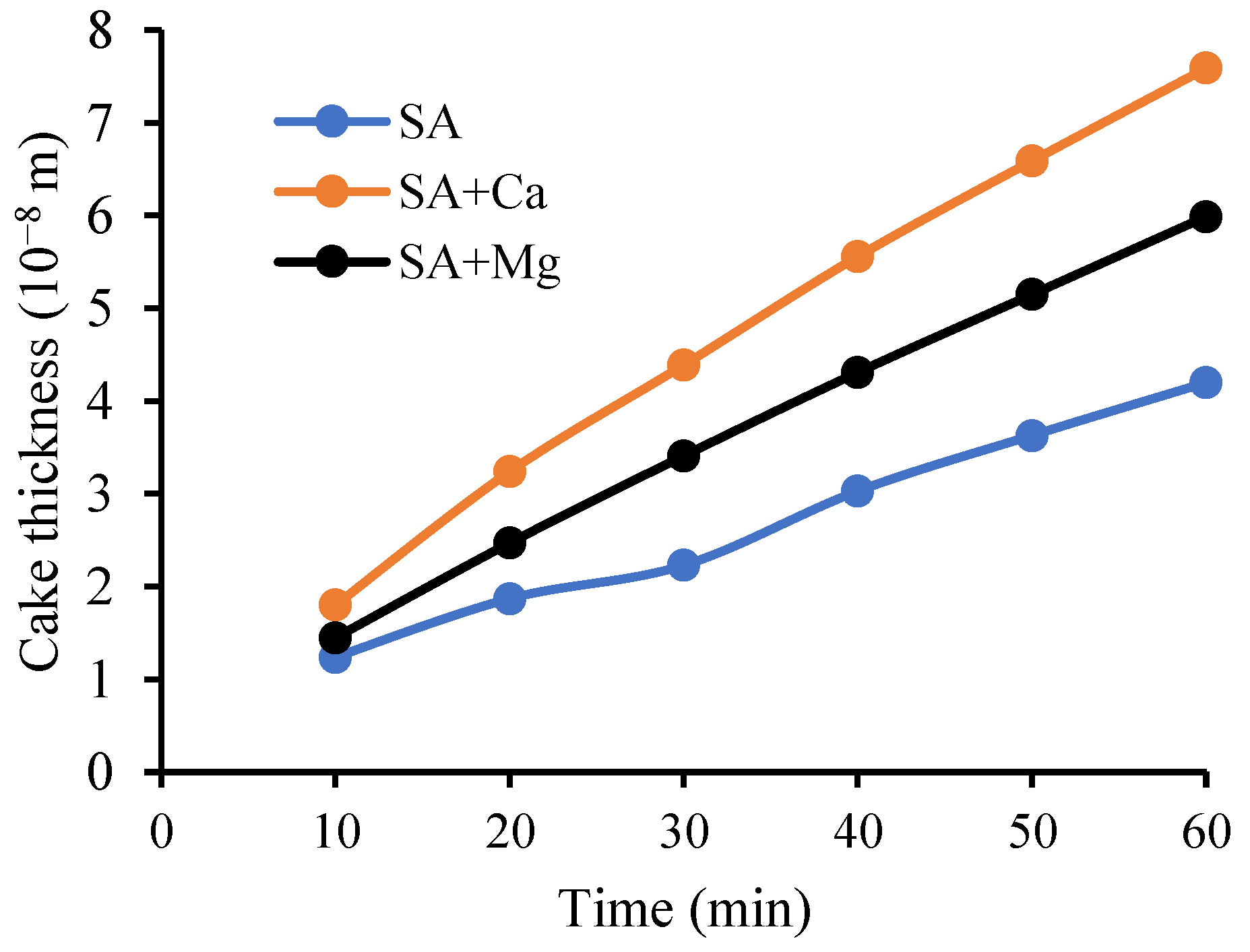
4.6. Cake Layer Build-Up
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arahman, N.; Mulyati, S.; Rahmah, M.; Takagi, R. The removal of fluoride from water based on applied current and membrane types in electrodialyis. J. Fluor. Chem. 2016, 191, 97–102. [Google Scholar] [CrossRef]
- Sheng, A.L.K.; Bilad, M.R.; Osman, N.B.; Arahman, N. Sequencing batch membrane photobioreactor for real secondary effluent polishing using native microalgae: Process performance and full-scale projection. J. Clean. Prod. 2017, 168, 708–715. [Google Scholar] [CrossRef]
- Arahman, N.; Mulyati, S.; Rahmah, M.; Takagi, R.; Matsuyama, H. Removal pro file of sulfate ion from mix ion solution with diff erent type and configuration of anion exchange membrane in elctrodialysis. J. Water Process Eng. 2017, 20, 173–179. [Google Scholar] [CrossRef]
- Plisko, T.V.; Liubimova, A.S.; Bildyukevich, A.V.; Penkova, A.V.; Dmitrenko, M.E.; Mikhailovskii, V.Y.; Melnikova, G.B.; Semenov, K.N.; Doroshkevich, N.V.; Kuzminova, A.I. Fabrication and characterization of polyamide-fullerenol thin film nanocomposite hollow fiber membranes with enhanced antifouling performance. J. Membr. Sci. 2018, 551, 20–36. [Google Scholar] [CrossRef]
- Shahkaramipour, N.; Tran, T.N.; Ramanan, S.; Lin, H. Membranes with surface-enhanced antifouling properties for water purification. Membranes 2017, 7, 13. [Google Scholar] [CrossRef] [PubMed]
- Razali, M.; Didaskalou, C.; Kim, J.F.; Babaei, M.; Drioli, E.; Lee, Y.M.; Szekely, G. Exploring and exploiting the effect of solvent treatment in membrane separations. ACS Appl. Mater. Interface 2017, 9, 11279–11289. [Google Scholar] [CrossRef] [PubMed]
- Didaskalou, C.; Buyuktiryaki, S.; Kecili, R.; Fonte, C.P.; Szekely, G. Valorisation of agricultural waste with adsorption/nanofiltration hybrid process: From materials to sustainable process design. Green Chem. 2017, 19, 3116–3125. [Google Scholar] [CrossRef]
- Li, G.; Law, W.C.; Chan, K.C. Floating, highly efficient, and scalable graphene membranes for seawater desalination using solar energy. Green Chem. 2018, 20, 3689–3695. [Google Scholar] [CrossRef]
- Didaskalou, C.; Kupai, J.; Cseri, L.; Barabas, J.; Vass, E.; Holtz, T.; Szekely, G. Membrane-grafted asymmetric organocatalyst for an integrated synthesis-separation platform. ACS Catal. 2018, 8, 7430–7438. [Google Scholar] [CrossRef]
- Kumar, A.; Thakur, A.; Panesar, P.S. Lactic acid extraction using environmentally benign green emulsion ionic liquid membrane. J. Clean. Prod. 2018, 181, 574–583. [Google Scholar] [CrossRef]
- Lee, M.J.; Hamid, M.R.A.; Lee, J.; Kim, J.S.; Lee, Y.M.; Jeong, H.K. Ultrathin zeolitic-imidazolate framework ZIF-8 membranes on polymeric hollow fibers for propylene/propane separation. J. Membr. Sci. 2018, 559, 28–34. [Google Scholar] [CrossRef]
- Huang, A.; Feng, B. Synthesis of novel graphene oxide-polyimide hollow fiber membranes for seawater desalination. J. Membr. Sci. 2018, 548, 59–65. [Google Scholar] [CrossRef]
- Rana, D.; Matsuura, T. Surface modifications for antifouling membranes. Chem. Rev. 2010, 110, 2448–2471. [Google Scholar] [CrossRef] [PubMed]
- Motsa, M.M.; Mamba, B.B.; D’Haese, A.; Hoek, E.M.V.; Verliefde, A.R.D. Organic fouling in forward osmosis membranes: The role of feed solution chemistry and membrane structural properties. J. Membr. Sci. 2014, 460, 99–109. [Google Scholar] [CrossRef]
- Charfi, A.; Yang, Y.; Harmand, J.; Ben Amar, N.; Heran, M.; Grasmick, A. Soluble microbial products and suspended solids influence in membrane fouling dynamics and interest of punctual relaxation and/or backwashing. J. Membr. Sci. 2015, 475, 156–166. [Google Scholar] [CrossRef]
- Vargas, A.; Moreno-Andrade, I.; Buitrón, G. Controlled backwashing in a membrane sequencing batch reactor used for toxic wastewater treatment. J. Membr. Sci. 2008, 320, 185–190. [Google Scholar] [CrossRef]
- Suwal, S.; Doyen, A.; Bazinet, L. Characterization of protein, peptide and amino acid fouling on ion-exchange and filtration membranes: Review of current and recently developed methods. J. Membr. Sci. 2015, 496, 267–283. [Google Scholar] [CrossRef]
- Teychene, B.; Collet, G.; Gallard, H. Modeling of combined particles and natural organic matter fouling of ultra filtration membrane. J. Membr. Sci. 2016, 505, 185–193. [Google Scholar] [CrossRef]
- Popović, S.; Dittrich, M.; Cakl, J. Modelling of fouling of outside-in hollow-fiber membranes by TiO2particles. Sep. Purif. Technol. 2015, 156, 28–35. [Google Scholar] [CrossRef]
- Mallubhotla, H.; Belfort, G. Semiempirical Modeling of cross-flow microfiltration with periodic reverse filtration. Ind. Eng. Chem. Res 1996, 5, 2920–2928. [Google Scholar] [CrossRef]
- Hashino, M.; Katagiri, T.; Kubota, N.; Ohmukai, Y.; Maruyama, T. Effect of membrane surface morphology on membrane fouling with sodium alginate. J. Membr. Sci. 2011, 366, 258–265. [Google Scholar] [CrossRef]
- Xu, W.T.; Zhao, Z.P.; Liu, M.; Chen, K.C. Morphological and hydrophobic modifications of PVDF flat membrane with silane coupling agent grafting via plasma flow for VMD of ethanol-water mixture. J. Membr. Sci. 2015, 491, 110–120. [Google Scholar] [CrossRef]
- Charfi, A.; Jang, H.; Kim, J. Membrane fouling by sodium alginate in high salinity conditions to simulate biofouling during seawater desalination. Bioresour. Technol. 2017, 240, 106–114. [Google Scholar] [CrossRef] [PubMed]
- Rathore, A.S.; Kumar, V.; Arora, A.; Lute, S.; Brorson, K.; Shukla, A. Mechanistic modeling of viral filtration. J. Membr. Sci. 2014, 458, 96–103. [Google Scholar] [CrossRef]
- Kin, J.; Dole, P. Filtration model for hollow fi ber membranes with compressible cake formation. Desalination 2009, 240, 2–6. [Google Scholar]
- Zhang, H.; Gao, J.; Jiang, T.; Gao, D.; Zhang, S.; Li, H.; Yang, F. Bioresource technology a novel approach to evaluate the permeability of cake layer during cross-flow filtration in the flocculants added membrane bioreactors. Bioresour. Technol. 2011, 102, 11121–11131. [Google Scholar] [CrossRef] [PubMed]
- Mulder, M. Basic Principles of Membrane Technology, 4th ed.; Kluwer Academic Publisher: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Badrnezhad, R.; Mirza, B. Journal of industrial and engineering chemistry modeling and optimization of cross-flow ultrafiltration using hybrid neural network-genetic algorithm approach. J. Ind. Eng. Chem. 2014, 20, 528–543. [Google Scholar] [CrossRef]
- Netcher, A.C.; Duranceau, S.J. Modeling the improvement of ultra fi ltration membrane mass transfer when using biofiltration pretreatment in surface water applications. Water Res. 2016, 90, 258–264. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.; Liang, H.; Qu, F.; Shao, S.; Yu, H.; Liu, B. Role of backwash water composition in alleviating ultra filtration membrane fouling by sodium alginate and the effectiveness of salt backwashing. J. Membr. Sci. 2016, 499, 429–441. [Google Scholar] [CrossRef]
- Hao, Y.; Moriya, A.; Maruyama, T.; Ohmukai, Y.; Matsuyama, H. Effect of metal ions on humic acid fouling of hollow fiber ultrafiltration membrane. J. Membr. Sci. 2011, 376, 247–253. [Google Scholar] [CrossRef]
- Sarkar, D.; Chakraborty, D.; Naskar, M.; Bhattacharjee, C. Characterization and modeling of radial flow membrane (RFM) module in ultra filtration. Desalination 2014, 354, 76–86. [Google Scholar] [CrossRef]
- Paipuri, M.; Kim, S.H.; Hassan, O.; Hilal, N.; Morgan, K. Numerical modelling of concentration polarisation and cake formation in membrane filtration processes. Desalination 2015, 365, 151–159. [Google Scholar] [CrossRef]
- Garcia-Ivars, J.; Iborra-Clar, M.-I.; Alcaina-Miranda, M.-I.; Van der Bruggen, B. Comparison between Hydrophilic and Hydrophobic metal nanoparticles on the phase separation phenomena during formation of asymmetric polyethersulphone membranes. J. Membr. Sci. 2015, 493, 709–722. [Google Scholar] [CrossRef]
- Arahman, N.; Mulyati, S.; Lubis, M.R.; Razi, F.; Takagi, R.; Matsuyama, H. Modification of polyethersulfone hollow fiber memrbanes with different polymeric additives. Membr. Water Treat. 2016, 4, 355–365. [Google Scholar] [CrossRef]
| Membrane Type | Model I | Model II | |||||
|---|---|---|---|---|---|---|---|
| Constant | Standard Error | Constant | Standard Error | ||||
| A | B | SSE | R2 | Τ | SSE | R2 | |
| CA | 4920.28 | 1.24 | 0.00038 | 0.95 | 4772.56 | 0.000898 | 0.61 |
| Sample Solution | Relative Permeability Model Validation (R2) | ||
|---|---|---|---|
| Model I | Model II | Model III | |
| SA | 0.9998 | 0.9261 | 0.9943 |
| SA + Ca | 0.9999 | 0.9438 | 0.9837 |
| SA + Mg | 0.9994 | 0.9200 | 0.9898 |
| Rm (m−1) | Feed | Kc (m−2) | Rc Validation (R2) | |
|---|---|---|---|---|
| 5.75 × 1012 | SA | 0.7123 | 1.66 × 10−20 | 0.8622 |
| SA + Ca | 0.5372 | 4.94 × 10−21 | 0.6701 | |
| SA + Mg | 0.5500 | 9.42 × 10−21 | 0.7165 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arahman, N.; Satria, S.; Razi, F.; Bilad, M.R. The Effect of Ca and Mg Ions on the Filtration Profile of Sodium Alginate Solution in a Polyethersulfone-2-(methacryloyloxy) Ethyl Phosphorylchloline Membrane. Water 2018, 10, 1207. https://doi.org/10.3390/w10091207
Arahman N, Satria S, Razi F, Bilad MR. The Effect of Ca and Mg Ions on the Filtration Profile of Sodium Alginate Solution in a Polyethersulfone-2-(methacryloyloxy) Ethyl Phosphorylchloline Membrane. Water. 2018; 10(9):1207. https://doi.org/10.3390/w10091207
Chicago/Turabian StyleArahman, Nasrul, Suffriandy Satria, Fachrul Razi, and M. Roil Bilad. 2018. "The Effect of Ca and Mg Ions on the Filtration Profile of Sodium Alginate Solution in a Polyethersulfone-2-(methacryloyloxy) Ethyl Phosphorylchloline Membrane" Water 10, no. 9: 1207. https://doi.org/10.3390/w10091207
APA StyleArahman, N., Satria, S., Razi, F., & Bilad, M. R. (2018). The Effect of Ca and Mg Ions on the Filtration Profile of Sodium Alginate Solution in a Polyethersulfone-2-(methacryloyloxy) Ethyl Phosphorylchloline Membrane. Water, 10(9), 1207. https://doi.org/10.3390/w10091207







