Symbolic Regression-Based Genetic Approximations of the Colebrook Equation for Flow Friction
Abstract
1. Introduction
2. Methods Used, Preparation of Data and Software Tool, Results, Structure of Approximations, Accuracy and Comparative Analysis
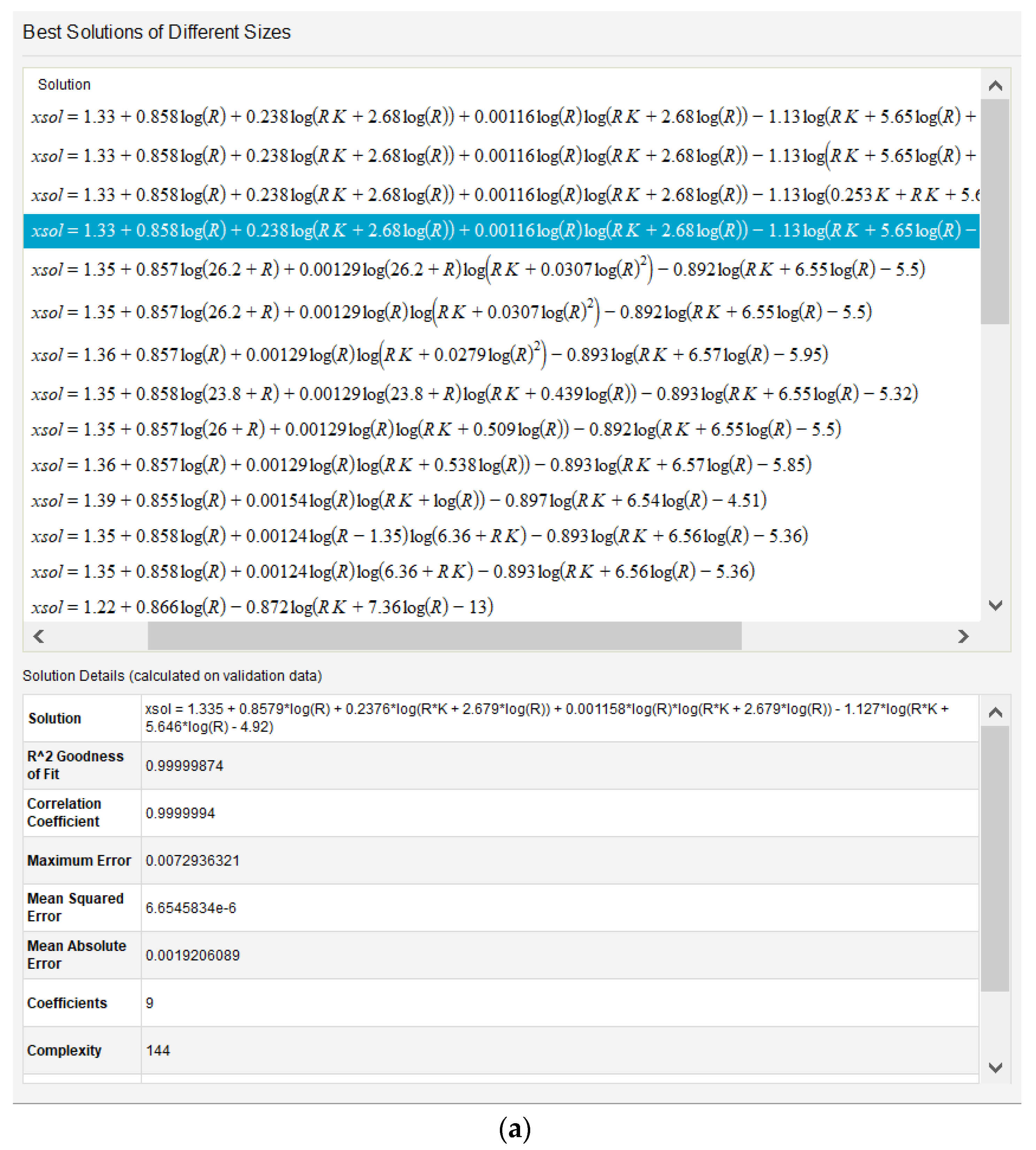
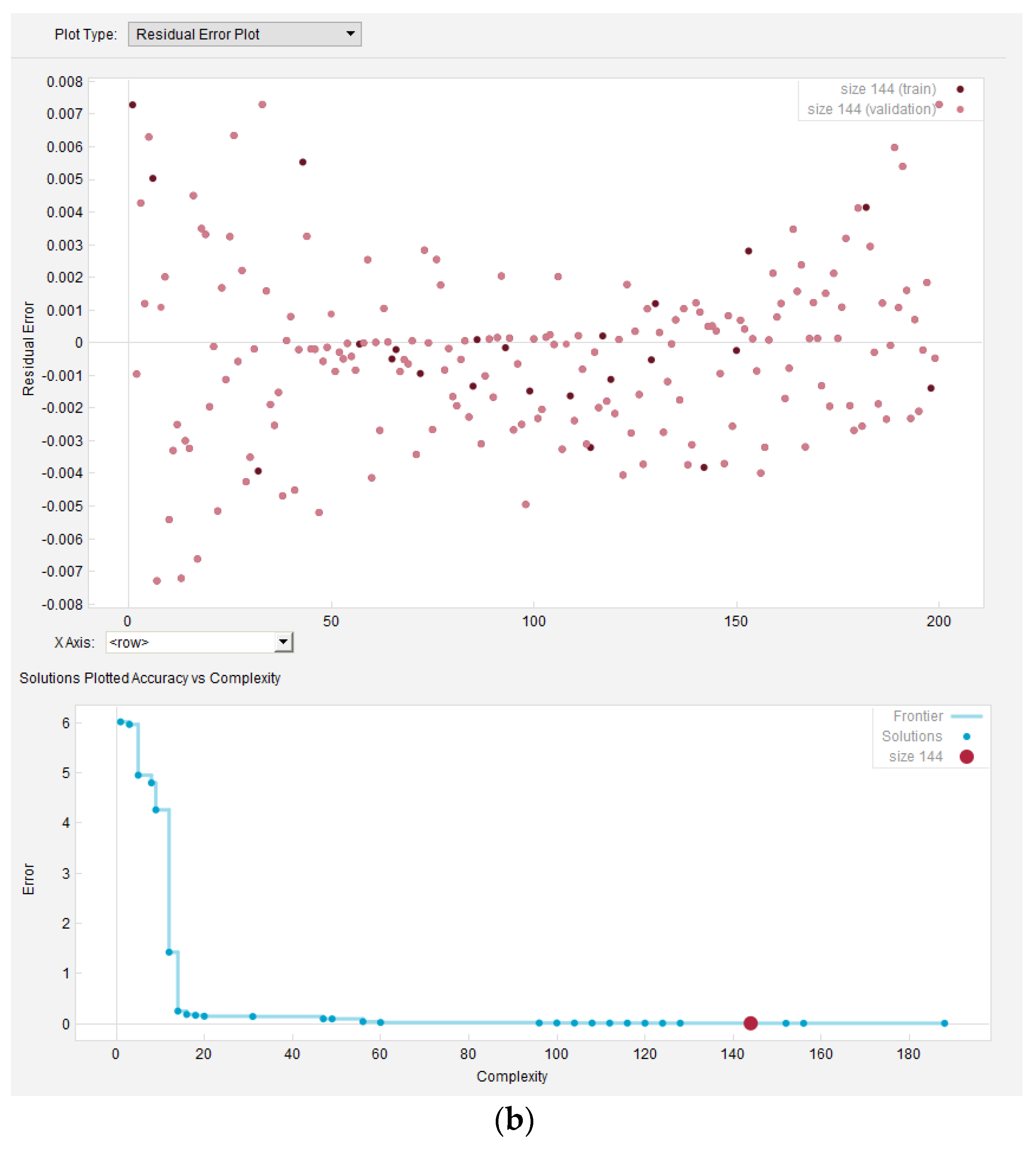
2.1. Input Parameters in Their Raw Form
2.2. Normalized Input Parameters
2.3. Discussion—Comparative Analysis
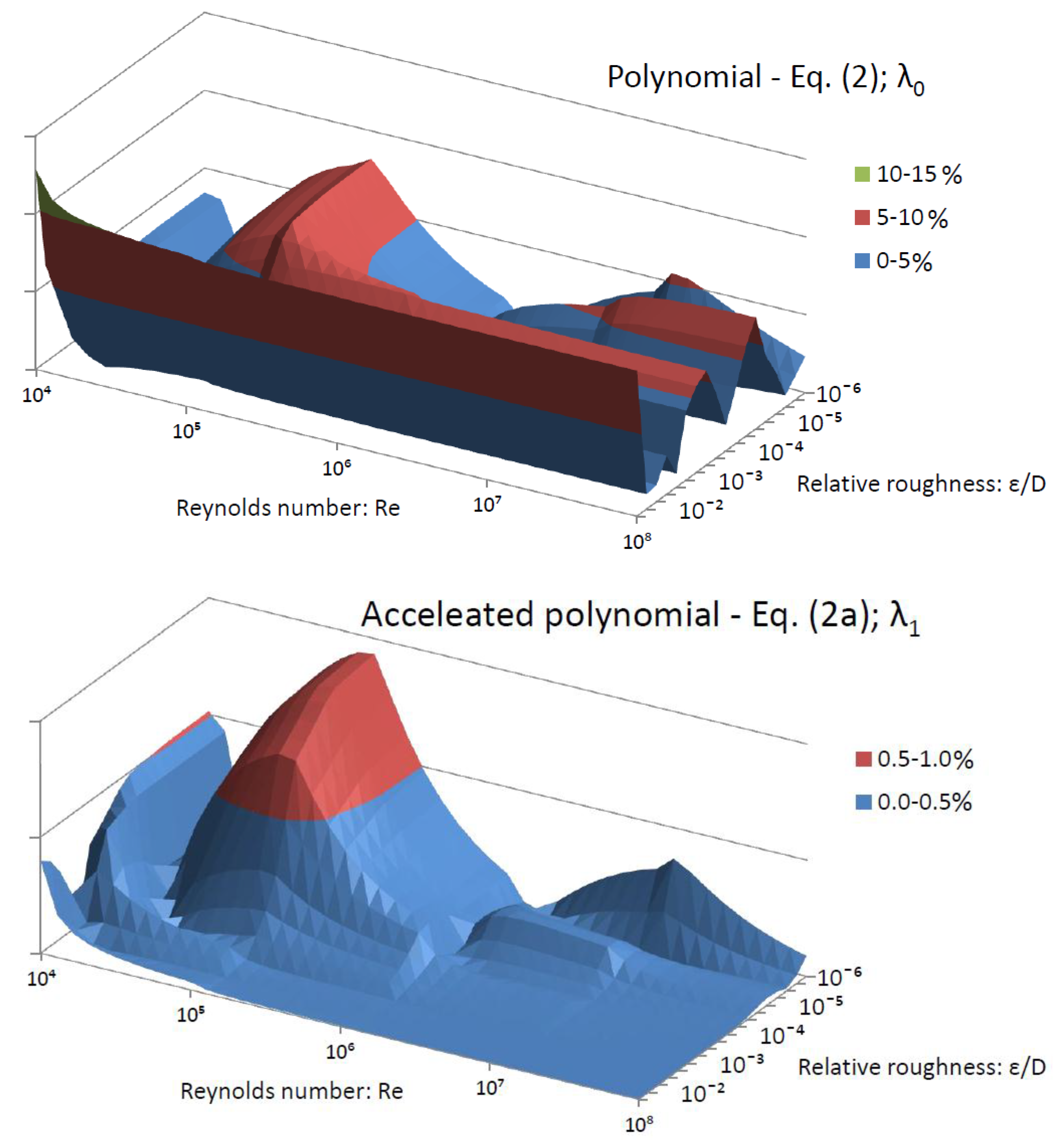
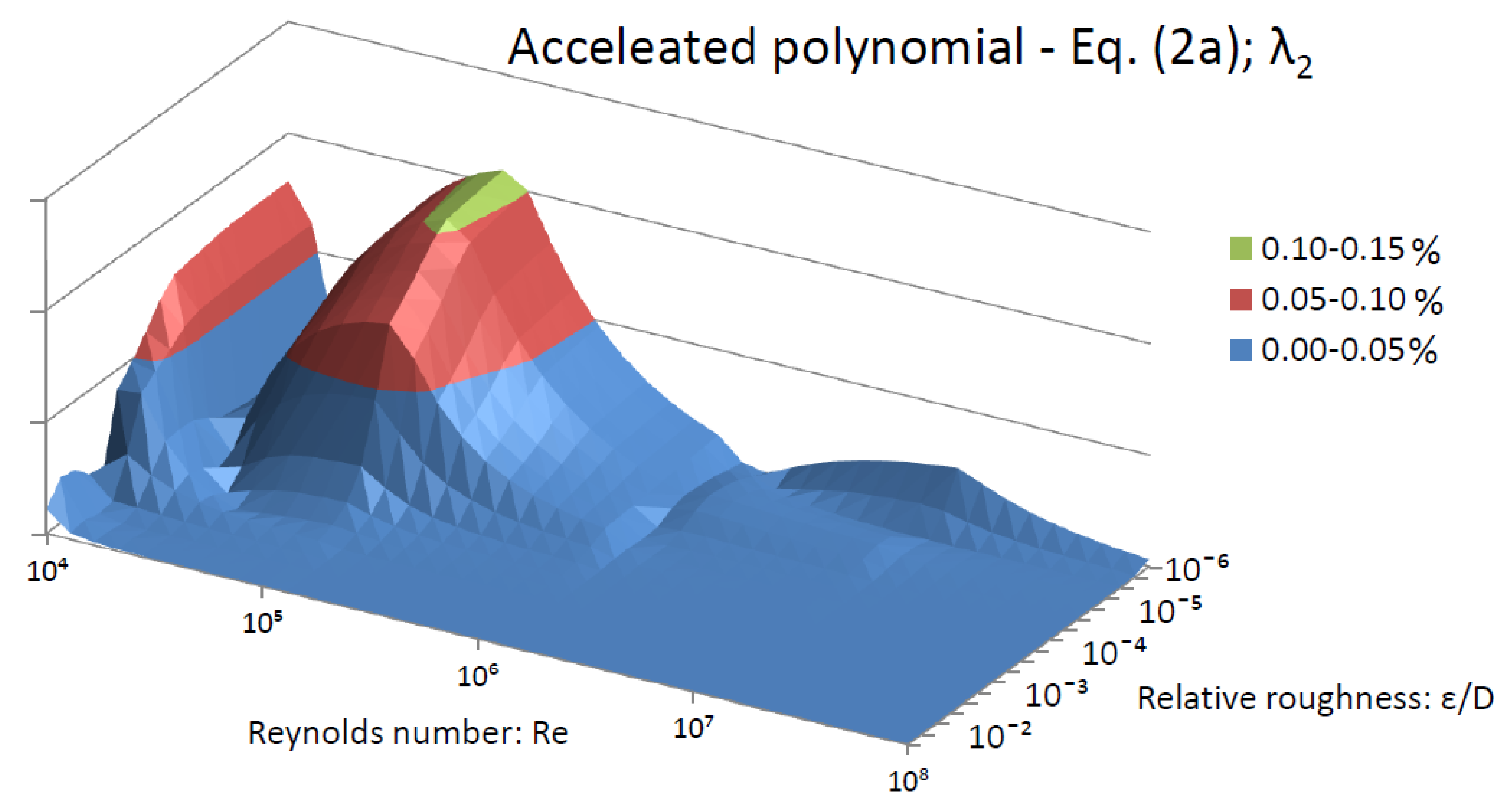
- Highly accurate: Compared with the similar approximations to the Colebrook equation, accelerated Equation (5a); with the relative error up to 0.28% and accelerated Equations (2a) and (6a) with the relative error up to 0.13% and 0.17%, respectively, are accurate as approximations by Bar [47] (0.2%), Chen [38] (0.36–0.18%), Zigrang and Sylvester [41] (0.14–0.08%, simpler: 1–0.775%), Fang et al. [48] (0.61–0.56%), Serghides [38] (0.14–0.0026%, simpler 0.35–0.27%), Buzzelli [49] (0.14–0.08%), Sonad and Goudar [50] (0.8–improved by Vatankhah and Kouchakzadeh [51]: 0.15%) and Romeo et al. [52] (0.14–0.008%); where the higher reported accuracy is achieved through genetic optimization [25,29]. These approximations are among the most accurate available to date [3,4,5,6,7,8], but at the same time in many cases much more complex compared to the approximations presented in our paper [4,11,12,13]. For example; approximations by Barr [47] and by Chen [38] contain two logarithmic expressions and two non-integer powers; by Romeo et al. [52], three logarithmic expressions and two non-integer powers, etc. which means that they introduce a higher computational burden to achieve the same accuracy. In this case, our Equation (2a), which after two steps of acceleration, contains only two logarithmic forms.
- Moderately accurate: Our Equation (6) with the relative error up to 2% does contain only two logarithmic expressions used for normalization and no non-integer power, and its accuracy can be compared with approximations by Swamee and Jain [53] (2.18–1.75%), Manadili [54] (2–1.5%), Brkić [42,55,56,57] (2–1.3%), Haland [58] (1.4–1.1%), etc., all with the same or higher complexity as Equation (6). Equation (2a) after the first step of acceleration with only one logarithmic function and with the relative error of up to 2.6% is even more efficient.
- Low accuracy: Our accelerated Equation (3a) is very simple with the relative error up to 5.35% but with only one peak of high error (otherwise up to 3% as can be seen from Figure 4); it is more accurate compared with approximations by Round [59] (10.9–5.5%), Eck [60] (8.2–5.7%) and Avci and Karagoz [61] (4.8–3.1%), Wood [62] (23.7–16.6%), Moody [63] (21.5–18.1%), etc.
3. Possible Simplifications
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Colebrook, C.F. Turbulent flow in pipes with particular reference to the transition region between the smooth and rough pipe laws. J. Inst. Civ. Eng. 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Colebrook, C.; White, C. Experiments with fluid friction in roughened pipes. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1937, 161, 367–381. [Google Scholar] [CrossRef]
- Gregory, G.A.; Fogarasi, M. Alternate to standard friction factor equation. Oil Gas J. 1985, 83, 120–127. [Google Scholar]
- Zigrang, D.J.; Sylvester, N.D. A review of explicit friction factor equations. J. Energy Resour. Technol. 1985, 107, 280–283. [Google Scholar] [CrossRef]
- Brkić, D. Review of explicit approximations to the Colebrook relation for flow friction. J. Pet. Sci. Eng. 2011, 77, 34–48. [Google Scholar] [CrossRef]
- Brkić, D. Determining friction factors in turbulent pipe flow. Chem. Eng. 2012, 119, 34–39. [Google Scholar]
- Winning, H.K.; Coole, T. Explicit friction factor accuracy and computational efficiency for turbulent flow in pipes. Flow Turbul. Combust. 2013, 90, 1–27. [Google Scholar] [CrossRef]
- Pimenta, B.D.; Robaina, A.D.; Peiter, M.X.; Mezzomo, W.; Kirchner, J.H.; Ben, L.H. Performance of explicit approximations of the coefficient of head loss for pressurized conduits. Rev. Bras. Eng. Agríc. E Ambient. 2018, 22, 301–307. [Google Scholar] [CrossRef]
- Brkić, D. Solution of the implicit Colebrook equation for flow friction using Excel. Spreadsheets Educ. 2017, 10, 2. Available online: http://epublications.bond.edu.au/ejsie/vol10/iss2/2 (accessed on 28 August 2018).
- Praks, P.; Brkić, D. One-log call iterative solution of the Colebrook equation for flow friction based on Padé polynomials. Energies 2018, 11, 1825. [Google Scholar] [CrossRef]
- Clamond, D. Efficient resolution of the Colebrook equation. Ind. Eng. Chem. Res. 2009, 48, 3665–3671. [Google Scholar] [CrossRef]
- Giustolisi, O.; Berardi, L.; Walski, T.M. Some explicit formulations of Colebrook–White friction factor considering accuracy vs. computational speed. J. Hydroinform. 2011, 13, 401–418. [Google Scholar] [CrossRef]
- Vatankhah, A.R. Approximate analytical solutions for the Colebrook equation. J. Hydraul. Eng. 2018, 144, 06018007. [Google Scholar] [CrossRef]
- Özger, M.; Yıldırım, G. Determining turbulent flow friction coefficient using adaptive neuro-fuzzy computing technique. Adv. Eng. Softw. 2009, 40, 281–287. [Google Scholar] [CrossRef]
- Brkić, D.; Ćojbašić, Ž. Intelligent flow friction estimation. Comput. Intell. Neurosci. 2016, 2016, 5242596. [Google Scholar] [CrossRef] [PubMed]
- Precup, R.E.; Preitl, S.; Bojan-Dragos, C.A.; Radac, M.B.; Szedlak-Stinean, A.I.; Hedrea, E.L.; Roman, R.C. Automotive applications of evolving Takagi-Sugeno-Kang fuzzy models. Facta Univ. Ser. Mech. Eng. 2017, 15, 231–244. [Google Scholar] [CrossRef]
- Dučić, N.; Ćojbašić, Ž.; Radiša, R.; Slavković, R.; Milićević, I. CAD/CAM design and genetic optimization of feeders for sand casting process. Facta Univ. Ser. Mech. Eng. 2016, 14, 147–158. [Google Scholar] [CrossRef]
- Shojaeizadeh, A.; Safaei, M.R.; Alrashed, A.A.; Ghodsian, M.; Geza, M.; Abbassi, M.A. Bed roughness effects on characteristics of turbulent confined wall jets. Measurement 2018, 122, 325–338. [Google Scholar] [CrossRef]
- Lebon, B.; Nguyen, M.Q.; Peixinho, J.; Shadloo, M.S.; Hadjadj, A. A new mechanism for periodic bursting of the recirculation region in the flow through a sudden expansion in a circular pipe. Phys. Fluids 2018, 30, 031701. [Google Scholar] [CrossRef]
- Brkić, D. Can pipes be actually really that smooth? Int. J. Refrig. 2012, 35, 209–215. [Google Scholar] [CrossRef]
- Sobol, I.M.; Turchaninov, V.I.; Levitan, Y.L.; Shukman, B.V. Quasi-Random Sequence Generator (Routine LPTAU51); Keldysh Institute of Applied Mathematics, Russian Academy of Sciences: Moscow, Russia, 1992. [Google Scholar]
- Schmidt, M.; Lipson, H. Distilling free-form natural laws from experimental data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef] [PubMed]
- Dubčáková, R. Eureqa: Software review. Genet. Program. Evol. Mach. 2011, 12, 173–178. [Google Scholar] [CrossRef]
- Samadianfard, S. Gene expression programming analysis of implicit Colebrook–White equation in turbulent flow friction factor calculation. J. Pet. Sci. Eng. 2012, 92, 48–55. [Google Scholar] [CrossRef]
- Ćojbašić, Ž.; Brkić, D. Very accurate explicit approximations for calculation of the Colebrook friction factor. Int. J. Mech. Sci. 2013, 67, 10–13. [Google Scholar] [CrossRef]
- Brkić, D. Discussion of “Gene expression programming analysis of implicit Colebrook–White equation in turbulent flow friction factor calculation” by Saeed Samadianfard. J. Pet. Sci. Eng. 2014, 124, 399–401. [Google Scholar] [CrossRef]
- Vatankhah, A.R. Comment on “Gene expression programming analysis of implicit Colebrook–White equation in turbulent flow friction factor calculation”. J. Pet. Sci. Eng. 2014, 124, 402–405. [Google Scholar] [CrossRef]
- Samadianfard, S.; Taghi Sattari, M.; Kisi, O.; Kazemi, H. Determining flow friction factor in irrigation pipes using data mining and artificial intelligence approaches. Appl. Artif. Intell. 2014, 28, 793–813. [Google Scholar] [CrossRef]
- Brkić, D.; Ćojbašić, Ž. Evolutionary optimization of Colebrook’s turbulent flow friction approximations. Fluids 2017, 2, 15. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Tang, P.T. Table-driven implementation of the logarithm function in IEEE floating-point arithmetic. ACM Trans. Math. Softw. (TOMS) 1990, 16, 378–400. [Google Scholar] [CrossRef]
- Pineiro, J.A.; Ercegovac, M.D.; Bruguera, J.D. Algorithm and architecture for logarithm, exponential, and powering computation. IEEE Trans. Comput. 2004, 53, 85–96. [Google Scholar] [CrossRef]
- Johansson, K.; Gustafsson, O.; Wanhammar, L. Implementation of elementary functions for logarithmic number systems. IET Comput. Digit. Tech. 2008, 2, 295–304. [Google Scholar] [CrossRef]
- Stoutemyer, D.R. Can the Eureqa symbolic regression program, computer algebra and numerical analysis help each other. Not. AMS 2013, 60, 713–724. [Google Scholar] [CrossRef]
- Korns, M.F. Accuracy in symbolic regression. In Genetic Programming Theory and Practice IX; Springer: New York, NY, USA, 2011; pp. 129–151. [Google Scholar]
- Bartz-Beielstein, T.; Branke, J.; Mehnen, J.; Mersmann, O. Evolutionary algorithms. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2014, 4, 178–195. [Google Scholar] [CrossRef]
- Brkić, D. Discussion of “Exact analytical solutions of the Colebrook-White equation” by Yozo Mikata and Walter S. Walczak. J. Hydraul. Eng. 2017, 143, 07017007. [Google Scholar] [CrossRef]
- Chen, N.H. An explicit equation for friction factor in pipe. Ind. Eng. Chem. Fundam. 1979, 18, 296–297. [Google Scholar] [CrossRef]
- Schorle, B.J.; Churchill, S.W.; Shacham, M. Comments on “An Explicit Equation for Friction Factor in Pipe”. Ind. Eng. Chem. Fundam. 1980, 19, 228–230. [Google Scholar] [CrossRef]
- Serghides, T.K. Estimate friction factor accurately. Chem. Eng. 1984, 91, 63–64. [Google Scholar]
- Zigrang, D.J.; Sylvester, N.D. Explicit approximations to the solution of Colebrook’s friction factor equation. AIChE J. 1982, 28, 514–515. [Google Scholar] [CrossRef]
- Brkić, D. New explicit correlations for turbulent flow friction factor. Nucl. Eng. Des. 2011, 241, 4055–4059. [Google Scholar] [CrossRef]
- Praks, P.; Kopustinskas, V.; Masera, M. Probabilistic modelling of security of supply in gas networks and evaluation of new infrastructure. Reliab. Eng. Syst. Saf. 2015, 144, 254–264. [Google Scholar] [CrossRef]
- Praks, P.; Kopustinskas, V.; Masera, M. Monte-Carlo-based reliability and vulnerability assessment of a natural gas transmission system due to random network component failures. Sustain. Resil. Infrastruct. 2017, 2, 97–107. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Advanced iterative procedures for solving the implicit Colebrook equation for fluid flow friction. Adv. Civ. Eng. 2018, 2018, 5451034. [Google Scholar] [CrossRef]
- Quan, L.P.; Nhan, T.A. Applying Computer algebra systems in approximating the trigonometric functions. Math. Comput. Appl. 2018, 23, 37. [Google Scholar] [CrossRef]
- Barr, D.I.H. Solutions of the Colebrook-White function for resistance to uniform turbulent flow. Proc. Inst. Civ. Eng. 1981, 71, 529–535. [Google Scholar] [CrossRef]
- Fang, X.; Xu, Y.; Zhou, Z. New correlations of single-phase friction factor for turbulent pipe flow and evaluation of existing single-phase friction factor correlations. Nucl. Eng. Des. 2011, 241, 897–902. [Google Scholar] [CrossRef]
- Buzzelli, D. Calculating friction in one step. Mach. Des. 2008, 80, 54–55. [Google Scholar]
- Sonnad, J.R.; Goudar, C.T. Turbulent flow friction factor calculation using a mathematically exact alternative to the Colebrook–White equation. J. Hydraul. Eng. 2006, 132, 863–867. [Google Scholar] [CrossRef]
- Vatankhah, A.R.; Kouchakzadeh, S. Discussion of “Turbulent flow friction factor calculation using a mathematically exact alternative to the Colebrook–White equation” by Jagadeesh R. Sonnad and Chetan T. Goudar. J. Hydraul. Eng. 2008, 134, 1187. [Google Scholar] [CrossRef]
- Romeo, E.; Royo, C.; Monzón, A. Improved explicit equations for estimation of the friction factor in rough and smooth pipes. Chem. Eng. J. 2002, 86, 369–374. [Google Scholar] [CrossRef]
- Swamee, P.K.; Jain, A.K. Explicit equations for pipe-flow problems. J. Hydraul. Div. 1976, 102, 657–664. [Google Scholar]
- Manadili, G. Replace implicit equations with signomial functions. Chem. Eng. 1997, 104, 129–130. [Google Scholar]
- Brkić, D. An explicit approximation of Colebrook’s equation for fluid flow friction factor. Pet. Sci. Technol. 2011, 29, 1596–1602. [Google Scholar] [CrossRef]
- Brkić, D. W solutions of the CW equation for flow friction. Appl. Math. Lett. 2011, 24, 1379–1383. [Google Scholar] [CrossRef]
- Brkić, D. Comparison of the Lambert W-function based solutions to the Colebrook equation. Eng. Comput. 2012, 29, 617–630. [Google Scholar] [CrossRef]
- Haaland, S.E. Simple and explicit formulas for the friction factor in turbulent pipe flow. J. Fluids Eng. 1983, 105, 89–90. [Google Scholar] [CrossRef]
- Round, G.F. An explicit approximation for the friction factor-Reynolds number relation for rough and smooth pipes. Can. J. Chem. Eng. 1980, 58, 122–123. [Google Scholar] [CrossRef]
- Eck, B. Technische Stromungslehre; Springer: New York, NY, USA, 1973. [Google Scholar]
- Avci, A.; Karagoz, I. A novel explicit equation for friction factor in smooth and rough pipes. J. Fluids Eng. 2009, 131, 061203. [Google Scholar] [CrossRef]
- Wood, D.J. An explicit friction factor relationship. Civil. Eng. 1966, 36, 60–61. [Google Scholar]
- Moody, L.F. An approximate formula for pipe friction factors. Trans. ASME 1947, 69, 1005–1011. [Google Scholar]
- Baker, G.A.; Graves-Morris, P. Padé Approximants. Encyclopedia of Mathematics and Its Applications; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Praks, P.; Brkić, D. Choosing the optimal multi-point iterative method for the Colebrook flow friction equation. Processes 2018, 6, 130. [Google Scholar] [CrossRef]

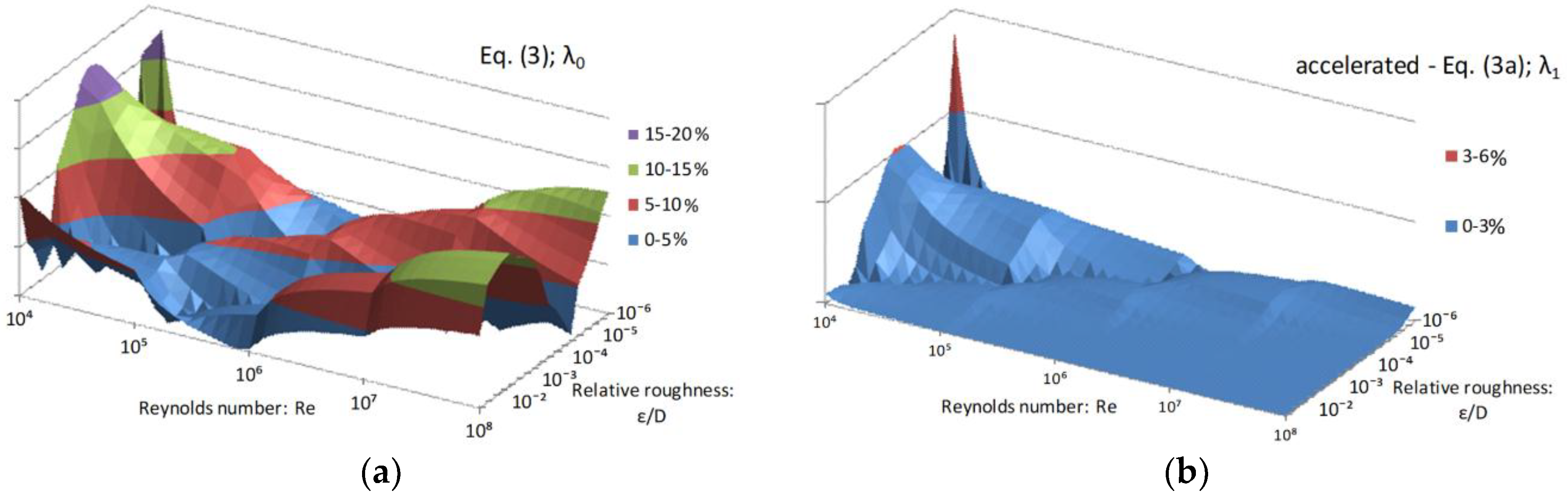
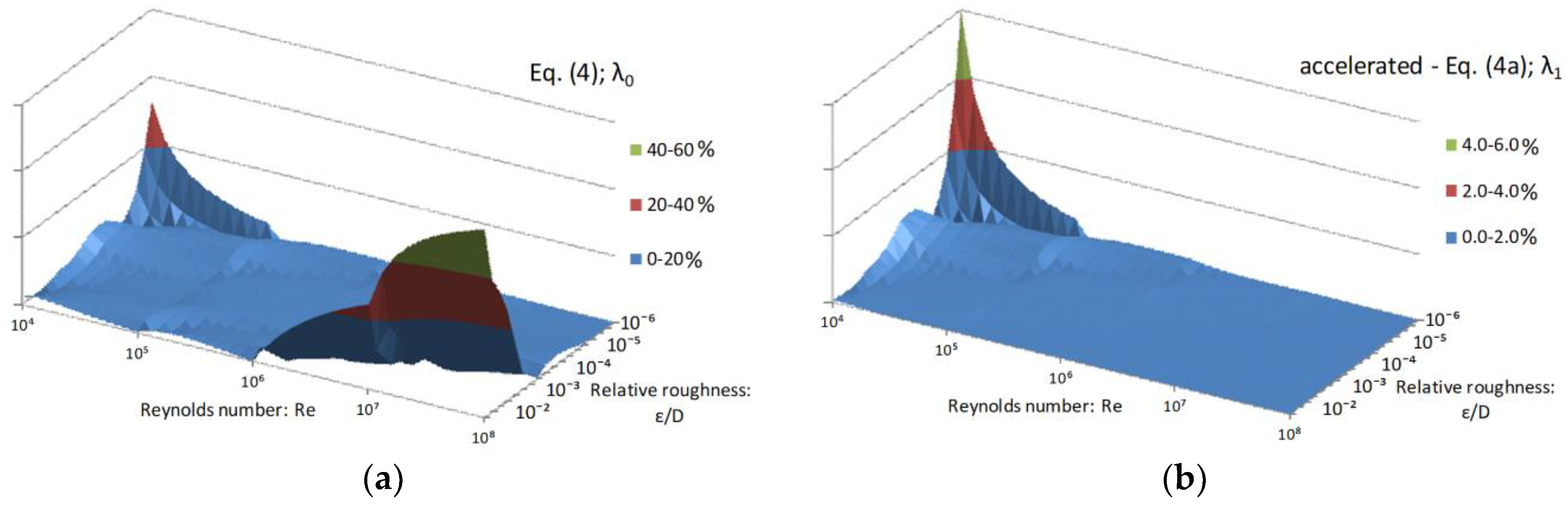
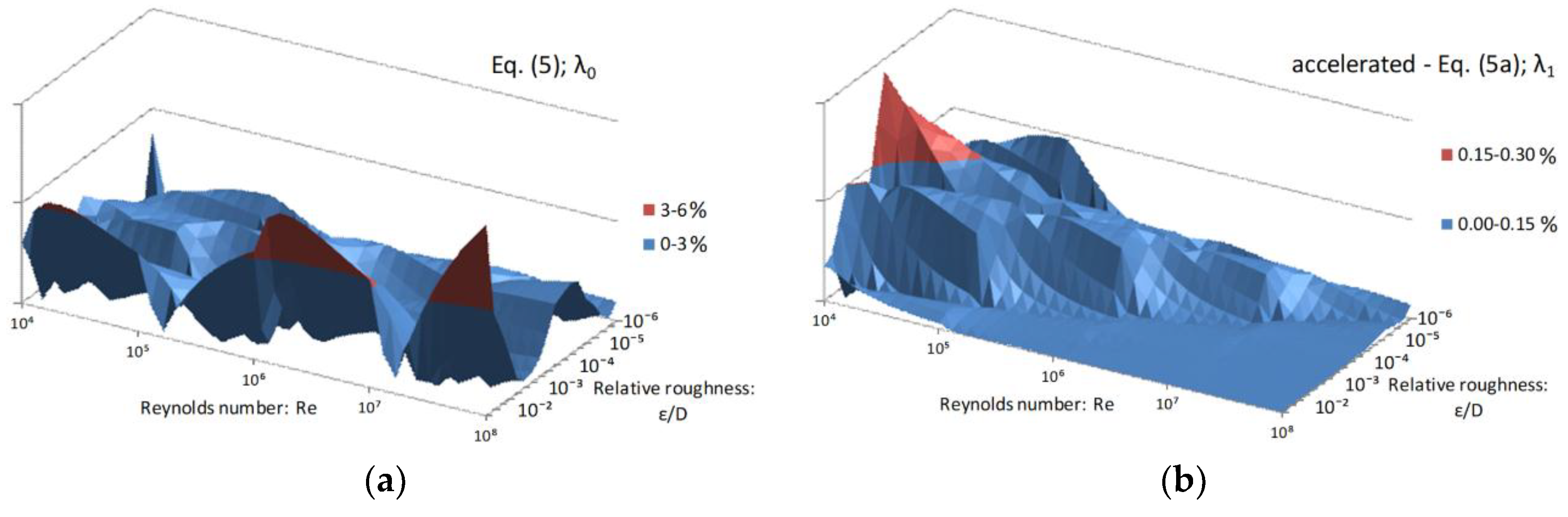
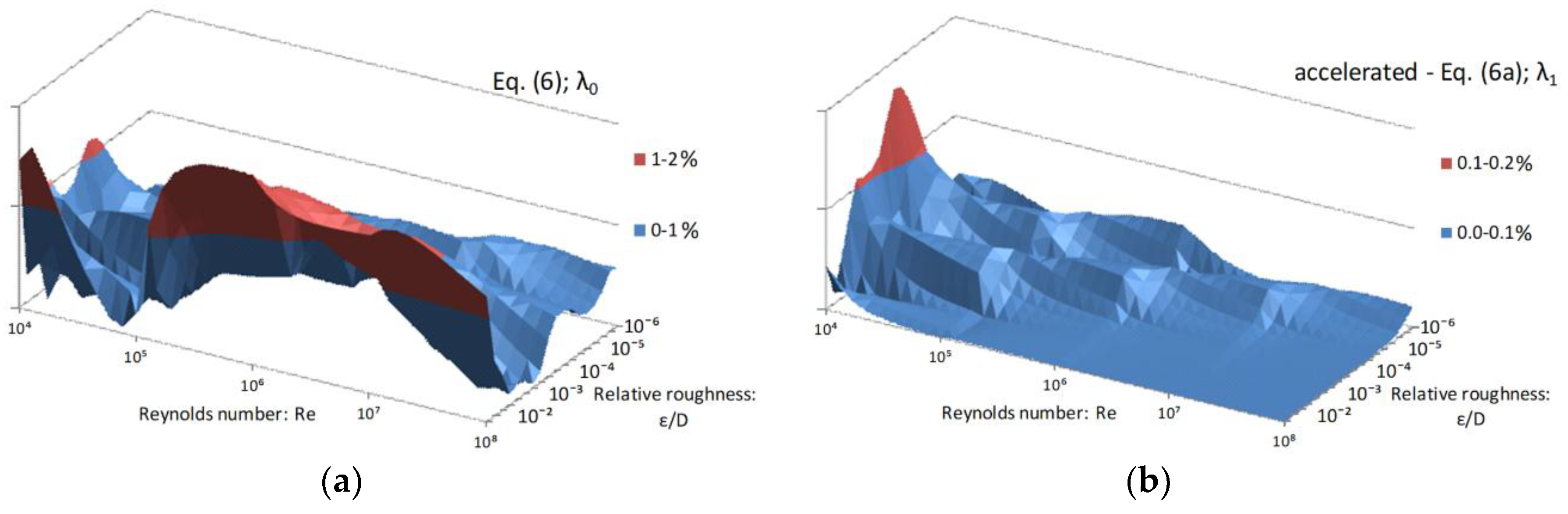
| Complexity: Number of log Functions | |||
|---|---|---|---|
| Accuracy | 1 | 2 | 3 |
| High | Equation (2a)—λ2→0.13% | Equation (6a)—λ1→0.17% Equation (5a)—λ1→0.28% | |
| Moderate | Equation (2a)—λ1→0.98% | Equation (6)—λ0→2% | |
| Low | Equation (5)—λ0→6% | Equation (4a)—λ1→6.29% Equation (3a)—λ1→5.35% | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Praks, P.; Brkić, D. Symbolic Regression-Based Genetic Approximations of the Colebrook Equation for Flow Friction. Water 2018, 10, 1175. https://doi.org/10.3390/w10091175
Praks P, Brkić D. Symbolic Regression-Based Genetic Approximations of the Colebrook Equation for Flow Friction. Water. 2018; 10(9):1175. https://doi.org/10.3390/w10091175
Chicago/Turabian StylePraks, Pavel, and Dejan Brkić. 2018. "Symbolic Regression-Based Genetic Approximations of the Colebrook Equation for Flow Friction" Water 10, no. 9: 1175. https://doi.org/10.3390/w10091175
APA StylePraks, P., & Brkić, D. (2018). Symbolic Regression-Based Genetic Approximations of the Colebrook Equation for Flow Friction. Water, 10(9), 1175. https://doi.org/10.3390/w10091175






