Effects of Guide Vane Placement Angle on Hydraulic Characteristics of Flow Field and Optimal Design of Hydraulic Capsule Pipelines
Abstract
1. Introduction
2. Theoretical Analysis
2.1. Design of the Piped Carriage
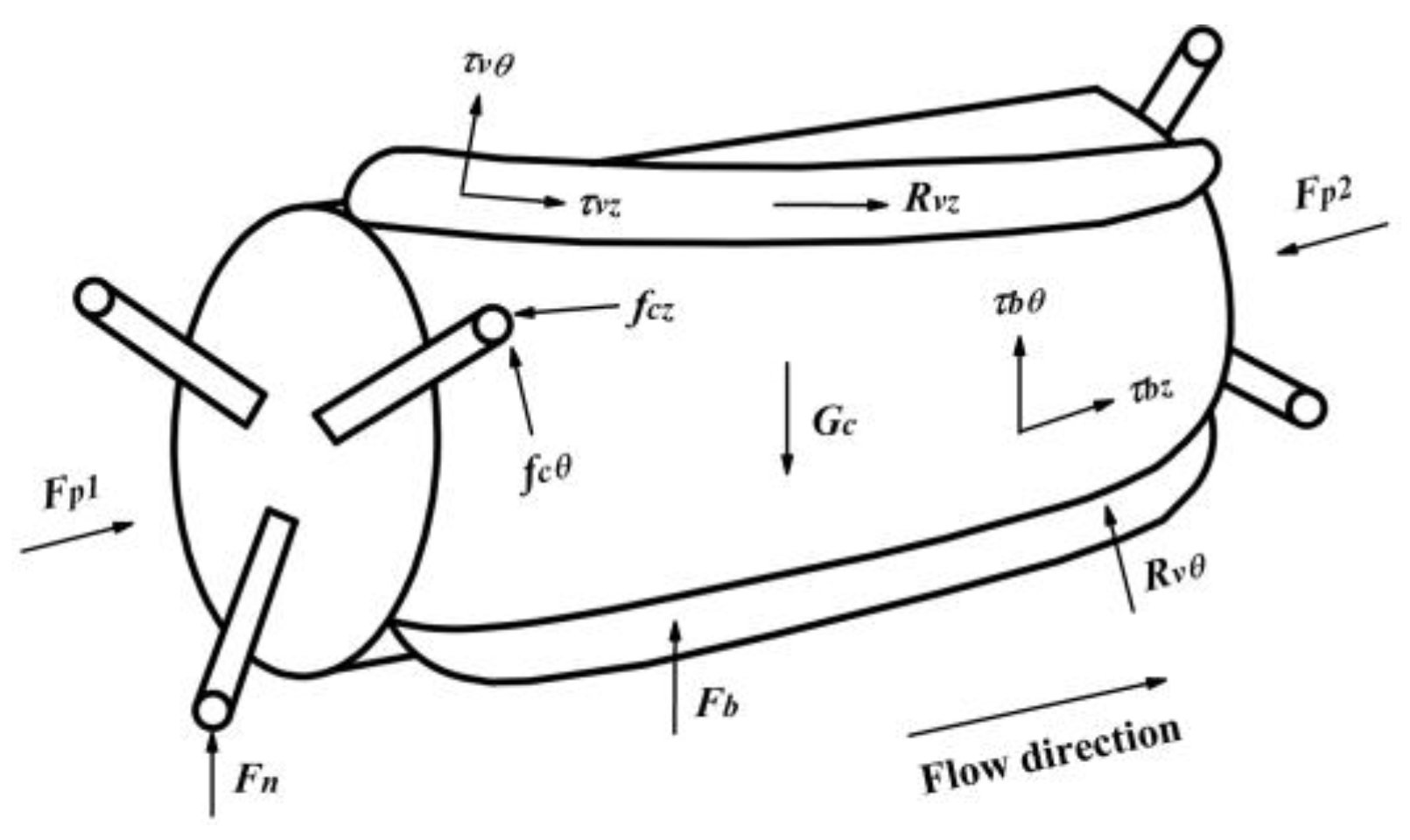
2.2. Force Analysis
- (1)
- The gravity of the piped carriage Gc was related to the basic materials of the piped carriage.
- (2)
- The pressure gradient force acting on the front and rear ends of the piped carriage Fp, which can be expressed aswhere Fp1 and Fp2 were the fluid pressures acting on the front and rear ends of the piped carriage, respectively.
- (3)
- The support force of the pipe wall against the piped carriage Fn. Six support forces acting on the contact points between the universal balls of the piped carriage and the inner wall of the pipes in different directions, and the directions of these support forces pointed towards the center of the conveying pipes from its interior wall.
- (4)
- The buoyancy of the piped carriage Fb was related to the internal volume of the barrel.
- (5)
- The rolling frictional resistance fc was decomposed into an axial force fcz and a circumferential force fcθ. These two forces can be expressed respectively aswhere μz was the axial rolling frictional resistance coefficient, μθ was the circumferential rolling frictional resistance coefficient.
- (6)
- The shear stress of the annular slit flow acting on the sidewall of the guide vanes τv was decomposed into an axial force τvz and a circumferential force τvθ. These two forces can be expressed respectively aswhere Vaz and Vaθ were the average axial speed and the average circumferential speed of the piped carriage respectively; Uvz and Uvθ were the average axial velocity and the average circumferential velocity of the annular slit flow in the near-wall areas of the guide vanes respectively; λv was the flow resistance coefficient in the near-wall areas of the guide vanes; ρ was the fluid density. In this article, the average circumferential speed and average angular speed of the piped carriage represented the circumferential rotating speed of the piped carriage, but the emphases expressed by these two physical parameters were different. The average axial velocity was analyzed by using the arc length, while the average angular velocity was analyzed by using the rotation angle.
- (7)
- The shear stress of the annular slit flow acting on the sidewall of the barrel τb was decomposed into an axial force τbz and a circumferential force τbθ. These two forces can be expressed respectively aswhere Usz and Usθ were the average axial velocity and the average circumferential velocity of the annular slit flow respectively; λb was the flow resistance coefficient in the near-wall areas of the barrel.
- (8)
- The fluid thrust acting on the guide vanes Rv was decomposed into an axial force Rvz and a circumferential force Rvθ. These two forces can be expressed respectively aswhere Cz and Cθ were the axial thrust coefficient and the circumferential thrust coefficient of the guide vanes respectively; ψ was the projected area coefficient of the guide vanes in the direction vertical to the pipe fluid; Uav was the average axial velocity of the pipe fluid.
- (9)
- The lift acting on the piped carriage Fl was related to the hydrodynamic pressure and the average axial velocity of the pipe fluid.
2.3. Motion Model
2.4. Rotating Characteristics
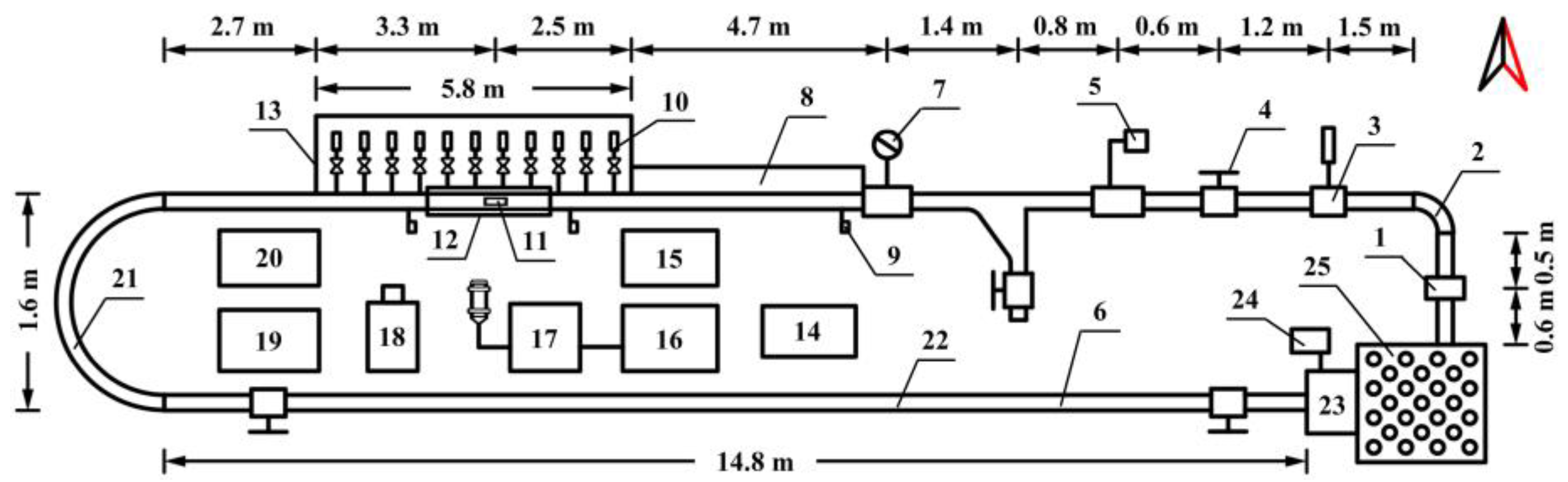
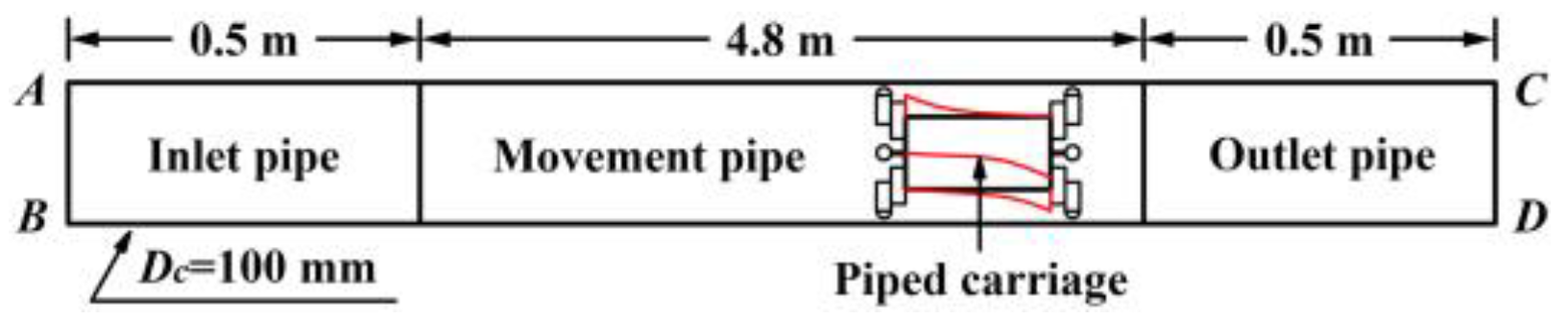
3. Materials and Methods
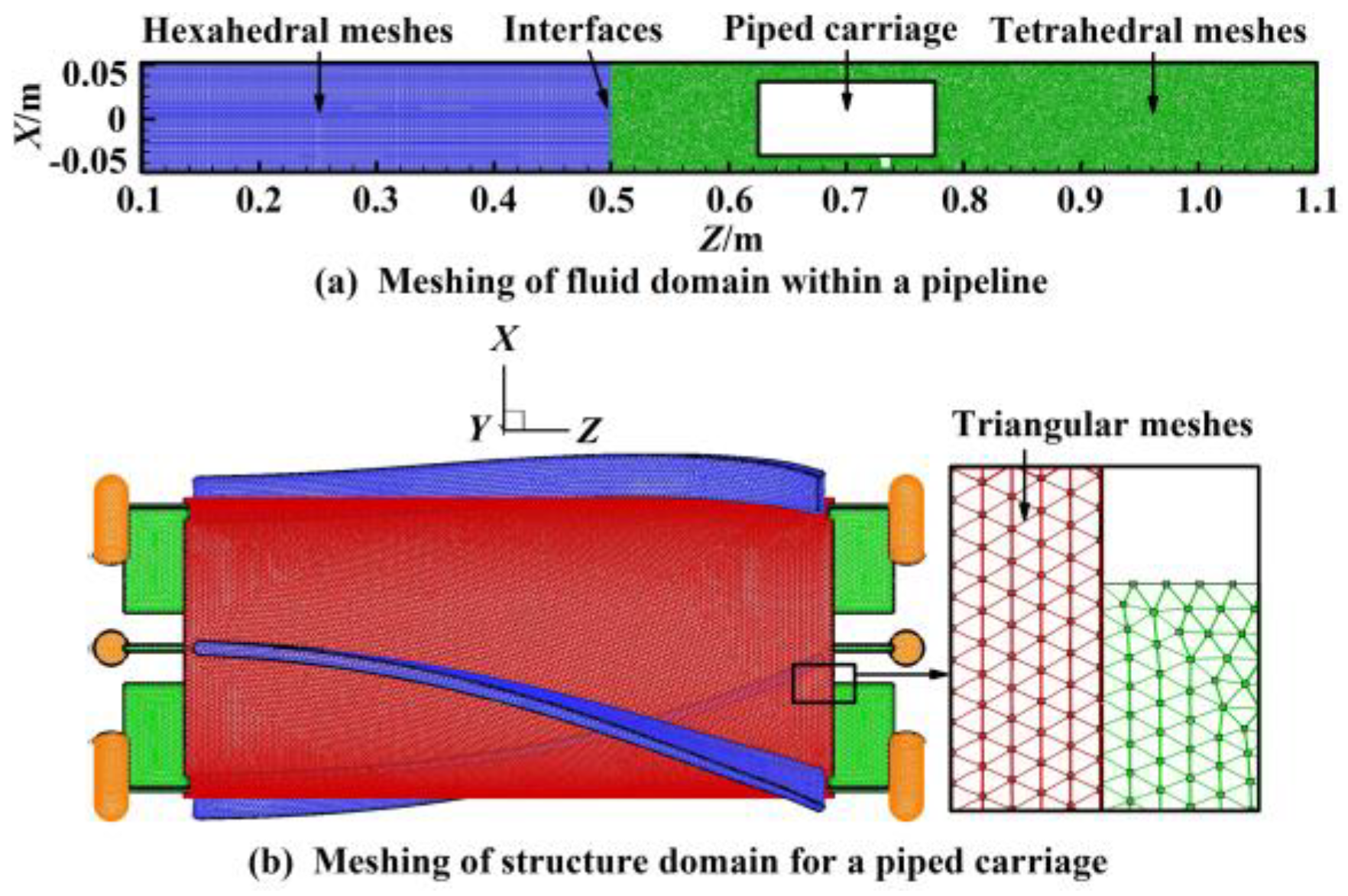
4. Bidirectional Fluid–Structure Interaction Calculation
4.1. Mathematical Model
4.2. Governing Equations of Fluid Domain
4.3. Motion Equations of Structural Domain
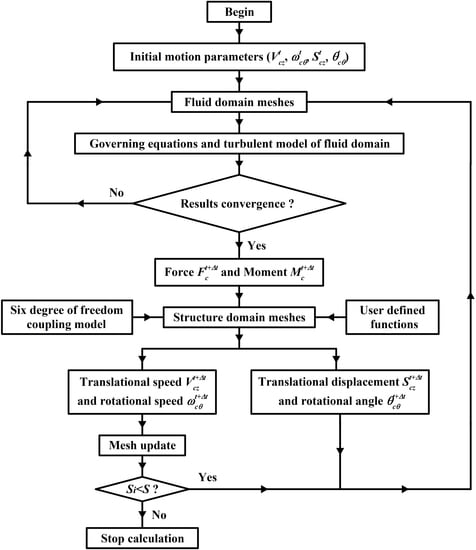
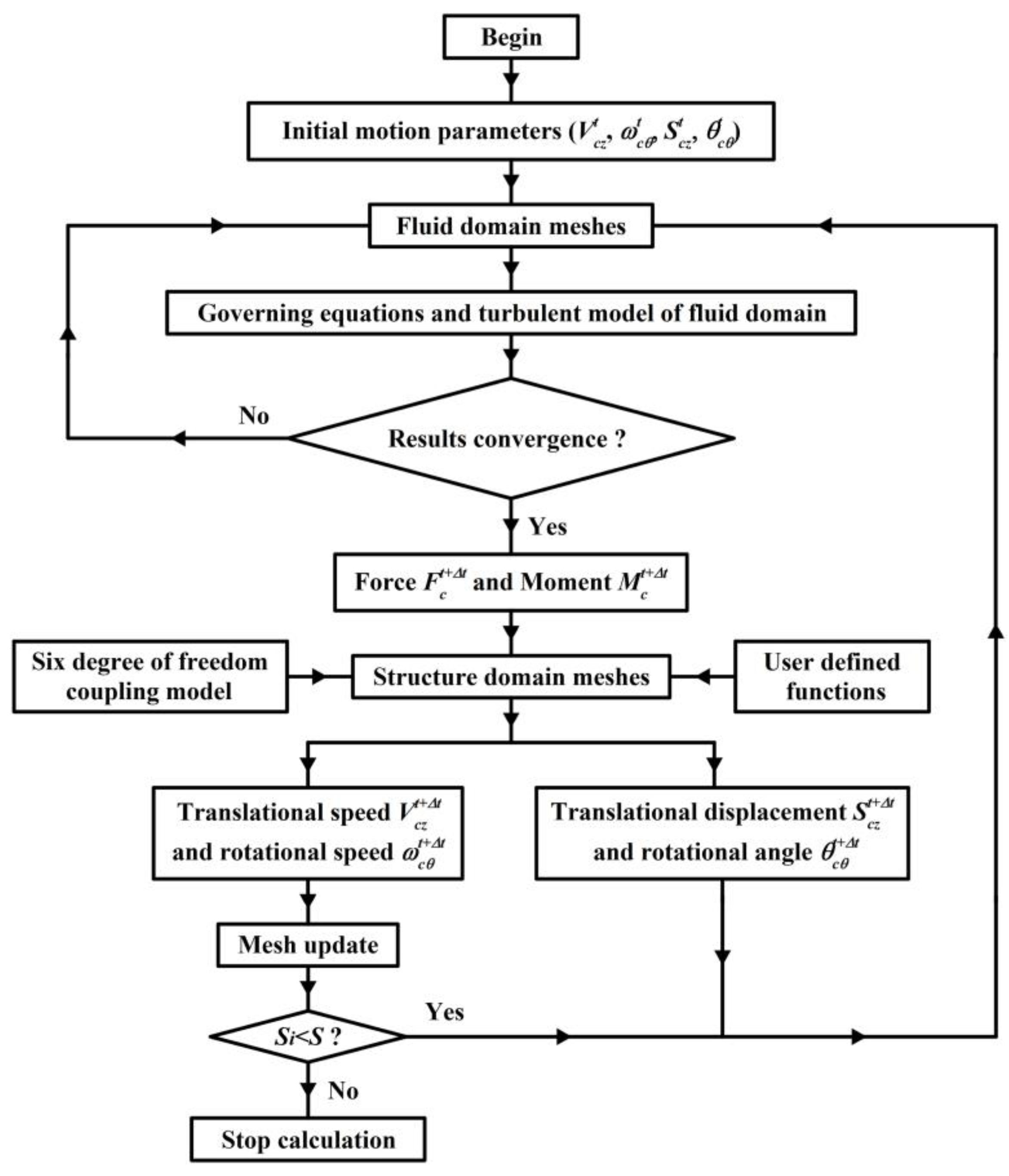
4.4. Bidirectional Fluid–Structure Interaction Algorithm
- (1)
- First of all, the motion parameters of the piped carriage needed to be set at the initial time t, including the instantaneous axial speed, ; the instantaneous angular speed, ; the instantaneous angle, ; and the instantaneous displacement, .
- (2)
- The instantaneous axial speed and the instantaneous angular speed at time t were regarded as the boundary conditions for the next iteration. The hydraulic characteristics at time t + ∆t were solved based on the governing equations and the turbulent model of the fluid domain. When the internal flow field was fully converged, the instantaneous resultant force and the instantaneous moment acting on the piped carriage at time t + ∆t were obtained.
- (3)
- The instantaneous axial speed and the instantaneous displacement of the piped carriage at t + ∆t were calculated, which were expressed as
- (4)
- The instantaneous angular speed and the instantaneous angle of the piped carriage at time t + ∆t were calculated, which were expressed as
- (5)
- Combined with the instantaneous displacement and the instantaneous angle at time t + ∆t, the piped carriage moved to a new location, and then the meshes of the fluid domain were updated by using the moving mesh technology.
- (6)
- The instantaneous axial speed and instantaneous angular speed at time t + ∆t were used as the boundary conditions for the next iteration. The above calculation steps were repeated again until the piped carriage arrived at the pre-defined locations in the computational domains.
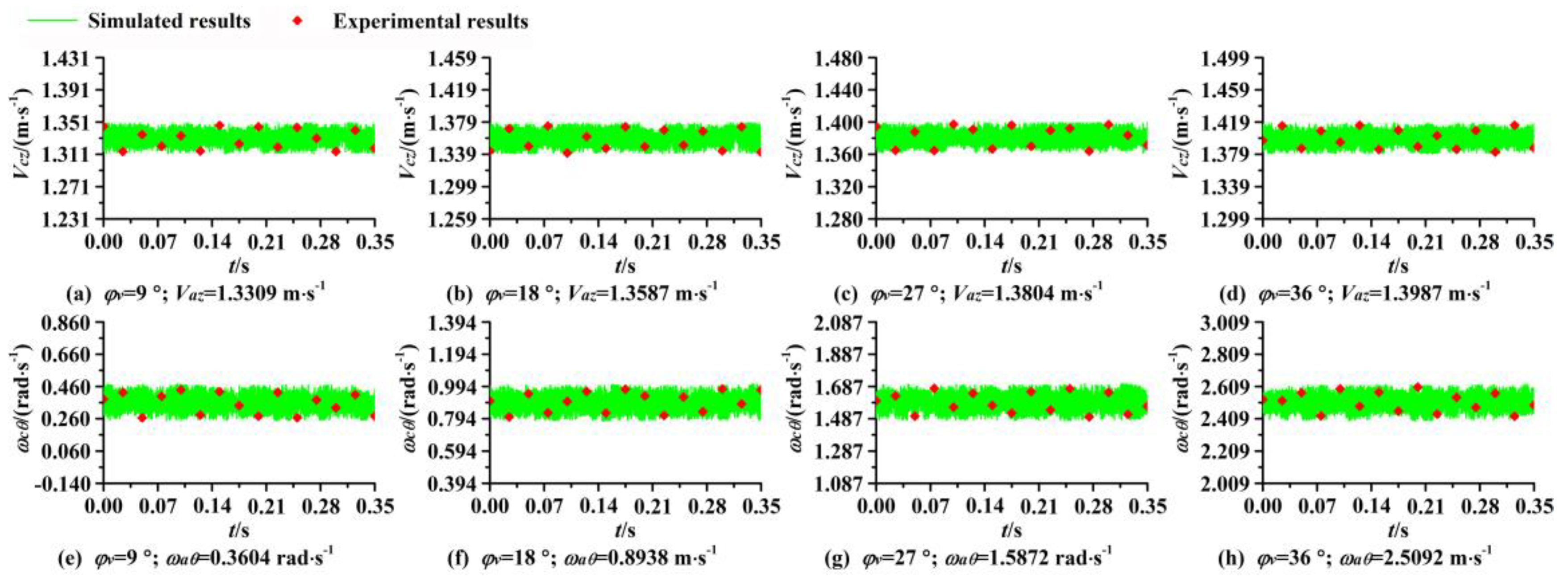
5. Verification of the Simulated Results
5.1. Instantaneous Speed
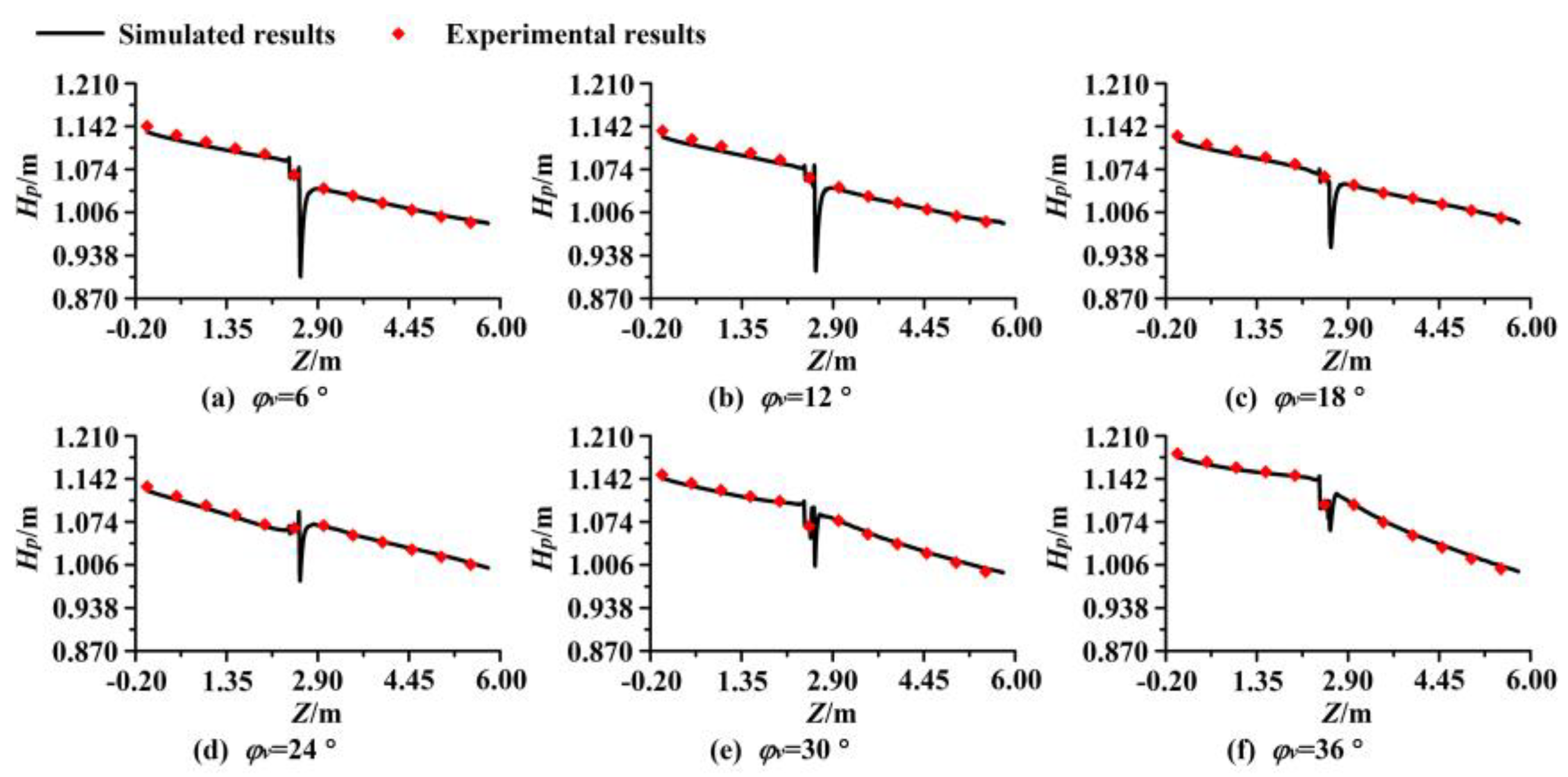
5.2. Piezometric Heads
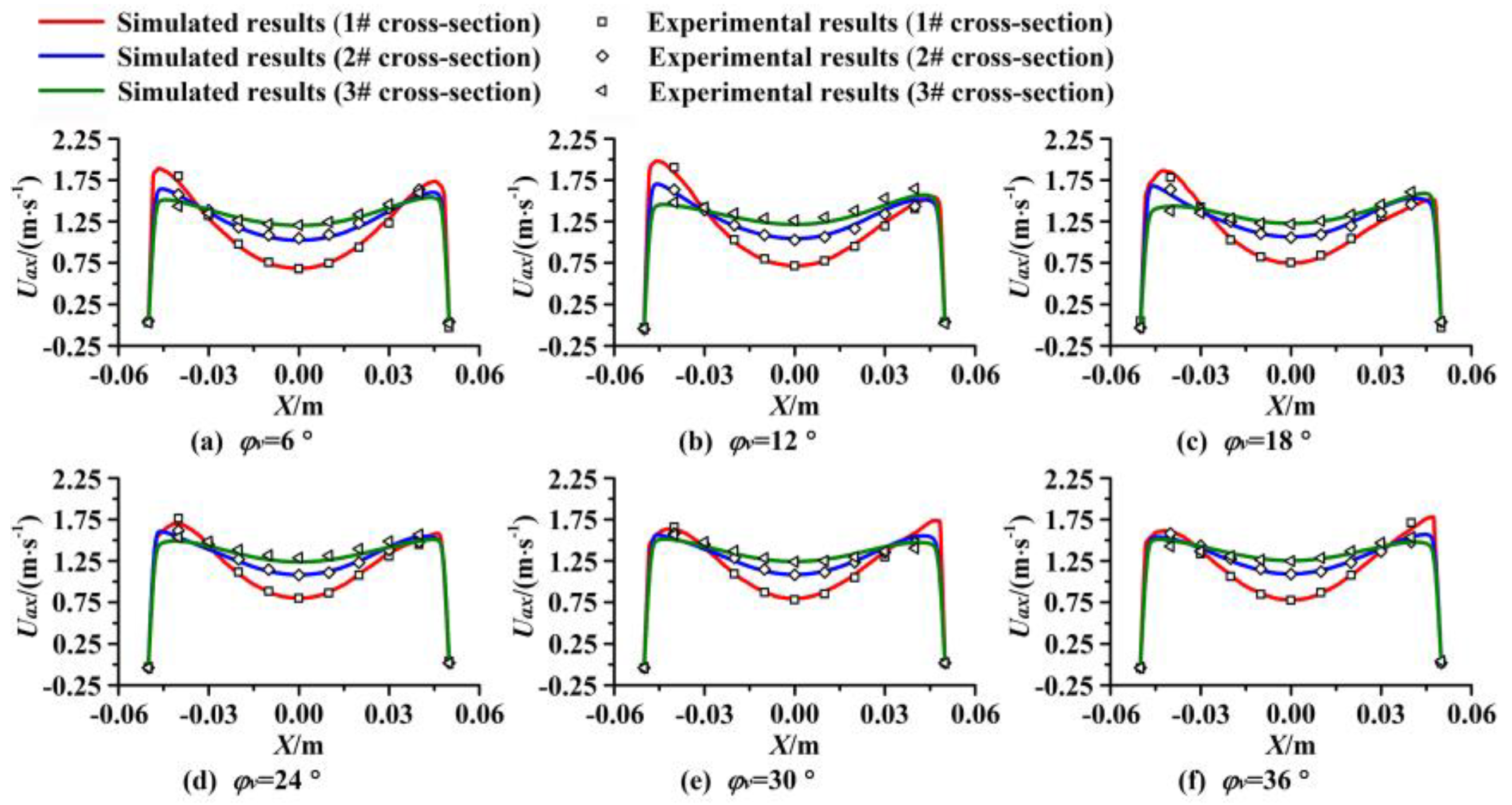
5.3. Velocity Distributions
6. Results and Discussion
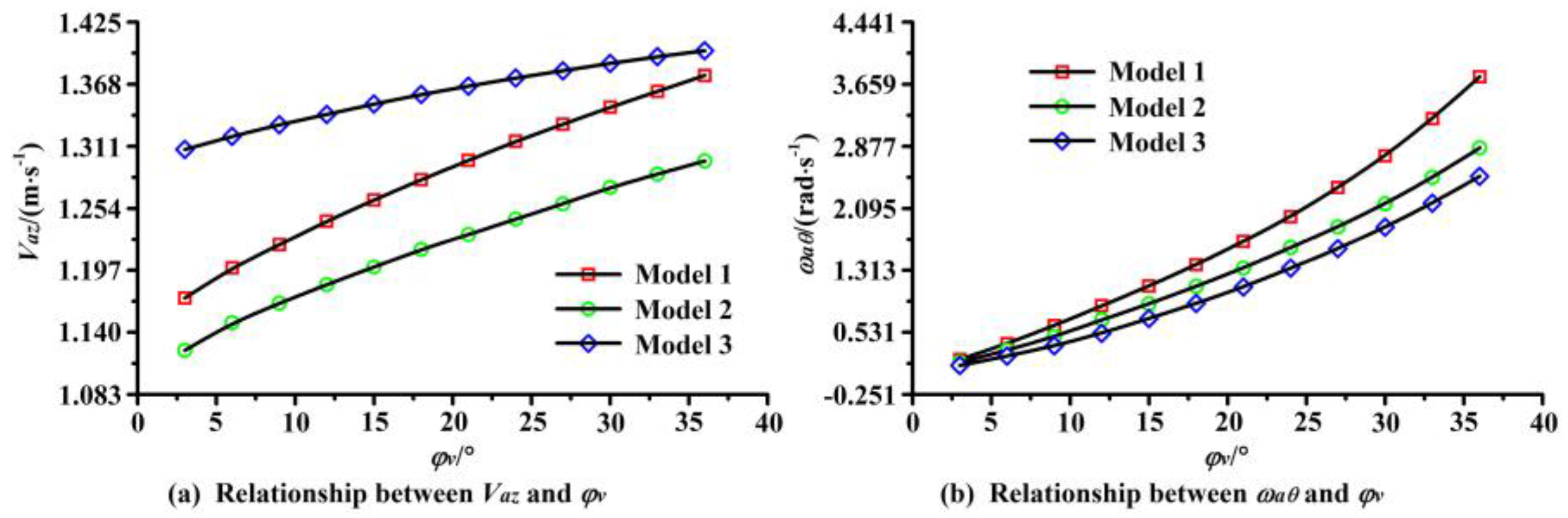
6.1. Average Speed Analysis
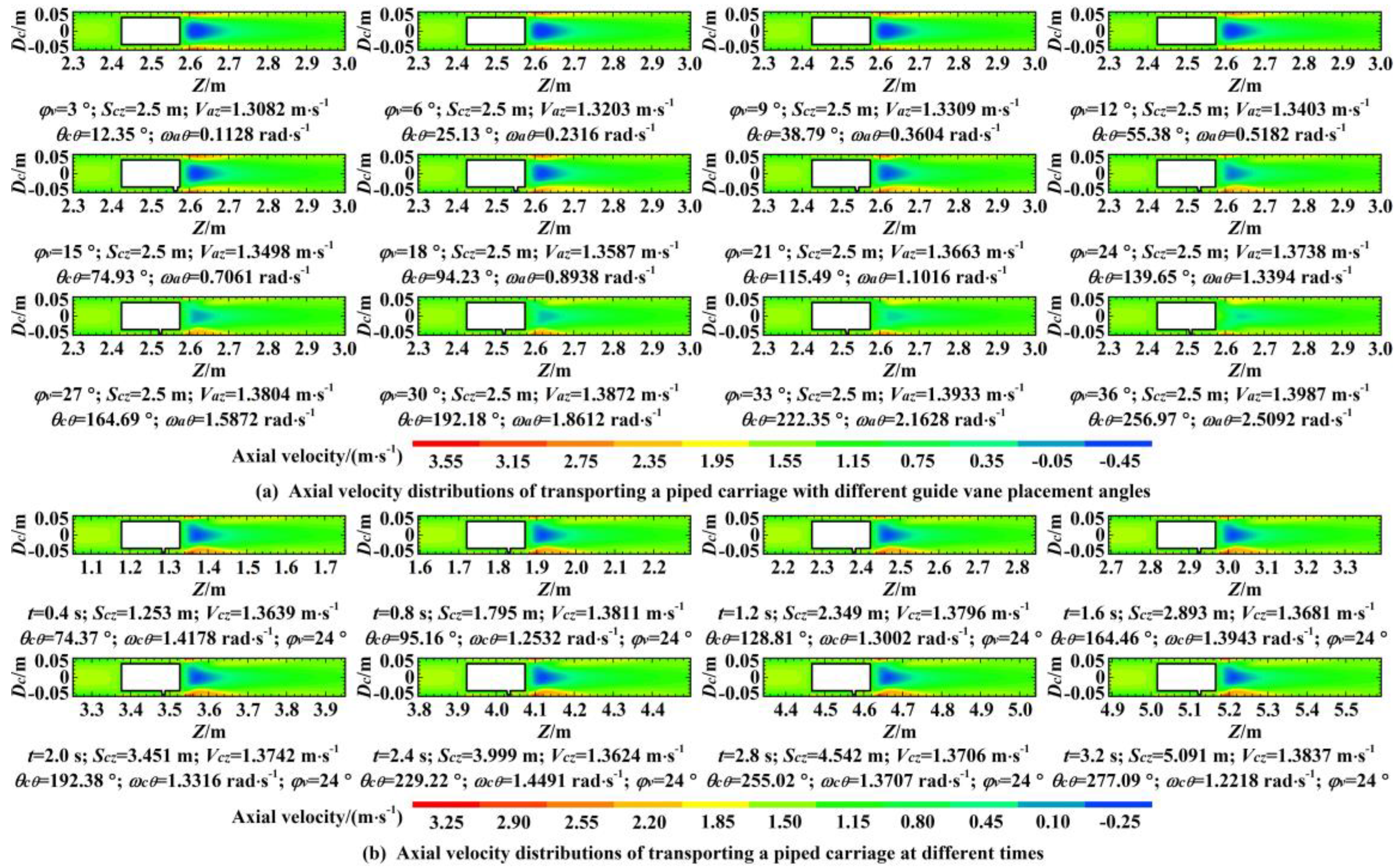
6.2. Axial Velocity Distributions
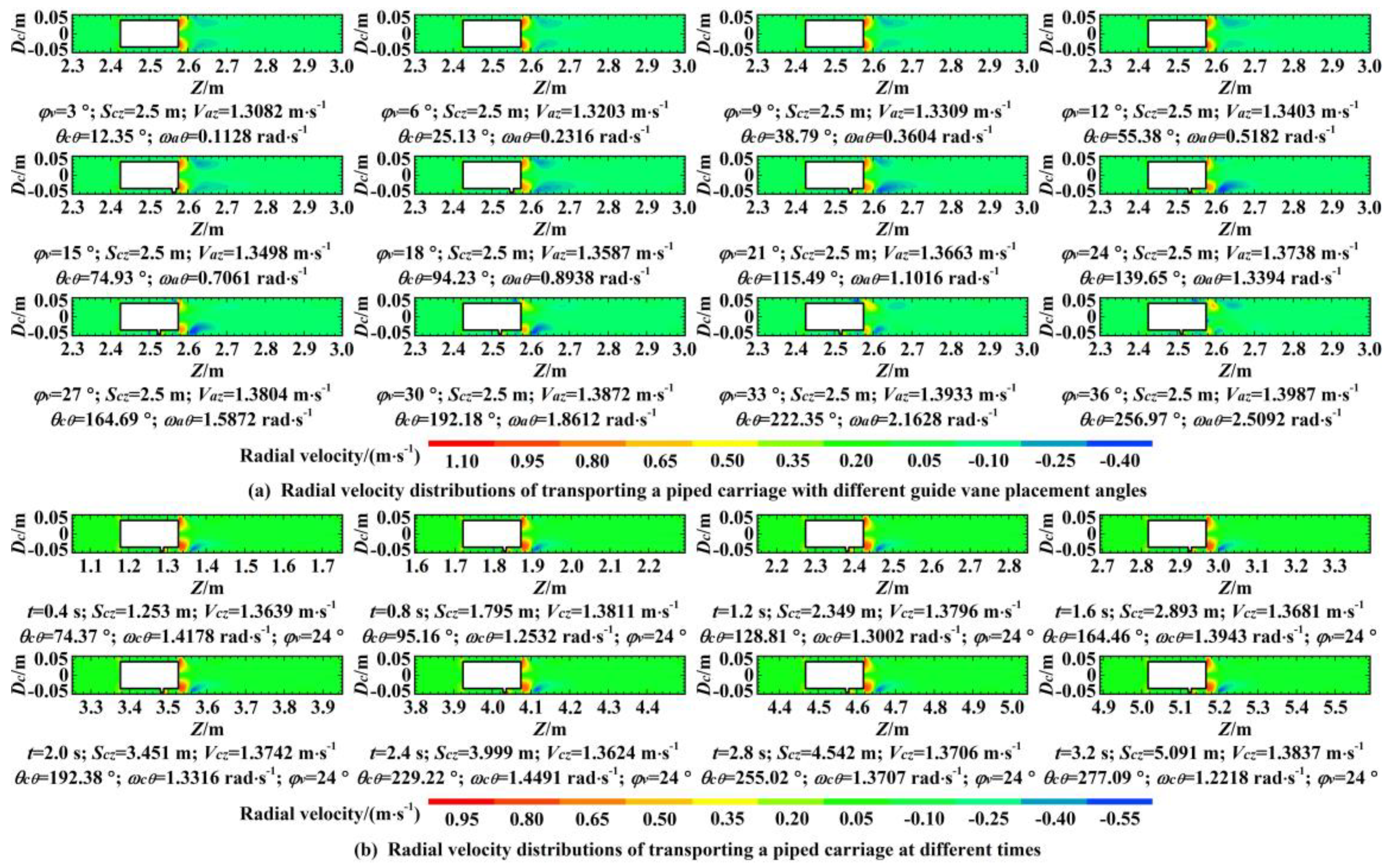
6.3. Radial Velocity Distribution
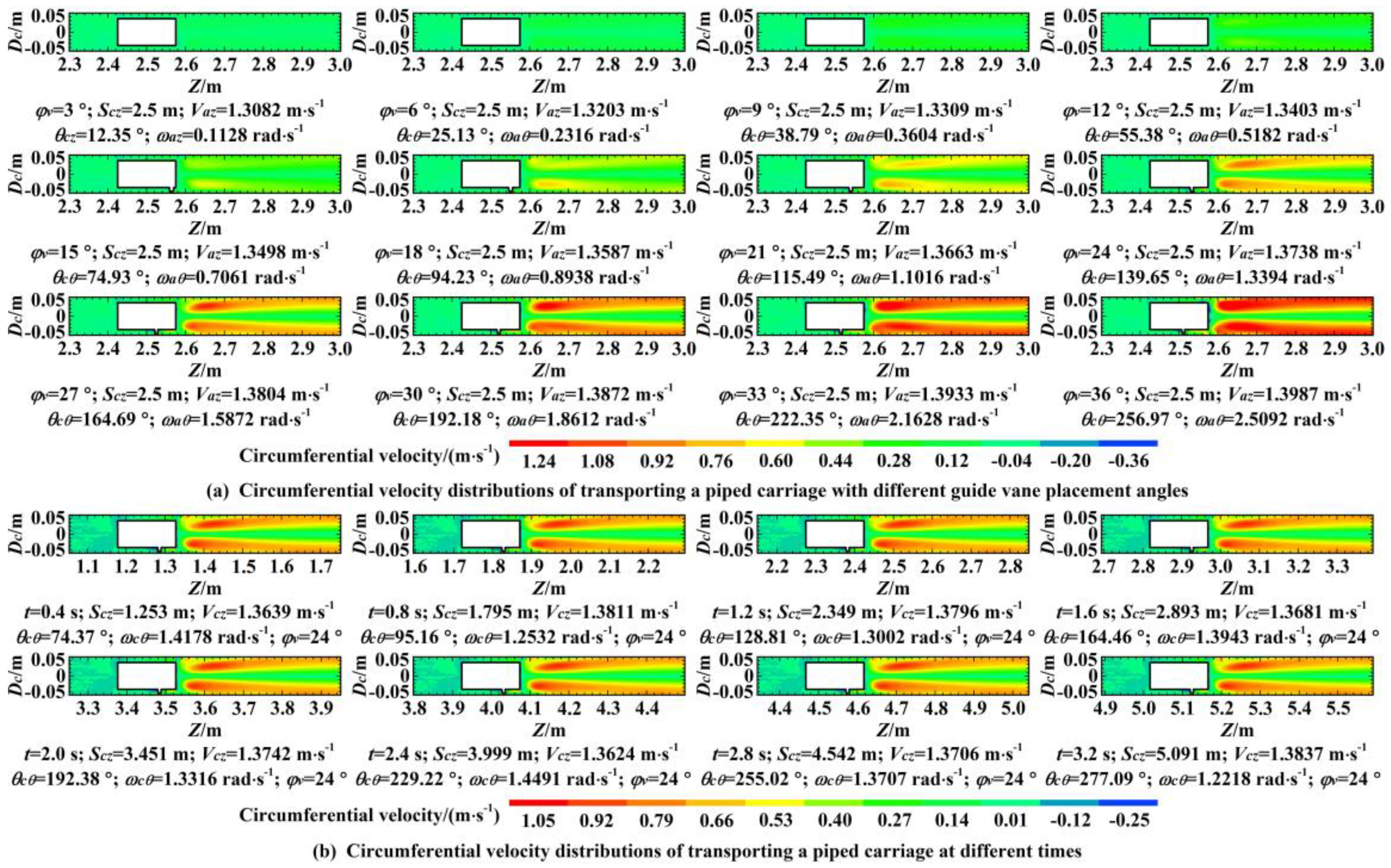
6.4. Circumferential Velocity Distribution
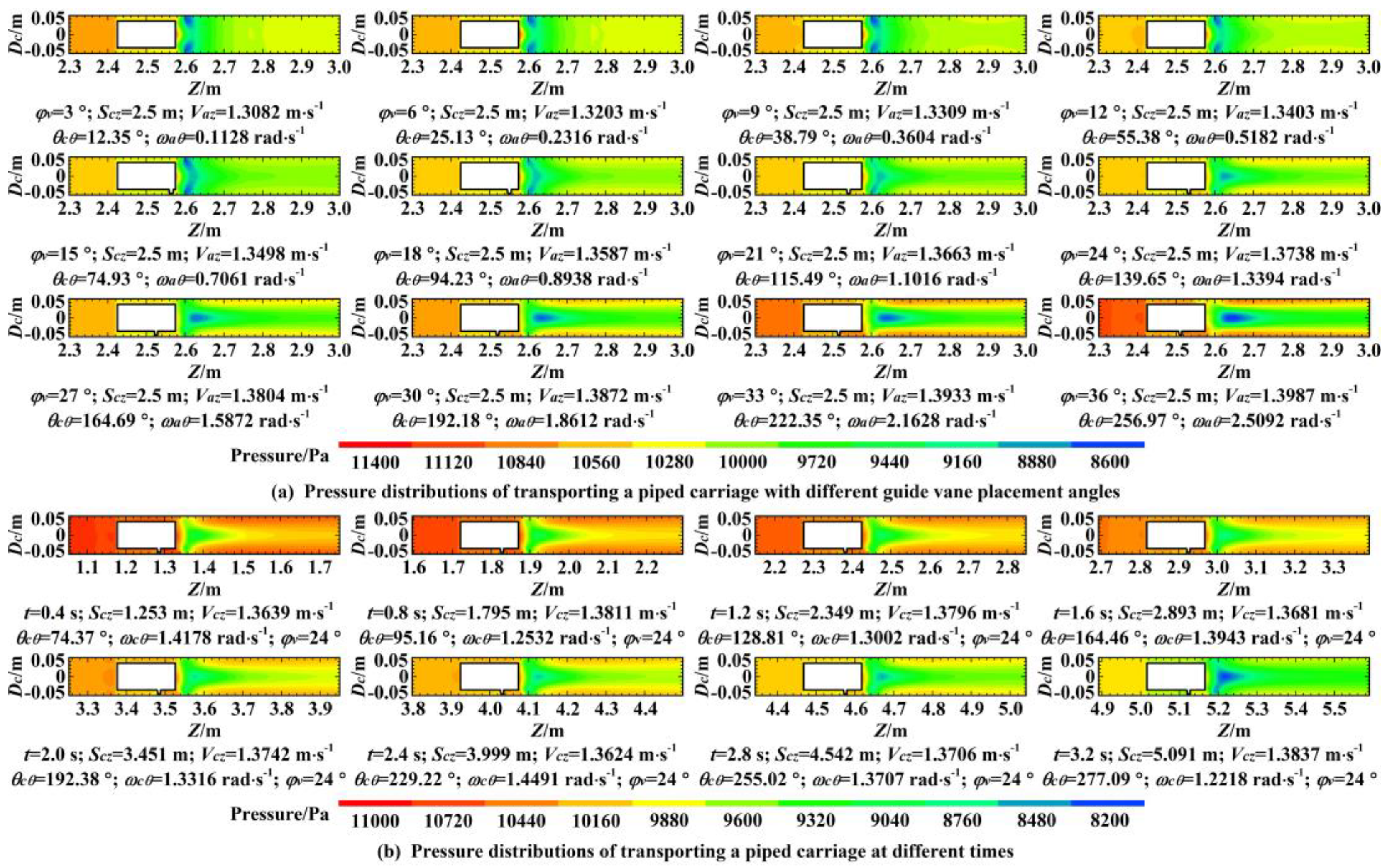
6.5. Pressure Distributions
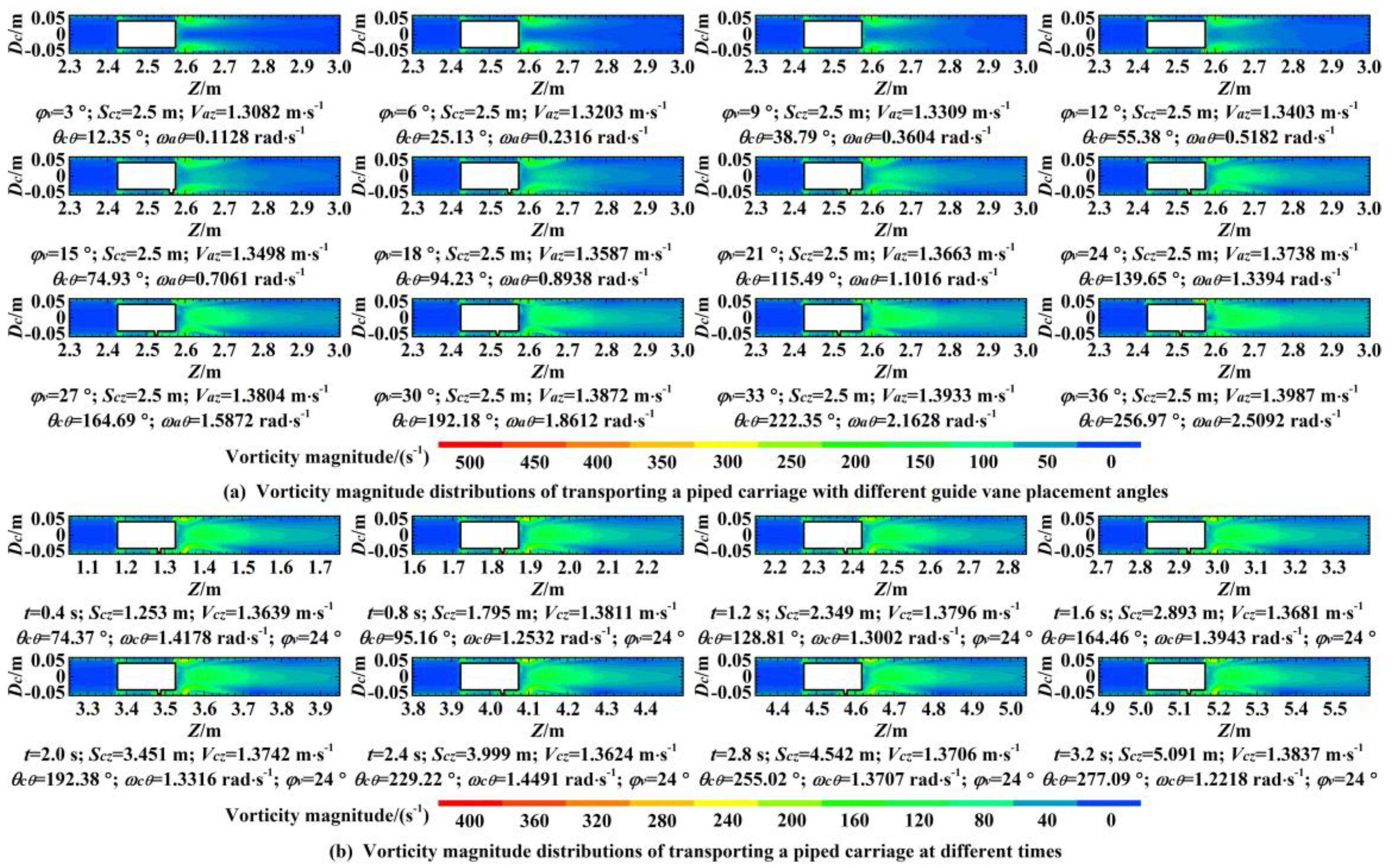
6.6. Vorticity Magnitude Distributions
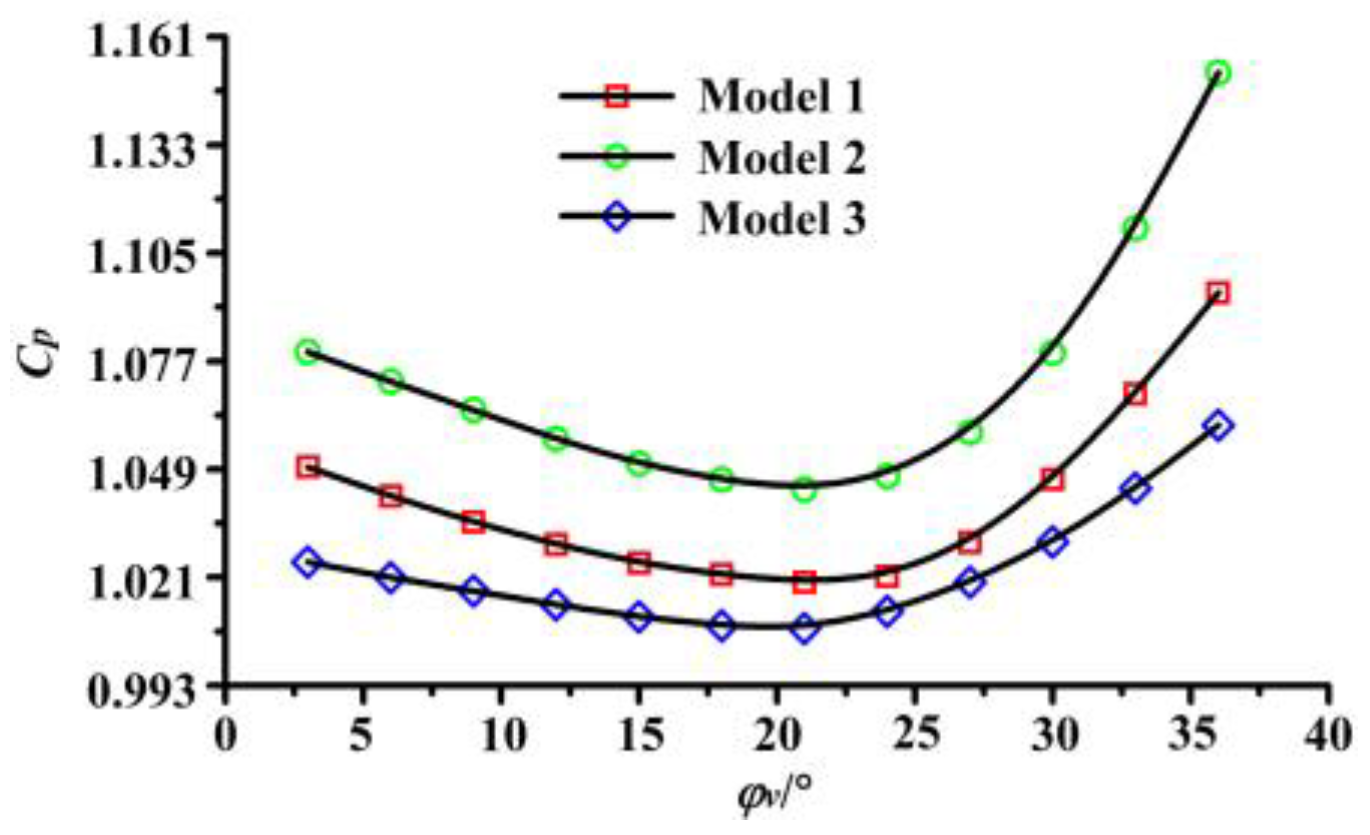
6.7. Pressure Drop Characteristics
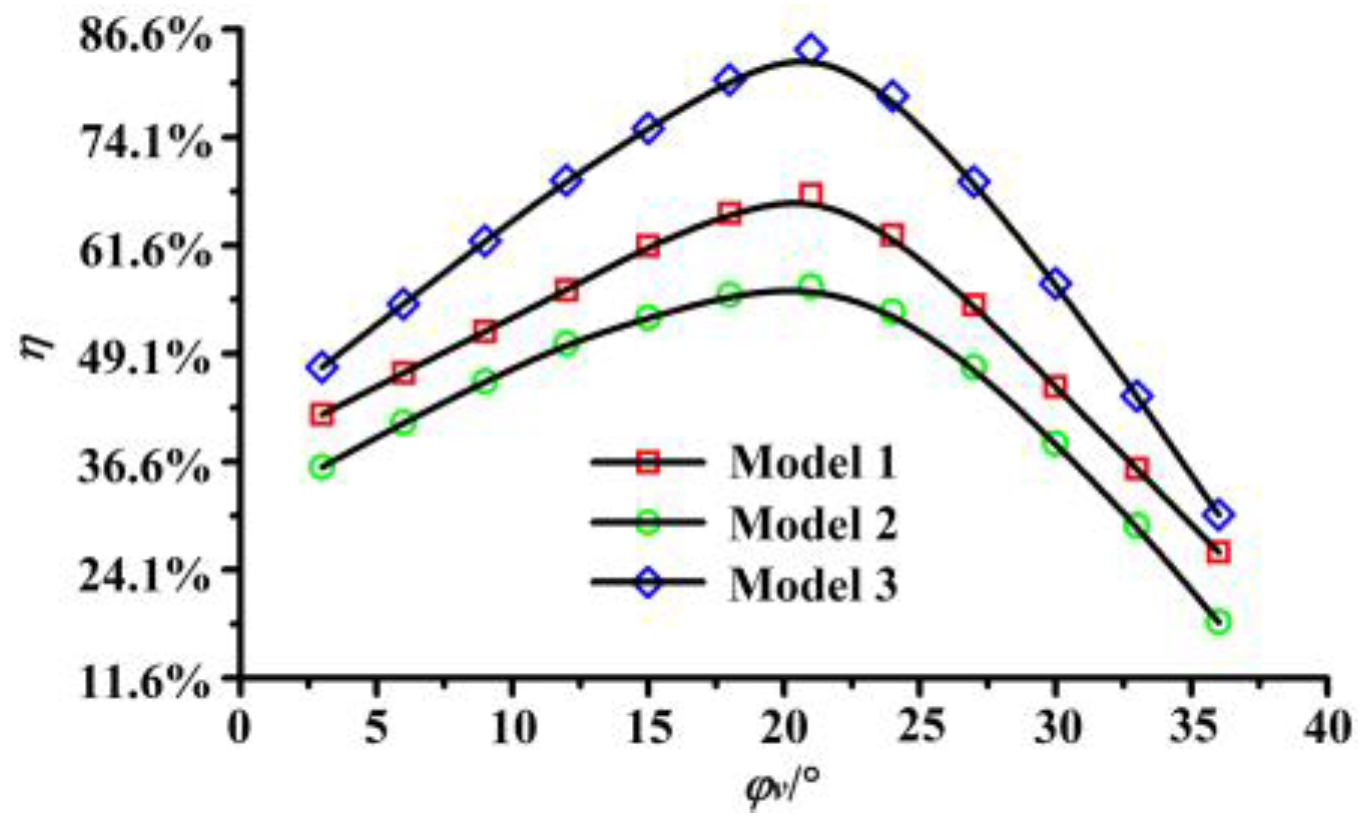
6.8. Mechanical Efficiencies
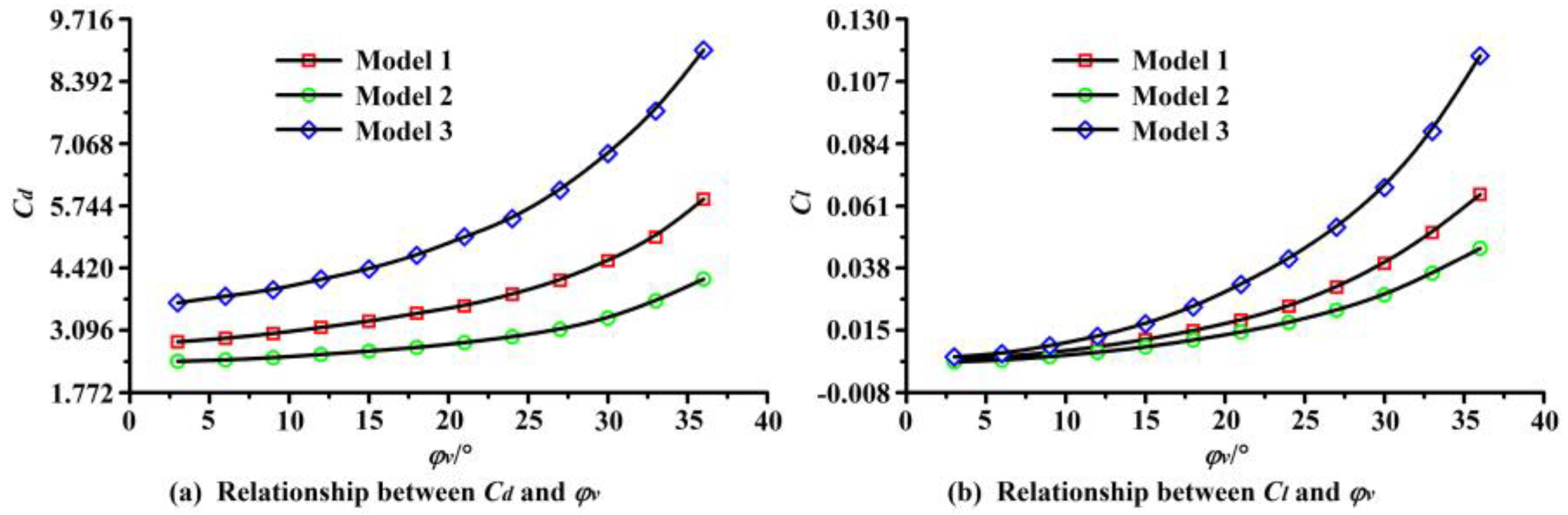
6.9. Force Statistics
7. An Optimization Model of HCPs
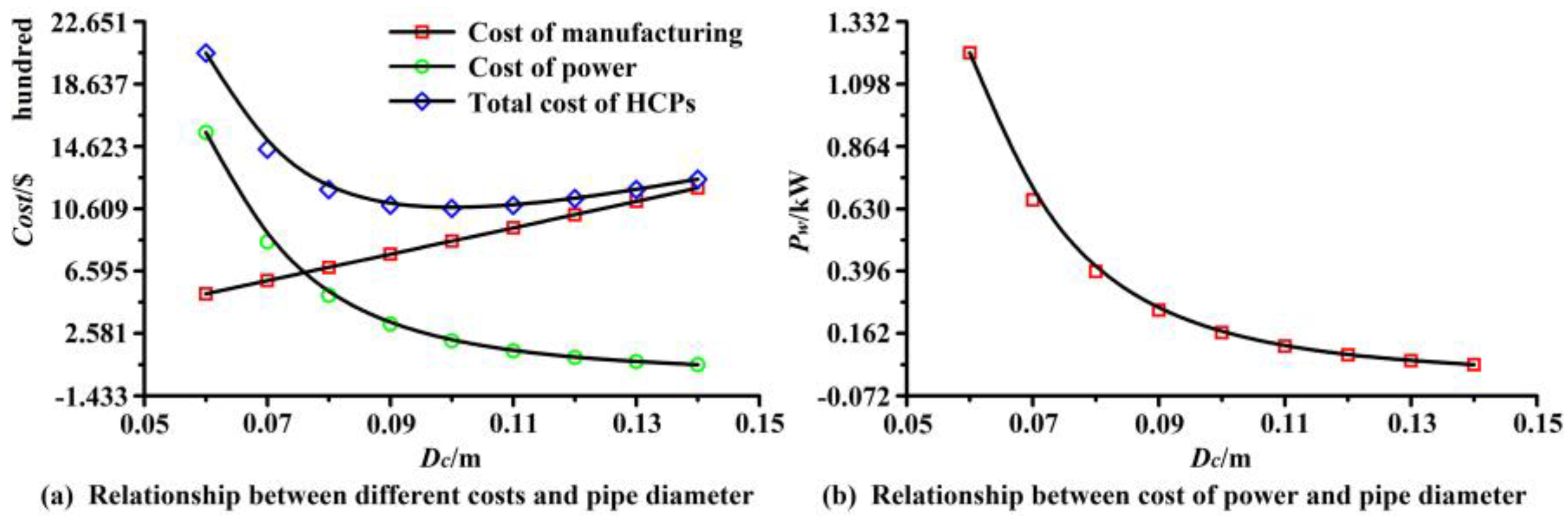
7.1. Cost of Pipeline
7.2. Cost of Piped Carriage
7.3. Cost of Power
7.4. Optimization Method
- (1)
- Assume the diameter of the pipeline Dc.
- (2)
- Obtain the total length of the conveying pipe through the dropping and receiving position of the piped carriage Lc.
- (3)
- Calculate the cost of pipelines and the piped carriage by adopting Equations (68) and (69) based on the materials for the pipelines and the piped carriages and market prices of these materials.
- (4)
- Determine and configure the physical parameters such as the diameter ratio of the piped carriage, the length of the barrel, the height of the guide vane, the length of the guide vane, the placement angle of the guide vane, as well as the transport loading based on the experimental schemes in Section 2.
- (5)
- Determine the diameter of the barrel dc, combined with the diameter of the pipelines.
- (6)
- Assume the value of the efficiency for the centrifugal pumping unit (0.6–0.75).
- (7)
- Calculate the total pressure drop of transporting the piped carriage by using the bidirectional fluid–structure interaction method ΔPtotal.
- (8)
- Assume the mixed pipe discharge Qm, based on the pipe discharge.
- (9)
- Calculate the cost of power consumption by using Equations (70) and (71) based on the unit price of electricity and the service life of the centrifugal pumping unit.
- (10)
- Calculate the total cost of HCPs, CostTotal, using Equations (64) and (65).
- (11)
- Repeat above Steps 1 to 10 for the various values of the pipe diameters to obtain the minimum value of the total cost of HCPs and its corresponding pipe diameter Dc.
- (12)
- Find out the optimal diameter of the conveying pipes in order to determine the various indicators for the optimization model of HCPs.
7.5. Design Example
8. Conclusions
- (1)
- With the increase of the guide vane placement angle, the average axial speeds of the piped carriage showed a logarithmic growth trend, while the average angular speeds showed an exponential growth trend.
- (2)
- With the increase of the guide vane placement angle, the affected areas of the axial velocity and radial velocity gradually decreased, and the affected areas of the circumferential velocity and vorticity magnitude gradually increased near the front end of the piped carriage. With the increase of the guide vane placement angle, both the average drag coefficient and the average lift coefficient of the piped carriage showed exponential growth.
- (3)
- The combined effects of both the energy dissipation and the energy conversion caused the local low-pressure areas to develop near the front end of the piped carriage, and the energy conversion caused the downstream pressure of the piped carriage to rise sharply again. With the increase of the guide vane placement angle, the average pressure drop coefficient of transporting the piped carriage first decreased and then increased, while the mechanical efficiency of transporting the piped carriage first increased and then decreased. The average pressure drop coefficient and mechanical efficiency of the piped carriage collectively indicated that the optimal placement angle of the guide vanes was 21° when the transport loading was 0.6 kg and the pipe discharge was 50 m3·h−1.
- (4)
- In the near-wall areas of the piped carriage, the axial velocity distributions, radial velocity distributions, circumferential velocity distributions, and vorticity magnitude distributions were basically the same, while the pressure distributions showed a gradually decreasing trend, when the piped carriage moved through the pipelines.
- (5)
- Based on the least cost principle, the optimization model of HCPs can output the optimal pipe diameter. A practical example has been completed in order to demonstrate the usage and effectiveness of this optimization model.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tachibana, M.; Matsumoto, Y. Basic studies on hydraulic capsule transportation: Part 1. Loss due to cylindrical capsules set in circular pipe flow. Bull. JSME 1981, 24, 987–994. [Google Scholar] [CrossRef]
- Liu, H.; Rhee, K.H. Behavior of non-uniform-density capsules in HCP. J. Pipeline 1987, 6, 307–318. [Google Scholar]
- Brown, R.A.S. Capsule pipeline research at the Alberta Research Council, 1985–1978. J. Pipeline 1987, 6, 75–82. [Google Scholar]
- Charles, M.E. The pipeline flow of capsules: Part 2: Theoretical analysis of the concentric flow of cylindrical forms. Can. J. Chem. Eng. 1962, 41, 46–51. [Google Scholar]
- Ellis, H.S. The pipeline flow of capsules: Part 5: An experimental investigation of the transport by water of single spherical capsules with density greater than that of the water. Can. J. Chem. Eng. 1964, 42, 155–161. [Google Scholar] [CrossRef]
- Round, G.F.; Bolt, L.H. The pipeline flow of capsules: Part 8: An experimental investigation of the transport in oil of single, denser-than-oil, spherical and cylindrical capsules. Can. J. Chem. Eng. 1965, 43, 197–205. [Google Scholar] [CrossRef]
- Kruyer, J.; Snyder, W.T. Relationship between capsule pulling force and pressure gradient in a pipe. Can. J. Chem. Eng. 1975, 53, 378–383. [Google Scholar] [CrossRef]
- Latto, B.; Chow, K.W. Hydrodynamic transport of cylindrical capsules in a vertical pipeline. Can. J. Chem. Eng. 1982, 60, 713–722. [Google Scholar] [CrossRef]
- Tomita, Y.; Yamamoto, M.; Funatsu, K. Motion of a single capsule in a hydraulic pipeline. J. Fluid Mech. 1986, 171, 495–508. [Google Scholar] [CrossRef]
- Kroonenberg, H.H.V.D. A mathematical model for concentric horizontal capsule transport. Can. J. Chem. Eng. 1987, 56, 538–543. [Google Scholar] [CrossRef]
- Polderman, H.G.; Velraeds, G.; Knol, W. Turbulent lubrication flow in an annular channel. J. Fluids Eng. 1986, 108, 185–192. [Google Scholar] [CrossRef]
- Chow, K.W. An Experimental Study of the Hydrodynamic Transport of Spherical and Cylindrical Capsules in a Vertical Pipeline. Master’s Thesis, McMaster University, Hamilton, ON, Canada, 1979. [Google Scholar]
- Sud, I.; Chaddock, J.B. Drag calculations for vehicles in very long tubes from turbulent flow theory. J. Fluid Eng. 1981, 103, 361–366. [Google Scholar] [CrossRef]
- Fujiwara, Y.; Tomita, Y.; Satou, H.; Funatsu, K. Characteristic of hydraulic capsule transport. JSME Int. J. 1994, 37, 89–95. [Google Scholar] [CrossRef]
- Cheng, C.C.; Liu, H. Tilt of stationary capsule in pipe. J. Hydraul. Eng. 1996, 122, 90–96. [Google Scholar] [CrossRef]
- Lenau, C.W.; El-Bayya, M.M. Unsteady flow in hydraulic capsule pipeline. J. Fluid Eng. 1996, 122, 1168–1173. [Google Scholar] [CrossRef]
- Huang, X.; Liu, H.; Marrero, T.R. Polymer drag reduction in hydraulic capsule pipeline. AIChE J. 1997, 43, 1117–1121. [Google Scholar] [CrossRef]
- Agarwal, V.C.; Mishra, R. Optimal design of a multi-stage capsule handling multi-phase pipeline. Int. J. Press. Vessels Pip. 1998, 75, 27–35. [Google Scholar] [CrossRef]
- Vlasak, P. An experimental investigation of capsules of anomalous shape conveyed by liquid in a pipe. Powder Technol. 1999, 104, 207–213. [Google Scholar] [CrossRef]
- Yanaida, K.; Tanaka, M. Drag coefficient of a capsule inside a vertical angular pipe. Powder Technol. 1997, 94, 239–243. [Google Scholar] [CrossRef]
- Azouz, I.; Shirazi, S.A. Numerical simulation of drag reducing turbulent flow in annular conduits. J. Fluid Eng. 1997, 119, 838–846. [Google Scholar] [CrossRef]
- Sun, X.H.; Li, Y.Y.; Yan, Q.F. Experimental study on starting conditions of the hydraulic transportation on the piped carriage. In Proceedings of the 20th National Conference on Hydrodynamics, Taiyuan, China; 425–431 August 2007. [Google Scholar]
- Wang, R.; Sun, X.H.; Li, Y.Y. Transportation characteristics of piped carriage with different Reynolds numbers. J. Drain. Irrig. Mach. Eng. 2011, 29, 343–346. [Google Scholar]
- Li, Y.Y.; Sun, X.H.; Yan, Y.X. Hydraulic characteristics of tube-contained raw material hydraulic transportation under different loads on the piped carriage. Trans. Chin. Soc. Agric. Mach. 2008, 39, 93–96. [Google Scholar]
- Zhang, X.L.; Sun, X.H.; Li, Y.Y.; Xi, X.N.; Guo, F.; Zheng, L.J. Numerical investigation of the concentric annulus flow around a cylindrical body with contrasted effecting factors. J. Hydrodyn. 2015, 27, 273–285. [Google Scholar] [CrossRef]
- Wang, J.; Sun, X.H.; Li, Y.Y. Analysis of pressure characteristics of tube-contained raw material pipeline hydraulic transportation under different discharges. In Proceedings of the International Conference on Electrical, Mechanical and Industrial Engineering (ICEMIE), Phuket, Thailand, 24–25 April 2016; pp. 44–46. [Google Scholar]
- Vlasak, P.; Berman, V. A contribution to hydrotransport of capsules in bend and inclined pipeline sections. Handb. Powder Technol. 2001, 10, 521–529. [Google Scholar]
- Ulusarslan, D. Comparison of experimental pressure gradient and experimental relationships for the low density spherical capsule train with slurry flow relationships. Powder Technol. 2008, 185, 170–175. [Google Scholar] [CrossRef]
- Khalil, M.F.; Kassab, S.Z.; Adam, I.G.; Samaha, M.A. Turbulent flow around single concentric long capsule in a pipe. Appl. Math. Model. 2010, 34, 2000–2017. [Google Scholar] [CrossRef]
- Asim, T.; Mishra, R. Computational fluid dynamics based optimal design of hydraulic capsule pipelines transporting cylindrical capsules. Powder Technol. 2016, 295, 180–201. [Google Scholar] [CrossRef]
- Asim, T.; Mishra, R.; Abushaala, S.; Jain, A. Development of a design methodology for hydraulic pipelines carrying rectangular capsules. Int. J. Press. Vessels Pip. 2016, 146, 111–128. [Google Scholar] [CrossRef]
- Li, Y.Y.; Sun, X.H.; Xu, F. Numerical simulation on the piped hydraulic transportation of tube-contained raw material based on FLOW-3D. Syst. Eng.-Theory Pract. 2013, 33, 262–266. [Google Scholar]
- Feng, J.; Huang, P.Y.; Joseph, D.D. Dynamic simulation of the motion of capsules in pipelines. J. Fluid Mech. 1995, 286, 201–227. [Google Scholar] [CrossRef]
- Jiang, Q.L.; Zhai, L.L.; Wang, L.Q.; Wu, D.Z. Fluid-structure interaction analysis of annular seals and rotor systems in multi-stage pumps. J. Mech. Sci. Technol. 2013, 27, 1893–1902. [Google Scholar] [CrossRef]
- Wang, S.B.; Li, S.B.; Song, X.Z. Investigations on static aeroelastic problems of transonic fans based on fluid-structure interaction method. Proc. Inst. Mech. Eng. Part A J. Power Energy 2016, 230, 685–695. [Google Scholar] [CrossRef]
- Carravetta, A.; Antipodi, L.; Golia, U.; Fecarotta, O. Energy saving in a water supply network by coupling a pump and a pump as turbine (PAT) in a turbopump. Water 2017, 9, 62. [Google Scholar] [CrossRef]
- Kosugi, S. Effect of traveling resistance factor on pneumatic capsule pipeline system. Powder Technol. 1999, 104, 227–232. [Google Scholar] [CrossRef]
- Li, Y.Y.; Sun, X.H.; Li, F.; Wang, R. Hydraulic characteristics of transportation of different piped carriages in pipe. J. Drain. Irrig. Mach. Eng. 2010, 28, 174–178. [Google Scholar]
- Zhang, C.J.; Sun, X.H.; Li, Y.Y.; Zhang, X.Q. Numerical simulation of hydraulic characteristics of cyclical slit flow with moving boundary of tube-contained raw materials pipelines hydraulic transportation. Trans. Chin. Soc. Agric. Eng. 2017, 33, 76–85. [Google Scholar]
- Teke, I.; Ulusarslan, D. Mathematical expression of pressure gradient in the flow of spherical capsules less dense than water. Int. J. Multiph. Flow 2007, 33, 658–674. [Google Scholar] [CrossRef]
- Ulusarslan, D.; Teke, I. Comparison of pressure gradient correlations for the spherical capsule train flow. Part. Sci. Technol. 2008, 26, 285–295. [Google Scholar] [CrossRef]
- Fan, F.; Liang, B.C.; Li, Y.R.; Bai, Y.C.; Zhu, Y.J.; Zhu, Z.X. Numerical investigation of the influence of water jumping on the local scour beneath a pipeline under steady flow. Water 2017, 9, 642. [Google Scholar] [CrossRef]
- Stancanelli, L.M.; Musumeci, R.E.; Foti, E. Computational fluid dynamics for modeling gravity currents in the presence of oscillatory ambient flow. Water 2018, 10, 635. [Google Scholar] [CrossRef]
- Vagnoni, E.; Andolfatto, L.; Richard, S.; Münch-Alligné, C.; Avellan, F. Hydraulic performance evaluation of a micro-turbine with counter rotating runners by experimental investigation and numerical simulation. Renew. Energy 2018, 126, 943–953. [Google Scholar] [CrossRef]
- Zi, D.; Wang, F.J.; Tao, R.; Hou, Y.K. Research for impacts of boundary layer grid scale on flow field simulation results in pumping station. J. Hydraul. Eng. 2016, 47, 139–149. [Google Scholar]
- Rahimi, H.; Schepers, J.G.; Shen, W.Z.; Ramos García, N.; Schneider, M.S.; Micallef, D.; Simao Ferreira, C.J.; Jost, E.; Klein, L.; Herráez, I. Evaluation of different methods for determining the angle of attack on wind turbine blades with CFD results under axial inflow conditions. Renew. Energy 2018, 125, 866–876. [Google Scholar] [CrossRef]
- Taghinia, H.; Rahman, M.; Lu, X. Effects of different CFD modeling approaches and simplification of shape on prediction of flow field around manikin. Energy Build. 2018, 170, 47–60. [Google Scholar] [CrossRef]
- Bambauer, F.; Wirtz, S.; Scherer, V.; Bartusch, H. Transient DEM-CFD simulation of solid and fluid flow in a three dimensional blast furnace model. Powder Technol. 2018, 334, 53–64. [Google Scholar] [CrossRef]
- Zhang, J.H.; Chao, Q.; Xu, B. Analysis of the cylinder block tilting inertia moment and its effect on the performance of high-speed electro-hydrostatic actuator pumps of aircraft. Chin. J. Aeronaut. 2018, 31, 169–177. [Google Scholar] [CrossRef]
- Lv, Z.; Huang, C.Z.; Zhu, T.H.; Wang, J.; Hou, R.G. A 3D simulation of the fluid field at the jet impinging zone in ultrasonic-assisted abrasive waterjet polishing. Int. J. Adv. Manuf. Technol. 2016, 87, 3091–3103. [Google Scholar] [CrossRef]
- Bailoor, S.; Annangi, A.; Seo, J.H.; Bhardwaj, R. Fluid–structure interaction solver for compressible flows with applications to blast loading on thin elastic structures. Appl. Math. Model. 2017, 52, 470–492. [Google Scholar] [CrossRef]
- Zhu, S.Q.; Hai-Yuan, L.I.; Chen, Z.H.; Huang, Z.G.; Zhang, H.H. Numerical investigations on missile separation of an aircraft based on CFD/CSD two-way coupling method. Eng. Mech. 2017, 34, 217–248. [Google Scholar]
- Yin, T.Y.; Pei, J.; Yuan, S.Q.; Osman, M.K.; Wang, J.B.; Wang, W.J. Fluid-structure interaction analysis of an impeller for a high-pressure booster pump for seawater desalination. J. Mech. Sci. Technol. 2017, 31, 5485–5491. [Google Scholar] [CrossRef]
- Zou, D.Y.; Xu, C.G.; Dong, H.B.; Liu, J. A shock-fitting technique for cell-centered finite volume methods on unstructured dynamic meshes. J. Comput. Phys. 2017, 345, 866–882. [Google Scholar] [CrossRef]
- Asim, T.; Algadi, A.; Mishra, R. Effect of capsule shape on hydrodynamic characteristics and optimal design of hydraulic capsule pipelines. J. Pet. Sci. Eng. 2018, 161, 390–408. [Google Scholar] [CrossRef]
- Zhu, M.L.; Yang, X.D.; Tian, F.W. The optimal design for long distance conduit of pumping station. J. Hydraul. Eng. 1998, S1, 106–109. [Google Scholar]
- Shu, D.F. The Research on Hydraulic Characteristics of Migration of Pipe Carriage under Different Diameter Ratios. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2010. [Google Scholar]
- Sun, L.; Sun, X.H.; Li, Y.Y.; Jing, Y.H. Cyclical slit flow of concentricity under different diameter ratios. Yellow River 2014, 36, 110–113. [Google Scholar]

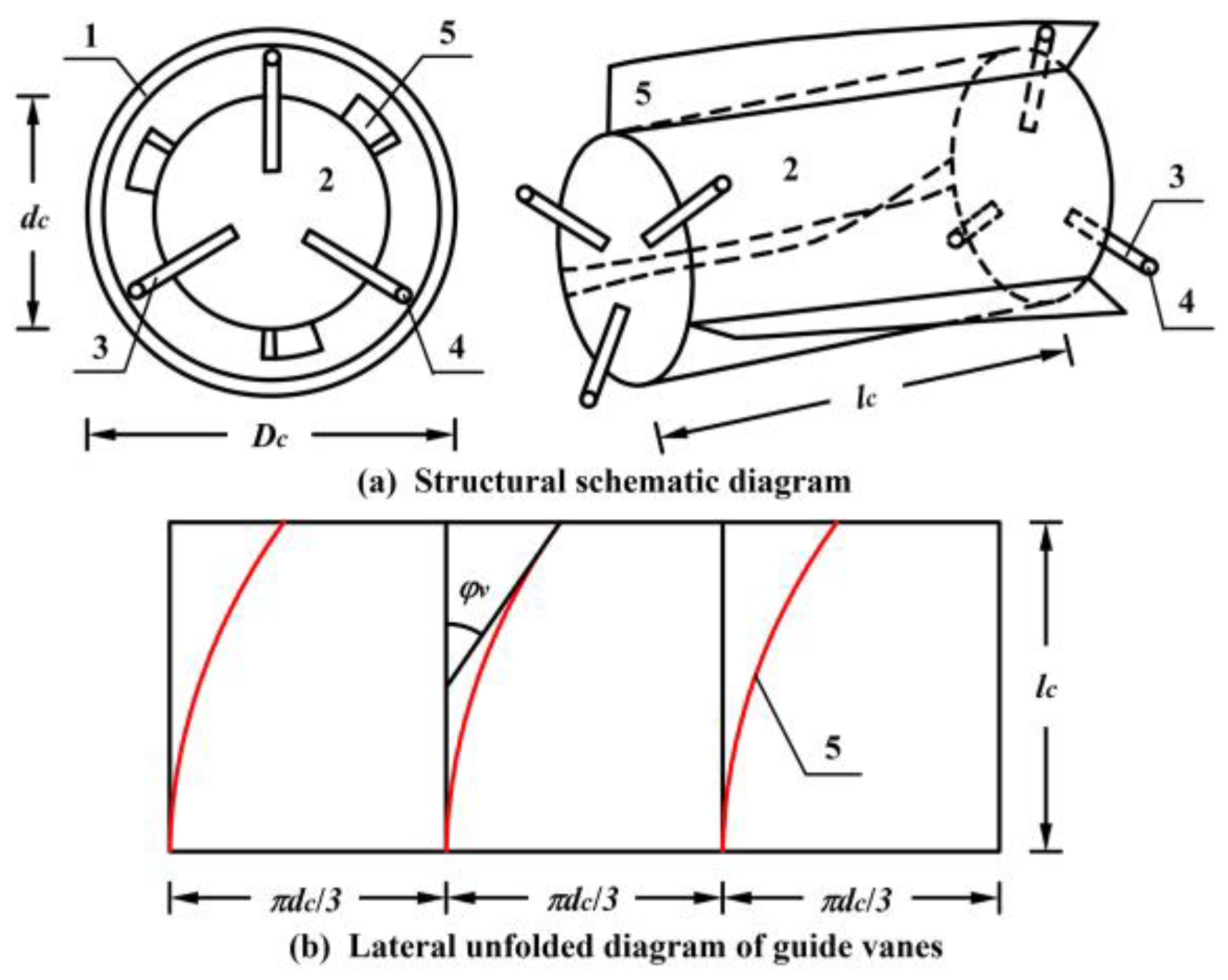
| Model of Piped Carriage | Model 1 | Model 2 | Model 3 | |
|---|---|---|---|---|
| Barrel | Length/mm | 100 | 150 | 150 |
| Diameter/mm | 70 | 60 | 70 | |
| Guide vane | Placement angle/° | 3/6/9/12/15/18/21/24/27/30/33/36 | ||
| Length/mm | 100 | 150 | 150 | |
| Height/mm | 10 | |||
| Transport loading/kg | 0.6 | |||
| Pipe discharge/(m3·h−1) | 50 | |||
| Mesh Size/m | Average Pressure of Inlet Cross-Section/Pa | |||||
|---|---|---|---|---|---|---|
| φv = 6° | φv = 12° | φv = 18° | φv = 24° | φv = 30° | φv = 36° | |
| 0.0045 | 11,703.21 | 11,606.79 | 11,571.42 | 11,518.76 | 11,811.74 | 12,111.42 |
| 0.004 | 11,454.86 | 11,369.96 | 11,309.38 | 11,323.09 | 11,558.04 | 11,888.51 |
| 0.0035 | 11,265.38 | 11,218.73 | 11,143.02 | 11,172.16 | 11,381.96 | 11,707.97 |
| 0.003 | 11,159.14 | 11,097.55 | 11,049.43 | 11,080.63 | 11,266.71 | 11,598.59 |
| 0.0025 | 11,101.31 | 11,023.58 | 10,967.94 | 11,010.39 | 11,201.29 | 11,527.81 |
| 0.002 | 11,057.74 | 10,981.52 | 10,922.61 | 10,962.48 | 11,158.22 | 11,485.09 |
| Boundary Name | Boundary Condition |
|---|---|
| Inlet of the horizontal pipe model | Velocity Inlet |
| Outlet of the horizontal pipe model | Pressure Outlet |
| Static wall of the horizontal pipe model | Stationary Wall |
| Moving wall of the piped carriage | Translating Wall |
| Connecting cross-sections of different pipes | Interface |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Sun, X.; Li, Y.; Zhang, X.; Zhang, X.; Yang, X.; Li, F. Effects of Guide Vane Placement Angle on Hydraulic Characteristics of Flow Field and Optimal Design of Hydraulic Capsule Pipelines. Water 2018, 10, 1378. https://doi.org/10.3390/w10101378
Zhang C, Sun X, Li Y, Zhang X, Zhang X, Yang X, Li F. Effects of Guide Vane Placement Angle on Hydraulic Characteristics of Flow Field and Optimal Design of Hydraulic Capsule Pipelines. Water. 2018; 10(10):1378. https://doi.org/10.3390/w10101378
Chicago/Turabian StyleZhang, Chunjin, Xihuan Sun, Yongye Li, Xueqin Zhang, Xuelan Zhang, Xiaoni Yang, and Fei Li. 2018. "Effects of Guide Vane Placement Angle on Hydraulic Characteristics of Flow Field and Optimal Design of Hydraulic Capsule Pipelines" Water 10, no. 10: 1378. https://doi.org/10.3390/w10101378
APA StyleZhang, C., Sun, X., Li, Y., Zhang, X., Zhang, X., Yang, X., & Li, F. (2018). Effects of Guide Vane Placement Angle on Hydraulic Characteristics of Flow Field and Optimal Design of Hydraulic Capsule Pipelines. Water, 10(10), 1378. https://doi.org/10.3390/w10101378