Modified Richards’ Equation to Improve Estimates of Soil Moisture in Two-Layered Soils after Infiltration
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Soil Moisture Measurement
2.3. Theory
2.3.1. Governing Equations
2.3.2. Modified Solution Equation with Parameters of Soil Properties for Upper Soil Layer
2.3.3. Analytical Formulation with Slope for Deeper Soil Layer
2.4. Data Statistics and Analysis
3. Results
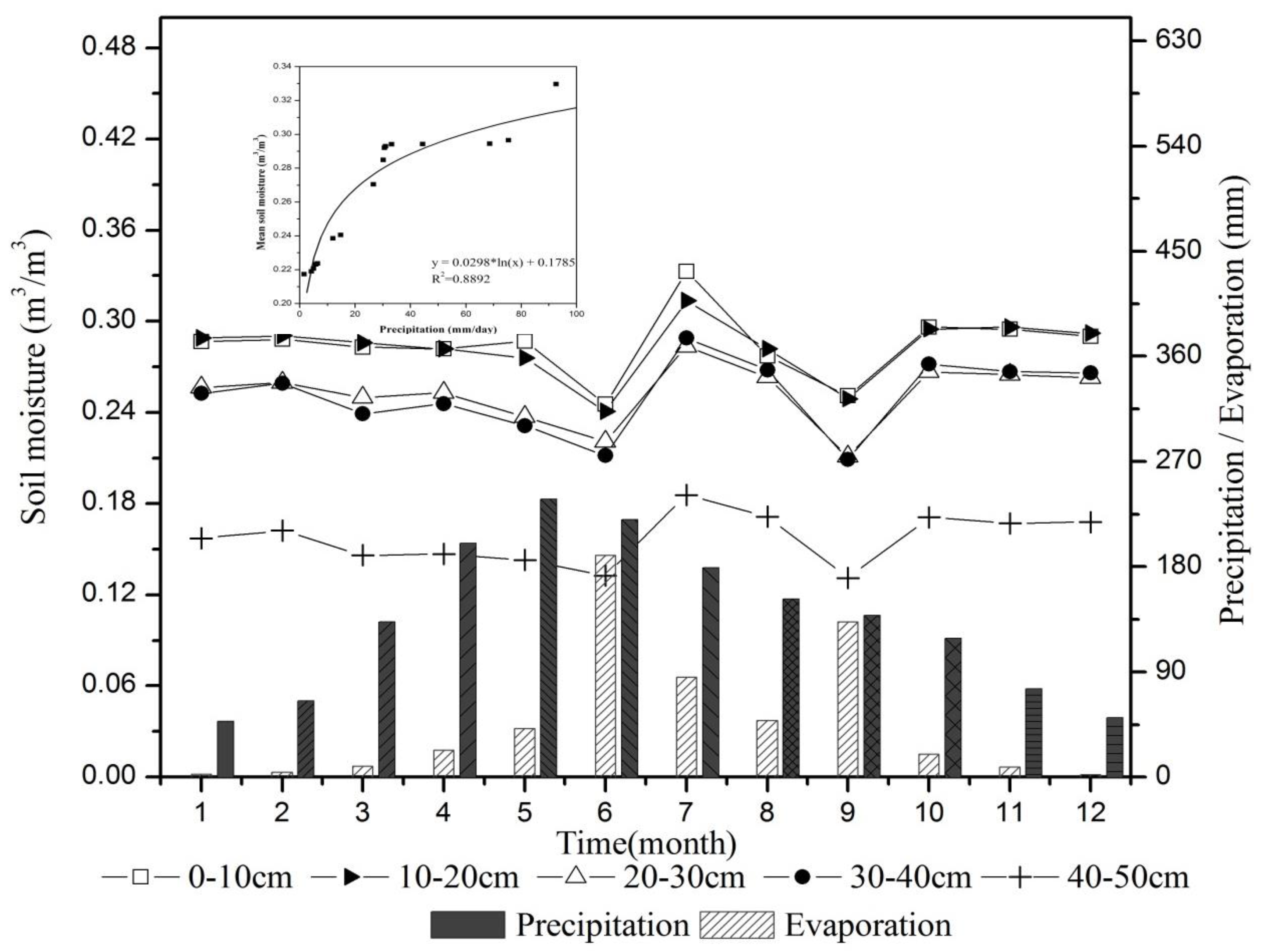
3.1. Temporal Analysis of Soil Moisture in Vertically Layered Soils
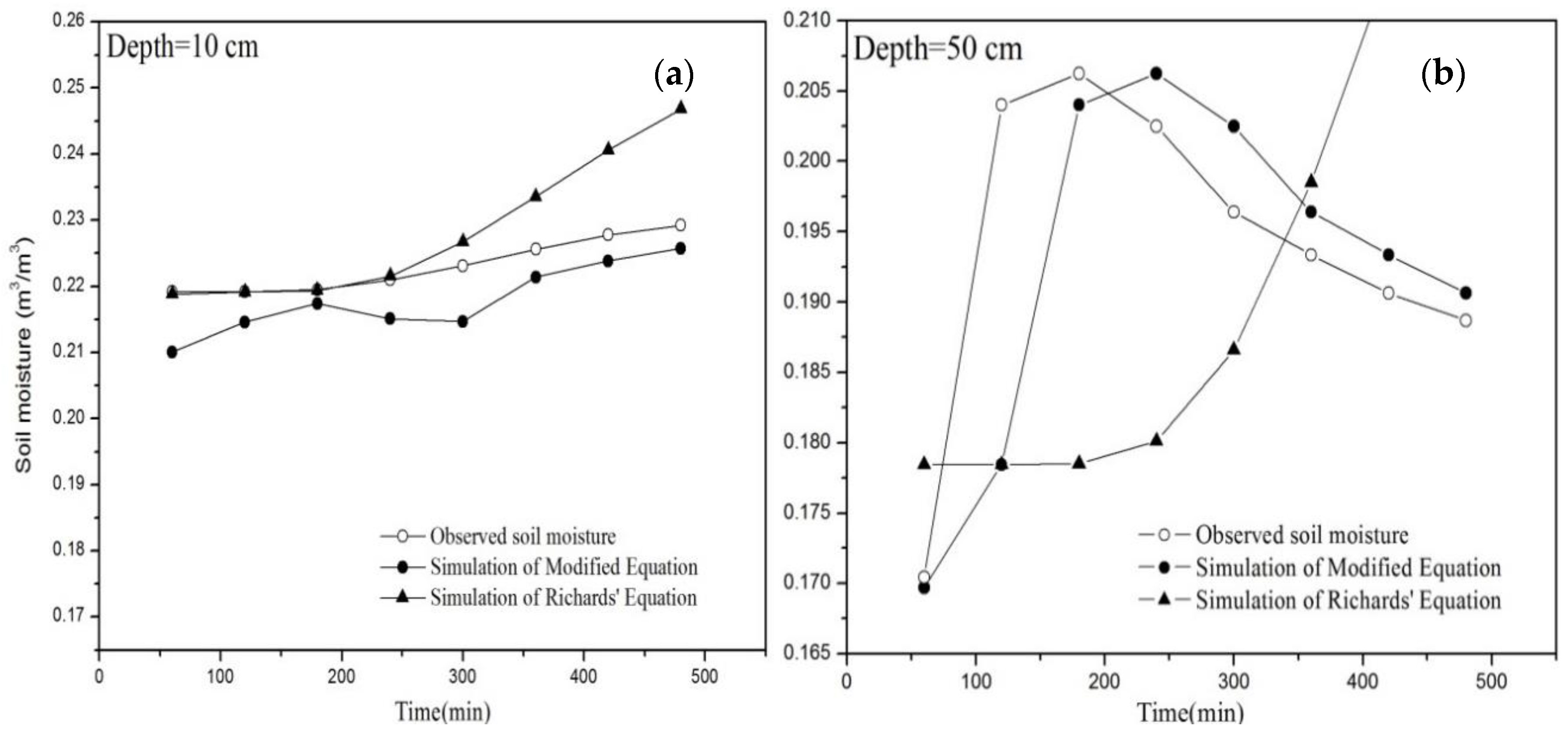
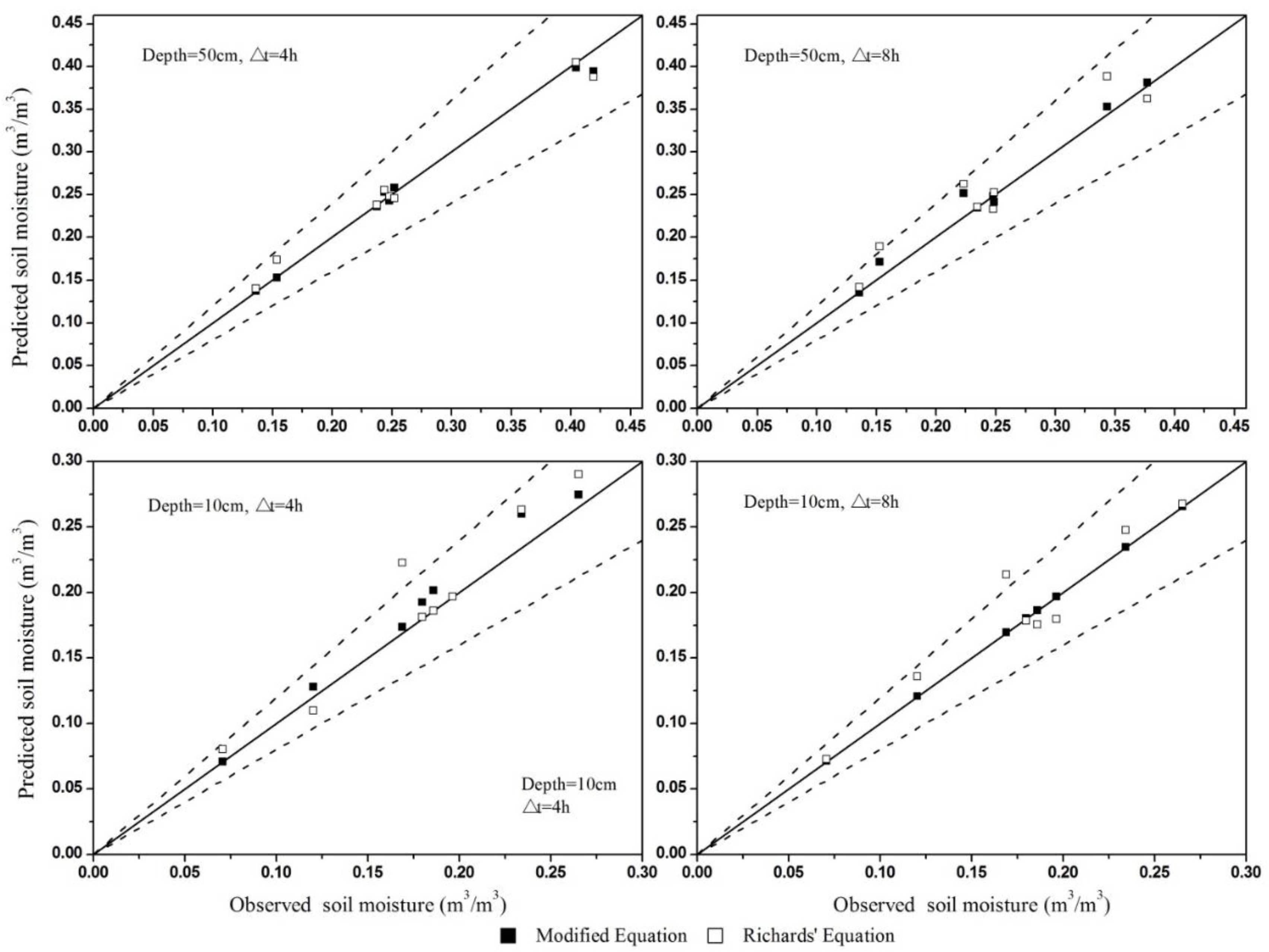
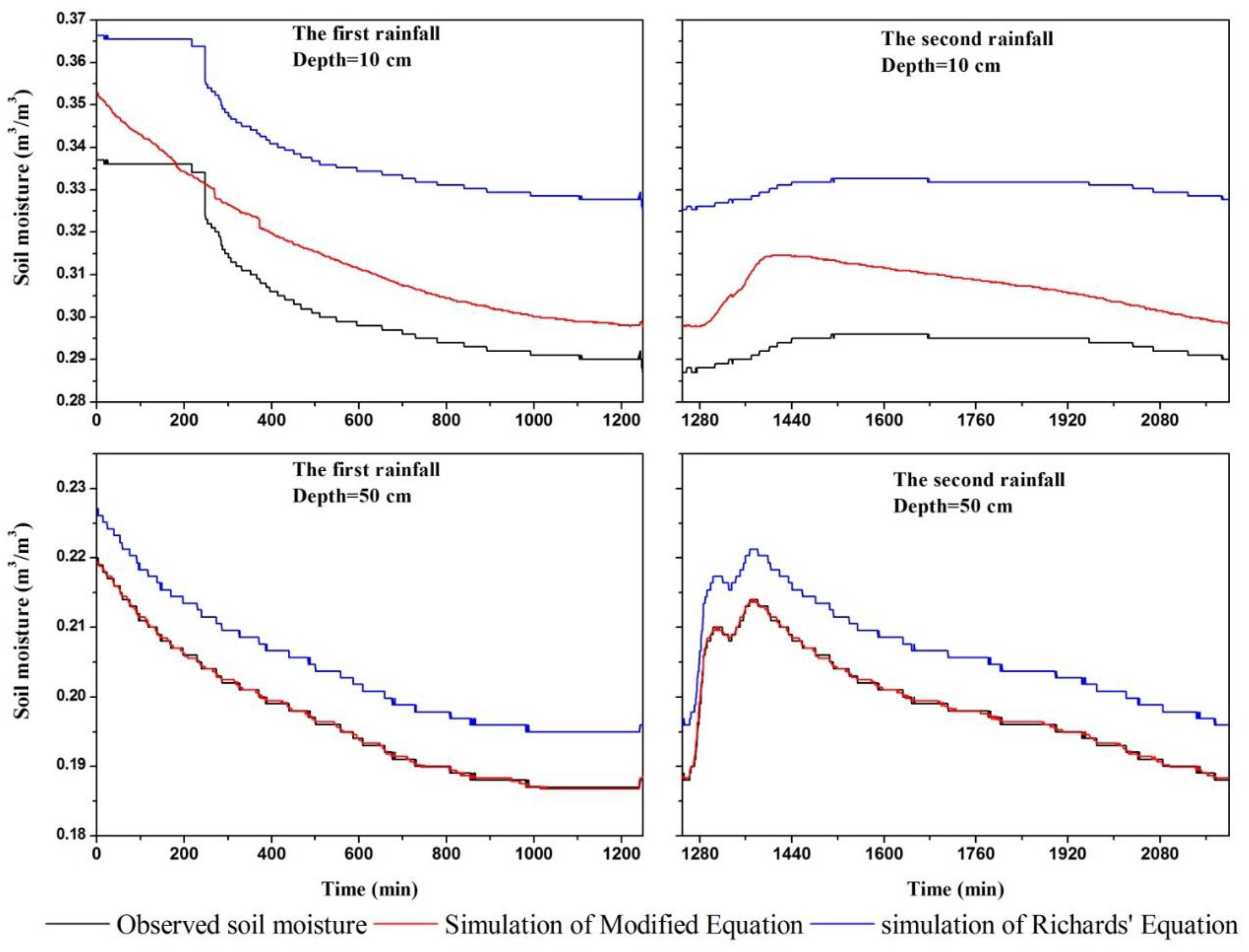
3.2. Comparison of Simulation Results of Modified and Original Richards’ Equation for Two Soil Layers
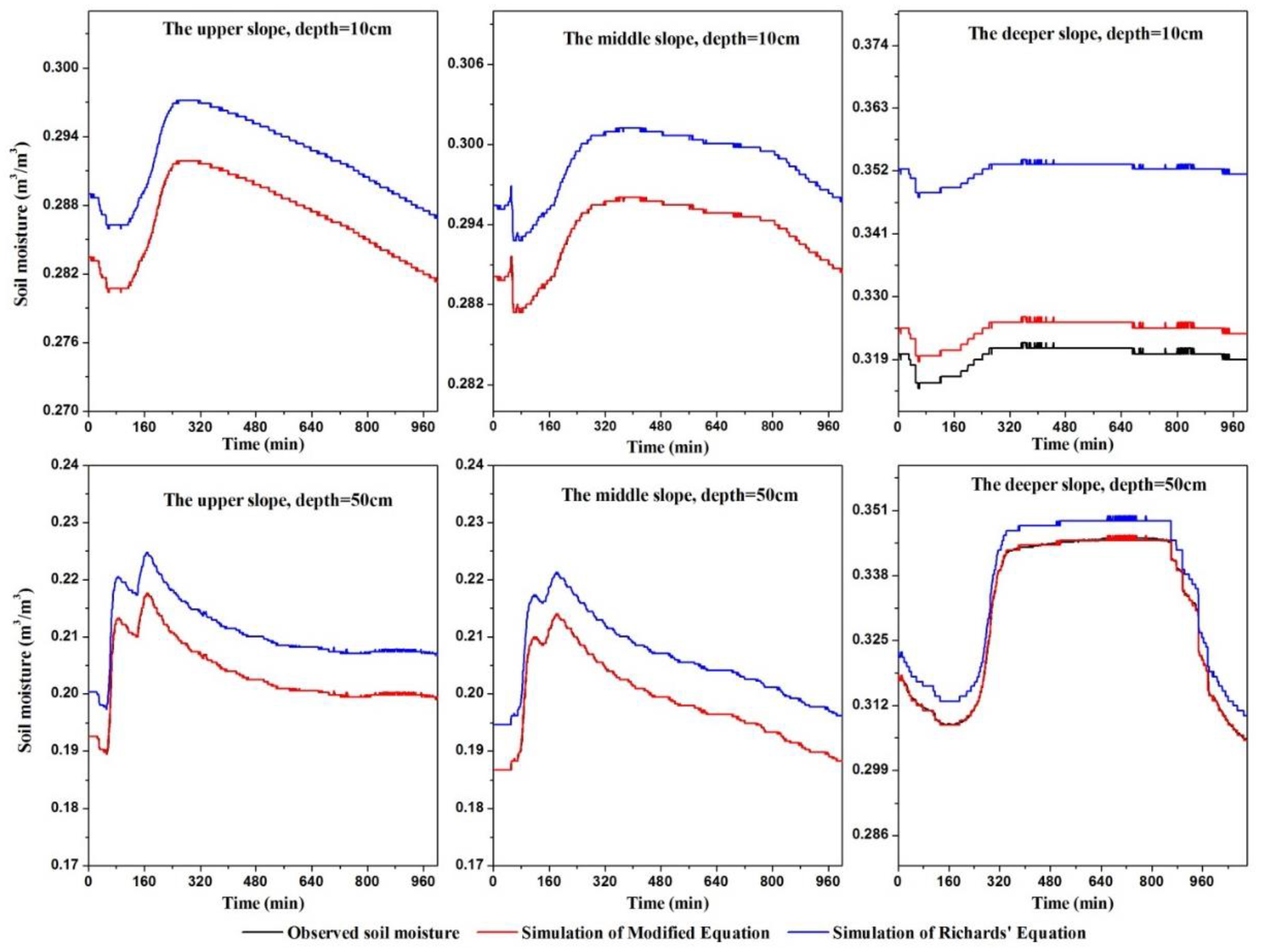
3.3. Spatiotemporal Variability in Soil Moisture Estimates
4. Discussion
4.1. Impact of Overland Flow on Simulations of Soil Moisture in Upper Soil Layer in Longer Rainy Periods
4.2. Effect of Downslope Flow on Accuracy of Simulations in Different Slope Positions
5. Conclusions
- Although Richards’ equation is one of the most widely used infiltration equations in hydrological models, the original analytical solutions have a limited ability to estimate soil moisture traces during infiltration on a hillslope.
- The spatial–temporal variations in soil moisture are controlled by diverse environmental control factors, such as hillslope and soil properties. However, these factors are difficult to express using the original Richards’ equation because of the difficulty in summarizing the related parameters. As far as we know, this is the first attempt to express environmental factors using in situ layered parameters in the infiltration equation.
- The simulation results calculated by the modified Richards’ equation with layered parameters were better than those calculated by the original equation. However, the bias between the simulations using the modified Richards’ equation and the observed values was higher for the upper soil layers. The accuracy of simulations varied depending on the slope position and the length of the rainy period, because of the effects of lateral downslope flow and overland flow during infiltration.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Richards, L.A. Capillary conduction of liquids through porous mediums. Phys. J. Gen. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.C.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.T.; Kanae, S.; Kowalczyk, E.; Lawrence, D.; et al. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [PubMed]
- Laio, F.; Porporato, A.; Ridolfi, L.; Rodriguez-Iturbe, I. Plants in water-controlled ecosystems: Active role in hydrologic processes and response to water stress—II. Probabilistic soil moisture dynamics. Adv. Water Resour. 2001, 24, 707–723. [Google Scholar] [CrossRef]
- Lewis, M.R. The rate of infiltration of water in irrigation practice. Trans. Am. Geophys. Union 1937, 18, 361–368. [Google Scholar] [CrossRef]
- Reeves, M.; Miller, E.E. Estimating infiltration for erratic rainfall. Water Resour. Res. 1975, 11, 102–110. [Google Scholar] [CrossRef]
- Baron, G. Abramowitz, A-handbook of mathematical functions. Computing 1967, 2, 169. [Google Scholar] [CrossRef]
- Bruce, R.R.; Thomas, A.W.; Whisler, F.D. Prediction of infiltration into layered field soils in relation to profile characteristics. Trans. Asae 1976, 19, 693–698. [Google Scholar] [CrossRef]
- Wang, G.; Fang, Q.; Wu, B.; Yang, H.; Xu, Z. Relationship between soil erodibility and modeled infiltration rate in different soils. J. Hydrol. 2015, 528, 408–418. [Google Scholar] [CrossRef]
- Xue, B.-L.; Wang, L.; Yang, K.; Tian, L.; Qin, J.; Chen, Y.; Zhao, L.; Ma, Y.; Koike, T.; Hu, Z.; et al. Modeling the land surface water and energy cycles of a mesoscale watershed in the central Tibetan Plateau during summer with a distributed hydrological model. J. Geophys. Res. Atmos. 2013, 118, 8857–8868. [Google Scholar] [CrossRef]
- Rossi, M.J.; Ares, J.O. Overland flow from plant patches: Coupled effects of preferential infiltration, surface roughness and depression storage at the semiarid Patagonian Monte. J. Hydrol. 2016, 533, 603–614. [Google Scholar] [CrossRef]
- Botter, G.; Porporato, A.; Rodriguez-Iturbe, I.; Rinaldo, A. Basin-scale soil moisture dynamics and the probabilistic characterization of carrier hydrologic flows: Slow, leaching-prone components of the hydrologic response. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Heathman, G.C.; Larose, M.; Cosh, M.H.; Bindlish, R. Surface and profile soil moisture spatio-temporal analysis during an excessive rainfall period in the Southern Great Plains, USA. Catena 2009, 78, 159–169. [Google Scholar] [CrossRef]
- Chu, S.T. Infiltration during an unsteady rain. Water Resour. Res. 1978, 14, 461–466. [Google Scholar] [CrossRef]
- Xue, B.-L.; Wang, L.; Li, X.; Yang, K.; Chen, D.; Sun, L. Evaluation of evapotranspiration estimates for two river basins on the Tibetan Plateau by a water balance method. J. Hydrol. 2013, 492, 290–297. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; D’Odorico, P.; Porporato, A.; Ridolfi, L. On the spatial and temporal links between vegetation, climate, and soil moisture. Water Resour. Res. 1999, 35, 3709–3722. [Google Scholar] [CrossRef]
- Wang, G.; Jiang, H.; Xu, Z.; Wang, L.; Yue, W. Evaluating the effect of land use changes on soil erosion and sediment yield using a grid-based distributed modelling approach. Hydrol. Process. 2012, 26, 3579–3592. [Google Scholar] [CrossRef]
- Zhou, Q.; Driscoll, C.T.; Moore, S.E.; Kulp, M.A.; Renfro, J.R.; Schwartz, J.S.; Cai, M.; Lynch, J.A. Developing Critical Loads of Nitrate and Sulfate Deposition to Watersheds of the Great Smoky Mountains National Park, USA. Water Air Soil Pollut. 2015, 226, 255. [Google Scholar] [CrossRef]
- Martinez-Fernandez, J.; Ceballos, A. Mean soil moisture estimation using temporal stability analysis. J. Hydrol. 2005, 312, 28–38. [Google Scholar] [CrossRef]
- Huang, X.; Shi, Z.H.; Zhu, H.D.; Zhang, H.Y.; Ai, L.; Yin, W. Soil moisture dynamics within soil profiles and associated environmental controls. Catena 2016, 136, 189–196. [Google Scholar] [CrossRef]
- Gomez-Plaza, A.; Martinez-Mena, M.; Albaladejo, J.; Castillo, V.M. Factors regulating spatial distribution of soil water content in small semiarid catchments. J. Hydrol. 2001, 253, 211–226. [Google Scholar] [CrossRef]
- Takagi, K.; Lin, H.S. Changing controls of soil moisture spatial organization in the Shale Hills Catchment. Geoderma 2012, 173, 289–302. [Google Scholar] [CrossRef]
- Western, A.W.; Bloschl, G. On the spatial scaling of soil moisture. J. Hydrol. 1999, 217, 203–224. [Google Scholar] [CrossRef]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Rao, S.G. Role of slope on infiltration: A review. J. Hydrol. 2018, 557, 878–886. [Google Scholar] [CrossRef]
- Lv, M.; Hao, Z.; Liu, Z.; Yu, Z. Conditions for lateral downslope unsaturated flow and effects of slope angle on soil moisture movement. J. Hydrol. 2013, 486, 321–333. [Google Scholar] [CrossRef]
- Kim, H.J.; Sidle, R.C.; Moore, R.D. Shallow lateral flow from a forested hillslope, Influence of antecedent wetness. Catena 2005, 60, 293–306. [Google Scholar] [CrossRef]
- Sun, H.; Meerschaert, M.M.; Zhang, Y.; Zhu, J.; Chen, W. A fractal Richards’ equation to capture the non-Boltzmann scaling of water transport in unsaturated media. Adv. Water Resour. 2013, 52, 292–295. [Google Scholar] [CrossRef] [PubMed]
- Corradini, C.; Melone, F.; Smith, R.E. Modeling local infiltration for a two-layered soil under complex rainfall patterns. J. Hydrol. 2000, 237, 58–73. [Google Scholar] [CrossRef]
- Menziani, M.; Pugnaghi, S.; Vincenzi, S. Analytical solutions of the linearized Richards equation for discrete arbitrary initial and boundary conditions. J. Hydrol. 2007, 332, 214–225. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G.A. Studies on soil physics Part I—The flow of air and water through soils. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar]
- Philip, J.R. Theory of Infiltration. Adv. Hydrosci. 1969, 5, 215–296. [Google Scholar]
- Wang, Y.; Hu, W.; Zhu, Y.; Shao Ma Xiao, S.; Zhang, C. Vertical distribution and temporal stability of soil water in 21-m profiles under different land uses on the Loess Plateau in China. J. Hydrol. 2015, 527, 543–554. [Google Scholar] [CrossRef]
- Horton, R.E. Analysis of Runoff-Plot Experiments With Varying Infiltration-Capacity. Eos Trans. Am. Geophys. Union 1939, 20, 693–711. [Google Scholar] [CrossRef]
- Hillel, D. A descriptive theory of fingering during infiltration into layered soils. Soil Sci. 1988, 146, 207–217. [Google Scholar] [CrossRef]
- Philip, J.R. Sorption and infiltration in heterogeneous media. Aust. J. Soil Res. 1967, 5, 1–10. [Google Scholar] [CrossRef]
- Talsma, T.; Parlange, J.Y. One-dimensional vertical infiltration. Aust. J. Soil Res. 1972, 10, 143–150. [Google Scholar] [CrossRef]
- Clothier, B.E.; White, I. Measurement of sorptivity and soil-water diffusivity in the field. Soil Sci. Soc. Am. J. 1981, 45, 241–245. [Google Scholar] [CrossRef]
- Cook, F.J.; Broeren, A. Six methods for determining sorptivity and hydraulic conductivity with disc permeameters. Soil Sci. 1994, 157, 2–11. [Google Scholar] [CrossRef]
- Parlange, J.Y. Theory of water-movement in soils: 1. One-dimensional absorption. Soil Sci. 1971, 111, 134–137. [Google Scholar] [CrossRef]
- Rathfelder, K.; Abriola, L.M. Mass conservative numerical-solutions of the head-based richards equation. Water Resour. Res. 1994, 30, 2579–2586. [Google Scholar] [CrossRef]
- Haverkamp, R.; Vauclin, M.; Touma, J.; Wierenga, P.J.; Vachaud, G. Comparison of numerical-simulation models for one-dimensional infiltration. Soil Sci. Soc. Am. J. 1977, 41, 285–294. [Google Scholar] [CrossRef]
- Su, L.; Wang, J.; Qin, X.; Wang, Q. Approximate solution of a one-dimensional soil water infiltration equation based on the Brooks-Corey model. Geoderma 2017, 297, 28–37. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Properties of porous media affecting fluid flow. J. Irrig. Drain. Div. 1966, 92, 61–88. [Google Scholar]
- Philip, J.R. Hillslope infiltration—Planar slopes. Water Resour. Res. 1991, 27, 109–117. [Google Scholar] [CrossRef]
- Jackson, C.R. Hillslope infiltration and lateral downslope unsaturated flow. Water Resour. Res. 1992, 28, 2533–2539. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A.; Miller, D. Handbook of Mathematical Functions With Formulas, Graphs and Mathematical Tables. J. Appl. Mech. 1965, 32, 239. [Google Scholar] [CrossRef]
- Liao, K.; Zhou, Z.; Lai, X. Evaluation of different approaches for identifying optimal sites to predict mean hillslope soil moisture content. J. Hydrol. 2017, 547, 10–20. [Google Scholar] [CrossRef]
- Smith, R.E.; Chery, D.L. Rainfall excess model from soil-water flow theory. J. Hydraul. Div. Asce 1975, 101, 404–406. [Google Scholar]

| Parameters | Texture | n | Sand | Silt | Clay | ρ | θn | D(θ) | α | Ks |
|---|---|---|---|---|---|---|---|---|---|---|
| (%) | (%) | (%) | (g/cm3) | (cm3/cm3) | (/cm) | (m/d) | ||||
| Values | loam | 0.5 | 49.44 | 45.04 | 5.52 | 1.4576 | 0.5 | 0.001 | 5 | 0.000132 |
| Temporal Statistics | 0–10 cm | 10–20 cm | 20–30 cm | 30–40 cm | 40–50 cm |
|---|---|---|---|---|---|
| Mean (%) | 31.58% | 30.83% | 23.04% | 24.65% | 16.28% |
| Standard Deviation (SD) | 0.037708 | 0.018525 | 0.006102 | 0.01508 | 0.015195 |
| Coefficient of Variation (CV) | 11.94% | 6.01% | 9.33% | 6.12% | 2.65% |
| Date | Root Mean Square Error (RMSE) | Bias | Relative Error | |||
|---|---|---|---|---|---|---|
| Modified Equation | Richards’ Equation | Modified Equation | Richards’ Equation | Modified Equation | Richards’ Equation | |
| 2016/9/26 | 0.0057 | 0.0083 | 0.0052 | −0.0053 | 2.41% | 2.19% |
| 2016/10/7 | 0.0108 | 0.0199 | 0.0090 | 0.0197 | 3.36% | 7.47% |
| 2016/11/21 | 0.0061 | 0.0050 | 0.0047 | −0.0032 | 1.84% | 1.18% |
| 2017/3/24 | 0.0010 | 0.0080 | 0.0010 | −0.0080 | 0.66% | 5.20% |
| 2017/4/13 | 0.0037 | 0.0066 | 0.0026 | −0.0061 | 1.68% | 3.75% |
| 2017/5/13 | 0.0272 | 0.0428 | 0.0030 | 0.02342 | 1.06% | 7.85% |
| Average | 0.0091 | 0.0151 | 0.0042 | 0.0034 | 1.84% | 4.61% |
| Date | Root Mean Square Error | Bias | Relative Error | |||
|---|---|---|---|---|---|---|
| Modified Equation | Richards’ Equation | Modified Equation | Richards’ Equation | Modified Equation | Richards’ Equation | |
| 2016/9/26 | 0.0100 | 0.0233 | 0.0024 | 0.0019 | 1.47% | 1.98% |
| 2016/10/7 | 0.0016 | 0.0150 | 0.0013 | −0.0052 | 0.57% | 1.84% |
| 2016/11/21 | 0.0026 | 0.0063 | 0.0024 | −0.0062 | 1.43% | 3.63% |
| 2017/3/24 | 0.0010 | 0.0080 | 0.0010 | −0.0080 | 0.66% | 5.20% |
| 2017/4/13 | 0.0037 | 0.0066 | 0.0026 | −0.0061 | 1.68% | 3.75% |
| 2017/5/13 | 0.0579 | 0.0569 | 0.0046 | −0.0008 | 3.79% | 1.57% |
| Average | 0.0128 | 0.0194 | 0.0023 | −0.0041 | 1.60% | 2.99% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Liu, T.; Xue, B.; A., Y.; Wang, G. Modified Richards’ Equation to Improve Estimates of Soil Moisture in Two-Layered Soils after Infiltration. Water 2018, 10, 1174. https://doi.org/10.3390/w10091174
Zhu H, Liu T, Xue B, A. Y, Wang G. Modified Richards’ Equation to Improve Estimates of Soil Moisture in Two-Layered Soils after Infiltration. Water. 2018; 10(9):1174. https://doi.org/10.3390/w10091174
Chicago/Turabian StyleZhu, Honglin, Tingxi Liu, Baolin Xue, Yinglan A., and Guoqiang Wang. 2018. "Modified Richards’ Equation to Improve Estimates of Soil Moisture in Two-Layered Soils after Infiltration" Water 10, no. 9: 1174. https://doi.org/10.3390/w10091174
APA StyleZhu, H., Liu, T., Xue, B., A., Y., & Wang, G. (2018). Modified Richards’ Equation to Improve Estimates of Soil Moisture in Two-Layered Soils after Infiltration. Water, 10(9), 1174. https://doi.org/10.3390/w10091174






