Abstract
Widely used in hydraulics, the Colebrook equation for flow friction relates implicitly to the input parameters; the Reynolds number, Re and the relative roughness of an inner pipe surface, ε/D with an unknown output parameter; the flow friction factor, λ; λ = f (λ, Re, ε/D). In this paper, a few explicit approximations to the Colebrook equation; λ ≈ f (Re, ε/D), are generated using the ability of artificial intelligence to make inner patterns to connect input and output parameters in an explicit way not knowing their nature or the physical law that connects them, but only knowing raw numbers, {Re, ε/D}→{λ}. The fact that the used genetic programming tool does not know the structure of the Colebrook equation, which is based on computationally expensive logarithmic law, is used to obtain a better structure of the approximations, which is less demanding for calculation but also enough accurate. All generated approximations have low computational cost because they contain a limited number of logarithmic forms used for normalization of input parameters or for acceleration, but they are also sufficiently accurate. The relative error regarding the friction factor λ, in in the best case is up to 0.13% with only two logarithmic forms used. As the second logarithm can be accurately approximated by the Padé approximation, practically the same error is obtained also using only one logarithm.
1. Introduction
The Colebrook equation for flow friction is one of the most used formulas in hydraulics, which is a branch of civil engineering, that deals with the conveyance of liquids through pipes. It is also widely used in mechanical, petroleum and chemical engineering, etc., wherever flow through pipes occur. It is an empirical relation developed by Colebrook [1] based on his experiment with White [2]. The experiment dealt with flow of air/liquid through artificially roughened pipes; Equation (1):
In Equation (1), λ is the Darcy flow friction factor, Re is the Reynolds number, and ε/D is the relative roughness of inner pipe surface (all three quantities are dimensionless).
In the Colebrook equation, the flow friction factor λ is implicitly given, λ = f (λ, Re, ε/D) where it can be expressed in an explicit way only approximately [3,4,5,6,7,8], λ ≈ f (Re, ε/D) or otherwise the original equation can be solved iteratively [9,10]. Today, it is important not only to have accurate but also computationally efficient approximations [11,12,13]. Here, we used the ability of artificial intelligence to connect input data; in our case the Reynolds number, Re and the relative roughness of inner pipe surface, ε/D with the output parameter; in our case the flow friction factor, λ not knowing the structure of the Colebrook equation [14,15,16,17]. We used the ability of artificial intelligence to connect input with output data to form patterns not knowing the nature of the data or the physical law that connects them (a similar approach is valid for other branches of hydraulics [18,19]). In that way, we tried to avoid the computationally expensive logarithmic law on which the Colebrook equation is based. As a final product we developed few low-cost but very accurate explicit approximations to the Colebrook equation.
2. Methods Used, Preparation of Data and Software Tool, Results, Structure of Approximations, Accuracy and Comparative Analysis
The main idea is to use the ability of artificial intelligence to connect input data sets; in our case the Reynolds number, Re and the relative roughness of inner pipe surface, ε/D with the output data set; in our case the flow friction factor, λ; {Re, ε/D}→{λ}, not knowing the physical law which connects input to output. Sign “→” practically represents the Colebrook equation; Equation (1), but the genetic programming tool is not aware of that fact. To prepare data to feed the genetic programming tool, we covered the whole practical domain of applicability of the Colebrook equation; which is for the Reynolds number, Re between 4000 and 108 (whole turbulent flow covered) and for the relative roughness of inner pipe surface, ε/D up to 0.05 (pipe covered from practically smooth to the very rough) [20] with a mesh which consists of 90 thousand intersection points {Re, ε/D} for which we calculated very accurately the flow friction factor, λ using the Colebrook equation; Equation (1); Figure 1a,b.
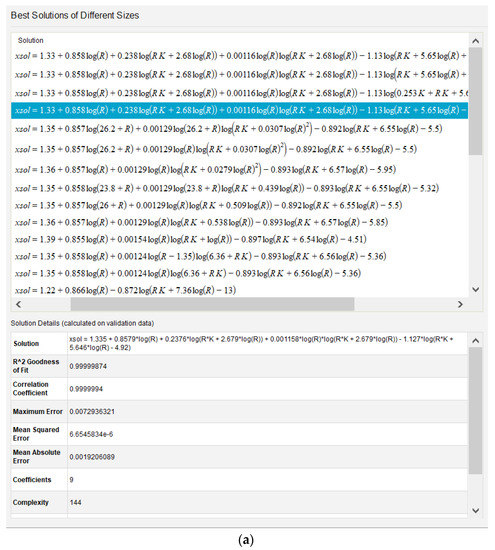
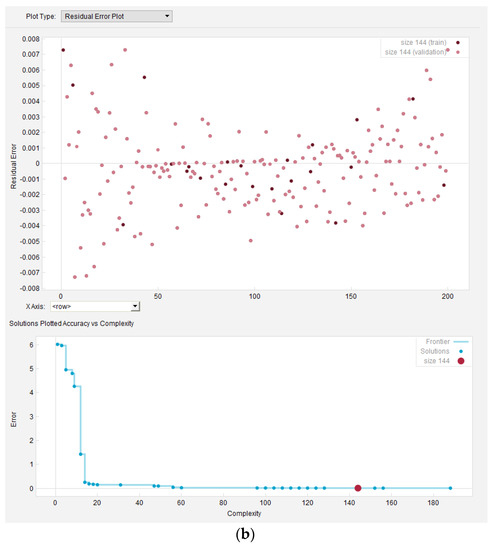
Figure 1.
(a) An example of Eureqa [computer software] interface: Best approximate solutions of the Colebrook equation with various complexity, which were automatically found by Eureqa. (b) An example of Eureqa [computer software] interface: The residual error plot of a selected analytical model for 200 pairs together with an accuracy vs complexity plot of solutions.
Having 90 thousand combinations; in order to test robustness of the symbolic regression algorithms we fed the genetic programming tool with 200 triplets {Re, ε/D}i, {λ}i (see Supplementary Material attached to this paper) hoping that it will connect {Re, ε/D}i→{λ}i accurately. The input sample was generated according to the uniform density function of each input variable. The low-discrepancy Sobol sequences were employed [21]. These so-called quasirandom sequences have useful properties. In contrary to random numbers, quasirandom numbers cover the space more quickly and evenly. Thus, they leave very few holes. We used [computer software] Eureqa by Nutonian, Inc., Boston, MA, as a genetic programming tool [22,23]. The symbolic regression approach adopted herein [24,25,26,27,28,29] is based upon genetic programming wherein a population of functions is allowed to breed and mutate with the genetic propagation into subsequent generations based on survival-of-the-fittest criteria [30]. The main goal of this study is to make accurate and computationally cheap explicit approximations of the Colebrook equation, where computationally cheap means to contain the least possible number of logarithmic functions and non-integer powers [31,32,33,34,35,36].
We can see that approximations found by Eureqa [computer software] have the form {R, K}→xsol, where the symbol R denotes the Reynolds number, K represents relative roughness and . All accurate models are computationally expensive, as they contain many logarithmic terms with different arguments. Thus, we can see that Eureqa itself requires human knowledge, in order to obtain an accurate but still a computationally cheap approximation of the Colebrook equation. Consequently, we will combine several approaches in this paper: Eureqa [computer software] [22,23], the fixed-point iteration [9] and Padé approximation [10]. According to our numerical experiments, Eureqa seems to be useful especially for finding a computationally cheap rational approximation of the Colebrook solution, which serves as a good starting point for the fixed-point iteration method (acceleration). Finally, the Padé approximation is used as a cheap but very accurate approximation of the logarithm in the second and the successful iterations of the fixed-point method.
2.1. Input Parameters in Their Raw Form
Using the input parameters in their raw form {Re, ε/D}i→{λ}i, Eureqa, the used genetic programming tool gives a set of approximations in polynomial forms [12]. Knowing that logarithmic expressions and non-integer powers are expensive for computation, we hoped that we have fully accomplished our task. Unfortunately, Eureqa gives a number of not very accurate solutions and here we show Equation (2) with the relative error of λ0 even up to 16.56% in respect to the accurate λ, where the relative error [5,26] is defined as (|λaccurate − λ|/λaccurate)·100%, where λaccurate is calculated in an iterative procedure using the original implicitly given Colebrook equation [6,9]; Equation (1), while λ is obtained through the presented approximations; Equations (2)–(6). In Equation (2), “↔” means related but not sufficiently accurate:
On the other hand, we found that the accuracy can increase significantly using one fixed-point iterative cycle of acceleration [9]; Equation (2a), after which accuracy of λ1 increases up to 0.98%.
In Equation (2a), “≈” means reasonably accurate enough and arguments of logarithms are defined by; Equation (2b):
The simple fixed-point iterative procedure [6,9]; Equation (2a) in case of the Colebrook equation is fast; λ0→16.56%, λ1→0.98%, λ2→0.13%, etc. (Figure 2). Thus, using only two logarithmic forms, high accuracy of λ2→0.13% is reached. Results are in the form {λ}0↔{Re, ε/D}0, {λ}1 ≈ {log10(λ0)}1, {λ}2≈{log10(log10(λ0))}2, etc., where “↔” means related but not sufficiently accurate, while “≈” is reasonably accurate enough. This approach with acceleration is widely used in development of approximations of the Colebrook equation [37,38,39,40,41,42]. The error can be further reduced by using one more accelerating step as shown, or using genetic algorithms [25,29,36], Excel fitting tool [27] or the Monte Carlo method [43,44].
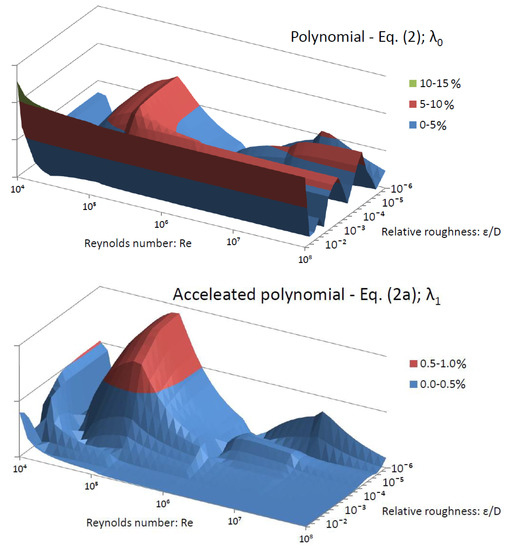
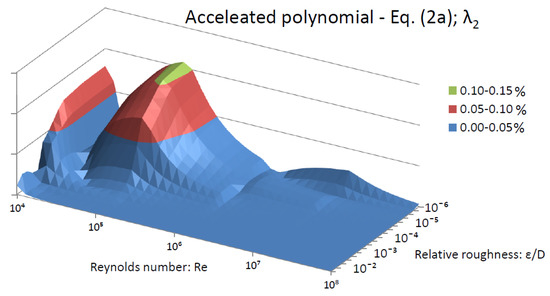
Figure 2.
Distribution of the relative error of λ over the domain of applicability of the Colebrook equation introduced by polynomial Equation (2)—(up), Equation (2a) after first step of fixed-point acceleration—(middle), and the second step of acceleration—(down); relative error up to 16.56%, up to 0.98% and up to 0.13% respectively.
2.2. Normalized Input Parameters
Unfortunately, in our case using the input parameters in their raw form the accuracy was not at a high level without acceleration, so having previous experience with the same problem where we used Artificial Neural Network [15,16] to simulate results, we normalized parameters a = log10(Re), b = −log10(ε/D), in order to avoid discrepancy in the scale which are in raw form 1000 < Re < 108 and ε/D << 1 and after normalization 3.5 < a < 8 and 1.3 < b < 6.5 (Eureqa, software used a as genetic programming tool also suggested to us a data normalization process) [34,35,36]. The normalization gives relatively good results, and the genetic programming tool generated more accurate results without knowing that the logarithmic form of the Colebrook equation was originally used but only knowing the predicted input and output datasets; Figure 3:

Figure 3.
Genetic programming tool makes λ ≈ f (a,b) without knowing the physical law that connects a and b.
Using our previous experience [15] with the training of the Artificial Neural Network where very good results were achieved through the normalization of parameters; a = log10(Re), b = −log10(ε/D), the genetic programming tool generated a dozen equations with different levels of accuracy and complexity, but fortunately none of them contain logarithms or non-integer power terms. Here, we present the four most successful explicit approximations; Equations (3)–(6). Adding one additional logarithmic form for acceleration using one additional fixed-point iterative step [9,45]; Equation (2a), the accuracy of the approximations increases significantly (about 10 times); Equations (3a)–(6a). Results are in the form {λ}0↔{a = log10(Re), b = −log10(ε/D)}0, {λ}1≈{log10(λ0)}1, {λ}2≈{log10(log10(λ0))}2, etc., where “↔” means related but not sufficiently accurate, while “≈” is reasonably accurate enough.
Distribution of the relative error over the domain of applicability of the Colebrook equation introduced by these four approximations is presented in Figure 4, Figure 5, Figure 6 and Figure 7.
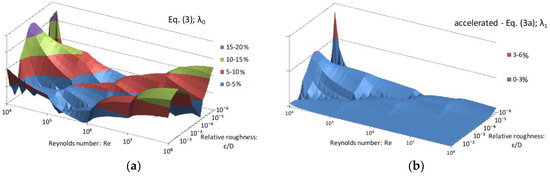
Figure 4.
Distribution of the relative error of λ over the domain of applicability of the Colebrook equation introduced by Equation (3)—(a), and accelerated Equation (3a)—(b); relative error up to 20% and up to 5.35%, respectively.
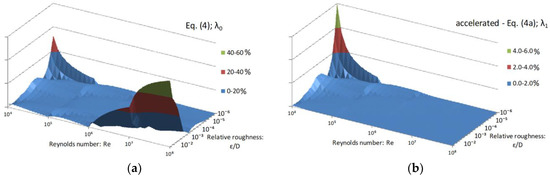
Figure 5.
Distribution of the relative error of λ over the domain of applicability of the Colebrook equation introduced by Equation (4)—(a), and accelerated Equation (4a)—(b); relative error up to 60% and up to 6.29%, respectively.
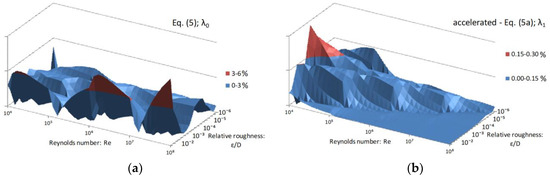
Figure 6.
Distribution of the relative error of λ over the domain of applicability of the Colebrook equation introduced by Equation (5)—(a), and accelerated Equation (5a)—(b); relative error up to 6% and up to 0.28%, respectively.
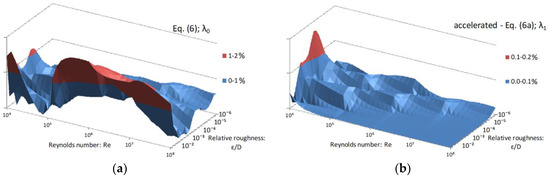
Figure 7.
Distribution of the relative error of λ over the domain of applicability of the Colebrook equation introduced by Equation (6)—(a), and accelerated Equation (6a)—(b); relative error up to 2% and up to 0.17%, respectively.
2.3. Discussion—Comparative Analysis
In general, the relative error of approximations of the Colebrook equation is not uniformly dispersed over the domain of applicability of the Colebrook equation [7,29], where the more complex is not always more accurate which can be noticed by comparing Equation (3) and Equation (4) and related Figure 4 and Figure 5, respectively. According to Eureqa, the software package which generated the approximations, Equation (5) is three times more complex compared with Equation (3), while Equation (4) is 1.5 times more complex compared with Equation (3). Using genetic algorithms [25,29] or the Excel fitting tool [27], there is a possibility to increase the accuracy of the presented approximations by changing their parameters near the current value. If the structure of the approximations remains unchanged, the complexity remains also unchanged while accuracy can increase [4,12,13], or in other words, the structure of the equations remains unchanged while the values of the coefficient change in order to fit better values obtained through the Colebrook equation. In that way error from Figure 4, Figure 5, Figure 6 and Figure 7 can decrease but also the distribution of the error over the domain of applicability changes [7,29].
To summarize our findings, we made Table 1, in which the maximum relative errors of approximations compared to the accurate λ are expressed as a function of complexity.

Table 1.
The maximal relative errors of approximations as a function of complexity.
It is clear that polynomial approximation was accelerated through the fixed-point iterative procedure; Equation (2a) shows better performances compared with those with normalized input parameters; Equations (3a)–(6a). For example, Equation (2a) with two logarithmic functions (used for acceleration) gives a relative error of no more than λ2→0.13% compared with the approximately same error of Equation (6a) with three logarithmic forms (two for normalization and one for acceleration); Equation (6a)—λ1→0.17%. Also, the expression for λ0 in case of Equation (2) is a polynomial while Equations (4)–(6) contain sinus trigonometric function [46]. After this careful analysis it can be concluded that it is better to use computationally expensive logarithmic functions for acceleration through Equation (2a) and not for normalization.
All approximations can be classified as highly accurate, moderate and with a low level of accuracy:
- Highly accurate: Compared with the similar approximations to the Colebrook equation, accelerated Equation (5a); with the relative error up to 0.28% and accelerated Equations (2a) and (6a) with the relative error up to 0.13% and 0.17%, respectively, are accurate as approximations by Bar [47] (0.2%), Chen [38] (0.36–0.18%), Zigrang and Sylvester [41] (0.14–0.08%, simpler: 1–0.775%), Fang et al. [48] (0.61–0.56%), Serghides [38] (0.14–0.0026%, simpler 0.35–0.27%), Buzzelli [49] (0.14–0.08%), Sonad and Goudar [50] (0.8–improved by Vatankhah and Kouchakzadeh [51]: 0.15%) and Romeo et al. [52] (0.14–0.008%); where the higher reported accuracy is achieved through genetic optimization [25,29]. These approximations are among the most accurate available to date [3,4,5,6,7,8], but at the same time in many cases much more complex compared to the approximations presented in our paper [4,11,12,13]. For example; approximations by Barr [47] and by Chen [38] contain two logarithmic expressions and two non-integer powers; by Romeo et al. [52], three logarithmic expressions and two non-integer powers, etc. which means that they introduce a higher computational burden to achieve the same accuracy. In this case, our Equation (2a), which after two steps of acceleration, contains only two logarithmic forms.
- Moderately accurate: Our Equation (6) with the relative error up to 2% does contain only two logarithmic expressions used for normalization and no non-integer power, and its accuracy can be compared with approximations by Swamee and Jain [53] (2.18–1.75%), Manadili [54] (2–1.5%), Brkić [42,55,56,57] (2–1.3%), Haland [58] (1.4–1.1%), etc., all with the same or higher complexity as Equation (6). Equation (2a) after the first step of acceleration with only one logarithmic function and with the relative error of up to 2.6% is even more efficient.
- Low accuracy: Our accelerated Equation (3a) is very simple with the relative error up to 5.35% but with only one peak of high error (otherwise up to 3% as can be seen from Figure 4); it is more accurate compared with approximations by Round [59] (10.9–5.5%), Eck [60] (8.2–5.7%) and Avci and Karagoz [61] (4.8–3.1%), Wood [62] (23.7–16.6%), Moody [63] (21.5–18.1%), etc.
3. Possible Simplifications
As already noted, the main goal is to produce not only accurate, but also computationally low cost [11,12,13,29] explicit approximations of the Colebrook equation. Trigonometric functions are used in Equations (4)–(6) and in their accelerated versions Equations (4)–(6), which is not in common use related to the approximations of the Colebrook equation. These trigonometric functions can also have a higher computational cost. On the other hand, use of the Padé approximation sin(x) ≈ x·(60 − 7x2)/(60 + 3x2) can potentially overwhelm the problem [64]. The Padé approximation x·(60 − 7x2)/(60 + 3x2) within the domain of interest; −0.08821 < x < 1.18456; compared with sin(x) can introduce the relative error up to 0.068%. Within the same domain, Eureqa gives a number of approximations for sin(x), but we have chosen to present here one accurate but relatively simple; sin(x) ≈ x − x2/5350.6747 − x3/6.0171 + x5/127.4678 with the relative error up to 0.003%. This error of approximations for sin(x) also has impact on the final error of our approximations; Equations (4)–(6) and their accelerated pairs; Equations (4a)–(6a).
Also, the Colebrook equation can be transformed in the mathematically equivalent form Equation (7) that is more suitable for further Padé simplifications. The main idea is to use already computed parameter b= −log10(ε/D) and to use the Padé polynomial in the form ln (1 − θ), where θ is given by Equation (8). In Equation (7), both 2·log10(3.71) ≈ 1.1387478 and 2/ln(10) ≈ 0.8686 are constant, while b = log10(ε/D) is recycled as already evaluated during the normalization of input parameters.
Note that Equation (7) does not work for ε/D = 0, but Equation (1) does work; for practical application in the case of a smooth regime, both relations works; for example, even for very smooth surfaces as for ε/D = 10−9. In practice [20], pipes are never that smooth to reach the value ε/D = 0.
Our proposed acceleration through Equation (2a) and Equations (3a)–(6a), can go further through Equation (7a), where b = −log10(ε/D) and λ0 from Equations (2)–(6).
The idea to eliminate the remained logarithmic form from the accelerated equations using the Padé approximation [64] for ln(1 − θ) where θ is defined by Equation (8) in this case is not sustainable because of a wide domain of θ that contains a value between −30,394.85651 and −2.92065 × 10−6 within the practical domain of the Colebrook equation; 4000 < Re < 108 and 0 < ε/D < 0.05.
Regarding the normalization of the input parameter a = log10(Re), we hoped also to use the fact that the practical domain of the Reynolds number Re, is from 4000 to 108 which has as a consequence log10(Re) ≈ log10(1 + Re), where for ln(1 + y) numerous approximations are available, but mostly for the argument z around 0. This is because some computer algebra systems and programming languages provide a special natural logarithm plus 1 function alternatively named to give more accurate results for values of x close to zero compared to using ln(1 + y) directly. In our case this is not of interest, knowing that for y = Re; y >> 1. Of course, to use only numbers between 1 and 10, we can use the rule ln(Re) = ln(z10n) = ln(z) + nln(10) where n = len(int(z)) and z = Re/10n; len is a function which calculates number of digits in a number while int is a function which gives a number down to the nearest integer; ln(10) = 2.30258509. A similar method can be used for the normalized parameter b = −log10(ε/D) where ε/D is between 0 and 0.05.
A fast but still reliable Padé approximation useful for the Colebrook equation has been recently introduced in [10]. The logarithm term , where argument z~1 is approximated by the rational function:
In this case, only one logarithm is computed and is stored in the computer memory: , whereas is approximated by and by Equation (9) as
where is defined in Equation (2b). When the Padé approximation (9) is applied to Equation (2a) and the starting point is estimated by Equation (2), the maximum relative error of Equation (10) is negligible: 5 × 10−10%. Thus, Equation (10) is very accurate when the iterative process defined by Equation (2a) is initiated by a good starting point (A comparison of iterative methods for solving the Colebrook equation is given in [65]). Consequently, the argument z of Equation (9) is very close to one in all cases within the domain of interest of the Colebrook equation [10].
4. Conclusions
Evaluation of hydraulic resistance, i.e., computation of flow friction factor, λ is one of the main tasks encountered in engineering practice wherever flow of fluid through closed conduits occur. Up to now, the empirical Colebrook Equation (1) which is implicitly given by a flow friction factor, λ is still accepted as an informal standard after 80 years. Obvious disadvantages of an implicit relationship inspired numerous efforts to derive as accurate possible explicit equivalent; λ ≈ f (Re, ε/D) to the original Colebrook equation; λ = f (Re, ε/D, λ). Nowadays, the requirement is not only to develop accurate, but also computationally efficient approximations to the Colebrook equation, which inspired us to use the ability of artificial intelligence to recognize patterns not knowing their true physical laws. Using genetic programming we developed a few accurate approximations to the Colebrook equation avoiding extensive use of computationally expensive logarithmic forms on which Colebrook’s relation is based. The most accurate approximations presented here have a relative error of up to 0.13% with only two and three logarithmic forms used which makes it very balanced in the ratio between accuracy and computational efficiency. The polynomial expression Equation (2) accelerated through the two steps of fixed-point iterative procedure; Equation (2a) introduced the relative error up to 0.13% using only two logarithmic functions. Practically the same error is introduced, when only one logarithmic function is computed, whereas the second logarithm is approximated by the Padé approximation. On the other hand, Equation (6a) reaches approximately the same accuracy using three logarithmic functions (two for normalization of input parameters and one for fixed-point acceleration) and using also one sinus trigonometric function. Therefore, a polynomial function can be recommended because it is cheaper for computation and because acceleration through the fixed-point iterative procedure is more efficient compared with the normalization of input parameters.
Our genetic approximations are valid only for a turbulent regime, i.e., for a simulation of the Colebrook equation. A transition from a laminar to a turbulent regime is rapid and it is not covered by the Colebrook formula. Our previous work with artificial neural networks shows that this transition cannot be simulated easily using artificial intelligence techniques. We found that the Colebrook equation can be simulated extremely accurately by a neural network with 50 neurons in the hidden layer. However, with the transition from laminar to turbulent regime included, even such complex network with 50 neurons introduces a very high error in this critical zone even after long lasting and complex strategies of training. Similar findings are also valid for the genetic approach.
Supplementary Materials
200 triplets {Re, ε/D}i, {λ}i used to feed the genetic programming tool are available online at http://www.mdpi.com/2073-4441/10/9/1175/s1. We used: Eureqa [computer software], Nutonian, Inc., Boston, MA, USA to generate the presented approximations. Data used to feed the software are based on the Colebrook equation; Equation (1) of this paper. The dataset of 200 combinations of {Re, ε/D}→{λ} was chosen using Sobol quasirandom sequences among 90 thousand generated triplets.
Author Contributions
The paper is a product of joint efforts of the authors who worked together on models of natural gas distribution networks. P.P. has a scientific background in applied mathematics and programming while D.B. in control and applied computing in mechanical and petroleum engineering. Based on his idea, P.P. generated the proposed explicit approximations of the Colebrook equation using Eureqa [computer software] and Padé approximation, while D.B. tested the methods and controlled the results. D.B. wrote the draft of this paper, while P.P. updated it according to the reviewers’ suggestions.
Funding
Resources to cover the Article Processing Charge are provided by the European Commission. This communication is registered in the internal system for publication PUBSY of the Joint Research Centre of the European Commission under No. JRC113016.
Conflicts of Interest
The authors declare no conflict of interest. The views expressed are those of the authors and may not in any circumstances be regarded as stating an official position of the European Commission or of the VŠB - Technical University of Ostrava.
References
- Colebrook, C.F. Turbulent flow in pipes with particular reference to the transition region between the smooth and rough pipe laws. J. Inst. Civ. Eng. 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Colebrook, C.; White, C. Experiments with fluid friction in roughened pipes. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1937, 161, 367–381. [Google Scholar] [CrossRef]
- Gregory, G.A.; Fogarasi, M. Alternate to standard friction factor equation. Oil Gas J. 1985, 83, 120–127. [Google Scholar]
- Zigrang, D.J.; Sylvester, N.D. A review of explicit friction factor equations. J. Energy Resour. Technol. 1985, 107, 280–283. [Google Scholar] [CrossRef]
- Brkić, D. Review of explicit approximations to the Colebrook relation for flow friction. J. Pet. Sci. Eng. 2011, 77, 34–48. [Google Scholar] [CrossRef]
- Brkić, D. Determining friction factors in turbulent pipe flow. Chem. Eng. 2012, 119, 34–39. [Google Scholar]
- Winning, H.K.; Coole, T. Explicit friction factor accuracy and computational efficiency for turbulent flow in pipes. Flow Turbul. Combust. 2013, 90, 1–27. [Google Scholar] [CrossRef]
- Pimenta, B.D.; Robaina, A.D.; Peiter, M.X.; Mezzomo, W.; Kirchner, J.H.; Ben, L.H. Performance of explicit approximations of the coefficient of head loss for pressurized conduits. Rev. Bras. Eng. Agríc. E Ambient. 2018, 22, 301–307. [Google Scholar] [CrossRef]
- Brkić, D. Solution of the implicit Colebrook equation for flow friction using Excel. Spreadsheets Educ. 2017, 10, 2. Available online: http://epublications.bond.edu.au/ejsie/vol10/iss2/2 (accessed on 28 August 2018).
- Praks, P.; Brkić, D. One-log call iterative solution of the Colebrook equation for flow friction based on Padé polynomials. Energies 2018, 11, 1825. [Google Scholar] [CrossRef]
- Clamond, D. Efficient resolution of the Colebrook equation. Ind. Eng. Chem. Res. 2009, 48, 3665–3671. [Google Scholar] [CrossRef]
- Giustolisi, O.; Berardi, L.; Walski, T.M. Some explicit formulations of Colebrook–White friction factor considering accuracy vs. computational speed. J. Hydroinform. 2011, 13, 401–418. [Google Scholar] [CrossRef]
- Vatankhah, A.R. Approximate analytical solutions for the Colebrook equation. J. Hydraul. Eng. 2018, 144, 06018007. [Google Scholar] [CrossRef]
- Özger, M.; Yıldırım, G. Determining turbulent flow friction coefficient using adaptive neuro-fuzzy computing technique. Adv. Eng. Softw. 2009, 40, 281–287. [Google Scholar] [CrossRef]
- Brkić, D.; Ćojbašić, Ž. Intelligent flow friction estimation. Comput. Intell. Neurosci. 2016, 2016, 5242596. [Google Scholar] [CrossRef] [PubMed]
- Precup, R.E.; Preitl, S.; Bojan-Dragos, C.A.; Radac, M.B.; Szedlak-Stinean, A.I.; Hedrea, E.L.; Roman, R.C. Automotive applications of evolving Takagi-Sugeno-Kang fuzzy models. Facta Univ. Ser. Mech. Eng. 2017, 15, 231–244. [Google Scholar] [CrossRef]
- Dučić, N.; Ćojbašić, Ž.; Radiša, R.; Slavković, R.; Milićević, I. CAD/CAM design and genetic optimization of feeders for sand casting process. Facta Univ. Ser. Mech. Eng. 2016, 14, 147–158. [Google Scholar] [CrossRef]
- Shojaeizadeh, A.; Safaei, M.R.; Alrashed, A.A.; Ghodsian, M.; Geza, M.; Abbassi, M.A. Bed roughness effects on characteristics of turbulent confined wall jets. Measurement 2018, 122, 325–338. [Google Scholar] [CrossRef]
- Lebon, B.; Nguyen, M.Q.; Peixinho, J.; Shadloo, M.S.; Hadjadj, A. A new mechanism for periodic bursting of the recirculation region in the flow through a sudden expansion in a circular pipe. Phys. Fluids 2018, 30, 031701. [Google Scholar] [CrossRef]
- Brkić, D. Can pipes be actually really that smooth? Int. J. Refrig. 2012, 35, 209–215. [Google Scholar] [CrossRef]
- Sobol, I.M.; Turchaninov, V.I.; Levitan, Y.L.; Shukman, B.V. Quasi-Random Sequence Generator (Routine LPTAU51); Keldysh Institute of Applied Mathematics, Russian Academy of Sciences: Moscow, Russia, 1992. [Google Scholar]
- Schmidt, M.; Lipson, H. Distilling free-form natural laws from experimental data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef] [PubMed]
- Dubčáková, R. Eureqa: Software review. Genet. Program. Evol. Mach. 2011, 12, 173–178. [Google Scholar] [CrossRef]
- Samadianfard, S. Gene expression programming analysis of implicit Colebrook–White equation in turbulent flow friction factor calculation. J. Pet. Sci. Eng. 2012, 92, 48–55. [Google Scholar] [CrossRef]
- Ćojbašić, Ž.; Brkić, D. Very accurate explicit approximations for calculation of the Colebrook friction factor. Int. J. Mech. Sci. 2013, 67, 10–13. [Google Scholar] [CrossRef]
- Brkić, D. Discussion of “Gene expression programming analysis of implicit Colebrook–White equation in turbulent flow friction factor calculation” by Saeed Samadianfard. J. Pet. Sci. Eng. 2014, 124, 399–401. [Google Scholar] [CrossRef]
- Vatankhah, A.R. Comment on “Gene expression programming analysis of implicit Colebrook–White equation in turbulent flow friction factor calculation”. J. Pet. Sci. Eng. 2014, 124, 402–405. [Google Scholar] [CrossRef]
- Samadianfard, S.; Taghi Sattari, M.; Kisi, O.; Kazemi, H. Determining flow friction factor in irrigation pipes using data mining and artificial intelligence approaches. Appl. Artif. Intell. 2014, 28, 793–813. [Google Scholar] [CrossRef]
- Brkić, D.; Ćojbašić, Ž. Evolutionary optimization of Colebrook’s turbulent flow friction approximations. Fluids 2017, 2, 15. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Tang, P.T. Table-driven implementation of the logarithm function in IEEE floating-point arithmetic. ACM Trans. Math. Softw. (TOMS) 1990, 16, 378–400. [Google Scholar] [CrossRef]
- Pineiro, J.A.; Ercegovac, M.D.; Bruguera, J.D. Algorithm and architecture for logarithm, exponential, and powering computation. IEEE Trans. Comput. 2004, 53, 85–96. [Google Scholar] [CrossRef]
- Johansson, K.; Gustafsson, O.; Wanhammar, L. Implementation of elementary functions for logarithmic number systems. IET Comput. Digit. Tech. 2008, 2, 295–304. [Google Scholar] [CrossRef]
- Stoutemyer, D.R. Can the Eureqa symbolic regression program, computer algebra and numerical analysis help each other. Not. AMS 2013, 60, 713–724. [Google Scholar] [CrossRef]
- Korns, M.F. Accuracy in symbolic regression. In Genetic Programming Theory and Practice IX; Springer: New York, NY, USA, 2011; pp. 129–151. [Google Scholar]
- Bartz-Beielstein, T.; Branke, J.; Mehnen, J.; Mersmann, O. Evolutionary algorithms. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2014, 4, 178–195. [Google Scholar] [CrossRef]
- Brkić, D. Discussion of “Exact analytical solutions of the Colebrook-White equation” by Yozo Mikata and Walter S. Walczak. J. Hydraul. Eng. 2017, 143, 07017007. [Google Scholar] [CrossRef]
- Chen, N.H. An explicit equation for friction factor in pipe. Ind. Eng. Chem. Fundam. 1979, 18, 296–297. [Google Scholar] [CrossRef]
- Schorle, B.J.; Churchill, S.W.; Shacham, M. Comments on “An Explicit Equation for Friction Factor in Pipe”. Ind. Eng. Chem. Fundam. 1980, 19, 228–230. [Google Scholar] [CrossRef]
- Serghides, T.K. Estimate friction factor accurately. Chem. Eng. 1984, 91, 63–64. [Google Scholar]
- Zigrang, D.J.; Sylvester, N.D. Explicit approximations to the solution of Colebrook’s friction factor equation. AIChE J. 1982, 28, 514–515. [Google Scholar] [CrossRef]
- Brkić, D. New explicit correlations for turbulent flow friction factor. Nucl. Eng. Des. 2011, 241, 4055–4059. [Google Scholar] [CrossRef]
- Praks, P.; Kopustinskas, V.; Masera, M. Probabilistic modelling of security of supply in gas networks and evaluation of new infrastructure. Reliab. Eng. Syst. Saf. 2015, 144, 254–264. [Google Scholar] [CrossRef]
- Praks, P.; Kopustinskas, V.; Masera, M. Monte-Carlo-based reliability and vulnerability assessment of a natural gas transmission system due to random network component failures. Sustain. Resil. Infrastruct. 2017, 2, 97–107. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Advanced iterative procedures for solving the implicit Colebrook equation for fluid flow friction. Adv. Civ. Eng. 2018, 2018, 5451034. [Google Scholar] [CrossRef]
- Quan, L.P.; Nhan, T.A. Applying Computer algebra systems in approximating the trigonometric functions. Math. Comput. Appl. 2018, 23, 37. [Google Scholar] [CrossRef]
- Barr, D.I.H. Solutions of the Colebrook-White function for resistance to uniform turbulent flow. Proc. Inst. Civ. Eng. 1981, 71, 529–535. [Google Scholar] [CrossRef]
- Fang, X.; Xu, Y.; Zhou, Z. New correlations of single-phase friction factor for turbulent pipe flow and evaluation of existing single-phase friction factor correlations. Nucl. Eng. Des. 2011, 241, 897–902. [Google Scholar] [CrossRef]
- Buzzelli, D. Calculating friction in one step. Mach. Des. 2008, 80, 54–55. [Google Scholar]
- Sonnad, J.R.; Goudar, C.T. Turbulent flow friction factor calculation using a mathematically exact alternative to the Colebrook–White equation. J. Hydraul. Eng. 2006, 132, 863–867. [Google Scholar] [CrossRef]
- Vatankhah, A.R.; Kouchakzadeh, S. Discussion of “Turbulent flow friction factor calculation using a mathematically exact alternative to the Colebrook–White equation” by Jagadeesh R. Sonnad and Chetan T. Goudar. J. Hydraul. Eng. 2008, 134, 1187. [Google Scholar] [CrossRef]
- Romeo, E.; Royo, C.; Monzón, A. Improved explicit equations for estimation of the friction factor in rough and smooth pipes. Chem. Eng. J. 2002, 86, 369–374. [Google Scholar] [CrossRef]
- Swamee, P.K.; Jain, A.K. Explicit equations for pipe-flow problems. J. Hydraul. Div. 1976, 102, 657–664. [Google Scholar]
- Manadili, G. Replace implicit equations with signomial functions. Chem. Eng. 1997, 104, 129–130. [Google Scholar]
- Brkić, D. An explicit approximation of Colebrook’s equation for fluid flow friction factor. Pet. Sci. Technol. 2011, 29, 1596–1602. [Google Scholar] [CrossRef]
- Brkić, D. W solutions of the CW equation for flow friction. Appl. Math. Lett. 2011, 24, 1379–1383. [Google Scholar] [CrossRef]
- Brkić, D. Comparison of the Lambert W-function based solutions to the Colebrook equation. Eng. Comput. 2012, 29, 617–630. [Google Scholar] [CrossRef]
- Haaland, S.E. Simple and explicit formulas for the friction factor in turbulent pipe flow. J. Fluids Eng. 1983, 105, 89–90. [Google Scholar] [CrossRef]
- Round, G.F. An explicit approximation for the friction factor-Reynolds number relation for rough and smooth pipes. Can. J. Chem. Eng. 1980, 58, 122–123. [Google Scholar] [CrossRef]
- Eck, B. Technische Stromungslehre; Springer: New York, NY, USA, 1973. [Google Scholar]
- Avci, A.; Karagoz, I. A novel explicit equation for friction factor in smooth and rough pipes. J. Fluids Eng. 2009, 131, 061203. [Google Scholar] [CrossRef]
- Wood, D.J. An explicit friction factor relationship. Civil. Eng. 1966, 36, 60–61. [Google Scholar]
- Moody, L.F. An approximate formula for pipe friction factors. Trans. ASME 1947, 69, 1005–1011. [Google Scholar]
- Baker, G.A.; Graves-Morris, P. Padé Approximants. Encyclopedia of Mathematics and Its Applications; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Praks, P.; Brkić, D. Choosing the optimal multi-point iterative method for the Colebrook flow friction equation. Processes 2018, 6, 130. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).