1. Introduction
Drought gradually happens with a lack of rainfall for a long period of time (i.e., months or years). This natural disaster is considered to be the most complex and least understood by many scientists. The impact of drought varies with respect to the affected areas. The damage may include impacts on the social and agriculture sectors, and the economy [
1]. In 2007, it was reported that, because of the tremendously hot temperature, heat waves, and heavy rainfalls, extreme events would accumulate and become more frequent [
2]. Although Malaysia experiences a tropical climate and receives more than 2000 mm of total rainfall annually, over the recent years, the country has experienced several drought episodes. For example, the state of Melaka faced a serious water shortage when water levels in the dams fell under critical levels in 1991, and the Durian Tunggal dam, which serves as a major water supply dam, ran dry [
3]. In 1998, an El Nino-related drought severely hit the states of Selangor, Kedah, and Penang, which caused severe social and environmental impacts across the country [
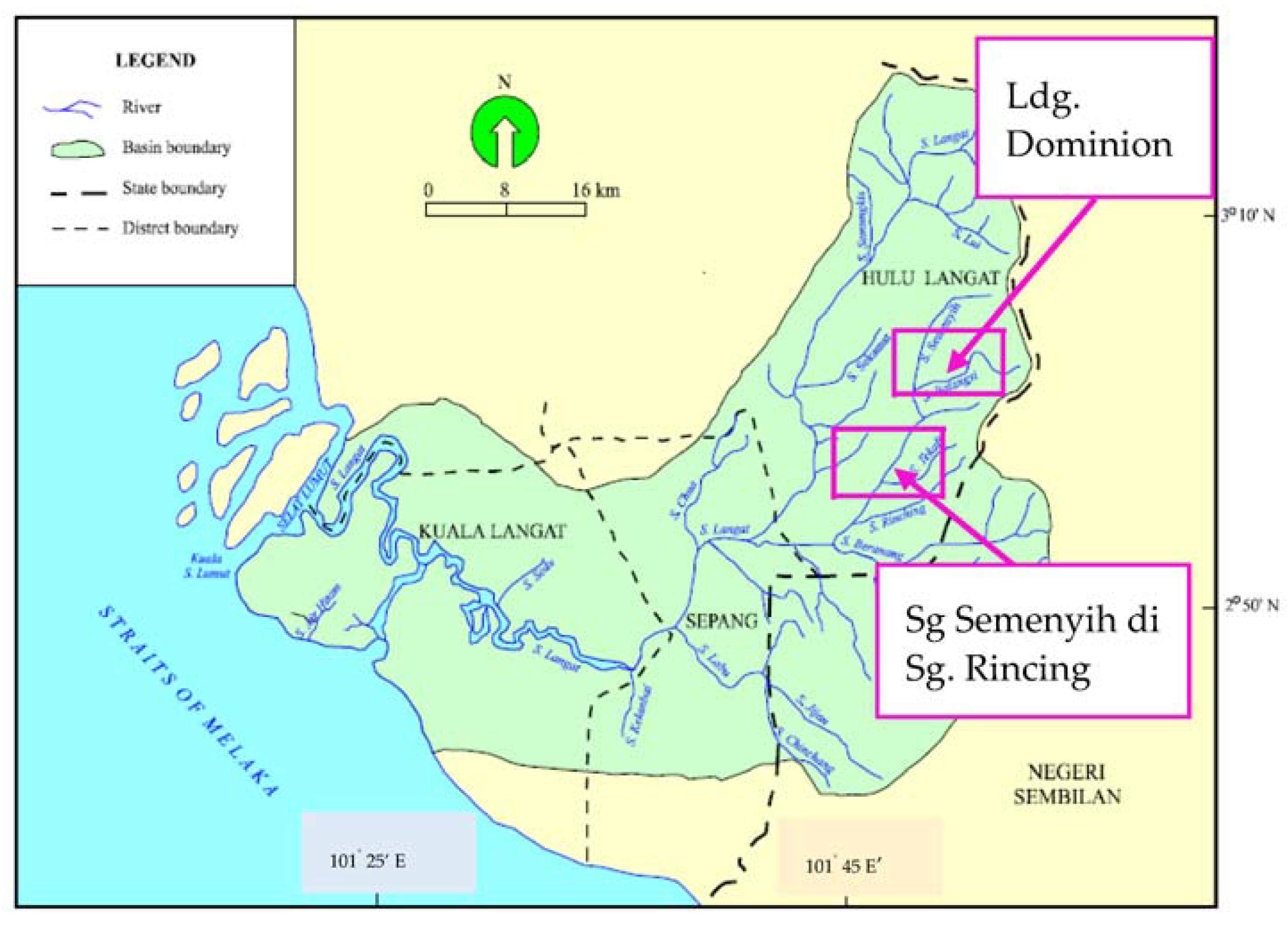
3]. This drought caused water rationing and hardship for 1.8 million residents of Kuala Lumpur and other towns in Klang Valley. The Langat River Basin also experienced a rise in temperature nearly 5° higher than usual on many days in March and April 2016 [
4]. A research study applied the standardized precipitation index (SPI) to evaluate dry conditions using the data from 10 gauging stations throughout peninsular Malaysia, and found that extreme dry conditions are becoming more frequent than extreme wet conditions [
5]. Thus, emphasis should be placed on measures to reduce the impact of dry conditions, although the authorities usually put more focus on reducing extreme wet conditions (i.e., floods).
Drought is generally analyzed by means of drought indices, which are effectually a function of precipitation and other hydrometeorological variables [
6]. Different drought indices have been discovered and are used in different nations [
6]. Hydrologists have defined four major categories of drought, namely, meteorological drought, agricultural drought, hydrological drought, and socioeconomic drought [
1]. Drought monitoring by indices in specific areas must be based on the availability of hydrometeorological data and the capability of the index to dependably detect spatial and temporal differences through a drought event. Nevertheless, no single indicator or index alone can precisely describe the onset and severity of the event. Numerous climate and water supply indices are used to describe the severity of any drought event. Although none of the major indices is inherently superior to the rest in all circumstances, some indices are better suited for certain uses than others [
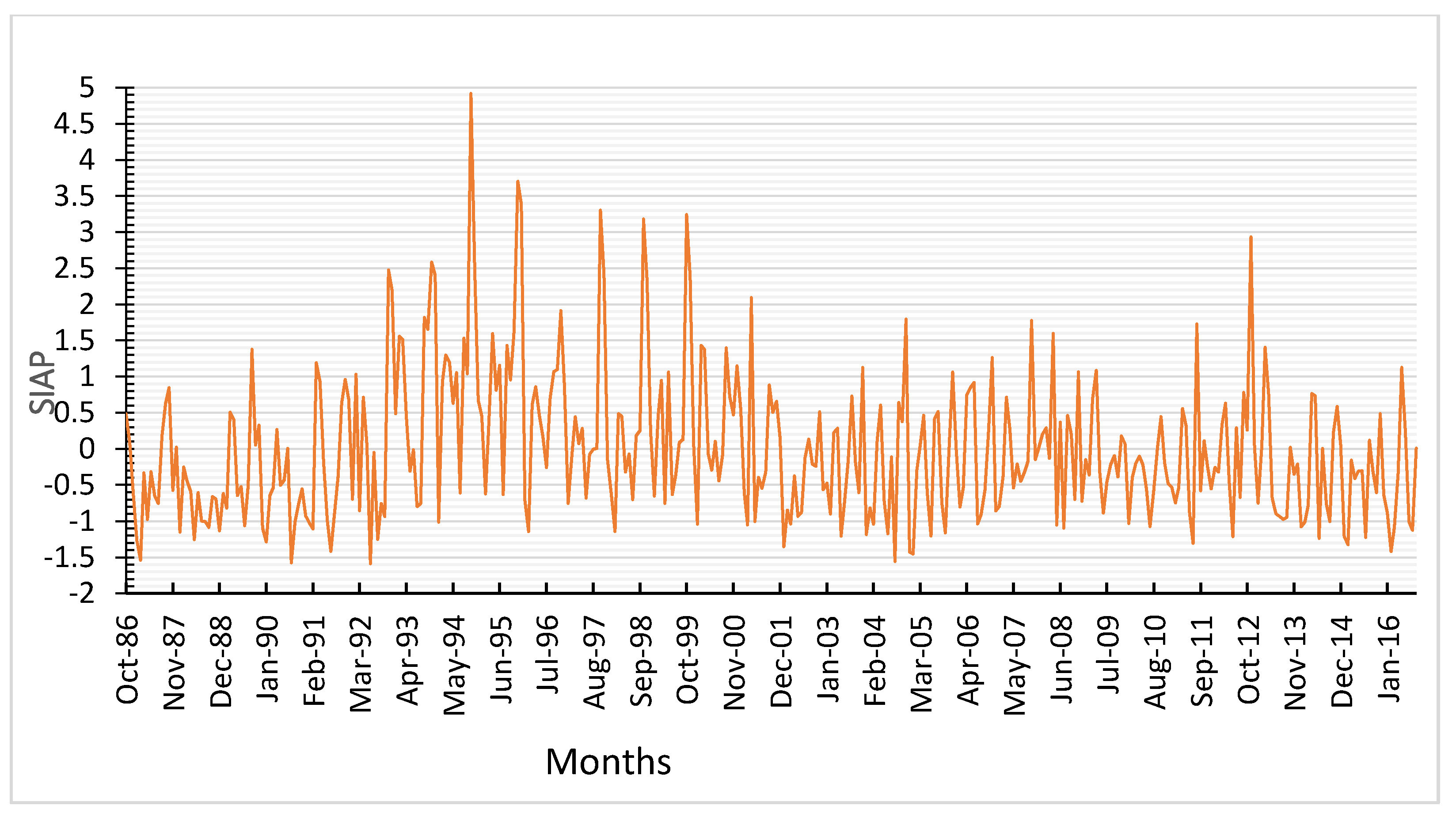
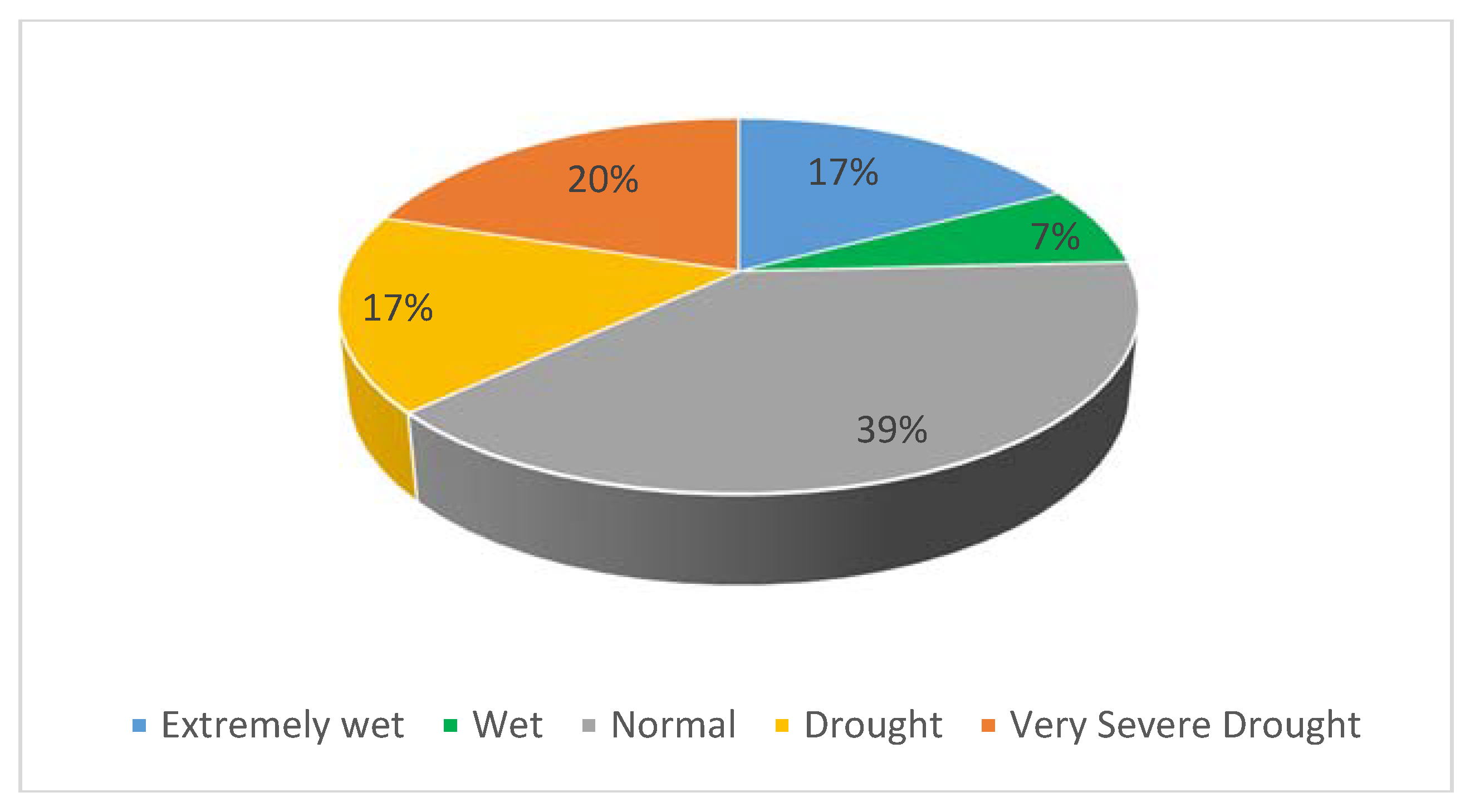
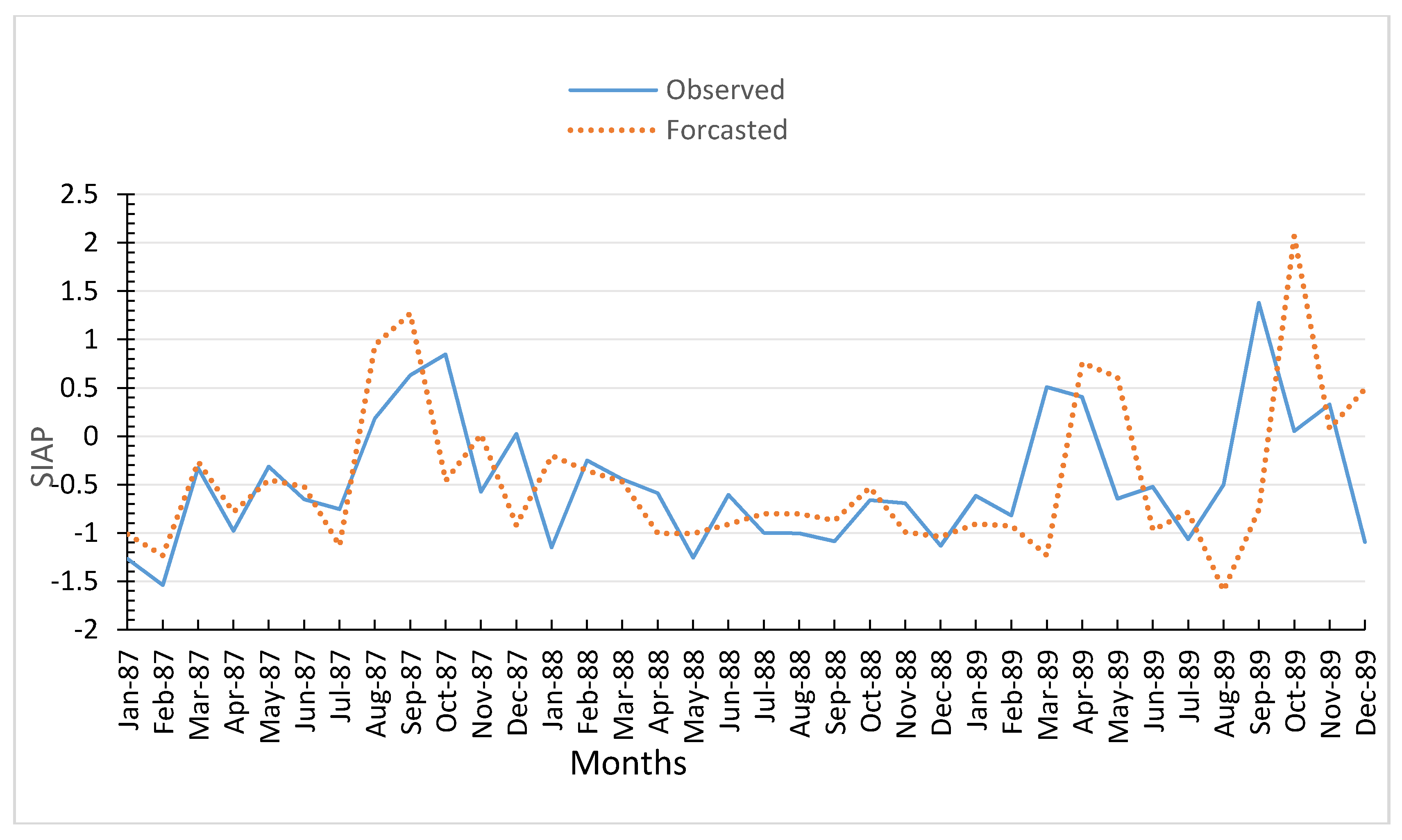
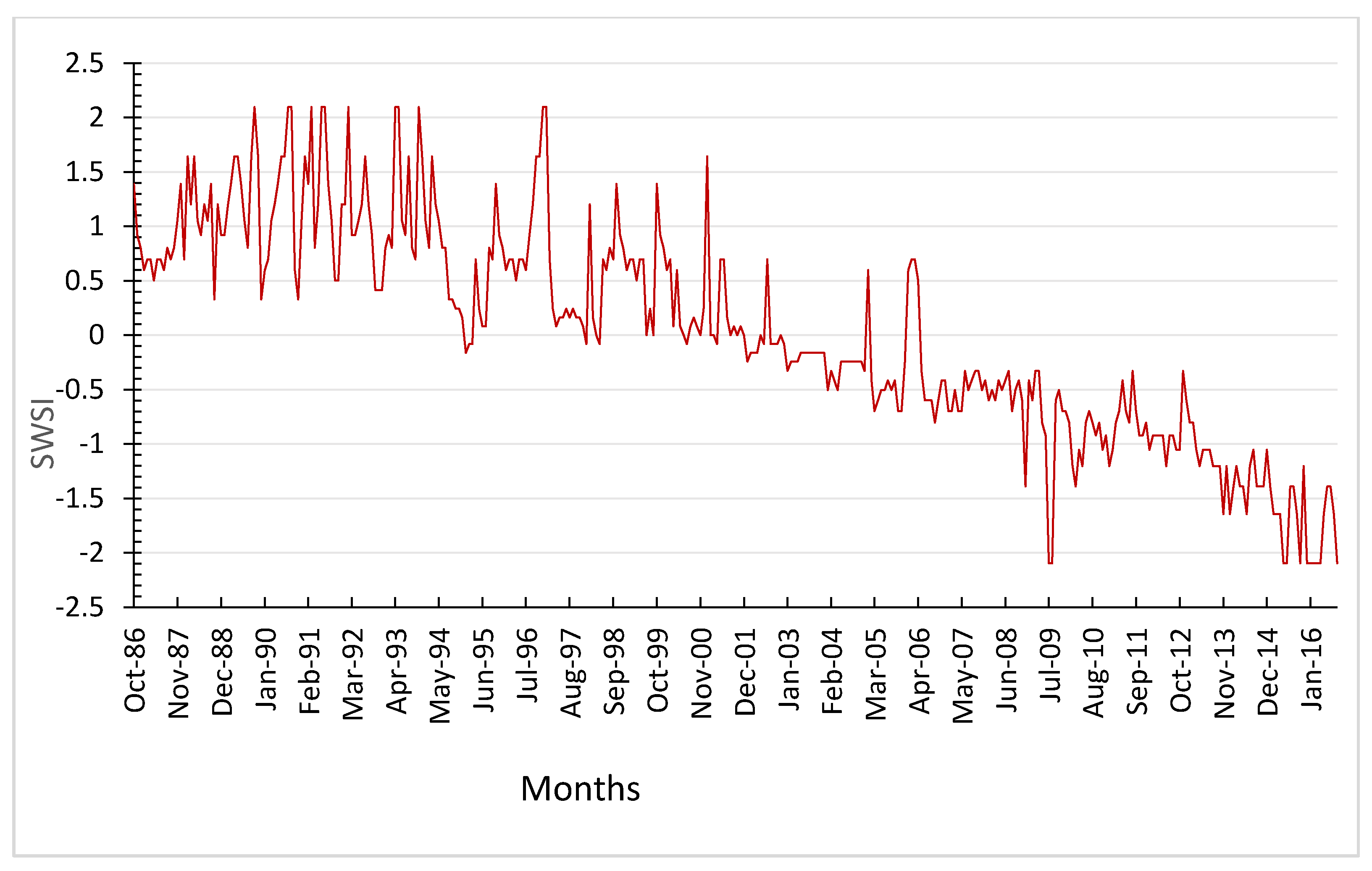
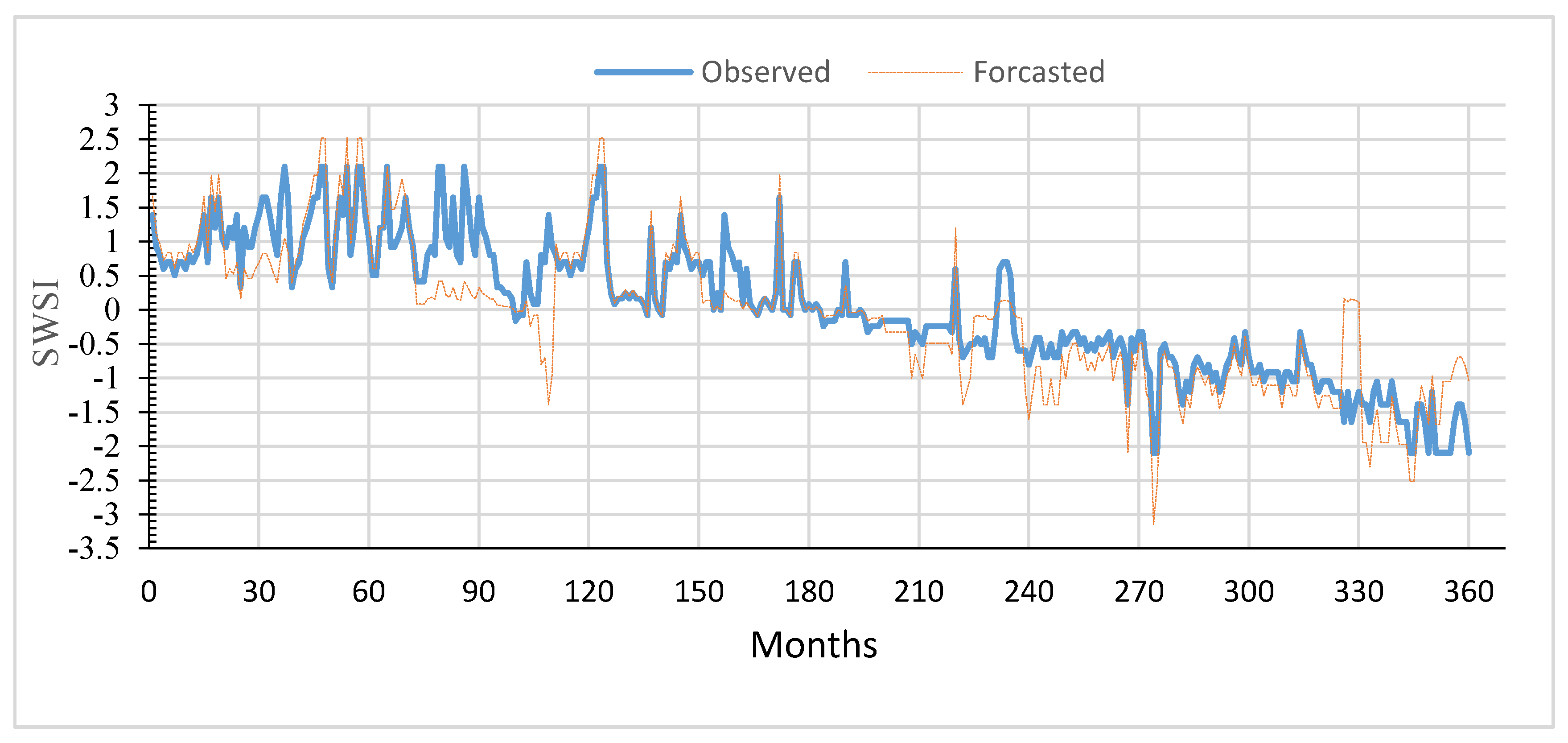
7]. In this study, the first objective was to assess the drought using two drought indices (DIs), the Standard Index of Annual Precipitation (SIAP) and the Standardized Water Storage Index (SWSI), to represent meteorological and hydrological droughts, respectively. The SIAP and SWSI were chosen for their simplicity, and they do not require parameter estimation. Gourabi [
8] used SIAP and the dependable rainfall index (DRI) for the recognition of drought years in several areas in Iran, and to analyze the effects on rice yield and water surface. Sing et al. [
9] used SIAP and a few other indices to assess the drought spells in the Almora district of Uttarakhand, India. On the other hand, to calculate SWSI, the Standardized Drought Assessment Toolbox (SDAT), developed by Farahmand and AghaKouchak in 2015 [
10], is used. The SDAT methodology standardizes the marginal probability of drought-related variables (e.g., precipitation, soil moisture, and relative humidity) using the empirical distribution function of the data. This approach does not require an assumption of the representativeness of a parametric distribution function to describe drought-related variables. Additionally, the nonparametric framework does not require a parameter estimation and goodness-of-fit evaluation, which makes the SDAT framework computationally much more efficient. Wang et al. [
11] used four drought indices, including SWSI, in order to assess the intensity and timing of drought events in the upper and middle Yangtze River Basin in China. In the second objective of this study, artificial neural network (ANN)–based models coupled with a wavelet were developed and their performance evaluation was carried out for both SIAP and SWSI models.
Many researchers have developed and applied various models to predict hydrological events, which could be divided into two major types, conceptual models (CM) and data-based models (DDM) [
12]. The conceptual models usually incorporate simplified schemes of physical laws and are generally nonlinear, time-invariant, and deterministic, with parameters that are representative of watershed characteristics. However, when they are calibrated to a given set of hydrological signals (time series), there is no guarantee that the conceptual models can predict accurately when they are used to extrapolate beyond the range of calibration or verification experience [
13,
14]. It was also a bit difficult to understand the nature of these kind of models, so, in order to use such kind of models it was very important that, in order to get better results, one should have all of the knowledge about the models and its parameters [
15]. However, DDM, which are basically numerical and based on biological neuron systems, recently known as an artificial brain or intelligence, have received more attention in water related applications because of their ease, fast progress time, and less data necessity. The ANN- or data-driven models have become increasingly popular in hydrologic forecasting because they are effective at dealing with the nonlinear characteristics of hydrological data [
16]. Among the various machine learning methods, artificial neural networks (ANNs), which include back-propagation neural network (BPNN), radial basis function (RBF) neural network, generalized regression neural network (GRNN), Elman neural network, and multilayer feed-forward (MLFF) network, are among the most popular techniques for hydrological time series forecasting [
17]. Although data driven models have attained high levels in the hydrological field, there is still space present to improve the forecasting methods [
18]. Hydrological processes are non-linear and arbitrary. By simply applying such models on an original time series, the facts of alteration are overlooked, so that prediction correctness is reduced [
19].
In the last decade, wavelet transform has become a widely applied technique for analyzing variations, periodicities, and trends in time series [
20,
21]. Wavelet transform, which can produce a good local representation of the signal, in both the time and frequency domains, provides considerable information on the structure of the physical process to be modelled. Discrete wavelet transformation provides a decomposition of original time series. Subseries decomposed by discrete wavelet transform, from original time series, provide detailed information about the data structure and its periodicity [
22]. The attributes of each subseries are different. The wavelet components of the original time series improve on a forecasting model by giving useful information on various resolution levels [
23]; however, not much research has applied a wavelet for drought forecasting. A major limitation of artificial neural networks (ANNs) is their inability to deal with nonstationary data. To overcome this limitation, researchers have increasingly begun to use a wavelet analysis to preprocess the inputs of the hydrologic data. Shabri [
24] proposed a hybrid wavelet–least square support vector machine (WLSSVM) model that combines the wavelet method and the LSSVM model for monthly stream flow forecasting. Belayneh and Adamowski [
25] studied drought forecasting using machine learning techniques and found that coupled wavelet neural network models were the most accurate for forecasting three month SPI (SPI 3) and six month SPI (SPI 6) values over lead times of one and three months in the Awash River Basin in Ethiopia. Therefore, in this study, coupling wavelets with ANN was expected to provide significant improvements in the model performance.