Abstract
Accurately forecasting streamflow values is essential to achieve an efficient, integrated water resources management strategy and to provide consistent support to water decision-makers. We present a simple, low-cost, and robust approach for forecasting monthly and yearly streamflows during the current hydrological year, which is applicable to headwater catchments. The procedure innovatively combines the use of well-known regression analysis techniques, the two-parameter Gamma continuous cumulative probability distribution function and the Monte Carlo method. Several model performance statistics metrics (including the Coefficient of Determination R2; the Root-Mean-Square Error RMSE; the Mean Absolute Error MAE; the Index of Agreement IOA; the Mean Absolute Percent Error MAPE; the Coefficient of Nash-Sutcliffe Efficiency NSE; and the Inclusion Coefficient IC) were used and the results showed good levels of accuracy (improving as the number of observed months increases). The model forecast outputs are the mean monthly and yearly streamflows along with the 10th and 90th percentiles. The methodology has been successfully applied to two headwater reservoirs within the Guadalquivir River Basin in southern Spain, achieving an accuracy of 92% and 80% in March 2017. These risk-based predictions are of great value, especially before the intensive irrigation campaign starts in the middle of the hydrological year, when Water Authorities have to ensure that the right decision is made on how to best allocate the available water volume between the different water users and environmental needs.
1. Introduction
Nowadays, water authorities and decision-makers are facing considerable challenges in achieving a sustainable and integrated water resources management system, especially, in water-stressed areas. They must make responsible management decisions on the optimum allocation of the available water volume from a wide range of possible sources (regulated or non-regulated rivers, groundwater resources, water re-use schemes, desalination plants, etc.) between the demands of, usually, multi-sectoral water users (urban, agriculture, industry, tourism, energy, etc.).
Not only must these decisions meet water demand, but they must protect this natural and finite resource, the environmental needs, the environmental impacts, the increase of legal requirements on water quality, the social equity, the costs, and the promotion of economic growth. Additionally, the effects of climate change on spatial distribution and temporal climate variability, coupled with an ever-increasing population, are altering traditional approaches to water resources planning, management, and decision processes [1,2].
To cope with this situation, a wide variety of conservation policies from supply augmentation (i.e., new infrastructures, such as reservoirs, desalination plants, rainwater harvesting, grey and black water reuse schemes, water transfers, groundwater recharge, etc.) to water demand reduction (i.e., water use efficiency, water restrictions, pricing policies, governance, etc.) can be adopted at the basin scale [3].
Therefore, advanced hydrological information and the provision of accurate streamflow forecasts is one of the key aspects to provide consistent support to decision-makers. Short-term forecasting, such as hourly or daily forecasting, is crucial for flood warning and sediment control. Medium-term forecasting based on monthly, seasonal, or annual time scales is fundamental in deciding on critical aspects of the current hydrological year, such as reservoir outflows planning, scheduling irrigation releases, allocating water to downstream users, drought mitigation, and managing river treaties or implementing compact compliance [4]. Long-term forecasting is key for planning investment in new strategic water infrastructures (such as reservoirs or water transfers between different catchments) as well as to inform the preparation of the River Basin Management Plans (required by the Water Framework Directive 2000/60/CE).
In Mediterranean countries (for example Spain), where agriculture plays an important socio-economic role, the critical decision point is in the middle of the hydrological year just before intensive irrigation campaigns commence (usually in April [5]). Whilst typical annual precipitation peaks generally occur during the months of January, February, and March, peak agricultural water demands occur precisely during the most water-stressed months of June, July, and August [6]. Therefore, water supply infrastructures, such as reservoirs, provide an important source of water storage during the wet season and are the essential infrastructure to efficiently deal with spatial and temporal climate irregularities distinctive of the Mediterranean area.
At a seasonal level, a skilful streamflow forecast may allow for more efficient water allocation and predictable trade-offs between flows for energy, irrigation, urban water supplies, environmental services, etc. Such forecasts often allow us to address anticipated conditions and not simply react to existing conditions, potentially reducing climate-related risks and offering opportunities [7,8]. The importance of achieving an adequate level of accuracy when predicting streamflows has been highlighted by many authors [9,10,11,12]. There is a wide variety of methods that have been used to build streamflow prediction models. Streamflow forecasting models fall into two general categories: Process-driven and data-driven [4,12,13]. Shalamu [4] and Yu et al. [13] have provided a very detailed description and review of the different models, limitations, and applications.
Data-driven models can use many different methods, for example: (i) The support vector machine, genetic programming, and seasonal autoregressive techniques [14]; (ii) artificial intelligence-based rainfall–runoff models that include the Artificial Neural Network (ANN), Wavelet, and SARIMAX (Seasonal Auto Regressive Integrated Moving Average with exogenous input concepts) [15]; and (iii) high dimensional vine copulas, conditional bivariate copula simulations, and a quantile-copula function [16], etc. More recently, Myronidis et al. [17] successfully used ARIMA (autoregressive integrated moving average) models to forecast the mean monthly streamflow values for the next three months and to predict the evolution of drought indices in Cyprus.
On the other hand, conceptual hydrologic models replicating observed historical data sets have traditionally been used for predicting the future. However, some of their shortcomings might come from aspects, such as the quality, accuracy, and completeness of the input requirements. Their complexity is due to the number of required input variables, the difficulty to capture certain hydrological phenomena (such as the snow storage and melting processes), and the computational time, as well as the calibration and parameter optimization processes, which can be also challenging. Gragne et al. [18] proposed to address these difficulties by complementing conceptual models with simple error models and thus their results present more accurate inflow forecasts into hydropower reservoirs several hours ahead.
Currently, the use of seasonal climate predictions is becoming more commonplace. For example, Khedun et al. [19] presented a copula-based precipitation-forecasting model that produces a notable improvement in simulating negative precipitation anomalies during “La Niña” and negative Pacific Decadal Oscillation. Also, Liu et al. [20] presented a probabilistic wavelet–support vector regression model for streamflow forecasting with rainfall and climate information input that consistently generates more reliable predictions for daily and monthly forecasts as compared with the best single-member wavelet-support vector models and the adaptive neuro-fuzzy inference system.
Nevertheless, in Spain, the level of accuracy achieved by the seasonal climate forecasts provided by the Spanish Meteorological Agency (AEMET or Agencia Estatal de Metereología) [21] for the year of 2017–2018 has not been as good as expected. For example, in February 2018, AEMET predicted that, for the south-eastern quarter of Spain, March, April, and May would be much drier than average, whereas March 2018 has been the wettest month registered to date.
Additionally, the Guadalquivir River Basin Authority (who is responsible for making the strategic decisions on controlled released outflows from reservoirs) still does not have an established common streamflow forecast model or procedure to predict reservoir inflows. These decisions are based on their vast knowledge and experience managing water resources in this area, especially during drought and periods of water scarcity when critical decisions and actions must be taken [22]. Usually, these decision-makers are not familiar with very complex models or specialised software, so they typically require simple, but sufficiently robust and reliable, tools.
This research contributes towards the development of a user-guided, novel, simple, low cost, and robust methodology to forecast streamflows within the current hydrological year. This is applicable to headwater systems and can provide support to strategic water management decisions. The methodology has been successfully applied to two headwater reservoirs located at the upper area of the Genil River (Guadalquivir River Basin), namely, Quéntar and Canales.
The model forecast outputs are the mean monthly and yearly streamflows along with the 10th and 90th percentiles (although the model offers flexibility to easily modify the percentiles if needed). The model was first put into operation in October 2016 and the model output forecasts achieved satisfactory results, with a relative error varying from 8% (Canales) to 18% (Quéntar). These risk-based forecasts are not only useful for water reservoir operators and authorities, but also to all stakeholders involved in the planning, management, and decision-making processes. The model also has the ability to incorporate seasonal climate predictions and climate change effects.
The aim of this work was to develop a simple and low cost statistical model (data-driven) to forecast monthly and annual streamflows during the current hydrologic year. To achieve this, the specifications were set to:
- Use free hydrological data sources available in the public domain (to be downloaded in an easy, free, and quick manner from a reliable, official online resource where possible);
- minimise the number of hydrological variables;
- integrate easily and regularly new observed hydrological data in the model (an automatic process where possible);
- minimise computational and simulation running times (instantaneously where possible); and
- offer a user-friendly interface.
2. Materials and Methods
2.1. Overview
The proposed methodology is to predict the probabilistic monthly and annual streamflows during the current hydrological year. It innovatively combines the use of well-known regression analysis techniques (between relevant hydrological variables), the two-parameter gamma continuous cumulative probability distribution function and the Monte Carlo simulation. It is based on a probabilistic comparison of the progression of the current hydrological year (in terms of cumulative monthly precipitation or cumulative monthly streamflow) with the historical data series.
Figure 1 shows the flowchart of this methodology (described in detail in the following sections and applied to two cases of study detailed in Section 3).
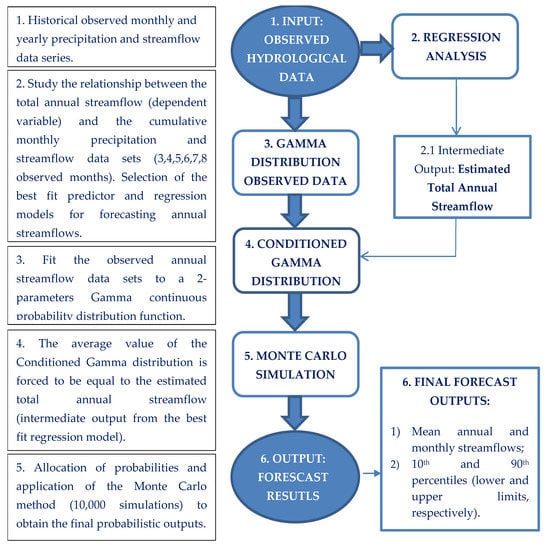
Figure 1.
Flowchart of the methodology.
2.2. Model Time Step, Data Sources, and Treatment
A monthly time step has been considered adequate for this work since the results are to support strategic and management decisions associated with annual or quarterly cycles. Therefore, the predictions from the model might not be applicable to other reservoir operations (for example, hydropower plants or flood forecasting) with lower time scale data requirements (hours, days).
It is also important to understand the phenomena that will be picked up within the selected monthly time step for each particular catchment area (for example, snow storage and melting processes, subterranean inflows, etc.).
Free hydrological data sources available in the public domain have been used to inform this work (as detailed in Section 3.2). The data can be downloaded in an easy, free, and fast manner from a reliable and official online resource.
The data requirements were the historical precipitation and streamflow monthly data sets for each particular catchment of study. It is recommended to apply the methodology when there is good quality input data and at least 30 years of observed data (although 40 years would be desirable to increase the forecasts’ accuracy). The minimum number of observed years should be greater in those catchments with a greater standard deviation.
From the observed data series, the cumulative precipitation and streamflow monthly time series were calculated for the first three observed months (Oct to Dec), four observed months (Oct to Jan), five observed months (Oct to Feb), six observed months (Oct to March), seven observed months (Oct to April), and eight observed months (Oct to May). The reason why the assessment starts with the first three cumulative observed months is to ensure that sufficiently good correlation coefficient values were achieved in the regression analysis.
With this input data, the model provides monthly and yearly streamflow forecasts for the rest of the current hydrological year monthly, starting the forecasts from January, as shown in Table 1.

Table 1.
Relationship between the observed and forecasted periods.
2.3. Simple Regression Analysis and Best Fit Predictor
For the proposed methodology, we used simple regression analysis techniques. We sought to predict the total annual streamflow (hereinafter referred to as Aannual) from relevant hydrological descriptors. We selected the cumulative monthly precipitation (hereinafter referred to as Pcum) and the cumulative monthly streamflow (hereinafter referred to as Acum) as the best predictors.
The analysis assumed that the hydrological cycle (from October to September) for a specific basin is in balance at the end of the hydrological year. Therefore, a greater correlation between the total annual streamflow and the cumulative monthly time sets was expected as the number of observed months increases.
The results from the regression analysis were subsequently assessed using the coefficient of determination (R2). This allowed us to select the best fit regression model and best fit hydrological predictor (cumulative rainfall or cumulative streamflow) for each specific month of study. The estimated total annual streamflow from the regression models is an intermediary output (to be used as an input to obtain the conditioned gamma, as shown in Figure 1).
It is important to note that the best fit regression model and the best fit predictor do not necessarily need to be same for all the observed months of study. In fact, it might vary depending on the predominant hydrological process given at each specific month or season of the year (snow storage and melting processes, subterranean inflows, seasonal extreme, and sporadic rainfall events). In this situation, a combined regression model should be used to achieve the best correlation values and forecast results.
2.4. Two-Parameter Gamma Cumulative Probability Distribution Function
The next step was fitting the historical annual streamflow data series to a two-parameter gamma (α,β) cumulative probability distribution function (CDF).
There is extensive literature describing the properties, parameters estimation, and applications of the two-parameters gamma (α,β) CDF [23]. This distribution has been shown to fit well to rainfall and streamflow data sets, respectively, and, therefore, has been widely applied to hydrological data-driven models, such as those described in the studies of Buishand [24], Stephenson et al. [25], Wang and Nathan [26], Chen et al. [27], and Chowdhury et al. [28].
A random variable, X, is said to have a two-parameter gamma continuous probability density function if its distribution is given by:
where α and β are the shape and scale parameters, respectively.
The gamma CDF is given by:
The mean, E(x), and variance, V(x), are given by Equations (4) and (5), respectively:
From Equations (4) and (5), we can estimate the mean and variance of the observed series and the parameters α and β, as follows:
β = V (x)/E (x)
α = E(x)2/β
This distribution provides the non-exceedance (or maximum) probability that the total annual streamflow will take a value less than or equal to a determined value as well as the maximum total annual streamflow value associated to a specific probability value.
It is important to check how well the gamma distribution fits with the observed data series of annual streamflows for each case study. Section 3.4 shows that for the two case studies, the gamma CDF was found to provide a very good fit to the total annual streamflow distribution.
2.5. Conditioned Two-Parameter Gamma Cumulative Probability Distribution Function (Using the Output from the Regression Models)
To obtain the conditioned gamma distribution function, we determined the influence of the estimated total annual streamflow (from the regression models, Section 2.3) on the gamma CDF (fitted to the observed data, Section 2.4).
To do that, we imposed the condition that the mean value of the new conditioned gamma CDF is equal to the result obtained from the regression model (‘’ or estimated total annual streamflow). The value of the scale parameter, β, is kept the same as that already obtained from the gamma CDF (fitted to the observed total annual streamflow data sets).
Based on this, the shape parameter, α, of the conditioned gamma was re-calculated as follows:
αcond (Conditioned Gamma) = Mean (Conditioned Gamma)/β =
= Estimated total annual streamflow (from the regression analysis)/β
= Estimated total annual streamflow (from the regression analysis)/β
We then estimated the conditioned gamma CDF using Equation (3) and the two-parameters (αcond,β).
It is important to highlight that whilst the gamma CDF is a fixed curve (since this is derived from the observed and complete hydrological years), the conditioned gamma CDF curve will vary from month to month depending on the output obtained from the regression models. In fact, the conditioned gamma CDF curve will move to the right or left of the gamma CDF, depending on whether the prediction is for a wetter or drier hydrological year than the mean historical year, respectively. If the conditioned gamma CDF is close to the observed gamma CDF this means that the current hydrological year is expected to be similar to the mean observed hydrological year.
The conditioned gamma distribution function (αcond,β) allowed us to assign a probability to each year of the historical series based on their total annual streamflow. Therefore, we obtained greater probabilities for those observed years whose annual streamflow is similar to the estimated annual streamflow (‘’) and lower probabilities for those observed years whose annual streamflow differs from the estimated annual streamflow. For each year of the historical series, we have its probability (p), given by:
where x is the observed annual streamflow of the historical records (hm3), αcond is the shape parameter of the conditioned gamma, and is the scale parameter of the gamma distribution (the same as per the non-conditioned gamma distribution).
2.6. Monte Carlo Method
The Monte Carlo Method is a numerical statistical method that allows the replication of random behaviour of real, non-dynamic systems through the generation of random numbers to which an event is assigned based on their probability distribution [29].
Our model generates 10,000 random input numbers in the interval [0,1]. Each of these random numbers is assigned to one year of the observed streamflows series according to the conditioned gamma CDF (which already integrates the output from the regression model). Therefore, we obtained 10,000 random observed years (from the historical series) according to the probability of success.
From the statistical analysis of those, we obtained three probabilistic forecasts: Optimistic, average, and pessimistic. For our case study, we assigned the 90th percentile to the optimistic streamflow forecast and the 10th percentile to the pessimistic forecast, though the user can easily modify these values if needed.
2.7. Model Running Time, Test, and Validation
The model takes just a few seconds to run the simulations and provide the forecast results. Therefore, this tool provides a significant improvement in saving simulation and computational times when compared with more complex and sophisticated models.
To verify the model performance, measure its predictive accuracy, and identify potential limitations, several metrics, including the root-mean-square error (RMSE) and determination coefficient (R2), were used (as shown in Section 3).
2.8. Application and Limitations
The total annual streamflow was chosen as the prediction target (instead of the precipitation) to avoid the need of using an additional model to transform the precipitation into streamflow.
However, it is important to note that if there are rapid and significant land use changes within the catchment of study, these might alter the observed hydrological cycle within the basin. In this situation, the model might generate misleading streamflow forecasts. For example, a recent and rapid increase in impermeable area would generate a greater volume of surface water flows and quick streamflow peaks than the historical observed catchment response [30]. In this case, the precipitation as the prediction target (instead of the streamflow) might be more appropriate and an additional model to transform the precipitation into the streamflow contribution might be required.
The proposed methodology does not consider the contributing inflows from upstream systems (for example, regulated outflow releases from other reservoirs upstream). Therefore, this methodology is applicable to headwater systems located at upper catchment areas.
There is no limitation in catchment size, however, those catchments with considerable climatic irregularity or very rare seasonal sporadic rainfall events are difficult to predict and should be carefully studied prior to progressing the modelling works (since this methodology is based on a statistical treatment of the known past to predict the future).
3. Application to Canales and Quéntar Reservoirs (Upper Guadalquivir River Basin, Spain)
3.1. Study Area Description
The Guadalquivir River is the main river in southern Spain that provides water to a total population of over four million people and over eight hundred thousand hectares for irrigation purposes. This system is currently formed by an interconnected system of 64 functioning dams [31]. Although there are alternative water resources from aquifers, springs, and water re-use schemes, nowadays, reservoirs are the essential infrastructure to efficiently deal with spatial and temporal climate irregularities distinctive of this catchment area. Figure 2 shows the location of the Guadalquivir River Basin in Spain and the area of study.
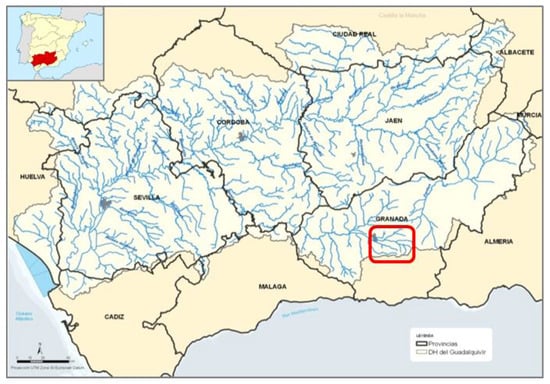
Figure 2.
Location of the Guadalquivir River Basin [31] in Spain and the area of study (Latitude: 37.15855 Longitude: −3.470605).
The Guadalquivir River has a total contributing catchment area of 57,527 km2 and is delimited by Sierra Morena to the north, the Betic mountain to the south, and the Atlantic Ocean. The altitude at the mountainous borders varies between 1000 m Above Ordenance Datum (AOD) and 3480 m AOD, which contrasts with the lower altitudes of the Guadalquivir River valley. The climate is Mediterranean, which is defined by the warm temperatures (16.8 °C annual average) and the irregularity of precipitations (550 mm annual average). The rains are frequently torrential and occur after long periods of drought and high temperatures, with a distinct susceptibility to erosion [31]. Figure 3 shows the mean annual precipitation and temperature, altitude, and land uses in the Guadalquivir River Basin.
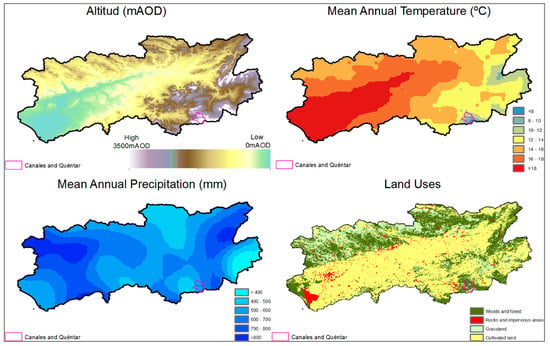
Figure 3.
Guadalquivir River Basin (a) altitude, (b) mean annual temperature, (c) mean annual precipitation, and (d) land uses.
The Guadalquivir River Basin Authority (GRBA) is responsible for the elaboration of the Guadalquivir River Basin Management Plan (according to the European Water Framework Directive 2000/60/CE) as well as the administration and control of the hydraulic public domain [31]. Last year, the GRBA published the draft version of the Guadalquivir River Basin Special Drought Management Plan (2017). This document establishes the general water management principles and course of action for different drought and water scarcity threshold scenarios for each sub-catchment area [32], but does not incorporate any streamflow forecast model or procedure.
The two headwater reservoirs of study are the Quéntar and Canales, located at the upper area of the Genil River within the Granada administrative area and to the south-east of the Guadalquivir River Basin (refer to Figure 2 and Figure 4).
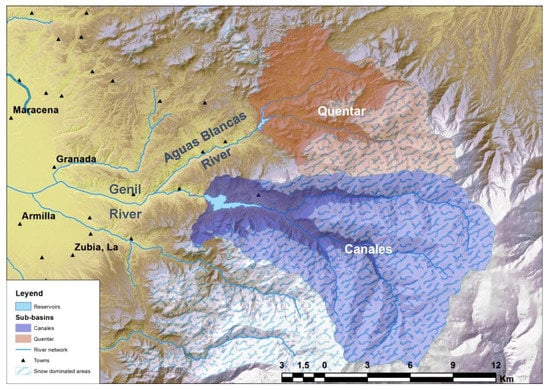
Figure 4.
Location of Canales reservoir sub-basin (Latitude: 37.15855 Longitude: −3.470605) and the Quéntar reservoir sub-basin (Latitude: 37.206527 Longitude: −3.433458). Source: own elaboration.
The Canales reservoir is located in the upstream area of the Genil River (close to Sierra Nevada), close to the town of Güejar Sierra, with a total contributing catchment area of 176.5 km2. The dam was built in 1989 with a total capacity of 70 hm3 and average streamflow of 80.42 hm3/year. This catchment area is affected by snow storage and melting processes in the Sierra Nevada. The snow appears between the months of November and May, reaching the maximum accumulation of snow in March with an average water-equivalent volume of 20 hm3 [33].
The Quéntar reservoir is located on the Aguas Blancas River (tributary of the Genil River), with a total contributing catchment area of 101.2 km2. This dam was built in 1975 with a total volume capacity of 13.5 hm3. The average streamflow is 28.84 hm3/year. This catchment area is affected by subterranean inflows due to the aquifer and lithology present in the region.
These two reservoirs form the key infrastructure that mainly provide water for urban and irrigation purposes. Urban water consumers are formed by the Granada city and fourteen towns of its metropolitan area, with up to 300,000 inhabitants. The Vega Alta del Río Genil traditional irrigations cover over 4000 hectares and are fed by an extensive irrigation channel system that diverts water from the Genil River (downstream of the Canales and Quéntar reservoirs).
This system is currently supplemented by a network of thirteen operating underground water wells located in the upper area of the Vega de Granada aquifer (south-east of the city of Granada, on both banks of the Monachil River and the A-395 motorway). These were built by the GRBA after the serious social, economic, and environmental consequences suffered during and after the 1992–1995 drought period (during which Canales and Quéntar reservoirs were depleted). The objective of these works was to supplement the existing surface water resources (provided by the Canales-Quéntar system) with the extraction of groundwater to serve the urban water supply of Granada and the metropolitan area. In 1995, the GRBA delivered this infrastructure to Emasagra (Local Water and Sewage Company) to guarantee its correct management, operation, and maintenance. Since then, Emasagra has been responsible for its management, while the GRBA is responsible for the supervision, reservoir management, and compliance with water allocation.
During years of average precipitation, water demands can be met with surface water resources. However, in years of below-normal precipitation, typically higher underground water volume extractions and/or reductions in per right allocation are required. During prolonged periods of drought and water scarcity, the urban water supply has theoretically been assigned priority of use over agricultural demand.
Strategic decisions made by the GRBA on the controlled released outflows from the Quéntar-Canales system are critical to ensure the most resource-efficient, cost-efficient, and sustainable allocation of the available water resources. These decisions are especially relevant before the intensive irrigation campaign starts (usually in April), when the water authorities must make responsible management decisions about the best allocation of the available water volume between different water consumers and environmental needs for the rest of the hydrological year.
However, despite their vital importance, decisions made by the GRBA are mainly based on the current water storage in reservoirs instead of using the results from streamflow forecast models. Therefore, we believe the proposed tool can positively contribute towards the development of a practical, quick, and reliable tool to support water authorities and managers on the strategic decision process to achieve a sustainable water resources management approach.
3.2. Data Sources and Treatment
The ‘Automatic Hydrological Information System (SAIH)’ is a free and public online portal maintained by the Guadalquivir River Basin Authority in Spain [34]. The SAIH offers information, such as streamflow, reservoir outflows, rainfall, reservoir level, temperature, etc. for up to 57 reservoirs, 52 non-regulated rivers, 20 canals, and 10 hydro power plants. Other information on rain, snow, and temperature gauging stations across the basin is also offered. The available temporal data sets vary depending on the specific sub-catchment area, but usually these are available from 1989. The information can be downloaded in an hourly, daily, or monthly time step.
The historical monthly precipitation and streamflow data series for Canales (from October 1988 to present) and Quéntar (from October 1977 to present) were obtained. From this information, the cumulative precipitation and streamflow monthly time series for the first three, four, five, six, seven, and eight observed months were determined (as described in Section 2.2).
3.3. Regression Analysis, Correlation, and Selection of the Best Fit Estimator and Regression Model
A complete statistical study was carried out to assess the correlation between the total annual streamflow and the cumulative monthly precipitation and streamflow sets. Figure 5 and Figure 6 show the regression analysis for the first three, four, five, six, seven, and eight observed months for Canales and Quéntar, respectively.
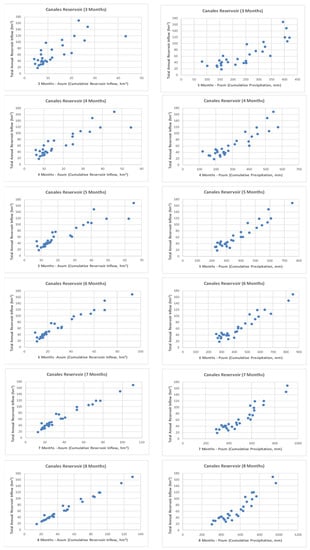
Figure 5.
Canales reservoir: Regression analysis for the first three, four, five, six, seven, and eight months using the cumulative monthly reservoir inflow and precipitation.
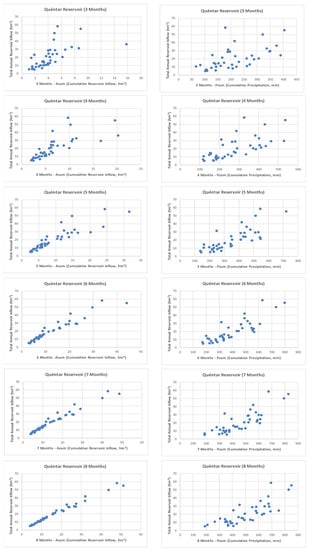
Figure 6.
Quéntar reservoir: Regression analysis for the first three, four, five, six, seven, and eight months using the cumulative monthly reservoir inflow and precipitation.
From a visual inspection of Figure 5 and Figure 6, it can easily be observed how the correlation is greater as the number of observed months increases. This is corroborated by the R2 values shown in Table 2.

Table 2.
Coefficient of determination (R2) from the regression analysis.
Table 2 shows the results obtained for the Canales and Quéntar reservoirs.
The comparative critical assessment of the coefficient of determination (R2) allowed us to select the best fit regression model and best fit hydrological predictor (cumulative rainfall or cumulative streamflow) for each reservoir and specific month of study. The estimated total annual streamflow from the regression models is an intermediary output (to be used as an input to obtain the conditioned gamma).
Table 2 shows that that the lineal regression model is the best fit model for the Canales reservoir. It can be observed that the cumulative precipitation presents the best R2 values (varying from 0.7253 to 0.9083) for the first three, four, and five observed months whilst the cumulative streamflow achieves the best R2 values (varying from 0.9429 to 0.9839) for the six, seven, and eight observed months. This fact is considered to be due to the influence of snow storage and melting processes distinctive of this basin. The Canales catchment river hydrograph shows a pluvio-nival pattern with two flow peaks. The first one was in January and February due to the surface water runoff from rainfall events. The second one was around April and May due to snow-melt water flows from the Sierra Nevada.
Therefore, the Canales regression model follows the equation:
where Aannual is the annual streamflow (hm3), xcum. is the cumulative monthly precipitation (for the first three, four, and five observed months in mm) and cumulative monthly streamflow (for the first six, seven, and eight months in hm3), and a and b are the lineal regression model coefficients.
Table 2 shows that the regression model (linear with logarithmic transformation) is the best fit model for the Quéntar reservoir. It can be observed that the cumulative streamflow presents the best R2 values (varying from 0.5442 to 0.9894) for all the months of study. The most important hydrological process given within the Quéntar catchment is due to the underground aquifer flows. The snow storage and melting processes are not relevant if compared with the Canales reservoir. Therefore, the base flow contribution into the total annual reservoir inflow is important. This might be the reason why the strongest correlation is found between the cumulative monthly streamflow and the annual streamflow.
Therefore, the Quéntar regression model follows the equation:
where Acum. is the cumulative monthly streamflow (hm3), and c and d are the regression model coefficients.
The estimated annual streamflow (‘’) can therefore be estimated from the obtained regression models, which are based on complete hydrological years (from October to September, both inclusive) of observed precipitation and streamflow data. That is, the regression models should contain all the historical records up to September of the last year that is needed to be forecasted.
3.4. Two-Parameter Gamma Cumulative Probability Distribution Function (Observed Data) and Conditioned Gamma Cumulative Probability Distribution Function (Using the Output from the Regression Models)
Following the methodology described in Section 2.4 and Section 2.5, we obtained two-parameter gamma CDF for each reservoir of study shown in Figure 7. It was found that the gamma distribution fits very well with rainfall in general [35] and particularly with the observed series of annual streamflows for the two reservoirs of study. We obtained a correlation coefficient (R) of 0.99 and 0.98 for Quéntar and Canales, respectively, between the observed annual streamflow series and those given by the distribution function.
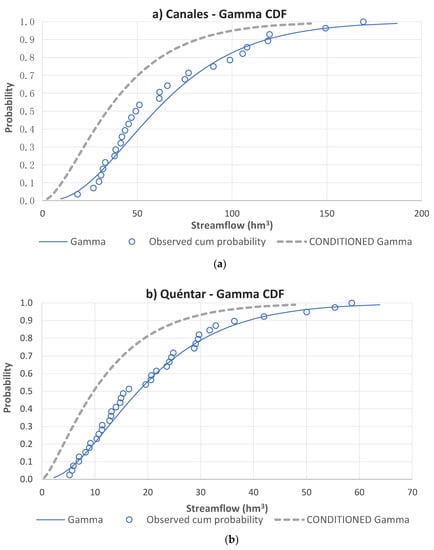
Figure 7.
Two-parameter gamma CDF and conditioned gamma distribution—1st April 2017: (a) Canales reservoir (observed data October 1988–September 2016); and (b) Quéntar reservoir: (observed data October 1977–September 2016).
It can be seen from Figure 7 that the forecast given by the model in April 2017 for Canales and Quéntar was for a drier year than the mean historical hydrological year (since the conditioned gamma distribution was to the left side of the gamma CDF), which was what happened last year.
3.5. Assigning Probabilities and Application of Monte Carlo Method
As explained in Section 2.6, we obtained 10,000 random observed years (from the historical series) using the Monte Carlo simulation method.
From the statistical analysis, we obtained three forecasts: Optimistic, average, and pessimistic. For our case study, we assigned the 90th percentile to the optimistic forecast and the 10th percentile to the pessimistic forecast, but the user can easily modify these values if needed.
Figure 8 shows, as an example, the April 2017 forecast output graph for the Quéntar reservoir model (six observed months and six forecast months). Lines in blue correspond to each observed year and the dotted red line to the historical average year. The orange line is the model average forecast output while the yellow dotted lines are the 90th and 10th percentiles forecasts (optimistic and pessimistic, respectively).
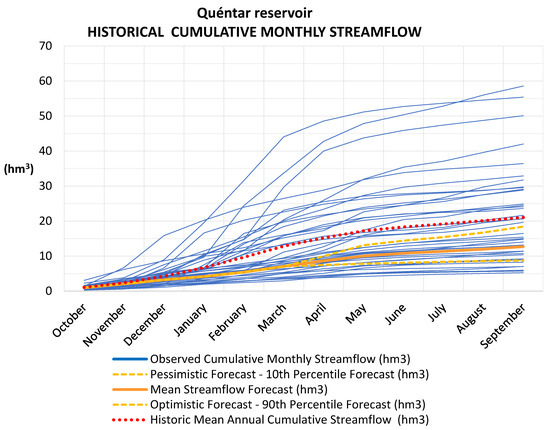
Figure 8.
Example of typical model forecast outputs results compared with the historical observed streamflow data.
3.6. Model Validation
To verify the model performance and measure its predicting accuracy, the following metrics were applied [36]:
- (a)
- Coefficient of determination (R2);
- (b)
- root-mean-square error (RMSE);
- (c)
- Mean Absolute Error (MAE);
- (d)
- Index of Agreement (IOA);
- (e)
- Mean Absolute Percent Error (MAPE);
- (f)
- Coefficient of Nash-Sutcliffe efficiency (NSE); and
- (g)
- Inclusion Coefficient (IC) defined as the percentage of times that the observed streamflow falls within the 10th and 90th percentiles (our pessimistic and optimistic forecast values).
The results are listed in Table 3 and Table 4 for Canales and Quéntar, respectively. The performance indices presented in Table 3 show that the model performs relatively better at forecasting annual rather than monthly streamflows. This highlights the difficulty of forecasting the monthly streamflow distribution along the hydrological year. This may be because the snow melt processes occurring in the Canales catchment area are more difficult to predict monthly (due to its variability).

Table 3.
Canales reservoir: Performance test results.

Table 4.
Quéntar reservoir: Performance test results.
The monthly forecast results achieved for the Canales (R2 values vary from 0.53 to 0.83 and average of 0.69) reservoir are better than those found for the Quéntar reservoir (R2 values vary from 0.23 to 0.51 and average of 0.41). The optimal results in our study are given for the Canales reservoir for the seven observed months that achieved the highest R2 = 0.83 and lowest MAPE = 32.45.
The results also show that, generally, the model performs better as the number of observed months increases (the values of R2, IOA, and NSE increase while the values of RMSE, MAE, and MAPE decrease). The higher values of error correspond to those observed hydrological years where hydrographs differ considerably from the mean historical observed year. Particularly, the worst MAPE value for the Canales and Quéntar reservoirs occurs in the driest years of 1994–1995 and 2004–2005.
To gain better insight into the model performance in relation to the lower and upper forecasts (i.e., 10th and 90th percentiles, respectively), the inclusion coefficient was calculated. An inclusion coefficient of approximately 80% for the monthly streamflow forecasts and higher than 80% for the annual forecasts was achieved. These results show that the 10 and 90 percentiles are representative values to support risk-based management decisions for these specific catchments.
Figure 9 and Figure 10 present the observed and estimated monthly and yearly streamflow hydrographs (with six months of observed data) for the Canales and Quéntar reservoirs, respectively. The model predicted the entire historical set relatively well, with a tendency to slightly overestimate the flows. The error distribution suggests that the model is less likely to be more effective in forecasting hydrograph peaks (very dry or very wet years).
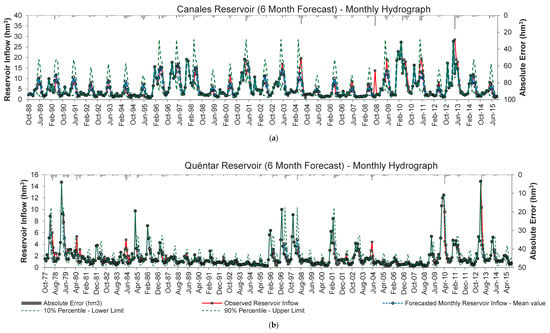
Figure 9.
Observed monthly streamflows (hm3) and predictions using the model with the first six months of observed data of the hydrological year and 10th and 90th percentiles (lower and upper limits) (hm3) of the (a) Canales reservoir and (b) Quéntar reservoir.
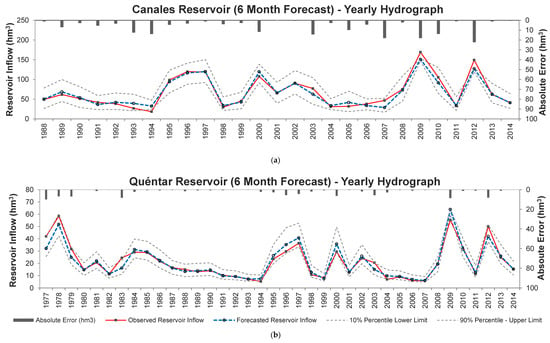
Figure 10.
Observed annual streamflows (hm3) and predictions using the model with the first six months of observed data of the hydrological year and 10th and 90th percentiles (lower and upper limits) (hm3) of the (a) Canales reservoir and (b) Quéntar reservoir
Myronidis et al. [17] developed ARIMA models to forecast the mean monthly streamflows for the next three months and for 10 different catchments in Cyprus, achieving moderate accuracy. The results achieved R2 values varying from 0.10 to 0.63 (average of 0.37) and MAPE values varying from 25.02 to 1112.38. Myronidis et al. acknowledged similar results achieved by other authors also using ARIMA models. Their optimal results obtained in this study were found for catchment number 6, which achieved the highest R2 = 0.63 and lowest MAPE = 25.02.
If we compare the ARIMA model results with those achieved in this study (Table 3 and Table 4), in average terms, our model performed similarly or even slightly better at providing results for a longer forecasted period (for up to nine months in advance), using a simpler methodology.
Given that the model has been developed to support management decisions associated with annual or quarterly cycles, we consider that the model is fit for its purpose and the results obtained are satisfactory.
3.7. Model Outputs
The proposed method can be implemented using mathematical programming software or simply using an Excel ® spreadsheet.
Figure 11 shows the user-friendly interface (taken from our model implemented in Excel). The user only needs to introduce the observed monthly rainfall and streamflow information in the dark grey columns and press the button called “Run the model”. Almost instantly, the user can see the numerical results and associated graphs on the right hand side of the screen showing the probabilistic mean total annual streamflow and the monthly distribution as well as the optimistic and pessimistic forecasts.
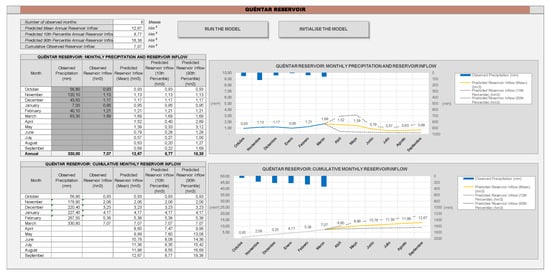
Figure 11.
Example of typical model input requirements and outputs results.
Figure 8 shows the historical data set of observed years and the historical average monthly streamflow as well as the prediction. This graph helps the user to quickly see how far the current hydrological year is from the mean historical hydrological year as well as similar historical observed years.
3.8. First Operational Year 2016–2017: Results
The model was first put into operation in October 2016. Figure 12 presents a comparative analysis of the annual and monthly streamflow forecasts with the observed values.
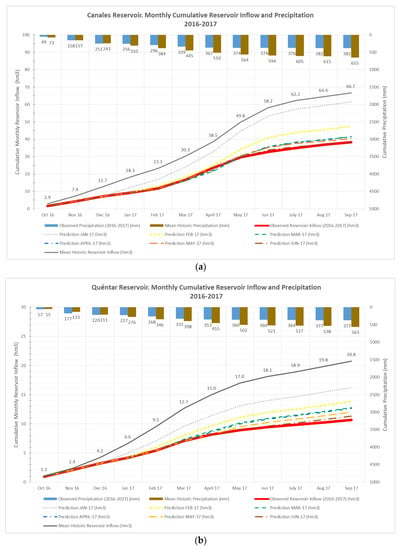
Figure 12.
Predictions of annual and monthly cumulative streamflow (hm3) and observed annual and monthly cumulative streamflow (hm3) of the (a) Canales reservoir and (b) Quéntar reservoir.
It can be observed that the 2016–2017 hydrological year was predicted to be drier than the average historical year and all predictions were between the average year shown in dark grey and the observed values shown in red. It can also be appreciated that the prediction given in January was below, but closer, to the average historical year, whilst as the number of observed months increased, the predictions were getting closer to the observed data.
It was observed for the Canales reservoir that the accuracy of the prediction output achieved in March 2017 (for the 2016/2017 total annual streamflow) was very good at approximately 92%. The forecast annual streamflow value was 41.52 hm3 whilst the observed value was 38.34 hm3 (compared with the observed historical mean annual streamflow of 66.71 hm3). Logically, the prediction results improved as the number of observed months increased.
For the Quéntar reservoir, the accuracy of the prediction given in March 2017 (for the 2016/2017 total annual streamflow) was slightly lower than the Canales reservoir, thus, achieving an accuracy of 80%, which is good. The total annual streamflow forecast was 12.65 hm3 whilst the observed value was 10.68 hm3 (compared with the observed historical mean annual streamflow of 20.81 hm3).
We investigated in more detail whether the Quéntar model could be improved. A more detailed evaluation of the behaviour and influence of the interannual underground flow in the total annual contribution to the reservoir was carried out. It was found that there is a relatively small correlation between the annual streamflow and with the previous years. It was also examined whether when applying the Monte Carlo simulation, the median value might provide better forecasts than using the mean value. Even though for the hydrological year of 2016–2017, the median provided better forecast results, when assessing the historical data, the mean value provided more accurate forecast results. For this particular sub-basin, we also concluded that the minimum number of observed years (to minimise the error) should be 40 years.
The model allows for the inclusion of seasonal predictions, for example, those provided by the AEMET in Spain. The seasonal probability prediction values estimated for the next quarter of the current year assigned to each tertile (wet, normal, and dry) are applied to the model outputs by multiplying them with seasonal predictions (upper, central, and lower estimations). Equally, the model allows the integration of climate change effects by scoring and weighing recent years of the historic data.
4. Conclusions and Future Research Directions
In Mediterranean countries, risk-based streamflows forecasts are critical, especially, before the intensive irrigation campaign starts (usually in April). During this time, water authorities must make responsible management decisions on the best allocation of the available water volume between different water users and environmental needs.
This research contributes towards the development of a user-guided, simple, low cost, and robust procedure for forecasting monthly and annual streamflows during the current hydrological year.
The methodology is innovative because of its combination of well-known techniques and its ability to achieve satisfactory and reliable results. Firstly, regression analysis techniques were applied to obtain the relationship between the total annual streamflow and the cumulative monthly rainfall and monthly streamflow. Secondly, the historical streamflow data sets were fitted to a two-parameter gamma continuous and cumulative probability distribution function. The estimated total annual streamflow output obtained from the regression analysis was made to be equal to the mean value of a new distribution, named the conditioned two-parameter gamma cumulative probability distribution function. This new distribution allowed the allocation of the probability for each year of the historical data set based on the estimated annual streamflow (from the regression analysis) and the gamma distribution (previously fitted to the historical data set). Finally, the Monte Carlo simulation was applied to obtain 10,000 simulations. The model outputs were the probabilistic mean annual and monthly streamflows along with the 10th and 90th percentiles (which can be easily modified by the user if needed). This allows decision-makers to adopt a water resource management risk-based approach, which can be adjusted to their own needs.
The method was successfully applied to two headwater reservoirs located at the upper area of the Genil River (Guadalquivir River Basin), namely, the Quéntar and Canales. Several metrics (including MAE, MAPE, IOA, RMSE, R2, and NSE) were used during the validation process, which showed good levels of accuracy and increased with the number of months observed. The model was first put into operation during the last hydrological year (2016–2017), obtaining accuracy levels of 92% and 80% respectively, for Canales and Quéntar, for the annual streamflow forecast given in March 2017.
The regression analysis shows that the best descriptor for forecasting the total annual streamflow for the Quéntar reservoir was the cumulative monthly streamflow (due to the influence of the subterranean flows). For Canales, the cumulative precipitation was the best predictor for the first three, four, and five months observed whilst the cumulative streamflow was the best predictor for the six, seven, and eight months observed. It is important to highlight that the best fit regression model and best fit predictor may vary depending on the predominant hydrological process at each specific basin and season of the year. In this situation, a combined regression model should be used to achieve the best correlation and predictive results.
The key advantages of this procedure are: (i) The use of relatively simple algorithms and well-known techniques, which can be easily implemented in an excel spreadsheet; (ii) the use of a minimum number of hydrological variables (streamflow and precipitation); (iii) the model saves substantial computational time (the model takes just a few seconds to run the simulations); (iv) the model does not depend on other software to achieve the results; (v) the model offers an intuitive user interface, which can be easily used by anyone; and (vi) the results achieved are similar or slightly better than those achieved with other more complex models.
The method also has some limitations: (i) It is applicable to headwater systems; (ii) if there are new rapid and significant land use changes within the catchment of study (not reflected in the historical data sets), the model might not capture these changes and may generate misleading streamflow forecasts; and (iii) whilst there is no limitation in catchment size, catchments with considerable climatic irregularity or very rare seasonal sporadic rainfall are difficult to predict and should be carefully studied.
To obtain the best results, this methodology should be applied when there is good quality input data and, at least, 30 years of observed data (although 40 years would be desirable to increase the forecast accuracy). The minimum number of observed years should be greater in those catchments with a greater standard deviation. The performance of the model can be further improved (and reduce prediction errors) by increasing the number of observed years.
Current and future research is in line with the full integration of seasonal climate predictions as well as the effects of climate change. Equally, we are working towards the integration of this model with other types of hydrological models (conceptual or distributed models) to check whether the accuracy could be further improved.
We conclude that the proposed methodology to forecast streamflows presented in this paper, although simple and of low cost, provides satisfactory, consistent, and robust results with a relatively small error margin. The outputs of this model can help with the early detection of critical events, such as droughts and periods of water scarcity, and support strategic water management decisions. This can improve resource and cost efficiency when deciding on optimum water allocation.
Author Contributions
Both authors have contributed equally to the research.
Funding
This research was funded by Fundación Centro Andaluz de Investigaciones del Agua (CETAQUA) and EMASAGRA S.A.
Acknowledgments
We acknowledge B.Eng. Nanton for his collaboration in this work, and CETAQUA and EMASAGRA S.A. for the economic support and technical feed-back. The authors thank Mediero, Ruiz Castro and MEng. Yeste. for their help during the revision. Finally, the constructive comments given by the reviewers and editor helped considerably to improve the quality of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pérez-Blanco, C.D.; Gómez, C.M. Drought management plans and water availability in agriculture: A risk assessment model for a Southern European basin. Weather Clim. Extrem. 2014, 4, 11–18. [Google Scholar] [CrossRef]
- Paneque, P. Drought Management Strategies in Spain. Water 2015, 7, 6689–6701. [Google Scholar] [CrossRef]
- Tanaka, S.K.; Zhu, T.; Lund, J.R.; Howitt, R.E.; Jenkins, M.W.; Pulido, M.A.; Tauber, M.; Ritzema, R.S.; Ferreira, I.C. Climate Warming and Water Management Adaptation for California. Clim. Chang. 2006, 76, 361–387. [Google Scholar] [CrossRef]
- Shalamu, A. Monthly and Seasonal Streamflow Forecasting in the Rio Grande Basin. PhD. Thesis, New Mexico State University, Las Cruces, NM, USA, 2009. [Google Scholar]
- Guadalquivir River Basin Authority. Plan Hidrológico de la Demarcación Hidrográfica del Guadalquivir (Guadalquivir River Basin Management Plan). 2016. Available online: http://www.chguadalquivir.es (accessed on 6 March 2018).
- Jódar, J.; Carpintero, E.; Martos-Rosillo, S.; Ruiz-Constán, A.; Marín-Lechado, C.; Cabrera-Arrabal, J.A.; González-Dugo, M.P. Combination of lumped hydrological and remote-sensing models to evaluate water resources in a semi-arid high altitude ungauged watershed of Sierra Nevada (Southern Spain). Sci. Total Environ. 2018, 625, 285–300. [Google Scholar] [CrossRef] [PubMed]
- Helmuth, M.E.; Moorhead, A.; Thomson, M.C.; Williams, J. Climate Risk Management in Africa: Learning from Practice; International Research Institute for Climate and Society, The Earth Institute at Columbia University: New York, NY, USA, 2007. [Google Scholar]
- Delorit, J.; Gonzalez Ortuya, E.C.; Block, P. Evaluation of model-based seasonal streamflow and water allocation forecasts. Hydrol. Earth Syst. Sci. 2017, 21, 4711–4725. [Google Scholar] [CrossRef]
- Coulibaly, P.; Anctil, F.; Bobee, B. Daily reservoir inflow forecasting using artificial neural networks with stopped training approach. J. Hydrol. 2000, 230, 244–257. [Google Scholar] [CrossRef]
- Baratti, R.; Cannas, B.; Fanni, A.; Pintus, M.; Sechi, G.M.; Toreno, N. River flow forecast for reservoir management through neural networks. Neurocomputing 2003, 55, 421–437. [Google Scholar] [CrossRef]
- Collischonn, W.; Morelli Tucci, C.E.; Clarke, R.T.; Chan Chou, S.; Guilhon, L.G.; Cataldi, M.; Allasia, D. Medium-range reservoir inflow predictions based on quantitative precipitation forecasts. J. Hydrol. 2007, 344, 112–122. [Google Scholar] [CrossRef]
- Wang, W. Stochasticity, Nonlinearity and Forecasting of Streamflow Processes; IOS Press: Beijing, China, 2006. [Google Scholar]
- Yu, X.; Zhang, X.; Qin, H. A data-driven model based on Fourier transform and support vector regression for monthly reservoir inflow forecasting. J. Hydro-Environ. Res. 2018, 18, 12–24. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, S.; Chen, H.; Zhou, Y. Comparative study of monthly inflow prediction methods for the Three Gorges Reservoir. Stoch. Environ. Res. Risk Assess. 2014, 28, 555–570. [Google Scholar] [CrossRef]
- Nourani, V.; Kisi, Ö.; Komasi, M. Two hybrid artificial intelligence approaches for modeling rainfall–runoff process. J. Hydrol. 2011, 402, 41–59. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, P.; Zhang, Y. A Probabilistic Wavelet–Support Vector Regression Model for Streamflow Forecasting with Rainfall and Climate Information Input. J. Hydrometeorol. 2015, 16, 2209–2229. [Google Scholar] [CrossRef]
- Myronidis, D.; Ioannou, K.; Fotakis, D.; Dorflinger, G. Streamflow and hydrological drought trend analysis and forecasting in Cyprus. Water Resour. Manag. 2018, 32, 1759–1776. [Google Scholar] [CrossRef]
- Gragne, A.S.; Sharma, A.; Mehrotra, R.; Alfredsen, K. Improving real-time inflow forecasting into hydropower reservoirs through a complementary modelling framework. Hydrol. Earth Syst. Sci. 2015, 19, 3695–3714. [Google Scholar] [CrossRef]
- Khedun, C.P.; Mishra, A.K.; Singh, V.P.; Giardino, J.R. A copula-based Precipitation forecasting model: Investigating the interdecadal modulation of ENSO’s impacts on monthly precipitation. Water Resour. Res. 2014, 50, 580–600. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, P.; Chen, X.; Guan, Y. A multivariate conditional model for streamflow prediction and spatial precipitation refinement. J. Geophys. Res. Atmos. 2015, 120, 10116–10129. [Google Scholar] [CrossRef]
- Ministerio de Agricultura y Pesca, Alimentación y Medio Ambiente, Gobierno de España. Agencia Estatal de meteorología. Available online: http://www.aemet.es/en/serviciosclimaticos/prediccion_estacional (accessed on 1 March 2018).
- Guadalquivir River Basin Authority. Plan especial de actuación en situaciones de alerta y eventual sequía de la cuenca hidrográfica del Guadalquivir. (Guadalquivir Drought Management Plan). 2007. Available online: http://www.chguadalquivir.es (accessed on 6 March 2018).
- Thom, H.C.S. A note on the gamma distribution. Mon. Weather Rev. 1958, 86, 117–122. [Google Scholar] [CrossRef]
- Buishand, T.A. Some remarks on the use of daily rainfall model. J. Hydrol. 1978, 36, 295–308. [Google Scholar] [CrossRef]
- Stephenson, D.B.; Kumar, K.R.; Doblas-Reyes, F.J.; Chauvin, E.; Pezzulli, S. Extreme daily rainfall events and their impact on Ensemble Forecast of the Indian Moonsoon. Mon. Weather Rev. 1999, 127, 1954–1966. [Google Scholar] [CrossRef]
- Wang, Q.J.; Nathan, R.J. A method for coupling daily and monthly time scales in stochastic generation of rainfall series. J. Hydrol. 2007, 346, 122–130. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. A daily stochastic weather generator for preserving low-frequency of climate variability. J. Hydrol. 2010, 388, 480–490. [Google Scholar] [CrossRef]
- Chowdhury, A.F.M.; Lockart, N.; Willgoose, G.; Kuczera, G.; Kiem, A.S.; Manage, N.P. Development and evaluation of a stochastic daily rainfall model with long-term variability. Hydrol. Earth Syst. Sci. 2017, 21, 6541–6558. [Google Scholar] [CrossRef]
- Rubinstein, R.Y.; Kroese, D.P. Simulation and the Monte Carlo Method; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Stathis, D.; Sapountzis, M.; Myronidis, D. Assessment of land-use change effect on a design storm hydrograph using the SCS curve number method. Fresenius Environ. Bull. 2010, 19, 1928–1934. [Google Scholar]
- Guadalquivir River Basin Authority Web Page. Available online: http://www.chguadalquivir.es (accessed on 6 March 2018).
- Guadalquivir River Basin Authority. Draft Guadalquivir River Basin Special Drought Management Plan. 2017. Available online: http://www.chguadalquivir.es (accessed on 6 March 2018).
- Arenillas, M.; Cobos, G.; Navarro, J. Datos Sobre La Nieve y Los Glaciares en Las Cordilleras Españolas; El programa ERHIN (1984–2008); Ministerio de Medio Ambiente y Medio Rural y Marino: Madrid, Spain, 2008. [Google Scholar]
- Guadalquivir River Basin Authority. Automatic Hydrological Information System (SAIH). Available online: http://www.chguadalquivir.es/saih/ (accessed on 6 March 2018).
- Myronidis, D.; Stathis, D.; Ioannou, K.; Fotakis, D. An integration of statistics temporal methods to track the effect of drought in a shallow Mediterranean Lake. Water Resour. Manag. 2012, 26, 4587–4605. [Google Scholar] [CrossRef]
- Mediero, L.; Garrote, L.; Martín-Carrasco, F.J. Probabilistic calibration of a distributed hydrological model for flood forecasting. Hydrol. Sci. J. 2011, 56, 1129–1149. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).