Simulation of the Water Dynamics and Root Water Uptake of Winter Wheat in Irrigation at Different Soil Depths
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Site
2.2. Experimental Design
2.3. Irrigation Design
2.4. Measurement Methods
3. The Model for the Soil Water Dynamics of Winter Wheat in Irrigation at Different Soil Depths
3.1. Governing Equation
3.2. Initial Condition
3.3. Boundary Conditions
3.4. Model Parameter Calibration
3.5. Model Evaluation
4. Results and Discussion
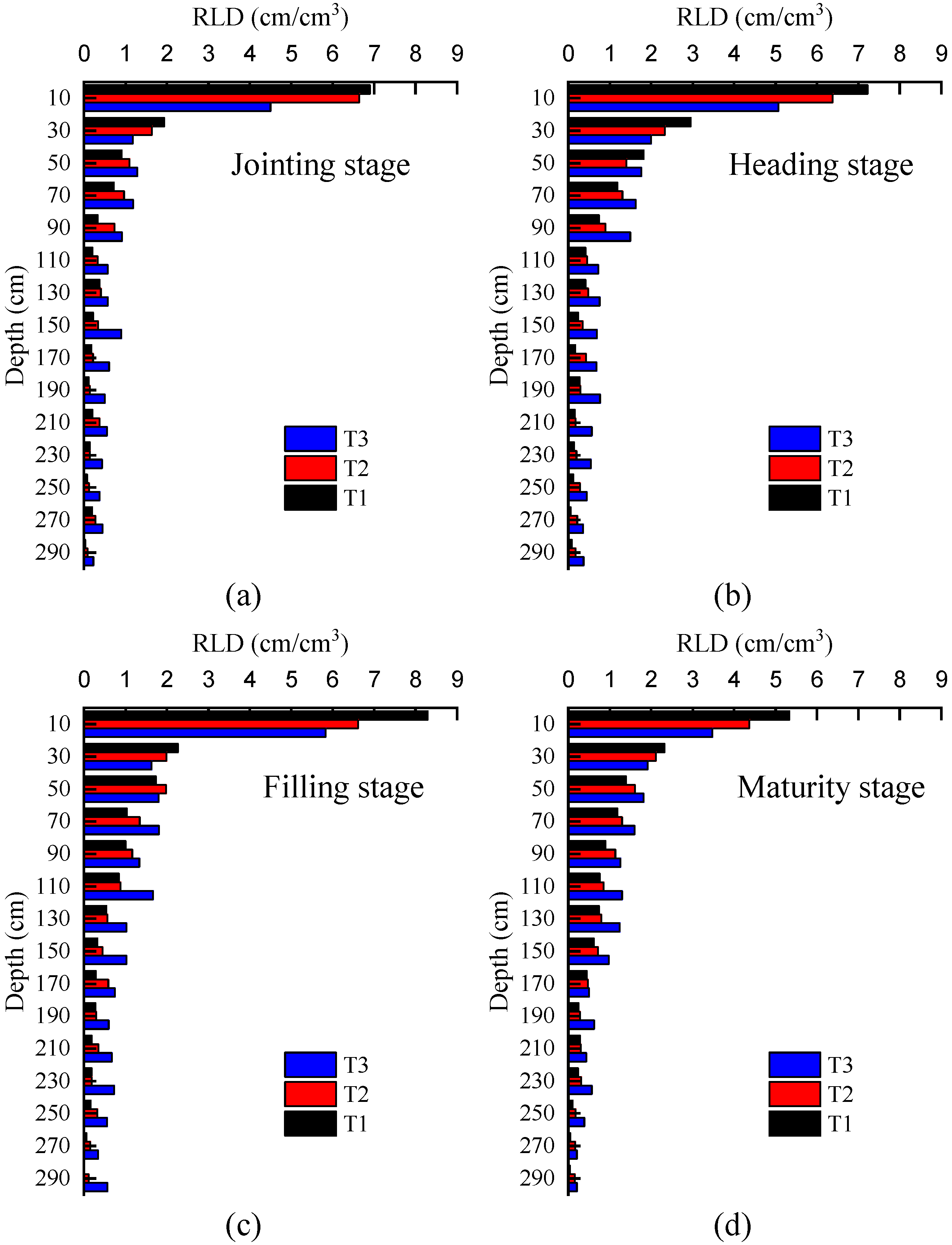
4.1. Spatial and Temporal Distributions of Winter Wheat at Different Irrigation Depths
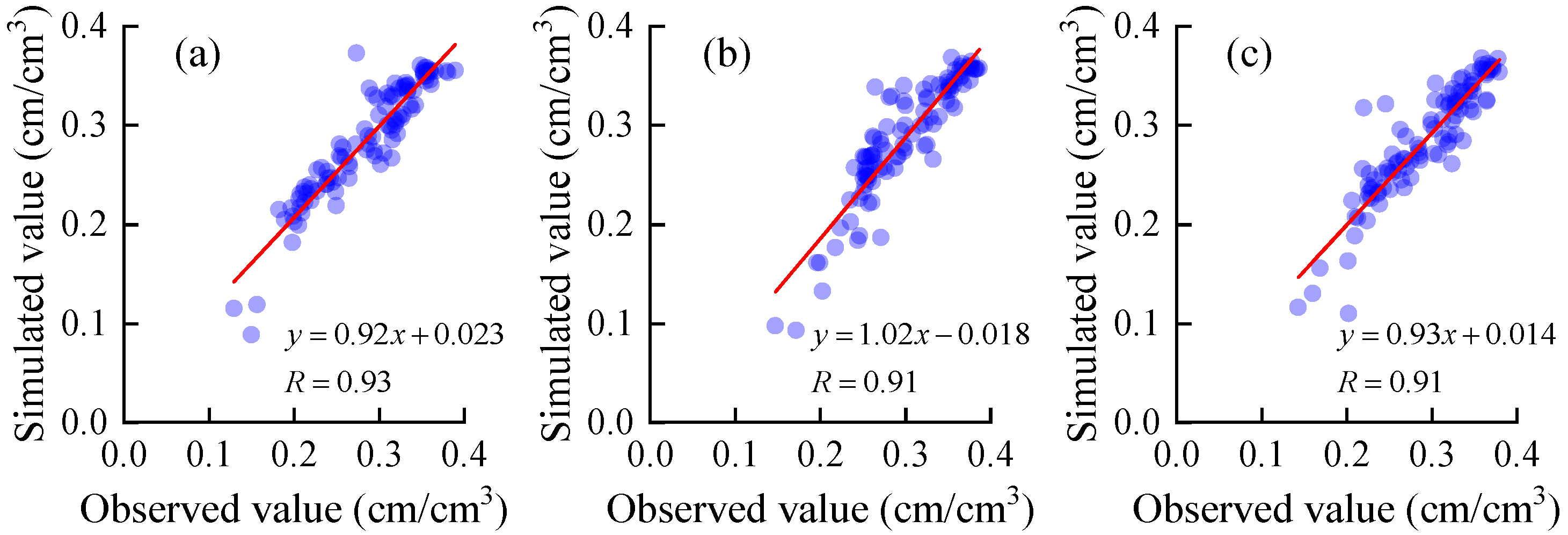
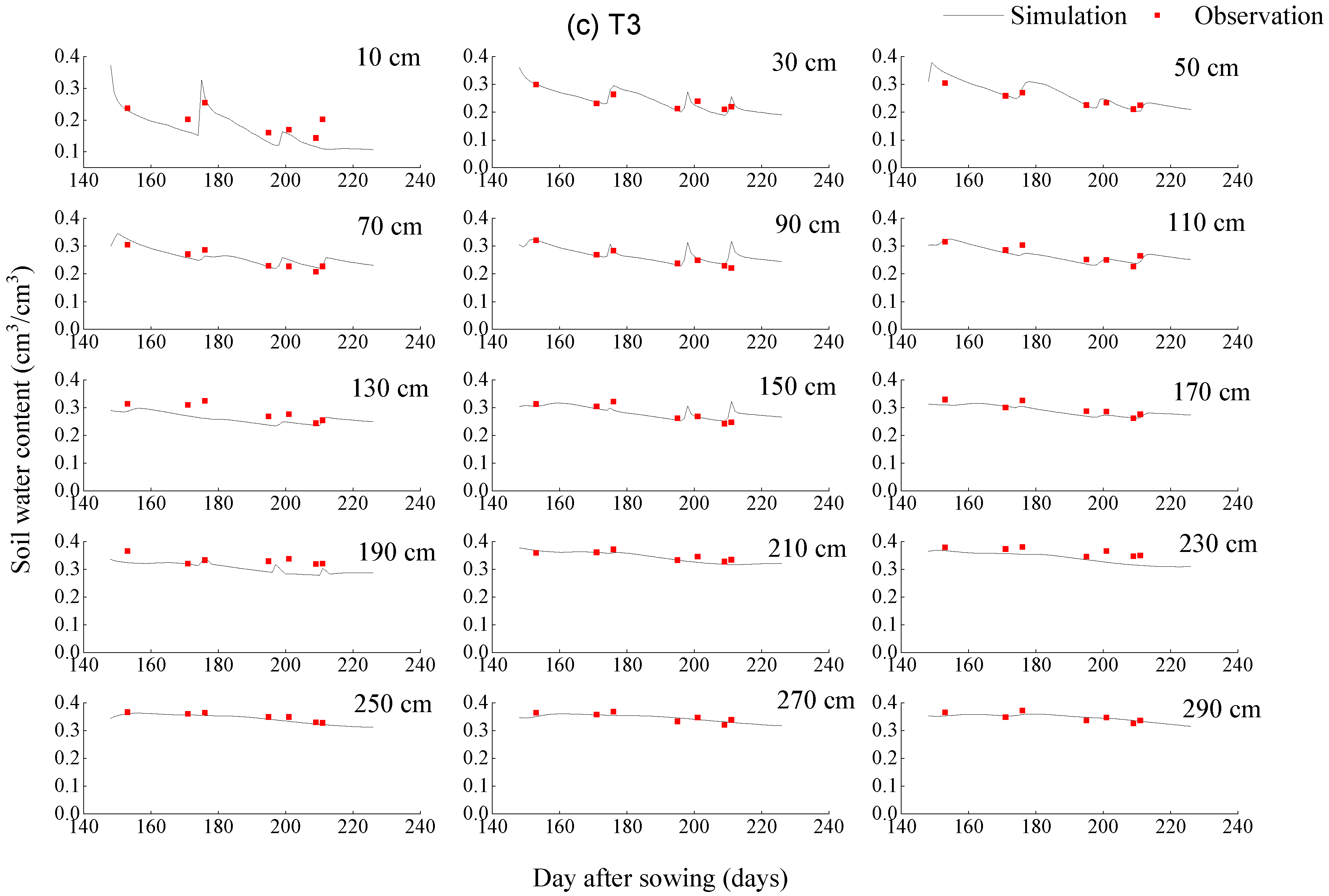
4.2. Evaluation of the Soil Water Movement Model in Irrigation at Different Soil Depths
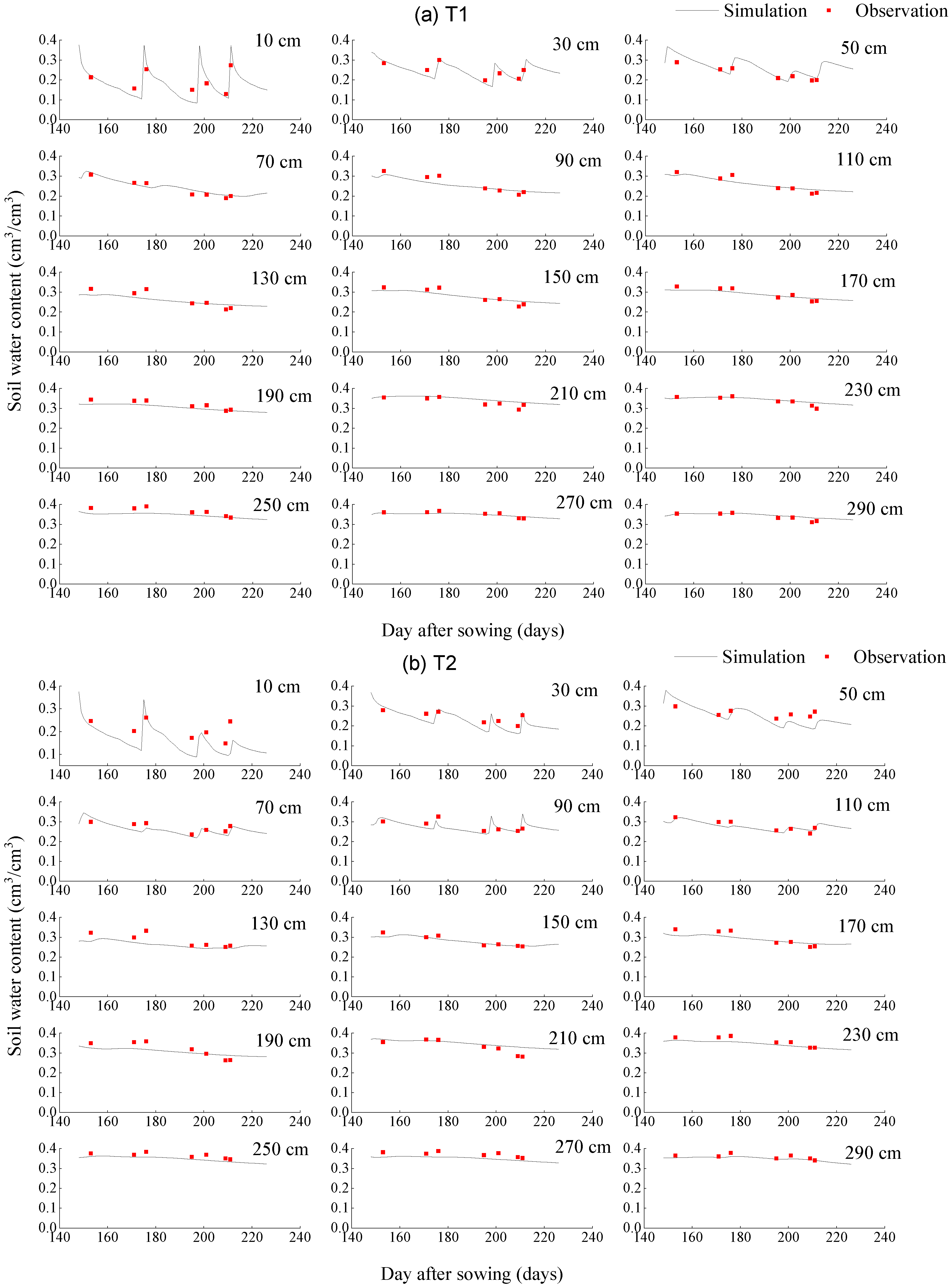
4.3. Simulation Analysis of Soil Water Dynamics at Different Irrigation Depths
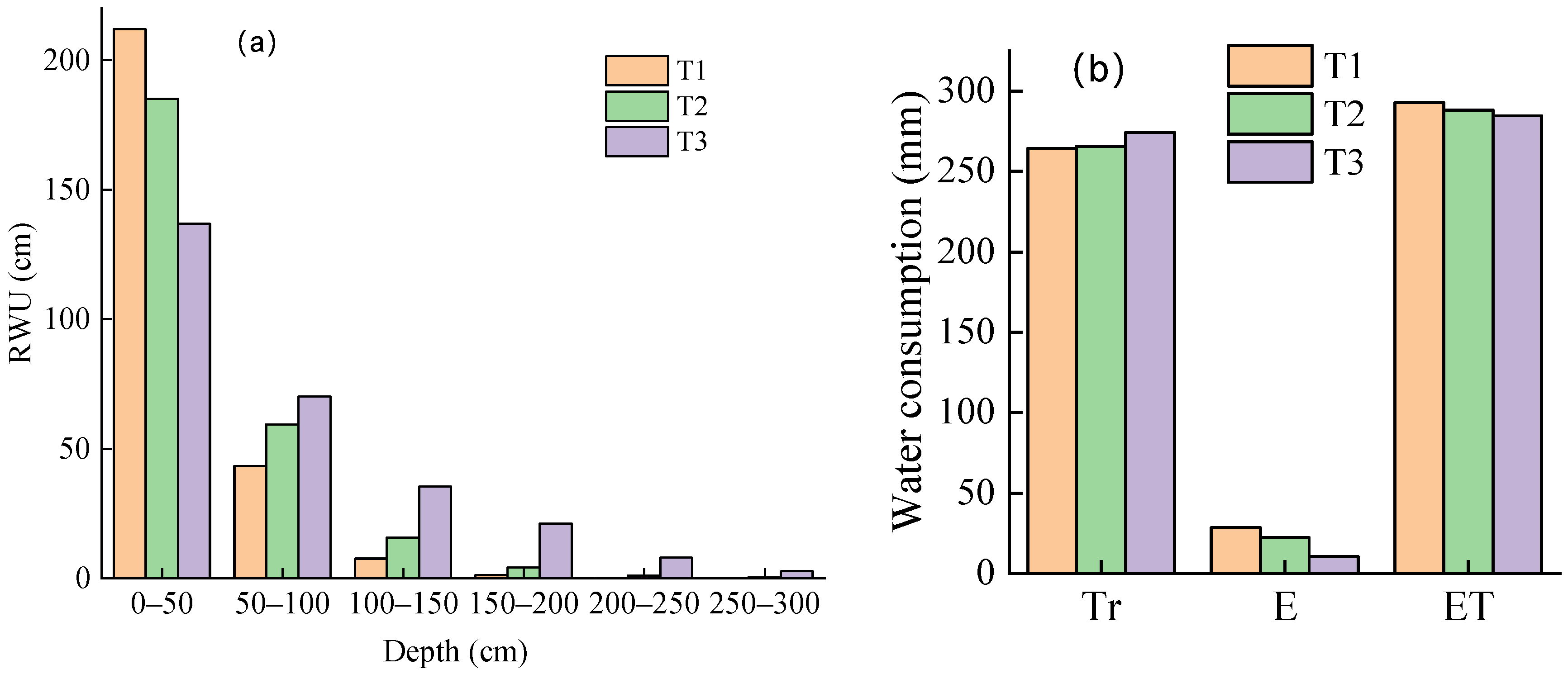
4.4. Simulation Analysis of RWU of Winter Wheat During Irrigation at Different Soil Depths
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, H.T.; Li, B.G.; Ren, T.S. Soil proifle characteristics of high-productivity alluvial cambisols in the North China Plain. J. Integr. Agric. 2015, 14, 765–773. [Google Scholar] [CrossRef]
- Yang, J.Y.; Mei, X.R.; Huo, Z.G.; Yan, C.R.; Ju, H.; Zhao, F.H.; Liu, Q. Water consumption in summer maize and winter wheat cropping system based on SEBAL model in Huang-Huai-Hai Plain, China. J. Integr. Agric. 2015, 14, 2065–2076. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Pei, D.; Chen, S.Y. Root growth and soil water utilization of winter wheat in the North China Plain. Hydrol. Process. 2004, 18, 2275–2287. [Google Scholar] [CrossRef]
- Wang, X.Q.; Wang, F.H.; Dong, Y.H.; Yu, Z.W.; Li, Z.J. Study on the ecological effect in wheat field of different planting patterns. Chin. J. Eco-Agric. 2005, 13, 119–122. (In Chinese) [Google Scholar]
- Dong, Z.Q.; Zhang, L.H.; Lv, L.H.; Li, Q.; Liang, S.B.; Jia, X.L. Effects of different irrigation methods on photosynthetic rate and yield of winter wheat. Agric. Res. Arid Areas 2015, 33, 1–7. (In Chinese) [Google Scholar] [CrossRef]
- Man, J.G.; Shi, Y.; Yu, Z.W.; Zhang, Y.L. Root growth, soil water variation and grain yield response of winter wheat to supplemental irrigation. Plant Prod. Sci. 2015, 19, 193–205. [Google Scholar] [CrossRef]
- Lv, G.H.; Song, J.Q.; Bai, W.B.; Wu, Y.F.; Liu, Y.; Kang, Y.H. Effects of different irrigation methods on micro-environments and root distribution in winter wheat fields. J. Integr. Agric. 2015, 14, 1658–1672. [Google Scholar] [CrossRef]
- Wang, L.C.; Shi, J.C.; Zuo, Q.; Zheng, W.J.; Zhu, X.M. Optimizing parameters of salinity stress reduction function using the relationship between root-water-uptake and root nitrogen mass of winter wheat. Agric. Water Manag. 1996, 196, 142–152. [Google Scholar] [CrossRef]
- Wang, J.D.; Gong, S.H.; Xu, D.; Yu, Y.D. Effects of irrigation models on the space distribution of root system and yield of winter wheat. J. Hydraul. Eng. 2011, 42, 1239–1246. (In Chinese) [Google Scholar]
- Lv, G.H.; Kang, Y.H.; Li, L.; Wan, S.Q. Effect of irrigation methods on root development and profile soil water uptake in winter wheat. Irrig. Sci. 2010, 28, 387–398. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, H.; Sun, C.T.; Gao, Y.; Gong, X.W.; Sun, J.S.; Wang, W.N. Root development of transplanted cotton and simulation of soil water movement under different irrigation methods. Water 2017, 9, 503. [Google Scholar] [CrossRef]
- Kashiwagi, J.; Morito, Y.; Jitsuyama, Y.; An, P.; Inoue, T.; Inagaki, M. Effects of Root Water Uptake Efficiency on Soil Water Utilization in Wheat (Triticum aestivum L.) under Severe Drought Environments. J. Agron. Crop Sci. 2015, 201, 161–172. [Google Scholar] [CrossRef]
- Feng, G.L.; Liu, C.M. Studies on the control of soil water profile and root distribution. Acta Geogr. Sin. 1997, 52, 461–469. (In Chinese) [Google Scholar] [CrossRef]
- Xue, Q.; Zhu, Z.; Musick, J.T.; Stewart, B.A.; Dusek, D.A. Root growth and water uptake in winter wheat under deficit irrigation. Plant Soil 2003, 257, 151–161. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Yuan, X.L. A field study on the relationship of soil water content and water uptake by winter wheat root system. Acta Agric. Boreall-Sin. 1995, 10, 99–104. (In Chinese) [Google Scholar] [CrossRef]
- Feng, G.L.; Liu, C.M. Analysis of root system growth in relation to soil water extraction pattern by winter wheat under water limiting conditions. J. Nat. Resour. 1998, 13, 235–241. (In Chinese) [Google Scholar] [CrossRef]
- Guo, F.; Ma, J.J.; Zheng, L.J.; Sun, X.H.; Guo, X.H.; Zhang, X.L. Estimating distribution of water uptake with depth of winter wheat by hydrogen and oxygen stable isotopes under different irrigation depths. J. Integr. Agric. 2016, 15, 891–906. [Google Scholar] [CrossRef]
- Wang, B.; Zheng, L.J.; Ma, J.J.; Sun, X.H.; Guo, X.H.; Guo, F. Effective root depth and water uptake ability of winter wheat by using water stable isotopes in the Loess Plateau of China. Int. J. Agric. Biol. Eng. 2016, 9, 27–35. [Google Scholar] [CrossRef]
- Wang, B.; Ma, J.J.; Sun, X.H.; Guo, X.H.; Di, N.; Huang, J. The influence of water regulation on root morphology and drought tolerance of winter wheat. Water Sav. Irrig. 2017, 22, 62–64. (In Chinese) [Google Scholar] [CrossRef]
- Di, N.; Ma, J.J.; Sun, X.H.; Guo, X.H.; Huang, J. Effect of irrigation depth on root morphology of winter wheat. China Rural Water Hydropower 2016, 59, 49–52. (In Chinese) [Google Scholar] [CrossRef]
- Huang, J.; Sun, X.H.; Ma, J.J.; Guo, X.H.; Di, N. Effects of deep irrigation on water consumption and water use efficiency of winter wheat. Agric. Res. Arid Areas 2017, 35, 220–226. (In Chinese) [Google Scholar] [CrossRef]
- Shang, S.H.; Li, X.C.; Mao, X.M.; Lei, Z.D. Simulation of water dynamics and irrigation scheduling for winter wheat and maize in seasonal frost areas. Agric. Water Manag. 2004, 68, 117–133. [Google Scholar] [CrossRef]
- Kang, S.Z.; Zhang, F.C.; Zhang, J.H. A simulation model of water dynamics in winter wheat field and its application in a semiarid region. Agric. Water Manag. 2001, 49, 115–129. [Google Scholar] [CrossRef]
- Jha, S.K.; Gao, Y.; Liu, H.; Huang, Z.D.; Wang, G.S.; Liang, Y.P.; Duan, A.W. Root development and water uptake in winter wheat under different irrigation methods and scheduling for North China. Agric. Water Manag. 2017, 182, 139–150. [Google Scholar] [CrossRef]
- He, K.K.; Yang, Y.H.; Yang, Y.M.; Chen, S.Y.; Hu, Q.L.; Liu, X.J.; Gao, F. HYDRUS Simulation of Sustainable Brackish Water Irrigation in a Winter Wheat-Summer Maize Rotation System in the North China Plain. Water 2017, 9, 536. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soil. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Feddes, R.A.; Bresler, E.; Neuman, S.P. Field test of a modified numerical model for water uptake by root system. Water Resour. Res. 1974, 10, 1199–1206. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Numerical Model for Water and Solute Movement in and below the Root Zone; United States Department of Agriculture, Agricultural Research Service U.S. Salinity Laboratory: Riverside, CA, USA, 1987.
- Kang, S.Z.; Liu, X.M.; Xiong, Y.Z. SPAC Water Transport Theory and Its Application; Water Resources and Electric Power Press: Beijing, China, 1994. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Requirements; FAO Irrigation and Drainage Paper No.56; FAO: Rome, Italy, 1998. [Google Scholar]
- Liu, C.M.; Dou, Q.C. Evapotranspiration calculation in soil–plant–atmosphere continuum models. Adv. Water Sci. 1992, 3, 255–263. (In Chinese) [Google Scholar] [CrossRef]
- Yang, S.Y.; Yan, P.; Mei, X.Y.; Sun, X.B. Effects of different soil water deficits on roots of winter wheat. J. Triticeae Crop. 2007, 27, 309–313. (In Chinese) [Google Scholar] [CrossRef]
- He, H.; Kang, S.Z.; Cao, H.X. Effect of lateral depth on root and seedling growth and water use efficiency of winter wheat. Trans. CSAE 2001, 17, 31–33. (In Chinese) [Google Scholar] [CrossRef]
- Han, N.N.; Wang, Y.R.; Sun, S.H.; Jin, J.H.; Guo, X.Y. Experimental Study on Effects of Irrigation on Water Consumption and Yield of Winter Wheat. Water Sav. Irrig. 2010, 4, 4–7. (In Chinese) [Google Scholar]
- Kang, S.Z.; Lu, Z.; Liang, Y.L.; Cai, H.J. Effects of limited irrigation on yield and water use efficiency of winter wheat on the Loess Plateau of China. Agric. Water Manag. 2002, 55, 203–216. [Google Scholar] [CrossRef]
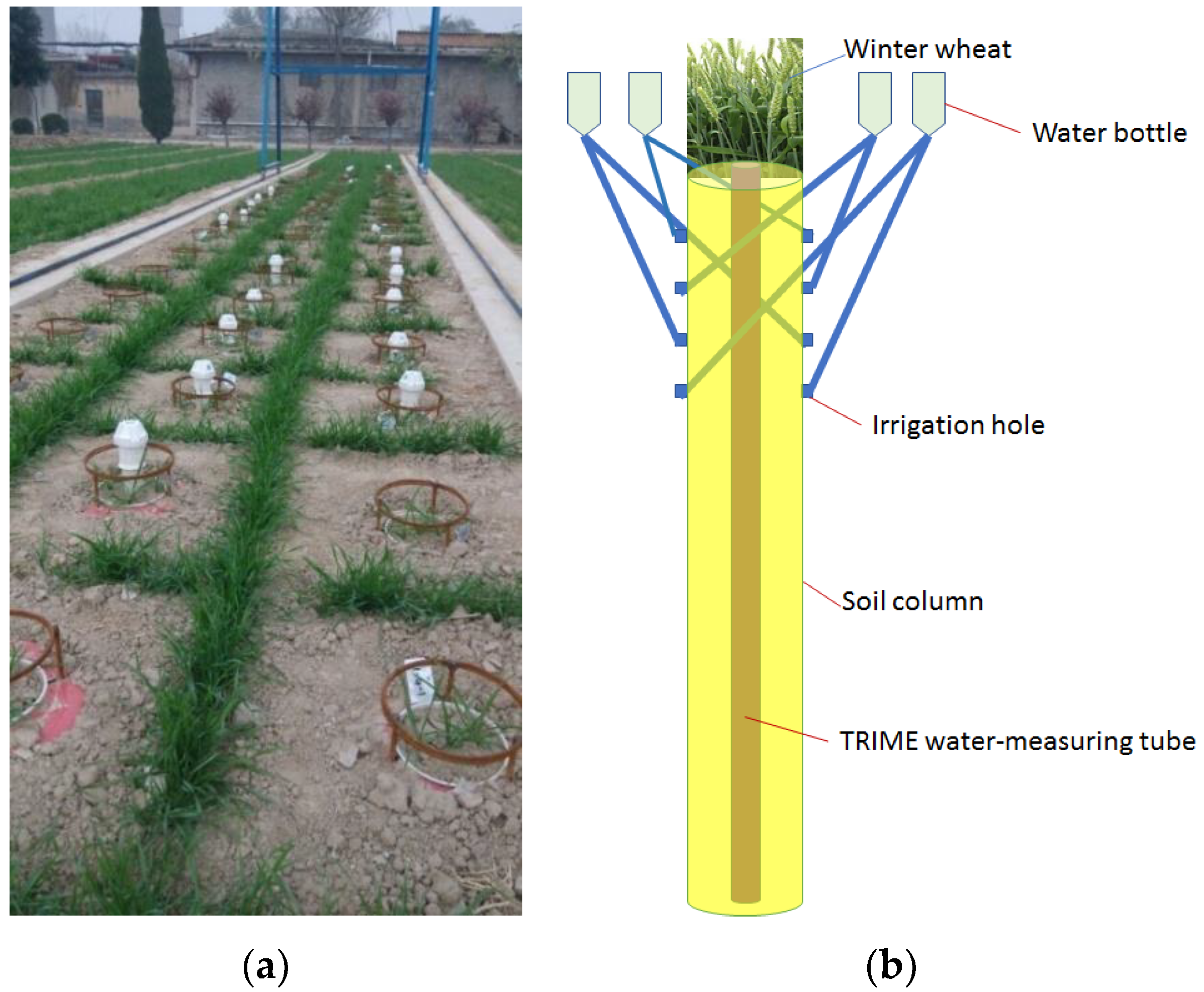


| Depths | Soil Texture Composition (%) | Soil Texture | Bulk Density | Field Capacity | ||
|---|---|---|---|---|---|---|
| (cm) | 0.02–2 mm | 0.002–0.02 mm | <0.002 mm | (g/cm3) | (cm3/cm3) | |
| 0–20 | 34.4 | 49.0 | 16.6 | Silty clay loam | 1.49 | 0.295 |
| 20–50 | 33.6 | 50.0 | 16.4 | Silty clay loam | 1.61 | 0.277 |
| 50–90 | 33.3 | 45.8 | 20.9 | Silty clay loam | 1.62 | 0.291 |
| 90–160 | 29.8 | 49.3 | 20.9 | Silty clay loam | 1.63 | 0.304 |
| 160–210 | 22.3 | 53.0 | 24.7 | Silty clay loam | 1.54 | 0.340 |
| 210–300 | 25.4 | 51.7 | 22.9 | Silty clay loam | 1.51 | 0.317 |
| Treatment | Irrigation Time | Irrigation Hole Depth (cm) | Amount of Irrigation Per Hole (mm) | Maximum Root Depth (cm) | Irrigation Scheme Depth (cm) |
|---|---|---|---|---|---|
| T1 | 20 December | 0 | 67.5 | 100 | 0 |
| 8 March | 0 | 67.5 | 200 | 0 | |
| 4 April | 0 | 67.5 | 300 | 0 | |
| 27 April | 0 | 67.5 | 300 | 0 | |
| 10 May | 0 | 67.5 | 300 | 0 | |
| T2 | 20 December | 0 | 67.5 | 100 | 0 |
| 8 March | 0, 30 | 66.5,1 | 200 | 40 | |
| 4 April | 0, 30, 60, 90 | 43.1, 9.3, 8.4, 6.7 | 300 | 120 | |
| 27 April | 0, 30, 60, 90 | 20, 15, 16, 16.5 | 300 | 120 | |
| 10 May | 0, 30, 60, 90 | 14.1, 18, 16.2, 19.2 | 300 | 120 | |
| T3 | 20 December | 0 | 67.5 | 100 | 0 |
| 8 March | 0, 30, 60, 90, 120 | 60.8, 2.1, 1.8, 1.8, 1 | 200 | 140 | |
| 4 April | 0, 30, 60, 90, 120, 150, 180 | 34, 12.5, 7.1, 7.9, 0, 1.6, 4.4 | 300 | 210 | |
| 27 April | 0, 30, 60, 90, 120, 150, 180 | 10, 15, 14, 13, 7, 7.7, 0.8 | 300 | 210 | |
| 10 May | 0, 30, 60, 90, 120, 150, 180 | 3.7, 11.6, 13.8, 13.9, 11.3, 10.9, 2.4 | 300 | 210 |
| Soil Layer (cm) | θr (cm3/cm3) | θs (cm3/cm3) | α | n | ks (cm/hour) | h50 (cm) | hcc (cm) | hc (cm) |
|---|---|---|---|---|---|---|---|---|
| 0–20 | 0.032 | 0.418 | 0.060 | 1.526 | 1.780 | −378.35 | −5272.42 | −47.76 |
| 20–50 | 0.045 | 0.406 | 0.045 | 1.435 | 1.792 | |||
| 50–90 | 0.060 | 0.402 | 0.078 | 1.387 | 0.793 | |||
| 90–130 | 0.040 | 0.415 | 0.063 | 1.446 | 0.601 | |||
| 130–210 | 0.025 | 0.442 | 0.044 | 1.598 | 0.407 | |||
| 210–300 | 0.033 | 0.450 | 0.050 | 1.645 | 0.133 |
| Treatment | a | b | c | d | f | R |
|---|---|---|---|---|---|---|
| T1 | 8.28 | 0.0348 | 5.00 | 0.0084 | 199 | 0.96 |
| T2 | 6.50 | 0.0266 | 7.00 | 0.0098 | 192 | 0.93 |
| T3 | 5.50 | 0.0130 | 7.00 | 0.0260 | 205 | 0.86 |
| Treatment | MAE (cm3/cm3) | MRE (%) | RMSE (cm3/cm3) |
|---|---|---|---|
| T1 | 0.016 | 6.17 | 0.021 |
| T2 | 0.022 | 7.95 | 0.028 |
| T3 | 0.017 | 6.38 | 0.025 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Sun, X.; Ma, J.; Lei, T.; Zheng, L.; Wang, P. Simulation of the Water Dynamics and Root Water Uptake of Winter Wheat in Irrigation at Different Soil Depths. Water 2018, 10, 1033. https://doi.org/10.3390/w10081033
Guo X, Sun X, Ma J, Lei T, Zheng L, Wang P. Simulation of the Water Dynamics and Root Water Uptake of Winter Wheat in Irrigation at Different Soil Depths. Water. 2018; 10(8):1033. https://doi.org/10.3390/w10081033
Chicago/Turabian StyleGuo, Xianghong, Xihuan Sun, Juanjuan Ma, Tao Lei, Lijian Zheng, and Pu Wang. 2018. "Simulation of the Water Dynamics and Root Water Uptake of Winter Wheat in Irrigation at Different Soil Depths" Water 10, no. 8: 1033. https://doi.org/10.3390/w10081033
APA StyleGuo, X., Sun, X., Ma, J., Lei, T., Zheng, L., & Wang, P. (2018). Simulation of the Water Dynamics and Root Water Uptake of Winter Wheat in Irrigation at Different Soil Depths. Water, 10(8), 1033. https://doi.org/10.3390/w10081033





