An Optimal Model for Water Resources Risk Hedging Based on Water Option Trading
Abstract
1. Introduction
2. Methodology
2.1. Concept of Water Option Contracts
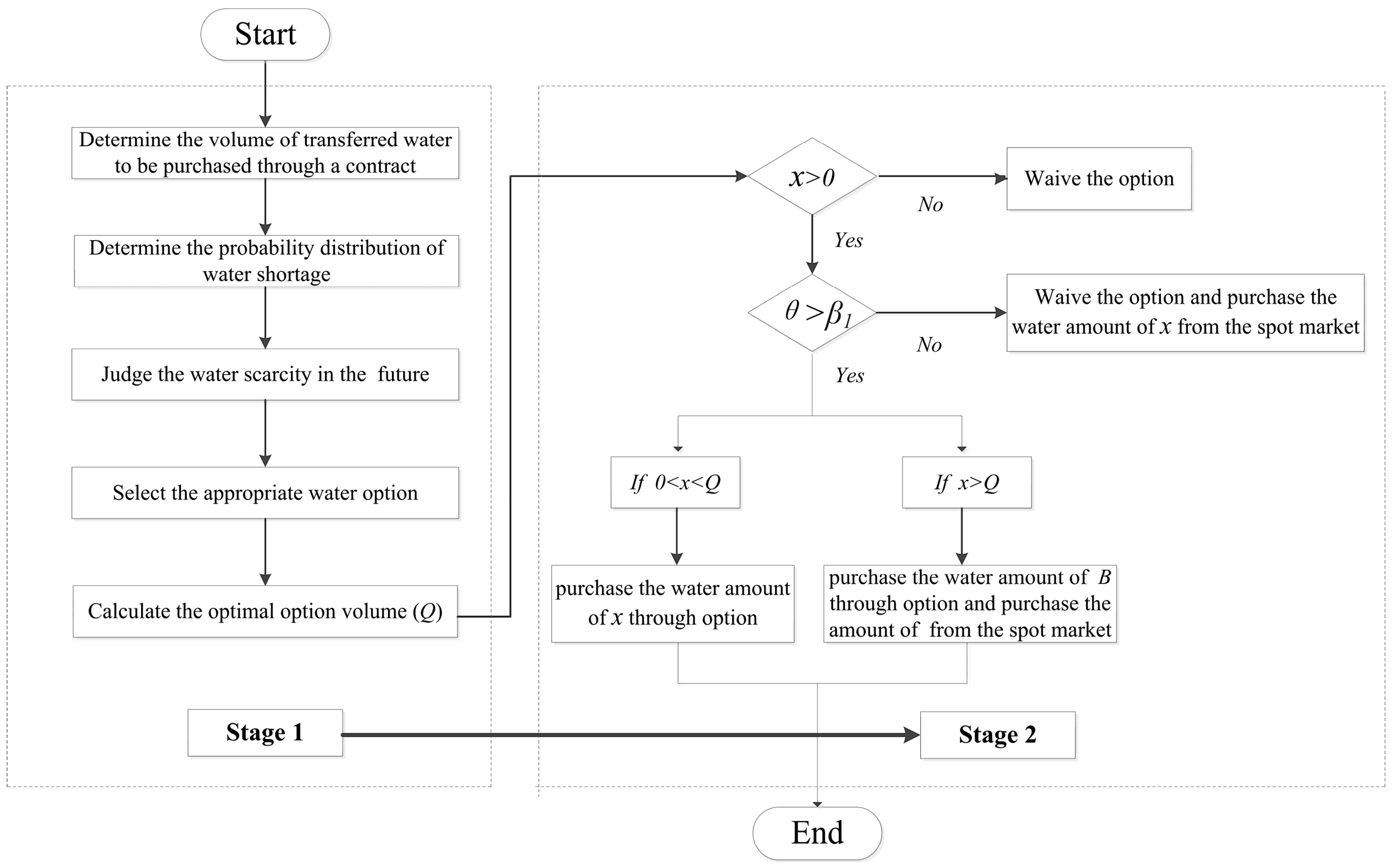
2.2. Two-Stage Water Option Trading Decision Model
2.3. Description of the Uncertainties
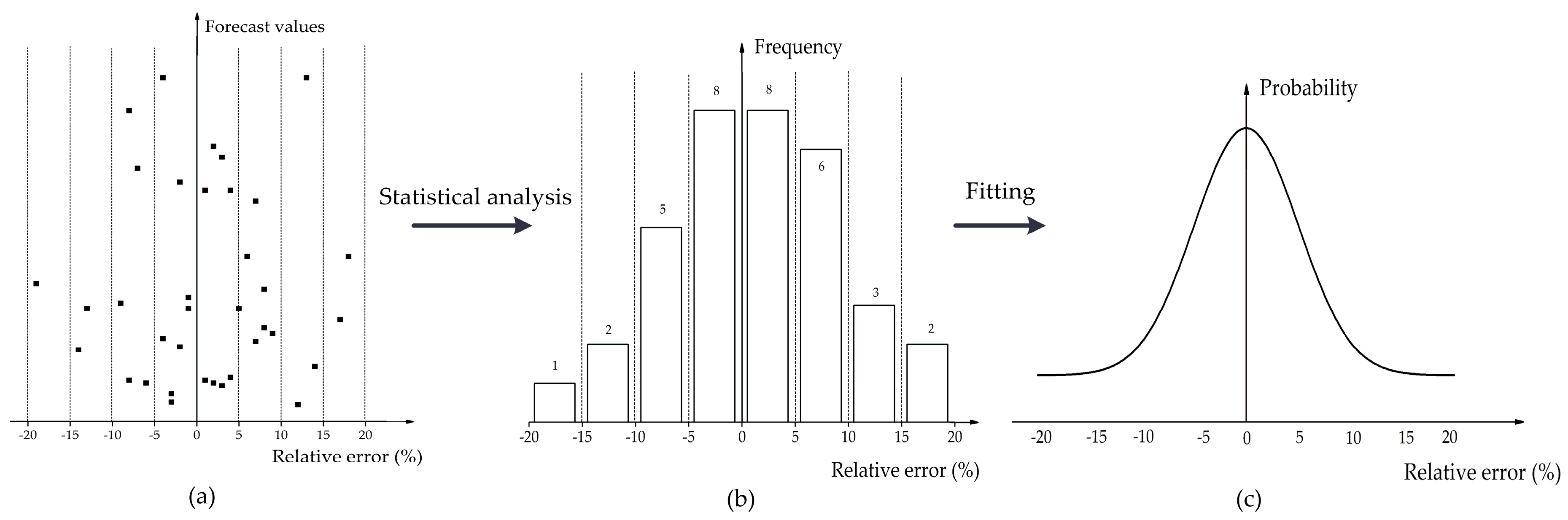
2.3.1. Uncertainty of Water Runoffs
2.3.2. Uncertainty of Spot Market Price
2.4. Option Trading Model Establishment and Solution
2.4.1. Optimization Model
- (1)
- represents the expected cost when the spot market price is lower than the exercise price, i.e., , and the option is not executed. Thus, the users need to pay the premium () and the cost () of buying water from the spot market.
- (2)
- indicates the expected cost when the spot market price is higher than the option price and there is no shortage of water, i.e., and . Thus, the users do not exercise the option and just need to pay the premium ().
- (3)
- represents the expected cost when the spot market price is higher than the option price and the water deficit is less than , i.e., and . Thus, the users need to pay the premium () and the cost of water purchased through the option market .
- (4)
- refers to the expected cost when the spot market price is higher than the option price and the water deficit is more than , i.e., and . Thus, the users need to pay the premium (), the cost () of water purchased through the option market, and the cost () of buying water from the spot market.The constraint conditions are
2.4.2. Model Solution
3. Case Study
3.1. Case Description
3.1.1. Description of the Uncertainties
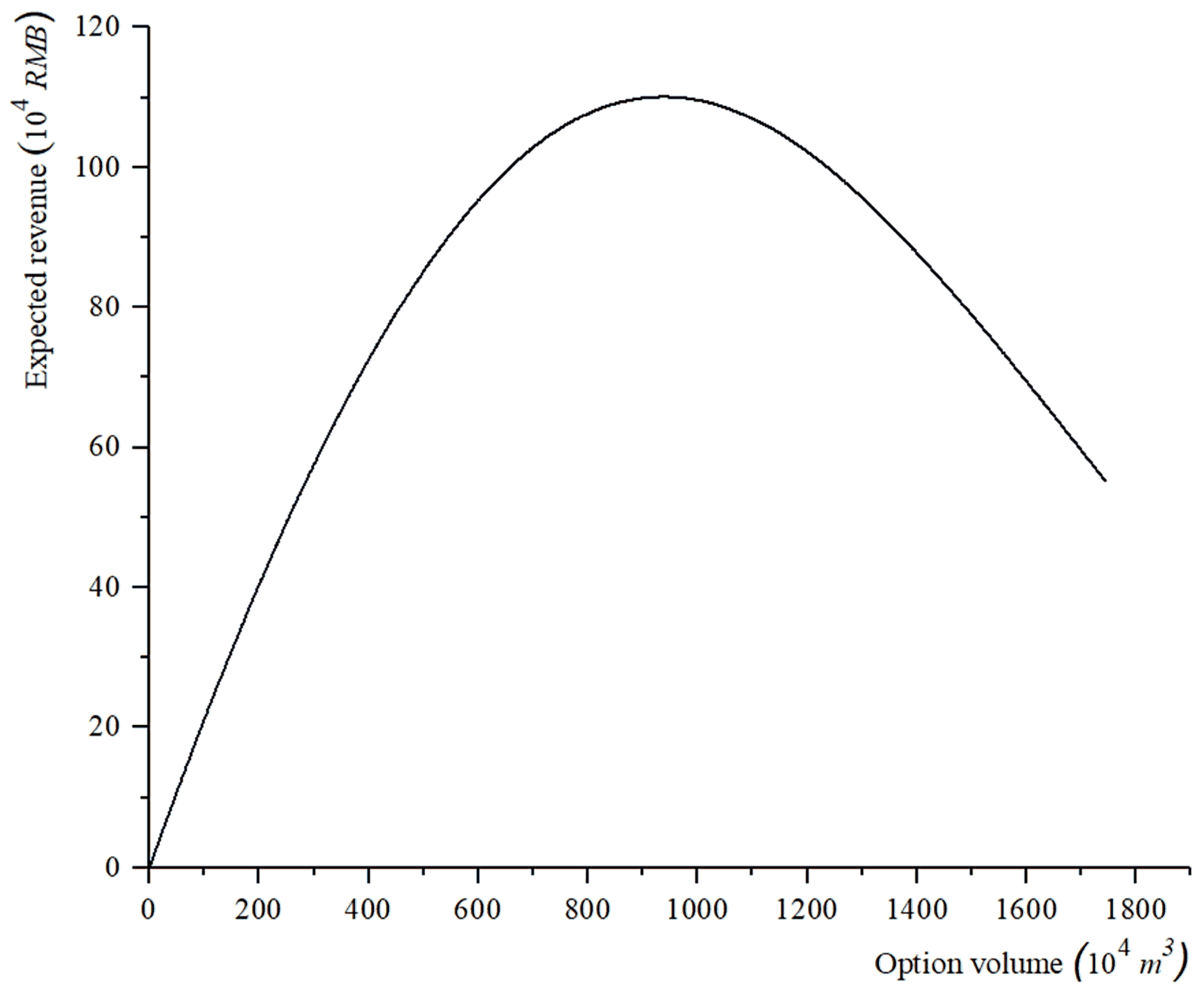
3.1.2. Option Trading Model Application and Solution
3.2. Discussions
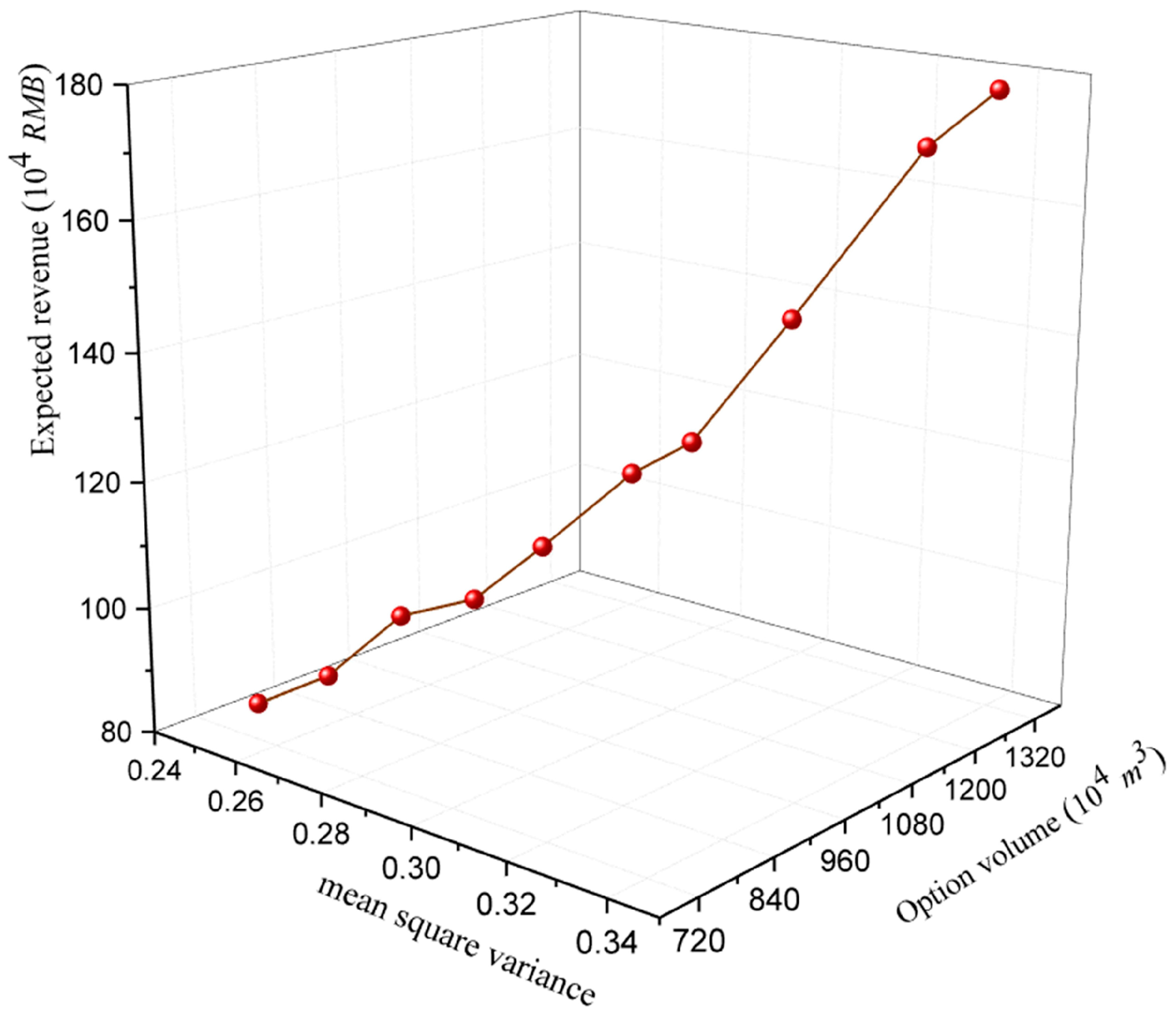
3.2.1. The Influence of the Uncertainty of the Local Runoff Forecast on the Model
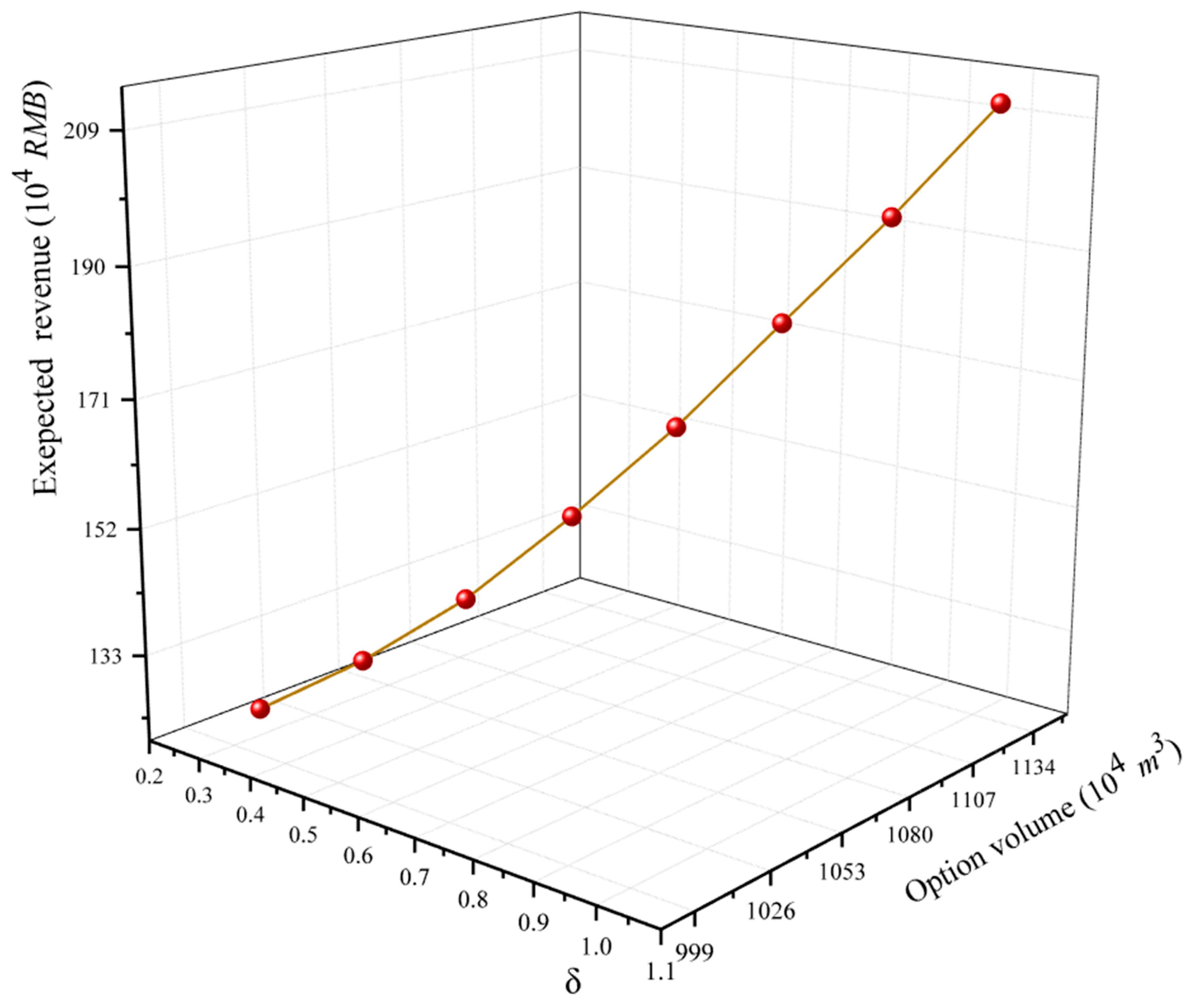
3.2.2. The Influence of the Fluctuation of Spot Market Price on the Model
3.2.3. Application of the Proposed Method
4. Conclusions
- (1)
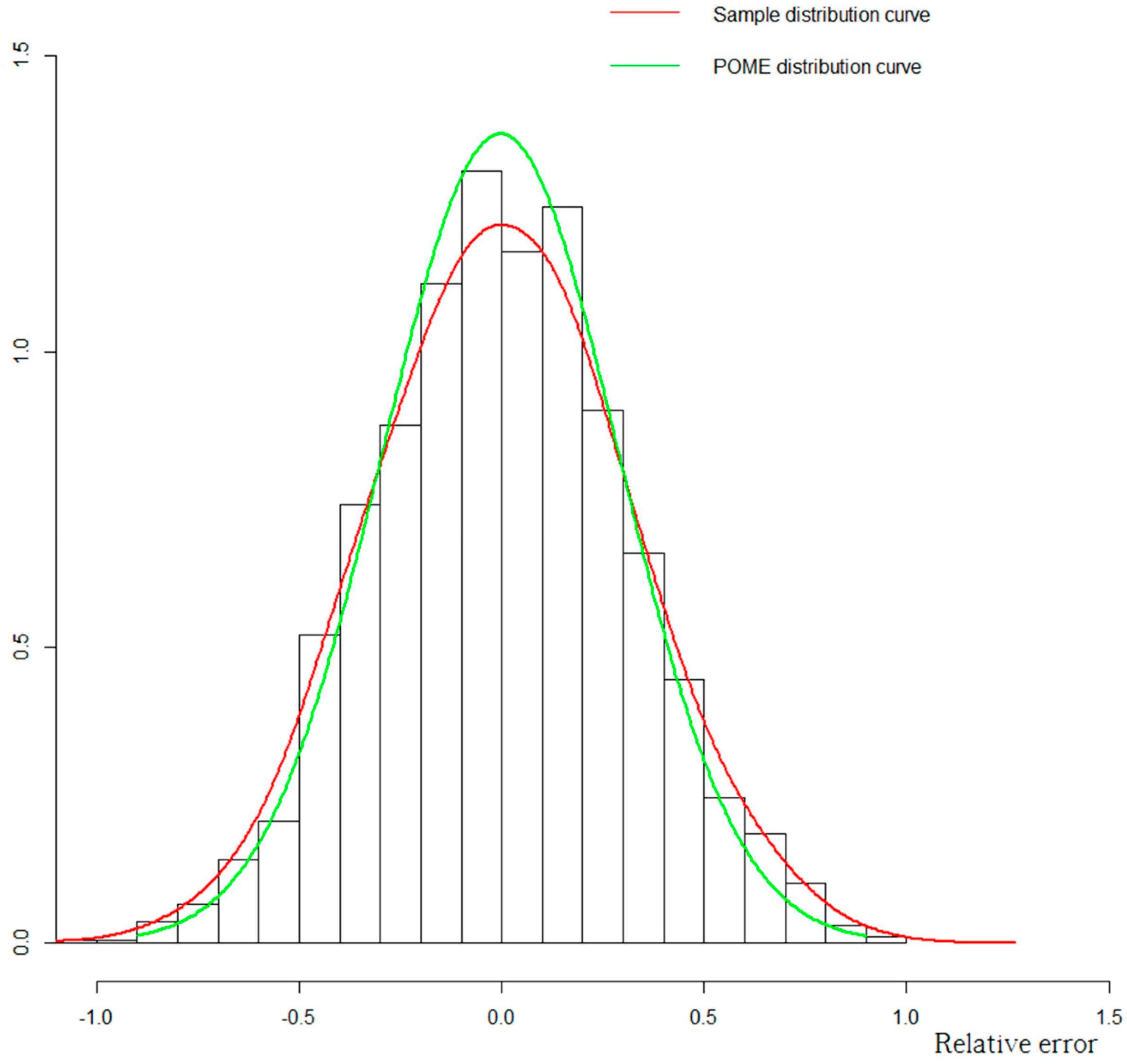
- We derived the relative error distribution of forecasted runoffs based on the principle of maximum entropy (POME), and then described the uncertainty of water deficit.
- (2)
- From the perspective of water users, the model of water scarcity risk hedging based on water option trading is established. The dichotomy method was employed to solve the model and to find the optimal water option trading strategy.
- (3)
- The proposed methodology was applied to an intake area of an inter-basin water transfer project in China. Additionally, different scenarios are set up to explore the effect of the uncertainty degree of local runoffs prediction and the spot market price on the optimal options trading volume and the expected revenue of the optimal options .
Author Contributions
Funding
Conflicts of Interest
References
- Kumar, A.; Sharma, M.P. Assessment of risk of GHG emissions from Tehri hydropower reservoir, India. Hum. Ecol. Risk Assess. Int. J. 2016, 22, 71–85. [Google Scholar] [CrossRef]
- You, J.J.; Wang, Z.J.; Gan, H.; Jiang, Y.Z. Current status and prospect of study in china on water allocation of inter-basin diversion projects. South North Water Transf. Water Sci. Technol. 2008, 3, 6. [Google Scholar]
- Zhong, P.; Wang, H.; Liu, J.; Chen, X.; Chen, K. Optimal dispatching model for Shenzhen water resources system. J. Hehai Univ. 2003, 31, 616–620. [Google Scholar]
- Chen, J.; Zhong, P.A.; Xu, B.; Zhao, Y.F. Risk analysis for real-time flood control operation of a reservoir. J. Water Resour. Plan. Manag. 2015, 141, 04014092. [Google Scholar] [CrossRef]
- Zhu, F.; Zhong, P.A.; Sun, Y.; Yeh, W.W.G. Real-time optimal flood control decision making and risk propagation under multiple uncertainties. Water Resour. Res. 2017, 53, 10635–10654. [Google Scholar] [CrossRef]
- Antonelli, M.; Tamea, S. Food-water security and virtual water trade in the middle east and North Africa. Int. J. Water Resour. Dev. 2015, 31, 326–342. [Google Scholar] [CrossRef]
- Grafton, R.Q.; Landry, C.; Libecap, G.D.; Mcglennon, S.; O’Brien, R. An integrated assessment of water markets: Australia, Chile, China, South Africa and the USA. Cent. Water Econ. Environ. Policy Pap. 2010, 5. [Google Scholar] [CrossRef]
- Fu, J.; Zhong, P.A.; Zhu, F.; Chen, J.; Wu, Y.N.; Xu, B. Water resources allocation in transboundary river based on asymmetric Nash–Harsanyi Leader–Follower game model. Water 2018, 10, 270. [Google Scholar] [CrossRef]
- Ha, M.; Gao, Z. Optimization of water allocation decisions under uncertainty: The case of option contracts. J. Ambient. Intell. Humaniz. Comput. 2017, 8, 809–818. [Google Scholar] [CrossRef]
- Brookshire, D.S.; Ganderton, P.T. Introduction to special section on water markets and banking: Institutional evolution and empirical perspectives. Water Resour. Res. 2004, 40, 547. [Google Scholar] [CrossRef]
- Jercich, S.A. California’s 1995 water bank program: Purchasing water supply options. J. Water Resour. Plan. Manag. 1997, 123, 59–65. [Google Scholar] [CrossRef]
- Calatrava, J.; Garrido, A. Spot water markets and risk in water supply. Agric. Econ. 2015, 33, 131–143. [Google Scholar] [CrossRef]
- Porkka, M.; Kummu, M.; Siebert, S.; Florke, M. The role of virtual water flows in physical water scarcity: The case of central Asia. Int. J. Water Resour. Dev. 2012, 28, 453–474. [Google Scholar] [CrossRef]
- Wichelns, D. Virtual water and water footprints offer limited insight regarding important policy questions. Int. J. Water Resour. Dev. 2010, 26, 639–651. [Google Scholar] [CrossRef]
- Hansen, K.; Kaplan, J.; Kroll, S. Valuing options in water markets: A laboratory investigation. Environ. Resour. Econ. 2014, 57, 59–80. [Google Scholar] [CrossRef]
- Hansen, K.; Williams, J. Valuing risk: Options in California water markets. Am. J. Agric. Econ. 2010, 90, 1336–1342. [Google Scholar] [CrossRef]
- Cheng, W.C.; Hsu, N.S.; Cheng, W.M.; Yeh, W.W.G. Optimization of European call options considering physical delivery network and reservoir operation rules. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Tomkins, C.D.; Weber, T.A. Option contracting in the California water market. J. Regul. Econ. 2010, 37, 107–141. [Google Scholar] [CrossRef]
- Rey, D.; Calatrava, J.; Garrido, A. Optimisation of water procurement decisions in an irrigation district: The role of option contracts. Aust. J. Agric. Resour. Econ. 2016, 60, 1–25. [Google Scholar] [CrossRef]
- Kasprzyk, J.R.; Reed, P.M.; Kirsch, B.R.; Characklis, G.W. Managing population and drought risks using many-objective water portfolio planning under uncertainty. Water Resour. Res. 2009, 45, 170. [Google Scholar] [CrossRef]
- Cui, J.; Schreider, S. Modelling of pricing and market impacts for water options. J. Hydrol. 2009, 371, 31–41. [Google Scholar] [CrossRef]
- Holburt, M.B.; Atwater, R.W.; Quinn, T.H. Water marketing in southern California. J. Am. Water Works Assoc. 1988, 80, 38–45. [Google Scholar] [CrossRef]
- Michelsen, A.M.; Young, R.A. Optioning agricultural water rights for urban water supplies during drought. Am. J. Agric. Econ. 1993, 75, 1010–1020. [Google Scholar] [CrossRef]
- Mudança Climática. Climate Change Adaptation: The Pivotal Role of Water; UN-Water: Ginebra, Suiza, 2010. [Google Scholar]
- Villinski, M.T. A numerical quadrature approach to option valuation in water markets. Am. Agric. Econ. Assoc. 1999, 81, 1321. [Google Scholar]
- Ramos, A.G.; Garrido, A. Formal risk-transfer mechanisms for allocating uncertain water resources: The case of option contracts. Water Resour. Res. 2004, 40, 73–74. [Google Scholar]
- Ranjan, R. Factors affecting participation in spot and options markets for water. J. Water Resour. Plan. Manag. 2004, 136, 454–462. [Google Scholar] [CrossRef]
- Diao, Y.F.; Wang, B.D.; Liu, J. Study on distribution of flood forecasting errors by the method based on maximum entropy. J. Hydraul. Eng. 2007, 38, 591–595. [Google Scholar]
- Wheeler, S.; Bjornlund, H.; Shanahan, M.; Zuo, A. Price elasticity of water allocations demand in the goulburn–murray irrigation district. Aust. J. Agric. Resour. Econ. 2010, 52, 37–55. [Google Scholar] [CrossRef]
- Wuab, D.J.; Zhang, J.E. Optimal bidding and contracting strategies for capital-intensive goods. Eur. J. Oper. Res. 2002, 137, 657–676. [Google Scholar]
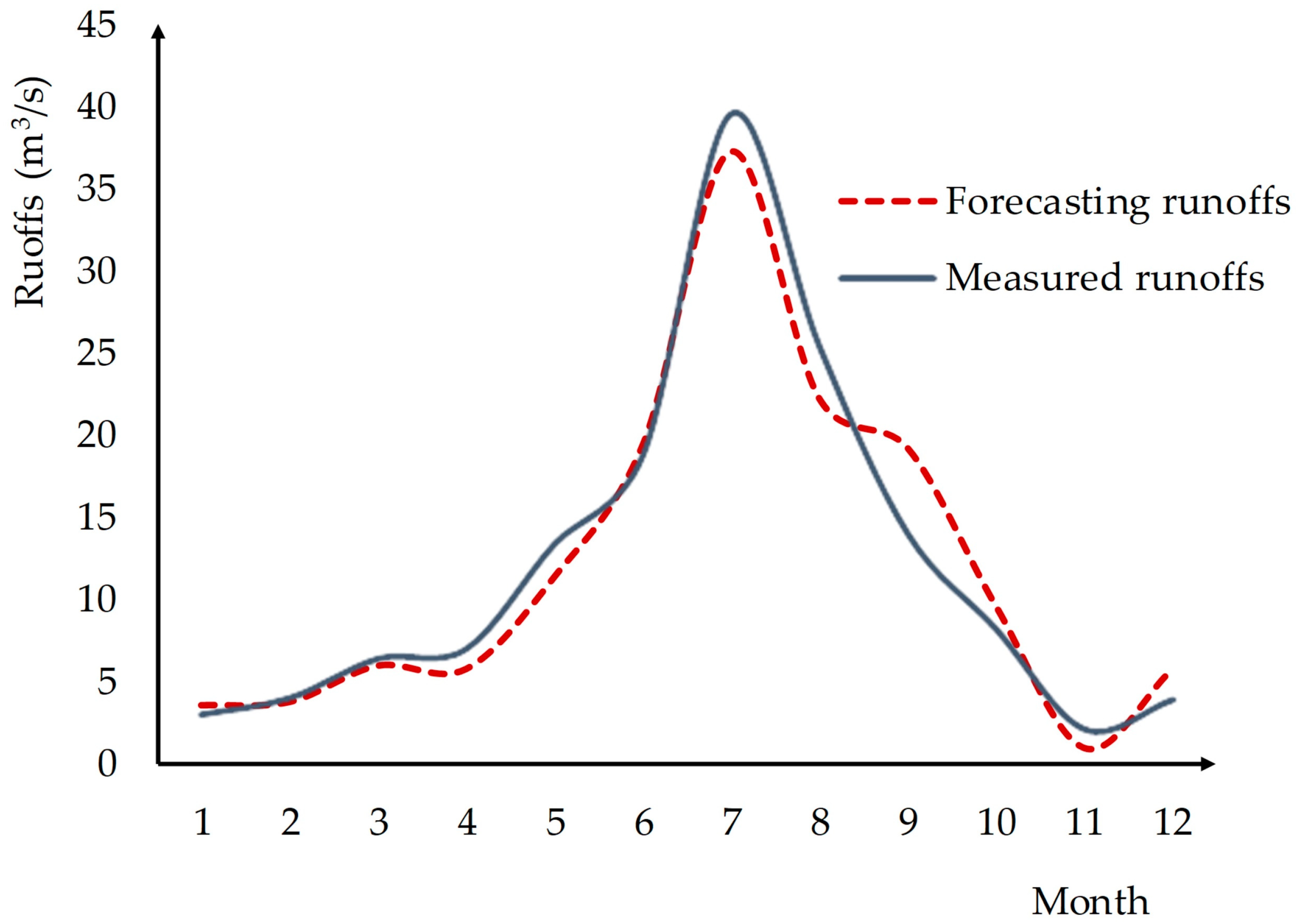
| Forecast Period | Forecasting Runoffs (m3/s) | Measured Runoffs (m3/s) | Absolute Error (m3/s) | Relative Error |
|---|---|---|---|---|
| January | 3.6 | 3 | −0.6 | −0.2 |
| February | 3.8 | 4 | 0.2 | 0.05 |
| March | 6 | 6.4 | 0.4 | 0.06 |
| April | 5.8 | 7 | 1.2 | 0.17 |
| May | 11.4 | 13.4 | 2 | 0.15 |
| June | 19.4 | 18.8 | −0.6 | −0.03 |
| July | 37.2 | 39.6 | 2.4 | 0.06 |
| August | 22.2 | 25.4 | 3.2 | 0.13 |
| September | 19.2 | 14 | −5.2 | −0.37 |
| October | 9.6 | 8.2 | −1.4 | −0.17 |
| November | 1 | 2.1 | 1.1 | 0.52 |
| December | 5.8 | 3.9 | −1.9 | −0.49 |
| Average | 12.1 | 12.2 | 0.1 | 0.20 |
| W (104 m3) | β1 (104 RMB) | β2 (104 RMB) | μ | δ | m1 | m3 |
|---|---|---|---|---|---|---|
| 3000 | 2 | 0.1 | 2.5 | 0.3 | 0.00116156 | 0.000219 |
| m2 | 0.25 | 0.26 | 0.27 | 0.28 | 0.29 | 0.3 | 0.31 | 0.32 | 0.33 | 0.34 |
|---|---|---|---|---|---|---|---|---|---|---|
| Q* (104 m3) | 755 | 800 | 849 | 897 | 936 | 1008 | 1029 | 1115 | 1263 | 1299 |
| N (104 RMB) | 83 | 88 | 98 | 101 | 110 | 121 | 127 | 145 | 169 | 178 |
| W (104 m3) | β1 (104 RMB) | β2 (104 RMB) | μ | λ0 | λ1 | λ2 | λ3 |
|---|---|---|---|---|---|---|---|
| 3000 | 2 | 0.1 | 2.5 | 0.3133 | −0.0326 | −5.879 | −0.0136 |
| m2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
|---|---|---|---|---|---|---|---|---|
| Q* (104 m3) | 1008 | 1026 | 1044 | 1063 | 1081 | 1099 | 1118 | 1136 |
| N (104 RMB) | 124 | 131 | 140 | 152 | 165 | 180 | 195 | 211 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, H.; Zhong, P.-A.; Chen, J.; Xu, B.; Wu, Y.; Zhu, F. An Optimal Model for Water Resources Risk Hedging Based on Water Option Trading. Water 2018, 10, 1026. https://doi.org/10.3390/w10081026
Yan H, Zhong P-A, Chen J, Xu B, Wu Y, Zhu F. An Optimal Model for Water Resources Risk Hedging Based on Water Option Trading. Water. 2018; 10(8):1026. https://doi.org/10.3390/w10081026
Chicago/Turabian StyleYan, Haibin, Ping-An Zhong, Juan Chen, Bin Xu, Yenan Wu, and Feilin Zhu. 2018. "An Optimal Model for Water Resources Risk Hedging Based on Water Option Trading" Water 10, no. 8: 1026. https://doi.org/10.3390/w10081026
APA StyleYan, H., Zhong, P.-A., Chen, J., Xu, B., Wu, Y., & Zhu, F. (2018). An Optimal Model for Water Resources Risk Hedging Based on Water Option Trading. Water, 10(8), 1026. https://doi.org/10.3390/w10081026





