1. Introduction
A debris flow is one of the most dangerous types of mass movement because, depending on the rheology and topography, it can reach a very high speed and large run-out distance. Important study aspects of the initiation process of a debris flow are the mechanism and boundary condition, because they determine the meteorological threshold conditions and further evolution, and will provide clues for future mitigation strategies [
1].
One can make different classifications of initiation mechanisms based on different viewpoints [
1]. It was among others [
2,
3], who stressed the importance of the infiltration capacity of the soil as a key factor for either the development of shallow landslides or surficial erosion and transport of material by overland flow, that might create different types of flow like mass movements. Effective overland flow driven triggering processes are mainly concentrated in channels where high water discharges, and severe erosion and transport lead to high solid concentrations generating debris flows [
4,
5,
6,
7,
8,
9]. Material is supplied to these debris flows by detachment and transport of the bed material, but also through lateral erosion of the channel bed. The channel can be partly or totally blocked by landslide dams. High runoff discharges eroding these landslide dams can also lead to initiation and rapid grow of debris flows [
10,
11,
12]. Landslide damming can also be initiated by rapid incision of the channel bed destabilizing the side walls [
13]. With infiltrating driven triggering mechanisms, shallow landslides are generated, which may or may not transform into debris flows. This failure mechanism by infiltrating water can occur in channel beds filled with loose material [
14] and on planar slopes where shallow landslides can also transform into debris flows [
15,
16,
17,
18]. The transformation of a failed mass into a debris flow is rather complex and depends on various hydro-mechanical processes related to pore pressure development and supply of abundant overland flow water further mobilizing the failed mass [
19,
20,
21,
22,
23].
Several authors analyzed partly the role of hydro-mechanical and morphometric factors controlling the type of initiation of debris flows. Berti [
24] analyzed the hydrological factors for the generation of debris flows in typical source areas in the Italian Alps by modelling overland flow in the channel bed from a source area as a response to rainfall impulses. Kean [
25] proposed an integrated hydro-geotechnical dynamic model to describe sediment transport by overland flow and consequently mass failure transforming into debris flow surges. Hu [
26] highlighted the initial soil moisture, and thus infiltration capacity as a controlling factor for the type of initiation; wet soils created mainly surficial runoff, erosion, and incision; bank failure; and damming and debris flow development, while dry soils showed mainly infiltration and landslide failure and debris flow initiation [
1]. Zhuang et al. [
1] focused more on the slope gradient as a controlling factor for different types of initiation. Their flume studies revealed that at gentler slope gradients around 10° ± 2°, incision and bank failure is dominant, creating channel damming and dam failure, inducing debris flows. At intermediate slopes around 15° ± 3°, erosion of bed material occurs at high discharges. The high sediment transport capacity with high sediment concentrations is sufficient to create debris flows. At steeper slopes around 21° ± 4°, bed failure by infiltrating overland flow water with debris flow formation is the most dominant process.
Meteorological thresholds for the initiation of debris flows are closely related to the process of initiation. In many studies about these meteorological thresholds, no clear distinction was made between the types of triggering [
27]. The assessment of these thresholds in relation to various morphometric and geological factors was made in most cases using statistical techniques [
28,
29,
30].
Until now, only isolated aspects of the hydrological triggering system of debris flows have been studied. There is a need for a comprehensive framework which gives insight in the controlling factors for the evolution of different triggering systems in upstream channels of debris flow gullies. Therefore this paper will try to give answers on the following questions:
What type of hydro-mechanical triggering mechanisms for debris flows can we distinguish in upstream channels of debris flow prone gullies?
What are the main parameters and in what way are they controlling the type and temporal sequence of these triggering processes?
What is the influence of hydro-mechanical parameters and related triggering processes on the meteorological thresholds for debris flow initiation?
In order to answer these questions we have carried out a number of flume tests to detect the conditions for different types of hydro-mechanical triggering mechanisms of debris flows (
Section 2). Based on the process information revealed by these experiments we will develop an integrated hydro-mechanical model describing these triggering processes (
Section 3). The model will be calibrated and validated using indicator values obtained from the processes measured in the flume (
Section 4). Virtual model simulations will be carried out in a schematic hypothetical source area of a catchment to make a framework of the type and sequence of these triggering processes as a function of slope angle and the hydraulic conductivity of the bed material (
Section 5). The model will also be used for sensitivity analyses to study the influence of important geometrical and hydro-mechanical parameters and the related type of initiation process on rainfall intensity-duration threshold curves, for the start of debris flows (
Section 6).
3. Integrated Model (1D) for Debris Flow Initiation in Upstream Channels
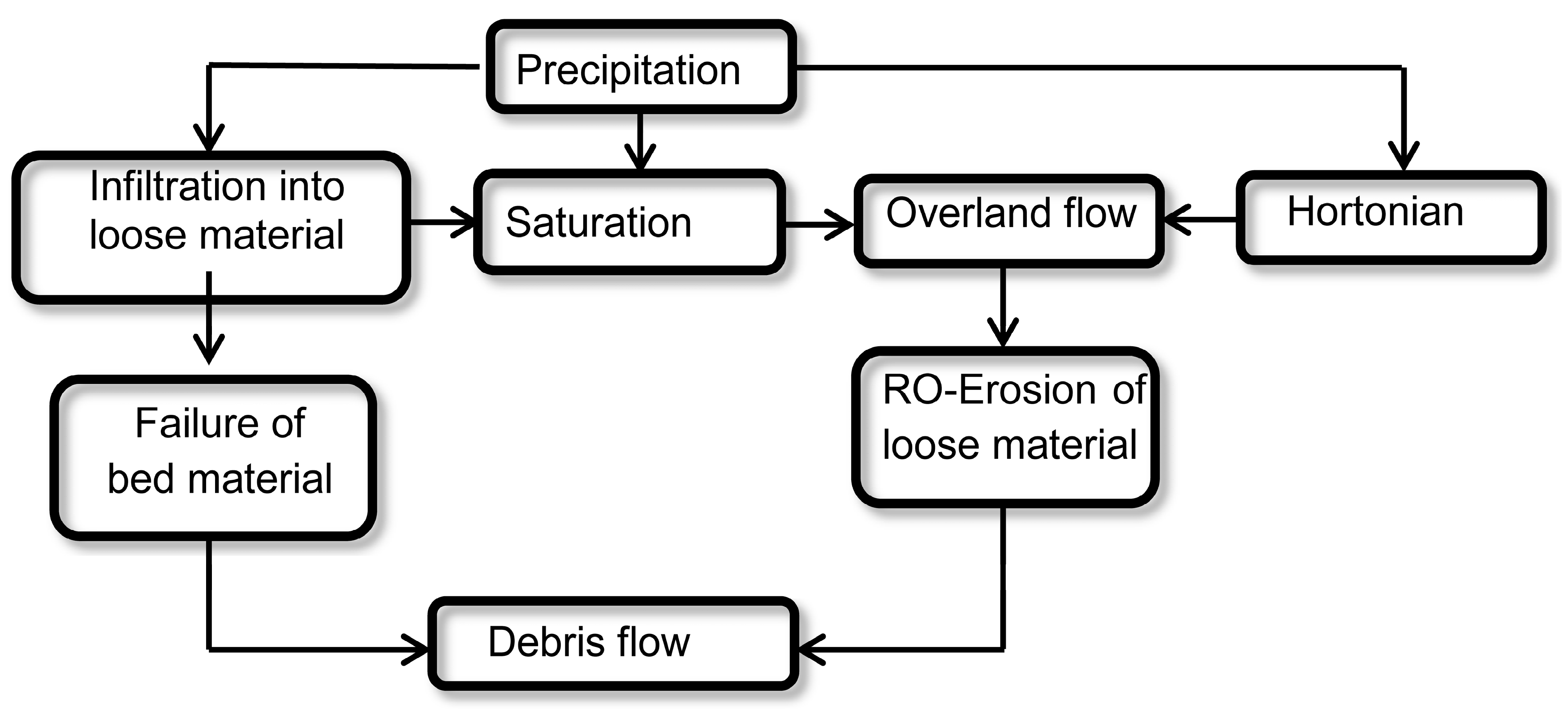
The flume test observations brought us to the concept of the triggering of debris flows caused by Hortonion and saturation overland flow initiating surficial erosion of bed material. Bed failure and entrainment of material was initiated by infiltration and subsurface flow leading to instability. First, we have to simulate the hydrological component of the triggering mechanisms of debris flows. For that we need the mass balance equation for overland (Equation (1a)) and through flow (Equation (1b)), which is given by:
where
qf is overland flow discharge per unit width (m
3 m
−1 s
−1);
qs is subsurface discharge per unit width (m
3 m
−1 s
−1);
hf is thickness of overland flow (m);
hs (m) is thickness of subsurface flow, ∂
x (m) is distance along the slope,
t is the time (s), and
B1–2 are terms (m s
−1) describing the inflow or outflow of water from the flow system, which is defined as follows:
where
r (m s
−1) describes the external input of rain into and
if (m s
−1) the outflow of water by infiltration out of the overland flow system (Equation (2a)) (see also
Figure 1). When there is no supply of rain, like in our flume experiments,
r = 0. In the case of subsurface flow,
if in Equation (2b) is considered now as an inflow term of the subsurface flow system. If
hf/Δ
t is larger than the infiltration capacity,
Ks (m s
−1) of the bed material the latter one is the limiting factor. Therefore the infiltration term
if of Equation (2) is the minimum (min) value of the infiltration capacity
Ks (m s
−1) and the current water depth (
hf), which can infiltrate in one time step Δ
t into the bed material:
We introduce here a general momentum equation for the water flow processes [
33]:
For turbulent overland flow, the parameters
and
in Equation (4a) can be defined as follows:
where
n is Manning’s
n and
S0 the slope gradient of the bed material.
For subsurface flow we can write according to Darcy’s law:
where
qs is the amount of subsurface flow water per unit width (m
3 m
−1 s
−1),
is slope angle (degrees), and
hs is the height of the flowing water component in the soil matrix (m). By comparing Equation (6) with the general momentum Equation (4b) we can define the parameters
and
for subsurface flow:
A combination of the mass balance Equation (1) with Equation (4) delivers an expression for overland flow or subsurface flow discharge (
qf,
qs) [
33]:
The 1D model is implemented in a fixed Eulerian frame where the variation in water flow variables is described at fixed coordinate points at a distance Δ
x along the slope as a function of time step Δ
t. A numerical solution for Equation (8) is given by [
33]:
where
qx,
and
should be read as
qf,s f,s and
f,s, respectively.
To simulate the initiation of debris flows by mass failure we used the equation for the infinite slope equilibrium model [
31], which is the trigger for failure:
where
F is the safety factor; failure occurs when
F = 1;
s and
(k N m
−3) are the saturated bulk density of the material and water, respectively;
is friction angle of the material;
z and
hs are the thickness of the soil and the height of the groundwater layer, respectively;
hs can be solved with Equation (6) and (9), respectively.
The overall stability of the bed material expressed with the safety factor (F) for the infinite slope model was calculated as an average of the safety factor of the different nodes. The inflow of water into the flume is coming from upstream, and therefore the pore pressure gradient is decreasing downstream. This means that the safety factor is always increasing downstream, and therefore the average approach of the safety factor over the length of the sample in the flume seems a reasonable approximation of the overall safety factor.
For estimating the transport capacity on steep slopes Rickenmann [
34,
35] proposed a bedload transport equation based on a shear stress approach, where discharge, bed slope gradient, and material grading are used as parameters to characterize flow hydraulics.
For steeper slopes, in the range of 0.03 <
S < 0.2 (1.7°–11.3°), Rickenmann [
34] performed a regression analysis with the steep flume data on bed load transport obtained at ETH Zurich that resulted in the equation:
where
D90 and
D30 are grain sizes at which 90% and 30%, respectively, by weight of the material are finer;
ds is the mass density of the solids,
S is the slope gradient, and
qc is the critical flow discharge for bedload entrainment. The experimental slopes were in the range of 0.03 >
S > 0.20 (1.7°–11.3°), and the
D90 of the material ranged between 0.9 and 2 cm and
D30 between 0.06 and 1 cm with inflow rates of 10–30 L s
−1. In the section below, we will calibrate Equation (11) for the steeper slopes in our flumes.
The integrated model developed in this section is able to describe the different types of hydro-mechanical triggering mechanisms for debris flows. It delivers us the physical parameters, which controls these processes, which will be applied in our virtual simulations in
Section 5 and
Section 6.
In the next section, we will calibrate our model on some process indicator values obtained from our flume tests.
4. Calibration and Validation of the Theoretical Model on the Basis of Flume Test Results
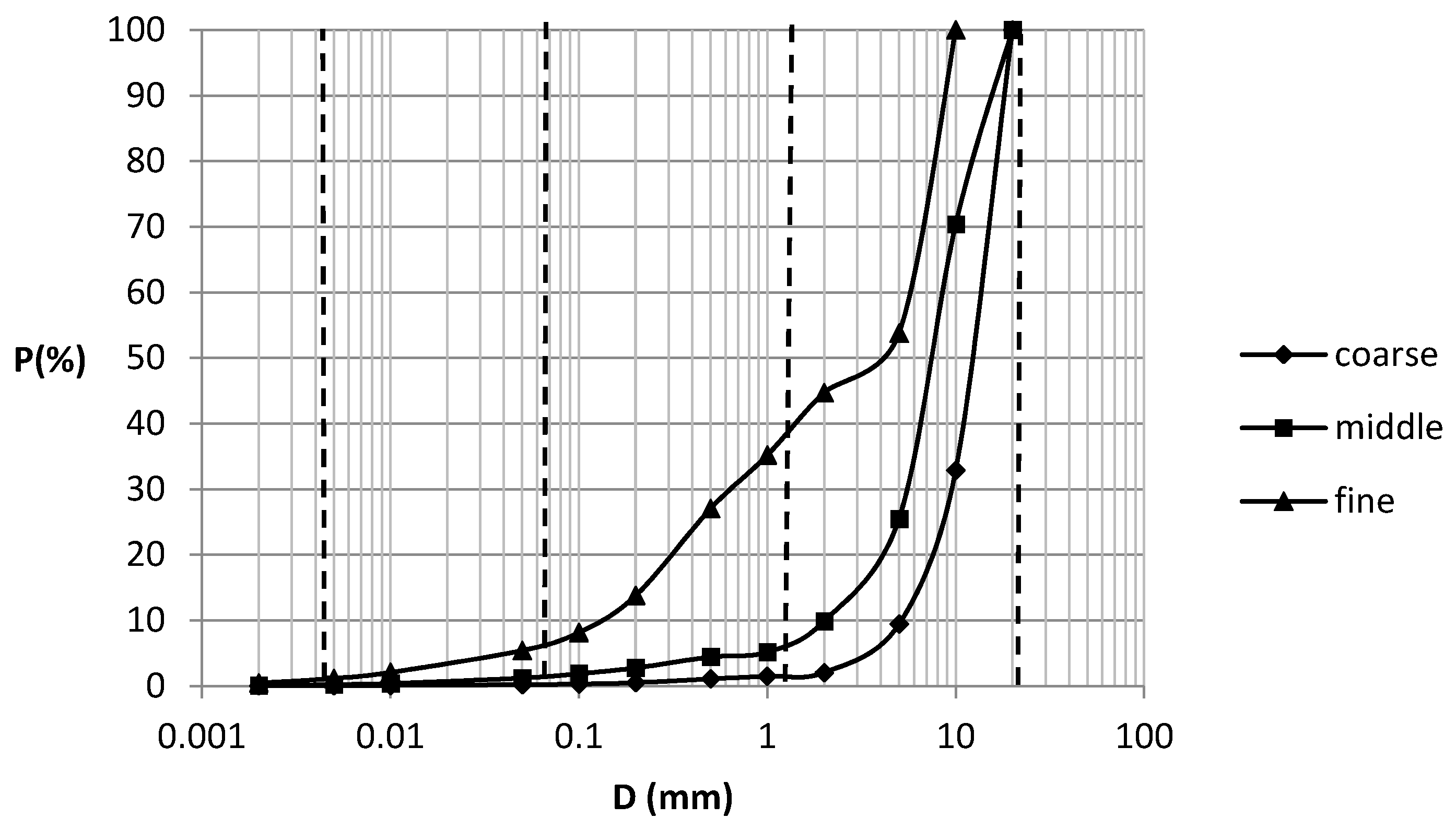
We will use here a number of process indicator values measured during the flume experiments to calibrate and validate the outcomes of our theoretical model. These are saturation or Hortonian overland flow, time to overland flow, maximum pore pressure, time to bed failure, and solid concentration by overland flow erosion. Hortonian overland flow and the time to Hortonian overland flow in the model is declared when surface water hf reaches the lower end of the bed material, while the bed material is still not saturated (hs < Zs). Saturation overland flow and the time towards it is declared when hs = Zs over the entire bed. Pore pressure is calculated each time step according to Equation (10b). The discharge of hf + hs is reported each time step at the end of the flume. Bed failure is declared as mentioned earlier when the average safety factor F over the bed length reaches the value of 1.
For the flume simulations, the distance between the nodes (Δx) was 0.1 m and the time interval (Δt) was 0.2 s.
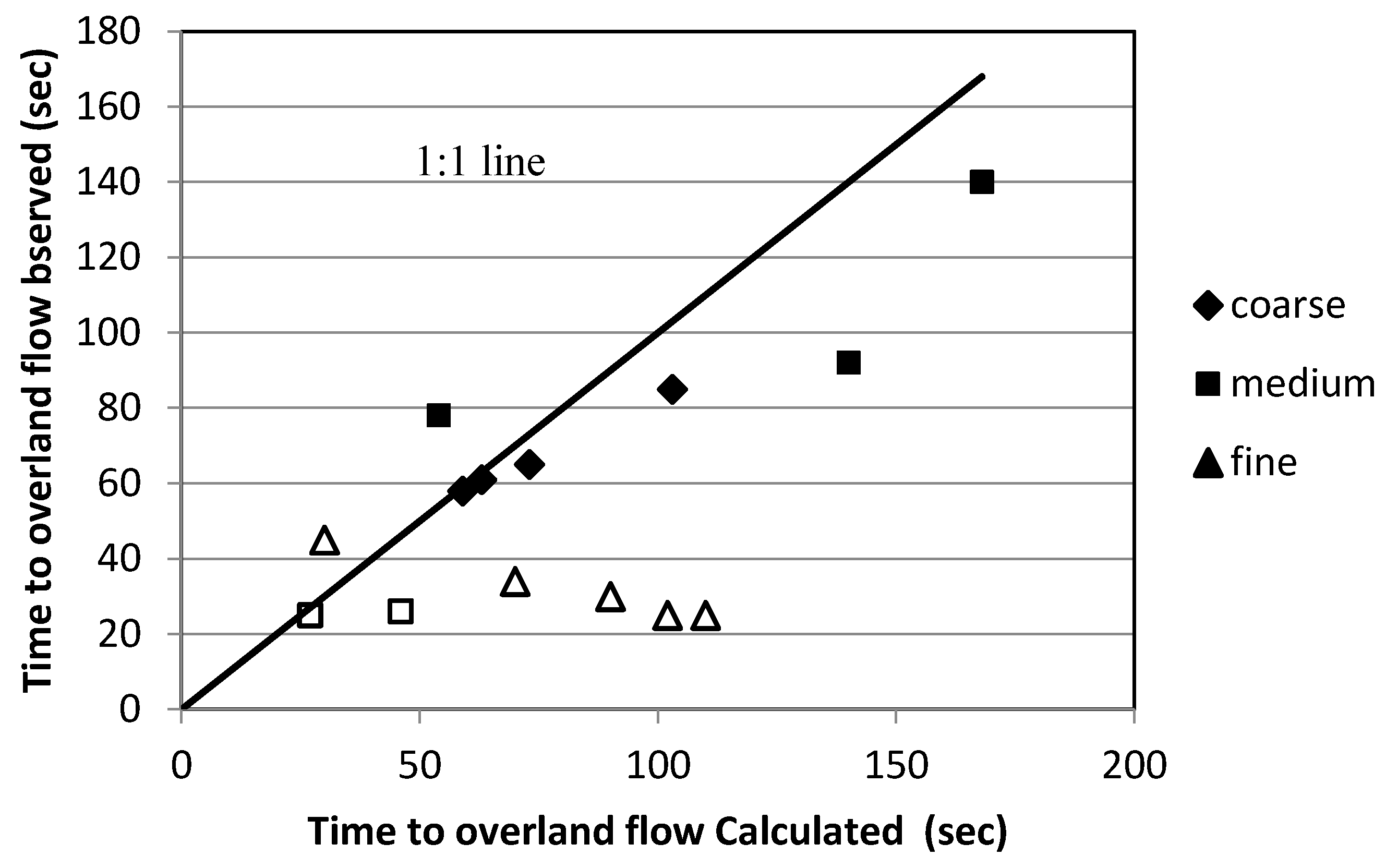
Figure 4 shows the relation between observed and calculated time to overland flow for the different flume tests. There is a moderate 1:1 correlation between observed and predicted time to overland flow for the medium and coarse sediments and for the fine sediments, showing Hortonian overland flow there is no correlation at all. The deviations in observed and predicted time to overland flow can be ascribed to the variation in density of the bed material in combination with a poor estimate of the
Ks value based on a limited amount of measurements, which was used as input for the modelling (see
Section 2.1). However the model was able to predict the type of overland flow according to what was observed during the flume tests (see
Table 2).
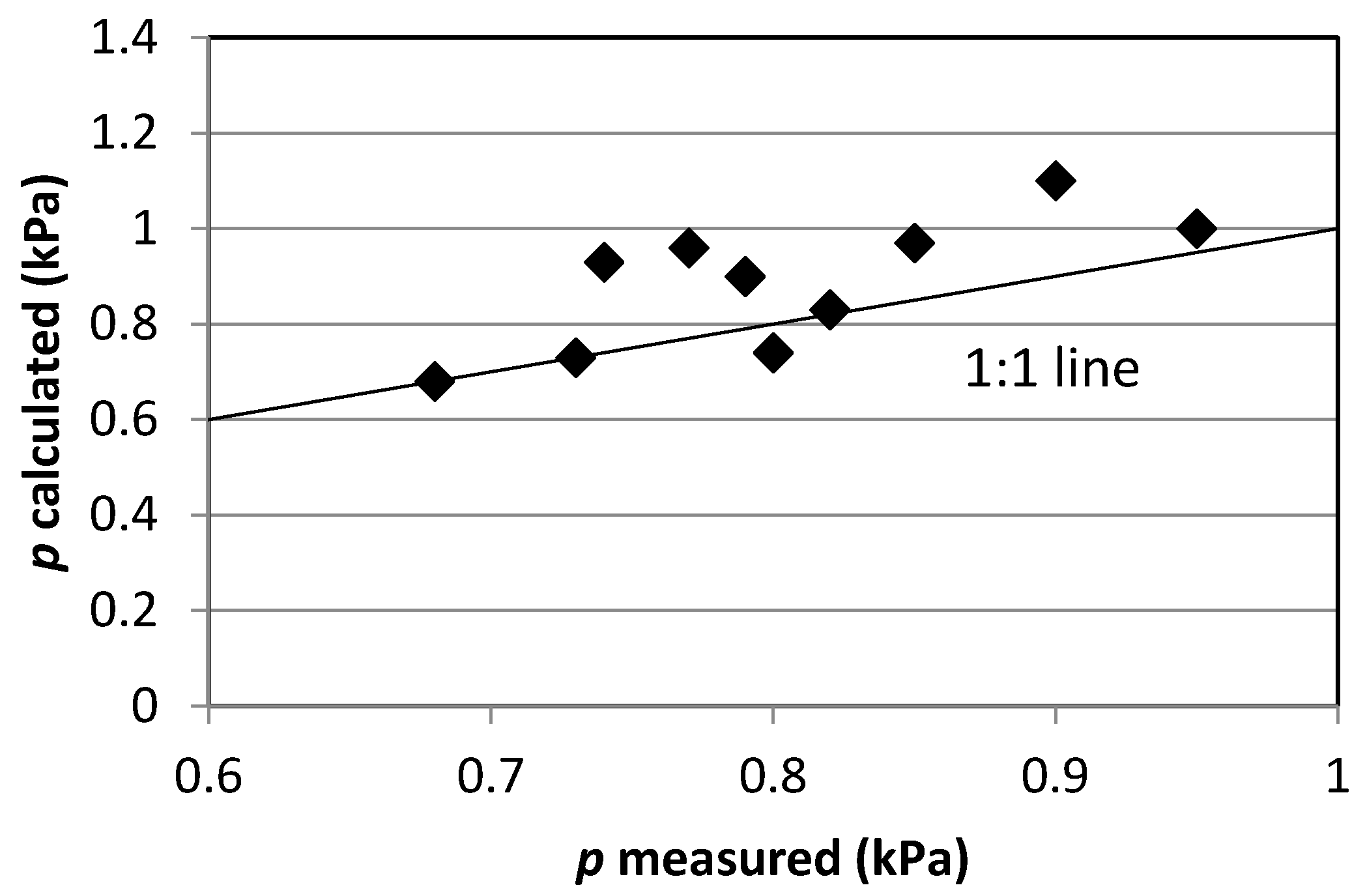
Despite the malfunctioning of some pore pressure sensors we were able to make a 1:1 comparison between the average maximum measured pore pressure for the three sensors (
Figure 1) and the average calculated maximum pore pressure (
Figure 5).
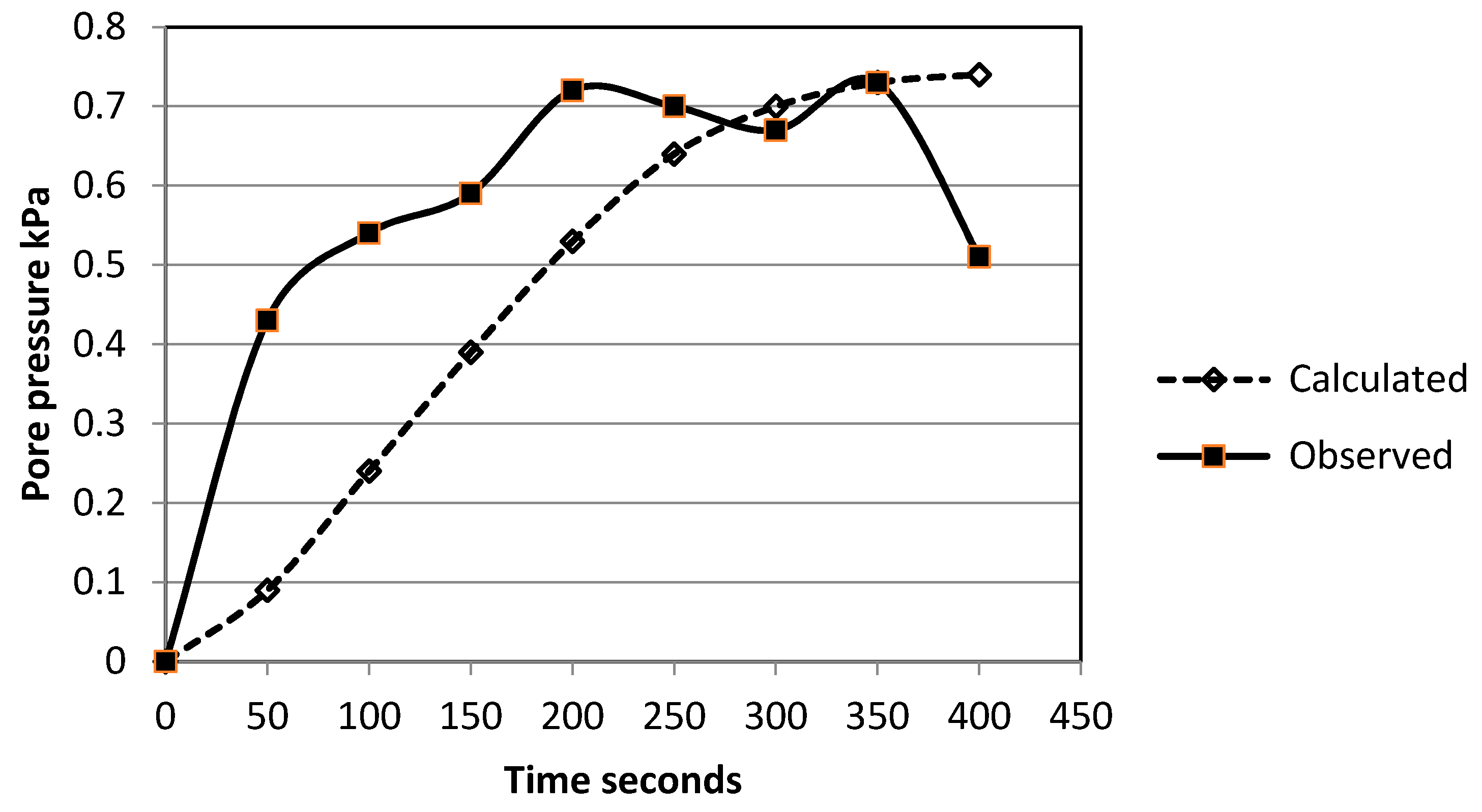
The Figure shows that in many cases there is a slight overestimation of the calculated pore pressure. Time series of measured pore pressure of the three sensors compared to modelled temporal pore pressure development showed that in most cases the onset towards maximum pore pressure for the three sensors was more irregular compared to the calculated development of the pore pressures (
Figure 6). This can be ascribed to the variation in density, which occurred during the compaction of the sediment layers or (and) the imperfect response of the sensors.
In relation to pore pressure development we compared the time to failure for the different test runs on the different materials. Since the time towards average maximum calculated and measured pore pressure coincided more or less, one would expect also corresponding calculated and measured failure times.
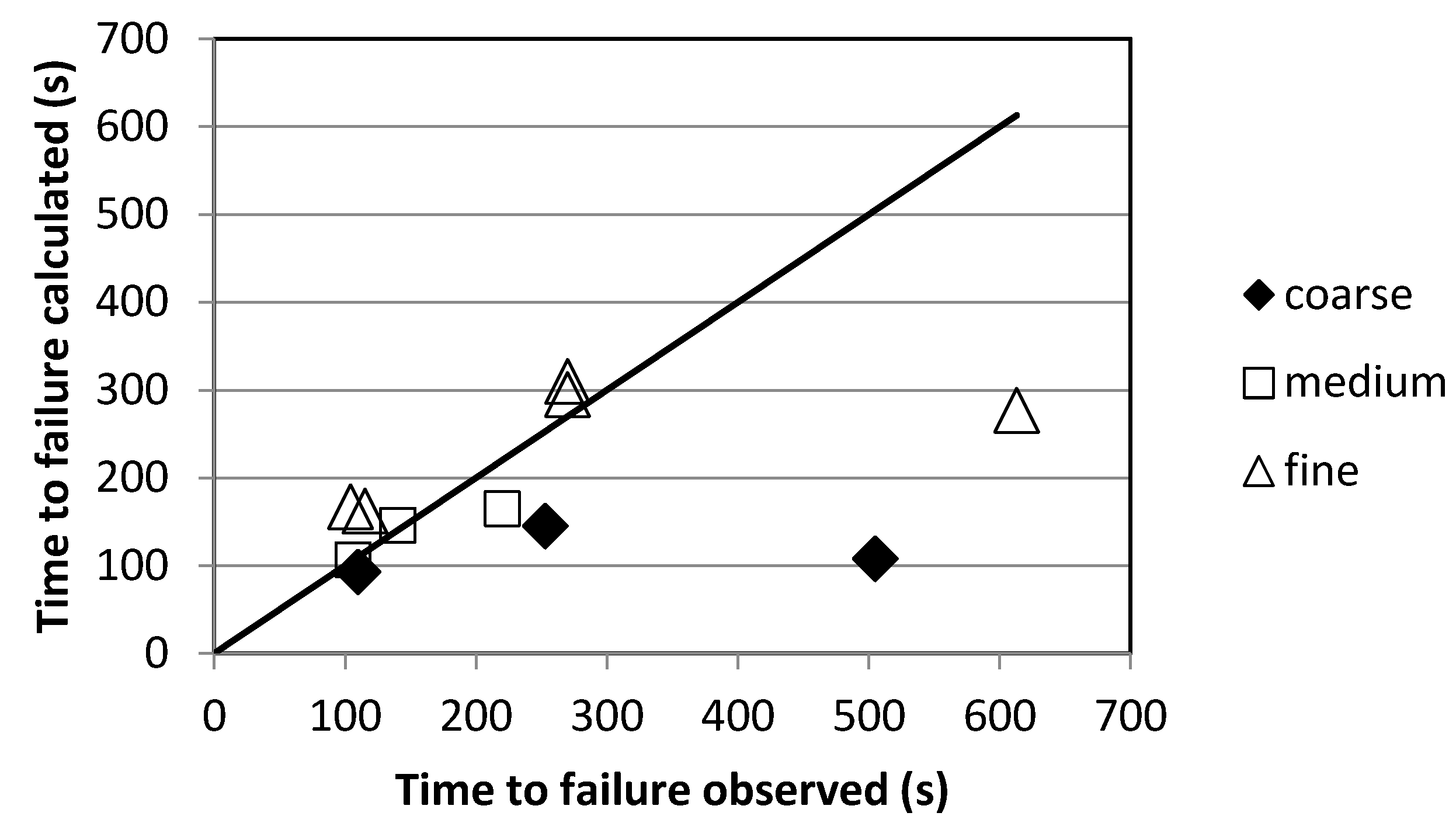
Table 2 and
Figure 7 show that the match between observed and calculated failure time is reasonable except for two outliers (coarse-20°; fine-18°).
Figure 7 shows further that the calculated time to failure seems to be underestimated for the coarse material and, although not so clear, overestimated for practically all the tests on the medium and fine materials. This suggests that the percolation rate is lower, and hence the observed time to failure is higher for the coarser bed materials and higher for finer bed materials. The average volumetric concentrations of the runoff water are 0.62, 0.65, and 0.70 for the coarse, medium, and fine bed materials, respectively. However, we would expect lower percolation rates (and therefore higher times to failure) in finer bed materials with higher concentrations of runoff water and more fine material and vise versa: higher percolation rates on the courser bed materials with lower runoff concentrations. We must conclude that the effect of concentration and gradient of the sediment in the water is not visible in our observed time to failure. Therefore, the deviations between calculated and observed values must be ascribed to the heterogeneity of the material, incorrect estimate of the friction values, and
Ks values and bulk density of the percolating water, and incorrect assessment of the overall safety factor.
We calibrated also the parameters of the Rickenmann [
35] equation, (Equation (11)) on our flume tests, which were carried out on slopes ranging between 0.25 >
S > 0.36 (14°–20°), with grain sizes for 0.9 >
d90 > 2 and 0.05 >
d30 > 1 cm, and with flow rates 0.5 >
qf > 15 L s
−1 m
−1.
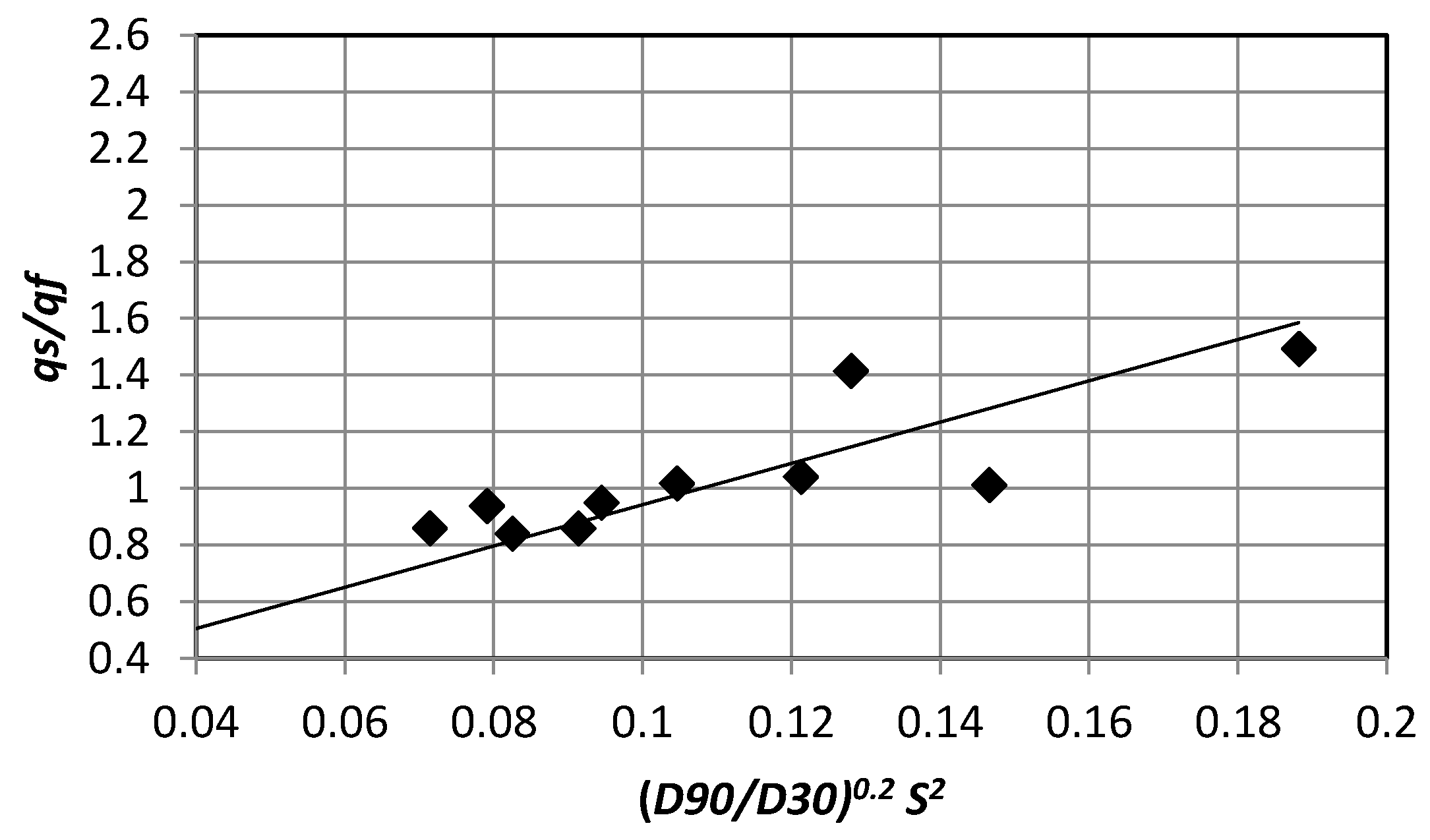
Figure 8 shows the best linear fit between
qsolid/
qf and (
d90/
d30)
0.2S2, which delivered the following modified equation for slopes between 14° and 20°:
which gives for
ds = 2.6:
The calibration revealed that qc in Equation (11) becomes zero or practically zero in Equation (12). At slopes larger than 15° the down slope component of the grain weight may reduce the critical shear stress τc which in our case obviously reduced to nearly zero.
We may conclude that the model is able to predict in a reasonable way essential process indicators for different hydrological triggering processes of debris flows in upstream channels. In the next section, we will apply the model on the field scale to predict hydro-mechanical triggering patterns for debris flows as a function of the hydrological conductivity of the bed material and the channel slope gradient.
6. Sensitivity Analyses for Parameters Influencing the Rain Intensity-Duration (I-D) Threshold Curves for Different Initiation Processes of Debris Flows
In the foregoing, we revealed the influence of
Ks and bed slope gradient on the sequence of processes mechanisms involved in the initiation of debris flows. We want to investigate here the effect of the other parameters (including
Ks and slope gradient) on rainfall thresholds in terms of intensity duration (I-D) curves for the triggering of debris flows by two main process mechanism: initiation by Hortonian overland flow (R
hE-I) and bed failure (BF-I). As we have seen in
Table 4 and
Table 5, debris flow initiation by saturation overland flow (R
sE-I) can only take place around 16 degrees. At lower slope angles, sediment concentrations are too low to call it a debris flow (
Table 4). At higher slope angles, we have bed failure before saturation overland flow can take place.
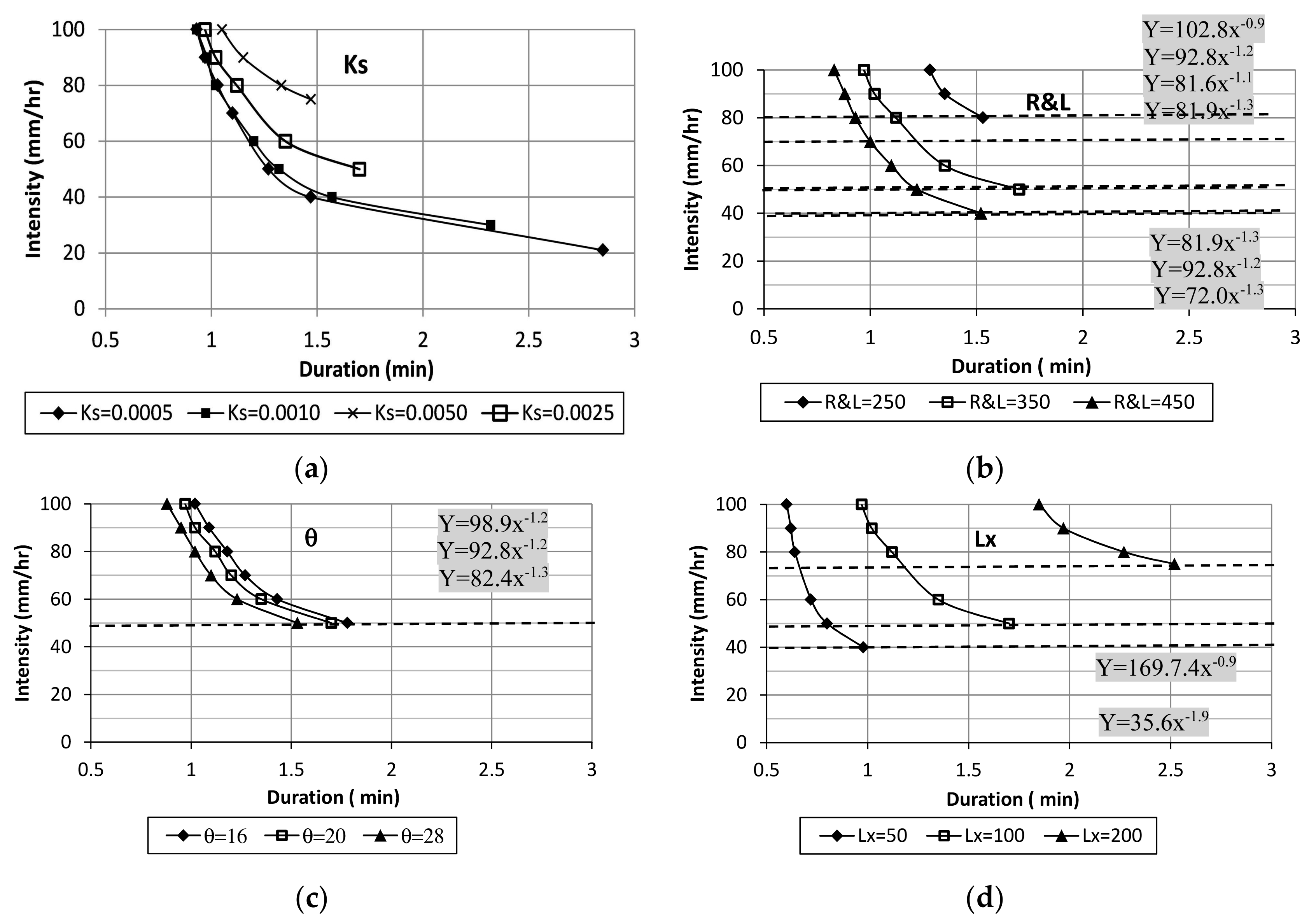
Figure 10 shows the effect of different parameters on the I-D curves for debris flows initiated by Hortonian overland flow. The intensity and duration value of a rain event which creates overland flow that just reaches the end of the channel bed with a sediment concentration of >0.2, is defined by us as a threshold rain event for debris flow initiation. The intensity and duration values for a variety of different critical rain events were plotted in a graph with on the Y-axis the intensity and on X-axis the duration. In this way, an intensity duration (ID) curve can be constructed.
Table 3 gives an overview of the range of the different parameters and the default values (in bold italic), which were used in the simulation and which give a realistic representation of geometric and geotechnical parameters for source area conditions The threshold curves for debris flow initiation by Hortonian overland flow are shown in
Figure 10. In this figure, the threshold curves, which are constructed using the default values given in
Table 3, are depicted with open rectangular markers. They are equal in all the sub-figures. This enables one to compare for the different parameters the difference between the ultimate curves and the default curve. For each selected parametric value there is an ultimate minimum rain intensity below which not enough overland flow, and thus a debris flow can be initiated, irrespective the duration (D) of the rain event (see horizontal dotted lines).
The simulations show that at intensities below this critical dotted line the overland flow water never reach the lower end of the bed due to a too high infiltration rate on its pathway compared to the supplied amount of water (direct rain input and surrounding overland flow), and finally bed failure may be the primary triggering process.
The most obvious selected parameter for overland flow initiation is the hydraulic conductivity
Ks. Other parameters are related to geometry of the source area (see
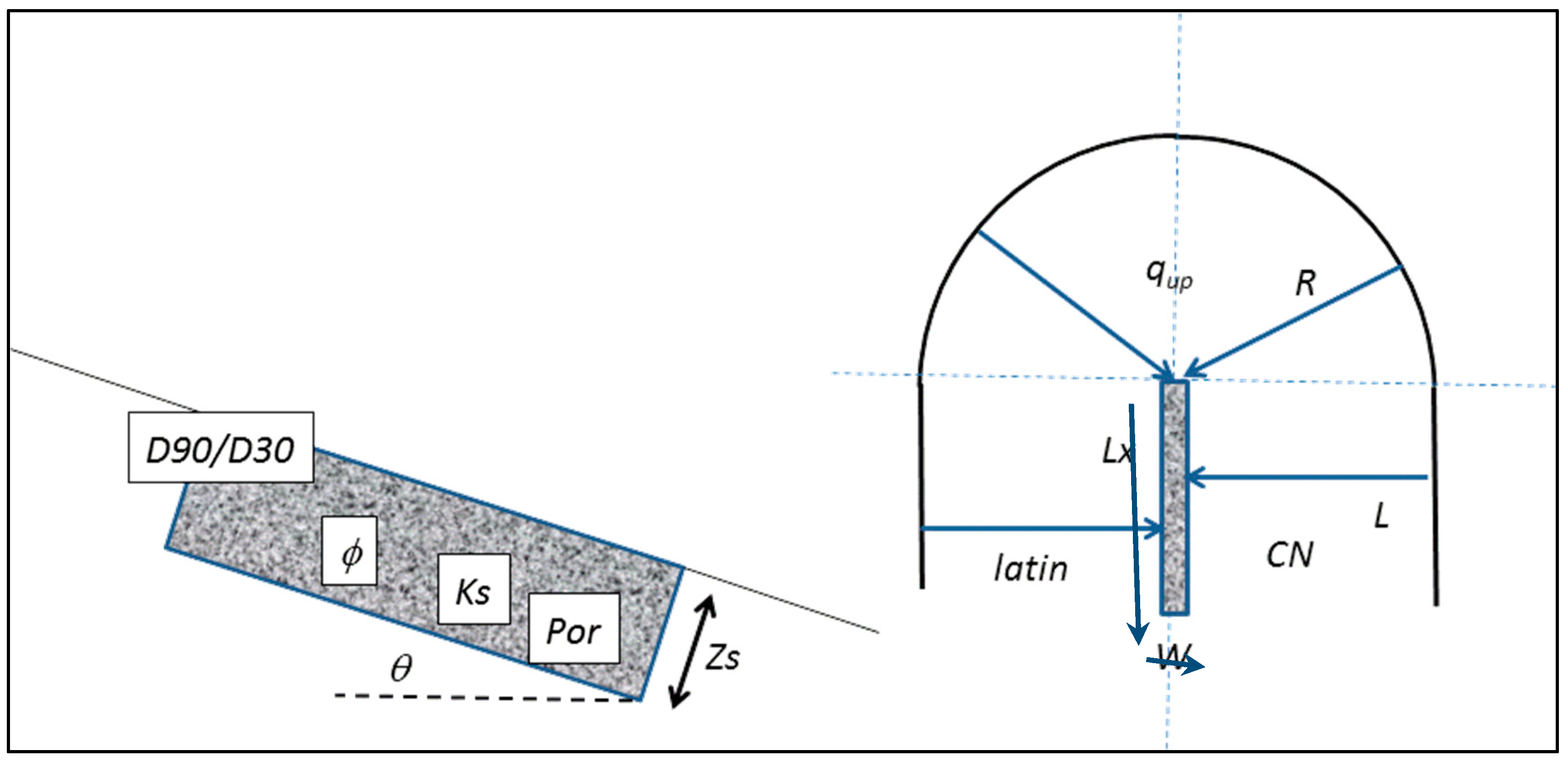
Figure 6) like length of the lateral slopes along the channel (
L), radius of the upstream area of the channel (
R), Length (
Lx) and width (
W) of the channel bed, channel bed gradient (
θ), and further Manning’s
n of the bed material.
We saw in the forgoing that Hortonian overland flow plays a dominant role for
Ks values <0.005 m s
−1.
Figure 10a shows the influence of the
Ks value on the I-D threshold curves for runoff erosion initiation (R
hE-I). The range of
Ks values was chosen between 0.0005 and 0.005 m s
−1. The figure shows that for
Ks values lower than 0.001 m s
−1 there is nearly no effect of
Ks on the position of the I-D curve, but there is a difference in the minimum intensity values (dotted lines) below which no debris flow can occur. A slight difference can be observed for lower intensities (<60 mm h
−1). Higher
Ks values (>0.001 m s
−1) have a larger influence on the I-D curves. (
Figure 10a).
The simulations show that the scale of the source area and lateral slopes (
R&
L), the length of the river bed (
Lx), and the width of the bed (
W) have the largest effect on the position of the threshold curve for the initiation of debris flow by Hortonian overland flow (
Figure 10b,d,f, respectively). The threshold curves are less sensible for the effect of the slope gradient
θ and Manning’s
n of the bed material (
Figure 10c,e respectively).
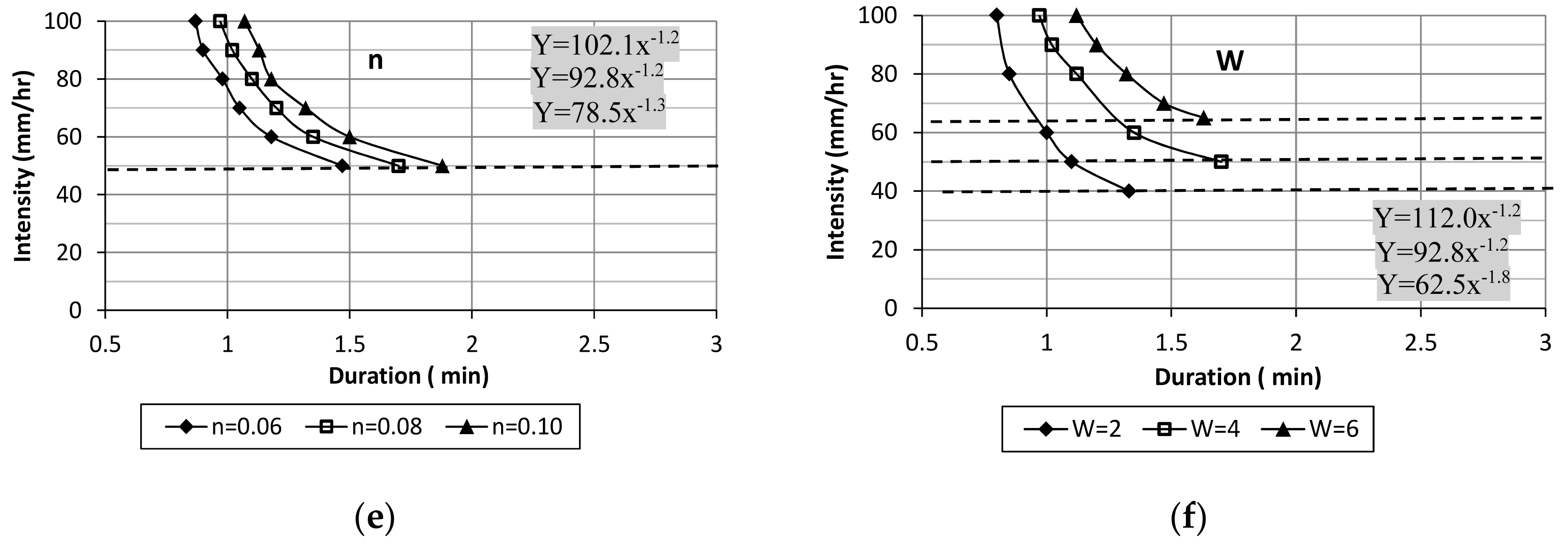
Figure 11 shows the influence of the different geotechnical and geometrical factors on the threshold values for the triggering of debris flows by bed failure. The range in
Ks values for which bed failure (BF-I) is the dominant process were chosen between 0.001 and 0.1 m s
−1 with a default value of 0.01 m s
−1. The effect of the selected range in geometric values
R&L,
Lx,
W,
θ, and
Zs (
Figure 11b,d,f–h, respectively) seems to be more or less the same. Less effect has the porosity (
Por) of the bed material and the
φ values (
Figure 11c,e, respectively). No effect had the hydraulic conductivity
Ks (
Figure 11a), which is related to the simplicity of the model describing instantaneous downward percolation for these high permeable bed materials. Interesting was to see that at lower
Ks values (around 0.001 m s
−1) and higher rain intensities, the rate of groundwater storage, and therefore the critical duration for failure, was nearly the same (
Figure 11a).
The I-D curves obtained by our simulations suggest that the duration range was strongly influenced by the type of initiation. Debris flows initiated by Hortonian overland flow seems to be initiated within several minutes while debris flow initiated by bed failure within one to two hours. I-D curves find in the literature give threshold curves with a larger duration range of one to several hours. The relative quick response to debris flow initiation can be explained by the large effect we give in our simulations to the contributing slopes with sparse vegetation and low infiltration rates, which in other areas may be minor due to higher infiltration rates of denser vegetation and lower overland flow rates. The use of the curve number method also explains the quick response to initiation, because it does not take into account the effect of the initial moisture content which for dry soils gives larger infiltration rates and time to ponding in the first period of a rain event. It also does not simulate the travel time towards the channel. The relative quick response for channel bed failure initiation was also found by Berti [
24] dealing with nearly impermeable rock slopes in the source area.
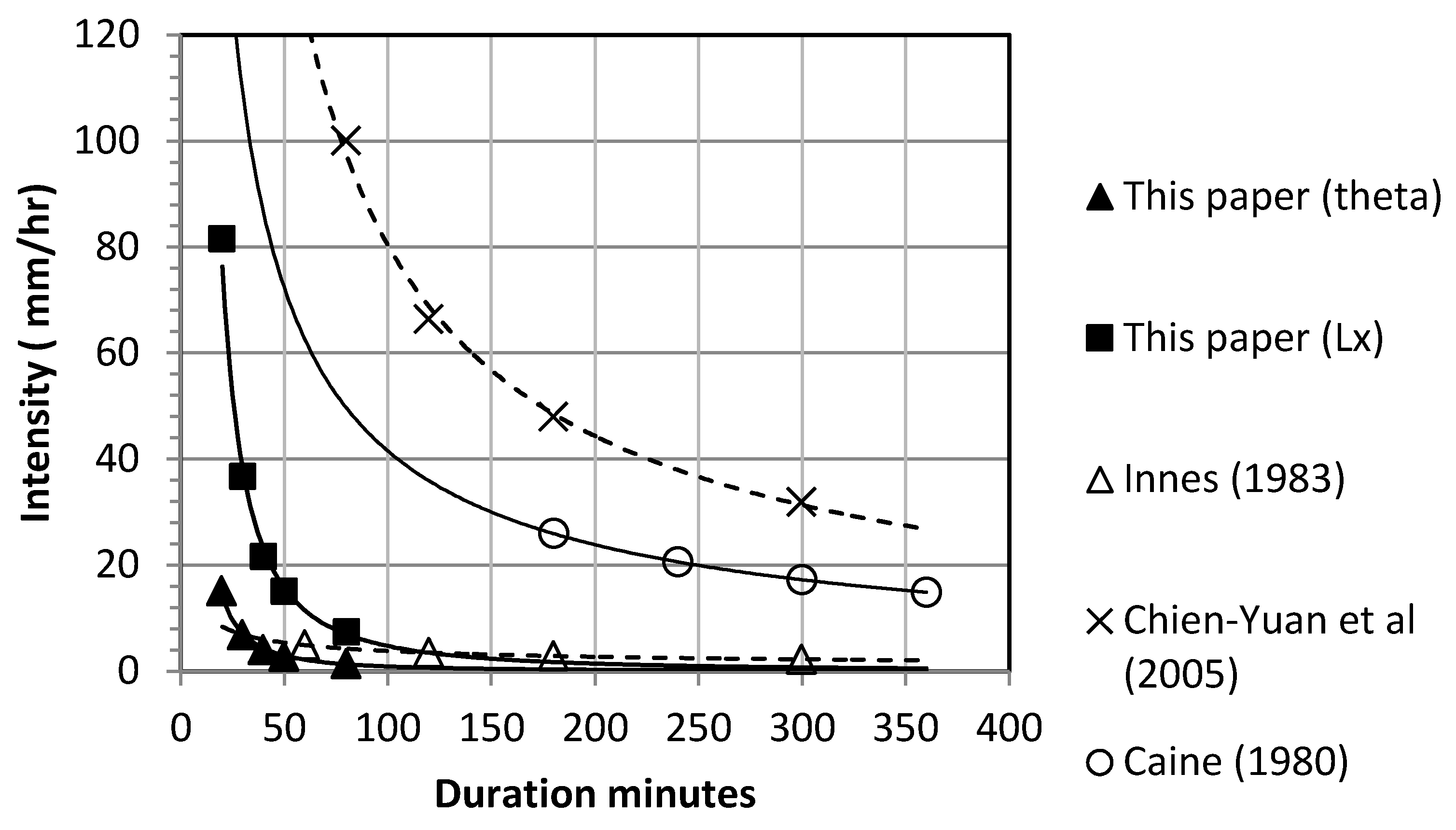
Figure 12 compares two extreme I-D curves [
37,
38], and one in between the two [
39] obtained worldwide with the two extreme curves produced in our simulation. The minimum curve in our simulation was related to the maximum channel slope (28°), and the maximum threshold curve was related to the largest length (
Lx) of the channel bed.
Figure 12 shows that a simple variation of parameters for the initiation of debris flows in channel beds of source areas, which gives already a significant range in variation compared to the range in threshold values for debris flows worldwide. The figure shows that, for reasons given above, our simulated curves are positioned in the lower part of the domain covered by all the curves obtained from different parts of the world.
We have shown in this section that the I-D curves for debris flows triggered by overland flow and bed failure are especially sensitive to the morphometric parameters of the source area and less sensitive to the hydro-mechanical parameters. The I-D curves for debris flows, triggered by the overland flow process are more sensitive to these parameters than the I-D curves related to the bed failure triggering process (compare
Figure 10 and
Figure 11). The sensitivity of these curves for these process parameters cover a range, which is quite significant compared with the ultimate range of I-D curves found worldwide.
7. Discussion
This paper unraveled the effect of different hydro-mechanical processes on the initiation of debris flows. It is focused on the initiation in channels and it gives a detailed insight in the influence of different hydro-mechanical process mechanisms in the source area on the type of debris flow initiation. It shows how the hydrologic conductivity (Ks) and slope gradient (θ) determine the sequence of various process mechanisms.
Our simulations suggest that the type of initiation and related factors have also a clear influence on the values of the I-D curve as shown in
Figure 10 and
Figure 11. These I-D curves, determined by our two simulated process mechanisms, Hortonian overland flow and bed failure show a relative quick response of debris flow initiation compared to what is generally provided by the literature. Our calculations were focused on the initiation of debris flows in the source area in channel beds surrounded by slopes with scarce vegetation and rather impermeable soils. A quick response (within one hour) was also observed by Berti [
24] where, as in our simulations, debris flows were initiated in the source area by the dominant effect of run-on water to the channel delivered by a bare, impermeable catchment upstream.
The assessment of rainfall threshold values for debris flow initiation are based in most cases on statistical empirical approaches using large data sets without detailed knowledge of the different triggering processes and its influencing factors [
2,
29]. Our quantitative approach to analyze the threshold conditions for debris flow initiation gives a more detailed insight in the effect of different parameters than the indicative parameters used in statistical techniques. Apart from the fact that no distinction is made in the mechanism of initiation, important morphometric characteristics, like channel width, slope, length, and thickness of bed material are ignored in most cases. As a consequence, the prediction of the probability debris flow initiation on the basis of rainfall for individual catchments can be very inaccurate. Further investigations must reveal the accuracy of both approaches to predict the initiation of debris flows.
The CN value, which we used in the simulation of overland flow on the contributing slopes, reflects in a lumped way the dynamic soil and land use characteristics. Especially the amount of storage of water before the time to ponding, and thus the estimate of the total overland flow production of a rain event can be rather inaccurate, especially for rain events with shorter durations. The use of a more detailed infiltration model incorporating the effect of the initial moisture content will give better predictions. However, in this paper we did not unravel in detail the effect of these soil and land use characteristics on threshold conditions for debris flow initiation, but used a constant CN value as input for the run-on simulation to the channel bed. Initial moisture conditions in the channel bed, which will affect the permeability and hence the boundary conditions for the initiation of overland flow were not considered either in this paper. The effect of the initial moisture content of the bed material is minor due to the large amounts of influx of water and the relative coarse material in the channel bed.
In this paper we mentioned the transport capacity of overland flow as a limiting factor for the initiation of debris flows. On slopes (<±16°) sediment concentrations are too low (<0.2) to call it a debris or hyper-concentrated flow. For these lower channel gradients we did not consider the effect of the delivery of extra material by side wall collapses and failure of landslide dams [
1,
13,
40], which may lead downstream to a rapid loading of the fluid and an instantaneous transformation into a debris flow
The initiation of debris flows by bed failure is also more complex since it depends on certain boundary conditions related to pore pressure development at failure and a large amount of runoff water, which must be supplied during failure to keep the material moving [
20,
22,
23,
41,
42].
It is interesting to analyze the potential in development further downstream of debris flows triggered by bed failure (BF-I) with high solid concentrations. On steeper slopes failure of the bed material occurs under lower groundwater heights (
hs), and therefore after failure much additional overland flow water is needed to maintain the movement further down slope. Important is also the mechanism of erosion and erosive power of both types of debris flows further downstream in order to grow to a mature debris flow [
6,
43,
44,
45,
46,
47].
8. Conclusions
We could distinguish in our flume tests three types of hydro-mechanical processes which may trigger debris flows in channel beds of first order source areas. These are erosion and transport by intensive Horton overland flow (ROh-I), saturation overland flow (ROs-I), and by infiltrating water causing failure of channel bed material (BF-I). On the basis of these flume tests, an integrated hydro-mechanical model was developed, which was calibrated and validated with a number of process indicators measured during the flume tests. We were able to assess by means of this model the influence of important parameters on the mode of debris flow initiation. The hydraulic conductivity of the bed sediments is an important factor controlling the type and sequence of processes triggering debris flows. At lower Ks values, Hortonian overland will be the first process to start debris flows followed by bed failure or saturation overland flow. At higher Ks values, triggering by Hortonian overland flow is not possible anymore in this relatively coarse bed material, and triggering by bed failure will be the dominant process if the slope gradient is steep enough (>16°). Therefore, the slope gradient of the channel bed is a second important factor controlling the type of hydro-mechanical triggering. On gentler slopes which remain stable under saturated conditions, saturation overland flow might create debris flows if slope gradient is not too gentle, and therefore sediment concentration too low to call it a debris flow.
We further analyzed also the effect of different important morphometric and hydro-mechanical parameters on meteorological thresholds for triggering debris flows by overland flow or bed failure, respectively. With respect to overland flow triggering, the morphometric factors related to the size of the source area and width and length of the channel bed have the largest influence on the position of the I-D curves. Meteorological thresholds for bed failure triggering are also sensitive to morphometric parameters while the hydro-mechanical parameters have relative less influence on these threshold values.