Hybrid Numerical Scheme of Preissmann Slot Model for Transient Mixed Flows

Abstract

The Preissmann slot model is one of the most widely used models to conceptualize both free-surface and pressurized flows in urban drainage systems. Despite its simplicity and wide range of applications, numerical solutions of the Preissmann slot model suffer from the spurious oscillations, especially when flow conditions switch from free-surface flow to pressurized flow. To overcome this problem, a new hybrid numerical flux solver of the Preissmann slot model is proposed herein, in which the upwind flux solver is combined with the centered flux solver. Numerical experiments are conducted for multiple flow conditions such as typical filling, pipe-filling, and transition-flow conditions. The numerical results indicate that the proposed scheme generally outperforms the conventional flux schemes for various hydraulic conditions and wave velocities. The proposed scheme should be useful to further enhance integrated urban water modeling in which transient mixed flow conditions significantly impact the simulation accuracy during extreme floods.

1. Introduction

Numerical modeling of sewer-pipe flow is of significant importance for a wide range of urban water problems such as urban inundation analysis, detecting the damage of a sewer pipe, or design of the sewer system. The type of flows in a sewer-pipe system is a free-surface flow but, during extreme flood events, it often becomes a partly free surface, partly pressurized flow (mixed flow) or fully pressurized flow. The numerical modeling of transient mixed flows is associated with infrastructure damage or operational problems. However, it is difficult to find a straightforward way because two different flow regimes should be considered in the same domain. When using two governing equations, it is difficult to track the mixed flow interfaces and switch smoothly between the two systems. Previous research [1,2] has shown that a compressible one-dimensional fluid equation with a linearized pressure law is an attractive alternative for modeling of transient mixed flows in pipe; however, a compressible fluid system is more complex to solve than a one-dimensional shallow water system usually used to represent open channel flows. The Preissmann slot model can avoid this difficulty and has been widely used to solve multiple flow conditions in sewer systems [3,4,5,6,7,8,9].

Unfortunately, the Preissmann slot model suffers from the spurious oscillations when the flow condition switches from open-channel flow to pressurized flow [10]. The conventional remedy for this problem is to reduce the impact of the acoustic-wave velocity by increasing the slot width [11,12]. However, this remedy can reduce the accuracy of the numerical solution because of the wider slot width and lower wave speed compared with the physical values. [13] presents an exact Riemann flux solver of the Preissmann slot model for highly transient mixed flows. However, the exact Riemann flux solver is not practical because it requires a large amount of computation for the iteration procedure. In addition, this method could not fully remove the spurious oscillations [6]. Ref. [3] proposed two methods based on the Roe’s flux scheme to prevent spurious oscillations. The first method is to introduce the artificial viscosity, which gradually increases with respect to the wave velocity. The second method uses the numerical filter to smooth variables such as water depth and momentum across the cells. Although both two methods can reduce the numerical oscillation within a certain level and stabilize the numerical results, oscillations can still be significant even with a comparatively moderate acoustic-wave speed of 100 m/s [14]. Leon [15] proposed a funnel-shaped slot to alleviate the abrupt change of wave velocity and the modified-shaped slot resulted in nonoscillatory solutions. However, this method is specifically tailored for a pipe with circular cross section. Malekpour and Karney [10] investigated the source of the spurious oscillation and proposed the modified Harten–Lax–van Leer (HLL) flux estimation based on the HLL flux proposed by Leon [15]. Their method removes the spurious oscillations even with acoustic-wave speed as high as 1000 m/s and produces accurate results for a wide range of cases. However, it requires tuning two additional parameters for each case, which may hinder the general application of this method.

The formulation of boundary conditions is also not a trivial issue in numerical modeling of sewer-pipe systems. The treatment of boundary conditions is strongly associated with the stability and accuracy of the numerical solution. Recently, ref. [16] presented a robust formulation that can represent a wide range of boundary conditions such as drop shafts, reservoirs, junctions, and dead ends. They considered common boundaries as junctions connected to an arbitrary number of pipes, and their method works well for a wide range of problems. However, equations for the implicit nonlinear system must be solved at each junction for each time step, which is not an easy task and may be an obstacle to applying this method.

In a general sense, the numerical flux solver for hyperbolic conservation laws can be categorized as either an upwind scheme or a centered (symmetric) scheme [17,18]. The upwind flux solvers, also called “Godunov-type schemes” or “approximated Riemann flux solvers,” are based on Riemann approaches or the equivalent and are suitable for capturing sharp water profiles such as shocks. Because of their superior performance, the upwind flux solver has been preferred over general hyperbolic conservation systems such as compressible flow, hydrodynamics systems, and shallow water systems, etc. [3,13,16,19,20,21]. However, for the Preissmann slot model, the monotonicity is not guaranteed by the widely used Riemann flux solvers because of the highly irregular shapes of pipes connected to the hypothetical slot, as presented in numerous previous works [5,10,22], whereas it is preserved for a regular-shaped flow domain. Conversely, the centered flux schemes are more diffusive than the upwind flux schemes, although they often over-smooth the water profile. The present study is based on the simple idea that a more diffusive flux solver may be required when flow is near the conduit roof [10,14].

The objective of this study is to develop a new hybrid numerical scheme of the Preissmann slot model and, through numerical experiments, demonstrate its applicability for a wide range of transient mixed-flow conditions. To achieve a more stable and accurate numerical scheme, the hybrid scheme combines both the upwind flux solver and the centered flux, although the proposed scheme is more than a combination of existing schemes. We also propose a modified formulation for boundary conditions, originally developed by [16,23], to explicitly compute the junction boundary. Numerical experiments are conducted to demonstrate the improved performance of the proposed method over conventional schemes for multiple flow conditions such as typical filling (Test 1), pipe-filling (Test 2), and transition-flow conditions (Test 3).

2. Numerical Model

2.1. Governing Equation

The hyperbolic conservative form of the continuity and momentum equations of free surface flow in uniform open channels and pipes can be written as follows:

$$\frac{\partial U}{\partial t}+\frac{\partial F}{\partial x}=S,$$

(1)

where $U$, $F$, and $S$ are vectors representing flow variables, fluxes, and source terms, respectively. These terms are written as follows:

$$U=\left[\begin{array}{c}A\\ Q\end{array}\right],F=\left[\begin{array}{c}Q\\ \frac{Q^2}{A}+\frac{A\overline{p}}{\rho }\end{array}\right],S=\left[\begin{array}{c}0\\ gA\left(S_0-S_f\right)\end{array}\right],$$

(2)

where $A$ is the flow cross-sectional area, $Q$ is the flow discharge, $\overline{p}$ is the average pressure over the flow cross-sectional area, $\rho$ is the density of water, g is the acceleration due to gravity, $S_0$ is the slope of the pipe, and $S_f$ is the energy slope, which can be expressed by Manning’s formula as follows:

$$S_f=\frac{{n_m}^{2}Q\left|Q\right|}{A^2{R}^{4/3}},$$

(3)

where $R$ is hydraulic radius and $n_m$ is Manning’s coefficient. Note that the friction surface on a slot is ignored following a basic assumption of Preissmann slot model [15].

The pressure head of pressurized flow is conceptualized as the open-channel flow depth in the Preissmann slot model. Because the acoustic-wave velocity is hypothetically equivalent to the velocity of a gravity wave, the slot width is $T_s=g{A}_f/a^2$, where $A_f$ is the conduit cross-sectional area and $a$ is the acoustic-wave velocity of the pipe.

Equation (1) can be discretized by the finite volume and forward Euler method as follows:

$$U_i^{n+1}=U_i^n-\frac{\Delta t}{\Delta x}\left(F_{i+1/2}^n-F_{i-1/2}^n\right)+\Delta t{S}^n,$$

(4)

where the superscript n is the time-step index, the subscript i is the index for the ith computational cell, $\Delta t$ is the time step, $\Delta x$ is the length of a computational cell, and $F_{i+1/2}$ is the numerical flux between cells i and i + 1.

The numerical flux function $F_{i+1/2}\left(U_L,U_R\right)$ is estimated by using $U_L=U_i$ and $U_R=U_{i+1}$ in the spatially first-order finite-volume numerical scheme with piecewise constant variable in the cell, where $U_L$ and $U_R$ represent the left and right variable vectors at cell-interface i + 1/2. The values of $U_L$ and $U_R$ can be reconstructed for the higher-order spatial estimate. Here, we consider the total variation diminishing scheme with piecewise linear distribution of variables. The $U_L$ and $U_R$ are reconstructed as

$$U_L=U_i+\frac{1}{2}\phi \left(r_i\right)\Delta U_{i-1/2},U_R=U_{i+1}-\frac{1}{2}\phi \left(r_{i+1}\right)\Delta U_{i+1/2},$$

(5)

where

$$\Delta U_{i-1/2}=U_i-U_{i-1},\Delta U_{i+1/2}=U_{i+1}-U_i,r_i=\frac{\Delta U_{i+1/2}}{\Delta U_{i-1/2}},r_{i+1}=\frac{\Delta U_{i+3/2}}{\Delta U_{i+1/2}},$$

(6)

and $\phi$ is a slope-limiter function. Among the variety of slope-limiter functions, the minmod limiter is used herein for stability. The minmod limiter is

$$\phi \left(r\right)=\max \left[0,\min \left(r,1\right)\right].$$

(7)

Note that the minmod limiter is the most diffusive and stable limiter.

2.2. Upwind Flux Solver

The Riemann flux solver for the Godunov-type numerical scheme is constructed based on an analysis of the eigenstructure of the system. Since an exact Riemann flux solver is impractical because of its high computational cost, an approximate Riemann flux solver should be used in practical applications [24]. In this study, we consider Roe’s flux and HLL flux schemes.

Roe’s flux scheme determines the approximate solution by solving a constant-coefficient linear system instead of the original nonlinear system. The system of Equation (1) is linearized as

$$\frac{\partial U}{\partial t}+\widehat{J}\left(U_L,U_R\right)\frac{\partial U}{\partial x}=S,$$

(8)

where $\widehat{J}$ is a Jacobian matrix at inter-cells and is assumed constant between two cells. The Riemann problem can then be solved as a linear hyperbolic system at each cell interface as

$$F_{i+1/2}^{\mathrm{Roe}}=\frac{1}{2}\left(F_L-F_R\right)-\left|\widehat{J}\left(U_L,U_R\right)\right|\left(U_R-U_L\right),$$

(9)

$$\widehat{J}\left(U_L,U_R\right)=R\left(U_L,U_R\right)\cdot \left|\Lambda \left(U_L,U_R\right)\right|\cdot R^{-1}\left(U_L,U_R\right),$$

(10)

where $R$ is the eigenvector matrix and $\Lambda$ is the diagonal corresponding eigenvalue matrix. The final stage of the algorithm is to find a suitable average interface state to determine $\widehat{J}$. As long as the space of the numerical solution is smooth, any reasonable average would probably give the right results. However, when discontinuities or shocks are present in the solution, the estimate of the average interface states becomes very important to find the right solution. Here, we use the average interface state as follows:

$$\overline{A}=\sqrt{A_L{A}_R},\overline{Q}=\frac{\sqrt{A_R}{Q}_L+\sqrt{A_L}{Q}_R}{\sqrt{A_R}+\sqrt{A_L}},\overline{c}=\sqrt{g\frac{I_R-I_L}{A_R-A_L}}$$

(11)

where $c$ is the gravity wave velocity and $I=Ay$.

In the HLL approach, the solution of the Riemann problem is approximated by an intermediate region $U_{\ast }$, which is the constant state separated from the left and right states $U_L$ and $U_R$ by two infinitely thin shock waves. The numerical flux $F_{i+1/2}$ is computed by the HLL flux solver as follows:

$$F_{i+1/2}^{\mathrm{HLL}}=\{\begin{array}{cc}{F}_L& \mathrm{if}{S}_L>0,\hfill \\ \frac{S_R{F}_L-S_L{F}_R+S_L{S}_R\left(U_R-U_L\right)}{S_R-S_L}& \mathrm{if}{S}_L\le 0\mathrm{and}{S}_R\ge 0,\hfill \\ F_R& \mathrm{if}{S}_R<0,\hfill \end{array}$$

(12)

where $F_L$ and $F_R$ represent left and right flux vectors at cell-interface i + 1/2, respectively, and $S_L$ and $S_R$ left and right wave speeds, which are calculated as follows [15]:

$$S_L=u_L-M_L,S_R=u_R-M_R$$

(13)

where $u_L$ and $u_R$ are left and right flow velocities, respectively, and $M_K(M=L,R)$ is

$$M_K=\{\begin{array}{cc}\sqrt{\left(\frac{A_{\ast }{\overline{p}}_{\ast }}{\rho }-\frac{A_K{\overline{p}}_K}{\rho }\right)\frac{A_{\ast }}{A_K\left(A_{\ast }-A_K\right)}}& {\mathrm{if}\mathrm{A}}_{\ast }{\text{>}}_K\hfill \\ c_K& \mathrm{otherwise}\hfill \end{array}$$

(14)

where the subscript “*” represents the star (intermediate) region and both $A_{\ast }$ and ${\overline{p}}_{\ast }$ are the functions of flow depth of the star region ($y_{\ast }$). The variables of the star region can be estimated from the characteristic of the system. Ref. [1] suggests several different approaches for approximating $y_{\ast }$ based on two shock-wave approximations, two rarefaction-wave approximations, and the linearization of the governing equations. For example, the estimate based on the linearized governing equation is

$$A_{\ast }=\frac{A_R+A_L}{2}+\frac{\overline{A}}{2\overline{c}}\left(u_L-u_R\right),$$

(15)

where $\overline{A}=\left(A_R+A_L\right)/2$ and $\overline{c}=\left(c_R+c_L\right)/2$. However, in our experience all three approaches mentioned above result in spurious oscillations when the flow switches from open-channel flow to pressurized flow, which is consistent with the observation of [4]. They investigated the effect of Equation (15) and concluded that the intermediate state could be adjusted to admit optimal numerical viscosity. They proposed following the adjusted estimate of star region flow depth as follows:

$$y_{\ast }=K_a\max \left[y_{i-NS},y_{i-NS+1},\dots ,y_{i-1},y_i,y_{i+1},\dots ,y_{i+NS-1},y_{i+NS}\right],$$

(16)

where $K_a$ and $NS$ are parameters that must be tuned empirically. The problem of Equation (16) is that both parameters significantly affect the performance of the numerical scheme and should be calibrated for each case. Unlike the experiment, there usually is no reference data in an actual sewer network, which can significantly hinder the practical application of Equation (16). Therefore, the method proposed by [4] is not considered herein.

2.3. Centered Flux Solver

The main feature of the centered scheme lies in its simplicity. This scheme does not require explicit knowledge of the eigenstructure of the system, nor the availability of a Riemann solver. The classical centered schemes include the Lax–Wendroff (LW) scheme and the Lax–Friedrichs (LF) scheme. The two-step version of the Lax–Wendroff scheme is

$$F_{i+1/2}^{\mathrm{LW}}=F\left(Q_{i+1/2}^{\mathrm{LW}}\right),Q_{i+1/2}^{\mathrm{LW}}=\frac{1}{2}\left(Q_i^n+Q_{i+1}^n\right)-\frac{1}{2}\frac{\Delta t}{\Delta x}\left(F\left(Q_{i+1}^n\right)-F\left(Q_i^n\right)\right).$$

(17)

The Lax–Friedrichs scheme is

$$F_{i+1/2}^{\mathrm{LF}}=\frac{1}{2}\left(F\left(Q_i^n\right)+F\left(Q_{i+1}^n\right)\right)-\frac{1}{2}\frac{\Delta x}{\Delta t}\left(Q_{i+1}^n-Q_i^n\right).$$

(18)

Note that the two-step version of LW scheme was derived by estimating intermediate variables at n + 1/2 from LF scheme. Therefore, it is a second-order method in temporal and different with the first-order forward Euler method. Although these two schemes are pioneering works in the centered scheme, they are not suitable for a modern finite-volume numerical scheme. The LW scheme does not preserve monotonicity and often results in spurious oscillations. The LW scheme, however, usually results in excessively diffusive numerical solutions. Vasconcelos et al. [25] pointed out that the LF scheme is not appropriate for flow regime transition problems because a huge difference in the wave velocities before and after the shock front results in very small Courant numbers in the free-surface portion of the flow, which in turn exacerbates the diffusive nature of the LF scheme and compromises the representation of the pipe-filling bore.

The first-order centered (FORCE) flux, proposed by Toro and Billett [26], is another option for a centered scheme. The FORCE flux is derived as the deterministic version of the staggered-grid random choice method, and the FORCE flux is an arithmetic mean of the LF and LW fluxes:

$$F_{i+1/2}^{\mathrm{FO}}=\frac{1}{2}\left(F_{i+1/2}^{\mathrm{LW}}+F_{i+1/2}^{\mathrm{LF}}\right).$$

(19)

The FORCE flux is less diffusive than the conventional LF scheme and it preserves the monotonicity. It was applied to Euler and molecular hydrodynamics equation, and the high-order extension of the FORCE scheme was also presented on two-dimensional unstructured meshes by Toro et al. [17].

Because the centered flux schemes are more diffusive than the upwind flux schemes, we expect the spurious oscillations to be reduced by the centered flux schemes. However, the diffusive flux schemes may affect the numerical accuracy whereas the upwind schemes usually do not result in spurious oscillations when the flow depth is lower than the conduit roof. Therefore, the following simple hybrid flux is proposed:

$$F_{i+1/2}^{\mathrm{Hybrid}}=\{\begin{array}{cc}{F}_{i+1/2}^{\mathrm{FO}}& \hfill \mathrm{if}\left(y_L-D\right)\left(y_R-D\right)<0,\\ F_{i+1/2}^{\mathrm{HLL}}& \hfill \mathrm{otherwise}.\end{array}$$

(20)

where D is the height of pipe. The strategy of the hybrid scheme is straightforward: FORCE flux is implemented only if the flow switches from the open-channel flow to the pressurized flow; otherwise, HLL flux is implemented.

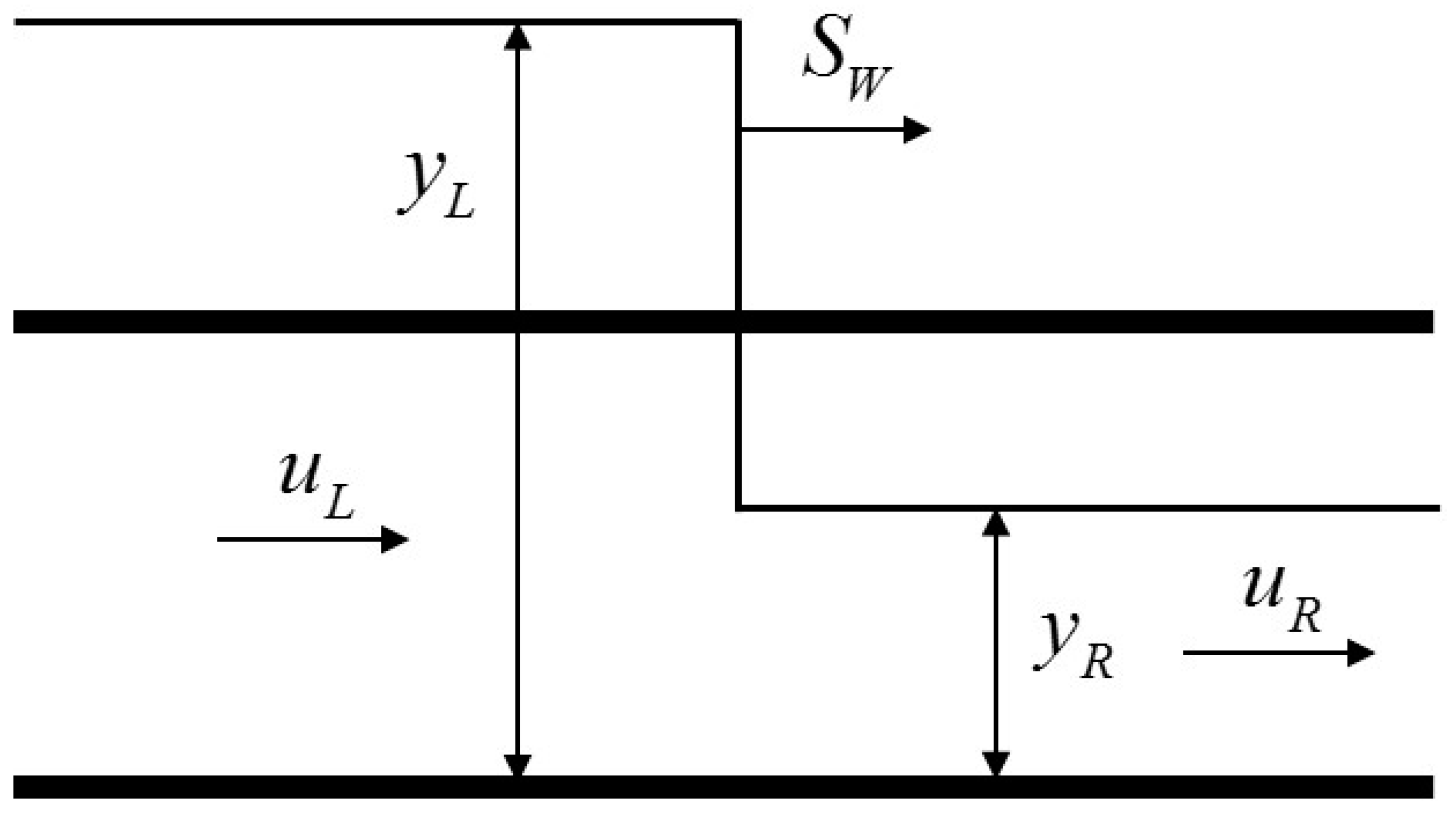
2.4. Boundary Computation

Various types of boundaries should be considered for a typical storm-sewer system. These include drop shafts, reservoirs, junctions, dead ends, and control gates, etc. Leon et al. [27] generalized the various types of boundary conditions as an N-way junction problem. In general, 2N + 1 variables are unknown for an N-way junction; namely, the piezometric depth y_b and the flow discharge Q_b at each pipe boundary, and the water depth y_d at the junction pond. Therefore, 2N + 1 equations must be solved for an N-way junction. The first equation is obtained from the Riemann invariants between the pipe boundary and the neighboring cell as $du\pm \left(c/A\right)dA=0$. The Riemann invariants are solved as follows Leon et al. [27]:

$$u_{b_j}^{n+1}-u_{b_j}^n\pm \left(c_{b_j}^{n+1}+c_j^n\right)\frac{A_{b_j}^{n+1}-A_j^n}{A_{b_j}^{n+1}-A_j^n}=0,$$

(21)

where the positive (negative) sign is used for inflowing (outflowing) pipes, the subscript b refers to the boundary, and j is the pipe index.

The second equation is usually given by the following energy equation:

$$y_b^{n+1}-y_p^{n+1}+\frac{{\left(u_{b_j}^{n+1}\right)}^2}{2g}\mp k_j\frac{u_b^{n+1}\left|u_b^{n+1}\right|}{2g}=0,$$

(22)

where k is the local head-loss coefficient and the subscript p is the depth of the junction pond. When the inflowing pipe is decoupled from the junction, the different boundary conditions can be used as presented in Leon et al. [27].

The last equation is given by the mass-balance equation of the junction pond:

$$A_p\frac{\partial y_p}{\partial t}={\displaystyle \sum _j^N{A}_{b_j}{u}_{b_j}},$$

(23)

where A_p is the vertical cross-sectional area of the junction pond. Leon et al. [27] used the backward Euler method to discretize Equation (24) as follows:

$$A_p\frac{y_p{}^{n+1}-y_p{}^n}{\Delta t}={{\displaystyle \sum _j^N\left(A_{b_j}{u}_{b_j}\right)}}^{n+1}$$

(24)

The combination of Equations (21), (22) and (24) can represent wide range of boundary conditions such as drop shafts, reservoirs, junctions, and dead ends, as has been verified through several test problems. However, this approach requires 2N + 1 nonlinear equations to be solved at a junction in an implicit manner. The convergence of the nonlinear system could be difficult to achieve for a large number of connected junctions. To avoid this difficulty, the above approach is modified in this study. The explicit form of Equation (25) is

$$A_p\frac{y_p{}^{n+1}-y_p{}^n}{\Delta t}={{\displaystyle \sum _j^N\left(A_{b_j}{u}_{b_j}\right)}}^n$$

(25)

Note that Equation (25) is derived from Equation (23) by using the forward Euler method. This simple change makes the problem much easier. Equation (25) can be solved separately, so the boundary conditions at each pipe can be solved in separate manner.

3. Numerical Results

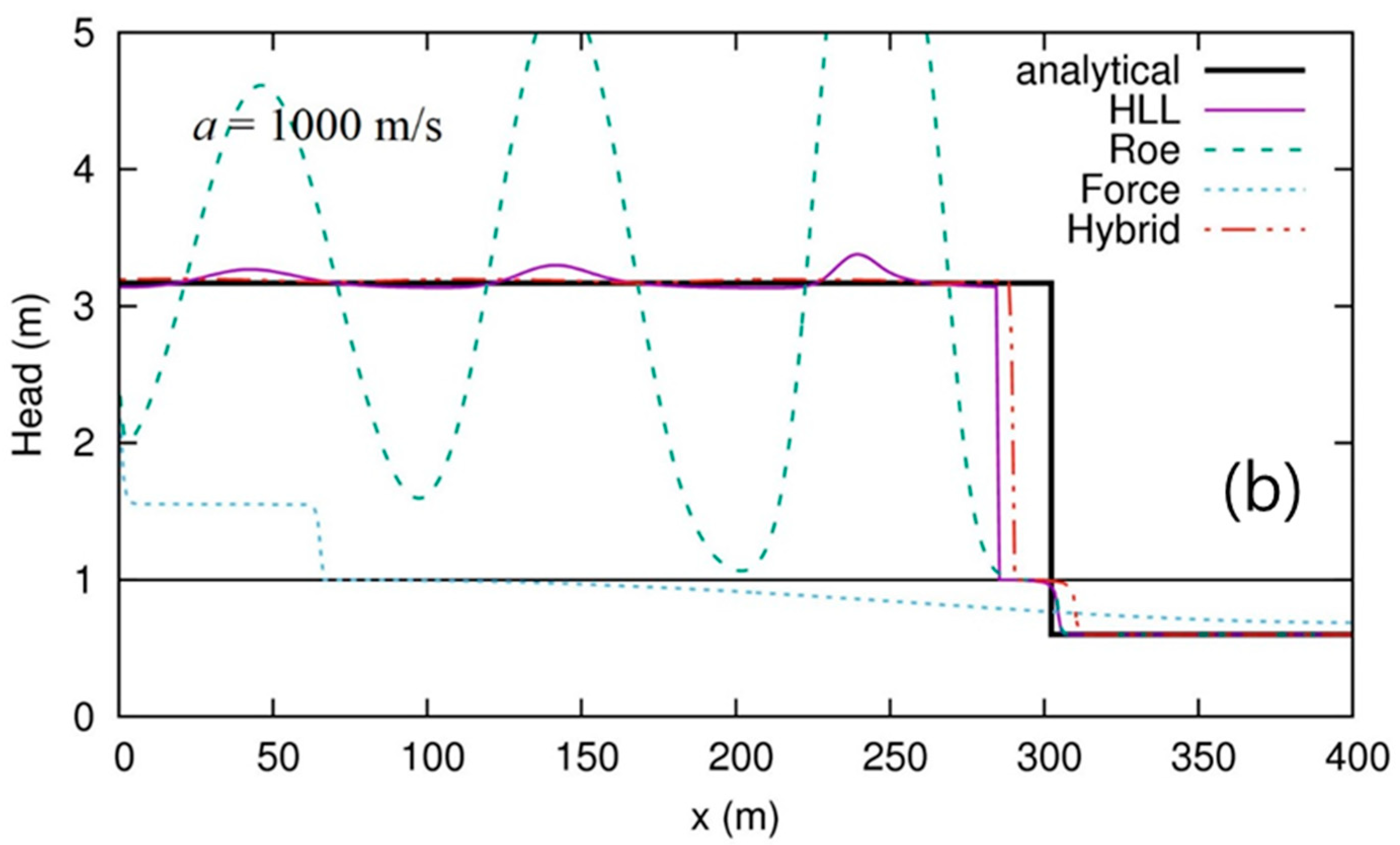
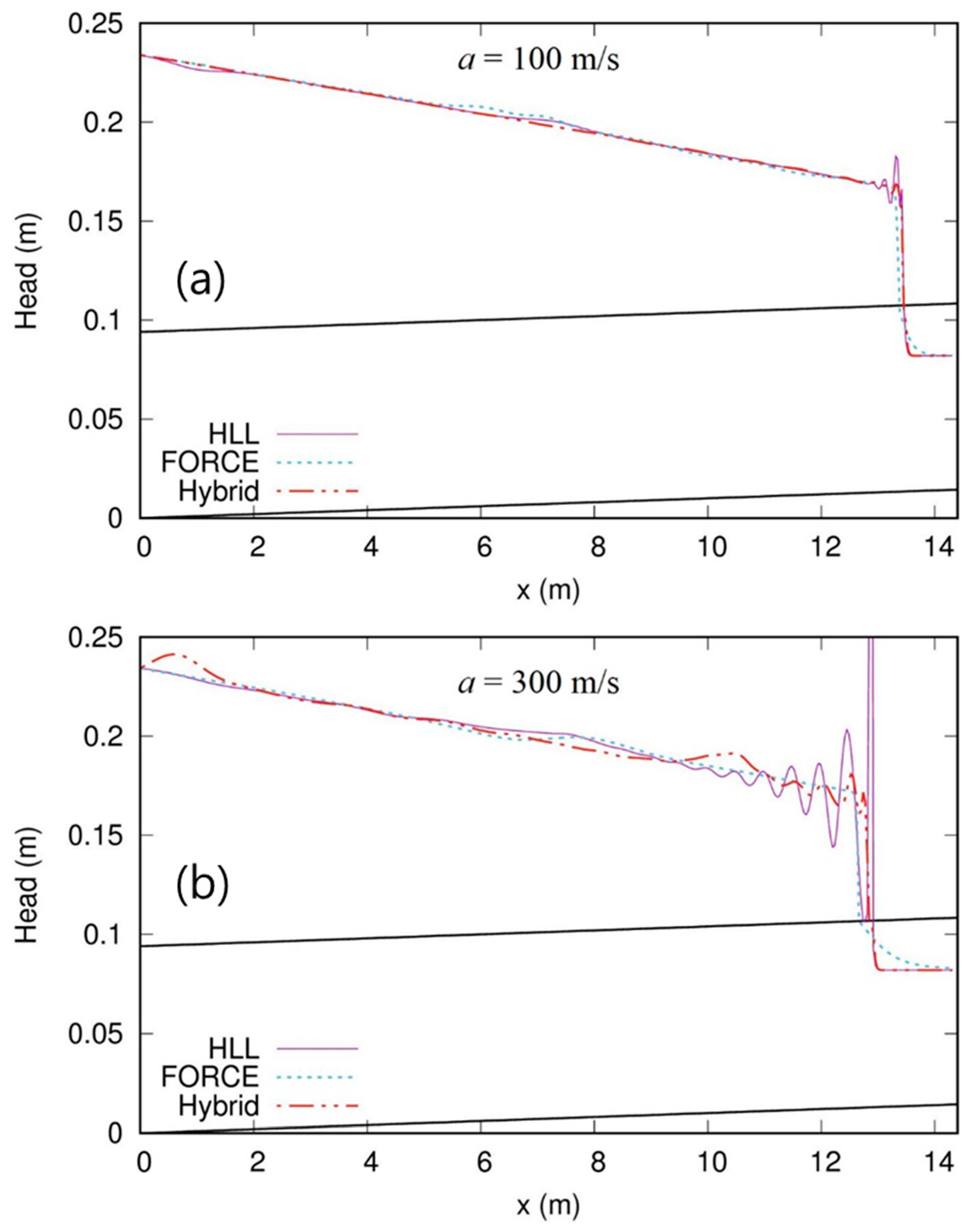
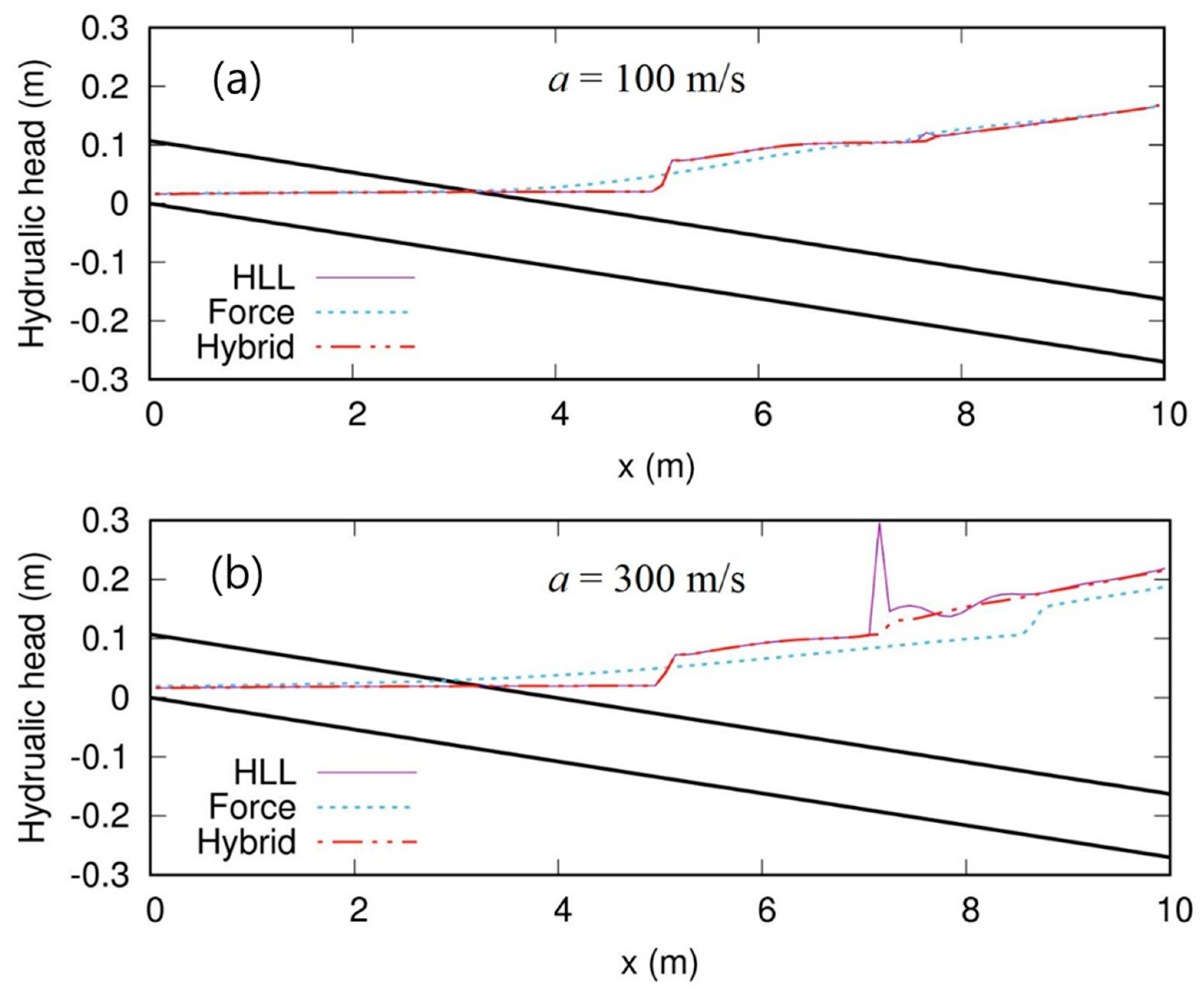
3.1. Test 1: Typical Filling Bore Problem

For Test 1, a typical filling bore problem with an analytical solution, introduced by Malekpour and Karney [10], is used to understand the cause of the numerical oscillations. Figure 1 shows the description of typical filling bore problem and details regarding the experiments process can be found in Malekpour and Karney [10]. With the condition $y_R=0.6\mathrm{m}$ and $u_R=0$, the analytical solution can be obtained by using the traveling-wave method as $S_W=10.077\mathrm{m}/\mathrm{s}$, $u_L=4.044\mathrm{m}/\mathrm{s}$, and $y_L=3.167\mathrm{m}$.

The Courant–Friedrichs–Lewy (CFL) number is set to 0.5 and two acoustic-wave velocities ($a=100,1000\mathrm{m}/\mathrm{s}$) are considered to estimate the performance of numerical schemes with relatively low and high values of wave velocity. The number of numerical cells is 400, as used in the study of Malekpour and Karney [10]. The values at intermediate region for HLL scheme are estimated by Equation (15) for all test problems in this paper.

Figure 2 compares the analytical solution with the numerical solutions computed by HLL, Roe, FORCE, and hybrid flux schemes using the spatially first-order piecewise constant variables in cells. Both upwind schemes, HLL and Roe, produce spurious oscillations near the shock-wave front whereas FORCE and hybrid schemes do not. In particular, the Roe scheme produces the most significant oscillations for both cases with $a=100,1000\mathrm{m}/\mathrm{s}$, presumably because it is the least diffusive of the four flux schemes while preserving the sharp water profile near the shock-wave front. Conversely, the FORCE scheme produces a smoothed water profile compared with the other flux schemes. Over-smoothing of the water profile becomes more significant when a higher acoustic-wave velocity, $a=1000\mathrm{m}/\mathrm{s}$, is applied. Smoothed hydraulic-head profiles are also found in the other three schemes with high acoustic-wave velocity near the shock-wave front, although the magnitude of over-smoothing is smaller than those of FORCE. This result implies that the high acoustic-wave velocity in the Preissmann slot model may cause not only the computational instability but also the reduced accuracy in a practical aspect. Overall, of the four flux schemes, the proposed hybrid scheme performs the best.

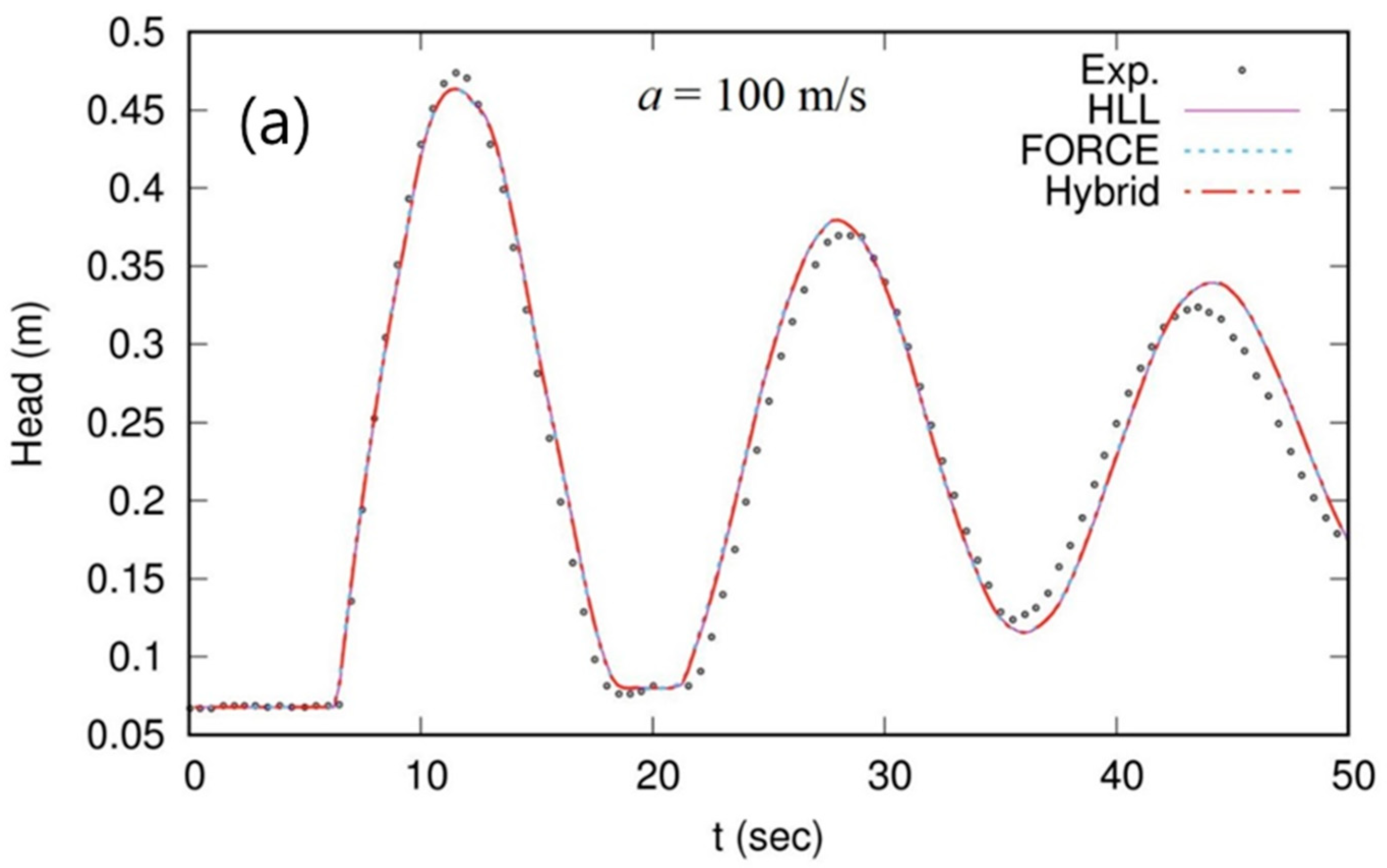
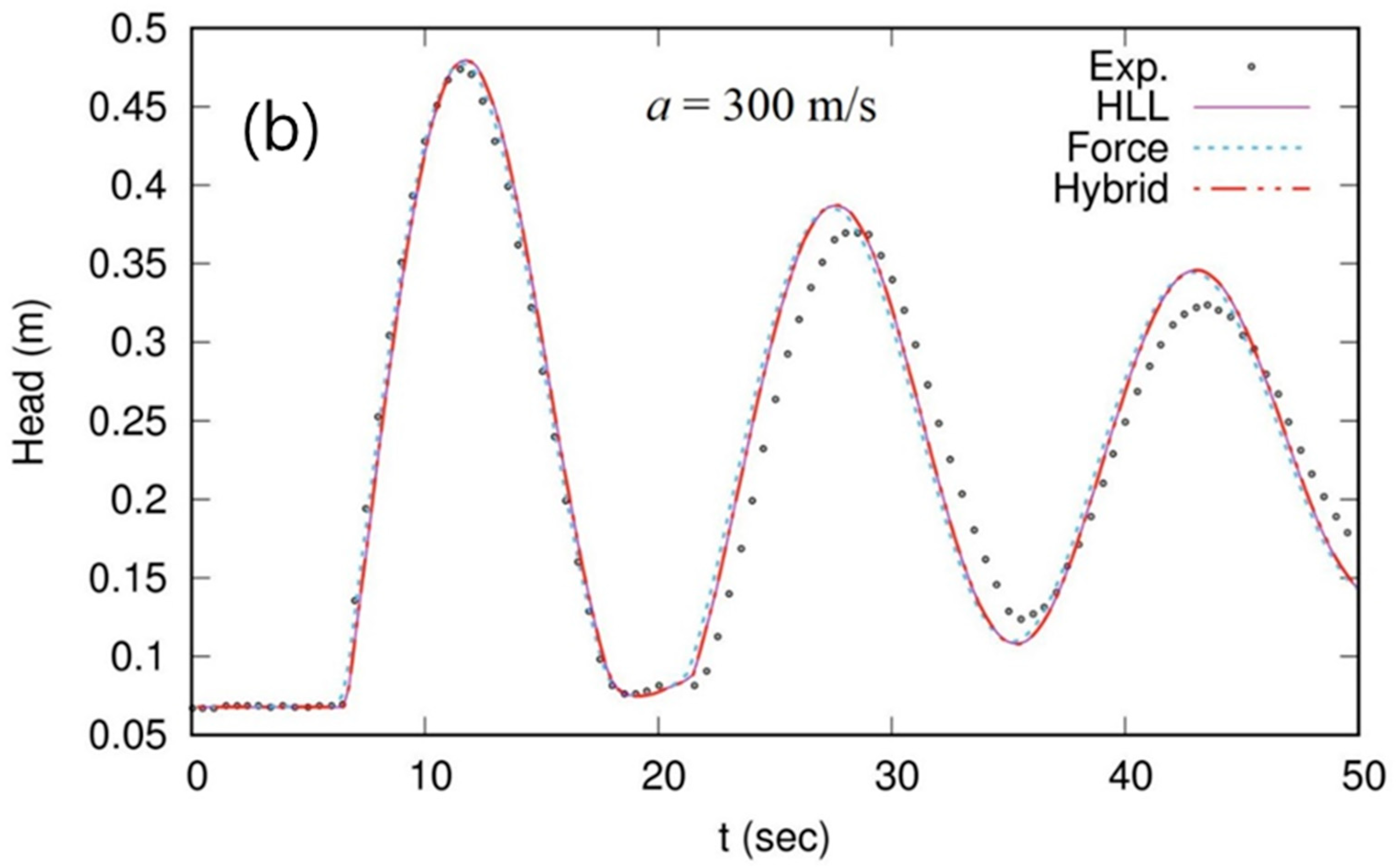
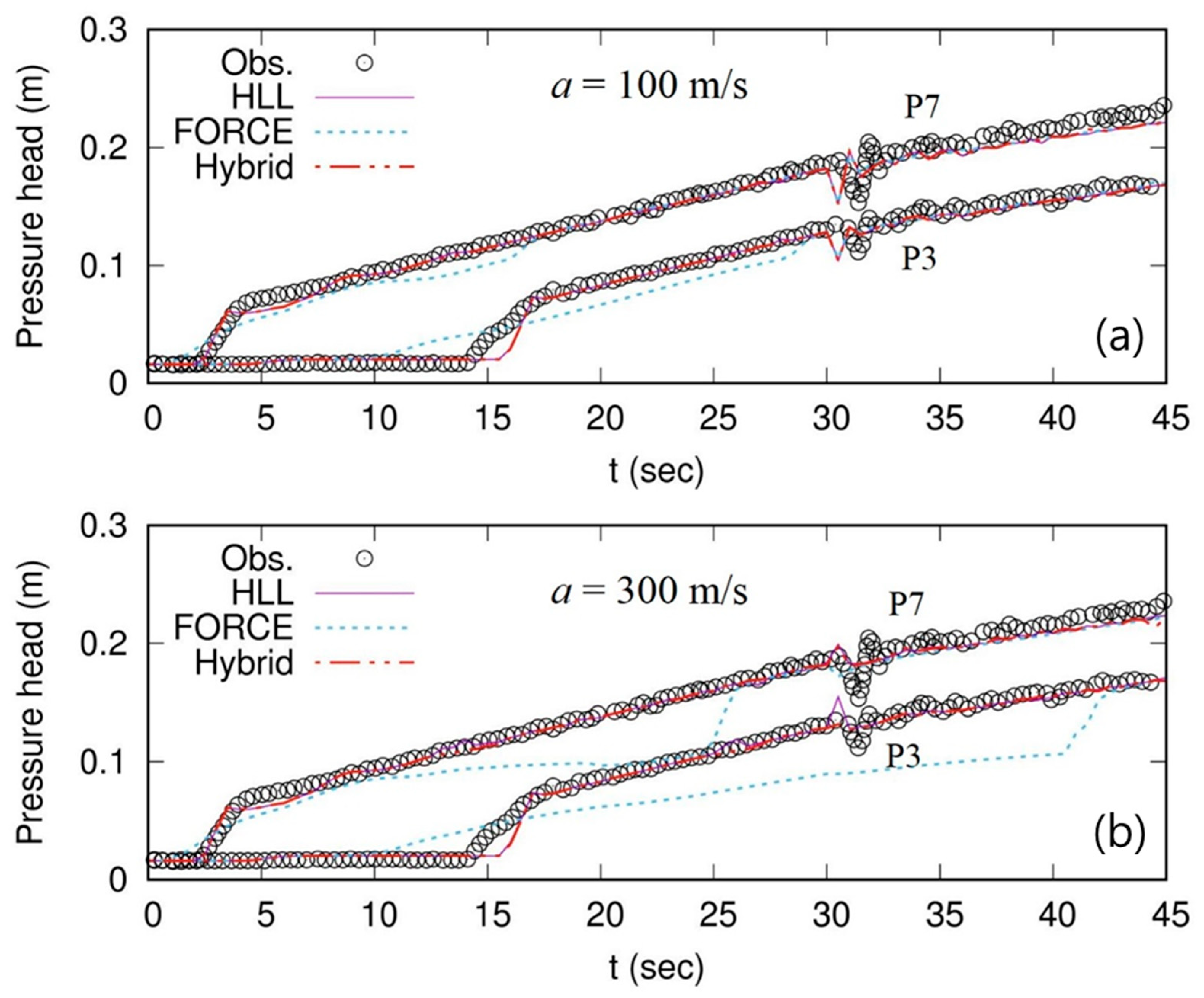
3.2. Test 2. Pipe-Filling Bore Experiment

For Test 2, a laboratory experiment performed by Vasconcelos and Wright [25] is used to compare the performance of the numerical schemes. Figure 3 shows the temporal variations of the observed and simulated water levels at the downstream tank. All numerical flux schemes reproduce the observed phenomena of the experiment except for the Roe flux scheme. The Roe flux scheme fails to reproduce this experiment because of the instability caused by spurious oscillations. Figure 4 compares the hydraulic-head profiles obtained from different flux schemes at 6 s. Apparently, the HLL scheme causes the most spurious oscillations of the three flux schemes. The spurious oscillation is more significant with $a=300\mathrm{m}/\mathrm{s}$ than with $a=100\mathrm{m}/\mathrm{s}$. The FORCE scheme produces the most stable results but the profile is over-smoothed near pipe-filling bores as compared with the other two flux schemes. The hybrid scheme has the best result with $a=100\mathrm{m}/\mathrm{s}$ whereas it suffers from spurious oscillations with $a=300\mathrm{m}/\mathrm{s}$. Note that the FORCE scheme, which is the most diffusive flux scheme of the three schemes, also produces spurious oscillations with $a=300\mathrm{m}/\mathrm{s}$. The results of this study are comparable to Figure 7(A) in Vasconcelos et al. [14]. Their results, obtained by using a modified Roe scheme, are more oscillatory than the results presented herein. Although the spurious oscillations are not perfectly removed in the case of high acoustic-wave velocity, the hybrid scheme performs satisfactorily for all cases in Test 2.

3.3. Test 3: Transition Flows in Pipe Experiment

The laboratory experiment, conducted at the Hydraulics Laboratory of the University of Calabria by Trajkovic et al. [12], is used for Test 3. This experiment evaluates how rapid changes affect the opening or closing of the sluice gates. In this study, we simulate the type-A set of experiments of Trajkovic et al. [12]. The initial condition for the experiment is an inflow rate of 0.0013 m³/s. The downstream sluice gate is totally opened, and the upstream sluice gate is opened by 0.014 m. A transient flow is generated after the downstream sluice gate is rapidly closed. Thirty seconds after the gate closes, the gate is partially reopened by 0.008 m. The pressure head appears 4.6 and 0.6 m upstream from the downstream sluice gate. The CFL number is set to 0.5 and two acoustic-wave velocities ($a=100,300\mathrm{m}/\mathrm{s}$) are considered to estimate the performance of the numerical schemes with relatively low and high wave velocity. The number of numerical cells is 100.

Figure 5 shows the observed and simulated pressure head 4.6 and 0.6 m upstream from the downstream sluice gate. The results of the HLL and hybrid schemes match well with the observed data overall whereas the FORCE scheme does not reproduce the observed pressure heads, even with a relatively low acoustic-wave speed $a=100\mathrm{m}/\mathrm{s}$. We hypothesize that the FORCE scheme is too diffusive to capture a filling bore propagation to a satisfactory level for this problem. The effect of the diffusive numerical flux is more significant when high acoustic-wave speed is adopted, which is also shown in Test 1. Figure 6 shows the hydraulic-head profile at 30 s. The HLL and hybrid scheme produce very similar profiles with $a=100\mathrm{m}/\mathrm{s}$. However, the HLL scheme causes significant spurious oscillations with $a=300\mathrm{m}/\mathrm{s}$ at x = 7.5 m, whereas the hybrid scheme does not. For both cases, the FORCE scheme produces diffusive filling bore profiles. Although the acoustic-wave speed of 1000 m/s is also tested, the results are not presented here because all numerical schemes fail to simulate due to spurious oscillations. Note that the hybrid scheme proposed herein can, to a certain degree, alleviate the instability from spurious oscillations, but the very high acoustic-wave speed of over 1000 m/s still can cause numerical instability, depending on the situation.

4. Conclusions

We propose a hybrid flux solver of the Preissmann slot model and evaluate it for the improved numerical analysis of transient mixed flows in sewer-pipe systems. The new hybrid scheme combines the upwind flux solver and the centered flux solver to exploit the benefits of the two different approaches. A modified treatment scheme for general boundary conditions, such as junctions, which was originally developed by Leon et al. [27], is also proposed and applied.

Three numerical test problems are investigated to verify the proposed hybrid flux scheme. The proposed scheme is usually more stable than the conventional HLL scheme and less diffusive than the central flux schemes such as the Force scheme. For Test 1, which is a typical filling bore problem with an analytical solution in a rectangular pipe, the hybrid scheme performs the best of the four different flux schemes with high and low wave celerity (a = 100, 1000 m/s). Tests 2 and 3 are experimental simulations of transient mixed flows in a circular pipe connected between two water tanks. The hybrid scheme performs generally better than the other conventional flux schemes. In particular, the Roe scheme, which is known as the least diffusive scheme, often results in spurious oscillations and fails the computations.

In addition to improved numerical accuracy and stability, another advantage of the hybrid scheme is its simplicity of application compared with the other methods presented in Vasconcelos et al. [26] and Malekpour and Karney [10]. Regardless of the shape of the cross section, the hybrid method can be applied to any type of pipe without adjusting additional parameters. The hybrid method is usually stable with a wave velocity ranging from ~100 to ~300 m/s through various test simulations. There remains, however, a limitation in terms of spurious oscillations, especially with a very high value of the wave velocity, such as a = 1000 m/s for two test problems. It remains difficult to present a threshold for the wave velocity that causes a numerical instability because it depends strongly on the problem. A more rigorous analysis of the relation between numerical stability and wave velocity is left for future work. The proposed scheme would be useful to further enhance integrated urban water modeling in which transient mixed flow conditions impact the simulation accuracy, especially for extreme flooding. We are currently pursuing a demonstration of the proposed method for real-world applications in a large urban area, and the results will be reported in the near future.